Подробный разбор симплекс-метода / Хабр
Пролог
Недавно появилась необходимость создать с нуля программу, реализующую алгоритм симплекс-метода. Но в ходе решения я столкнулся с проблемой: в интернете не так уж много ресурсов, на которых можно посмотреть подробный теоретический разбор алгоритма (его обоснование: почему мы делаем те или иные шаги) и советы по практической реализации — непосредственно, алгоритм. Тогда я дал себе обещание — как только завершу задачу, напишу свой пост на эту тему. Об этом, собственно, и поговорим.
Замечание. Пост будет написан достаточно формальным языком, но будет снабжен комментариями, которые должны внести некоторую ясность. Такой формат позволит сохранить научный подход и при этом, возможно, поможет некоторым в изучении данного вопроса.
§1. Постановка задачи линейного программирования
Определение:
Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств.
Общая задача линейного программирования (далее – ЛП) имеет вид:
§2. Каноническая форма задачи ЛП
Каноническая форма задачи ЛП:
Замечание: Любая задача ЛП сводится к канонической.
Алгоритм перехода от произвольной задачи ЛП к канонической форме:
- Неравенства с отрицательными умножаем на (-1).
- Если неравенство вида (≤), то к левой части добавляем – добавочную переменную, и получаем равенство.
- Если неравенство вида (≥), то из левой части вычитаем , и получаем равенство.
- Делаем замену переменных:
- Если , то
- Если — любой, то , где
Замечание:
Будем нумеровать по номеру неравенства, в которое мы его добавили.
Замечание: ≥0.
§3. Угловые точки. Базисные/свободные переменные. Базисные решения
Определение:
Точка называется угловой точкой, если представление возможно только при .
Иными словами, невозможно найти две точки в области, интервал проходящий через которые содержит (т.е. – не внутренняя точка).
Графический способ решения задачи ЛП показывает, что нахождение оптимального решения ассоциируется с угловой точкой. Это является основной концепцией при разработке симплекс-метода.
Определение: Пусть есть система m уравнений и n неизвестных (m < n). Разделим переменные на два множества: (n-m) переменные положим равными нулю, а остальные m переменных определяются решением системы исходных уравнений. Если это решение единственно, то тогда ненулевые m переменных называют базисными; нулевые (n-m) переменных – свободными (небазисными), а соответствующие результирующие значения переменных называют базисным решением.
§4. Симплекс-метод
Симплекс-метод позволяет эффективно найти оптимальное решение, избегая простой перебор всех возможных угловых точек. Основной принцип метода: вычисления начинаются с какого-то «стартового» базисного решения, а затем ведется поиск решений, «улучшающих» значение целевой функции.
Необходимые условия для применения симплекс-метода:
- Задача должна иметь каноническую форму.
- У задачи должен быть явно выделенный базис.
Определение:
Явно выделенным базисом будем называть вектора вида:, т.е. только одна координата вектора ненулевая и равна 1.
Замечание: Базисный вектор имеет размерность (m*1), где m – количество уравнений в системе ограничений.
Для удобства вычислений и наглядности обычно пользуются симплекс-таблицами:
- В первой строке указывают «наименование» всех переменных.
- В первом столбце указывают номера базисных переменных, а в последней ячейке – букву Z (это строка функционала).
- В «середине таблицы» указывают коэффициенты матрицы ограничений — aij.
- Последний столбец – вектор правых частей соответствующих уравнений системы ограничений.

- Крайняя правая ячейка – значение целевой функции. На первой итерации ее полагают равной 0.
Замечание:
Базис – переменные, коэффициенты в матрице ограничений при которых образуют базисные вектора.
Замечание: Если ограничения в исходной задаче представлены неравенствами вида ≤, то при приведении задачи к канонической форме, введенные дополнительные переменные образуют начальное базисное решение.
Замечание: Коэффициенты в строке функционала берутся со знаком “-”.
Алгоритм симплекс-метода:
1. Выбираем переменную, которую будем вводить в базис. Это делается в соответствии с указанным ранее принципом: мы должны выбрать переменную, возрастание которой приведет к росту функционала. Выбор происходит по следующему правилу:
- Если задача на минимум – выбираем максимальный положительный элемент в последней строке.
- Если задача на максимум – выбираем минимальный отрицательный.

Такой выбор, действительно, соответствует упомянутому выше принципу: если задача на минимум, то чем большее число вычитаем – тем быстрее убывает функционал; для максимума наоборот – чем большее число добавляем, тем быстрее функционал растет.
Замечание: Хотя мы и берем минимальное отрицательное число в задаче на максимум, этот коэффициент показывает направление роста функционала, т.к. строка функционала в симплекс-таблице взята со знаком “-”. Аналогичная ситуация с минимизацией.
Определение: Столбец симплекс-таблицы, отвечающий выбранному коэффициенту, называется
2. Выбираем переменную, которую будем вводить в базис. Для этого нужно определить, какая из базисных переменных быстрее всего обратится в нуль при росте новой базисной переменной. Алгебраически это делается так:
- Вектор правых частей почленно делится на ведущий столбец
- Среди полученных значений выбирают минимальное положительное (отрицательные и нулевые ответы не рассматривают)
Определение:
Такая строка называется ведущей строкой и отвечает переменной, которую нужно вывести из базиса.
Замечание: Фактически, мы выражаем старые базисные переменные из каждого уравнения системы ограничений через остальные переменные и смотрим, в каком уравнении возрастание новой базисной переменной быстрее всего даст 0. Попадание в такую ситуацию означает, что мы «наткнулись» на новую вершину. Именно поэтому нулевые и отрицательные элементы не рассматриваются, т.к. получение такого результата означает, что выбор такой новой базисной переменной будет уводить нас из области, вне которой решений не существует.
3. Ищем элемент, стоящий на пересечении ведущих строки и столбца.
Определение: Такой элемент называется ведущим элементом.
4. Вместо исключаемой переменной в первом столбце (с названиями базисных переменных) записываем название переменной, которую мы вводим в базис.
5. Далее начинается процесс вычисления нового базисного решения. Он происходит с помощью метода Жордана-Гаусса.
- Новая Ведущая строка = Старая ведущая строка / Ведущий элемент
- Новая строка = Новая строка – Коэффициент строки в ведущем столбце * Новая Ведущая строка
Замечание:
Преобразование такого вида направлено на введение выбранной переменной в базис, т.
6. После этого проверяем условие оптимальности. Если полученное решение неоптимально – повторяем весь процесс снова.
§5. Интерпретация результата работы симплекс-метода
1. Оптимальность
Условие оптимальности полученного решения:
- Если задача на максимум – в строке функционала нет отрицательных коэффициентов (т.е. при любом изменении переменных значение итогового функционала расти не будет).
- Если задача на минимум – в строке функционала нет положительных коэффициентов (т.е. при любом изменении переменных значение итогового функционала уменьшаться не будет).
2. Неограниченность функционала
Однако, стоит отметить, что заданный функционал может не и достигать максимума/минимума в заданной области. Алгебраический признак этого можно сформулировать следующим образом:
При выборе ведущей строки (исключаемой переменной) результат почленного деления вектора правых частей на ведущий столбец содержит только нулевые и отрицательные значения.
Фактически, это значит, что какой бы рост мы не задавали новой базисной переменной, мы никогда не найдем новую вершину. А значит, наша функция не ограничена на множестве допустимых решений.
3. Альтернативные решения
При нахождении оптимального решения возможен еще один вариант – есть альтернативные решения (другая угловая точка, дающая то же самое значение функционала).
Алгебраический признак существования альтернативы:
После достижения оптимального решения имеются нулевые коэффициенты при свободных переменных в строке функционала.
Это значит, что при росте соответствующей переменной с нулевым коэффициентом значение функционала не изменится и новое базисное решение будет также давать оптимум функционала.
Эпилог
Данная статья направлена на более глубокое понимание теоретической части. В замечаниях и пояснениях здесь можно получить ответы на вопросы, которые обычно опускают при изучении этого метода и принимают априори. Однако, надо понимать, что многие методы численной оптимизации основаны на симплекс-методе (например, метод Гомори, М-Метод) и без фундаментального понимания вряд ли получится сильно продвинуться в дальнейшем изучении и применении всех алгоритмов этого класса.
Однако, надо понимать, что многие методы численной оптимизации основаны на симплекс-методе (например, метод Гомори, М-Метод) и без фундаментального понимания вряд ли получится сильно продвинуться в дальнейшем изучении и применении всех алгоритмов этого класса.
Чуть позже напишу статью о практической реализации симплекс-метода, а также несколько статей о Методе искусственных переменных (М-Метод), Методе Гомори и Методе ветвей и границ.
Спасибо за внимание!
P.S.
Если уже сейчас Вы мучаетесь с реализацией симплекс-метода, советую почитать книгу А. Таха Введение в исследование операций — там все неплохо разобрано и в теории, и на примерах; а также посмотрите примеры решения задач matburo.ru — это поможет с реализацией в коде.
Симплекс метод — процесс решения проблем
Цель этой минилекции – познакомить вас с практическим применением симплекс-метода решения проблем, предложенного Басадуром. После ее прочтения станут понятны основы этого мощного творческого метода решения проблем.
Что собой представляет симплекс метод
Вне всякого сомнения, проблемы бывают разного характера и масштаба. Но важно только то, что они могут быть разрешены. Однако прежде чем предпринять действия для решения проблемы, важно сначала осознать ее. Тем не менее, наиболее значимые шаги в процессе решения проблем часто упускаются из виду. Это означает, что оптимальный выход из ситуации не удается найти или сама проблема определена неверно. Симплекс метод – это метод преодоления трудностей, который учитывает такие ошибки и предотвращает их. Эту модель разработал американский гуру в сфере творчества Марино (Мин) Сидни Басадур, который представил свой метод в книге «Сила инноваций». Он также является изобретателем запатентованной системы мышления Simplexity. Симплекс-метод решения проблем, разработанный Басадуром, включает несколько шагов, пройдя которые группа людей получает возможность найти креативные решения. С помощью Simplex-метода легче определить задачу, а затем предложить и реализовывать способы ее преодоления.
Алгоритм симплекс метода по Басадуру: три фазы
Басадур разделил разработанный им симплекс-метод решения задач на три фазы, которые включают восемь шагов.
Фаза 1: Постановка проблемы
Эта первая фаза связана с первыми тремя шагами симплекс-процесса решения задач: поиск проблемы, выяснение деталей и формирование четкой задачи. Только после этого задача может быть сформулирована правильно. Когда станет ясно, в чем заключена проблема, появится возможность отследить ее истоки в организационной структуре.
Фаза 2: Процесс поиска решений
После фокусировки на описании проблемы симплекс-метод переходит ко второй фазе, заключающейся в поиске возможных решений. Выполняются следующие шаги: поиск идей, способных привести к устранению проблемы, выбор и оценка этих идей. На этом этапе предлагается как можно больше творческих идей, которые могут помочь разрешить сложившуюся ситуацию.
Фаза 3: Реализация решения
Когда преодоление проблемы близко, следует третья и последняя фаза. Она содержит три заключительных шага симплекс-процесса Басадура, а именно: планирование всех необходимых действий, обеспечение поддержки с вовлечением в решение проблемы всех сотрудников и последний шаг – принятие требуемых мер и их реализация. В этой фазе важно, чтобы решение было тщательно проработано. Его внедрение должно осуществляться профессионально. Кроме того, при реализации решения нужно позаботиться о пространстве для маневра, чтобы в случае необходимости можно было корректировать свои действия.
Она содержит три заключительных шага симплекс-процесса Басадура, а именно: планирование всех необходимых действий, обеспечение поддержки с вовлечением в решение проблемы всех сотрудников и последний шаг – принятие требуемых мер и их реализация. В этой фазе важно, чтобы решение было тщательно проработано. Его внедрение должно осуществляться профессионально. Кроме того, при реализации решения нужно позаботиться о пространстве для маневра, чтобы в случае необходимости можно было корректировать свои действия.
Симплекс-метод решения проблем: восемь шагов
Шаг 1: Поиск проблемы
На этом этапе лучше всего не пытаться сразу же найти выход из ситуации. Для начала необходимо прояснить суть проблемы и ее симптомы. Причина выяснится позже. В ходе этого шага, к примеру, потребуется определить желания и потребности не только клиентов и поставщиков, но и сотрудников. В отличие от многих других методов решения проблем в симплекс-процессе Басадура на первом этапе проблема еще не известна. Для ускорения шага 1 могут быть заданы вспомогательные вопросы, например такие:
Для ускорения шага 1 могут быть заданы вспомогательные вопросы, например такие:
- Какие полезные рекомендации могут предложить клиенты?
- Как отреагируют клиенты на попытку расширить взаимодействие?
- Что не так в обслуживании клиентов на текущий момент?
Шаг 2: Выяснение деталей
Этот этап включает в себя сбор информации, касающейся текущей ситуации и, возможно, самой проблемы. На первом этапе были выяснены симптомы проблемы, и на основе этого понадобится собрать имеющиеся факты. Что организации уже известно о рассматриваемой проблеме? Собранные сведения должны быть проанализированы и оценены. Наиболее значимые данные будут играть важную роль на следующих этапах. Опять же, могут быть полезны дополнительные вопросы, такие как:
- Какие претензии предъявлялись за последний год?
- Как клиенты относятся к проблеме?
- Предпринимались ли какие-либо действия?
- Существуют ли предложения по улучшению ситуации?
Шаг 3: Определение проблемы
Область проблем выяснена, поэтому теперь можно определить конкретную проблему. Важно объяснить проблему не слишком пространно, но и не слишком ограниченно. Ответы на ряд вопросов «почему?» помогают понять ситуацию в целом. Отдельные детали помогают описать проблему. Как это работает, можно понять на следующем примере:
Важно объяснить проблему не слишком пространно, но и не слишком ограниченно. Ответы на ряд вопросов «почему?» помогают понять ситуацию в целом. Отдельные детали помогают описать проблему. Как это работает, можно понять на следующем примере:
Вопрос: «Почему мы хотим улучшить обслуживание наших клиентов?»
Ответ: «Потому что клиентов в настоящее время отсылают туда-обратно в различные контактные центры. Им нужен постоянный человек для контактов, который будет в курсе происходящего».
Определено, что проблема касается работы отдела обслуживания клиентов, который по большей части не связывает клиента с нужным человеком.
Шаг 4: Поиск решения
В рамках симплекс-процесса этот шаг связан с широким кругом идей, которые могли бы способствовать решению проблемы. Структурные подразделения и отдельные сотрудники играют в этом важную роль. Неплохой идеей будет создание проектной группы, которая бы разрабатывала креативные решения. Такой групповой поиск идей по принципу «мозгового штурма» не подразумевает критики идей друг друга. Это препятствовало бы творческому процессу. На этом этапе должны быть разработаны возможные варианты решения проблемы.
Это препятствовало бы творческому процессу. На этом этапе должны быть разработаны возможные варианты решения проблемы.
Шаг 5: Выбор и оценка
Пришло время рассмотреть предложенные идеи более подробно. Цель этапа состоит в том, чтобы решить, какая идея лучше всего подходит для решения задачи. Лучше всего начать с создания критериев оценки, позволяющих провести объективный анализ. Идея, наиболее соответствующая этим критериям, обычно является самым лучшим решением проблемы. На этом этапе вспомогательные вопросы также могут ускорить процесс. В частности, лучше уточнить:
- Какое влияние окажет выбранное решение?
- Понадобятся ли какие-либо расходы в связи с выбранным решением?
- Сколько времени и усилий потребуется для реализации задачи?
Шаг 6: Планирование
Теперь, когда выбор сделан, пришло время для составления плана действий. Проще говоря, понадобится четко распределить действия и обязанности, предоставив возможность каждому трудиться над выполнением задачи. Обычно решение незначительных проблем не требует большого количества действий. В случае более серьезных проблем лучшим выбором будет официальное участие в управлении проектом.
Обычно решение незначительных проблем не требует большого количества действий. В случае более серьезных проблем лучшим выбором будет официальное участие в управлении проектом.
Шаг 7: Обеспечение взаимодействия
Хотя это может показаться излишним, но важно учитывать вовлеченность сотрудников на протяжении всего процесса. Только при условии согласия с решением они будут стремиться к успешному завершению задачи. Решение проблем часто связано с нововведениями. Сотрудникам нередко трудно изменить привычный стиль работы. Вот почему они должны осознавать негативные последствия проблемы и ценность внедряемых изменений.
Шаг 8: Принятие мер
План действий может быть реализован только в том случае, если будет обеспечена достаточная поддержка. Этот шаг заслуживает такого же внимания, как и другие. В конце концов, если план не будет реализован, проблема не будет решена. Будет полезным по ходу дела оценивать результаты и проверять, насколько значительно уменьшилась решаемая проблема.
Симплекс-метод решения проблем: цикличность метода
Симплекс-процесс, предложенный Басадуром для преодоления проблем – простая, но мощная модель решения задач. Однако этот процесс не является линейным, он имеет циклический характер. Это означает наличие возможностей для постоянного совершенствования. Вот почему решение задач с помощью симплекс-метода Басадура часто сравнивают с циклом Деминга (PDCA): планирование, действие, проверка, корректировка. После завершения финального этапа следует вернуться к первому шагу для дальнейшей корректировки решения проблемы.
Симплекс метод решения проблем — презентация в PowerPoint
Если вы бизнес-тренер и планируете использовать эту мини-лекцию в своих тренингах, то:
- Рекомендуем прочитать статью о том как сделать свою мини-лекцию живой и интересной.
- Скачайте презентацию в формате PowerPoint для визуальной поддержки вашей мини-лекции.
Премиальный контент
Ссылка на скачивание этой презентации и другой премиальный контент доступны подписчикам платных тарифов. Оформите платную подписку на сайте “Технология тренинга” и получите полный доступ к 13 готовым тренингам, 256 слайдам, 112 минилекциям, 619 упражнениям, 41 видео и т.д. Это совсем не дорого.
Оформите платную подписку на сайте “Технология тренинга” и получите полный доступ к 13 готовым тренингам, 256 слайдам, 112 минилекциям, 619 упражнениям, 41 видео и т.д. Это совсем не дорого.
Нет аккаунта? Зарегистрируйтесь Есть аккаунт? Войдите
Алгоритм и пример симплекс-метода (ММЭ). Пример решения симплекс-методом
Пример 5.1. Решить следующую задачу линейного программирования симплекс-методом:
Решение:
I итерация:
1 этап: формирование исходной симплекс-таблицы.
Исходная задача линейного программирования задана в стандартной форме. Приведем ее к каноническому виду путем введения в каждое из ограничений-неравенств дополнительной неотрицательной переменной, т. е.
е.
В полученной системе уравнений примем в качестве разрешенных (базисных) переменные х3, х4, х5, х6, тогда свободными переменными будут х1,х2. Выразим базисные переменные через свободные:
Приведем целевую функцию к следующему виду:
На основе полученной задачи сформируем исходную симплекс-таблицу:
Таблица 5.3
Исходная симплекс-таблица
СП БП | Оценочные отношения | |||
18 | 1 | 3 | ||
16 | 2 | 1 | ||
5 | 0 | 1 | ||
21 | 3 | 0 | ||
0 | –2 | –3 |
2 этап: определение базисного решения.
Согласно определению базисного решения свободные переменные равны нулю, а значения базисных переменных – соответствующим значениям свободных чисел, т.е.:
.
3 этап: проверка совместности системы ограничений ЗЛП.
На данной итерации (в таблице 5.3) признак несовместности системы ограничений (признак 1) не выявлен (т.е. нет строки с отрицательным свободным числом (кроме строки целевой функции), в которой не было бы хотя бы одного отрицательного элемента (т.е. отрицательного коэффициента при свободной переменной)).
4 этап: проверка ограниченности целевой функции.
На данной итерации (в таблице 5.3) признак неограниченности целевой функции (признак 2) не выявлен (т.е. нет колонки с отрицательным элементом в строке целевой функции (кроме колонки свободных чисел), в которой не было бы хотя бы одного положительного элемента).
5 этап: проверка допустимости найденного базисного решения.
Так как найденное базисное решение не содержит отрицательных компонент, то оно является допустимым.
6 этап: проверка оптимальности.
Найденное базисное решение не является оптимальным, так как согласно признаку оптимальности (признак 4) в строке целевой функции не должно быть отрицательных элементов (свободное число данной строки при рассмотрении данного признака не учитывается). Следовательно, согласно алгоритму симплекс-метода переходим к 8 этапу.
8 этап: определение разрешающего элемента.
8.1. Определение разрешающей колонки.
Так как найденное базисное решение допустимое, то поиск разрешающей колонки будем производить по следующей схеме: определяем колонки с отрицательными элементами в строке целевой функции (кроме колонки свободных чисел). Согласно таблице 5.3, таких колонок две: колонка «х1» и колонка «х2». Из таких колонок выбирается та, которая содержит наименьший элемент в строке целевой функции. Она и будет разрешающей. Колонка «х2» содержит наименьший элемент (–3) в сравнении с колонкой «х1». Следовательно, ее принимаем в качестве разрешенной.
Она и будет разрешающей. Колонка «х2» содержит наименьший элемент (–3) в сравнении с колонкой «х1». Следовательно, ее принимаем в качестве разрешенной.
8.2. Определение разрешающей строки.
Для определения разрешающей строки находим положительные оценочные отношения свободных чисел к элементам разрешающей колонки, строка, которой соответствует наименьшее положительное оценочное отношение, принимается в качестве разрешенной.
Таблица 5.4
Исходная симплекс-таблица
В таблице 5.4 наименьшее положительное оценочное отношение соответствует строке «х5», следовательно, она будет разрешающей.
Элемент, расположенный на пересечение разрешающей колонки и разрешающей строки, принимается в качестве разрешающего. В нашем примере – это элемент , который расположен на пересечении строки «х5» и колонки «х2».
9 этап: преобразование симплекс-таблицы.
Разрешающий элемент показывает одну базисную и одну свободную переменные, которые необходимо поменять местами в симплекс-таблице, для перехода к новому «улучшенному» базисному решению. В данном случае это переменные х5 и х2, в новой симплекс-таблице (таблице 5.5) их меняем местами.
9.1. Преобразование разрешающего элемента.
Разрешающий элемент таблицы 5.4 преобразовывается следующим образом:
Полученный результат вписываем в аналогичную клетку таблицы 5.5.
9.2. Преобразование разрешающей строки.
Элементы разрешающей строки таблицы 5.4 делим на разрешающий элемент данной симплекс-таблицы, результаты вписываются в аналогичные ячейки новой симплекс-таблицы (таблицы 5.5). Преобразования элементов разрешающей строки приведены в таблице 5.5.
9.3. Преобразование разрешающей колонки.
Элементы разрешающей колонки таблицы 5.4 делим на разрешающий элемент данной симплекс-таблицы, а результат берется с обратным знаком. Полученные результаты вписываются в аналогичные ячейки новой симплекс-таблицы (таблицы 5.5). Преобразования элементов разрешающей колонки приведены в таблице 5.5.
Полученные результаты вписываются в аналогичные ячейки новой симплекс-таблицы (таблицы 5.5). Преобразования элементов разрешающей колонки приведены в таблице 5.5.
9.4. Преобразование остальных элементов симплекс-таблицы.
Преобразование остальных элементов симплекс-таблицы (т.е. элементов не расположенных в разрешающей строке и разрешающей колонке) осуществляется по правилу «прямоугольника».
К примеру, рассмотрим преобразование элемента, расположенного на пересечении строки «х3» и колонки «», условно обозначим его «х3». В таблице 5.4 мысленно вычерчиваем прямоугольник, одна вершина которого располагается в клетке, значение которой преобразуем (т.е. в клетке «х3»), а другая (диагональная вершина) – в клетке с разрешающим элементом. Две другие вершины (второй диагонали) определяются однозначно. Тогда преобразованное значение клетки «х3» будет равно прежнему значению данной клетки минус дробь, в знаменателе которой разрешающий элемент (из таблицы 5. 4), а в числителе произведение двух других неиспользованных вершин, т.е.:
4), а в числителе произведение двух других неиспользованных вершин, т.е.:
«х3»: .
Аналогично преобразуются значения других клеток:
«х3 х1»: ;
«х4»: ;
«х4 х1»: ;
«х6»: ;
«х6 х1»: ;
«»: ;
«х1»: .
В результате данных преобразований получили новую симплекс- таблицу (таблица 5.5).
II итерация:
1 этап: составление симплекс-таблицы.
По результатам симплекс-преобразований предыдущей итерации составляем новую симплекс-таблицу:
Таблица 5.5
Симплекс-таблица II итерации
СП БП | Оценочные отношения | |||
–(3/1)=–3 | ||||
–(1/1)=–1 | ||||
5/1=5 | 0/1=0 | (1)–1=1 | ||
–(0/1)=0 | ||||
–(–3/1)=3 |
2 этап: определение базисного решения.
В результате проведенных симплекс-преобразований получили новое базисное решение (таблица 5.5):
.
Как видно, при данном базисном решении значение целевой функции =15, что больше чем при предыдущем базисном решении.
3 этап: проверка совместности системы ограничений.
Не совместность системы ограничений в соответствии с признаком 1 в таблице 5.5 не выявлена.
4 этап: проверка ограниченности целевой функции.
Неограниченность целевой функции в соответствии с признаком 2 в таблице 5.5 не выявлена.
5 этап: проверка допустимости найденного базисного решения.
Найденное базисное решение в соответствии с признаком 3 допустимое, так как не содержит отрицательных компонент.
6 этап: проверка оптимальности найденного базисного решения.
Найденное базисное решение в соответствии с признаком 4 не оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5. 5) содержится отрицательный элемент: –2 (свободное число данной строки при рассмотрении данного признака не учитывается). Следовательно, переходим к 8 этапу.
5) содержится отрицательный элемент: –2 (свободное число данной строки при рассмотрении данного признака не учитывается). Следовательно, переходим к 8 этапу.
8 этап: определение разрешающего элемента.
8.1. Определение разрешающей колонки.
Найденное базисное решение допустимое, определяем колонки с отрицательными элементами в строке целевой функции (кроме колонки свободных чисел). Согласно таблице 5.5, такой колонкой является только одна колонка: «х1». Следовательно, ее принимаем в качестве разрешенной.
8.2. Определение разрешающей строки.
Согласно полученным значениям положительных оценочных отношений в таблице 5.6, минимальным является отношение, соответствующее строке «х3». Следовательно, ее принимаем в качестве разрешенной.
Таблица 5.6
Симплекс-таблица II итерации
СП БП | Оценочные отношения | |||
3 | 1 | –3 | 3/1=3 – min | |
11 | 2 | –1 | 11/2=5,5 | |
5 | 0 | 1 | – | |
21 | 3 | 0 | 21/3=7 | |
15 | –2 | 3 |
9 этап: преобразование симплекс-таблицы.
Преобразования симплекс-таблицы (таблицы 5.6) выполняются аналогично, как и в предыдущей итерации. Результаты преобразований элементов симплекс-таблицы приведены в таблице 5.7.
III итерация
1 этап: построение новой симплекс-таблицы.
По результатам симплекс-преобразований предыдущей итерации составляем новую симплекс-таблицу:
Таблица 5.7
Симплекс-таблица III итерации
СП БП | Оценочные отношения | |||
3/1=3 | (1)–1=1 | –3/1=–3 | ||
–(2/1)=–2 | ||||
–(0/1)=0 | ||||
–(3/1)=–3 | ||||
–(–2/1)=2 |
2 этап: определение базисного решения.
В результате проведенных симплекс-преобразований получили новое базисное решение (таблица 5.7):
.
3 этап: проверка совместности системы ограничений.
Не совместность системы ограничений в соответствии с признаком 1 в таблице 5.7 не выявлена.
4 этап: проверка ограниченности целевой функции.
Неограниченность целевой функции в соответствии с признаком 2 в таблице 5.7 не выявлена.
5 этап: проверка допустимости найденного базисного решения.
Найденное базисное решение в соответствии с признаком 3 допустимое, так как не содержит отрицательных компонент.
6 этап: проверка оптимальности найденного базисного решения.
Найденное базисное решение в соответствии с признаком 4 не оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5.7) содержится отрицательный элемент: –3 (свободное число данной строки при рассмотрении данного признака не учитывается). Следовательно, переходим к 8 этапу.
Следовательно, переходим к 8 этапу.
8 этап: определение разрешающего элемента.
8.1. Определение разрешающей колонки.
Найденное базисное решение допустимое, определяем колонки с отрицательными элементами в строке целевой функции (кроме колонки свободных чисел). Согласно таблице 5.7, такой колонкой является только одна колонка: «х5». Следовательно, ее принимаем в качестве разрешенной.
8.2. Определение разрешающей строки.
Согласно полученным значениям положительных оценочных отношений в таблице 5.8, минимальным является отношение, соответствующее строке «х4». Следовательно, ее принимаем в качестве разрешенной.
Таблица 5.8
Симплекс-таблица III итерации
СП БП | Оценочные отношения | |||
3 | 1 | –3 | – | |
5 | –2 | 5 | 5/5=1 – min | |
5 | 0 | 1 | 5/1=5 | |
12 | –3 | 9 | 12/9=1? | |
21 | 2 | –3 |
9 этап: преобразование симплекс-таблицы.
Преобразования симплекс-таблицы (таблицы 5.8) выполняются аналогично, как и в предыдущей итерации. Результаты преобразований элементов симплекс-таблицы приведены в таблице 5.9.
IV итерация
1 этап: построение новой симплекс-таблицы.
По результатам симплекс-преобразований предыдущей итерации составляем новую симплекс-таблицу:
Таблица 5.9
Симплекс-таблица IV итерации
СП БП | Оценочные отношения | |||
–(–3/5)=3/5 | ||||
5/5=1 | –2/5 | (5)–1= | ||
–(1/5)=–1/5 | ||||
–(9/5)=–9/5 | ||||
–(–3/5)=3/5 |
2 этап: определение базисного решения.
В результате проведенных симплекс-преобразований получили новое базисное решение, согласно таблице 5.9 решение следующее:
.
3 этап: проверка совместности системы ограничений.
Не совместность системы ограничений в соответствии с признаком 1 в таблице 5.9 не выявлена.
4 этап: проверка ограниченности целевой функции.
Неограниченность целевой функции в соответствии с признаком 2 в таблице 5.9 не выявлена.
5 этап: проверка допустимости найденного базисного решения.
Найденное базисное решение в соответствии с признаком 3 допустимое, так как не содержит отрицательных компонент.
6 этап: проверка оптимальности найденного базисного решения.
Найденное базисное решение в соответствии с признаком 4 оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5.9) нет отрицательных элементов (свободное число данной строки при рассмотрении данного признака не учитывается).
7 этап: проверка альтернативности решения.
Найденное решение является единственным, так как в строке целевой функции (таблица 5.9) нет нулевых элементов (свободное число данной строки при рассмотрении данного признака не учитывается).
Ответ: оптимальное значение целевой функции рассматриваемой задачи =24, которое достигается при .
Пример 5.2. Решить вышеприведенную задачу линейного программирования при условии, что целевая функция минимизируется:
Решение:
I итерация:
1 этап: формирование исходной симплекс-таблицы.
Исходная задача линейного программирования задана в стандартной форме. Приведем ее к каноническому виду путем введения в каждое из ограничений-неравенств дополнительной неотрицательной переменной, т. е.
е.
В полученной системе уравнений примем в качестве разрешенных (базисных) переменные х3, х4, х5, х6, тогда свободными переменными будут х1,х2. Выразим базисные переменные через свободные:
Приведем целевую функцию к следующему виду:
На основе полученной задачи сформируем исходную симплекс-таблицу:
Таблица 5.10
Исходная симплекс-таблица
СП БП | Оценочные отношения | |||
18 | 1 | 3 | ||
16 | 2 | 1 | ||
5 | 0 | 1 | ||
21 | 3 | 0 | ||
0 | –2 | –3 |
2 этап: определение базисного решения.
Согласно определению базисного решения свободные переменные равны нулю, а значения базисных переменных – соответствующим значениям свободных чисел, т.е.:
.
3 этап: проверка совместности системы ограничений ЗЛП.
На данной итерации (в таблице 5.10) признак несовместности системы ограничений (признак 1) не выявлен (т.е. нет строки с отрицательным свободным числом (кроме строки целевой функции), в которой не было бы хотя бы одного отрицательного элемента (т.е. отрицательного коэффициента при свободной переменной)).
4 этап: проверка ограниченности целевой функции.
На данной итерации (в таблице 5.10) признак неограниченности целевой функции (признак 2) не выявлен (т.е. нет колонки с положительным элементом в строке целевой функции (колонка свободных чисел не рассматривается), в которой не было бы хотя бы одного положительного элемента).
5 этап: проверка допустимости найденного базисного решения.
Так как найденное базисное решение не содержит отрицательных компонент, то оно является допустимым.
6 этап: проверка оптимальности найденного базисного решения.
Найденное базисное решение в соответствии с признаком 4 оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5.10) нет положительных элементов (свободное число данной строки при рассмотрении данного признака не учитывается).
7 этап: проверка альтернативности решения.
Найденное решение является единственным, так как в строке целевой функции (таблица 5.10) нет нулевых элементов (свободное число данной строки при рассмотрении данного признака не учитывается).
Ответ: оптимальное значение целевой функции рассматриваемой задачи =0, которое достигается при .
Пример 5.3. Решить следующую задачу линейного программирования симплекс-методом:
Решение:
I итерация
1 этап: составление исходной симплекс-таблицы.
Задача линейного программирования задана в каноническом виде. Составим расширенную матрицу и выделим с помощью метода Жордана-Гаусса базисные переменные. Примем в качестве базисных – переменные х1 и х2.
Умножим (поэлементно) первую строку на –3 и сложим со второй:
.
Умножим вторую строку на :
.
Сложим вторую с первой строкой:
.
В результате система ограничений примет следующий вид:
Выразим базисные переменные через свободные:
Выразим целевую функцию также через свободные переменные, для этого подставим полученные значения базисных переменных в целевую функцию:
.
Запишем целевую функцию в следующем виде:
.
Составим исходную симплекс-таблицу:
Таблица 5.11
Исходная симплекс-таблица
СП БП | Оценочные отношения | |||
–1 | 0 | |||
0 | 2 | |||
4 | – | –3 |
2 этап: определение базисного решения.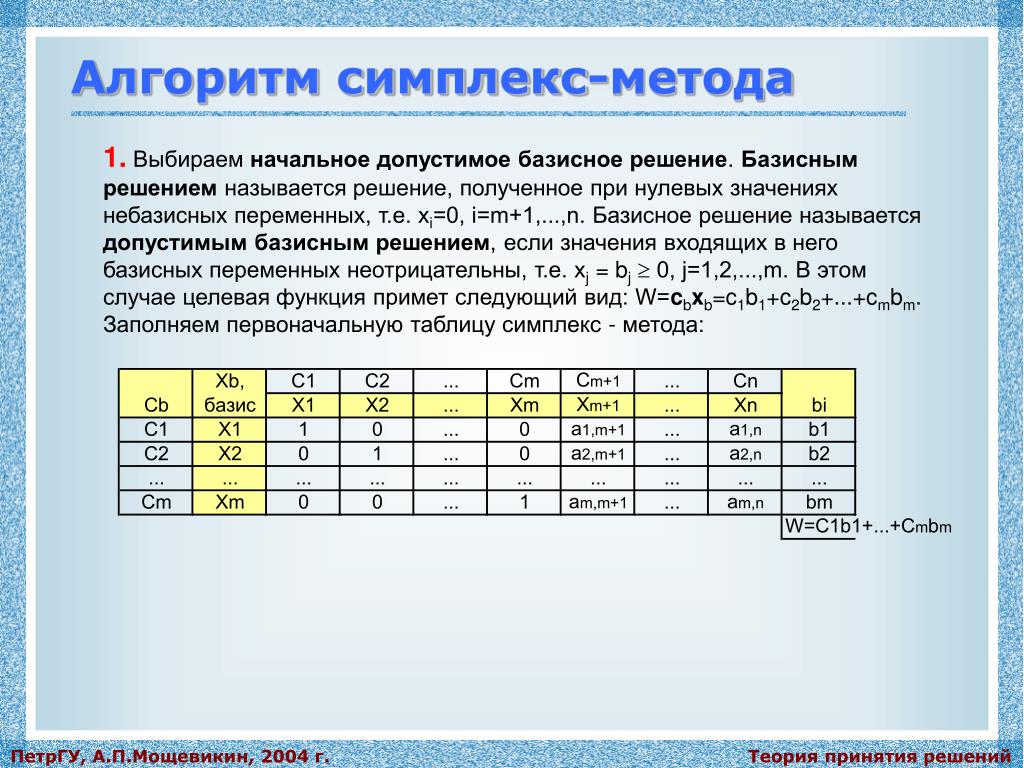
Согласно определению базисного решения свободные переменные равны нулю, а значения базисных переменных – соответствующим значениям свободных чисел, т.е.:
.
Найденное базисное решение является вырожденным, т.к. имеется базисная переменная х2, равная нулю.
3 этап: проверка совместности системы ограничений ЗЛП.
Так как в таблице 5.11 имеется строка с отрицательным свободным числом (–1), в которой нет ни одного отрицательного элемента (т.е. отрицательного коэффициента при свободной переменной), то согласно признаку несовместности (признак 1) система ограничений данной задачи не совместна (строка целевой функции при рассмотрении данного признака не учитывается). Следовательно, рассматриваемая задача линейного программирования не имеет решения.
Ответ: рассматриваемая задача линейного программирования не имеет решения в силу несовместности ее системы ограничений.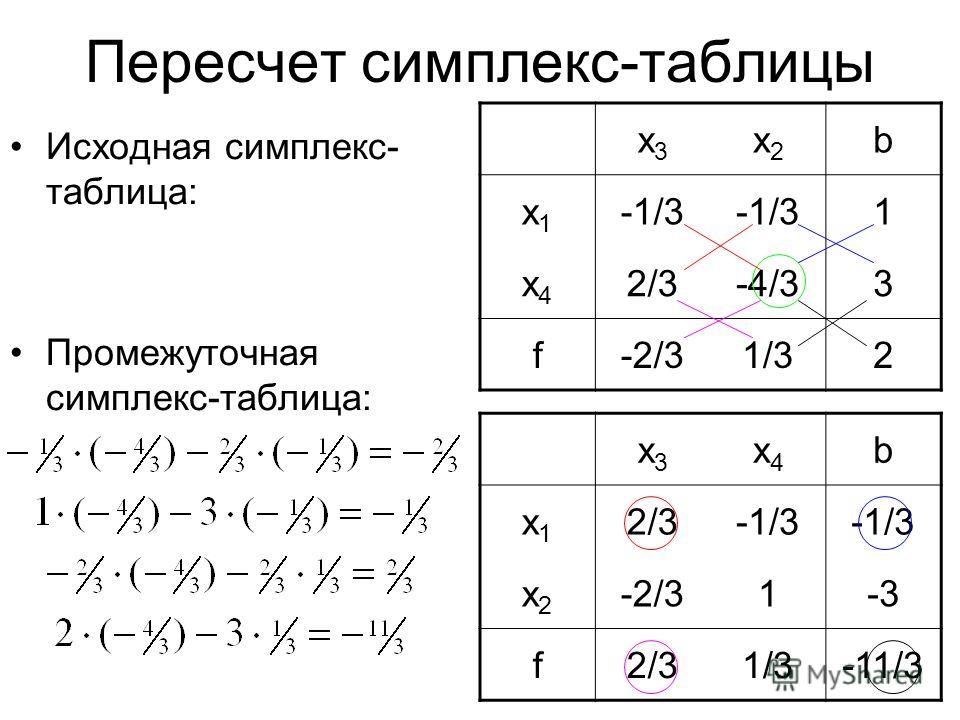
МЕТОД — Энциклопедия по экономике
Итак, для нахождения оптимальной производственной программы необходимо такое решение системы многих уравнений с многими неизвестными, при котором критерий (целевая функция) достигает оптимума. Система уравнений и неравенств (24.1) — (24.5), (24.7) обладает следующим свойством она линейна относительно неизвестных. Это означает, что неизвестные входят в уравнения, неравенства и критерий лишь в первой степени и что отсутствуют произведения неизвестных. Методом решения подобных задач, которые носят название задач линейного программирования, служит так называемый симплекс-метод. Симплекс-метод изложен в целом ряде книг. Ограничимся лишь его технико-экономической интерпретацией. [c.413]Решение задачи (24.1) — (24.7) нахождения оптимальной производственной программы симплекс-методом осуществляется на ЭВМ в два этапа на первом этапе отыскивается допустимый план на втором — происходит улучшение допустимого плана до оптимального. В целом можно сказать, что решение задачи нахождения [c.
 413]
413]Упорядоченный перебор интересующих нас допустимых планов, нахождение допустимых планов требуют огромной вычислительной работы, которая осуществляется на ЭВМ. Симплекс-метод, согласно которому ЭВМ осуществляет упорядоченный перебор и находит оптимальное решение, является наиболее распространенным экономико-математическим методом. [c.414]
Наиболее распространенным методом решения важных практических задач планирования и управления является линейное программирование. С помощью симплекс-метода решаются задачи планирования производственной программы предприятия, объединения, способствующие получению максимального эффекта при ограниченных материальных и трудовых ресурсах. Распределительный метод линейного программирования позволяет выбрать оптимальные варианты планов транспортных перевозок решать задачи по оптимизации планов загрузки оборудования и др. [c.78]
Для решения задачи (I) автор предлагает использовать метод ветвей и границ, а для нахождения решения семейства задач (II) -использовать методы линейного программирования (например.
 симплекс -метод).
[c.120]
симплекс -метод).
[c.120]Рассмотрим некоторые особенности этого метода. В качестве-основы может быть выбран алгоритм симплекс-метода (например, мультипликативный), в котором на каждой итерации в явном виде вычисляется вектор симплексных множителей по формуле [c.99]
Вычислительная схема реализации расчетов по модели (2)— (9) на основе мультипликативного алгоритма симплекс. — метода показана на рисунке. [c.100]
Симплекс-метод представляет собой технику решения задач с ограничивающими факторами при помощи компьютера (соответствующие расчеты можно сделать и вручную, но это очень трудоемко, даже при относительно несложных задачах). Будучи ограниченным только аппаратными или программными возможностями (т.е. особенностями прикладной программы или объемом памяти компьютера), симплекс-метод позволяет решать задачи с огромным количеством товаров/услуг и ограни- [c.370]
Симплекс-метод — это техника решения многопродуктовых задач в условиях ограничений, чаще реализуемая с помощью компьютера. [c.378]
[c.378]
Для решения симплекс-методом (на компьютере) технический консультант спортклуба сформулировал задачу о размещении кресел [c.389]
Наконец, рассмотрим многокритериальные симплекс-методы,, основанные на использовании симплекс-таблицы линейного программирования. Эти методы очень близки к методам параметрического программирования и состоят в переходе из некоторой исходной точки (скажем, точки А см. рис. 6.9) в соседнюю эффективную точку. При этом, в отличие от методов взвешивания, понятие весов не используется. Многокритериальные симплекс-методы имеют те же самые достоинства и1 недостатки, что и параметрические методы. [c.311]
Стандартные программные пакеты для персональных компьютеров реализуют в этом случае симплекс-метод, который представляет собой итеративный пошаговый процесс. Он начинается с выбора одного возможного решения с последующим замещением его, если результат может быть улучшен. Этот перебор продолжается до тех пор, пока дальнейшее улучшение невозможно.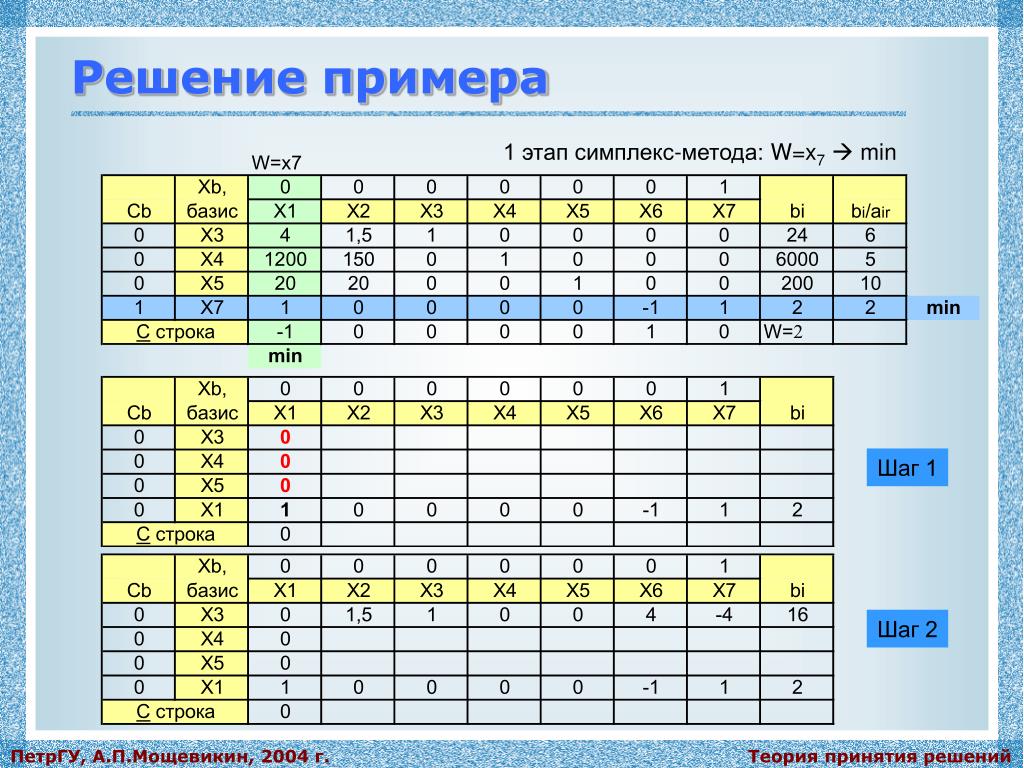 Таким образом будет получено оптимальное решение.
[c.280]
Таким образом будет получено оптимальное решение.
[c.280]
В этих случаях используется симплекс-метод, который представляет собой итеративную (пошаговую) процедуру для определения оптимального решения задачи линейного программирования. Расчеты по симплекс-методу начинают с определения допустимого решения, а затем отыскиваются другие допустимые решения и проверяются возможности их улучшения. Переход от одного решения к другому продолжается до тех пор, пока новые улучшения не будут невозможны. Широко распространены стандартные компьютерные программы, которые используют симплекс-метод для решения таких управленческих задач, которые можно представить как задачи линейного программирования. [c.220]
Нахождение оптимального решения. В случае, когда в целевой функции только две переменные и количество ограничений небольшое, для нахождения оптимального решения можно использовать графический метод и метод проб и ошибок. В более сложных случаях, которые возникают на практике, необходимы специальные пакеты программного обеспечения, например симплекс-метод. [c.382]
[c.382]
Следует отметить, что метод проб и ошибок, а также графический метод полезны в случае двух или, возможно, трех переменных. Для решения проблемы линейного программирования со многими переменными эти методы непрактичны. Стандартные программные пакеты для персональных компьютеров реализуют в этом случае симплекс-метод, который представляет собой итеративный пошаговый процесс. Он начинается выбором одного возможного решения с последующим замещением его, если результат можно улучшить. Этот перебор продолжается до тех пор, пока дальнейшее улучшение перестает быть возможным. [c.385]
Весьма типичной задачей, решаемой с помощью линейного программирования, является транспортная задача. Ее смысл заключается в минимизации грузооборота при доставке товаров широкого потребления от производителя к потребителю, с оптовых складов и баз в розничные торговые предприятия. Она решается симплекс-методом или распределительным методом. [c.163]
Задачи с помощью линейного программирования решаются двумя способами симплекс-методом и распределительном методом. [c.41]
[c.41]
Симплекс-метод см. Баканов М. И., Шеремет А. Д. Теория экономического анализа. — М. Финансы и статистика, 1998.-С. 162- 171. Приведенный в учебнике пример также может служить материалом для практических занятий. [c.42]
Известно, что в случае двух переменных решение задачи математического программирования можно провести не только аналитически (например, используя симплекс-метод), но и графически. В нашем примере интерес представляет только целочисленное решение. [c.221]
Линейное программирование — математический метод, предназначенный для выявления оптимального решения из большого числа возможных вариантов решения задачи, у которой условия позволяют запись в виде линейных соотношений. Линейное программирование применяется для решения задач типа распределение ресурсов, формирование комбинации кормов, составление портфеля инвестиций, выбор производственной программы. Для постановки задачи линейного программирования необходимо ввести переменные (определяемые) величины, выразить через эти переменные ограничивающие условия и целевую функцию.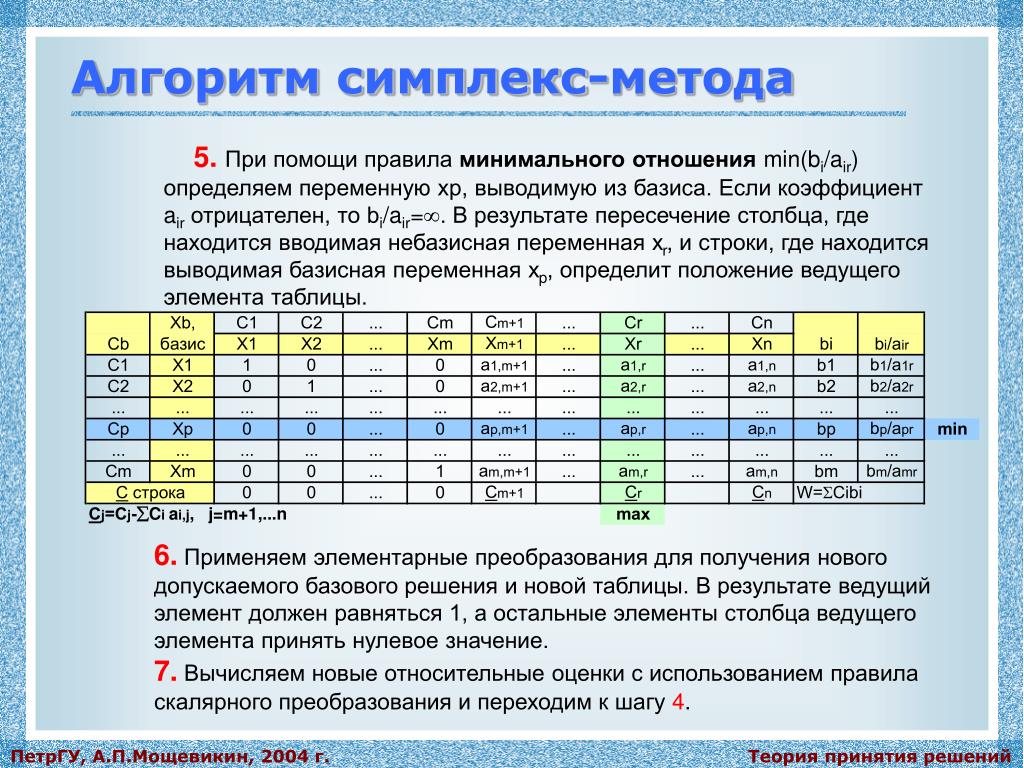 Для решения задач линейного программирования используют симплекс-метод или графический метод (при наличии двух переменных в решаемой задаче).
[c.122]
Для решения задач линейного программирования используют симплекс-метод или графический метод (при наличии двух переменных в решаемой задаче).
[c.122]
Симплекс-метод (аналитическое решение задач линейного программирования) — это алгоритм формального пересчета вариантов решения задачи с последовательным движением к оптимальному решению. Каждый шаг алгоритма расчетов улучшает предыдущее решение. [c.122]
Рассмотрим алгоритм симплекс-метода на основе числового примера — оптимизационной задачи, включающей пять неизвестных и три ограничивающих условия. [c.122]
Решение. В результате решения задачи симплекс-методом найдем оптимальное решение х = 1 х = 7, 5 1 =29,5, где верхний индекс переменных — номер задачи. [c.127]
Результаты решения симплекс-методом задачи 2 х = 1,2 j f = 7 L2 = 29,4 задачи 3 х = 0,75 xf = 8 L3 = 29,25. [c.128]
Решение задачи ЛП осуществляется модифицированным симплекс-методом с мультипликативным представлением обратной матрицы и двусторонними границами для переменных и ограничений. [c.179]
[c.179]
С учетом возможностей современных ППП, использующих модифицированный симплекс-метод с мультипликативным представлением матрицы, отнесение очередного вектора к классу векторов, обеспечивающих совместность или несовместность, требует проведения всего нескольких итераций после модификации обобщенной матрицы [c.207]
Раскрыв любую книгу по управлению финансами, изданную в России, или переведенный с английского учебник по корпоративным финансам, едва ли не с первых страниц натыкаешься на обилие сложных формул, интегралов и производных, а также на множество терминов, таких как финансовый рычаг, модель Дюпона и т. п. Изыски финансовой механики безусловно важны и полезны. Но все симплекс-методы и оптимизационные модели ни на шаг не приближают нас к составлению бюджетов компании. Например, к пониманию того, чем бюджет отличается от сметы. [c.37]
Имеется три источника AI, А2, А3 располагающие соответствующими мощностями и четыре потребителей Btj B2, В3 и В4 (мвт). При известных стоимостях передачи единицы мощности С, t от i источника к j потребителю ( без учёта потерь мощности ) найти оптимальный Уед распределения электрической мощности от источников к потребителям, при котором затраты на передачу минимальны и определить оптимальную конфигурацию электрической сети. Решение задачи осуществить можно симплекс методом, либо распределительным методом либо методом потенциалов.
[c.10]
При известных стоимостях передачи единицы мощности С, t от i источника к j потребителю ( без учёта потерь мощности ) найти оптимальный Уед распределения электрической мощности от источников к потребителям, при котором затраты на передачу минимальны и определить оптимальную конфигурацию электрической сети. Решение задачи осуществить можно симплекс методом, либо распределительным методом либо методом потенциалов.
[c.10]
Блок 6 — машинное решение модели. Для решения данной экономико-математической модели может быть использован алгоритм, разработанный сотрудниками ЦЭМИ АН СССР, который предусматривает решение с помощью мультипликативного симплекс-метода. В результате машинного решения должна быть получена распечатка ленты, описание которой дано а разделе Выходная информация . . . . . . …. [c.157]
Данная задача решается с применением симплекс-метода, описание которого приводится ниже. [c.179]
Оптимизация компаундирования значительно повышает рентабельность продукции при полном использовании запасов компонентов. Но для получения таких результатов необходимо обеспечить быстроту расчетов, что возможно только при применении ЭЦВМ. Решение простейшего варианта задачи о смешении симплекс-методом вручную продолжается около 15 дней, тогда как решение более сложной задачи на ЭЦВМ при наличии готовой
[c.135]
Но для получения таких результатов необходимо обеспечить быстроту расчетов, что возможно только при применении ЭЦВМ. Решение простейшего варианта задачи о смешении симплекс-методом вручную продолжается около 15 дней, тогда как решение более сложной задачи на ЭЦВМ при наличии готовой
[c.135]
Рассмотренный метод оптимизации производственной программы. НПЗ в постановке (2)—(9)-реализован на ЭВМ М-22 . Ниже приводится общая схема вычисления по данному методу. Условия (4)—(8) формируются в виде отдельного. информационного массива. Он используется только при решении вспомогательной задачи (12). Основой предлагаемой вычислительной схемы является алгоритм мультипликативного симплекс-метода, к которому стыкуются алгоритмы решения вспомогательной задачи и усреднения. Для решения вспомогательнбй задачи может использоваться основная программа. Однако в связи/с ее небольшими размерами был разработан и реализован на ЭВМ более экономный прямой алгоритм симплекс метода с верхними ограничениями на переменные. Следует отметить, что предлагаемый подход может реализован и другой вычислительной схемой, отличной от приводимой ниже. Ее отличие состоит в том, что алгоритм решения вспомогательной задачи.подключается только после получения оптимального решения, основной задачи. Практическая проверка обеих вычислительных схем не показала существенного преимущества ни одной из них.
[c.100]
Следует отметить, что предлагаемый подход может реализован и другой вычислительной схемой, отличной от приводимой ниже. Ее отличие состоит в том, что алгоритм решения вспомогательной задачи.подключается только после получения оптимального решения, основной задачи. Практическая проверка обеих вычислительных схем не показала существенного преимущества ни одной из них.
[c.100]
На /-и итерации процедуры исходной информацией шага а) является положительный вектор весов X = Х15. .., Я ]. Задача (3.9) решается с помощью симплекс-метода ее решение, обозначаемое х1, используется для построения вспомогательной информации, которая состоит в расчете значений вектора критериев в соседних с х вершинах многогранного множества (3.7). При этом рассматриваются только те вершины, которые принадлежат эффективному множеству решений. Пусть на Z-й итерации таких вершин [c.307]
AB D, содержащий все выпуклые комбинации этих точек (он заштрихован на рис. 6.9), содержит и неэффективные точки. Среди методов построения эффективных вершин можно выделить два основных направления. Это методы взвешивания и многокритериальные симплекс-методы.
[c.310]
Это методы взвешивания и многокритериальные симплекс-методы.
[c.310]
Становление современного математического аппарата оптимальных экономических решений началось в 40-е годы, благодаря первым работам Н. Винера, Р. Беллмана, С. Джонсона, Л. Канторовича. Задача линейного программирования впервые математически сформулирована Л. В. Канторовичем в 1939 г. на примере задачи раскроя материалов для Ленинградского фанерного треста. В 1947 г. Дж. Данциг предложил универсальный алгоритм решения задач линейного программирования, названный им симплекс-методом. В 1941 г. Хичкок и независимо от него в 1947 г. Купсман формулируют транспортную задачу, в 1945 г. Стиглер — задачу о диете. В 1952 г. было проведено первое успешное решение задачи линейного программирования на ЭВМ Sea в Национальном бюро стандартов США. [c.102]
М301. Мультипликативный симплекс-метод решения общей задачи линейного программирования [c.35]
Симплексный метод, библиотека scipy и нелинейное программирование в линейном программировании на Python
Симплексный метод, scipy библиотека и нелинейное программирование для решения задач
- Основное определение симплекс-метода
- Принцип метода Big M для решения линейного программирования
- решение Excel
- Python вызывает optimize package и scipy для решения линейного программирования
- Программирование на Python для реализации симплексного метода
- Сравнение
- Нелинейное программирование
Основное определение симплекс-метода:
В общих задачах линейного программирования, когда количество переменных в системе линейных уравнений больше, чем количество уравнений, будет неопределенное количество решений, и симплекс-метод является общим метод решения задач линейного программирования. Конкретные шаги заключаются в том, чтобы найти один за другим симплекс из системы линейных уравнений, и каждый симплекс может получить набор решений, а затем оценить, увеличивает ли решение или уменьшает значение целевой функции, и решить, какой симплекс выбрать в форма следующего шага. Через итерацию оптимизации, пока целевая функция не достигнет максимального или минимального значения. Другими словами, симплекс-метод придерживается основной идеи «гарантировать, что каждая итерация лучше предыдущей»: сначала найдите базовое возможное решение, определите его и посмотрите, является ли оно оптимальным решением; если нет, следовать Преобразовать определенное правило в другое улучшенное и лучшее базовое выполнимое решение, а затем определить; если это все еще не так, преобразовать снова и повторить. Поскольку количество основных возможных решений ограничено, оптимальное решение задачи может быть получено после конечного числа преобразований. Если проблема не имеет оптимального решения, этот метод также можно использовать для оценки.
Конкретные шаги заключаются в том, чтобы найти один за другим симплекс из системы линейных уравнений, и каждый симплекс может получить набор решений, а затем оценить, увеличивает ли решение или уменьшает значение целевой функции, и решить, какой симплекс выбрать в форма следующего шага. Через итерацию оптимизации, пока целевая функция не достигнет максимального или минимального значения. Другими словами, симплекс-метод придерживается основной идеи «гарантировать, что каждая итерация лучше предыдущей»: сначала найдите базовое возможное решение, определите его и посмотрите, является ли оно оптимальным решением; если нет, следовать Преобразовать определенное правило в другое улучшенное и лучшее базовое выполнимое решение, а затем определить; если это все еще не так, преобразовать снова и повторить. Поскольку количество основных возможных решений ограничено, оптимальное решение задачи может быть получено после конечного числа преобразований. Если проблема не имеет оптимального решения, этот метод также можно использовать для оценки.
Принцип метода Big M для решения линейного программирования:
Метод Big M сначала преобразует задачу линейного программирования в стандартную форму. Если система уравнений ограничений содержит единичную матрицу I, то был получен начальный допустимый базис. В противном случае добавьте тысячи неотрицательных искусственных переменных в левую часть системы уравнений ограничений, чтобы вектор-столбец коэффициентов, соответствующий искусственной переменной, и вектор-столбец коэффициентов других переменных образовали единичную матрицу. Используя единичную матрицу в качестве начального базиса, можно получить начальное базовое допустимое решение. Чтобы получить начальное базовое возможное решение исходной проблемы, искусственная переменная должна быть заменена из базовой переменной на неосновную переменную посредством итеративного процесса как можно скорее. По этой причине отрицательный коэффициент -M с большим абсолютным значением может быть присвоен искусственной переменной в целевой функции. Таким образом, пока в базовых переменных есть искусственные переменные, целевая функция не может быть максимизирована. Последующие вычисления такие же, как и для решения с симплексной таблицей, и M нужно только рассматривать как большое положительное число. Если искусственные переменные включены в базовые переменные симплексной оптимальной таблицы, это означает, что не существует допустимого решения исходной задачи. В противном случае оставшаяся часть оптимального решения, исключая искусственные переменные, является начальным основным допустимым решением исходной задачи.
Таким образом, пока в базовых переменных есть искусственные переменные, целевая функция не может быть максимизирована. Последующие вычисления такие же, как и для решения с симплексной таблицей, и M нужно только рассматривать как большое положительное число. Если искусственные переменные включены в базовые переменные симплексной оптимальной таблицы, это означает, что не существует допустимого решения исходной задачи. В противном случае оставшаяся часть оптимального решения, исключая искусственные переменные, является начальным основным допустимым решением исходной задачи.
тема:
Используйте пакет для решения:
Excel использует метод Big M для решения линейного программирования:
# Импорт пакета from scipy import optimize import numpy as np #OK c, A_ub, B_ub c = np.array([50,100]) A_ub = np.array([[1,1],[2,1],[0,1]]) B_ub = np.array([300,400,250]) #Решать res =optimize.linprog(-c,A_ub,B_ub) print(res)
результат:
import numpy as np
def pivot(d,bn):
l = list(d[0][:-2])
jnum = l. index(max(l)) # Номер перевода
m = []
for i in range(bn):
if d[i][jnum] == 0:
m.append(0.)
else:
m.append(d[i][-1]/d[i][jnum])
inum = m.index(min([x for x in m[1:] if x!=0])) # Перенести нижний индекс
s[inum-1] = jnum
r = d[inum][jnum]
d[inum] /= r
for i in [x for x in range(bn) if x !=inum]:
r = d[i][jnum]
d[i] -= r * d[inum]
def solve(d,bn):
flag = True
while flag:
if max(list(d[0][:-1])) <= 0: # Пока все коэффициенты не будут меньше или равны 0
flag = False
else:
pivot(d,bn)
def printSol(d,cn):
for i in range(cn - 1):
if i in s:
print("x"+str(i)+"=%.2f" % d[s.index(i)+1][-1])
else:
print("x"+str(i)+"=0.00")
print("objective is %.2f"%(-d[0][-1]))
d = np.loadtxt("./data.txt", dtype=np.float)
(bn,cn) = d.shape
s = list(range(cn-bn,cn-1)) # Базовый список переменных
solve(d,bn)
printSol(d,cn)
index(max(l)) # Номер перевода
m = []
for i in range(bn):
if d[i][jnum] == 0:
m.append(0.)
else:
m.append(d[i][-1]/d[i][jnum])
inum = m.index(min([x for x in m[1:] if x!=0])) # Перенести нижний индекс
s[inum-1] = jnum
r = d[inum][jnum]
d[inum] /= r
for i in [x for x in range(bn) if x !=inum]:
r = d[i][jnum]
d[i] -= r * d[inum]
def solve(d,bn):
flag = True
while flag:
if max(list(d[0][:-1])) <= 0: # Пока все коэффициенты не будут меньше или равны 0
flag = False
else:
pivot(d,bn)
def printSol(d,cn):
for i in range(cn - 1):
if i in s:
print("x"+str(i)+"=%.2f" % d[s.index(i)+1][-1])
else:
print("x"+str(i)+"=0.00")
print("objective is %.2f"%(-d[0][-1]))
d = np.loadtxt("./data.txt", dtype=np.float)
(bn,cn) = d.shape
s = list(range(cn-bn,cn-1)) # Базовый список переменных
solve(d,bn)
printSol(d,cn)
данные данные:
Результаты:
Сравнивая два результата с точки зрения ценности, два метода в основном одинаковы с небольшой ошибкой, но результат симплексного метода более точен как целочисленное значение.
# coding=utf-8
from scipy.optimize import minimize
import numpy as np
# demo 2
#Calculate (2 + x1) / (1 + x2) - минимальное значение 3 * x1 + 4 * x3 x1, x2, x3 в диапазоне от 0,1 до 0,9
def fun(args):
a,b,c,d=args
v=lambda x: (a+x[0])/(b+x[1]) -c*x[0]+d*x[2]
return v
def con(args):
# Ограничения делятся на eq и ineq
#eq означает, что результат функции равен 0; ineq означает, что выражение больше или равно 0
x1min, x1max, x2min, x2max,x3min,x3max = args
cons = ({'type': 'ineq', 'fun': lambda x: x[0] - x1min},\
{'type': 'ineq', 'fun': lambda x: -x[0] + x1max},\
{'type': 'ineq', 'fun': lambda x: x[1] - x2min},\
{'type': 'ineq', 'fun': lambda x: -x[1] + x2max},\
{'type': 'ineq', 'fun': lambda x: x[2] - x3min},\
{'type': 'ineq', 'fun': lambda x: -x[2] + x3max})
return cons
if __name__ == "__main__":
# Определить постоянное значение
args = (2,1,3,4) #a,b,c,d
# Установить диапазон параметров / ограничения
args1 = (0. 1,0.9,0.1, 0.9,0.1,0.9) #x1min, x1max, x2min, x2max
cons = con(args1)
# Установить первоначальное предположение
x0 = np.asarray((0.5,0.5,0.5))
res = minimize(fun(args), x0, method='SLSQP',constraints=cons)
print(res.fun)
print(res.success)
print(res.x)
1,0.9,0.1, 0.9,0.1,0.9) #x1min, x1max, x2min, x2max
cons = con(args1)
# Установить первоначальное предположение
x0 = np.asarray((0.5,0.5,0.5))
res = minimize(fun(args), x0, method='SLSQP',constraints=cons)
print(res.fun)
print(res.success)
print(res.x)
результат:
Симплекс-метод. Алгоритм симплекс-метода. Особенности табличного симплекс-метода. Понятия модифицированного симплекс-метода и двойственного симплекс-метода
Информатика и выч. техника \ Информатика
Страницы работы
16 страниц (Word-файл)
Посмотреть все страницы
Скачать файл
Фрагмент текста работы
Задачей оптимизации в
математике называется задача о нахождении экстремума вещественной функции в
некоторой области. Как правило, рассматриваются области, принадлежащие и заданные набором равенств и
неравенств.
Как правило, рассматриваются области, принадлежащие и заданные набором равенств и
неравенств.
3.1. Описание
Задача линейного программирования состоит в том, что необходимо максимизировать или минимизировать некоторый линейный функционал на многомерном пространстве при заданных линейных ограничениях.
Каждое из линейных неравенств на переменные ограничивает полупространство в соответствующем линейном пространстве. В результате все неравенства ограничивают некоторый многогранник (возможно, бесконечный), называемый также полиэдральным конусом.
Уравнение W(x) = c, где
W(x) – максимизируемый (или
минимизируемый) линейный функционал, порождает гиперплоскость L(c). Зависимость от c порождает семейство параллельных гиперплоскостей.
При этом экстремальная задача приобретает следующую формулировку: требуется
найти такое наибольшее c,
что гиперплоскость L(c)
пересекает многогранник хотя бы в одной точке. Заметим, что пересечение
оптимальной гиперплоскости и многогранника будет содержать хотя бы одну
вершину, причем их будет более одной, если пересечение содержит ребро или k-мерную грань. Поэтому
максимум функционала можно искать в вершинах многогранника. Принцип
симплекс-метода состоит в том, что выбирается одна из вершин многогранника,
после чего начинается движение по его рёбрам от вершины к вершине в сторону
увеличения значения функционала. Когда переход по ребру из текущей вершины в
другую вершину с более высоким значением функционала невозможен, считается, что
оптимальное значение c
найдено.
Заметим, что пересечение
оптимальной гиперплоскости и многогранника будет содержать хотя бы одну
вершину, причем их будет более одной, если пересечение содержит ребро или k-мерную грань. Поэтому
максимум функционала можно искать в вершинах многогранника. Принцип
симплекс-метода состоит в том, что выбирается одна из вершин многогранника,
после чего начинается движение по его рёбрам от вершины к вершине в сторону
увеличения значения функционала. Когда переход по ребру из текущей вершины в
другую вершину с более высоким значением функционала невозможен, считается, что
оптимальное значение c
найдено.
Сущность симплекс-метода состоит в том, что если число
неизвестных больше числа уравнений, то данная система неопределенная с
бесчисленным множеством решений. Для решения системы все неизвестные
произвольно подразделяются на базисные и свободные. Число базисных переменных
определяется числом линейно-независимых уравнений. Остальные неизвестные
свободные. Им придаются произвольные значения и затем подставляются в систему.
Любому набору свободных неизвестных можно придать бесчисленное множество
произвольных значений, которые дадут бесчисленное множество решений. Если все
свободные неизвестные приравнять к нулю, то решение будет состоять из значений
базисных неизвестных. Такое решение называется базисным.
Им придаются произвольные значения и затем подставляются в систему.
Любому набору свободных неизвестных можно придать бесчисленное множество
произвольных значений, которые дадут бесчисленное множество решений. Если все
свободные неизвестные приравнять к нулю, то решение будет состоять из значений
базисных неизвестных. Такое решение называется базисным.
В теории линейного программирования существует теорема, которая утверждает, что среди базисных решений системы можно найти оптимальное, а в некоторых случаях – несколько оптимальных решений, причем все они обеспечат экстремум целевой функции. Таким образом, если найти какой-то базисный план и затем улучшить его, то получится оптимальное решение. На этом принципе построен симплекс-метод.
Последовательность вычислений симплекс-методом можно разделить на две основные фазы:
1. нахождение исходной вершины множества допустимых решений;
2.
последовательный переход от вершины к вершине, ведущий к оптимизации
значения целевой функции.
В некоторых случаях исходное решение очевидно или его определение не требует сложных вычислений, – например, когда все ограничения представлены неравенствами вида «меньше или равно» (тогда нулевой вектор совершенно точно есть допустимое решение, хотя, скорее всего, далеко не оптимальное). В таких задачах первую фазу симплекс-метода можно вообще не проводить. Симплекс-метод соответственно делится на однофазный и
двухфазный.
3.2. Алгоритм симплекс-метода
Усиленная постановка задачи
Рассмотрим следующую задачу линейного программирования:
Теперь поставим эту задачу в эквивалентной усиленной форме. Необходимо максимизировать Z, где:
Здесь x – переменные из исходного линейного функционала; xs – новые
переменные, дополняющие старые таким образом, что неравенство переходит в
равенство; c –
коэффициенты исходного линейного функционала; Z – переменная, которую необходимо максимизировать. Полупространства и в пересечении
образуют многогранник, представляющий множество допустимых решений. Разница
между числом переменных и уравнений даёт число степеней свободы. Проще говоря,
если рассматривать вершину многогранника, это есть число рёбер, по которым
можно продолжать движение.
Полупространства и в пересечении
образуют многогранник, представляющий множество допустимых решений. Разница
между числом переменных и уравнений даёт число степеней свободы. Проще говоря,
если рассматривать вершину многогранника, это есть число рёбер, по которым
можно продолжать движение.
Тогда можно присвоить такому числу переменных значение 0 и назвать
Похожие материалы
Информация о работе
Скачать файл
4.2: Максимизация Симплекс-методом
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 37869
- Рупиндер Секон и Роберта Блум
- Колледж Де Анза
Цели обучения
В этом разделе вы научитесь решать задачи максимизации линейного программирования с использованием симплекс-метода:
- Определить и настроить линейную программу в стандартной форме максимизации
- Преобразование ограничений неравенства в уравнения с использованием резервных переменных
- Настройте начальную симплексную таблицу, используя целевую функцию и уравнения резерва
- Найдите оптимальную симплексную таблицу, выполнив операции поворота.

- Определите оптимальное решение по оптимальной симплексной таблице.
В предыдущей главе мы использовали геометрический метод для решения задач линейного программирования, но геометрический подход не работает для задач с более чем двумя переменными. В реальных жизненных ситуациях задачи линейного программирования состоят буквально из тысяч переменных и решаются компьютерами. Мы можем решить эти проблемы алгебраически, но это будет не очень эффективно. Предположим, нам дали задачу, скажем, с 5 переменными и 10 ограничениями. Выбрав все комбинации из пяти уравнений с пятью неизвестными, мы могли бы найти все угловые точки, проверить их на допустимость и найти решение, если оно существует. Но беда в том, что даже для задачи с таким небольшим количеством переменных мы получим более 250 угловых точек, и проверка каждой точки будет очень утомительна. Поэтому нам нужен метод, который имеет систематический алгоритм и может быть запрограммирован для компьютера. Метод должен быть достаточно эффективным, чтобы нам не пришлось оценивать целевую функцию в каждой угловой точке. У нас есть именно такой метод, и он называется симплексный метод .
У нас есть именно такой метод, и он называется симплексный метод .
Симплекс-метод был разработан во время Второй мировой войны доктором Джорджем Данцигом. Его модели линейного программирования помогли союзным войскам решить проблемы с транспортом и планированием. В 1979 году советский ученый Леонид Хачян разработал метод, названный алгоритмом эллипсоида, который должен был стать революционным, но, как оказалось, ничем не лучше симплексного метода. В 1984 году Нарендра Кармаркар, научный сотрудник AT&T Bell Laboratories, разработал алгоритм Кармаркара, который, как было доказано, в четыре раза быстрее, чем симплекс-метод для определенных задач. Но симплекс-метод по-прежнему работает лучше всего для большинства задач.
В симплексном методе используется очень эффективный подход. Он не вычисляет значение целевой функции в каждой точке; вместо этого он начинается с угловой точки области выполнимости, где все основные переменные равны нулю, а затем систематически перемещается от угловой точки к угловой точке, улучшая значение целевой функции на каждом этапе. Процесс продолжается до тех пор, пока не будет найдено оптимальное решение.
Процесс продолжается до тех пор, пока не будет найдено оптимальное решение.
Чтобы изучить симплекс-метод, мы попробуем довольно нетрадиционный подход. Сначала мы перечисляем алгоритм, а затем работаем над проблемой. Мы обосновываем обоснование каждого шага в процессе. Тщательное обоснование выходит за рамки данного курса.
Начнем с примера, который мы решили в предыдущей главе графическим методом. Это даст нам некоторое представление о симплекс-методе и в то же время даст нам возможность сравнить несколько допустимых решений, которые мы получили ранее с помощью графического метода. Но сначала приведем алгоритм симплекс-метода.
СИМПЛЕКСНЫЙ МЕТОД
- Поставьте задачу. То есть запишите целевую функцию и ограничения неравенства.
- Преобразуйте неравенства в уравнения. Это делается путем добавления одной резервной переменной для каждого неравенства.
- Построить начальную симплексную таблицу. Запишите целевую функцию в нижней строке.

- Самая отрицательная запись в нижней строке идентифицирует сводной столбец.
- Вычислите частные. Наименьшее частное определяет строку. Элемент на пересечении столбца, определенного на шаге 4, и строки, определенной на этом шаге, идентифицируется как опорный элемент. Частные вычисляются путем деления крайнего правого столбца на столбец, указанный в шаге 4. Частное, являющееся нулем, отрицательным числом или имеющим ноль в знаменателе, игнорируется.
- Выполните поворот, чтобы обнулить все остальные записи в этом столбце. Это делается так же, как и с методом Гаусса-Джордана.
- Когда в нижней строке больше нет отрицательных значений, мы закончили; в противном случае начинаем снова с шага 4.
- Прочитайте свои ответы. Получить переменные, используя столбцы с 1 и 0. Все остальные переменные равны нулю. Максимальное значение, которое вы ищете, отображается в правом нижнем углу.
Теперь мы используем симплекс-метод для решения примера 3. 1.1, решенного геометрически в разделе 3.1.
1.1, решенного геометрически в разделе 3.1.
Пример \(\PageIndex{1}\)
Ники работает на двух работах с частичной занятостью: работа I и работа II. Она никогда не хочет работать больше, чем в общей сложности 12 часов в неделю. Она определила, что на каждый час работы на Работе I ей нужно 2 часа времени на подготовку, а на каждый час работы на Работе II ей нужен один час времени на подготовку, и она не может тратить на подготовку более 16 часов. Если она зарабатывает 40 долларов в час на работе I и 30 долларов в час на работе II, сколько часов в неделю она должна работать на каждой работе, чтобы максимизировать свой доход?
Решение
При решении этой задачи будем следовать алгоритму, указанному выше.
ШАГ 1. Поставьте задачу. Запишите целевую функцию и ограничения.
Поскольку симплекс-метод используется для задач, состоящих из многих переменных, нецелесообразно использовать переменные \(x\), \(y\), \(z\) и т. д. Мы используем символы \(x_1\ ), \(x_2\), \(x_3\) и так далее.
Let
- \(x_1\) = количество часов в неделю, которое Ники будет работать на работе I и 9.0010
- \(x_2\) = количество часов в неделю, которое Ники будет работать на задании II.
Принято выбирать переменную, которая должна быть максимизирована как \(Z\).
Задача формулируется так же, как и в предыдущей главе.
\[\begin{array}{ll}
\textbf { Развернуть} & \mathrm{Z}=40 \mathrm{x}_{1}+30 \mathrm{x}_{2} \\
\ textbf { При условии: } & \mathrm{x}_{1}+\mathrm{x}_{2} \leq 12 \\
& 2 \mathrm{x}_{1}+\mathrm{x}_ {2} \leq 16 \\
& \mathrm{x}_{1} \geq 0 ; \mathrm{x}_{2} \geq 0
\end{array}\nonumber \]
ШАГ 2. Преобразовать неравенства в уравнения. Это делается путем добавления одной резервной переменной для каждого неравенства.
Например, чтобы преобразовать неравенство \(x_1 + x_2 ≤ 12\) в уравнение, мы добавляем неотрицательную переменную \(y_1\), и мы получаем
\[x_1 + x_2 + y_1 = 12 \nonumber \]
Здесь переменная \(y_1\) восполняет пробел и представляет величину, на которую \(x_1 + x_2\) меньше 12. В этой задаче, если Ники работает менее 12 часов, скажем, 10 , тогда \(y_1\) равно 2. Позже, когда мы прочитаем окончательное решение из симплексной таблицы, значения резервных переменных будут определять неиспользованные суммы.
В этой задаче, если Ники работает менее 12 часов, скажем, 10 , тогда \(y_1\) равно 2. Позже, когда мы прочитаем окончательное решение из симплексной таблицы, значения резервных переменных будут определять неиспользованные суммы.
Перепишем целевую функцию \(Z = 40x_1 + 30x_2\) в виде \(- 40x_1 — 30x_2 + Z = 0\).
После добавления резервных переменных наша задача выглядит следующим образом:
\[\begin{array}{ll}
\text { Целевая функция } & — 40x_1 — 30x_2 + Z = 0 \\
\text { С учетом ограничений: } &x_1+x_2+y_1=12\
&2x_1+x_2+y_2=16\
&x1 ≥ 0; x2 ≥ 0
\end{array} \nonumber \]
ШАГ 3. Построить исходную симплексную таблицу . Каждое ограничение неравенства отображается в отдельной строке. (Ограничения неотрицательности заставляют , а не появляться в виде строк в симплексной таблице.) Запишите целевую функцию в нижней строке.
Теперь, когда неравенства преобразованы в уравнения, мы можем представить задачу в виде расширенной матрицы, называемой исходной симплексной таблицей, следующим образом.
Здесь вертикальная линия отделяет левую часть уравнений от правой. Горизонтальная линия отделяет ограничения от целевой функции. Правая часть уравнения представлена столбцом C.
Читатель должен заметить, что последние четыре столбца этой матрицы выглядят как окончательная матрица для решения системы уравнений. Если мы произвольно выберем \(x_1 = 0\) и \(x_2 = 0\), мы получим
\[\left[\begin{array}{ccccc}
y_{1} & y_{2} & Z & | &С\
1&0&0 & | & 12 \
0 & 1 & 0 & | & 16 \\
0 & 0 & 1 & | & 0
\end{массив}\right]\nonumber \]
, что читается как
\[y_1 = 12 \quad y_2 = 16 \quad Z = 0 \nonumber \]
Решение, полученное путем произвольного присвоения значений некоторым переменным и последующего решения для оставшихся переменных, называется базовым решением , связанным с таблицей . Таким образом, приведенное выше решение является основным решением, связанным с исходной симплексной таблицей. Мы можем пометить базовую переменную решения справа от последнего столбца, как показано в таблице ниже.
ШАГ 4. Самая отрицательная запись в нижней строке идентифицирует сводной столбец.
Самая отрицательная запись в нижней строке -40; поэтому столбец 1 идентифицируется.
Вопрос Почему мы выбираем самую отрицательную запись в нижней строке?
Ответ Самая отрицательная запись в нижней строке представляет наибольший коэффициент в целевой функции — коэффициент, ввод которого увеличит значение целевой функции быстрее всего.
Симплекс-метод начинается с угловой точки, где все основные переменные, переменные с такими символами, как \(x_1\), \(x_2\), \(x_3\) и т. д., равны нулю. Затем он перемещается от угловой точки к соседней угловой точке, всегда увеличивая значение целевой функции. В случае целевой функции \(Z = 40x_1+ 30x_2\) имеет смысл увеличить значение \(x_1\), а не \(x_2\). Переменная \(x_1\) представляет количество часов в неделю, которые Ники работает на работе I. Поскольку работа I оплачивается 40 долларов в час, в отличие от работы II, на которой платят всего 30 долларов, переменная \(x_1\) увеличит целевую функцию на $40 за единицу увеличения переменной \(x_1\).
ШАГ 5. Вычислите частные. Наименьшее частное определяет строку. Элемент на пересечении столбца, определенного на шаге 4, и строки, определенной на этом шаге, идентифицируется как опорный элемент.
Следуя алгоритму, для вычисления частного делим записи в крайнем правом столбце на записи в столбце 1, исключая запись в нижней строке.
Наименьшее из двух частных, 12 и 8, равно 8. Следовательно, идентифицируется строка 2. Пересечение столбца 1 и строки 2 является записью 2, которая выделена. Это наш опорный элемент.
Вопрос Почему мы находим частное и почему наименьшее частное определяет строку?
Ответ Когда мы выбираем самую отрицательную запись в нижней строке, мы пытаемся увеличить значение целевой функции, вводя переменную \(x_1\). Но мы не можем выбрать любое значение для \(x_1\). Можем ли мы позволить \(x_1 = 100\)? Точно нет! Это потому, что Ники никогда не хочет работать более 12 часов на обеих работах вместе взятых: \(x_1 + x_2 ≤ 12\). Можем ли мы позволить \(x_1 = 12\)? Опять же, ответ отрицательный, потому что время подготовки к работе I в два раза превышает время, затрачиваемое на работу. Поскольку Ники никогда не хочет тратить на подготовку более 16 часов, максимальное время, которое она может работать, составляет 16 ÷ 2 = 8.9.0034
Можем ли мы позволить \(x_1 = 12\)? Опять же, ответ отрицательный, потому что время подготовки к работе I в два раза превышает время, затрачиваемое на работу. Поскольку Ники никогда не хочет тратить на подготовку более 16 часов, максимальное время, которое она может работать, составляет 16 ÷ 2 = 8.9.0034
Теперь вы видите цель вычисления частных; использование частных для определения опорного элемента гарантирует, что мы не нарушаем ограничения.
Вопрос Почему мы идентифицируем поворотный элемент?
Ответ Как мы упоминали ранее, симплекс-метод начинается с угловой точки, а затем переходит к следующей угловой точке, всегда улучшая значение целевой функции. Значение целевой функции улучшается за счет изменения количества единиц переменных. Мы можем добавить количество единиц одной переменной, отбросив единицы другой. Поворот позволяет нам сделать именно это.
Переменная, единицы которой добавляются, называется входной переменной , , а переменная, единицы которой заменяются, называется исходящей переменной . Входной переменной в приведенной выше таблице является \(x_1\), и она определяется самой отрицательной записью в нижней строке. Уходящая переменная \(y_2\) была идентифицирована наименьшим из всех частных.
Входной переменной в приведенной выше таблице является \(x_1\), и она определяется самой отрицательной записью в нижней строке. Уходящая переменная \(y_2\) была идентифицирована наименьшим из всех частных.
ШАГ 6. Выполните поворот, чтобы обнулить все остальные записи в этом столбце.
В главе 2 мы использовали поворот, чтобы получить эшелонированную форму строк расширенной матрицы. Поворот — это процесс получения 1 в местоположении поворотного элемента, а затем обнуления всех остальных записей в этом столбце. Итак, теперь наша задача состоит в том, чтобы сделать наш опорный элемент равным 1, разделив всю вторую строку на 2. Далее следует результат.
Чтобы получить ноль в записи первой над опорным элементом, умножаем вторую строку на -1 и прибавляем к строке 1. Получаем
Чтобы получить ноль в элементе ниже стержня, умножаем вторую строку на 40 и прибавляем к последней строке.
Теперь мы определяем основное решение, связанное с этой таблицей. Произвольно выбирая \(x_2 = 0\) и \(y_2 = 0\), мы получаем \(x_1 = 8\), \(y_1 = 4\) и \(z = 320\). Если мы напишем расширенную матрицу, левая часть которой представляет собой матрицу со столбцами, в которых одна единица, а все остальные элементы равны нулю, мы получим следующую матрицу, утверждающую то же самое.
Произвольно выбирая \(x_2 = 0\) и \(y_2 = 0\), мы получаем \(x_1 = 8\), \(y_1 = 4\) и \(z = 320\). Если мы напишем расширенную матрицу, левая часть которой представляет собой матрицу со столбцами, в которых одна единица, а все остальные элементы равны нулю, мы получим следующую матрицу, утверждающую то же самое.
\[\left[\begin{array}{ccccc}
\mathrm{x}_{1} & \mathrm{y}_1 & \mathrm{Z} & | & \mathrm{C} \\
0 & 1 & 0 & | & 4 \
1 & 0 & 0 & | & 8 \
0 & 0 & 1 & | & 320
\end{array}\right] \nonumber \]
Мы можем переформулировать решение, связанное с этой матрицей, как \(x_1 = 8\), \(x_2 = 0\), \(y_1 = 4\) , \(y_2 = 0\) и \(z = 320\). На этом этапе игры написано, что если Ники проработает 8 часов на работе I и ни одного часа на работе II, ее прибыль Z составит 320 долларов. Напомним из примера 3.1.1 в разделе 3.1, что (8, 0) была одной из наших угловых точек. Здесь \(y_1 = 4\) и \(y_2 = 0\) означают, что у нее останется 4 часа рабочего времени и никакого времени на подготовку.
ШАГ 7. Когда в нижней строке больше нет отрицательных значений, мы закончили; в противном случае мы начинаем снова с шага 4.
Поскольку в нижней строке все еще есть отрицательная запись, -10, нам нужно снова начать с шага 4. На этот раз мы не будем повторять детали каждого шага. , вместо этого мы укажем столбец и строку, которые дают нам опорный элемент, и выделим опорный элемент. Результат следующий.
Делаем опорный элемент 1, умножая строку 1 на 2, и получаем
Теперь, чтобы все остальные записи в этом столбце были равны нулю, мы сначала умножаем строку 1 на -1/2 и прибавляем к строке 2, а затем умножаем строку 1 на 10 и прибавляем к нижней строке.
У нас больше нет отрицательных записей в нижней строке, поэтому мы закончили.
Вопрос Почему мы закончили, если в нижней строке нет отрицательных значений?
Ответ Ответ лежит в нижней строке. Нижняя строка соответствует уравнению:
\[\begin{array}{l}
0 x_{1}+0 x_{2}+20 y_{1}+10 y_{2}+Z=400 \quad \text { or } \\
z=400-20 y 1-10 y 2
\end{array}\nonumber \]
Поскольку все переменные неотрицательны, максимальное значение \(Z\) может быть равно 400, и это произойдет только когда \(y_1\) и \(y_2\) равны нулю.
ШАГ 8. Прочитайте ваши ответы.
Теперь мы читаем наши ответы, то есть мы определяем базовое решение, связанное с окончательной симплексной таблицей. Опять же, мы смотрим на столбцы, в которых есть 1, а все остальные записи — нули. Поскольку столбцы с метками \(y_1\) и \(y_2\) не являются такими столбцами, мы произвольно выбираем \(y_1 = 0\) и \(y_2 = 0\), и мы получаем
\[\left[\begin{array}{ccccc}
\mathrm{x}_{1} & \mathrm{x}_{2} & \mathrm{Z} & | & \mathrm{C} \\
0 & 1 & 0 & | & 8 \\
1 & 0 & 0 & | & 4 \
0 & 0 & 1 & | & 400
\end{массив}\right] \nonumber \]
Матрица читается как \(x_1 = 4\), \(x_2= 8\) и \(z = 400\).
Окончательное решение гласит, что если Ники будет работать 4 часа на работе I и 8 часов на работе II, она максимизирует свой доход до 400 долларов. Поскольку обе переменные slack равны нулю, значит, она израсходовала бы все рабочее время, а также время на подготовку, и ничего не останется.
Эта страница под названием 4. 2: Максимизация с помощью симплексного метода распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Рупиндером Секоном и Робертой Блум с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
2: Максимизация с помощью симплексного метода распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Рупиндером Секоном и Робертой Блум с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Рупиндер Сехон и Роберта Блум
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Теги
- симплексный алгоритм
- источник@https://www.
 deanza.edu/faculty/bloomroberta/math21/afm3files.html.html
deanza.edu/faculty/bloomroberta/math21/afm3files.html.html
Линейное программирование: пример симплексного метода
- HOME
- ИЗБРАННОЕ
- КОНТАКТ
- КРЕДИТЫ
- Дом
- PHPСимплекс
- Помощь PHPSimple
- Исследование операций
- История
- Реальные случаи
- Теория
- Проблемы моделирования
- Симплексный метод
- Двухфазный симплексный метод
- Графический метод
- Примеры
- Проблемы моделирования
- Диетическая проблема
- Проблема перевозки войск
- Проблема перевозки грузов
- Проблема фруктовых деревьев
- Задача распределения персонала
- Задача минимальной дороги
- Проблема с местоположением
- Проблема фондовой биржи
- Симплексный метод
- Графический метод
- Проблемы моделирования
- Джордж Б.
 Данциг
Данциг- Биография
- Интервью
- Язык
- Испанский
- Английский
- Французский
- Португальский
Пример (часть 1): Симплекс-метод
Решите Симплекс-методом следующую задачу:
| Максимизация | Z = f(x,y) = 3x + 2y |
| предмет: | 2x + у ≤ 18 |
| 2x + 3y ≤ 42 | |
| 3x + у ≤ 24 | |
| х ≥ 0, у ≥ 0 |
Рассмотрим следующие шаги:
- Произведите замену переменных и нормализуйте знак независимых членов.
Внесено изменение в наименование переменной, устанавливающее следующие соответствия:
- x становится X1
- г становится X2
Поскольку независимые условия всех ограничений положительны, никаких дальнейших действий не требуется.
 В противном случае было бы умножение на «-1» в обеих частях неравенства (заметим, что эта операция также влияет на тип ограничения).
В противном случае было бы умножение на «-1» в обеих частях неравенства (заметим, что эта операция также влияет на тип ограничения). - Нормализация ограничений.
Неравенства становятся уравнениями путем добавления запаса , избытка и искусственные переменные в виде следующей таблицы:
Тип неравенства Появляющаяся переменная ≥ — избыток + искусственный = + искусственный ≤ + провисание В этом случае в каждое из ограничений типа ≤ вводится резервная переменная (X3, X4 и X5), для преобразования их в равенства, в результате чего получается система линейных уравнений:
2·Х1 + Х2 + Х3 = 18 2·Х1 + 3·Х2 + Х4 = 42 3·Х1 + Х2 + Х5 = 24 - Сопоставьте целевую функцию с нулем.

Z — 3·X1 — 2·X2 — 0·X3 — 0·X4 — 0·X5 = 0
- Напишите исходную таблицу симплекс-метода.
Исходная таблица симплекс-метода состоит из всех коэффициентов переменных решения исходной задачи и резерва, избыточных и искусственных переменных, добавленных на втором этапе (в столбцах, с P0 в качестве постоянного члена и Pi в качестве коэффициентов остальных переменных Xi) и ограничения (в строках). Столбец Cb содержит коэффициенты переменных, которые находятся в базе.
Первая строка состоит из коэффициентов целевой функции, а последняя строка содержит значение целевой функции и приведенных затрат Zj — Cj.
Последняя строка вычисляется следующим образом: Zj = Σ(Cbi·Pj) для i = 1..m, где если j = 0, то P0 = bi и C0 = 0, иначе Pj = aij. Хотя это первая таблица симплекс-метода и все Cb нулевые, поэтому расчет можно упростить, и к этому моменту Zj = -Cj.
Таблица I .  1-я итерация
1-я итерация3 2 0 0 0 Основание Кб Р0 Р1 Р2 Р3 Р4 Р5 Р3 0 18 2 1 1 0 0 Р4 0 42 2 3 0 1 0 Р5 0 24 3 1 0 0 1 З 0 -3 -2 0 0 0 - Состояние остановки.

Если целью является максимизация, когда в последней строке (строке индикатора) нет отрицательного значения между дисконтированными затратами (столбцы P1 ниже), достигается условие остановки.
В этом случае алгоритм достигает конца, так как возможности улучшения нет. Значение Z (столбец P0) является оптимальным решением задачи.
Другой возможный сценарий: все значения отрицательные или нулевые в столбце входных переменных базы. Это указывает на то, что проблема не ограничена и решение всегда будет улучшаться.
В противном случае последовательно выполняются следующие шаги.
- Выбор входных и выходных базовых переменных.
Сначала определяется входная базовая переменная. Для этого выбирается столбец, значение которого в строке Z меньше всех отрицательных значений. В этом примере это будет переменная X1 (P1) с коэффициентом -3.
Если есть два или более одинаковых коэффициента, удовлетворяющих вышеуказанному условию (случай равенства), то выбрать базовую переменную.

Столбец входной базовой переменной называется сводным столбцом (выделен зеленым цветом).
После получения входной базовой переменной определяется выходная базовая переменная. Решение основано на простом вычислении: разделить каждый независимый член (столбец P0) между соответствующим значением в сводном столбце, если оба значения строго положительны (больше нуля). Выбирается строка, результатом которой является минимальный балл.
Если какое-либо значение меньше или равно нулю, это частное не будет выполнено. Если все значения опорного столбца удовлетворяют этому условию, то будет достигнуто условие остановки и задача имеет неограниченное решение (см. теорию симплекс-метода).
В этом примере: 18/2 [=9], 42/2 [=21] и 24/3 [=8]
Член сводного столбца, который привел к меньшему положительному частному в предыдущем делении, указывает строку резервной переменной, выходящую из базы. В данном примере это X5 (P5) с коэффициентом 3.
 Этот ряд называется поворотный ряд (зеленый).
Этот ряд называется поворотный ряд (зеленый).Если два или более частных удовлетворяют условию выбора (случай равенства), выбирается другая базовая переменная (где это возможно).
Пересечение опорного столбца и сводной строки отмечает значение сводки , в этом примере 3.
- Обновление таблицы.
Новые коэффициенты таблицы рассчитываются следующим образом:
- В сводной строке каждое новое значение рассчитывается как:
Новое значение = Предыдущее значение / Сводка
- В остальных строках каждое новое значение рассчитывается как:
Новое значение = Предыдущее значение — (Предыдущее значение в сводном столбце * Новое значение в сводной строке)
Таким образом, стержень нормализуется (его значение становится равным 1), а другие значения стержневого столбца отменяются (аналогично методу Гаусса-Жордана).

Расчеты для строки P4 показаны ниже:
Предыдущий ряд P4 42 2 3 0 1 0 — — — — — — Предыдущее значение в сводном столбце 2 2 2 2 2 2 х х х х х х Новое значение в сводной строке 8 1 1/3 0 0 1/3 = = = = = = Новый ряд P4 26 0 7/3 0 1 -2/3 Таблица, соответствующая этой второй итерации:
Таблица II .  2-я итерация
2-я итерация3 2 0 0 0 Основание Кб Р0 Р1 Р2 Р3 Р4 Р5 Р3 0 2 0 1/3 1 0 -2/3 Р4 0 26 0 7/3 0 1 -2/3 Р1 3 8 1 1/3 0 0 1/3 З 24 0 -1 0 0 1 - В сводной строке каждое новое значение рассчитывается как:
- При проверке наблюдается условие остановки, которое не выполняется, так как в последней строке одно отрицательное значение -1.
 Итак, снова повторите шаги 6 и 7.
Итак, снова повторите шаги 6 и 7.- 6.1. Входной базовой переменной является X2 (P2), так как это переменная, соответствующая столбцу, где коэффициент равен -1.
- 6.2. Чтобы вычислить выходную базовую переменную, постоянные члены столбца P0) делятся на члены нового сводного столбца: 2 / 1/3 [= 6], 26 / 7/3 [= 78/7] и 8 / 1/ 3 [=24]. Поскольку меньшее положительное частное равно 6, выходная базовая переменная равна X3 (P3).
- 6.3. Новый стержень равен 1/3.
- 7. Обновление значений таблицы снова получается:
Таблица III. 3-я итерация 3 2 0 0 0 Основание Кб Р0 Р1 Р2 Р3 Р4 Р5 Р2 2 6 0 1 3 0 -2 Р4 0 12 0 0 -7 1 4 Р1 3 6 1 0 -1 0 1 З 30 0 0 3 0 -1
- Повторная проверка условия остановки показывает, что опорная строка имеет одно отрицательное значение, -1.
 Это означает, что оптимальное решение еще не достигнуто, и мы должны продолжить итерацию (шаги 6 и 7):
Это означает, что оптимальное решение еще не достигнуто, и мы должны продолжить итерацию (шаги 6 и 7):- 6.1. Входной базовой переменной является X5 (P5), так как это переменная, соответствующая столбцу, где коэффициент равен -1.
- 6.2. Чтобы вычислить выходную базовую переменную, постоянные члены (P0) делятся на члены нового сводного столбца: 6/(-2) [=-3] , 12/4 [=3] и 6/1 [= 6]. В этой итерации выходная базовая переменная равна X4 (P4).
- 6.3. Новый стержень 4.
- 7. Обновление значений таблицы снова получается:
Таблица IV. 4-я итерация 3 2 0 0 0 Основание Кб Р0 Р1 Р2 Р3 Р4 Р5 Р2 2 12 0 1 -1/2 1/2 0 Р5 0 3 0 0 -7/4 1/4 1 Р1 3 3 1 0 3/4 -1/4 0 З 33 0 0 5/4 1/4 0
- Конец алгоритма.

Отмечено, что в последней строке все коэффициенты положительные, значит, условие остановки выполнено.
Оптимальное решение задается значением Z в столбце постоянных условий (столбец P0), в примере: 33. В том же столбце показана точка, в которой оно достигает, наблюдая за соответствующими строками входных переменных решения. : X1 = 3 и X2 = 12.
Отмена изменения имени дает x = 3 и y = 12.
Решите с помощью PHPSimplex.
Copyright © 2006-2022 PHPSimplex. Все права защищены.
X
PHPSimple
Версия 0.81
Copyright © 2006-2022. Все права защищены.
Разработчик:
Даниэль Искьердо Гранха
Хуан Хосе Руис Руис
английский перевод:
Лучано Мигель Тобариа
Французский перевод:
Эстер Руте Руис
перевод на португальский:
Розан Бухес
Линейное программирование: симплекс-метод
Линейное программирование: симплекс-методЗадача линейного программирования
Вот первая проблема, с которой мы столкнулись.
| Развернуть | Р | = | 40x 1 | + | 30x 2 | ||
|---|---|---|---|---|---|---|---|
| Тема: | х 1 | + | 2x 2 | ≤ | 16 | ||
| х 1 | + | х 2 | ≤ | 9 | |||
| 3x 1 | + | 2x 2 | ≤ | 24 | |||
| х 1 | , | х 2 | ≥ | 0 |
Начальная система
Исходная система находится путем преобразования ограничений ≤ в ограничения = путем добавления резервной переменной.
Это тот же шаг, который мы предприняли в табличном методе.
| Развернуть | Р | = | 40x 1 | + | 30x 2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тема: | х 1 | + | 2x 2 | + | с 1 | = | 16 | ||||||
| х 1 | + | х 2 | + | с 2 | = | 9 | |||||||
| 3x 1 | + | 2x 2 | + | с 3 | = | 24 | |||||||
| х 1 | , | х 2 | , | с 1 | , | с 2 | , | с 3 | ≥ | 0 |
Начальная таблица
Таблицы — это причудливые имена для матриц. Теперь мы преобразуем систему линейных уравнений в матрицы. Однако здесь есть еще одна хитрость… мы перемещаем все переменные в левую часть, поэтому целевая функция становится равной -40×9.1343 1 — 30x 2 + P = 0. Мы также помещаем целевую функцию последней в таблицу и помещаем над ней линию увеличения, чтобы отделить ее от ограничений.
Теперь мы преобразуем систему линейных уравнений в матрицы. Однако здесь есть еще одна хитрость… мы перемещаем все переменные в левую часть, поэтому целевая функция становится равной -40×9.1343 1 — 30x 2 + P = 0. Мы также помещаем целевую функцию последней в таблицу и помещаем над ней линию увеличения, чтобы отделить ее от ограничений.
| х 1 | x 2 | с 1 | с 2 | с 3 | Р | справа | ||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 1 | 0 | 0 | 0 | 16 | ||
| 1 | 1 | 0 | 1 | 0 | 0 | 9 | ||
| 3 | 2 | 0 | 0 | 1 | 0 | 24 | ||
| -40 | -30 | 0 | 0 | 0 | 1 | 0 |
Базовые и небазовые переменные
В каждой строке таблицы будет базовая переменная, а целевая функция всегда будет базовой в нижней строке.
Каждая переменная соответствует столбцу в таблице. Если столбец очищен и содержит только один ненулевой элемент, то эта переменная является базовой переменной. Если столбец не очищен и содержит более одного ненулевого элемента, эта переменная не является базовой и значение этой переменной равно нулю.
Значения всех неосновных переменных (столбцы, содержащие более одного числа) равны нулю. В этой таблице это будет x 1 и x 2 .
Значения основных переменных находятся путем считывания решения из матрицы, полученной путем удаления неосновных столбцов.
| с 1 | с 2 | с 3 | Р | правая сторона | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 16 | с 1 | = | 16 | |||
| 0 | 1 | 0 | 0 | 9 | с 2 | = | 9 | |||
| 0 | 0 | 1 | 0 | 24 | с 3 | = | 24 | |||
| 0 | 0 | 0 | 1 | 0 | Р | = | 0 |
Подытожим, что у нас есть.
| Базовый | Небазовый |
|---|---|
| с 1 =16, с 2 =9, с 3 =24, P=0 | х 1 =0, х 2 =0 |
Связывание таблицы с таблицей
Давайте вспомним результаты, которые мы получили от табличного метода.
| Пт | х 1 | x 2 | с 1 | с 2 | с 3 | Выполнимо? | P = 40x 1 + 30x 2 |
|---|---|---|---|---|---|---|---|
| А | 0 | 0 | 16 | 9 | 24 | да | 0 |
| Б | 0 | 8 | 0 | 1 | 16 | да | 240 |
| С | 0 | 9 | -2 | 0 | 6 | нет | н/д |
| Д | 0 | 12 | -8 | -3 | 0 | нет | н/д |
| Е | 16 | 0 | 0 | -7 | -24 | нет | н/д |
| Ф | 9 | 0 | 7 | 0 | -3 | нет | н/д |
| Г | 8 | 0 | 8 | 1 | 0 | да | 320 |
| Н | 2 | 7 | 0 | 0 | 15 | да | 290 |
| я | 4 | 6 | 0 | -1 | 0 | нет | н/д |
| Дж | 6 | 3 | 4 | 0 | 0 | да | 330 |
Если вы сравните значения, полученные при чтении таблицы, вы увидите, что мы находимся в точке A , где x 1 = 0 и x 2 = 0.
Идентификация основных переменных для каждой строки
Каждая строка таблицы будет иметь одну базовую переменную для этой строки. Какая это переменная, можно довольно легко определить, не удаляя столбцы, соответствующие неосновным переменным.
Для столбцов, которые очищены и содержат только одну ненулевую запись, вы перемещаетесь вниз по столбцу, пока не найдете ненулевую запись. Каждый столбец будет иметь ненулевой элемент в другой строке. Переменная в этом столбце будет базовой переменной для строки с ненулевым элементом.
Это немного сбивает с толку, так что, возможно, это поможет.
- Столбец s 1 очищен, кроме первой строки. Поэтому s 1 является базовой переменной в первой строке.
- Столбец s 2 очищен, за исключением второй строки. Поэтому s 2 является базовой переменной во второй строке.
- Столбец s 3 очищен, за исключением третьей строки. Поэтому s 3 является базовой переменной в третьей строке.

- Столбец P очищен, за исключением нижней строки. Следовательно, P — основная переменная в нижней строке.
| Базовый | х 1 | x 2 | с 1 | с 2 | с 3 | Р | справа | ||
|---|---|---|---|---|---|---|---|---|---|
| с 1 | 1 | 2 | 1 | 0 | 0 | 0 | 16 | ||
| с 2 | 1 | 1 | 0 | 1 | 0 | 0 | 9 | ||
| с 3 | 3 | 2 | 0 | 0 | 1 | 0 | 24 | ||
| Р | -40 | -30 | 0 | 0 | 0 | 1 | 0 |
Симплексный метод
Мы видели, что находимся на пересечении линий x 1 = 0 и x 2 = 0. Это начало координат, а две неосновные переменные: x 1 и x 2 . Чтобы обойти допустимую область, нам нужно сойти с одной из линий x 1 = 0 или x 2 = 0 на одну из линий s 1 = 0, s 2 = 0 или s 3 = 0. Вопрос в том, в каком направлении двигаться?
Это начало координат, а две неосновные переменные: x 1 и x 2 . Чтобы обойти допустимую область, нам нужно сойти с одной из линий x 1 = 0 или x 2 = 0 на одну из линий s 1 = 0, s 2 = 0 или s 3 = 0. Вопрос в том, в каком направлении двигаться?
Выбор сводной колонки
Подумайте о целевой функции P = 40x 1 + 30x 2 . На каждую единицу, которую мы двигаем в направлении x 1 , мы получаем 40 в целевой функции. На каждую единицу, которую мы двигаем в направлении x 2 , мы получаем 30 в целевой функции. Думайте об этом как о каждом шаге, который вы делаете вправо (x 1 ), вы получаете 40 долларов, и за каждый сделанный вами шаг (направление x 2 ) вы получаете 30 долларов.
Что бы вы предпочли? Надеюсь, ваш ответ — зарабатывать 40 долларов за каждый шаг, который вы делаете. Если это не так, вы не очень хорошо поймете симплекс-метод.
Теперь подумайте о том, как эти 40 представлены в целевой функции таблицы. Когда мы поместили целевую функцию в таблицу, мы переместили переменные решения и их коэффициенты в левую часть и сделали их отрицательными. Следовательно, самое отрицательное число в нижней строке соответствует самому положительному коэффициенту целевой функции и указывает направление, в котором мы должны двигаться.
Сводной столбец — это столбец с самым отрицательным числом в нижней строке. Если в нижней строке нет минусов, остановитесь, все готово.
Положительное значение в нижней строке таблицы будет соответствовать отрицательному коэффициенту целевой функции, что означает, что движение в этом направлении фактически уменьшит значение цели. Это не то, что мы хотим сделать, если нам нужно максимальное значение, поэтому мы останавливаемся, когда в нижней строке целевой функции больше нет отрицательных значений.
Мы уходим от линии, соответствующей неосновной переменной в сводном столбце. Это означает, что переменная выходит из набора базовых переменных и становится небазовой.
Это означает, что переменная выходит из набора базовых переменных и становится небазовой.
Поместите стрелку под опорную колонку.
Выбор сводного ряда
Теперь, когда мы выбрали направление, нам нужно определить, как далеко мы должны двигаться в этом направлении. Помните, что мы сейчас находимся в точке A и движемся в направлении x 1 или вправо. Это означает, что мы можем перейти к пунктам E (16,0), F (9,0) или G (8,0).
- Точка E находится в точке (16,0) и является пересечением прямых x 2 = 0 и s 1 = 0. x 1 станет основной, а s 1 станет неосновной . Значение x 1 изменится с x 1 = 0 на x 1 = 16, если мы перейдем к точке E .
- Точка F находится в (9,0) и является пересечением линий x 2 = 0 и s 2 = 0.
 x 1 станет основным, а s 2 станет неосновным. Значение x 1 изменится с x 1 = 0 на x 1 = 9, если мы перейдем к точке F .
x 1 станет основным, а s 2 станет неосновным. Значение x 1 изменится с x 1 = 0 на x 1 = 9, если мы перейдем к точке F . - Точка G находится в (8,0) и является пересечением прямых x 2 = 0 и s 3 = 0. x 1 станет основной, а s 3 станет неосновной. Значение x 1 изменится с x 1 = 0 до x 1 = 8, если мы перейдем к точке G .
Давайте посмотрим, как мы можем узнать эту информацию из таблицы. Помните, мы пытаемся сделать это вообще без использования графа.
Сформируйте отношения между неотрицательными записями в правой части и положительными записями в сводном столбце для каждого из проблемных ограничений. Не найти соотношение для целевой функции. Не находите отношение, если элемент в сводном столбце отрицателен или равен нулю, но найдите отношение, если правая часть равна нулю.
| Базовый | х 1 | x 2 | с 1 | с 2 | с 3 | Р | справа | отношение | ||
|---|---|---|---|---|---|---|---|---|---|---|
| с 1 | 1 | 2 | 1 | 0 | 0 | 0 | 16 | 16/1 = 16 | ||
| с 2 | 1 | 1 | 0 | 1 | 0 | 0 | 9 | 9/1 = 9 | ||
| с 3 | 3 | 2 | 0 | 0 | 1 | 0 | 24 | 24/3 = 8 | ||
| Р | -40 | -30 | 0 | 0 | 0 | 1 | 0 | |||
| ↑ |
Не могли бы вы посмотреть на эти коэффициенты? 16, 9 и 8. И еще лучше, 16 связано со строкой, где s 1 является базовой, 9 связана со строкой, где s 2 является базовой, а 8 связана со строкой, где s 3 является основным.
И еще лучше, 16 связано со строкой, где s 1 является базовой, 9 связана со строкой, где s 2 является базовой, а 8 связана со строкой, где s 3 является основным.
Это означает, что мы можем сказать, насколько изменится x 1 , взглянув на соотношение. Мы также можем сказать, к какой строке мы будем двигаться, взглянув на переменную, которая является базовой для этой строки.
Какую строку выбрать? Ваша первая мысль может заключаться в том, что, поскольку мы получаем 40 долларов за каждую перемещаемую единицу, мы должны переместить как можно больше единиц. Если мы переместим 8 единиц, мы получим 40 × 8 = 320 долларов, если мы переместим 9 единиц, мы получим 40 × 9 = 360 долларов, а если мы переместим 16 единиц, мы получим 40 × 16 = 640 долларов. Есть одна очень большая проблема с однако такая цепочка рассуждений. Если мы переместимся больше, чем на 8, мы покинем достижимую область. Следовательно, мы должны переместиться на наименьшее возможное расстояние, чтобы остаться в допустимой области.
Сводная строка — это строка с наименьшим неотрицательным отношением. Если не удается найти неотрицательных отношений, останавливайтесь, задача не имеет решения.
Если одно из соотношений равно 0, это считается неотрицательным значением. Используй это.
Поместите стрелку рядом с наименьшим соотношением, чтобы указать основную строку.
| Базовый | х 1 | x 2 | с 1 | с 2 | с 3 | Р | справа | отношение | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| с 1 | 1 | 2 | 1 | 0 | 0 | 0 | 16 | 16/1 = 16 | |||
| с 2 | 1 | 1 | 0 | 1 | 0 | 0 | 9 | 9/1 = 9 | |||
| с 3 | 3 | 2 | 0 | 0 | 1 | 0 | 24 | 24/3 = 8 | ← | ||
| Р | -40 | -30 | 0 | 0 | 0 | 1 | 0 | ||||
| ↑ |
Переменная, являющаяся базовой для сводной строки, будет исключена из набора базовых. Ее заменит переменная из сводного столбца, входящая в набор базовых переменных.
Ее заменит переменная из сводного столбца, входящая в набор базовых переменных.
Пересечение опорной строки и опорного столбца называется опорным элементом. Обведите это.
вещей, которые мы можем сказать перед разворотом
Нам известно следующее.
- Целевая функция увеличивается на 40 на каждую единицу, которую мы перемещаем в x 1 направление и мы движемся на 8 единиц. Это означает, что целевая функция увеличится на 40×8 = 320. Поскольку сейчас она равна 0, она станет равной 320.
- Переменная x 1 заменит s 3 в качестве базовой переменной в третьей строке. Остальные строки сохранят свои основные переменные.
- Опорный столбец будет очищен, за исключением опорного элемента, который станет 1.
- Опорная строка не изменится, кроме как путем деления, чтобы сделать опорный элемент равным 1. В этом случае мы разделим все на 3.
- Увеличение x 1 будет 8.
- Графически мы будем в точке G , где x 2 и s 3 — неосновные.

- Столбцы s 1 , s 2 и P останутся очищенными, а их основные строки останутся прежними.
| Базовый | х 1 | x 2 | с 1 | с 2 | с 3 | Р | справа | ||
|---|---|---|---|---|---|---|---|---|---|
| с 1 | 0 | 1 | 0 | 0 | |||||
| с 2 | 0 | 0 | 1 | 0 | |||||
| x 1 | 1 | 2/3 | 0 | 0 | 1/3 | 0 | 8 | ||
| Р | 0 | 0 | 0 | 1 | 320 |
Поворот!
Используйте операции со строками, чтобы очистить сводной столбец. То есть, когда вы закончите, единственной записью в сводном столбце будет элемент в 3-й строке, где был опорный элемент.
То есть, когда вы закончите, единственной записью в сводном столбце будет элемент в 3-й строке, где был опорный элемент.
| Базовый | х 1 | x 2 | с 1 | с 2 | с 3 | Р | справа | ||
|---|---|---|---|---|---|---|---|---|---|
| с 1 | 0 | 4/3 | 1 | 0 | -1/3 | 0 | 8 | ||
| с 2 | 0 | 1/3 | 0 | 1 | -1/3 | 0 | 1 | ||
| х 1 | 1 | 2/3 | 0 | 0 | 1/3 | 0 | 8 | ||
| Р | 0 | -10/3 | 0 | 0 | 40/3 | 1 | 320 |
Интерпретация новой таблицы
На этот раз x 2 и s 3 столбцы не очищаются, поэтому они неосновные и их значение равно 0. x 1 является основным в третьей строке и его значение равно 8. s 1 является основным в первой строке и его значение равно 8. s 2 является основным во второй строке и его значение равно 1.
x 1 является основным в третьей строке и его значение равно 8. s 1 является основным в первой строке и его значение равно 8. s 2 является основным во второй строке и его значение равно 1.
| Базовый | Небазовый |
|---|---|
| x 1 =8, с 1 =8, с 2 =1, P=320 | х 2 =0, с 3 =0 |
Сравните это с таблицей, которую мы имели раньше, и вы увидите, что мы действительно находимся в точке G .
| Пт | х 1 | x 2 | с 1 | с 2 | с 3 | Выполнимо? | P = 40x 1 + 30x 2 |
|---|---|---|---|---|---|---|---|
| Г | 8 | 0 | 8 | 1 | 0 | да | 320 |
Повторение процесса
Пока в нижней строке есть отрицательные значения, значение целевой функции можно увеличить, переместив ее в новую точку.
Если вы посмотрите на целевую функцию, вы заметите, что есть только одно отрицательное значение, -10/3 в столбце x 2 . Это означает, что, двигаясь вверх (в x 2 направление), мы можем увеличить значение целевой функции. Мы будем двигаться от линии x 2 = 0, что означает, что мы будем двигаться вдоль линии s 3 = 0. Где бы мы ни оказались, x 2 займет место этой базовой переменной. Если бы мы двигались в направлении s 3 , это движение навредило бы нам.
Как далеко мы можем двигаться?
- Мы можем перейти к точке J , которая равна (6,3), так что увеличение x 2 будет 3. Эта точка находится на пересечении прямых s 3 = 0 и s 1 = 0, поэтому s 1 станет неосновным и будет заменено на x 2 как основное.
- Мы могли бы перейти к точке I , которая находится в точке (5,6), поэтому увеличение x 2 будет равно 6.
 Эта точка находится на пересечении прямых s 3 = 0 и s 2 = 0, поэтому s 2 станет неосновным и будет заменено на x 2 в качестве основного.
Эта точка находится на пересечении прямых s 3 = 0 и s 2 = 0, поэтому s 2 станет неосновным и будет заменено на x 2 в качестве основного. - Мы могли бы перейти к точке D , которая находится в точке (0,12), так что увеличение x 2 будет 12. Эта точка находится на пересечении линий s 3 = 0 и x 1 = 0, поэтому x 1 станет неосновным и будет заменен на x 2 в качестве основного.
Обратите внимание, что когда мы формируем отношения между неотрицательными элементами в правой части и положительными элементами в основной строке, мы получаем 6 при переходе к s 1 = 0 (точка I ), 3 при переходе к s 2 = 0 (точка J ) и 12 при переходе к x 1 = 0 (точка D ). Мы снова выбираем наименьшее отношение, чтобы оставаться в допустимой области.
| Базовый | х 1 | x 2 | с 1 | с 2 | с 3 | С | справа | отношение | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| с 1 | 0 | 4/3 | 1 | 0 | -1/3 | 0 | 8 | 8/(4/3) = 6 | |||
| с 2 | 0 | 1/3 | 0 | 1 | -1/3 | 0 | 1 | 1/(1/3) = 3 | ← | ||
| x 1 | 1 | 2/3 | 0 | 0 | 1/3 | 0 | 8 | 8/(2/3) = 12 | |||
| Р | 0 | -10/3 | 0 | 0 | 40/3 | 1 | 320 | ||||
| ↑ |
Вещи, которые мы можем сказать перед поворотом
Нам известно следующее.
- Целевая функция увеличивается на 10/3 на каждую единицу, которую мы перемещаем в направлении x 2 , и мы перемещаемся на 3 единицы. Это означает, что целевая функция увеличится на (10/3)×3 = 10. Поскольку сейчас 320, она станет 330.
- Переменная x 2 заменит s 2 в качестве базовой переменной во второй строке. Остальные строки сохранят свои основные переменные.
- Опорный столбец будет очищен, за исключением опорного элемента, который станет 1.
- Опорная строка не изменится, кроме как путем умножения, чтобы сделать опорный элемент равным 1. В этом случае мы умножим все на 3.
- Увеличение x 2 будет 3.
- Графически мы будем в точке J , где s 2 и s 3 неосновные.
- Столбцы s 1 , x 1 и P останутся очищенными, а их основные строки останутся прежними.
| Базовый | х 1 | x 2 | с 1 | с 2 | с 3 | Р | справа | ||
|---|---|---|---|---|---|---|---|---|---|
| с 1 | 0 | 0 | 1 | 0 | |||||
| х 2 | 0 | 1 | 0 | 3 | -1 | 0 | 3 | ||
| x 1 | 1 | 0 | 0 | 0 | |||||
| Р | 0 | 0 | 0 | 1 | 330 |
Шарнир
Хорошо, теперь мы развернёмся и найдём остальную информацию.
| Базовый | х 1 | x 2 | с 1 | с 2 | с 3 | Р | справа | ||
|---|---|---|---|---|---|---|---|---|---|
| с 1 | 0 | 0 | 1 | -4 | 1 | 0 | 4 | ||
| х 2 | 0 | 1 | 0 | 3 | -1 | 0 | 3 | ||
| x 1 | 1 | 0 | 0 | -2 | 1 | 0 | 6 | ||
| Р | 0 | 0 | 0 | 10 | 10 | 1 | 330 |
Интерпретация новой таблицы
На этот раз столбцы s 2 и s 3 не очищаются, поэтому они неосновные и их значение равно 0. x 1 является основным в третьей строке и его значение равно 6. s 1 является основным в первой строке и его значение равно 4. x 2 является основным во второй строке и его значение равно 3.
x 1 является основным в третьей строке и его значение равно 6. s 1 является основным в первой строке и его значение равно 4. x 2 является основным во второй строке и его значение равно 3.
| Базовый | Небазовый |
|---|---|
| х 1 = 6, х 2 = 3, с 1 = 4, Р=330 | с 2 =0, с 3 =0 |
Сравните это с таблицей, которую мы имели ранее, и вы увидите, что мы действительно находимся в точке J .
| Пт | х 1 | x 2 | с 1 | с 2 | с 3 | Выполнимо? | P = 40x 1 + 30x 2 |
|---|---|---|---|---|---|---|---|
| Дж | 6 | 3 | 4 | 0 | 0 | да | 330 |
Готово!
Поскольку в нижней строке нет отрицательных значений, перемещение в другую точку понизит значение целевой функции, а не повысит его. Поскольку мы пытаемся максимизировать значение целевой функции, это было бы контрпродуктивно. Мы останавливаемся, мы закончили.
Поскольку мы пытаемся максимизировать значение целевой функции, это было бы контрпродуктивно. Мы останавливаемся, мы закончили.
Решение
Максимальное значение P равно 330, когда x 1 = 6 и x 2 = 3. Значения резервных переменных: s 1 = 4, s 2 = 0 и s 3 = 0,
Оптимизация: симплексный метод максимизации. | Свапнил Бандгар | Analytics Vidhya
Фото взято из ВикипедииСимплекс-метод — это подход к ручному решению моделей линейного программирования с использованием резервных переменных, таблиц и сводных переменных в качестве средства поиска оптимального решения задачи оптимизации. Линейная программа — это метод достижения наилучшего результата при максимальном или минимальном уравнении с линейными ограничениями. Большинство линейных программ можно решить с помощью онлайн-решателя, такого как MatLab, но симплекс-метод — это метод решения линейных программ вручную. Для решения модели линейного программирования с помощью симплекс-метода необходимо выполнить следующие шаги:
● Стандартная форма
● Введение резервных переменных
● Создание таблицы
● Переменные сводки
● Создание новой таблицы
● Проверка оптимальности методов в вышеуказанные шаги и следует примеру модели линейного программирования, показанной ниже, на протяжении всего документа, чтобы найти оптимальное решение.
Максимизировать:
Чтобы определить Максимум, мы должны выполнить следующие шаги.
Шаги:
- Преобразование всех основных уравнений неравенства путем добавления резервных переменных. Также создайте целевую функцию, равную нулю, переместив все значения в одну сторону.
Уравнения после добавления резервной переменной (u,v,w)
Где u,v,w≥0
2. Симплексная таблица используется для выполнения строковых операций в модели линейного программирования, а также для проверки решения на оптимальность . Таблица состоит из коэффициента, соответствующего переменным линейного ограничения, и коэффициента целевой функции. В таблице ниже выделенная полужирным шрифтом верхняя строка таблицы указывает, что представляет каждый столбец. Следующие две строки представляют коэффициенты переменных линейного ограничения из модели линейного программирования, а последняя строка представляет коэффициенты переменных целевой функции.
Теперь создайте симплексную таблицу, создав коэффициенты всех уравнений субъекта и добавив уравнение объекта внизу.
3. Чтобы рассчитать коэффициент, мы можем выбрать минимальное значение из последней строки и выполнить следующие шаги.
Как идентифицировать столбец Pivot:
В приведенной выше таблице -6 — это наименьшее отрицательное число в последней строке. Это укажет, что столбец z будет содержать сводную переменную, которая выделена желтым цветом.
Как идентифицировать сводную строку:
Сводная переменная используется в операциях со строками, чтобы определить, какая переменная станет значением единицы, и является ключевым фактором при преобразовании значения единицы. Опорную переменную можно определить, посмотрев на нижнюю строку таблицы и индикатор. Предполагая, что решение не является оптимальным, выберите наименьшее отрицательное значение в нижней строке. Одно из значений, лежащих в столбце этого значения, будет опорной переменной. Чтобы найти индикатор, разделите бета-значения линейных ограничений на соответствующие им значения из столбца, содержащего возможную сводную переменную. Пересечение строки с наименьшим неотрицательным показателем и наименьшим отрицательным значением в нижней строке станет опорной переменной.
Пересечение строки с наименьшим неотрицательным показателем и наименьшим отрицательным значением в нижней строке станет опорной переменной.
Разделите сводной столбец на константу в соответствующей строке и определите значения.
Решение отношения дает нам значение (900/1 = 900) для первого ограничения, значение (350/1 = 350) для второго ограничения и значение третьего ограничения (400 /1 = 400) . Поскольку 350 является наименьшим неотрицательным отношением, опорное значение будет во второй строке, выделенной зеленым цветом, а пересечение опорной строки и столбца будет опорным элементом со значением 1, выделенным красным цветом.
Теперь, когда опорная переменная определена, мы можем работать над дальнейшим решением, чтобы оптимизировать ее.
4. Чтобы оптимизировать сводную переменную, ее необходимо преобразовать в единичное значение (значение 1). Так как здесь опорный элемент уже равен 1, нам не нужно делать его единичным значением.
5. После того, как значение единицы было определено, поработайте над формулой, которая сделает другие значения в столбце, содержащем значение единицы, равными нулю. Это связано с тем, что переменная резерва и другое значение переменной могут быть идентифицированы, и решение оптимизируется.
Формулы: R1=R1-R2 , R3=R3-R2 и R4=R4+6R2
Применение приведенных выше формул к нашей симплексной таблице приведет к приведенной ниже таблице.
Получено оптимальное решение, поскольку все значения в нижней строке больше или равны нулю.
Здесь основными переменными являются u, z, w и p.
Неосновными переменными являются x, v и y.
Отсюда мы можем получить значения переменных, как показано ниже:
x=0, y=0, v=0, u=550, w = 50, p = 2100, z = 350.
Теперь, чтобы проверить уравнение,
Максимальное оптимальное значение равно 2100 и находится при (0,0, 350) целевой функции.
Симплекс-метод — это метод определения оптимального значения линейной программы вручную. Метод дает оптимальное решение, удовлетворяющее заданным ограничениям, и дает максимальное значение дзета. Чтобы использовать симплекс-метод, данная модель линейного программирования должна иметь стандартную форму, в которую затем могут быть введены резервные переменные. Используя табличные и сводные переменные, можно найти оптимальное решение.
Метод дает оптимальное решение, удовлетворяющее заданным ограничениям, и дает максимальное значение дзета. Чтобы использовать симплекс-метод, данная модель линейного программирования должна иметь стандартную форму, в которую затем могут быть введены резервные переменные. Используя табличные и сводные переменные, можно найти оптимальное решение.
Базовые переменные — это переменные, которые неотрицательны с точки зрения оптимального решения.
Ограничения представляют собой ряд равенств и неравенств, являющихся набором критериев, которым необходимо удовлетворять при поиске оптимального решения.
Неравенство — это выражение, которое не имеет однозначного решения и отличается символами «больше» или «меньше» вместо традиционного знака равенства.
Линейная программа — это модель, используемая для достижения наилучшего результата при максимальном или минимальном уравнении с линейными ограничениями.
Неосновные переменные — это переменные, равные нулю с точки зрения оптимального решения.
Оптимальное решение модели линейного программирования максимизации — это значения, присвоенные переменным в целевой функции, чтобы получить наибольшее значение дзета. Оптимальное решение существовало бы в угловых точках графика всей модели.
Сводная переменная используется в операциях со строками для определения того, какая переменная станет значением единицы, и является ключевым фактором при преобразовании значения единицы.
Симплекс-метод — это подход к ручному решению моделей линейного программирования с использованием резервных переменных, таблиц и сводных переменных в качестве средства поиска оптимального решения задачи оптимизации.
Симплексная таблица используется для выполнения строковых операций в модели линейного программирования, а также для проверки оптимальности.
Переменные Slack — это дополнительные переменные, которые вводятся в линейные ограничения линейной программы для преобразования их из ограничений неравенства в ограничения равенства.
Стандартная форма является базовым форматом для всех линейных программ перед поиском оптимального решения.
Ссылка: Либретексты, Книга: Блитцер, Математическое мышление | Пирсон.
Симплексный алгоритм — табличный метод
.
|
Симплексный метод - Брайан Вейтч
Симплексный метод - Брайан Вейтчрешить систему неравенств
Описание
Спасибо за проверку моего приложения Row Reduction. Ознакомьтесь с симплексным методом на приложение хранить сейчас!
Посмотрите демонстрационное видео от того, как использовать это приложение.
Особенности:
- Решает стандартное максимальное, стандартное минимальное и нестандартное
- Позволяет вам самостоятельно работать с этим методом
- Предлагает подсказки по запросу
- Отменить операцию, если вы допустили ошибку
Нужно решить задачу линейного программирования? Закончили использовать симплекс-метод, но вы не
получающий
правильный ответ? Один из основных недостатков симплекс-метода заключается в том, что вы должны отслеживать
а
страница, полная утомительных вычислений И выберите правильные операции со строками. Когда вы впервые узнаете
это
технику трудно сделать и то, и другое правильно.
Когда вы впервые узнаете
это
технику трудно сделать и то, и другое правильно.
Симплекс-метод включает в себя использование последовательности «Если/Тогда», которая приводит вас к начальному Симплексному методу. Стол. Это приложение проведет вас через настройку и создаст исходную таблицу. Оттуда вы можете либо использовать метод самостоятельно или он поможет вам с помощью подсказок. Выберите операцию, и приложение создать новую таблицу для вас. Вы можете сосредоточиться исключительно на практике и экспериментировании.
Что делать, если вы делаете всю эту рукописную работу и все еще не можете получить ответ?
Вы также можете приобрести обновление Instant Solution. Введите систему уравнений и нажмите
РЕШЕНИЕ. Он сгенерирует все правильные операции со строками и таблицы и отобразит их все в
однажды. Теперь вы можете продолжить и попытаться найти свою ошибку.
Теперь вы можете продолжить и попытаться найти свою ошибку.
Счастливого обучения
Симплексный метод
Подборка скриншотов
Навыки и умения
Что я выучил...
Мое второе приложение!
Приложение симплексного метода было продолжением приложения Row
Приложение «Уменьшение».
Структура и поток были идентичными, поэтому я смог повторно использовать большую часть сокращения строк.
код. я написал это
app таким образом, чтобы я мог повторно использовать большую часть кода. Вот чему я научился... писать код
в таком случае
чтобы его можно было использовать в других проектах.
Что было сложно
Разница между приложением Row Reduction и Приложение «Симплексный метод» писал код для подсказок. Симплекс-метод достаточно сложно объяснить, и даже сложнее кодировать. Я узнал, что составление подробной блок-схемы метода помогло мне создать классы, методы и т.д. В основном Я узнал, что вы действительно должны планировать заранее.
Что я мог бы сделать лучше
Теперь, когда я узнал больше, я хотел бы вернуться и переделать это приложение. Я хочу очистить
классы, работающие с симплексным алгоритмом. Опция мгновенного решения распечатывает каждый
шаг
алгоритма. Мне пришлось создавать подпредставления программно. И я уверен, что смогу это сделать
очиститель
и более эффективным.
Политика конфиденциальности
В основном... я не собираю данные
Файлы cookie
Файлы cookie — это файлы с небольшим объемом данных, которые обычно используются как анонимные уникальные идентификаторы. Они отправляются в ваш браузер с веб-сайтов, которые вы посещаете, и хранятся во внутренней памяти вашего устройства.
Эта Служба не использует эти файлы cookie в явном виде. Однако приложение может использовать сторонние
код и библиотеки, которые используют файлы cookie для сбора информации и улучшения своих услуг.
У вас есть возможность либо принять, либо отказаться от этих файлов cookie и узнать, когда файл cookie
отправляются на ваше устройство. Если вы решите отказаться от наших файлов cookie, вы не сможете использовать
некоторые части этой Услуги.
Поставщики услуг
Я могу нанимать сторонние компании и частных лиц по следующим причинам:
Для облегчения нашего Сервиса; Для предоставления Сервиса от нашего имени; Для оказания услуг, связанных с Сервисом; или же Чтобы помочь нам проанализировать, как используется наш Сервис. Я хочу сообщить пользователям этого Сервиса, что эти третьи лица имеют доступ к вашим Персональные данные. Причина в том, чтобы выполнять возложенные на них задачи от нашего имени. Однако они обязаны не разглашать и не использовать информацию для каких-либо других целей.
Безопасность
Я ценю ваше доверие в предоставлении нам вашей личной информации, поэтому мы стремимся использовать
коммерчески приемлемые средства защиты. Но помните, что ни один метод
передача через Интернет или метод электронного хранения на 100% безопасен и
надежным, и я не могу гарантировать его абсолютную безопасность.
Но помните, что ни один метод
передача через Интернет или метод электронного хранения на 100% безопасен и
надежным, и я не могу гарантировать его абсолютную безопасность.
Ссылки на другие сайты
Эта служба может содержать ссылки на другие сайты. Если вы нажмете на стороннюю ссылку, вы быть направлены на этот сайт. Обратите внимание, что эти внешние сайты не управляются мной. Поэтому я настоятельно рекомендую вам ознакомиться с Политикой конфиденциальности этих веб-сайтов. У меня нет контролировать и не нести ответственности за содержание, политику конфиденциальности или практику любых сторонних сайтов или сервисов.
Конфиденциальность детей
Эти Услуги не предназначены для лиц моложе 13 лет. Я не собираю намеренно
личную информацию от детей младше 13 лет. В случае, если я узнаю, что
ребенок младше 13 лет предоставил мне личную информацию, я немедленно удаляю ее из
наши серверы. Если вы являетесь родителем или опекуном и знаете, что у вашего ребенка
предоставил нам личную информацию, пожалуйста, свяжитесь со мной, чтобы я мог сделать
необходимые действия.
В случае, если я узнаю, что
ребенок младше 13 лет предоставил мне личную информацию, я немедленно удаляю ее из
наши серверы. Если вы являетесь родителем или опекуном и знаете, что у вашего ребенка
предоставил нам личную информацию, пожалуйста, свяжитесь со мной, чтобы я мог сделать
необходимые действия.
Изменения в настоящей Политике конфиденциальности
Я могу время от времени обновлять нашу Политику конфиденциальности. Таким образом, вам рекомендуется просмотреть эту страницу периодически на любые изменения. Я сообщу вам о любых изменениях, опубликовав новую Политику конфиденциальности. Политика на этой странице. Эти изменения вступают в силу сразу после их публикации на этом сайте. страница.
Свяжитесь с нами
Если у вас есть какие-либо вопросы или предложения относительно моей Политики конфиденциальности, не стесняйтесь обращаться к нам
мне на jankyapps@gmail.



 index(max(l)) # Номер перевода
m = []
for i in range(bn):
if d[i][jnum] == 0:
m.append(0.)
else:
m.append(d[i][-1]/d[i][jnum])
inum = m.index(min([x for x in m[1:] if x!=0])) # Перенести нижний индекс
s[inum-1] = jnum
r = d[inum][jnum]
d[inum] /= r
for i in [x for x in range(bn) if x !=inum]:
r = d[i][jnum]
d[i] -= r * d[inum]
def solve(d,bn):
flag = True
while flag:
if max(list(d[0][:-1])) <= 0: # Пока все коэффициенты не будут меньше или равны 0
flag = False
else:
pivot(d,bn)
def printSol(d,cn):
for i in range(cn - 1):
if i in s:
print("x"+str(i)+"=%.2f" % d[s.index(i)+1][-1])
else:
print("x"+str(i)+"=0.00")
print("objective is %.2f"%(-d[0][-1]))
d = np.loadtxt("./data.txt", dtype=np.float)
(bn,cn) = d.shape
s = list(range(cn-bn,cn-1)) # Базовый список переменных
solve(d,bn)
printSol(d,cn)
index(max(l)) # Номер перевода
m = []
for i in range(bn):
if d[i][jnum] == 0:
m.append(0.)
else:
m.append(d[i][-1]/d[i][jnum])
inum = m.index(min([x for x in m[1:] if x!=0])) # Перенести нижний индекс
s[inum-1] = jnum
r = d[inum][jnum]
d[inum] /= r
for i in [x for x in range(bn) if x !=inum]:
r = d[i][jnum]
d[i] -= r * d[inum]
def solve(d,bn):
flag = True
while flag:
if max(list(d[0][:-1])) <= 0: # Пока все коэффициенты не будут меньше или равны 0
flag = False
else:
pivot(d,bn)
def printSol(d,cn):
for i in range(cn - 1):
if i in s:
print("x"+str(i)+"=%.2f" % d[s.index(i)+1][-1])
else:
print("x"+str(i)+"=0.00")
print("objective is %.2f"%(-d[0][-1]))
d = np.loadtxt("./data.txt", dtype=np.float)
(bn,cn) = d.shape
s = list(range(cn-bn,cn-1)) # Базовый список переменных
solve(d,bn)
printSol(d,cn)
 1,0.9,0.1, 0.9,0.1,0.9) #x1min, x1max, x2min, x2max
cons = con(args1)
# Установить первоначальное предположение
x0 = np.asarray((0.5,0.5,0.5))
res = minimize(fun(args), x0, method='SLSQP',constraints=cons)
print(res.fun)
print(res.success)
print(res.x)
1,0.9,0.1, 0.9,0.1,0.9) #x1min, x1max, x2min, x2max
cons = con(args1)
# Установить первоначальное предположение
x0 = np.asarray((0.5,0.5,0.5))
res = minimize(fun(args), x0, method='SLSQP',constraints=cons)
print(res.fun)
print(res.success)
print(res.x)