Площадь четырехугольника
Главная
→
Геометрия
→
Площадь четырехугольника
Площадь произвольного четырехугольника, формулы и калькулятор для вычисления в режиме онлайн. Для вычисления площади произвольного четырехугольника применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь произвольного четырехугольника или проверить уже выполненные вычисления.
В окончании статьи приведены ссылки для вычисления частных случаев четырехугольников: квадрата, трапеции, параллелограмма, прямоугольника, ромба.
Таблица с формулами площади четырехугольника (в конце страницы)
— Вычисления (показано) (скрыто)
— примечания (показано) (скрыто)
1
Площадь четырехугольника по диагоналям и углу между ними
. .. подготовка …
.. подготовка …
d
d2 — диагональ
α° — угол между диагоналями
2
Площадь четырехугольника через стороны и углы между этими сторонами
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
… подготовка …
a — сторона
b — сторона
c — сторона
d — сторона
α° — угол между сторонами
β° — угол между сторонами
3
Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты
Данная формула справедлива только для четырехугольников, вокруг которых можно описать окружность.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
.
a — сторона
b — сторона
c — сторона
d — сторона
4
Площадь четырехугольника в который можно вписать окружность
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
… подготовка …
a — сторона
b — сторона
c — сторона
d — сторона
r — радиус вписанной окружности
5
Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
… подготовка …
a — сторона
b — сторона
c — сторона
d — сторона
α° — угол между сторонами
β° — угол между сторонами
Примечание:
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади четырехугольника
| исходные данные (активная ссылка для перехода к калькулятору) | эскиз | формула | |
| 1 | диагональ и угол между ними | ||
| 2 | стороны и углы между этими сторонами | где , | |
| 3 | стороны (по Формуле Брахмагупты) | где | |
| 4 | стороны и радиус вписанной окружности | где | |
| 5 | стороны и углы между ними |
Площадь частных случаев четырехугольников
Для вычисления частных случаев четырехугольников можно воспользоваться формулами и калькуляторами, приведенными в других статьях сайта:
- площадь квадрата
- площадь трапеции
- площадь параллелограмма
- площадь прямоугольника
- площадь ромба
Определения
Четырехугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками.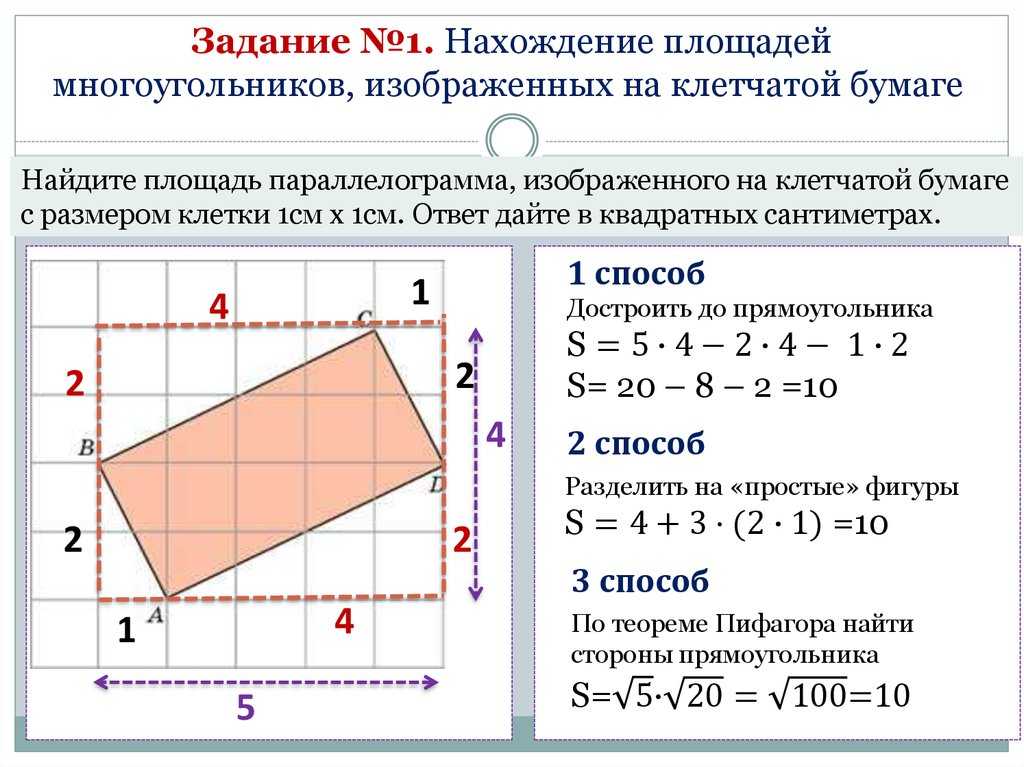
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь четырехугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
Как найти площадь прямоугольника – 9 формул с лайфхаками и примерами
Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.
Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.
По диагонали и стороне
Должна быть известна диагональ и любая из сторон. Действия:
- Найти квадрат диагонали, то есть умножить ее на саму себя.

- Найти квадрат известной стороны.
- Из квадрата диагонали вычесть квадрат стороны.
- Найти квадратный корень получившейся разности.
- Умножить его на известную сторону.
Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.
- Квадрат стороны = 3*3 = 9 см.
- Квадрат диагонали = 5*5 = 25 см.
- Вычитаю из квадрата диагонали квадрат стороны: 25-9 = 16 см.
- Нахожу квадратный корень получившейся разности. Корень из 16 = 4 см.
- Умножаю корень разности на известную сторону: 16*9 = 144 см.
Ответ: 144 см.
Обратите внимание
Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.
По стороне и диаметру описанной окружности
Вокруг любого прямоугольника можно описать окружность.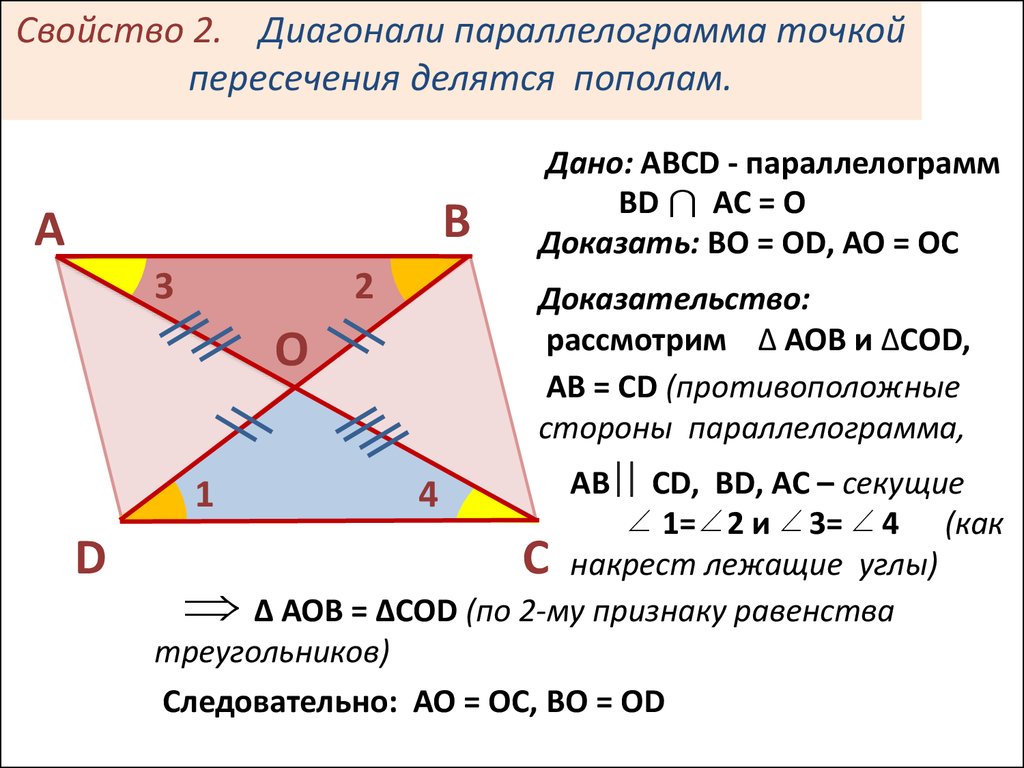 Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.
Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.
Действия:
- Найдите квадрат диаметра – умножьте диаметр на диаметр.
- Найдите квадрат известной стороны.
- Отнимите от квадрата диаметра квадрат стороны.
- Найдите квадратный корень разности.
- Умножьте квадратный корень на известную сторону.
Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.
- Квадрат диаметра: 10*10 = 100 см.
- Квадрат стороны: 8*8 = 64 см.
- Отнимаю от квадрата диаметра квадрат стороны: 100-64 = 36 см.
- Квадратный корень из 36 равен 6 см (потому что 6*6 = 36).
- Умножаю сторону на корень из разности: 8*6 = 48 см.
Ответ: 48 см.
Лайфхак
Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:
А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.
Диаметр равен двум радиусам, потому что радиус – это половина диаметра.
По радиусу описанной окружности и стороне
Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.
Другой способ:
- Найти квадрат радиуса (умножьте радиус на радиус).
- Умножить квадрат радиуса на 4.
- Найти квадрат известной стороны.
- Отнять от четырех радиусов в квадрате квадрат известной стороны (из второго отнять третье).
- Найти квадратный корень разности.
- Умножить корень на известную сторону.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.
- Квадрат радиуса: 5*5=25 см.
- Четыре квадрата радиуса: 4*25 = 100 см.
- Квадрат стороны: 6*6 = 36 см.
- Отнимаю от четырех радиусов в квадрате квадрат стороны: 100-36 = 64 см.
- Нахожу квадратный корень разности. Корень из 64 равен 8 см.

- Умножаю корень на сторону: 8*6 = 48 см.
Ответ: 48 см.
Помните
Радиус = половине диаметра.
Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.
По стороне и периметру – 1 способ
Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).
Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.
Пример. Периметр прямоугольника равен 14 см, а одна из сторон равна 3 см. Найдите площадь.
- Нахожу вторую сторону прямоугольника:
- P=2(a+b).
- P=2a+2b.
- 14= 2*3+2b.
- 14 = 6+2b.
- 2b = 14-6 = 8.
- b = 8/2.
- b = 4.
- Нахожу площадь по основной формуле. S = 3*4 = 12 см.
Ответ: 12 см.
По стороне и периметру – 2 способ
Действия такие:
- Умножьте периметр на сторону.

- Найдите квадрат стороны.
- Умножьте квадрат стороны на 2.
- Отнимите от произведения периметра и стороны два квадрата стороны (от первого отнимите третье).
- Поделите на 2.
Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.
- Умножаю периметр на сторону: 8*28 = 224 см.
- Нахожу квадрат стороны: 8*8 = 64 см.
- Умножаю квадрат стороны на два: 64*2 = 84 см.
- Отнимаю из первого третье: 224-84 = 140 см.
- Делю разность на два: 140/2 = 70 см.
Ответ: 70 см.
По диагонали и углу между диагоналями
Диагонали прямоугольника всегда равны.
Действия:
- Найти квадрат диагонали (умножить диагональ на саму себя).
- Найти половину этого квадрата – умножить его на 0,5.
- Найти синус угла между диагоналями.
- Умножить половину квадрата диагонали на синус угла между диагоналями.
Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.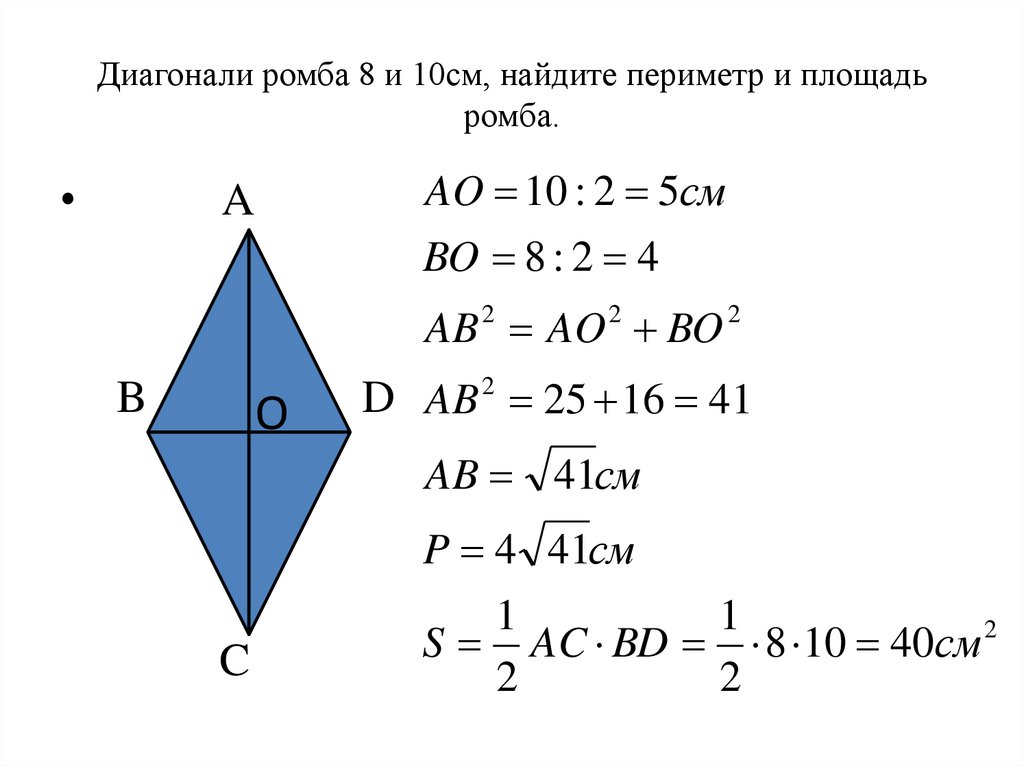
- Квадрат диагонали: 10*10 = 100 см.
- Половина этого квадрата: 0,5*100 = 50 см.
- Синус угла между диагоналями: sin 30 градусов = 0,5.
- Перемножаю половину квадрата и синус угла, чтобы найти площадь: 50*0,5 = 25 см.
Ответ: 25 см.
Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).
По радиусу описанной окружности и углу между диагоналями – первый способ
Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.
- Находим длину диагонали: 6*2 =12 см.
- Квадрат диагонали равен 144 см.
- Половина квадрата: 72 см.
- Синус 30 градусов равен 0,5.
- Умножаем половину квадрата на синус: 72*0,5 = 36 см.

Ответ: 36 см.
По радиусу описанной окружности и углу между диагоналями – второй способ
Действия:
- Найти квадрат радиуса (умножить радиус на радиус).
- Умножить квадрат радиуса на два.
- Найти синус угла между диагоналями.
- Умножить синус угла на два радиуса в квадрате.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.
- Квадрат радиуса: 6*6 = 36.
- Два радиуса в квадрате: 36*2 = 72.
- Синус 30 градусов равен 0,5.
- Произведение синуса и двух радиусов в квадрате: 72*0,5 = 36 см.
Ответ: 36 см.
Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.
ЕЖЕНЕДЕЛЬНАЯ РАССЫЛКА
Получайте самые интересные статьи по почте и подписывайтесь на наши социальные сети
ПОДПИСАТЬСЯВаш браузер устарел рекомендуем обновить его до последней версии
или использовать другой более современный.
порядок ее нахождения, свойства фигуры и пример решения
Геометрия
12.11.21
14 мин.
В геометрии при решении задач иногда требуется найти площадь прямоугольника через диагонали. Формула и ее применение позволяют вычислить эту величину. Однако с самого начала фигуру требуется идентифицировать, руководствуясь определенными признаками. Кроме того, полезно будет знать основные свойства и соотношения для расчета других параметров (периметра, сторон и т. д.).
Оглавление:
- Общие сведения
- Информация о фигуре
- Соотношения для вычислений
- Пример задания
В геометрии при решении задач иногда требуется найти площадь прямоугольника через диагонали. Формула и ее применение позволяют вычислить эту величину. Однако с самого начала фигуру требуется идентифицировать, руководствуясь определенными признаками. Кроме того, полезно будет знать основные свойства и соотношения для расчета других параметров (периметра, сторон и т.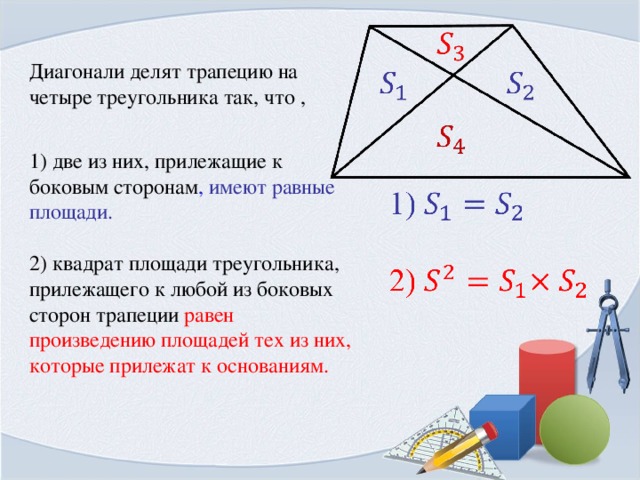 д.).
д.).
Общие сведения
В геометрии, как и во всех дисциплинах с физико-математическим уклоном, существует взаимосвязь между параметрами. Например, базовая формула площади прямоугольника зависит от длин его противоположных сторон. Впервые ее используют в пятом классе для решения простейших задач.
Однако на начальном уровне дается название фигуры, т. е. прямоугольник или квадрат. В старших классах встречаются задачи на идентификацию последних. На основании исследования принадлежности четырехугольника к определенному виду требуется вычислить некоторые его параметры. Если фигура определена неверно, расчеты будут выполнены некорректно.
Навык решения задач по геометрии необходим не только на вступительных экзаменах, тестировании и зачетах, но и для выполнения ремонта. Например, для комнаты прямоугольной формы нужно купить плитку и обои. Для этого необходимо вычислить площадь и правильно идентифицировать форму основания, т. е. пола или стены.
Однако перед рассмотрением признаков, свойств и формул, которые нужны для нахождения параметров фигуры, следует ознакомиться с теорией, дающей общее представление о прямоугольнике.
Четырехугольник, состоящий из равных и параллельных между собой противоположных сторон, которые образуют прямые углы, называется прямоугольником. Обозначается он четырьмя литерами — именами вершин. Например, UVWX. Специалисты рекомендуют соблюдать очередность в алфавитном порядке, поскольку в высших учебных заведениях преподавательский состав это требует от студентов.
Многие учащиеся делают ошибку, используя в качестве идентификации фигуры определение. Для примера следует рассмотреть квадрат и прямоугольник. У первого противолежащие стороны параллельны и будут равняться одному значению, а углы, образованные ими, равны 90 градусов. Признаки фигур позволяют точно классифицировать вид четырехугольника, а затем применить к нему соответствующие соотношения.
Признаки прямоугольника
Признак или идентификация — набор критериев, на основании которых четырехугольник можно отнести к определенному типу.
- Обозначить прямоугольник — UVWX. У него ∠U=∠V=∠W=90.
- На основании утверждения о сумме внутренних углов найти ∠Х: ∠Х = 360-90-90-90=90.
- Утверждение доказано.
Однако математики вывели 3 признака, которые помогут отличить прямоугольник от квадрата. К ним относятся:
- Смежные стороны не равны между собой.
- Диагонали при пересечении не образуют прямые углы.
- В прямоугольник невозможно вписать окружность, поскольку он не является правильным четырехугольником.
Первый признак строится из определения самой фигуры. Доказывается это очень просто. Следует начертить прямоугольник и обозначить его UVWX. Он состоит из следующих сторон: первая пара противоположных — UV=WX и вторая — VW=UX.
Диагонали в квадрате и прямоугольнике равны между собой. В этом случае для вычисления такого параметра, как площадь, можно брать любую диагональ (UW и VX). Основное отличие свойства пересечения последних — в квадрате они образуют прямой угол.
Если рассмотреть последний признак, нужно учесть, что окружность можно вписать только в правильные фигуры, т. е. их стороны должны быть эквивалентны между собой. Так можно легко идентифицировать прямоугольник. Однако требуется рассмотреть его основные свойства, которые могут быть полезными при решении задач по геометрии.
Основные свойства
Прямоугольник обладает такими же свойствами, что и квадрат. Однако есть некоторые отличия, состоящие из доказанных математиками утверждений и соотношений. Например, возможно найти площадь прямоугольника, зная диагонали. К свойствам можно отнести:
Например, возможно найти площадь прямоугольника, зная диагонали. К свойствам можно отнести:
- Вершины фигуры — основания прямых внутренних углов, сумма которых составляет 360 градусов.
- Равенство и параллельность взаимно противоположных сторон.
- Центр симметрии и окружности — точка пересечения диагоналей, которая делит их пополам. Кроме того, через нее можно провести среднюю линию.
- Подобие и равенство всех треугольников, которые образуются в результате пересечения его диагоналей.
Вычисление диагонали (UW=q) через известные смежные стороны (UV=u и VW=v). q 2 = u 2 + v 2.
- Диагональ — диаметр описанной окружности, D = q.
- Если диагонали пересекаются, образуются большие прямоугольные и малые равнобедренные треугольники.
- Медиана и высота, которые проведены из любой вершины, равны половине q.
- Диагональ не является биссектрисой.
Этих свойств недостаточно при решении задач.
В этом случае могут пригодиться формулы.
Соотношения для вычислений
В геометрии для удобства решения задач и описания формул применяются сокращенные записи. Пусть прямоугольник обозначается литерами UVWX. Его стороны — UV=u и VW=v, а диагонали — q. Все углы при вершинах эквивалентны 90 градусам. Если рассматривать градусные меры ∠, образованных пересечением двух диагоналей q, острый — w, а тупой — z. Кроме того, вокруг фигуры можно описать окружность с радиусом (R) и диаметром (D).
Начинающие математики часто путают ∠w и ∠z, подставляя в формулу площади через диагональ, размерность не того ∠. У прямоугольника существуют следующие параметры, являющиеся дополнительными: площадь (обозначается литерой «S» и является его размерностью) и периметр «P» (алгебраическая сумма длин 4 сторон).
Нахождение размерности и периметра
Базовое соотношение, по которому возможно вычислить периметр, имеет следующий вид: P=2u+2v. (0.5)=54,64 (м).
(0.5)=54,64 (м).
Задача любого типа должна решаться с минимальных количеством формул и вычислений. Алгоритм ее решения должен быть оптимален.
Таким образом, нахождение площади прямоугольника через диагональ позволяет существенно сократить объемы вычислений и время, потраченное на решение этой задачи.
Площадь прямоугольника формула 4. Как посчитать площадь прямоугольника: практические советы
Площадь прямоугольника, как не будет дерзко звучать, но это важное понятие. В повседневной жизни мы постоянно сталкиваемся с ним. Узнать размер полей, огородов, рассчитать количество краски, необходимой для побелки потолка, сколько понадобится обоев для оклейки ко
мнаты и другое.
Геометрическая фигура
Для начала поговорим о прямоугольнике. Это фигура на плоскости, которая имеет четыре прямых угла, а ее противоположные стороны равны. Стороны его привыкли называть длиной и шириной. Измеряют их в миллиметрах, сантиметрах, дециметрах, метрах и т. д. Теперь ответим на вопрос: «Как найти площадь прямоугольника?» Для этого необходимо длину умножить на ширину.
Измеряют их в миллиметрах, сантиметрах, дециметрах, метрах и т. д. Теперь ответим на вопрос: «Как найти площадь прямоугольника?» Для этого необходимо длину умножить на ширину.
Площадь=длина*ширина
Но еще одна оговорка: длина и ширина должны быть выражены в одинаковых единицах измерения, то есть метр и метр, а не метр и сантиметр. Записывается площадь латинской буквой S. Для удобства обозначим длину латинской буквой b, а ширину латинской буквой a, как показано на рисунке. Отсюда мы делаем вывод, что единицей измерения площади является мм 2 , см 2 , м 2 и т. д.
Рассмотрим на конкретном примере, как найти площадь прямоугольника. Длина b=10 ед. Ширина a=6 ед. Решение: S=a*b, S=10 ед.*6 ед., S=60 ед 2 . Задача. Как узнать площадь прямоугольника, если длина в 2 раза больше ширины и составляет 18 м? Решение: если b=18 м, тогда а=b/2, a=9 м. Как найти площадь прямоугольника, если известны обе стороны? Правильно, подставить в формулу. S=a*b, S=18*9, S=162 м 2 . Ответ: 162 м 2 . Задача. Сколько необходимо купить рулонов обоев для комнаты, если ее размеры составляют: длина 5,5 м ширина 3,5, а высота 3 м? Размеры рулона обоев: длина 10 м, ширина 50 см. Решение: сделаем рисунок комнаты.
Задача. Сколько необходимо купить рулонов обоев для комнаты, если ее размеры составляют: длина 5,5 м ширина 3,5, а высота 3 м? Размеры рулона обоев: длина 10 м, ширина 50 см. Решение: сделаем рисунок комнаты.
Площади противоположных сторон равны. Вычислим площадь стены с размерами 5,5 м и 3 м. S стены 1 =5,5*3,
S стены 1 =16,5 м 2 . Следовательно, противоположная стена имеет площадь равную 16,5 м 2 . Найдем площади следующих двух стен. Стороны их, соответственно, равны 3,5 м и 3 м. S стены 2 =3,5*3, S стены 2 =10,5 м 2 . Значит, и противоположная сторона равна 10,5 м 2 . Сложим все результаты. 16,5+16,5+10,5+10,5=54 м 2 . Как вычислить площадь прямоугольника, если стороны выражены в разных единицах измерения. Ранее мы вычисляли площади в м 2 , то и в этом случае будем использовать метры. Тогда ширина рулона обоев будет равна 0,5 м. S рулона =10*0,5, S рулона =5 м 2 . Теперь узнаем, сколько рулонов необходимо для оклейки комнаты. 54:5=10,8 (рулонов). Так как они измеряются целыми числами, то нужно купить 11 рулонов обоев.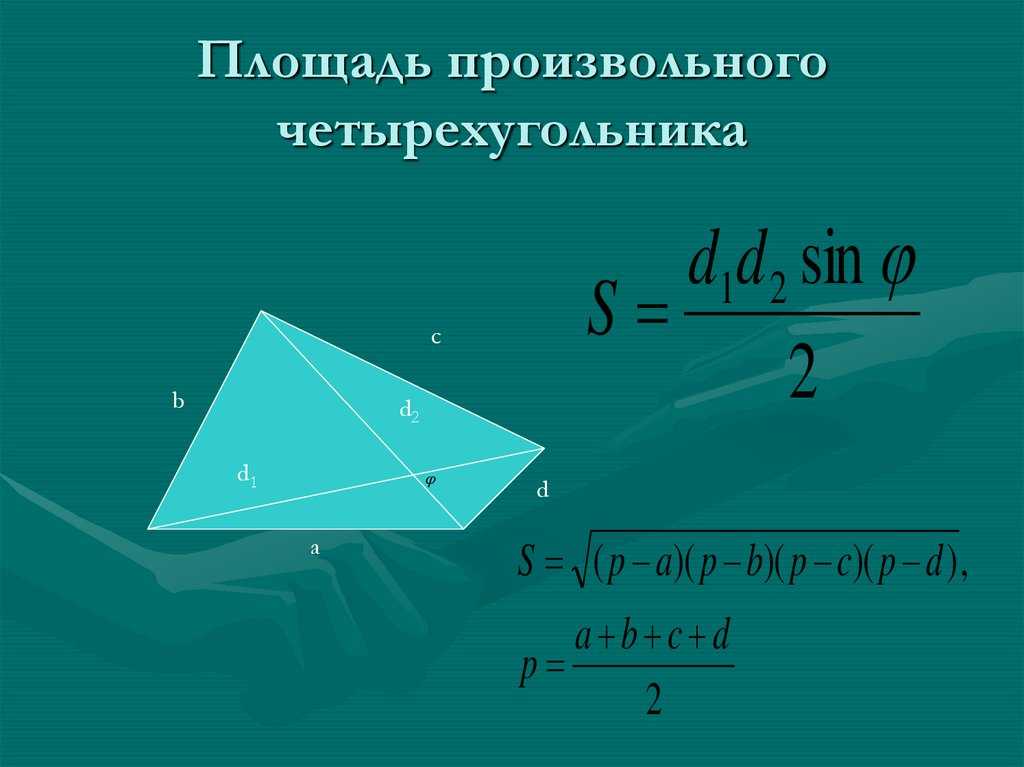 Ответ: 11 рулонов обоев. Задача. Как вычислить площадь прямоугольника, если известно, что ширина на 3 см короче длины, а сумма сторон прямоугольника составляет 14 см? Решение: пусть длина х см, тогда ширина (х-3) см. х+(х-3)+х+(х-3)=14, 4х-6=14, 4х=20, х=5 см — длина прямоугольника, 5-3=2 см — ширина прямоугольника, S=5*2, S=10 см 2 Ответ: 10 см 2 .
Ответ: 11 рулонов обоев. Задача. Как вычислить площадь прямоугольника, если известно, что ширина на 3 см короче длины, а сумма сторон прямоугольника составляет 14 см? Решение: пусть длина х см, тогда ширина (х-3) см. х+(х-3)+х+(х-3)=14, 4х-6=14, 4х=20, х=5 см — длина прямоугольника, 5-3=2 см — ширина прямоугольника, S=5*2, S=10 см 2 Ответ: 10 см 2 .
Резюме
Рассмотрев примеры, надеюсь, стало понятно, как найти площадь прямоугольника. Напомню, что единицы измерения длины и ширины должны совпадать, иначе получится неправильный результат, чтобы не допустить ошибок, читайте задание внимательно. Иногда сторона может быть выражена через другую сторону, не стоит бояться. Обратитесь к нашим решенным задачам, вполне возможно, они могут помочь. Но хоть раз в жизни мы сталкиваемся с нахождением площади прямоугольника.
Инструкция
Например, вам , что длина одной из сторон (а) равна 7 см, а периметр прямоугольника (P) равен 20 см. Так как периметр любой фигуры равен сумме длин ее сторон, а у прямоугольника противоположные стороны равны, то его периметр а будет выглядеть следующим образом: P = 2 x (a + b), или P = 2a + 2b.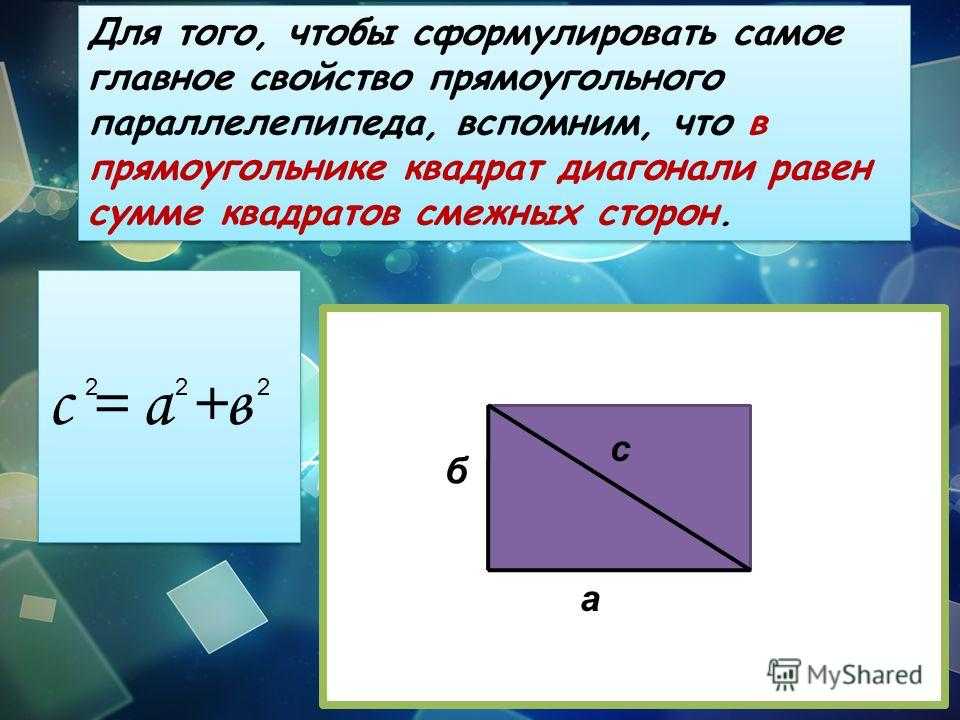 Из этой формулы следует, что найти длину второй стороны (b) можно с помощью несложной операции: b = (P – 2a) : 2. Так, в нашем случае сторона b будет равна (20 – 2 х 7) : 2 = 3 см.
Из этой формулы следует, что найти длину второй стороны (b) можно с помощью несложной операции: b = (P – 2a) : 2. Так, в нашем случае сторона b будет равна (20 – 2 х 7) : 2 = 3 см.
Теперь, зная длины обеих смежных сторон (a и b), вы сможете подставить их в формулу площади S = ab. В данном случае прямоугольника будет равна 7х3 = 21. Обратите на то, что единицами измерения будут уже не , а сантиметры квадратные, так как длин двух сторон единицы их измерения (сантиметры) вы тоже умножали друг на друга.
Источники:
- как находится периметр прямоугольника
Плоская фигура, состоящая из четырех сторон и четырех прямых углов. Из всех фигур площадь прямоугольника приходится вычислять чаще других. Это и площадь квартиры, и площадь садового участка, и площадь поверхности стола или полки. Например, чтобы просто оклеить комнату обоями, вычисляют площадь ее прямоугольных стен.
Инструкция
Кстати, из прямоугольника можно легко вычислить площадь .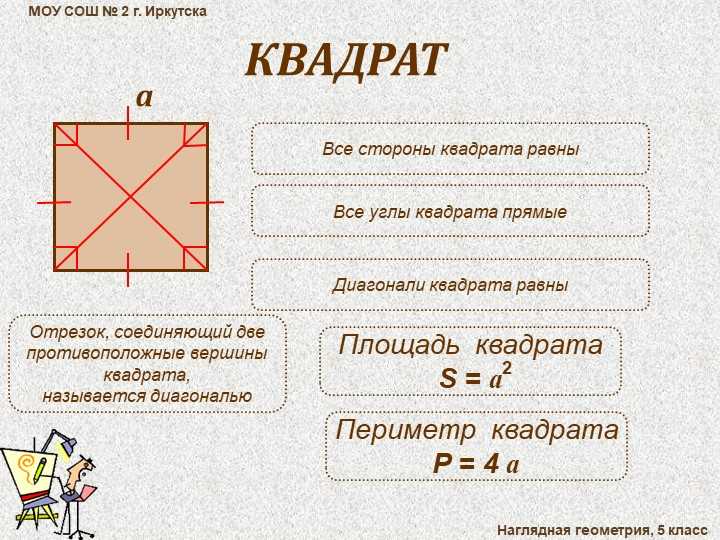 Достаточно достроить прямоугольный до прямоугольника так, чтобы гипотенуза стала диагональю прямоугольника . Тогда будет очевидно, что площадь такого прямоугольника равна произведению катетов треугольника, а площадь самого треугольника, соответственно, равна половине произведения катетов.
Достаточно достроить прямоугольный до прямоугольника так, чтобы гипотенуза стала диагональю прямоугольника . Тогда будет очевидно, что площадь такого прямоугольника равна произведению катетов треугольника, а площадь самого треугольника, соответственно, равна половине произведения катетов.
Видео по теме
Частный случай параллелограмма — прямоугольник – известен только в геометрии Евклида. У прямоугольника равны все углы, и каждый из них по отдельности составляет 90 градусов. Исходя из частных свойств прямоугольника , а также из свойств параллелограмма о параллельности противолежащих сторон можно найти стороны фигуры по заданным диагоналям и углу от их пересечения. Вычисление сторон прямоугольника основывается на дополнительных построениях и применении свойств получаемых фигур.
Инструкция
Буквой А отметьте точку пересечения диагоналей. Рассмотрите образованный построениями EFА. Согласно свойству прямоугольника его диагонали равны и пополам точкой пересечения А.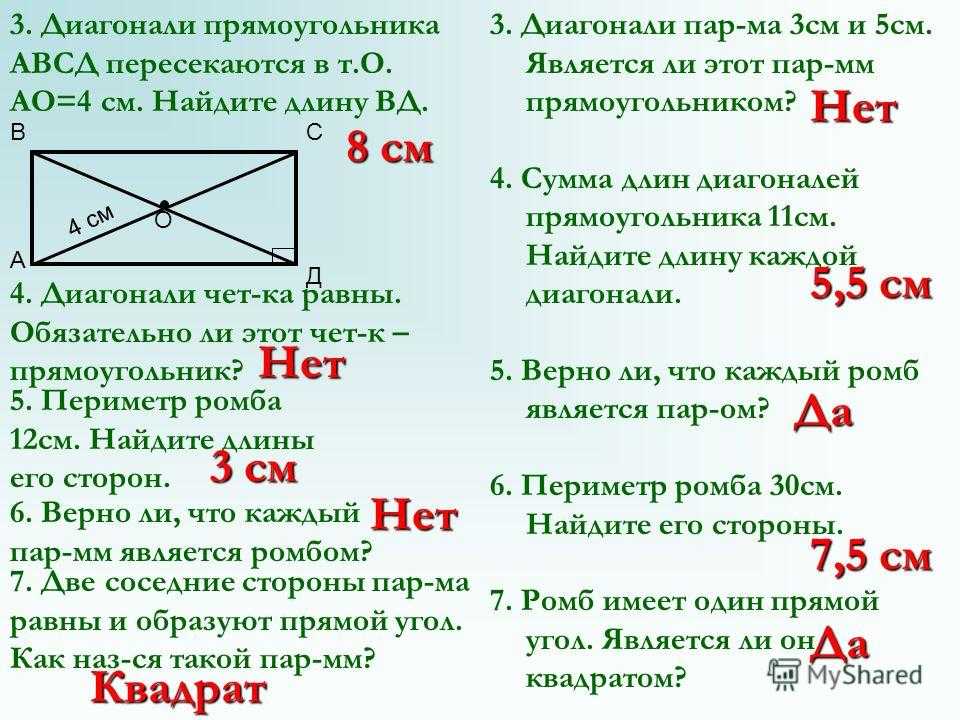 Вычислите значения FА и EА. Так как треугольник EFА равнобедренным и его стороны EА и FА равны между собой и соответственно равны половине диагонали EG.
Вычислите значения FА и EА. Так как треугольник EFА равнобедренным и его стороны EА и FА равны между собой и соответственно равны половине диагонали EG.
Далее вычислите первую EF прямоугольника . Данная сторона является третьей неизвестной стороной рассматриваемого треугольника EFА. Согласно теореме косинусов по соответствующей формуле найдите сторону EF. Для этого подставьте в формулу косинусов полученные ранее значения сторон FА EА и косинус известного угла между ними α. Вычислите и запишите полученное значение EF.
Найдите вторую сторону прямоугольника FG. Для этого рассмотрите другой треугольник EFG. Он является прямоугольным, где известны гипотенуза EG и катет EF. Согласно теореме Пифагора найдите второй катет FG по соответствующей формуле.
Относится к простейшим плоским геометрическим фигурам и является одним из частных случаев параллелограмма. Отличительная черта такого параллелограмма — прямые углы во всех четырех вершинах. Ограниченную сторонами прямоугольника площадь можно вычислить несколькими способами, используя размеры его сторон, диагонали и углы между ними, радиус вписанной окружности и т.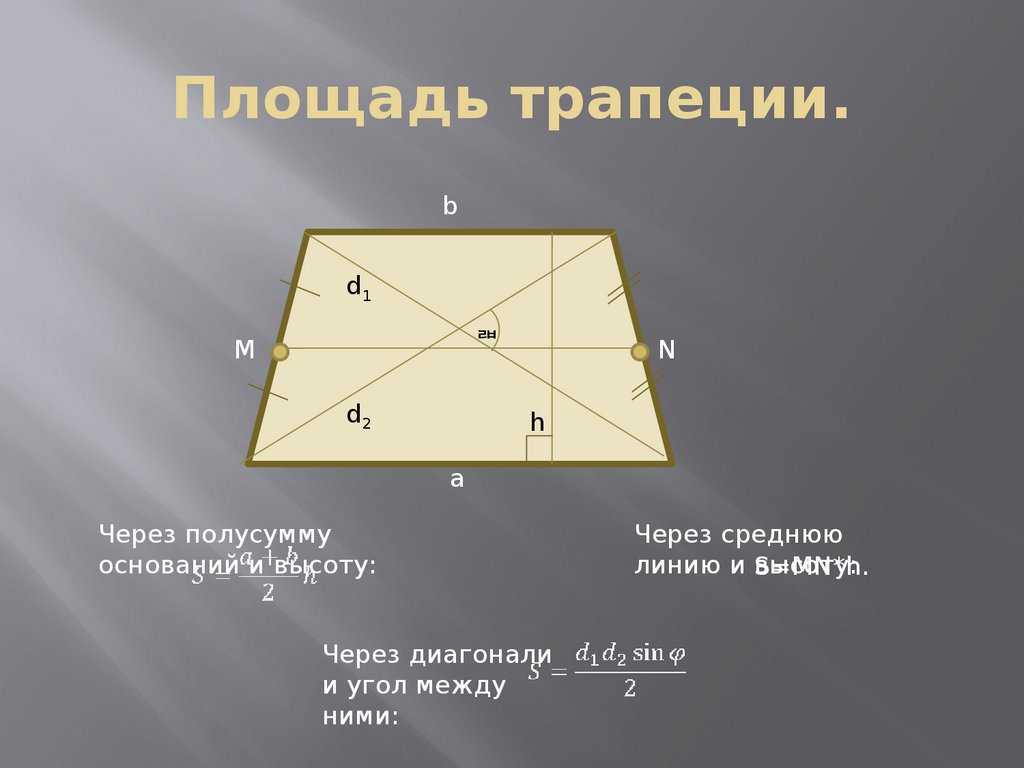 д.
д.
Инструкция
Если известна величина угла (α), который составляет диагональ прямоугольника с одной из его сторон, а также длина (С) этой диагонали, то для вычисления площади можно задействовать определения тригонометрических в прямоугольном . Прямоугольный треугольник здесь образуют две стороны четырехугольника и его диагональ. Из определения косинуса вытекает, что длина одной из сторон будет равна произведению длины диагонали на угла, величина известна. Из определения синуса можно вывести формулу длины другой стороны — она равна произведению длины диагонали на синус все того же угла. Подставьте эти тождества в формулу из предыдущего шага, и получится, что для нахождения площади надо перемножить синус и косинус известного угла, а также длины диагонали прямоугольника : S=sin(α)*cos(α)*С².
Если кроме длины диагонали (С) прямоугольника известна величина угла (β), который образуют диагонали, то для вычисления площади фигуры можно тоже задействовать одну из тригонометрических функций — синус.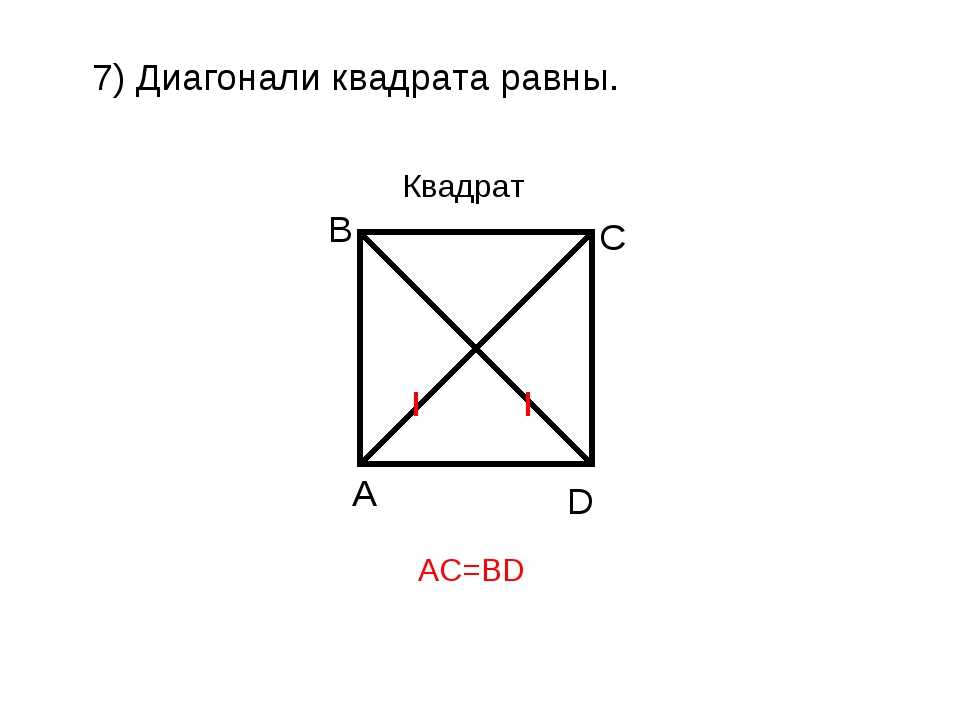 Возведите в квадрат длину диагонали и умножьте полученный результат на половину синуса известного угла: S=С²*sin(β)/2.
Возведите в квадрат длину диагонали и умножьте полученный результат на половину синуса известного угла: S=С²*sin(β)/2.
Если известен (r) вписанной в прямоугольник окружности, то для вычисления площади возведите эту величину во вторую степень и увеличьте результат в четыре раза: S=4*r². Четырехугольник, в который можно , будет являться квадратом, а длина его стороны равна диаметру вписанной окружности, то есть удвоенному радиусу. Формула получена подстановкой длин сторон, выраженных через радиус в тождество из первого шага.
Если известны длины (P) и одной из сторон (A) прямоугольника , то для нахождения площади внутри этого периметра вычислите половину произведения длины стороны на разницу между длиной периметра и двумя длинами этой стороны: S=A*(P-2*A)/2.
Видео по теме
С задачей найти периметр или площадь многоугольника сталкиваются не только ученики на уроках геометрии. Порой ее случается решать и взрослому человеку. Приходилось ли вам рассчитывать необходимое количество обоев для комнаты? Или, может быть, вы измеряли протяженность дачного участка, чтобы огородить его забором? Так знания основ геометрии иногда незаменимы для осуществления важных проектов.
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. где S — площадь треугольника,
— длины сторон треугольника,
— высота треугольника,
— угол между сторонами и,
— радиус вписанной окружности,
R — радиус описанной окружности,
Формулы площади квадрата
- Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.
- Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.S = 1 2 2 где S — Площадь квадрата,
— длина стороны квадрата,
— длина диагонали квадрата.
Формула площади прямоугольника
- Площадь прямоугольника равна произведению длин двух его смежных сторон
где S — Площадь прямоугольника,
— длины сторон прямоугольника.
Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма - Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
a · b · sin α
где S — Площадь параллелограмма,
— длины сторон параллелограмма,
— длина высоты параллелограмма,
— угол между сторонами параллелограмма.
Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. - Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей. где S — Площадь ромба,
— длина стороны ромба,
— длина высоты ромба,
— угол между сторонами ромба,
1 , 2 — длины диагоналей.
Формулы площади трапеции
- Формула Герона для трапеции
Где S — Площадь трапеции,
— длины основ трапеции,
— длины боковых сторон трапеции,
Начиная с 5 класса, ученики начинают знакомиться с понятием площадей разных фигур. 2$.
2$.
Диагонали разделяет прямоугольник на 4 фигуры – 4 треугольника. При этом треугольники попарно равны. Если провести диагональ в прямоугольнике, то она разделяет фигуру на два равных прямоугольных треугольника. Средняя оценка: 4.4 . Всего получено оценок: 214.
Полезный калькулятор для школьников и взрослых позволяет быстро вычислить площадь прямоугольника по двум его сторонам. Подобный расчет мы часто производим не только в рамках школьного курса геометрии, но и в повседневной жизни. Например, если нужно посчитать площадь комнаты при ремонте квартиры, для расчета необходимого количества материалов.
Удобная навигация по статье:
Как рассчитать площадь прямоугольникаПрямоугольником принято называть геометрическую плоскую фигуру, которая имеет параллельно расположенные противоположные стороны при углах в 90 градусов. В качестве длины этой геометрической фигуры выступает величина, которая имеет большую сторону. При этом, за ширину принимается величина меньшей стороны.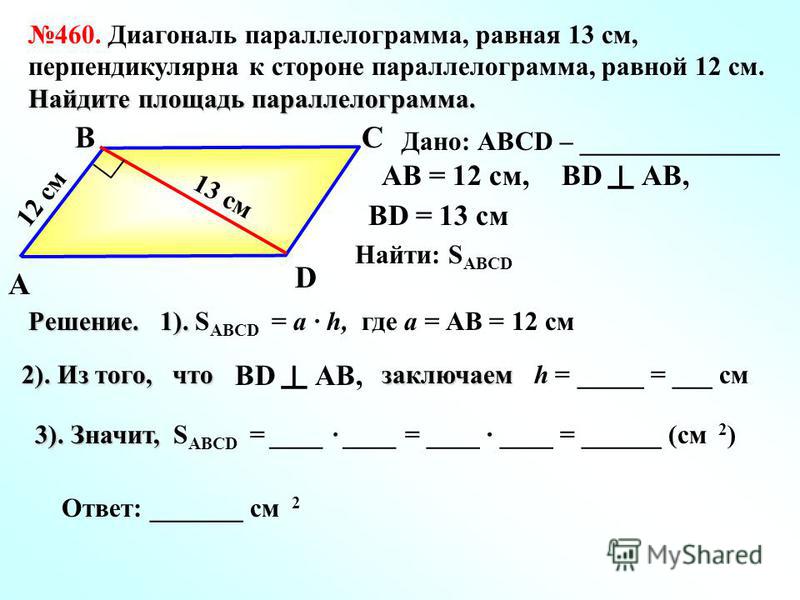 Для правильного вычисления площади прямоугольника Вам необходимо знать определённые параметры, которыми обладает данная фигура. В их числе:
Для правильного вычисления площади прямоугольника Вам необходимо знать определённые параметры, которыми обладает данная фигура. В их числе:
- диагональ;
- ширина;
- так называемый угол наклона к одной из сторон диагонали;
- длина.
Таким образом, произвести расчёт площади прямоугольника можно различными способами. Всё зависит от количества информации о фигуре, а именно, какие величины нам точно известны.
Как вычислить площадь прямоугольника, имея линейные параметры его сторон?
Давайте в качестве обозначения длины прямоугольника будем использовать букву «а», для его ширины – букву «b», а площадь геометрической фигуры обозначим буквой «S». Согласно этому, наша формула будет выглядеть следующим образом: S = a x b.
Зная линейные параметры прямоугольника, можно легко определить его периметр последующей формуле: P = 2(a + b), где в качестве обозначения периметра мы используем букву «P».
Как можно вычислить площадь прямоугольника, зная величину одну из его сторон и диагональ?
Как нам известно, диагональ делит любой прямоугольник на два так называемых прямоугольных треугольника. Давайте присвоим диагонали индекс «с», а длину стороны обозначим буквой «а». Теперь необходимо произвести следующий порядок действий:
Давайте присвоим диагонали индекс «с», а длину стороны обозначим буквой «а». Теперь необходимо произвести следующий порядок действий:
- для начала необходимо найти длину неизвестной стороны. Для этого мы используем формулу Пифагора: b = V c2 – a2.
- После этого, нам следует определить площадь нашей основной геометрической фигуры (прямоугольника) как площадь треугольника, умноженную на два: Sтр = ½ (а х в).
- Согласно вышеописанной схеме расчёта площадь прямоугольника в данном случае будет равна: S = 2 x Sтр = а х в.
В том случае, если нам известны периметр прямоугольника, а также длина одной из его сторон, то площадь этой геометрической фигуры можно вычислить, определив длину второй стороны (b = (P – 2xa), по такой формуле: S = a x b.
Если же нам известны размер диагонали прямоугольника, а также угол между стороной и самой диагональю, то площадь можно вычислить при помощи следующих тригонометрических функций: Sтр = ½ х с2 х sinФ х cosФ.
При этом, общая площадь в данном случае будет составлять S = 2 x Sтр.
Площадь прямоугольника. Видео-урок.
Площадь ромба по 2 диагоналям. Площадь ромба
Несмотря на то, что математика – царица наук, а арифметика – царица математики, самую большую сложность в изучении у школьников вызывает геометрия. Планиметрия – раздел геометрии, который изучает плоские фигуры. Одной из таких фигур является ромб. Большинство задач по решению четырехугольников сводятся к нахождению их площадей. Систематизируем известные формулы и различные способы расчета площади ромба.
Ромб – это параллелограмм, все четыре стороны которого равны. Напомним, что у параллелограмма есть четыре угла и четыре попарно параллельные равные стороны. Как любой четырехугольник, ромб имеет ряд свойств, которые сводятся к следующим: при пересечении диагонали образуют угол, равный 90 градусов (AC ⊥ BD), точка пересечения делит каждую на два равных отрезка. Диагонали ромба также являются биссектрисами его углов (∠DCA = ∠BCA, ∠ABD = ∠CBD и т.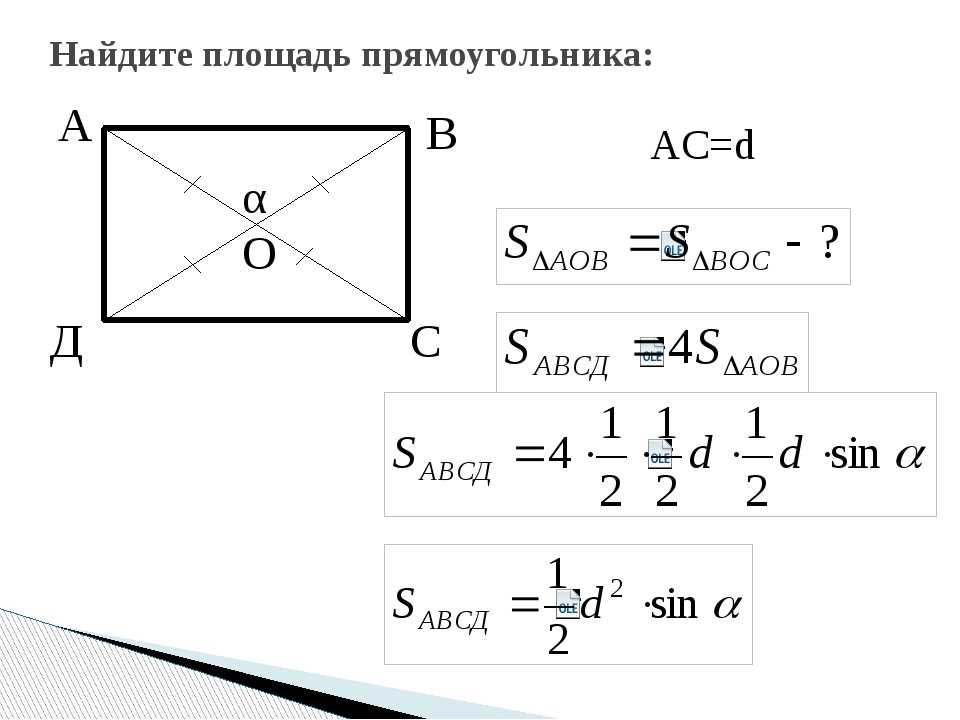 д.). Отсюда следует, что они делят ромб на четыре равных прямоугольных треугольника. Сумма длин диагоналей, возведенных во вторую степень, равна длине стороны во второй степени, умноженной на 4, т.е. BD 2 + AC 2 = 4AB 2 .
Существует множество методов, используемых в планиметрии для расчета площади ромба, применение которых зависит от исходных данных. Если известны длина стороны и любой угол, можно воспользоваться следующей формулой: площадь ромба равна квадрату стороны, умноженному на синус угла. Из курса тригонометрии известно, что sin (π – α) = sin α, а значит, в расчетах можно использовать синус любого угла – как острого, так и тупого. Частным случаем является ромб, у которого все углы прямые. Это квадрат. Известно, что синус прямого угларавен единице, поэтому площадь квадрата равна длине его стороны, возведенной во вторую степень.
д.). Отсюда следует, что они делят ромб на четыре равных прямоугольных треугольника. Сумма длин диагоналей, возведенных во вторую степень, равна длине стороны во второй степени, умноженной на 4, т.е. BD 2 + AC 2 = 4AB 2 .
Существует множество методов, используемых в планиметрии для расчета площади ромба, применение которых зависит от исходных данных. Если известны длина стороны и любой угол, можно воспользоваться следующей формулой: площадь ромба равна квадрату стороны, умноженному на синус угла. Из курса тригонометрии известно, что sin (π – α) = sin α, а значит, в расчетах можно использовать синус любого угла – как острого, так и тупого. Частным случаем является ромб, у которого все углы прямые. Это квадрат. Известно, что синус прямого угларавен единице, поэтому площадь квадрата равна длине его стороны, возведенной во вторую степень.
Если величина сторон неизвестна, воспользуемся длиной диагоналей. В этом случае площадь ромба равна половине произведения большой и малой диагоналей.
При известной длине диагоналей и величине любого угла площадь ромба определяется двумя способами. Первый: площадь – это половина квадрата большей диагонали, умноженная на тангенс половины градусной меры острого угла, т.е. S = 1/2*D 2 *tg(α/2), где D – большая диагональ, α – острый угол. Если вам известен размер меньшей диагонали, воспользуемся формулой 1/2*d 2 *tg(β/2), где d – меньшая диагональ, β – тупой угол. Напомним, что мера острого угла меньше 90 градусов (меры прямого угла), а тупой угол соответственно – больше 90 0 .
Площадь ромба можно отыскать, используя длину стороны (напомним, все стороны у ромба равны) и высоты. Высота – это перпендикуляр, опущенный на противоположную углу сторону или на ее продолжение. Чтобы основание высоты располагалось внутри ромба, ее следует опускать из тупого угла.
Иногда в задаче требуется отыскать площадь ромба, исходя из данных, относящихся к вписанной окружности.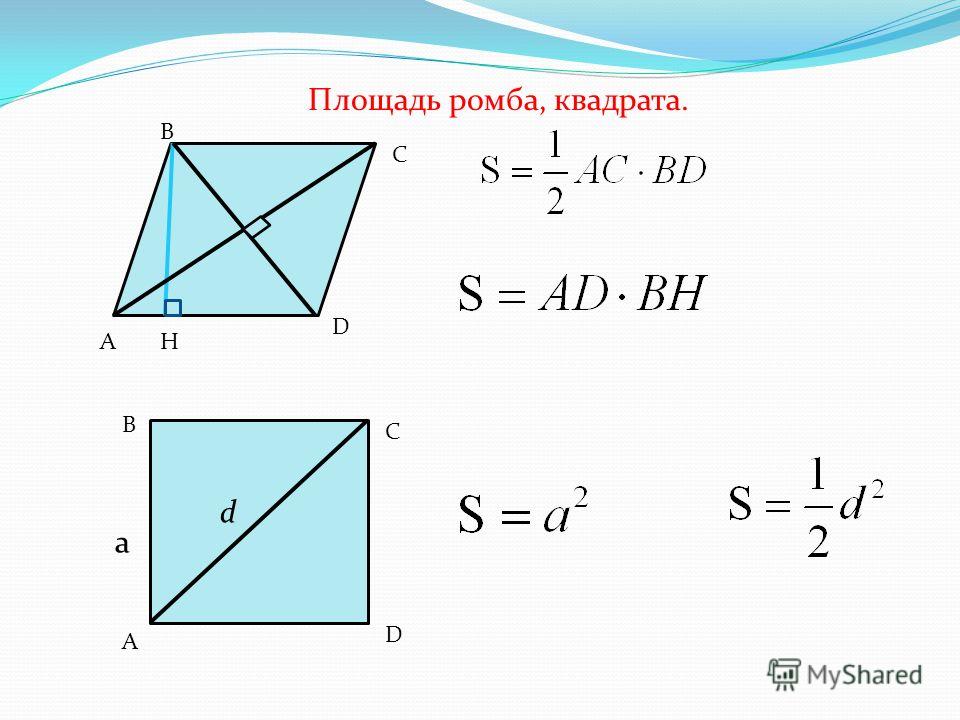 В этом случае необходимо знать ее радиус. Существуют две формулы, которыми можно воспользоваться для расчета. Итак, чтобы ответить на поставленный вопрос, можно удвоить произведение стороны ромба и радиуса вписанной окружности. Другими словами, необходимо умножить диаметр вписанной окружности на сторону ромба. Если в условии задачи представлена величина угла, то площадь находится через частное между квадратом радиуса, умноженном на четыре, и синусом угла.
В этом случае необходимо знать ее радиус. Существуют две формулы, которыми можно воспользоваться для расчета. Итак, чтобы ответить на поставленный вопрос, можно удвоить произведение стороны ромба и радиуса вписанной окружности. Другими словами, необходимо умножить диаметр вписанной окружности на сторону ромба. Если в условии задачи представлена величина угла, то площадь находится через частное между квадратом радиуса, умноженном на четыре, и синусом угла.
Как видите, существует множество способов для нахождения площади ромба. Конечно, чтобы запомнить каждый из них, потребуется терпение, внимательность и, конечно же, время. Но в дальнейшем вы сможете легко выбрать метод, подходящий для вашей задачи, и убедитесь, что геометрия – это несложно.
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. где S — площадь треугольника,
— длины сторон треугольника,
— высота треугольника,
— угол между сторонами и,
— радиус вписанной окружности,
R — радиус описанной окружности,
Формулы площади квадрата
- Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны. - Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.
S = 1 2 2 где S — Площадь квадрата,
— длина стороны квадрата,
— длина диагонали квадрата.
Формула площади прямоугольника
- Площадь прямоугольника равна произведению длин двух его смежных сторон
где S — Площадь прямоугольника,
— длины сторон прямоугольника.
Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма - Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.a · b · sin α
где S — Площадь параллелограмма,
— длины сторон параллелограмма,
— длина высоты параллелограмма,
— угол между сторонами параллелограмма.

Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. - Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей. где S — Площадь ромба,
— длина стороны ромба,
— длина высоты ромба,
— угол между сторонами ромба,
1 , 2 — длины диагоналей.
Формулы площади трапеции
- Формула Герона для трапеции
Где S — Площадь трапеции,
— длины основ трапеции,
— длины боковых сторон трапеции,
– это параллелограмм, у которого все стороны равны.
Ромб с прямыми углами называется квадратом и считается частным случаем ромба.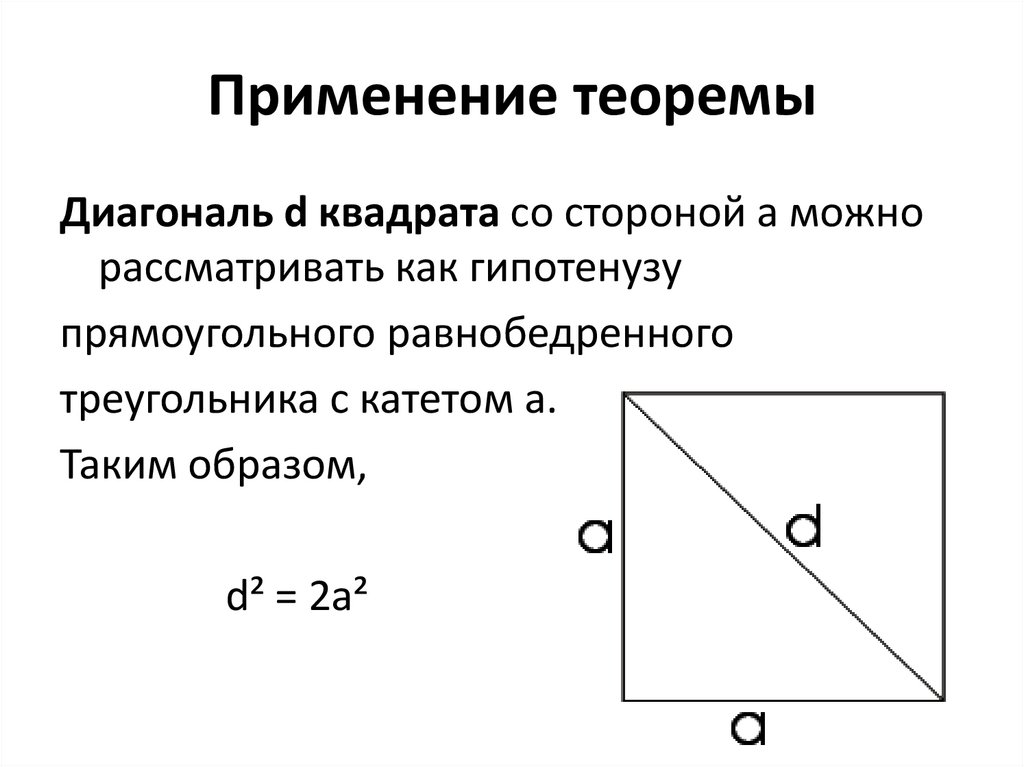 Найти площадь ромба можно различными способами, используя все его элементы – стороны, диагонали, высоту. Классической формулой площади ромба считается расчет значения через высоту.
Найти площадь ромба можно различными способами, используя все его элементы – стороны, диагонали, высоту. Классической формулой площади ромба считается расчет значения через высоту.
Пример расчета площади ромба по этой формуле очень прост. Необходимо только подставить данные и высчитать площадь.
Площадь ромба через диагонали
Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.
Формула площади ромба через диагонали представляет собой произведение его диагоналей, разделенное на 2.
Рассмотрим пример расчета площади ромба через диагонали. Пусть дан ромб с диагоналями
d1
=5 см и d2
=4. Найдем площадь.
Формула площади ромба через стороны подразумевает и применение других элементов. Если в ромб вписана окружность, то площадь фигуры можно просчитать по сторонам и ее радиусу:
Пример расчета площади ромба через стороны также весьма прост. Требуется только просчитать радиус вписанной окружности.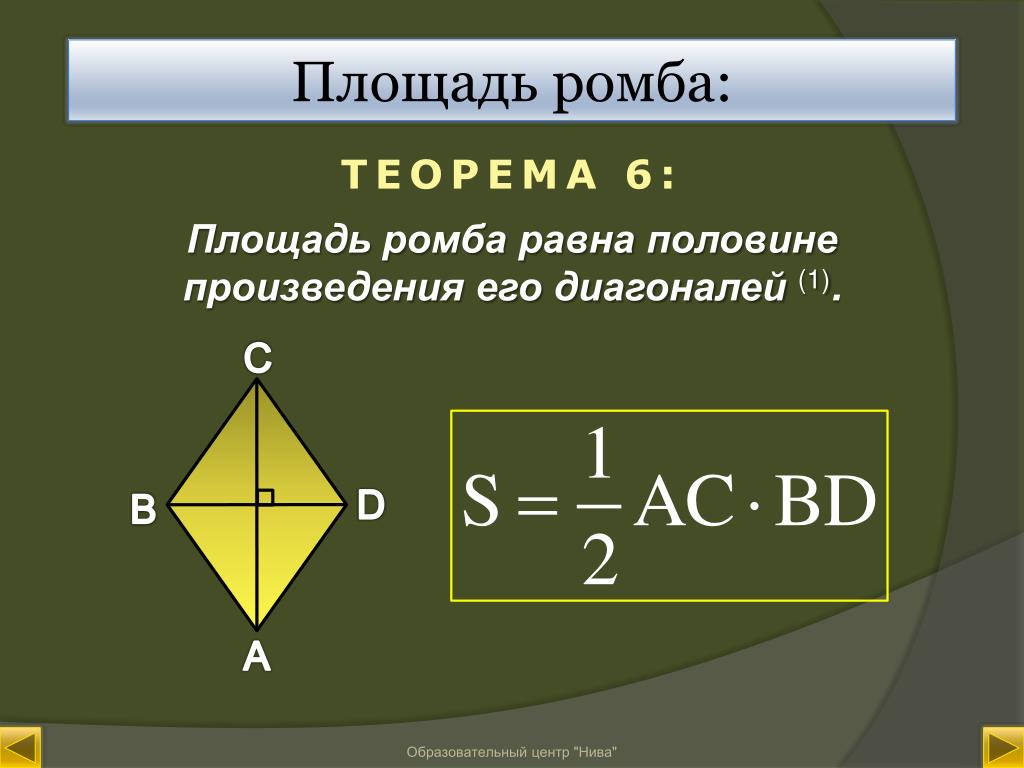 Его можно вывести из теоремы Пифагора и по формуле .
Его можно вывести из теоремы Пифагора и по формуле .
Площади ромба через сторону и угол
Формула площади ромба через сторону и угол используется очень часто.
Рассмотрим пример расчета площади ромба через сторону и угол.
Задача: Дан ромб, диагонали которого равны d1
=4 см,d2
=6 см. Острый угол равен α
= 30°. Найдите площадь фигуры через сторону и угол.
Для начала найдем сторону ромба. Используем для этого теорему Пифагора. Мы знаем, что в точке пересечения диагонали делятся пополам и образуют прямой угол. Следовательно:
Подставим значения:
Теперь мы знаем сторону и угол. Найдем площадь:
– это параллелограмм , у которого все стороны равны, то для него действуют все те же формулы, как и для параллелограмма, включая формулу нахождения площади через произведение высоты и стороны .
Площадь ромба можно найти, также зная его диагонали . Диагонали делят ромб на четыре абсолютно одинаковых прямоугольных треугольника . Если мы их рассортируем, так чтобы получить прямоугольник , то его длина и ширина будут равны одной целой диагонали и половине второй диагонали. Поэтому площадь ромба находится умножением диагоналей ромба, сокращенных на два (как площади получившегося прямоугольника).
Поэтому площадь ромба находится умножением диагоналей ромба, сокращенных на два (как площади получившегося прямоугольника).
Если в распоряжении только угол и сторона , то можно вооружиться диагональю в качестве помощника и начертить ее напротив известного угла. Тогда она разделит ромб на два конгруэнтных треугольника, площади которых в сумме дадут нам площадь ромба. Площадь каждого из треугольников будет равна половине произведения квадрата стороны на синус известного угла, как площадь равнобедренного треугольника . Поскольку таких треугольников два, то коэффициенты сокращаются, оставив только сторону во второй степени и синус:
Если внутри ромба вписать окружность , то его радиус будет относиться к стороне под углом 90° , что значит, что удвоенный радиус будет равен высоте ромба . Подставив вместо высоты h=2r в предыдущую формулу, получим площадь S=ha=2ra
Если же вместе с радиусом вписанной окружности, дана не сторона, а угол, то следует сначала найти сторону, проведя высоту таким образом, чтобы получить прямоугольный треугольник с заданным углом. Тогда сторона a
может быть найдена из тригонометрических отношений по формуле . Подставляя это выражение в ту же стандартную формулу площади ромба, выходит
Тогда сторона a
может быть найдена из тригонометрических отношений по формуле . Подставляя это выражение в ту же стандартную формулу площади ромба, выходит
Ромб — это частный случай параллелограмма. Он представляет собой плоскую четырехугольную фигуру, в которой все стороны равны. Данное свойство определяет то, что у ромбов параллельны противоположные стороны и равны противолежащие углы. Диагонали ромба пресекаются под прямым углом, точке их пересечения приходится на середину каждой диагонали, а углы из который они выходят делятся пополам. То есть они диагонали ромба являются биссектрисами углов. Исходя из приведенных определений и перечисленных свойств ромбов их площадь может быть определена различными способами.
1. Если известны обе диагонали ромба AC и BD, то площадь ромба может быть определена как половина произведения диагоналей.
S = ½ ∙ AC ∙ BD
где AC, BD — длина диагоналей ромба.
Чтобы понять почему это так, можно мысленно вписать в ромб прямоугольник таким образом, чтобы стороны последнего были перпендикулярны диагоналям ромба. Становится очевидным, что площадь ромба будет равна половине площади вписанного данным образом в ромб прямоугольника, длина и ширина которого будут соответствовать величине диагоналей ромба.
Становится очевидным, что площадь ромба будет равна половине площади вписанного данным образом в ромб прямоугольника, длина и ширина которого будут соответствовать величине диагоналей ромба.
2. По аналогии с параллелепипедом площадь ромба может быть на найдена как произведение его стороны, на высоту перпендикуляра с опущенного к данной стороне с противолежащей стороны.
S = а ∙ h
где а — сторона ромба;
h — высота перпендикуляра, опущенного на данную сторону.
3. Площадь ромба также равна квадрату его стороны, умноженному на синус угла α
.
S = a 2 ∙ sinα
где, a — сторона ромба;
α
— угол между сторонами.
4. Также площадь ромба может быть найдена через его сторону и радиус вписанной в него окружности.
S = 2 ∙ a ∙ r
где, a — сторона ромба;
r — радиус вписанной в ромб окружности.
Интересные факты
Слово ромб произошло от древнегреческого rombus, что в переводе означает «бубен». В те времена бубны действительно имели ромбовидную форму, а не круглую, как мы привыкли видеть их в настоящее время. С тех же времен произошло и название карточной масти «бубны». Очень широко ромбы различных видов используются в геральдике.
В те времена бубны действительно имели ромбовидную форму, а не круглую, как мы привыкли видеть их в настоящее время. С тех же времен произошло и название карточной масти «бубны». Очень широко ромбы различных видов используются в геральдике.
Найти площадь квадрата по диагонали
Квадрат — это правильный четырёхугольник, у которого все стороны и углы равны. У квадрата две диагонали, соединяющие несмежные вершины фигуры. Расчет площади квадрата по диагонали онлайн-калькулятором производится по формуле S=12*d2, где d — диагональ квадрата
Чтобы найти площадь квадрата по диагонали онлайн, понадобится несколько простых действий:
- указать размер диагонали и единицы измерения;
- выбрать, в каких единицах необходимо рассчитать площадь;
- получить ответ после нажатия на кнопку «Найти».
Нахождение площади квадрата по диагонали
Чтобы найти площадь квадрата по диагонали с помощью онлайн-калькулятора, нужно:
- Задать диагональ квадрата.
 Для наглядности возьмем квадрат со стороной 8 см и введем это значение в пустое поле калькулятора:
Для наглядности возьмем квадрат со стороной 8 см и введем это значение в пустое поле калькулятора:
Отметим, что при вводе некорректного значения калькулятор выдает предупреждение. Например, вот что будет, если ввести в поле для диагонали отрицательное значение: - Выберем размерности величин. Онлайн калькулятор позволяет работать с миллиметрами, сантиметрами и метрами, а также осуществляет конвертацию этих величин.
- Теперь нажмем «Найти» и получим решение с ответом:
Материалы, которые помогут вам лучше разобраться в теме:
- Площадь фигуры: понятие площади, свойства площади, квадрируемые фигуры
- Вычисление площади фигуры в полярных координатах
Ответ:
Решение
Ответ:
- list» :key=»`error-${eIdx}`» v-html=»e»/>
Похожие калькуляторы:
- Площадь треугольника (по 3 сторонам)
- Площадь треугольника (по 2 сторонам и углу)
- Площадь треугольника (по стороне и высоте)
- Площадь прямоугольного треугольника
- Площадь равнобедренного треугольника
- Площадь равностороннего треугольника
- Площадь квадрата (по стороне квадрата)
- Площадь прямоугольника
- Площадь треугольника (по 3 сторонам и радиусу описанной окружности)
- Площадь треугольника (по 3 сторонам и радиусу вписанной окружности)
- Площадь треугольника (по полупериметру и радиусу вписанной окружности)
- Площадь треугольника (по двум сторонам и одному углу)
- Площадь треугольника (по одной стороне и двум углам)
- Площадь треугольника (по радиусу описанной окружности и двум углам)
- Площадь круга (по радиусу)
- Площадь круга (по диаметру)
- Площадь круга (по длине окружности)
- Площадь ромба (по сторонам и углу между ними)
- Площадь ромба (по стороне и высоте)
- Площадь ромба (по диагоналям)
- Площадь параллелограмма (по сторонам и углу между ними)
- Площадь параллелограмма (по стороне и высоте)
- Площадь параллелограмма (по диагоналям и углу между ними)
- Площадь трапеции (по основаниям и высоте)
- Площадь трапеции (по средней линии и высоте)
- Площадь трапеции (по диагоналям и углу между ними)
- Площадь эллипса
- Площадь поверхности куба
- Площадь поверхности параллелепипеда
- Площадь поверхности сферы
- Площадь поверхности цилиндра
- Площадь поверхности конуса
Вычисление площади квадрата по диагонали онлайн
При отсутствии данных о длине стороны квадрата можно найти площадь фигуры другим способом.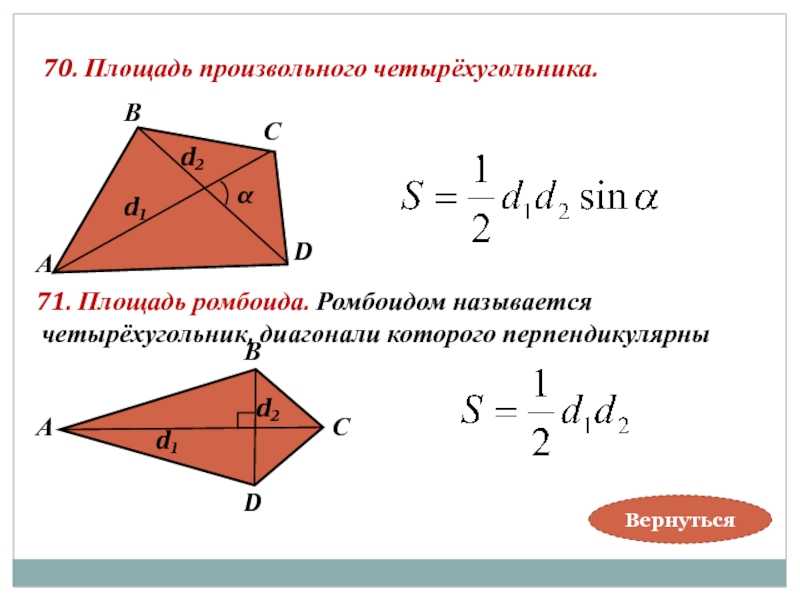 В данном случае можно не прибегать к услугам программных средств и все действия произвести самостоятельно. Но если величина диагонали содержит несколько знаков, то при возведении ее в квадрат есть вероятность допустить ошибку.
В данном случае можно не прибегать к услугам программных средств и все действия произвести самостоятельно. Но если величина диагонали содержит несколько знаков, то при возведении ее в квадрат есть вероятность допустить ошибку.
Рассчитать площадь квадрата по диагонали онлайн понадобится:
- школьникам, которые выполняют домашнее задание по геометрии;
- родителям для быстрого контроля;
- учителям, проверяющим работы класса;
- студентам, которым важен точный ответ, на который опираются дальнейшие вычисления.
Сервис выдает последовательное решение задачи с точным ответом. С помощью сайта Zaochnik можно осуществлять подготовку к занятиям без привлечения репетиторов, траты средств и лишнего времени.
Понравился калькулятор? Поделись с друзьями!
Площадь квадрата по диагонали
Площадь любой геометрической фигуры – это пространство, занимаемое двумерным объектом. Квадрат представляет собой двумерную геометрическую фигуру, которая определяется сторонами, которые равны по длине и перпендикулярны друг другу (угол между двумя сторонами составляет 90 градусов). Площадь квадрата — это количество квадратных единиц, необходимых для полного заполнения квадрата. Существуют разные способы вычисления площади квадрата.
Площадь квадрата — это количество квадратных единиц, необходимых для полного заполнения квадрата. Существуют разные способы вычисления площади квадрата.
Один из обычных и стандартных способов вычисления площади квадрата — это использование его диагоналей или сторон. Поскольку все стороны квадрата одинаковы, мы можем напрямую найти квадрат его стороны. Следовательно, площадь квадрата равна произведению любой из двух его сторон.
Но иногда длина стороны не указана, и мы знаем только длину диагонали квадрата. Зная прямоугольные треугольники, мы можем найти площадь квадрата по диагонали.
Что такое диагональ квадрата?
Диагональ — это линия, идущая от одного угла фигуры к противоположному углу и проходящая через центр фигуры. Диагонали квадрата всегда равны друг другу. В многоугольнике диагонали можно определить как линию, соединяющую две его несмежные вершины.
Связь между диагональю и стороной квадрата
Квадрат можно разделить на два прямоугольных треугольника, где диагональ квадрата равна длине гипотенузы треугольника.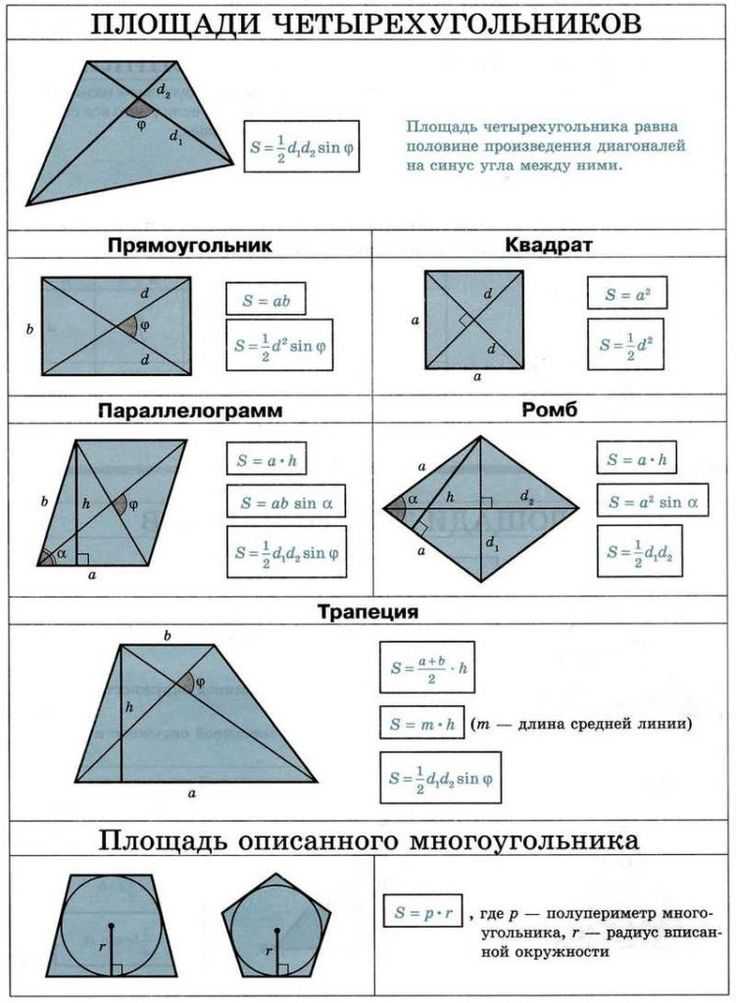 Теорема Пифагора, применимая к прямоугольным треугольникам, показывает связь между гипотенузой и сторонами прямоугольного треугольника.
Теорема Пифагора, применимая к прямоугольным треугольникам, показывает связь между гипотенузой и сторонами прямоугольного треугольника.
Таким образом, он также представляет отношение между диагональю квадрата (гипотенузой треугольника) и его сторонами.
(Изображение скоро будет загружено) 9{2}}\]
= \[a\sqrt{2}\]
= сторона \[\sqrt{2}\]
Формула площади квадрата по диагонали
По длине диагонали , площадь квадрата можно рассчитать как:
Площадь квадрата = ½ × d 2 единицы 2
Здесь «d» — длина любой из диагоналей. Также помните, что в квадрате диагонали равны.
Вычисление площади квадрата по диагонали
Мы знаем формулу нахождения площади квадрата по диагоналям. Теперь мы выведем эту формулу, используя следующие два метода.
Использование теоремы Пифагора
(Изображение будет загружено в ближайшее время)
На данном рисунке диагональ единиц длины «d» делит квадрат стороны «a» единиц на два прямоугольных треугольника. Теперь, применяя теорему Pythagoras в любом правом треугольнике,
Теперь, применяя теорему Pythagoras в любом правом треугольнике,
(гипотенуза) 2 = (основа) 2 + (перпендикуляр) 2
здесь,
Perpendicular = A
= A
= A
=
=
=
Гипотенуза = d
SO,
A 2 + A 2 = D 2
2A 2 = D 2
или, A 2 = D 2 /2
WELY 2 = D 2 /2 что площадь квадрата = a 2 = d 2 / 2Таким образом, площадь квадрата с использованием диагоналей = ½ × d 2 квадратных единиц.
Используя отношение между стороной и диагональю
Для квадрата со стороной «a» и диагональю «d», мы знаем, что
Площадь квадрата = сторона x сторона = a 2
Теперь, как мы получили выше,
Диагональ квадрата = сторона x √2 = a√2
Тогда, сторона квадрата, a = 1 /√2 x диагональ = d/√2
Таким образом, площадь квадрата = a 2
Площадь = (d/√2) 2
Площадь = d 2 /2
3 Площадь = 90½ x d 2
Площадь = ½ x (диагональ) 2
Таким образом, площадь квадрата с использованием диагоналей = ½ × d 2 квадратных шт.
Решенные примеры
Пример 1. Найдите стороны и площадь квадрата, если диагональ равна 6 см.
Решение: Возьмем квадрат со стороной x. Если квадрат разделить на два прямоугольных треугольника, то гипотенуза каждого треугольника равна диагонали квадрата. Как известно, диагональ равна 6 см.
Согласно теореме Пифагора,
x 2 + x 2 = 6 2
9Таким образом, длина сторона квадрата равна 3\[\sqrt{2}\] единиц.Чтобы найти площадь квадрата, когда дана диагональ, мы можем использовать любой из следующих методов:
Метод 1
Площадь квадрата = сторона x сторона =3\[\sqrt{2 }\] x 3\[\sqrt{2}\]
= 9 x 2 = 18 см 2
Метод 2
Площадь квадрата = ½ x d 2 = ½ x 6 x 6
= ½ x 36 = 18 см 2
92002 Пример длины диагонали квадрата по теореме Пифагора, если сторона равна 4 см.
Решение: Мы знаем, что все стороны квадрата равны по длине. Мы также знаем, что каждая вершина образует угол 90°. Теперь давайте разделим квадрат на два прямоугольных треугольника со сторонами, равными 4 см. Используя теорему Пифагора в одном из треугольников найдем третью сторону треугольника, являющуюся диагональю квадрата.
Пусть гипотенуза/диагональ равна ‘c’ см.
Следовательно, (гипотенуза) 2 = (основание) 2 + (перпендикулярный) 2
C 2 = 4 2 + 4 2
= C 2 + 160023 2
= C 2 + = 16024 = 16024 = 160023 2
= C 2 + 4 2
= C 2 + 4 2
= C 2 + 4 2
= C 2 + 4 2
= C 2 + 16
c = \[\sqrt{32}\] см
c = 4\[\sqrt{2}\]см
Длина диагонали 4\[\sqrt{2}\]см
Диагональ прямоугольника.
 Калькулятор
КалькуляторАвтор Доминик Черня, кандидат наук
Отзыв от Bogna Szyk
Последнее обновление: 11 марта 2022 г.
Содержание:- Как найти диагональ прямоугольника?
- Какова диагональ прямоугольника?
Наш калькулятор диагонали прямоугольника — это обширный инструмент, который быстро находит диагональ и другие параметры прямоугольника. Вы столкнулись с конкретной проблемой прямоугольника, и вы не знаете , как найти диагональ прямоугольника ? Попробуйте ввести пару параметров в поля рядом с текстом или продолжайте читать, чтобы узнать возможные 9 параметров.0269 диагональ прямоугольника формулы .
Типичный прямоугольник показан на рисунке ниже. Мы отметили пять основных величин, описывающих конкретный прямоугольник. Вы можете использовать их для получения формулы диагонали прямоугольника. Это:
- l — длина ,
- ширина ,
- α — угол между диагоналями ,
- r — радиус описанной окружности ,
- д — диагональ ,
и два других параметра, которые не показаны на картинке:
- A — площадь ,
- П — периметр .

Термин прямоугольник происходит от латинского rectangulus , который представляет собой комбинацию двух слов: rectus (правый, правильный) и angulus (угол). Это название происходит от того факта, что прямоугольник представляет собой четырехугольник с четырьмя прямыми углами (4 * 90° = 360°). Его противоположные стороны параллельны и имеют одинаковую длину, а две его диагонали пересекаются посередине и также имеют одинаковую длину.
Квадрат — это частный случай прямоугольника. Его определение состоит в том, что у него все четыре стороны одинаковой длины, или, альтернативно, угол между двумя диагоналями прямой. Попробуйте наши калькуляторы, посвященные квадратам. Они могут быстро оценить периметр, площадь и диагональ любого квадрата, который вам нужен, только по длине его стороны.
Центр прямоугольника равноудален от его вершин, поэтому на нем всегда можно описать окружность . С другой стороны, вы можете вписать окружность в прямоугольник, только если это квадрат .
Как найти диагональ прямоугольника?
Чтобы найти диагональ прямоугольника по формуле, вы можете разделить прямоугольник на два конгруэнтных прямоугольных треугольника, т. е. треугольники с одним углом 90°. Каждый треугольник будет иметь стороны длиной l и w и гипотенузой длины d . Вы можете использовать теорему Пифагора для оценки диагонали прямоугольника, которая может быть выражена следующей формулой:
d² = l² + w² ,
и теперь вы должны знать, как найти диагональ прямоугольника по явной формуле — просто извлеките квадратный корень:
d = √(l² + w²) .
Наш калькулятор диагонали прямоугольника позволяет использовать практически любые единицы измерения. Воспользуйтесь нашим конвертером длины или конвертером площади, чтобы узнать, как переключаться между различными единицами измерения (СИ и имперскими).
Какова диагональ прямоугольника?
Иногда вы не можете указать все две стороны прямоугольника.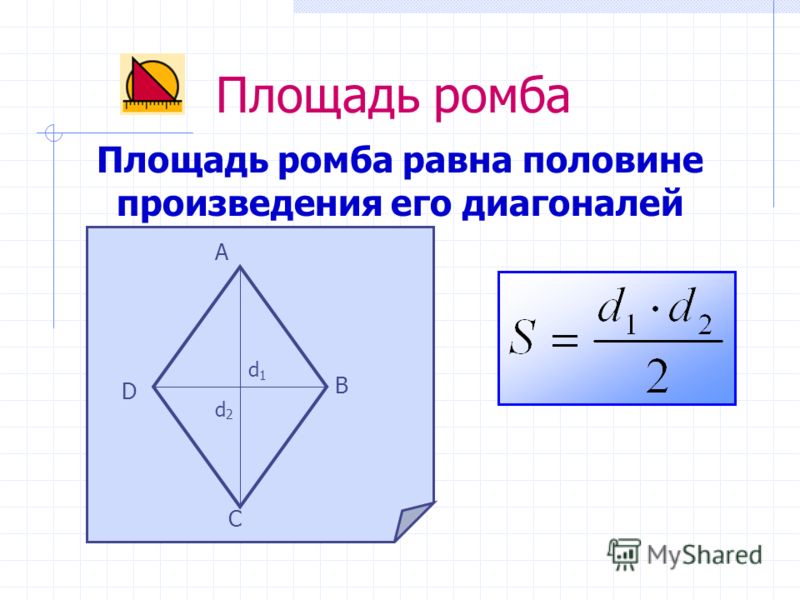 Как найти диагональ прямоугольника в этом случае? Ответ дает наш калькулятор диагонали прямоугольника. Сначала запишем три основных уравнения для площади, периметра и радиуса описанной окружности:
Как найти диагональ прямоугольника в этом случае? Ответ дает наш калькулятор диагонали прямоугольника. Сначала запишем три основных уравнения для площади, периметра и радиуса описанной окружности:
- Площадь прямоугольника:
A = w * l, - Периметр прямоугольника
P = 2 * w + 2 * l, - Радиус окружности прямоугольника
r = d/2.
С помощью приведенных выше уравнений мы теперь можем вывести различные формулы диагонали прямоугольника , которые используются калькулятором этой диагонали прямоугольника:
- Учитывая длину и ширину :
д = √(l² + w²), - Дано длина/ширина и площадь :
d = √(A²/l² + l²)илиd = √(A²/w² + w²), - Дано длина/ширина и периметр :
d = √(2l² - P*l + P²/4))илиd = √(2w² - P*w + P²/4), - Даны длина/ширина и угол :
d = w / sin(α/2)илиd = l / cos(α/2), - Учитывая площадь и периметр :
d = √(P² - 2*A), - Учитывая площадь и угол :
d = √(2 * A / sin(α)), - Учитывая периметр и угол :
d = P / (2*sin(α/2) + 2*cos(α/2)), - Дан радиус описанной окружности :
d = 2 * r.
Примечание: Угол α между диагоналями лежит перед длиной , как и на первом рисунке. Также помните, что калькулятор диагонали прямоугольника предполагает, что длина больше ширины!
Знаете ли вы, что существует особый прямоугольник, называемый золотым прямоугольником? Если нет, то воспользуйтесь нашим калькулятором золотых прямоугольников и узнайте, как построить золотые прямоугольники!
Доминик Черня, кандидат наук
Длинная сторона (l)
Короткая сторона (w)
Площадь (A)
Периметр (P)
Угол между диагоналями окружности (06)
Диагональ
Диагональ (d)
Посмотрите 21 похожий калькулятор 2d геометрии 📏
ПлощадьПлощадь прямоугольникаПлощадь полумесяца… Еще 18
Диагональ квадрата — формула, свойства, примеры
LearnPracticeDownload
Диагональ квадрата представляет собой отрезок, соединяющий любые две несмежные вершины. Квадрат имеет две диагонали, которые равны по длине и делят друг друга пополам под прямым углом. Формула диагонали квадрата используется для вычисления длины диагонали квадрата, когда известна длина его стороны.
Квадрат имеет две диагонали, которые равны по длине и делят друг друга пополам под прямым углом. Формула диагонали квадрата используется для вычисления длины диагонали квадрата, когда известна длина его стороны.
| 1. | Какова диагональ квадрата? |
| 2. | Что такое Диагональ формулы квадрата? |
| 3. | Вывод диагонали квадрата по формуле |
| 4. | Примеры использования диагональной формулы квадрата |
| 5. | Часто задаваемые вопросы о диагонали квадратной формулы |
Что такое диагональ квадрата?
Квадрат имеет две диагонали, каждая из которых образована соединением противоположных вершин квадрата. Обратите внимание на следующий квадрат, чтобы соотнести свойства диагоналей, приведенные ниже.
- Диагонали квадрата равны по длине.
- Они перпендикулярны друг другу.

- Они делят квадрат на два равных равнобедренных прямоугольных треугольника.
Что такое Диагональ формулы квадрата?
Диагональ формулы квадрата равна d = a√2; где «d» — диагональ, а «а» — сторона квадрата. Формула диагонали квадрата выводится по теореме Пифагора. Диагональ делит квадрат на два равнобедренных прямоугольных треугольника. Обе диагонали равны и делят друг друга пополам под прямым углом. Давайте разберемся, как вывести формулу для нахождения диагонали квадрата.
Вывод диагонали квадрата по формуле
В квадрате длина обеих диагоналей одинакова. Длина диагонали «d» квадрата со стороной «а» вычисляется по теореме Пифагора. Обратите внимание на следующий квадрат, чтобы увидеть, что длина диагонали обозначена буквой «d», а длина стороны обозначена буквой «a».
Диагональ квадрата Формула
Рассмотрим треугольник ADC в квадрате. Мы знаем, что все углы квадрата равны 9.0 °, поэтому, используя теорему Пифагора, мы можем найти гипотенузу, которая в данном случае равна «d».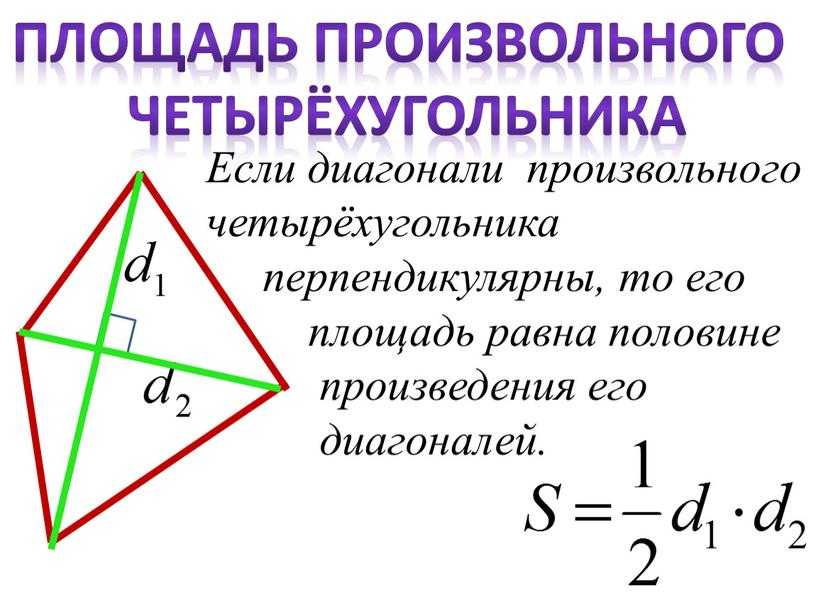
D 2 = A 2 + A 2
D = √ (A 2 + A 2 )
D = √ (2A 2 )
D = √ (2A 2 )
9666 D = √ (2A 2 )966 D = √ (2A 2 )9
D = √ (2A 2 ) 9000 3
D = √ (2A 2 )
D = √ (2A 2 )
D = √ (2A 2 )
D = √ (2A 2 ) √a 2
= √2a
Следовательно, диагональ квадрата равна: d = a√2
☛ Похожие статьи
- Диагонали прямоугольника 9006
- Диагональ куба Формула
- Диагональ формулы параллелограмма
- Диагональ многоугольника Формула
- Диагональ ромба
Примеры использования диагональной формулы квадрата
Пример 1: Найдите длину диагонали квадрата со стороной 14 единиц.
Решение:
Длина стороны квадрата: а = 14 единиц.

Используя формулу вычисления диагонали квадрата, длина диагонали d равна:
d = a√2
d = 14√2 или 19,8 единицы
Ответ: Длина каждой диагонали данного квадрата равна 19,8 единицы.
Пример 2: Длина диагонали квадрата составляет 3√2 единицы. Найдите длину стороны квадрата.
Решение:
Дано, что диагональ квадрата = 3√2 единицы.
Предположим, что длина стороны квадрата равна «а».
Согласно формуле диагонали квадрата, длина диагонали d равна:
d = a √2
3√2 = a √2
a = 3
Ответ: Длина стороны данного квадрата = 3 единицы.
Пример 3: Найдите длину диагонали квадрата, если его площадь 36 квадратных единиц.
Решение:
Площадь квадрата = 36 квадратных единиц
Мы знаем, что площадь квадрата = a 2 = 36
Следовательно, a = 6 единиц
Мы знаем, что диагональ формула квадрата: d = a√2
Следовательно, длина диагонали = a√2 = 6√2 = 8,49 ед.

Ответ: Длина диагонали квадрата = 8,49 ед.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами
Запишитесь на бесплатный пробный урок
Практические вопросы по диагонали квадрата
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о диагонали квадратной формулы
Что такое диагональ квадрата в математике?
Диагональ квадрата — это отрезок, соединяющий две несмежные вершины. Квадрат имеет две диагонали, которые равны по длине и делят друг друга пополам под прямым углом. Свойства диагоналей квадрата следующие:
- Они равны по длине.
- Они перпендикулярны друг другу.
- Они делят квадрат на два равных равнобедренных прямоугольных треугольника.

Какова формула диагонали квадрата?
Квадрат имеет две диагонали одинаковой длины, которые можно рассчитать по формуле d = a√2, где а — сторона квадрата.
Как рассчитать диагональ квадрата по формуле диагонали?
Чтобы вычислить длину диагонали квадрата, мы используем следующие шаги:
- Шаг 1: Проверьте длину стороны квадрата, a.
- Шаг 2: Подставьте значение «а» в формулу диагонали квадрата, d = a√2.
- Шаг 3: Запишите полученное значение в соответствующей единице измерения.
Как получить диагональ квадратной формулы?
Диагональ квадратной формулы можно вывести с помощью теоремы Пифагора.
- Шаг 1: Проведите диагонали квадрата.
- Шаг 2: Образуются два прямоугольных треугольника. Рассмотрим один из треугольников.
- Шаг 3: Две стороны прямоугольного треугольника будут одинаковыми, так как все стороны квадрата равны.
- Шаг 4: Примените теорему Пифагора и вычислите длину гипотенузы треугольника, являющегося диагональю квадрата.

Таким образом, диагональ d = √(a 2 + a 2 ) = (√2)a = a√2; где «а» — сторона квадрата.
Что такое «а» в диагонали квадратной формулы?
Так как квадрат имеет четыре равные стороны, поэтому в формуле диагонали квадрата «а» представляет сторону квадрата. Таким образом, диагональ квадратной формулы задается как d = a√2.
Диагональ квадрата равна его стороне?
Нет, диагональ квадрата не равна его стороне. Поскольку все углы квадрата равны 90°, диагональ квадрата становится гипотенузой треугольников, образуемых в квадрате.
Как найти диагональ квадрата, зная площадь?
Если известна площадь квадрата, можно вычислить длину стороны квадрата. Затем значение длины стороны можно использовать для нахождения диагонали квадрата с помощью формулы d = a√2. Например, если площадь квадрата составляет 81 кв. Сначала найдем длину его стороны, так как мы знаем, что площадь квадрата = a 2 . Следовательно, сторона «а» = √81 = 9 единиц. Теперь мы будем использовать это значение в формуле d = a√2, d = 9√2 = 12,72 единицы.
Теперь мы будем использовать это значение в формуле d = a√2, d = 9√2 = 12,72 единицы.
Как найти диагональ квадрата, если дана сторона?
Диагональ квадрата можно вычислить, если известна сторона. Диагональ квадратной формулы = a√2; где «а» — длина стороны. Данную длину стороны подставляют в эту формулу, чтобы получить длину диагонали. Например, если длина стороны квадрата равна 10 см, мы подставим в формулу значение d = a√2. Это означает, что длина диагонали (d) = a√2 = 10√2 = 14,14 см.
Как найти диагональ квадрата с периметром?
Диагональ квадрата можно вычислить, если известен периметр квадрата. Давайте разберемся в этом на примере. Например, если периметр квадрата равен 32 единицам, найдем диагональ, выполнив следующие шаги:
- Шаг 1: Мы знаем, что формула для нахождения периметра квадрата = 4 × длина стороны. После подстановки заданного значения периметра можно вычислить длину стороны квадрата. Здесь это будет Периметр квадрата = 4 × длина стороны.
 Это будет 32 = 4 × длина стороны. Следовательно, длина стороны будет равна 8 единицам.
Это будет 32 = 4 × длина стороны. Следовательно, длина стороны будет равна 8 единицам. - Шаг 2: Зная длину стороны, можно вычислить диагональ квадрата по формуле Диагональ квадрата = a√2; где «а» — длина стороны. Теперь мы можем подставить это значение в формулу Диагональ квадрата = a√2 = 8 × √2 = 11,313 единиц.
Рабочие листы по математике и визуальный учебный план
Как найти длину диагонали прямоугольника
Все ресурсы по базовой геометрии
9 Диагностические тесты 164 практических теста Вопрос дня Карточки Учитесь по концепции
← Предыдущая 1 2 3 4 Следующая →
Справка по базовой геометрии » Плоская геометрия » Четырехугольники » Прямоугольники » Как найти длину диагонали прямоугольника
Длина прямоугольника 12 дюймов, а ширина 5 дюймов. Чему равна диагональ прямоугольника?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы найти диагональ, воспользуемся теоремой Пифагора:
где = гипотенуза
или
Сообщить об ошибке
Одна сторона прямоугольника 7 дюймов, а другая 9 дюймов. Сколько сантиметров длина диагонали прямоугольника?
Сколько сантиметров длина диагонали прямоугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Вы можете найти диагональ прямоугольника, если у вас есть ширина и высота. Диагональ равна квадратному корню из квадрата ширины плюс квадрат высоты.
Сообщить об ошибке
Найдите длину диагонали.
Возможные ответы:
Правильный ответ:
Пояснение:
Прямоугольник можно разрезать на два равных прямоугольных треугольника, гипотенуза которых является диагональю прямоугольника.
Используйте теорему Пифагора, чтобы найти гипотенузу:
, где a и b — катеты, а c — гипотенуза
Сообщить об ошибке
Стандартная школьная баскетбольная площадка имеет длину 84 фута и ширину 50 футов.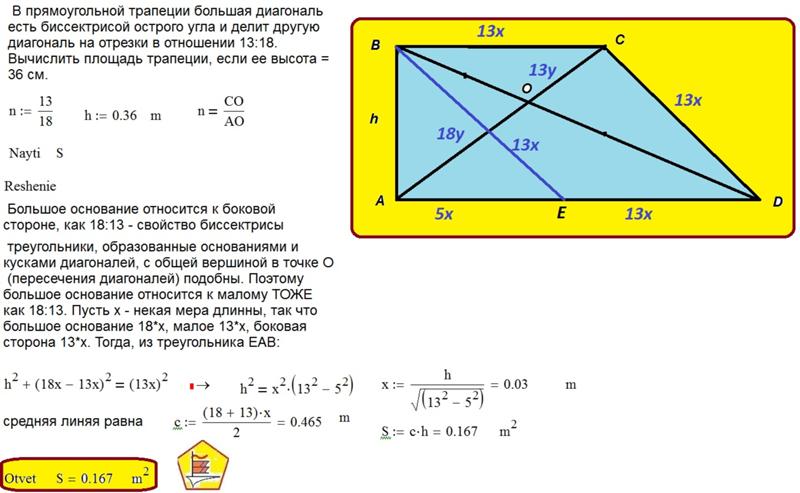 Во время тренировки тренер К. заставляет Кайри бежать из одного правого угла на одном конце площадки в левый угол на другом конце площадки. С точностью до фута, сколько пробежал Кирие?
Во время тренировки тренер К. заставляет Кайри бежать из одного правого угла на одном конце площадки в левый угол на другом конце площадки. С точностью до фута, сколько пробежал Кирие?
Возможные ответы:
Правильный ответ:
Объяснение:
Картинка очень помогает решить эту задачу, поэтому мы начнем с прямоугольной баскетбольной площадки.
Заметим, что расстояние, пройденное Кирие (обозначено красным), является диагональю нашего прямоугольника, который мы назовем . Нам также не следует, что эта диагональ делит наш прямоугольник на два конгруэнтных прямоугольных треугольника. Поэтому мы можем найти длину нашей диагонали, сосредоточившись на одном из этих треугольников и определив гипотенузу. Это можно сделать с помощью теоремы Пифагора, которая дает нам:
Извлечение квадратного корня дает нам
Округление до ближайшего фута дает ответ 98.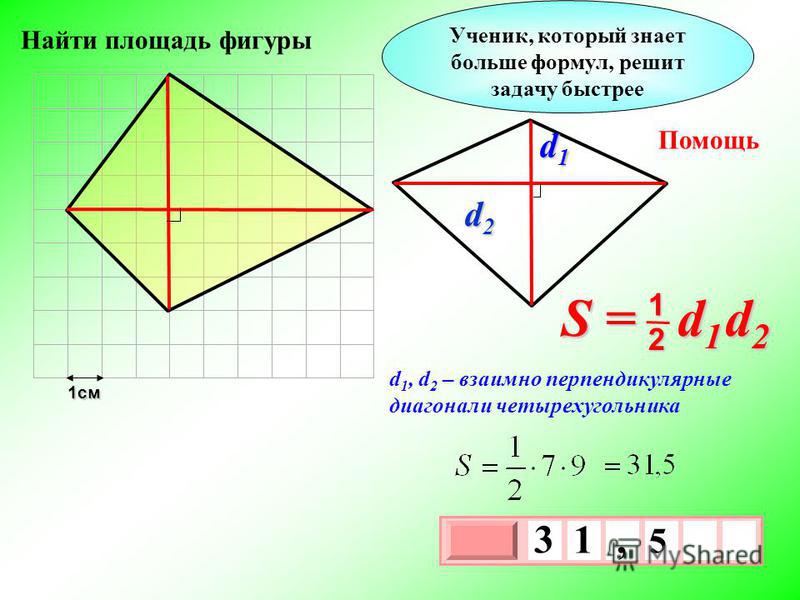
Сообщить об ошибке
Прямоугольник имеет высоту . Какова длина его диагонали, округленная до десятых?
Возможные ответы:
Правильный ответ:
Объяснение:
1. Используйте теорему Пифагора с и .
Сообщить об ошибке
Стороны прямоугольника ABCD равны 4 дюймам и 13 дюймам.
Какова длина диагонали прямоугольника ABCD?
Возможные ответы:
Правильный ответ:
Объяснение:
Диагональ прямоугольника делит прямоугольник на 2 прямоугольных треугольника со сторонами, равными сторонам прямоугольника, и с гипотенузой, являющейся диагональю. Все, что вам нужно сделать, это использовать теорему Пифагора:
где a и b — стороны прямоугольника, а c — длина диагонали.
Сообщить об ошибке
Найдите длину диагонали прямоугольника, имеющего длину и ширину .
Возможные ответы:
Правильный ответ:
Пояснение:
Диагональ прямоугольника также является гипотенузой прямоугольного треугольника, катетами которого являются длина и ширина прямоугольника.
Затем мы можем использовать теорему Пифгора, чтобы найти диагональ.
Для заданного прямоугольника
Сообщить об ошибке
Найдите длину диагонали прямоугольника, имеющего длину и ширину .
Возможные ответы:
Правильный ответ:
Пояснение:
Диагональ прямоугольника также является гипотенузой прямоугольного треугольника, катетами которого являются длина и ширина прямоугольника.
Затем мы можем использовать теорему Пифгора, чтобы найти диагональ.
Для заданного прямоугольника
Сообщить об ошибке
Найдите длину диагонали прямоугольника, имеющего длину и ширину .
Возможные ответы:
Правильный ответ:
Пояснение:
Диагональ прямоугольника также является гипотенузой прямоугольного треугольника, катетами которого являются длина и ширина прямоугольника.
Затем мы можем использовать теорему Пифгора, чтобы найти диагональ.
Для заданного прямоугольника
Сообщить об ошибке
Найдите длину диагонали прямоугольника, имеющего длину и ширину .
Возможные ответы:
Правильный ответ:
Пояснение:
Диагональ прямоугольника также является гипотенузой прямоугольного треугольника, катетами которого являются длина и ширина прямоугольника.
Затем мы можем использовать теорему Пифгора, чтобы найти диагональ.
Для заданного прямоугольника
Сообщить об ошибке
← Предыдущий 1 2 3 4 Далее →
Уведомление об авторских правах
Все ресурсы по базовой геометрии
9 Диагностические тесты 164 практических теста Вопрос дня Карточки Изучите концепцию
Площадь прямоугольника размером 24 x 16 и геометрические свойства, такие как симметрия, периметр прямоугольника, диагонали
Нам дано, что длина прямоугольника = 24,0 единицы, а ширина = 16,0 единицы. н.э. = до н.э. = 24,0 ед. А АВ = CD = 16,0 ед. Единицами могут быть любые единицы длины: дюймы, см, футы, мили, км и т. д. Геометрические свойства, которые мы вычислим Вычислим площадь, периметр, длину диагонали, радиус описанной окружности, площадь описанной окружности и углы, образуемые диагональю со сторонами. Вычисление площади прямоугольника Площадь этого прямоугольника = длина х ширина (длина х ширина) = 24,0 х 16,0 = 384,0 кв. шт. Вычисление периметра прямоугольникаПериметр этого прямоугольника = 2 * (длина + ширина) = 2 * (24,0 + 16,0) = 80,0 единиц Диагональ этого прямоугольника может быть вычислена с помощью теоремы Пифагора (или теоремы Пифагора). Треугольники ADC (или BDC) являются прямоугольными треугольниками. Итак, диагональ(и) можно рассматривать как гипотенузу прямоугольного треугольника. Таким образом, квадрат длины диагонали равен сумме квадратов длины и ширины. Длина диагоналей AC и BD = (24,0 2 + 16,0 2 ) (1/2) Итак, длина диагонали = 28,84 единицы Вычисление радиуса и площади описанной окружности На самом деле у прямоугольника нет вписанной окружности, которая касается каждой стороны. Однако действительно возможно нарисовать окружность, проходящую через все 4 вершины прямоугольника. Обе диагонали являются диаметрами окружности. Угол в полуокружности является прямым углом: каждый из 4 углов прямоугольника становится углом полукруга, когда мы рисуем описанную окружность. Радиус описанной окружности = половина длины диагонали = 28,84/2 единицы = 14,42 единицы Площадь описанной окружности = PI x радиус окружности2 = PI * 14,42 * 14,42 = 653,45 квадратных единиц Симметрия и оси симметрии Прямоугольник имеет 2 оси симметрии: прямую, проходящую через середины сторон AB и CD, и другую прямую, проходящую через середины сторон AD и BC. Оба проходят через точку E. Прямоугольник также является «изогональным» по своей природе, хотя это понятие вы, возможно, изучите или столкнетесь с ним позже. Вычисление угла, образованного диагональю со сторонами Мы можем использовать немного тригонометрии, чтобы вычислить это. Тангенс угла CAD = Тангенс угла ACB = ширина прямоугольника / длина прямоугольника = 16,0/24,0 = 0,67 Угол CAD = Угол ACB = tan -1 0,67 = 0,59 радиан = 33,69градусов и угол BAC = угол ACD = 90 градусов — угол CAD = 0,98 радиана = 56,31 градуса Примеры конгруэнтности и конгруэнтных треугольников Каждая диагональ делит прямоугольник на пару конгруэнтных треугольников. ДиагональBD делит прямоугольник на равные треугольники BAD и BCD. Доказательство: (a) Угол BAD = угол BCD = 90 градусов (прямой угол) (b) BD общая сторона обоих (гипотенуза) (c) BA = CD = 16,0 единиц (противоположные стороны прямоугольника равны) (d) AD = BC = 24,0 единицы (противоположные стороны прямоугольника равны) Используя (a) (b) и (c), два треугольника конгруэнтны, используя конгруэнтность RHS или HL (гипотенуза-катет). Или с использованием (c) (a) и (d) два треугольника конгруэнтны с использованием конгруэнтности SAS (сторона-угол-сторона) Аналогично можно доказать, что АС делит прямоугольник на два равных треугольника. Кроме того, две диагонали делят прямоугольник на две пары конгруэнтных треугольников (Треугольник AEB и треугольник CED конгруэнтны, треугольник BEC и треугольник AED конгруэнтны) Чтобы доказать, что треугольники AEB и треугольники CED равны: (a) AB = CD = 16,0 единиц (противоположные стороны прямоугольника равны) (б) Угол ABD = Угол CDB (AB параллелен CD, а BD — их секущая, это противоположные углы, значит, они равны) (c) Угол BAC = угол DCA (по той же причине, что и выше) (d) Угол BEA = угол CED (противоположные или вертикальные углы равны) Итак, мы можем доказать конгруэнтность двух треугольников с помощью ASA Congruence (используя (c) (a) (b)) Или мы можем доказать конгруэнтность двух треугольников с помощью конгруэнтности AAS (используя (d)(b)(a)) Аналогичным образом мы можем доказать, что треугольники BEC и AED равны. Помните: прямоугольник — это четырехугольник с 4 прямыми углами. Противоположные стороны равны. Все свойства, применимые к параллелограммам, применимы и к прямоугольникам. Квадрат можно рассматривать как частный случай прямоугольника, у которого все стороны равны. Каждый прямоугольник представляет собой выпуклый многоугольник и вписанный четырехугольник, диагональ которого представляет собой диаметр описанной окружности. Несколько примеров для иллюстрации похожих прямоугольников, преобразования размеров, коэффициента масштабирования и геометрического подобия.Эти учебные пособия по подобным треугольникам, масштабному коэффициенту и преобразованию размеров также могут быть полезны. Несколько примеров для иллюстрации подобных прямоугольников, преобразования размеров, масштабного коэффициента и геометрического подобияПример: Пусть текущий прямоугольник (с размерами 24,0 x 16,0) будет прямоугольником A. Теперь рассмотрим другой прямоугольник B (размерами 12,0 x 8,0) Оба эти прямоугольника геометрически подобны, так как отношения длин соответствующих сторон равны. Длина прямоугольника A : Длина прямоугольника B = Ширина прямоугольника A : Ширина прямоугольника B 24,0 : 12,0 = 16,0 : 8,0 = 2,0 : 1 А отношение их площадей: Площадь прямоугольника A : Площадь прямоугольника B = 384,0 : 96,0 = 4,0 : 1 Масштабный коэффициент между A:B = длина прямоугольника A : длина прямоугольника B = 24,0 : 12,0 = 2,0 Обратите внимание, что отношение площадей равно квадрату отношения соответствующих сторон (или масштабному коэффициенту). Это пример преобразования размера в 2D-фигурах: , когда все стороны фигуры умножаются на отношение R , площадь новой фигуры в R 2 умножается на площадь исходной фигуры. Несколько примеров для иллюстрации подобных прямоугольников, преобразования размеров, масштабного коэффициента и геометрического подобияПример: Пусть текущий прямоугольник (с размерами 24,0 x 16,0) будет прямоугольником A. Теперь рассмотрим другой прямоугольник B (размерами 6,0 x 4,0) Оба эти прямоугольника геометрически подобны, так как отношения длин соответствующих сторон равны. Длина прямоугольника A : Длина прямоугольника B = Ширина прямоугольника A : Ширина прямоугольника B 24,0 : 6,0 = 16,0 : 4,0 = 4,0 : 1 А отношение их площадей: Площадь прямоугольника A : Площадь прямоугольника B = 384,0 : 24,0 = 16,0 : 1 Масштабный коэффициент между A:B = длина прямоугольника A : длина прямоугольника B = 24,0 : 6,0 = 4,0 Обратите внимание, что отношение площадей равно квадрату отношения соответствующих сторон (или масштабному коэффициенту). Это пример преобразования размера в 2D-фигурах: , когда все стороны фигуры умножаются на отношение R , площадь новой фигуры в R 2 умножается на площадь исходной фигуры. Несколько примеров для иллюстрации подобных прямоугольников, преобразования размеров, масштабного коэффициента и геометрического подобияПример: Пусть текущий прямоугольник (с размерами 24,0 x 16,0) будет прямоугольником A. Теперь рассмотрим другой прямоугольник B (размерами 3,0 x 2,0) Оба эти прямоугольника геометрически подобны, так как отношения длин соответствующих сторон равны. Длина прямоугольника A : Длина прямоугольника B = Ширина прямоугольника A : Ширина прямоугольника B 24,0 : 3,0 = 16,0 : 2,0 = 8,0 : 1 А отношение их площадей: Площадь прямоугольника A : Площадь прямоугольника B = 384,0 : 6,0 = 64,0 : 1 Масштабный коэффициент между A:B = длина прямоугольника A : длина прямоугольника B = 24,0 : 3,0 = 8,0 Обратите внимание, что отношение площадей равно квадрату отношения соответствующих сторон (или масштабному коэффициенту). Это пример преобразования размера в 2D-фигурах: если все стороны фигуры умножить на коэффициент R площадь новой фигуры равна R 2 площадь исходной фигуры. Еще несколько примеров: Геометрические свойства прямоугольника размером 25 x 16. Геометрические свойства прямоугольника размером 25 x 17. Чтобы узнать больше о геометрических особенностях и свойствах прямоугольников, формулах, связанных с измерением и т. д., вы можете найти это полезным. чтобы прочитать свойства учебника Rectangle здесь. Многие из этих концепций являются частью программы по математике для 9 и 10 классов программы GCSE в Великобритании, Common Core Standards в США, программы ICSE/CBSE/SSC в Индии. Вы можете ознакомиться с нашими бесплатными и печатными рабочими листами для Common Core и GCSE. |
Что такое диагональ? — Определение, факты и примеры
Диагонали в геометрии
Многоугольник определяется как плоская или плоская двумерная замкнутая форма, ограниченная прямыми сторонами. Диагональ — это отрезок, соединяющий противоположные вершины (или углы) многоугольника. Другими словами, диагональ — это отрезок, соединяющий две несмежные вершины многоугольника. Он соединяет вершины многоугольника, исключая ребра фигуры.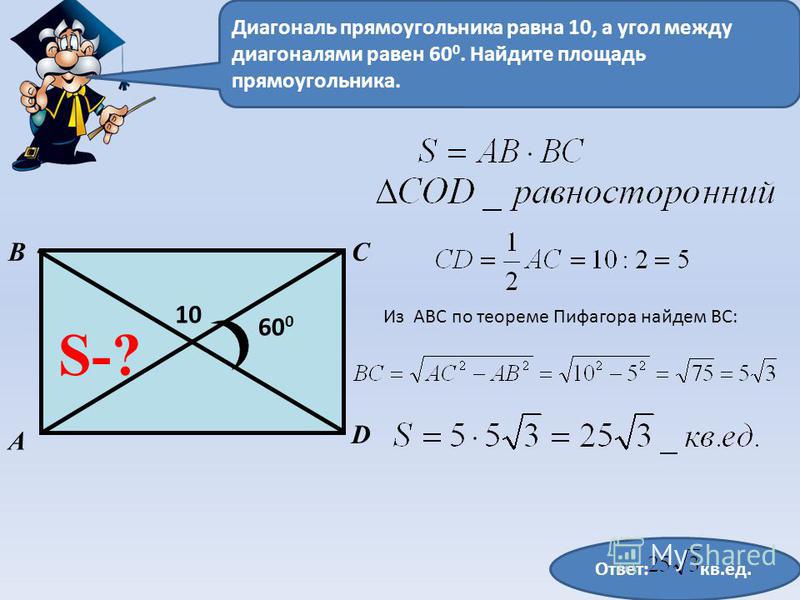 На следующих фигурах нарисованы диагонали:
На следующих фигурах нарисованы диагонали:
История диагонали
Слово «диагональ» происходит от древнегреческого слова diagonios , что означает «от угла к углу». И Евклид, и Страбон использовали его для описания линии, соединяющей две вершины прямоугольного параллелепипеда или ромба; позже он стал известен на латыни как diagonus (наклонная линия).
Диагонали многоугольника
Формула диагонали
Диагонали для многоугольников всех форм и размеров могут быть изготовлены и для любой формы; есть формула для определения количества диагоналей.
Количество диагоналей в многоугольнике с n вершинами = $\frac{n(n-3)}{2}$
Итак, по этой формуле мы можем легко вычислить количество диагоналей в многоугольнике.
В данной таблице показано количество диагоналей в различных многоугольниках:
Диагонали объемных фигур
Как и у многоугольников, у объемных фигур также есть диагонали. В зависимости от количества ребер количество и свойства диагоналей различаются для разных тел. На следующих телах проведены диагонали:
На следующих телах проведены диагонали:
Длина диагонали
Длина диагоналей любой формы зависит от размеров их сторон.
Длина диагонали квадрата
Длину диагонали квадрата можно определить по теореме Пифагора. Диагональ квадрата делит его на два прямоугольных треугольника. Применяя теорему Пифагора, мы можем найти длину диагонали (d) квадрата со стороной (a) как a$\sqrt{2}$.
Длина диагонали квадрата с каждой стороной a единиц = a$\sqrt{2}$ единиц 9{2}}$, где d — диагональ, l — длина, а b — ширина прямоугольника.
Решенные примеры
- Каково общее количество диагоналей в многоугольнике с 12 сторонами?
Решение:
Количество диагоналей в многоугольнике с n вершинами = $\frac{n(n-3)}{2}$
Следовательно, количество диагоналей в многоугольнике с 12 сторонами = $\frac{12(12-3)}{2}$ = 54
- Какова длина диагонали квадрата со стороной 6 см?
Решение:
Сторона, A = 6 см
Длина диагонала = a $ \ times \ sqrt {2} $
= 6 $ \ times \ sqrt {2} $ 9000 39666 = 6 $ \ times \ sqrt {2} $
66 = 6 $ \ times \ sqrt {2} $
66 = 6 $ \ times \ sqrt {2} $
66 = 6 $ \ sqrt {2} $
6 = 6 $ \ times \ sqrt {2} $
6 = 6 $ \ times \ sqrt {2} $
6 = 6 $ \ sqrt $\sqrt{2}$ см
- Рахул прогуливается по прямоугольному парку длиной 20 и шириной 15 метров.
 Определить диагональ прямоугольного парка.
Определить диагональ прямоугольного парка.
Решение:
Длина прямоугольного парка = 20 м, Ширина прямоугольного парка = 15 м 9{2}}$
= $\sqrt{400 + 225}$
= $\sqrt{625}$
= 25 m
Practice Problems
5
6
8
9
Правильный ответ: 9
Количество диагоналей в шестиугольнике (6 вершин) = $\frac{6(6-3)}{2}$ = 9
$\sqrt{10}$ см
2$\sqrt{ 10}$ см
10 см
20 см 9{2}}$ = $\sqrt{4+36}$ = $\sqrt{40}$ = $2\sqrt{10}$ см
6 см
24 см
3$\sqrt{2}$ см
24$\sqrt{2}$ см
Правильный ответ: 24 см
Диагональ квадрата со стороной a равна a$\sqrt{2}$ . Поскольку a$\sqrt{2}$ = 6$\sqrt{2}$, a должно быть 6 см.
Следовательно, периметр квадрата должен быть 4 × 6 см или 24 см.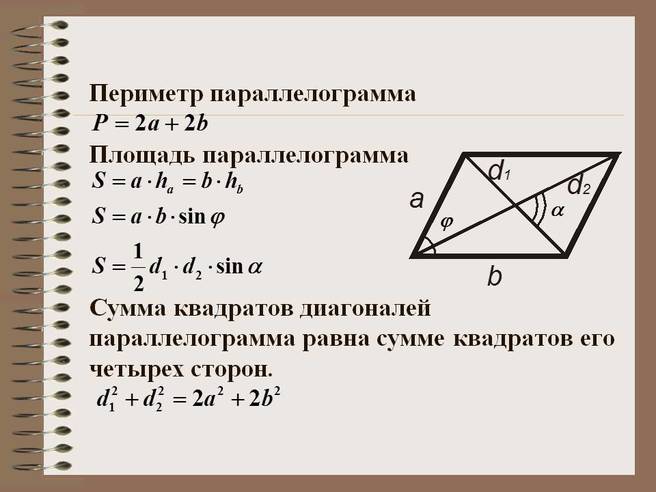

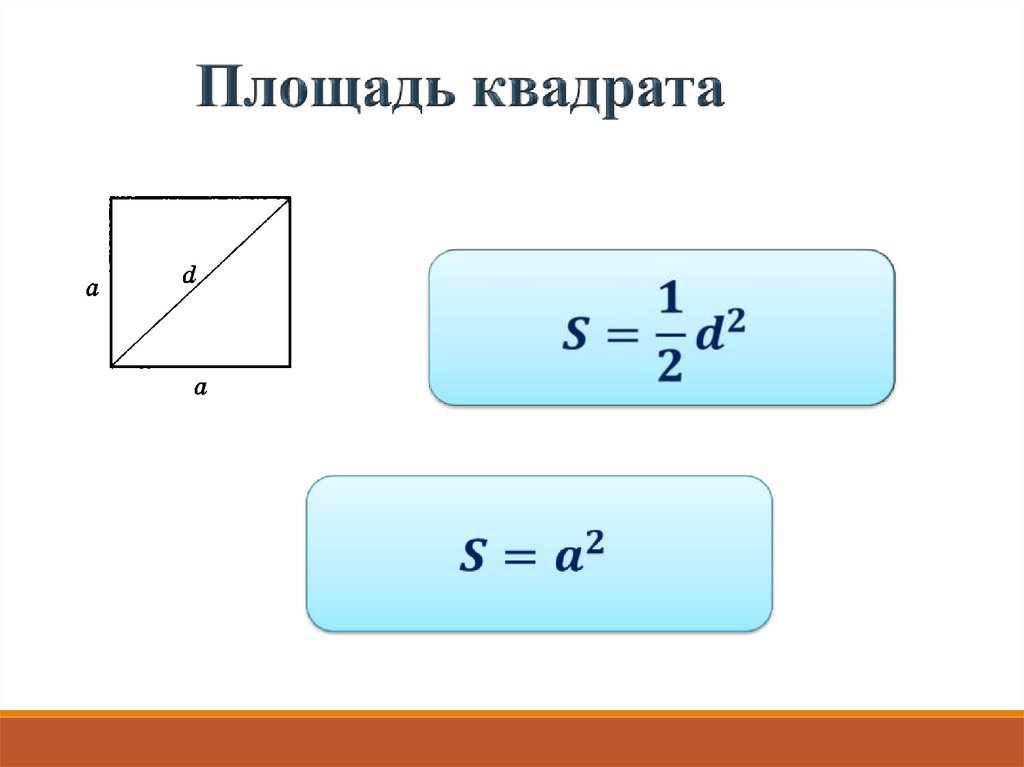





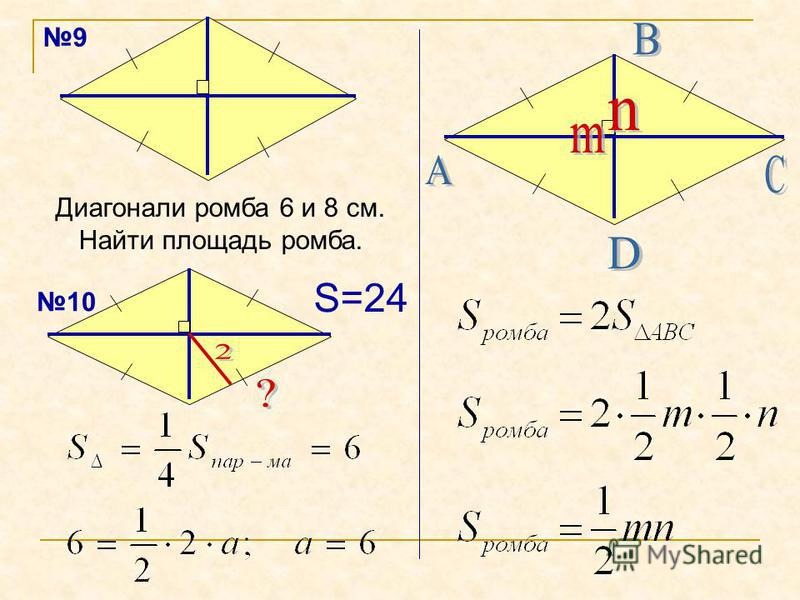 В этом случае могут пригодиться формулы.
В этом случае могут пригодиться формулы.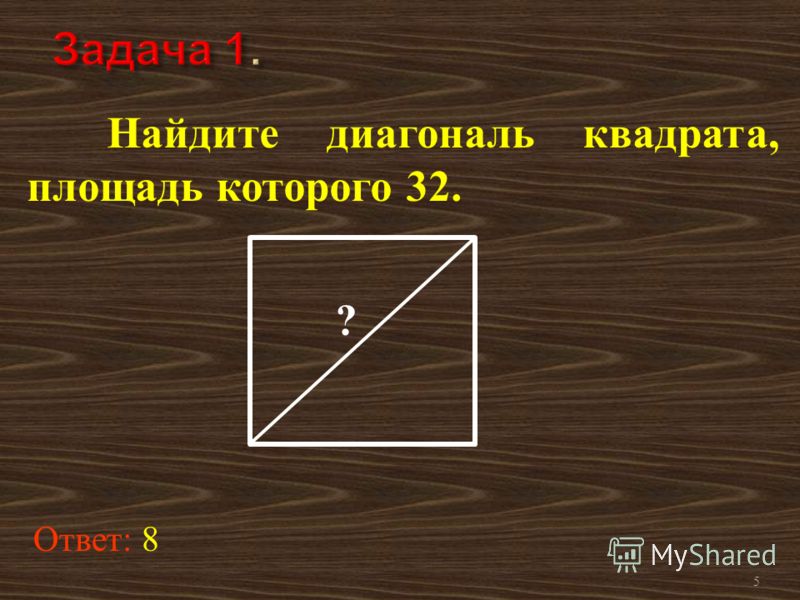

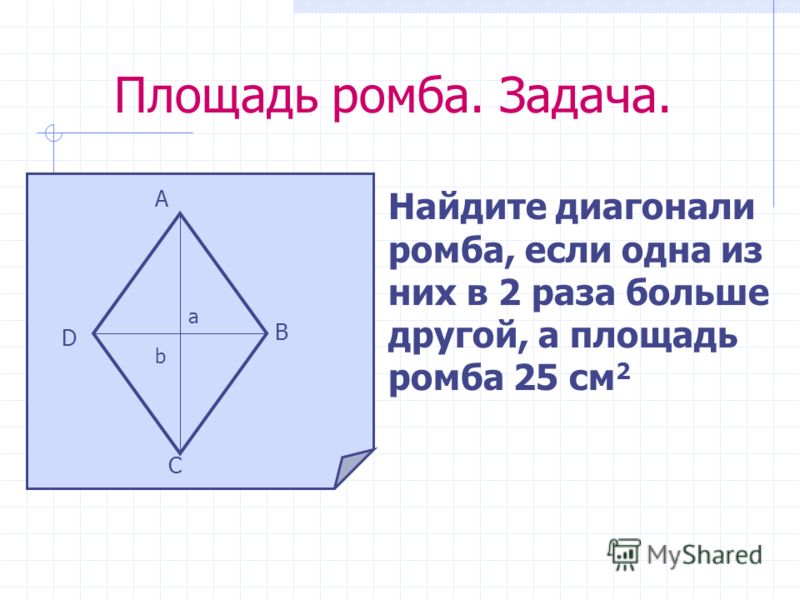
 Для наглядности возьмем квадрат со стороной 8 см и введем это значение в пустое поле калькулятора:
Для наглядности возьмем квадрат со стороной 8 см и введем это значение в пустое поле калькулятора: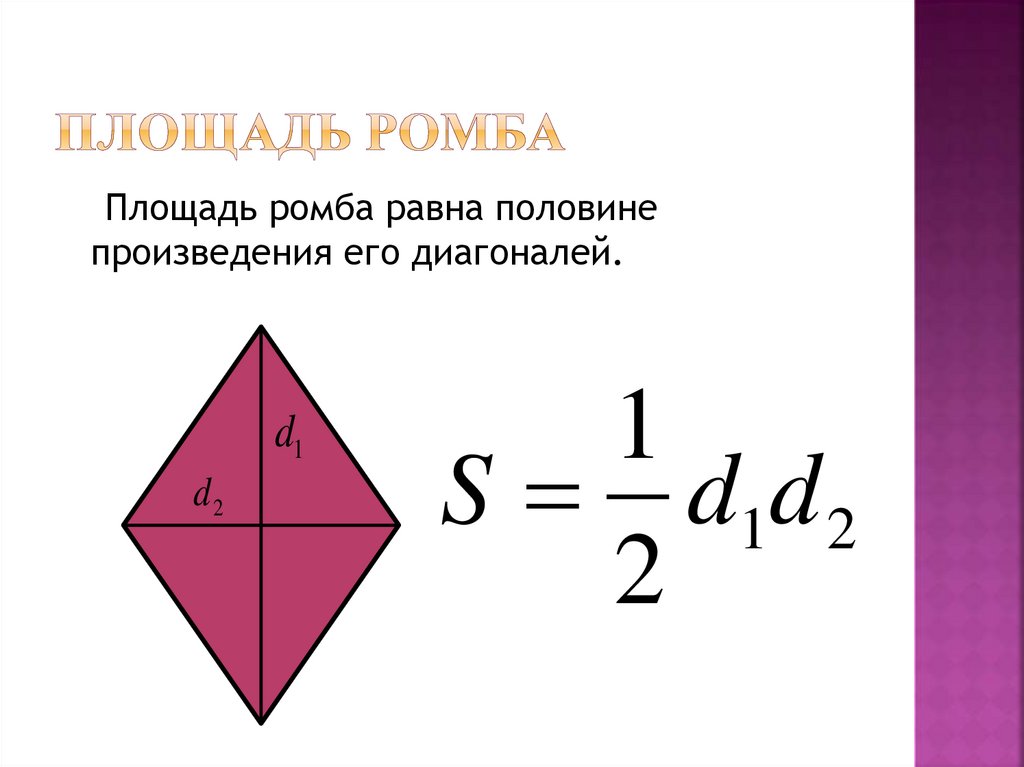


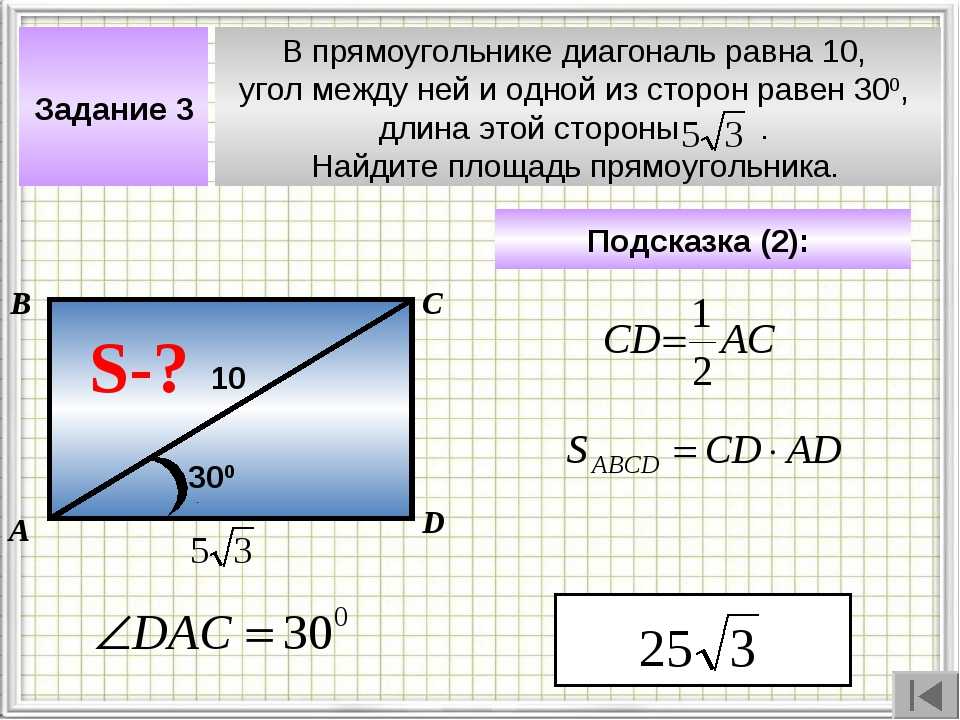

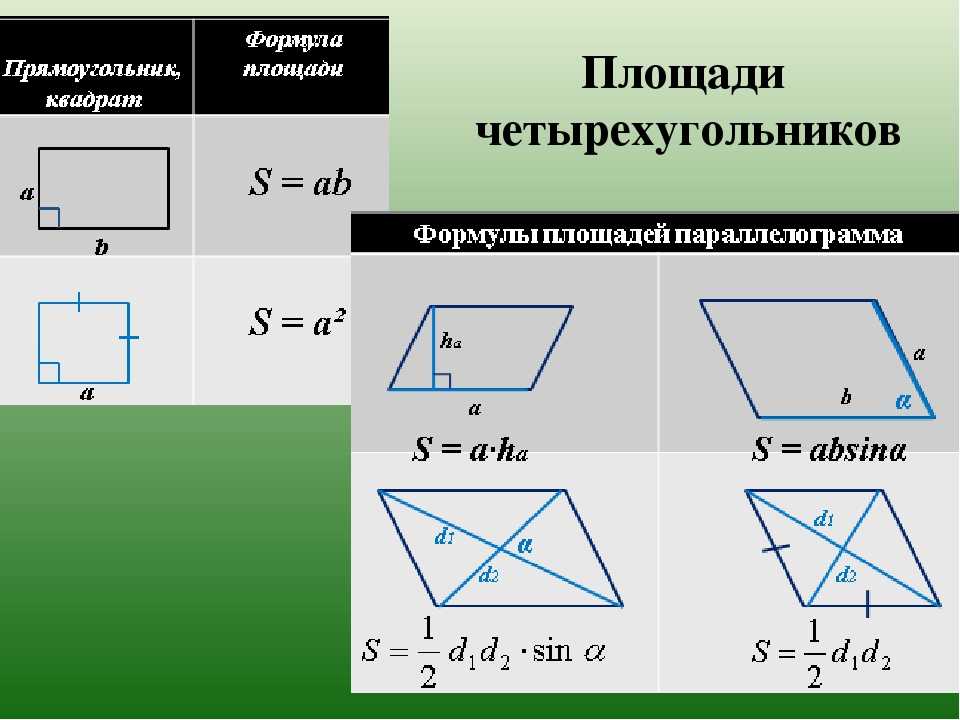

 Это будет 32 = 4 × длина стороны. Следовательно, длина стороны будет равна 8 единицам.
Это будет 32 = 4 × длина стороны. Следовательно, длина стороны будет равна 8 единицам.
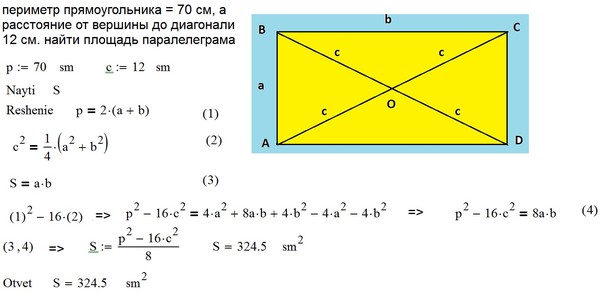 Это возможно только в предельном случае, когда длина и ширина равны и это квадрат.
Это возможно только в предельном случае, когда длина и ширина равны и это квадрат.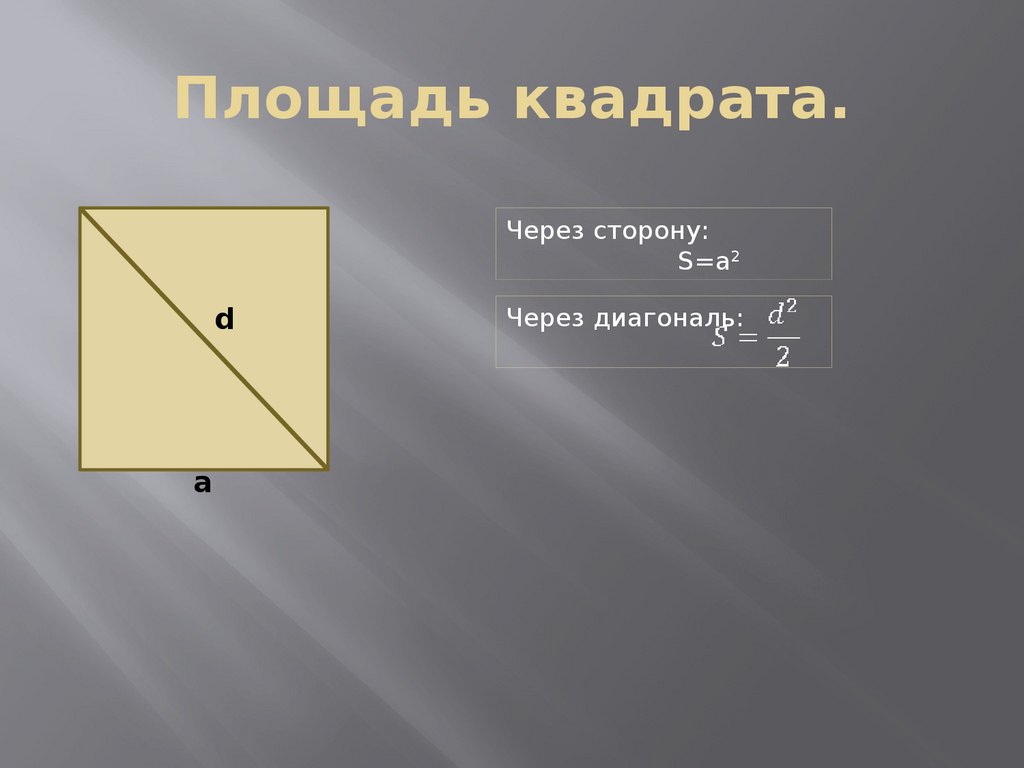


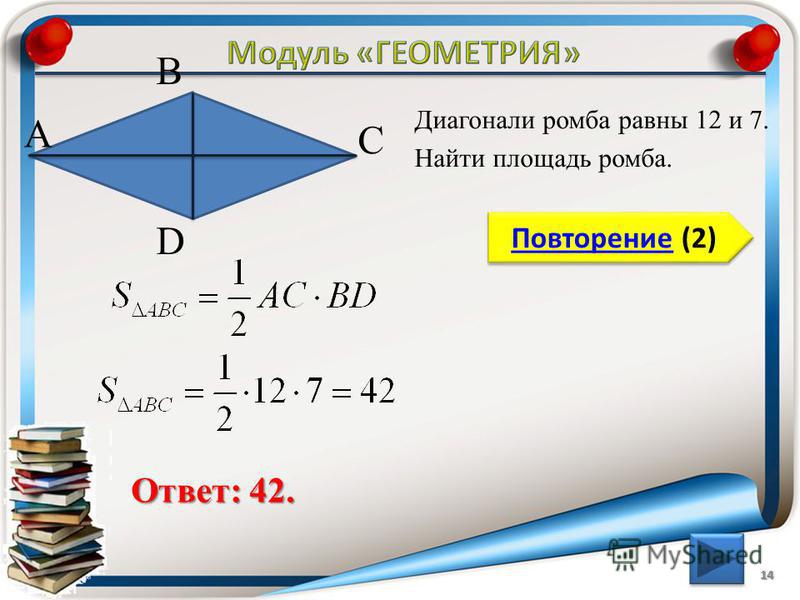



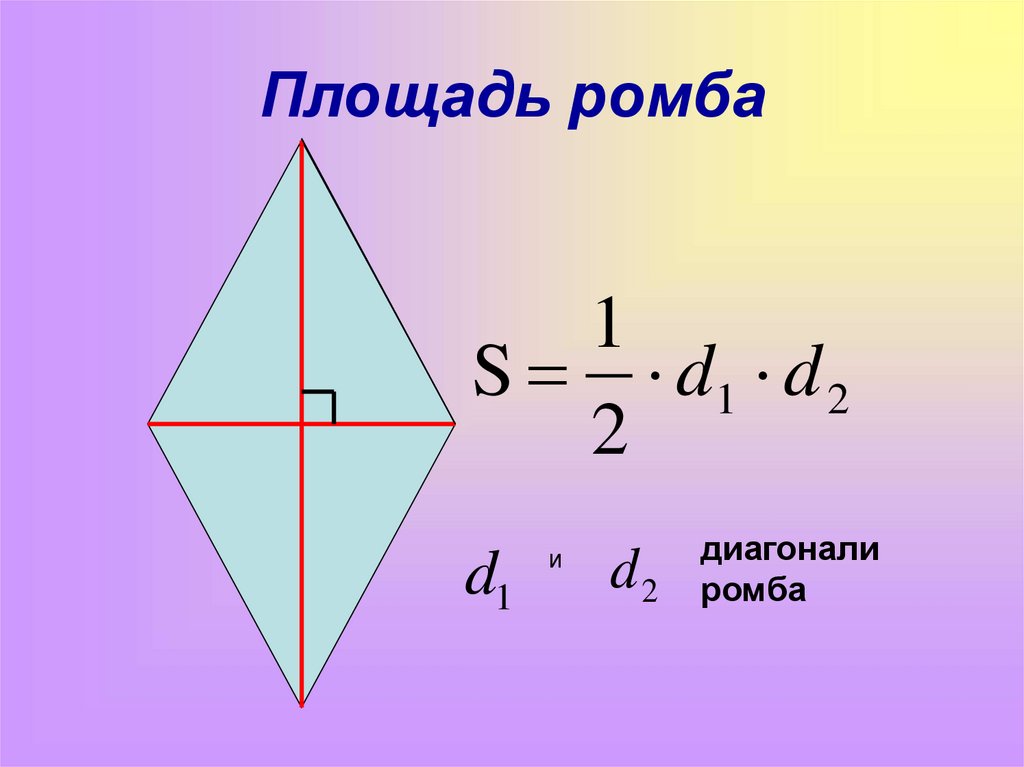 Определить диагональ прямоугольного парка.
Определить диагональ прямоугольного парка.