С векторы: Векторы в C++. Методы класса std::vector — push_back, clear, size

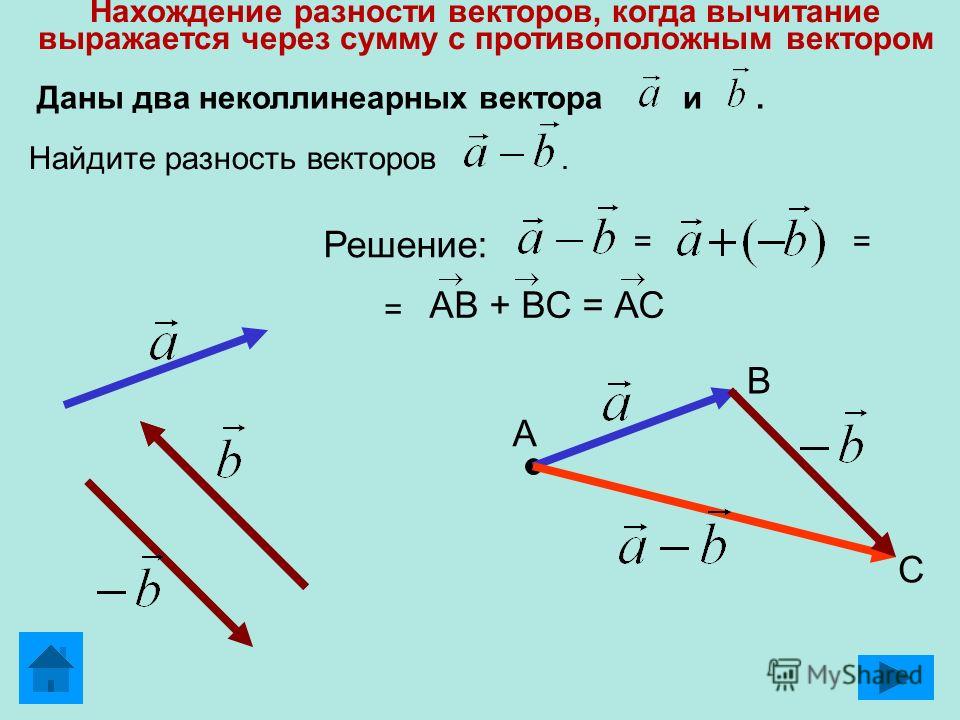
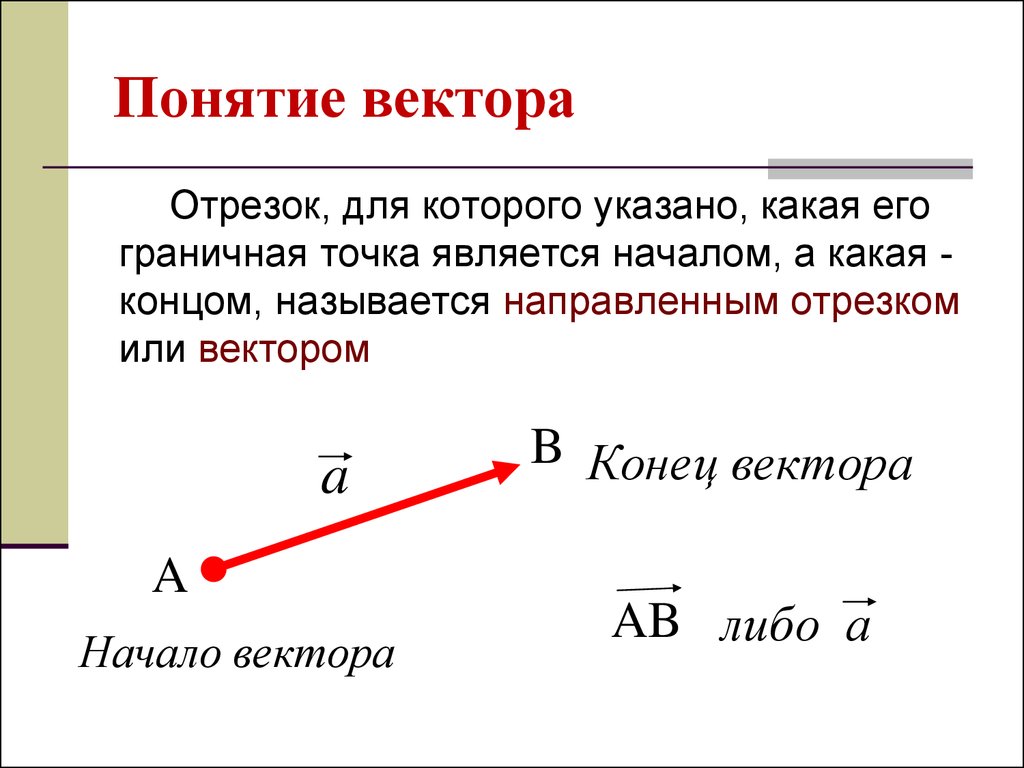
Векторы, действия с векторами

• Справочник
• Онлайн-калькуляторы
• Тесты с ответами

Векторы

• В

  • Векторное произведение
  • Векторное пространство
  • Векторы на плоскости и в пространстве

• Г

  • Геометрическая фигура угол

• Д

  • Деление отрезка в заданном соотношении
  • Длина вектора

• К

  • Компланарные векторы и условие компланарности
  • Координатная прямая (числовая прямая), координатный луч
  • Координаты вектора в ДСК

• Л

  • Линейная зависимость системы векторов

• Н

  • Нахождение вектора, перпендикулярного данному вектору
  • Нахождение координат вектора
  • Нахождение середины отрезка
  • Нахождение угла между векторами: примеры и решения

• О

  • Операции над n-мерными векторами
  • Операции над векторами в прямоугольной системе координат
  • Операции над векторами и их свойства
  • Ортогональные векторы и условие ортогональности
• П

  • Проекция вектора на ось и числовая проекция
  • Прямоугольная система координат на плоскости и в пространстве

• Р

  • Расстояние между точками

• С

  • Скалярное произведение векторов
  • Смешанное произведение векторов

• У

  • Условие коллинеарности векторов

• Выражения
• Действительные, рациональные, иррациональные числа
• Делимость
• Дифференциальные уравнения
• Интегралы, методы интегрирования
• Все темы по математике

• Курсовые работы
• Рефераты
• Контрольные работы
• Отчет по практике
• Эссе

Узнать подробнее

Проектная практика Строительная компания Renaissance Construction

• Вид работы:

  Отчёт по практике

• Выполнена:

  7 июля 2022 г.

• Стоимость:

  4 500 руб

Заказать такую же работу

Маленький сад возле жилого дома

• Вид работы:

  Курсовая работа

• Выполнена:

  23 мая 2022 г.

• Стоимость:

  4 800 руб

Заказать такую же работу

Дистанционный экзамен

Заказать такую же работу

Высшая математика

Заказать такую же работу

выполнить две практические работы

• Вид работы:

  Решение задач

• Выполнена:

  8 мая 2022 г.

• Стоимость:

  6 700 руб

Заказать такую же работу

В обоих файлах необходимо выполнить только вариант

• Вид работы:

  Решение задач

• Выполнена:

  30 апреля 2022 г.

• Стоимость:

  1 000 руб

Заказать такую же работу

Смотреть все работы по строительству

Не получается написать работу самому?

Доверь это кандидату наук!

Действия с векторами в координатах



Ранее мы рассмотрели правила сложения векторов и умножения вектора на число. Но рассмотрели их с принципиально-графической точки зрения. Посмотрим, как данные правила работают аналитически – когда нам известны координаты векторов в ортонормированном базисе  либо :

1) Правило сложения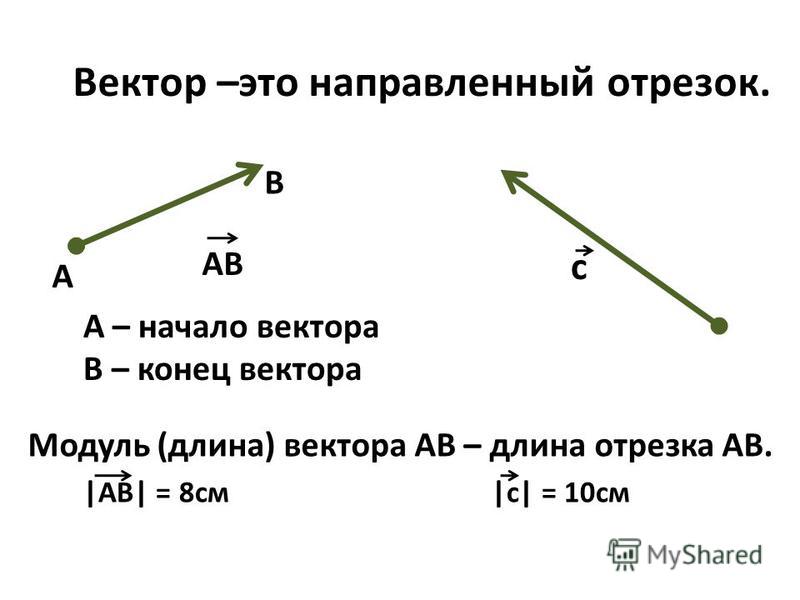 векторов. Пусть есть два вектора плоскости  и . Для того, чтобы сложить эти векторы, нужно сложить их соответствующие координаты: . Как просто. На всякий случай запишу частный случай – формулу разности векторов: .
Аналогичное правило справедливо для суммы любого количества векторов, добавим например, вектор , и результат понятен:
Если речь идёт о векторах в пространстве, то всё точно так же, только добавится дополнительная координата. Если даны векторы , то их суммой является вектор .

2) Правило умножения вектора на число. Ещё проще! Для того чтобы вектор  умножить на число , нужно каждую координату данного вектора умножить на число :
.
Для пространственного вектора  правило такое же:

Задача 7

Даны векторы  и . Найти  и

Решение чисто аналитическое:

Ответ:

Чертеж в подобных задачах строить не надо, тем не менее, геометрическая демонстрация будет весьма полезной.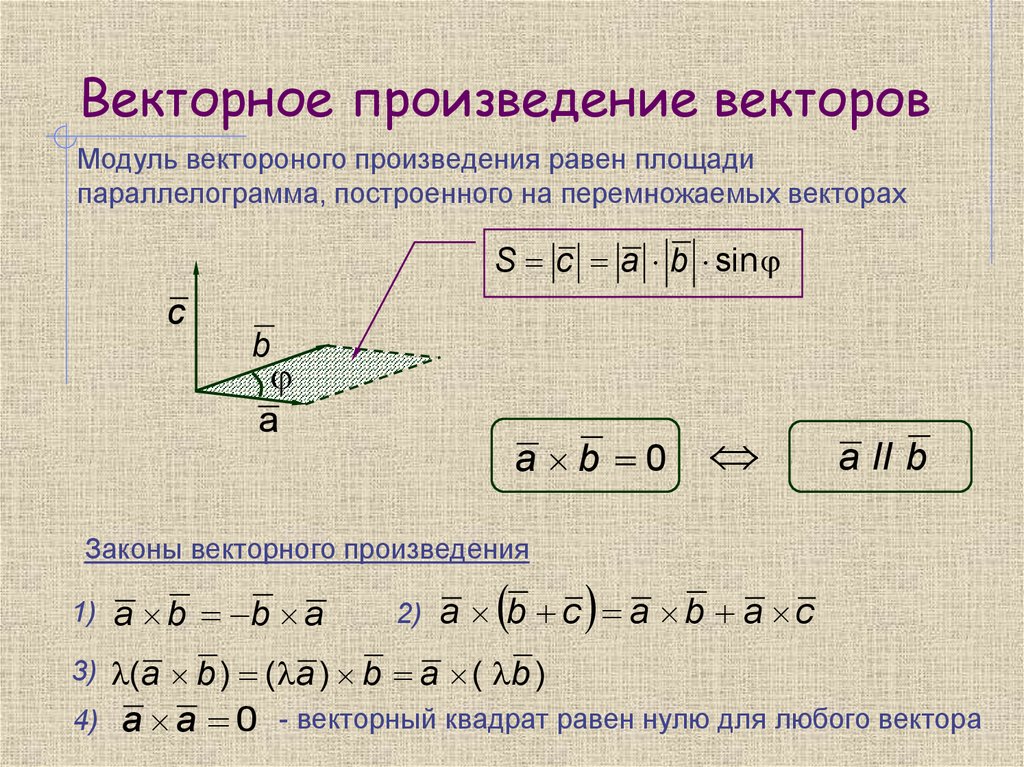 Если считать, что векторы заданы в ортонормированном базисе , то графическое решение задачи будет таким:

Коль скоро речь идет только о векторах, то оси рисовать не обязательно. Достаточно начертить базисные векторы, причём, где угодно. Ну и координатную сетку для удобства. Как видите, графический способ решения привёл к тем же результатам, что и аналитический способ решения. Ещё раз заметьте свободу векторов: любую из трёх «конструкций» можно переместить в любую точку плоскости.

Для векторов в пространстве можно провести аналогичные выкладки. Но там чертежи строить значительно сложнее, поэтому ограничусь аналитическим решением (на практике, собственно, бОльшего и не нужно):

Задача 8

Даны векторы  и . Найти  и

Решение: для действий с векторами справедлив обычный алгебраический приоритет: сначала умножаем, потом складываем:

Ответ:

И для самостоятельного решения занятный пример с векторами на плоскости:

Задача 9

Даны векторы . Найти  и

Решение и ответ в конце книги.

1.5.5. Как найти единичный вектор?

1.5.3. Как найти длину вектора?

| Оглавление |



Автор: Aлeксaндр Eмeлин

Создание, изменение и доступ к векторным элементам

В этой статье вы узнаете о векторах в программировании на R. Вы научитесь создавать их, получать доступ к их элементам с помощью различных методов и изменять их в своей программе.

Вектор — это базовая структура данных в R. Она содержит элементы того же типа. Типы данных могут быть логическими, целочисленными, двойными, символьными, сложными или необработанными.

Тип вектора можно проверить с помощью функции typeof() .

Еще одним важным свойством вектора является его длина. Это количество элементов в векторе, и его можно проверить с помощью функции 9.0007 длина() .

---

Как создать вектор в R?

Векторы обычно создаются с помощью функции c() .

Так как вектор должен иметь элементы одного типа, эта функция попытается привести элементы к одному типу, если они разные.

Приведение от младших к более высоким типам от логического к целому к двойному к символьному.

 > х <- с(1, 5, 4, 9, 0)
> тип(х)
[1] «двойной»
> длина (х)
[1] 5
> x <- c(1, 5.4, ИСТИНА, "привет")
> х
[1] «1» «5.4» «ИСТИНА» «привет»
> тип(х)
[1] "персонаж" 

Если мы хотим создать вектор последовательных чисел, очень полезен оператор : .

Пример 1: Создание вектора с помощью: оператора

 > х <- 1:7; Икс
[1] 1 2 3 4 5 6 7
> у <- 2:-2; у
[1] 2 1 0 -1 -2 

Более сложные последовательности могут быть созданы с помощью функции seq() , например определения количества точек в интервале или размера шага.

Пример 2. Создание вектора с помощью функции seq()

 > seq(1, 3, by=0.2) # указать размер шага
[1] 1,0 1,2 1,4 1,6 1,8 2,0 2,2 2,4 2,6 2,8 3,0
> seq(1, 5, length. out=4) # указать длину вектора
[1] 1,000000 2,333333 3,666667 5,000000
 

---

Как получить доступ к элементам вектора?

Доступ к элементам вектора можно получить с помощью векторной индексации. Вектор, используемый для индексации, может быть логическим, целочисленным или вектором символов.

---

Использование целочисленного вектора в качестве индекса

Индекс вектора в R начинается с 1, в отличие от большинства языков программирования, где индекс начинается с 0.

Мы можем использовать вектор целых чисел в качестве индекса для доступа к определенным элементам.

Мы также можем использовать отрицательные целые числа, чтобы вернуть все элементы, кроме указанных.

Но мы не можем смешивать положительные и отрицательные целые числа, в то время как индексация и действительные числа, если они используются, усекаются до целых чисел.

 > х
[1] 0 2 4 6 8 10
> x[3] # доступ к третьему элементу
[1] 4
> x[c(2, 4)] # доступ ко 2-му и 4-му элементам
[1] 2 6
> x[-1] # доступ ко всем элементам, кроме 1-го
[1] 2 4 6 8 10
> x[c(2, -4)] # нельзя смешивать положительные и отрицательные целые числа
Ошибка в x[c(2, -4)]: только 0 могут быть смешаны с отрицательными нижними индексами
> x[c(2. 4, 3.54)] # действительные числа усекаются до целых
[1] 2 4
 

---

Использование логического вектора в качестве индекса

Когда мы используем логический вектор для индексации, возвращается позиция, где логический вектор равен TRUE .

Эта полезная функция помогает нам фильтровать вектор, как показано ниже.

 > х[с(ИСТИНА, ЛОЖЬ, ЛОЖЬ, ИСТИНА)]
[1] -3 3
> x[x < 0] # фильтрация векторов по условиям
[1] -3 -1
> х [х > 0]
[1] 3
 

В приведенном выше примере выражение x>0 даст логический вектор (ЛОЖЬ, ЛОЖЬ, ЛОЖЬ, ИСТИНА) , который затем используется для индексации.

---

Использование вектора символов в качестве индекса

Этот тип индексации полезен при работе с именованными векторами. Мы можем назвать каждый элемент вектора.

 > x <- c("первый"=3, "второй"=0, "третий"=9)
> имена(х)
[1] "первый" "второй" "третий"
> х["секунда"]
второй
0
> х[с("первый", "третий")]
первая треть
3 9
 

---

Как изменить вектор в R?

Мы можем изменить вектор с помощью оператора присваивания.

Мы можем использовать методы, описанные выше, для доступа к определенным элементам и их модификации.

Если мы хотим обрезать элементы, мы можем использовать переназначения.

 > х
[1] -3 -2 -1 0 1 2
> х[2] <- 0; x # изменить 2-й элемент
[1] -3 0 -1 0 1 2
> х[х<0] <- 5; x # изменить элементы меньше 0
[1] 5 0 5 0 1 2
> х <- х[1:4]; x # обрезать x до первых 4 элементов
[1] 5 0 5 0
 

---

Как удалить вектор?

Мы можем удалить вектор, просто назначив NULL к нему.

 > х
[1] -3 -2 -1 0 1 2
> х <- NULL
> х
НУЛЕВОЙ
> х[4]
НУЛЕВОЙ
 

• ПРЕДЫДУЩИЙ
  Функция R switch()
• СЛЕДУЮЩИЙ
  R Матрица

Полное руководство по C++ Vector

В некоторых аспектах векторы похожи на массивы. Например, они оба являются контейнерами последовательности, что означает, что к ним можно обращаться последовательно. Хотя последовательно можно получить доступ к большему количеству структур данных, в этом руководстве вы узнаете, в частности, о векторах C++.

Что такое вектор C++?

Векторы — это последовательные контейнеры, в которых элементы расположены последовательно или в непрерывном порядке. Они могут изменять свой размер всякий раз, когда элемент вставляется или удаляется.

Рис: векторная диаграмма

Синтаксис:

Рис: векторный синтаксис

Здесь тип объекта — это тип данных объекта, например, int, string и т. д., за которым следует имя переменной.

Вставка и удаление элементов в векторе

В векторе C++ есть несколько функций, которые используются для добавления и удаления нескольких элементов из вектора. Вы изучите эти функции позже, но сначала вы должны понять, как эти элементы вставляются внутрь вектора.

Обычно элементы вставляются в конец вектора. Но всякий раз, когда элемент вставляется в указанную позицию, то есть в место, отличное от конца вектора, он сдвигает все элементы, которые были после этой позиции, в их новую позицию.

В случае удаления, если элементы удаляются с конца или указанной позиции, размер контейнера уменьшится на количество удаленных элементов. Это также удалит элементы, отличные от конца вектора, и заставит элементы сместиться в их новые позиции.

Функции-члены вектора C++

Векторные функции-члены C++ можно разделить на три типа:

• Модификаторы
• Итераторы
• Емкость

Модификаторы

: Как следует из названия, это функции, которые используются для модификации или изменения вектора. Например, assign() используется для очистки существующего значения и присвоения нового значения вектору.

Итераторы: функции итератора используются для перемещения или повторения элементов вектора. Например, функция end() используется для указания на последний элемент вектора.

Емкость: Функции, лежащие в емкости, имеют какое-то отношение к размеру, например, изменение размера вектора. Например, функция resize(n) используется для изменения размера вектора.

Модификаторы

• push_back(): Эта функция позволяет добавить новый элемент в конец вектора.
• pop_back(): используется для удаления или удаления последнего элемента из вектора.
• insert(): эта функция используется для добавления нового элемента перед указанной позицией внутри вектора.
• erase(): используется для удаления элемента из контейнера в указанной позиции или диапазоне.
• swap(): используется для обмена содержимым между векторами, но должен быть одного типа.
• assign(): используется для присвоения нового значения вектору путем замены старого значения.
• clear(): эта функция используется для удаления всех элементов из векторов.

Рис. Пример модификаторов

В этом примере вы видели использование различных функций-модификаторов, таких как assign(), push_back(), pop_back(), insert(), clear().

• Функция assign() назначает от 1 до 9 позиций в векторе. В этой функции первый параметр отображает количество значений, а второй параметр представляет значение, которое необходимо присвоить.
• push_back() добавляет значение 2 в конец вектора.
• pop_back() удаляет это последнее значение вектора.
• вставка () добавляет 7 к началу вектора, потому что в первом параметре, который указывает позицию, вы написали n.begin, что означает, что первый элемент указан, а во втором параметре вы добавили значение , т. е. 7,
• Наконец, функция clear() удаляет все элементы из контейнера.

Ниже показан вывод приведенного выше примера.

Рис: Пример вывода модификаторов

Итераторы

• begin(): эта функция возвращает итератор к первому элементу векторного контейнера.
• end(): эта функция возвращает итератор к последнему элементу векторного контейнера.
• cbegin(): эта функция аналогична функции begin(); единственное отличие состоит в том, что он не может изменять или модифицировать содержимое, на которое указывает.
• cend(): эта функция также возвращает итератор к последнему элементу вектора, как и функция end(), но разница в том, что она не может изменять содержимое, на которое указывает.

Рис. Пример итераторов

В этом примере вы использовали одну функцию модификатора push_back() и две функции итератора begin() и end(). После объявления вектора num вы увидели добавление в него значений с помощью функции push_back(). Затем вы использовали цикл for для печати тех значений, которые вы добавили, то есть 1,2,3,4,5. Здесь num.begin() указывает начало цикла, а num.end() указывает конечную точку цикла.

Ниже приведен вывод приведенного выше примера.

Рис. Пример вывода итераторов

Емкость

• size(): Эта функция используется для возврата количества элементов внутри вектора.

• max_size(): используется для возврата максимального размера вектора.

• resize(n): Эта функция используется для изменения размера контейнера, т. е. если заданный размер больше n, то лишние элементы удаляются. А если размер меньше n, то добавляются какие-то лишние элементы.

• capacity(): Эта функция возвращает размер, который в настоящее время выделен для вектора.

• empty(): проверяет, является ли вектор пустым или нет, и возвращает true, если вектор пуст, иначе возвращает false.

Рис. Пример емкости

В приведенном выше примере вы видели использование одной функции-модификатора push_back() и некоторых функций емкости, таких как size(), capacity(), max_size(), empty(), resize().

Как видно из приведенного ниже вывода, все эти функции выполняют свои собственные функции.

Функция size() возвращает размер контейнера, функция capacity() отображает размер, выделенный контейнеру в данный момент, и так далее.

Рис. Пример вывода емкости

Разница между вектором и массивом

Вектор	Массив
Размер вектора изменяется автоматически при вставке или удалении элементов.	Размер массива фиксирован; вы не можете изменить его после однократной инициализации его размера.
Вектор менее эффективен с точки зрения памяти.	Массив более эффективен; он занимает меньше памяти, чем вектор.
Синтаксис:              vector v1;	Синтаксис:              Int arr[5]={3,2,5,1,6};
Больше подходит, когда над элементами выполняются операции добавления и удаления.	Больше подходит для частого доступа к элементам из-за их индексной структуры.
Векторы могут хранить множество объектов.	Массив может хранить похожие или однородные элементы.

Получите прочную основу для Java, наиболее часто используемого языка программирования в разработке программного обеспечения, с помощью учебного курса сертификации Java.

Заключение

Векторы — это контейнеры последовательностей, которые могут изменять свой размер. В этом руководстве по векторам C++ вы узнали о различных функциях-членах векторов, их функциях и различиях между векторами и массивами.

У вас есть вопросы относительно векторов C++? Если у вас есть, пожалуйста, оставьте их в разделе комментариев. Мы поможем вам решить ваши вопросы. Чтобы узнать больше о том, как инициализировать Vectorin C++ и C++ String, ознакомьтесь с нашим руководством по C++.

Если вы, с другой стороны, ищете более всестороннее обучение, выходящее за рамки C++ и охватывающее самые востребованные языки программирования и навыки, необходимые сегодня, магистерская программа Full Stack Java Developer от Simplilearn окажется именно тем, что вам нужно.