Счет дробей онлайн: Калькулятор для сокращения дробей

Содержание

Тренажер «ДРОБИ» 5-11 классов на сложение, вычитание, умножение или деление | Клуб любителей математики

Данный тренажер является третьим в линейке тренажеров по математике для развития навыков устного счета с удобным, интуитивно-понятным интерфейсом.

Работа тренажера также основана на генерации примеров по математике с различными видами дробей, изучаемых в средних классах школы. Решение примеров способствует развитию скорости и качества устного счёта.

Приложение благоприятно влияет на умственную деятельность как детей, так и взрослых.

Режимы счёта

На странице настроек режима можно задавать необходимые параметры генерации примеров с дробями для любого класса.

Онлайн тренажер «Дроби» позволяет генерировать примеры с любыми видами дробей, с любым из четырёх арифметических действий: «сложение – вычитание» или «умножение – деление».

Кнопки на панели настроек работают по принципу «Вкл/Выкл». Если цвет кнопки зелёный — значит в примерах будут использоваться дроби того типа, который описывает кнопка. Если же цвет серый — этот тип дробей использоваться не будет.

В приложении отсутствуют режимы «Уравнение» и «Сравнение» из-за их избыточной сложности. Работа проходит только в режиме «Пример» с возможным использованием следующих типов дробей:

Разные знаменатели — в примере будут появляться обыкновенные дроби с разными знаменателями.

Неправильные дроби — в примере будут появляться обыкновенные неправильные дроби (числитель больше знаменателя).

Смешанные числа — в примере будут появляться смешанные числа (числа, состоящие из целой и дробной частей).

Десятичные дроби — в примере будут появляться дроби в десятичной записи.

Также имеется возможность включить обязательную проверку ответа на сокращение дробной части числа и выделение целой части числа (если имеется). Понять, нужно ли сокращать ответ можно по красному индикатору * на странице настроек и странице ввода ответа.

Все изменения настроек сразу применяются и Вы тут же можете увидеть как будет выглядеть новый пример в графе «Например». Когда подбор нужных характеристик окончен, нажмите на кнопку ПОЕХАЛИ.

Процесс счёта

Вверху представлены 4 кнопки быстрого доступа: к главной странице сайта, профилю пользователя. Также есть возможность включить/отключить звуковые уведомления или перейти к Подробному решению текущего примера.

Вы решаете заданый пример, вводите ответ по частям (целое, числитель, знаменатель) в соответствующие поля с помощью экранной клавиатуры, нажимаете на кнопку ПРОВЕРИТЬ. Если затрудняетесь дать ответ, воспользуйтесь подсказкой. После проверки ответа Вы увидите сообщение либо о правильно введенном ответе, либо об ошибке.

Количество правильных, неправильных ответов и число подсказок можно увидеть в соответствующих индикаторах.

Прогресс и достижения

Приложение также предусматривает небольшой соревновательный момент через получение медалей за безошибочность — правильное решение N примеров подряд.

Для получения медали, в зависимости от степени её «классности» (бронзовая, серебряная или золотая), необходимо безошибочно решить 20, 50 и 100 примеров соответственно. Медаль высшей категории заменяет собой предыдущую, и выдается единоразово. На полоске прогресса наглядно видно сколько примеров осталось решить для достижения цели. При получении медали прогресс не сбрасывается, таким образом чтобы получить, например, серебряную медаль достаточно решить еще 30 примеров безошибочно.

Если во время решения была использована подсказка, то верный ответ не идет в зачет прогресса. Ошибка же сразу обнуляется весь прогресс. Поэтому будьте максимально осторожны, если хотите получить медаль — один неверный шаг и придется начинать все с начала.

Узнать, получили ли Вы уже медаль за конкретный режим можно на странице «Статистика» в профиле или в самом приложении.

Такой интерфейс делает процесс решения математических примеров более интересным, являясь также простой мотивацией для детей.

Подробное решение примеров

В любой момент работы с тренажером вы можете перейти в разделу «Подробного решения примера», если обычной подсказки в виде верного ответа вам не достаточно.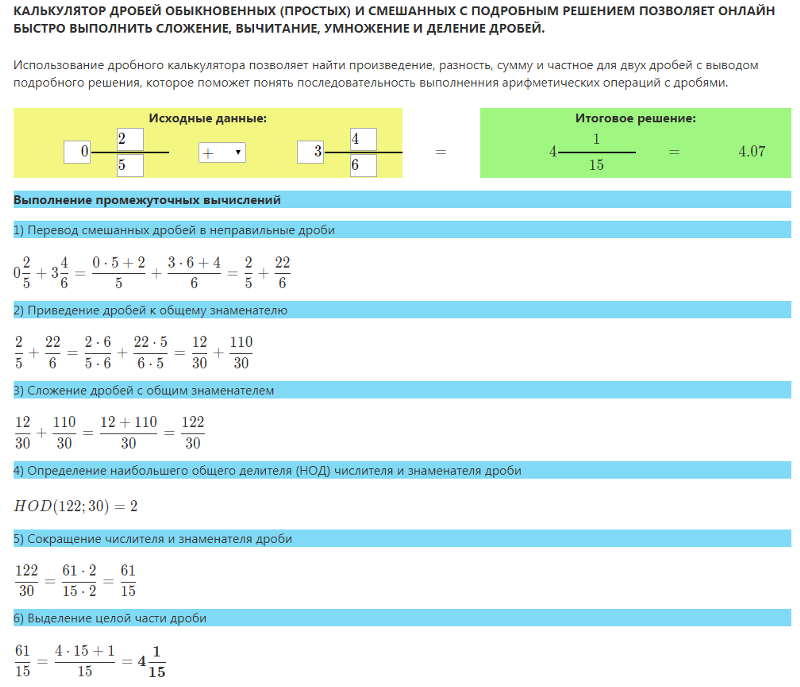 Для этого кликните на соответствующую иконку сверху, либо перелестнув страницу вниз.

Здесь вы сможете посмотреть подробное решение примера с дробями со всеми преобразованиями, сокращениями и упрощениями.

Дополнительная информация

Хотим также обратить внимание, что ссылка на какой-либо режим имеет довольно простой вид:

домен сайта + раздел приложения + кодировка данного режима

например: matematika.club/drobi/#60101

Таким образом Вы легко можете пригласить любого человека посоревноваться в решении арифметических примеров по математике, просто передав ему ссылку на текущий режим.

Действия с обыкновенными дробями. Умножение и деление

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

ДЕЙСТВИЯ С
ОБЫКНОВЕННЫМИ
ДРОБЯМИ
(умножение и
деление).
учитель математики I категории
Сухорукова Фарида Римовна
1. Умножение дробей и смешанных чисел
Контрольная работа
2. Взаимно обратные числа.
3. Деление дробей и смешанных чисел
Контрольная работа
Esc
выход
Умножение дробей и смешанных чисел
Произведение двух обыкновенных дробей
равно дроби, числитель которой равен произведению
числителей, а знаменатель — произведению
знаменателей данных дробей.
4 1 4 1 4
7 3 7 3 21
При умножении необходимо по возможности
сократить.
6 7 6 7 2 1 2
2
7 3 17 31 1 1 1
2
1
Чтобы умножить обыкновенную дробь на натуральное
число, нужно умножить числитель дроби на это число, а
знаменатель оставить тот же.

Сократить и выделить
целую часть.
4
4 3 12
5
3
1
7
7
7
7
1
4
4 3 4 1 4
3
15
15 5 5
5
При умножении смешанных чисел их сначала
обращают в неправильные дроби.
4 7 11 7 11 1 11
2
1
1
7 9 1 7 9 1 9
9
9
1
Вычислить
ПРОВЕРЬ
ОТВЕТЫ
(сократить,
выделить
целую часть)
7 3
11 4
5 14
7 15
21
44
2
3
5 6
6
7 25 35
4 1
2
3 2
5 3
3
1
2
5 3
3
3
1
5
1 3 5
2
6
4
2 1
2 1 2
5
5 6
4 2
2 4 12
7 3
В меню
Взаимно обратные числа
Два числа, произведение которых равно единице,
называют взаимно обратными числами
2 3 2 3
и
1
3 2 3 2
2 3 2 3 5 3
1 и
1 1
3 5
3 5 3 5
Выбери взаимно обратные дроби

5
7
5
11
4
13
1
2
5
1
3
2
1
5
13
4
3
2
4
В меню
Деление дробей и смешанных чисел
Чтобы поделить натуральное число на дробь,
следует число умножить на дробь обратную заданной.

3
4 4 4 16
1
4 4
5
4
3
3
3
3
Чтобы поделить дробь на натуральное число,
следует знаменатель дроби умножить на число.
4
4 3 4 1 4
3
7
7 1 7 3 21
4
4
4
3
7
7 3 21
или
Чтобы разделить одну обыкновенную дробь на другую,
надо умножить первую дробь на дробь, обратную второй.
1 3 1 4 1 4 4
5 4 5 3 5 3 15
4 1 4 4 4 4 16
1
3
5 4 5 1 5 1 5
5
2
1 1 1 10 1 10 2
2
5 10 1 5 1
5 1 1
Чтобы разделить одно смешанное число на другое, надо:
• преобразовать смешанные дроби в неправильные;
• умножить первую дробь на дробь, обратную второй;
• сократить полученную дробь;
• если получилась неправильная дробь преобразовать
неправильную дробь в смешанную.
4
1 9 9 9 4 1 4 4
1 2
5
4 5 4 5 9 5 1 5
1 3 6 4 2 4 8
3
1
1
5 4 5 31 5
5
5
2
Вычислить
ПРОВЕРЬ
ОТВЕТЫ
(сократить, выделить целую часть)
7 3 28
11 4 33
5 15
1
1
7 28
3
5 5
3
7 21
4
1 1
3
5
5 4
2
2
5
15
3
11
5
1 3
18
6
2
1
2 1 2
5
5
4
2
2 1 2
7
7
В меню

English Русский Правила

Онлайн калькулятор: Египетские дроби

Египетская дробь представляет собой сумму уникальных дробей с единичным числителем (единичные дроби). Существует бесконечное количество способов представить дробь в виде суммы единичных дробей. Было разработано несколько методов преобразования дроби в эту форму. Этот калькулятор можно использовать для преобразования дробного числа в египетскую дробь с использованием методов Расщепления, Голомба, Фибоначчи/Сильвестра, Двоичных чисел или методов Блейхера/Эрдеша ¹ . Введите любое число от 0 до 1 в виде десятичной или простой дроби, и калькулятор расширит его до суммы отдельных дробей. Калькулятор также может попытаться найти наилучший метод из перечисленных выше, минимизируя либо сумму знаменателей, либо максимальный знаменатель (подробнее о критериях наилучшего метода см. ниже).

Расширение египетской дроби

Обыкновенная дробь

Метод расширения Лучший метод: Сумма знаменателя Лучший метод: Максимальный знаменатель Двоичный остаток Блейхер/Эрдеш Фибоначчи/Сильвестр Голомб Разделение

Египетские дроби

Метод

Знаменатели

См. египетскую дробь к Преобразователь рациональных чисел для обратного преобразования.
Древние египтяне не использовали упомянутые выше методы разложения дроби для представления дроби в виде единичной суммы дробей. Мы можем считать это анализируя древние документы, сохранившиеся до наших дней. Приведенный ниже калькулятор использует упомянутые выше алгоритмы для расширения дробей с числителем 2 и нечетным знаменателем в диапазоне от 5 до 101 и сравнения результатов с папирусом Райнда (1650 г. до н. э.). Метод Голомба не участвует в сравнении, так как дает те же результаты, что и метод Фибоначчи/Сильвестра для данных папируса Райнда (и всех дробей с числителем = 2 в общем случае).

Папирус Ринда и алгоритмы разложения дробей

Критерии наилучшего алгоритмаТочное совпадение: Двоичный остатокТочное совпадение: Блейхер/ЭрдосТочное совпадение: Фибоначчи/СильвестрТочное совпадение: Папирус РиндТочное совпадение: РазделениеМинимизировать: Сумма знаменателяМинимизировать: Максимум знаменательMinimise : количество иероглифовMinimise : количество иероглифов 2Minimise : Количество терминов

Точность вычислений

Знаки после запятой: 2

Файл очень большой. Во время загрузки и создания может происходить замедление работы браузера.

Следующие критерии сравнения дают наилучшие результаты для исходных данных из папируса Райнда по сравнению с результатами всех методов:

Минимизация: Максимальный знаменатель
Минимизация: сумма знаменателя

Оба критерия сравнения выбирают расширение фракции папируса Райнда как лучшее в 46 из 49 случаев. Методы Фибоначчи/Сильвестра выигрывают для минимизации: количество иероглифов и минимизация: критерии подсчета терминов. Но если немного изменить способ подсчета иероглифов (если считать за один любой набор черточек, обозначающий числа от 2 до 9), расширение папируса Райнда будет лишь немного проигрывать методу Фибоначчи/Сильвестра.

Кевин Гонг, Египетские дроби, UC Berkeley Math 196 Spring 1992 ↩

 Древний Египет Египетская дробь Египтология дробь Математика Теория чисел Папирус Райнд дробь

Игры дроби для детей онлайн

Онлайн игры дроби для детей

Математические игры с дробями — отличный способ упростить дробь обучение. Идентификация, сравнение и преобразование дробей никогда не было проще! Вы можете превратить изучение математики в легкую прогулку с помощью интерактивных онлайн-игр с дробями.

Как познакомить детей с дробями?

Дроби как понятие могут быть немного трудными для понимания. В основном это связано с тем, что дроби ведут себя иначе, чем целые числа, поскольку дроби менее интуитивны по сравнению с ними. Когда ребенок начинает понимать дроби, речь уже не идет о счете чисел. Внезапно они увидят, что целое можно разделить на половинки, пятые или даже тридцать седьмые части. Дроби также подчиняются определенным правилам, которые на первый взгляд могут показаться маловероятными, например, чем больше знаменатель, тем меньше дробь и т. д. Но все эти правила важно понимать и помнить. Дроби тоже пишутся по-разному.

Вот почему очень важно сосредоточиться на эффективном ознакомлении детей с дробями, поскольку это закладывает основу для сложных тем, которые им предстоит пройти в математическом путешествии. Фракции следует знакомить юных учащихся, связывая их с реальной жизнью, используя множество визуальных эффектов и контекстов, а также делая их забавными и увлекательными.

Как сделать дроби интересными для детей?

Мы можем сделать дроби забавными для детей с помощью игр и занятий, основанных на примерах из реальной жизни. Онлайн-игры с дробями, такие как сложение и вычитание дробей с помощью манипулятивных действий, выбор правильного раздела, подсчет равных частей, запись целых чисел в виде дробей и многие другие, предназначены для учащихся 3, 4 и 5 классов, одновременно делая изучение дробей захватывающим.

Как игры помогают лучше понять дроби?

Веселые игры и задания помогают детям с легкостью осваивать сложные понятия. Они превращают фиаско фракций в веселье! Они обеспечивают гибкость обучения, позволяют детям понимать математические концепции в своем собственном темпе, а также включают в себя все общие преимущества игр.

Рекомендовано Фракции Рабочие листы

Просмотреть все 222 Рабочие листы

Часто задаваемые вопросы

Как учить дроби для детей?
Изучение того, как построить дробь и как части целого делятся на дроби, — все это концепции, которые можно практиковать в веселых играх с дробями.
После освоения основ, обычно с помощью числовой строки или манипуляций, учащиеся начнут изучать концепцию сложения и вычитания с дробями, а также использовать смешанные числа и преобразовывать их в неправильные дроби и из них.
Как учить дроби?
Фракции можно легко выучить с помощью простых игр для класса. Когда дети начнут визуализировать разбиения и смогут оценить решение, они будут на пути к освоению концепции дробей. Чем больше вы сможете сделать дробную практику увлекательной, тем более интересной будет концепция для учащихся. Чем нагляднее игра, тем лучше, чтобы учащиеся могли видеть, как концепция строится и трансформируется у них на глазах. В конце концов, повторяющаяся практика дробей в различных обучающих играх укрепляет их мастерство дробей.
Как помочь ребенку понять дроби?
Поскольку навыки усложняются с повышением класса, дробные игры для детей служат для закрепления этих навыков, которые требуют много практики, прежде чем полное понимание и мастерство. Понимание дробей может помочь детям делить предметы на равные части и называть дроби, а также научиться правильно складывать и вычитать дроби.
Как играть в фракционные игры онлайн?
Обучающие игры с дробями, в которых используется множество наглядных материалов, помогут учащимся увидеть дроби в действии и использовать мысленный взор для решения более сложных задач. Они могут помочь им сравнивать дроби и сопоставлять дроби со смешанными числами.
Какие развлечения лучше всего подходят для детей?
Дробные задания, включающие дроби пиццы, чрезвычайно интересны для детей, поскольку они изучают эквивалентные, похожие и непохожие дроби, а также их сравнение. Выпечка, когда дети преобразуют дроби в их эквиваленты, чтобы использовать их наилучшим образом, также является отличным способом попрактиковаться в дробях. Выпечка помогает преобразовывать смешанные числа, а также складывать и вычитать дроби.

No related posts.