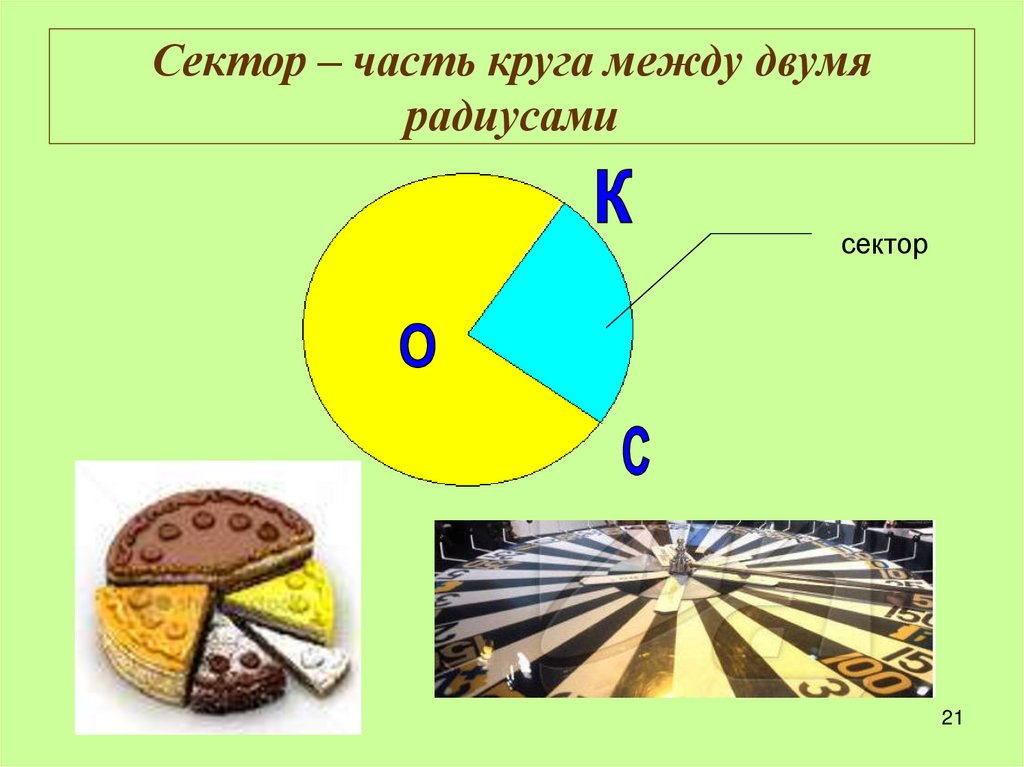
Формулы площади сектора круга и длины его дуги
Окружность — основная фигура в геометрии, свойства которой рассматривают в школе в 8 классе. Одна из типичных задач, связанных с окружностью, заключается в нахождении площади некоторой ее части, которая носит название кругового сектора. В статье приводятся формулы площади сектора и длины его дуги, а также пример их использования для решения конкретной задачи.
Понятие об окружности и круге
Перед тем как приводить формулу площади сектора окружности, рассмотрим, что собой представляет указанная фигура. Согласно математическому определению, под окружностью понимают такую фигуру на плоскости, все точки которой равноудалены от некоторой одной точки (центра).
Когда рассматривают окружность, то пользуются следующей терминологией:
- Радиус — отрезок, который проводится от центральной точки до кривой окружности. Его принято обозначать буквой R.
- Диаметр — это отрезок, который соединяет две точки окружности, но при этом проходит также через центр фигуры.
 Его обычно обозначают буквой D.
Его обычно обозначают буквой D. - Дуга — это часть кривой окружности. Измеряют ее либо в единицах длины, либо с использованием углов.
Круг — еще одна важная фигура геометрии, он представляет собой совокупность точек, которая ограничена кривой окружности.
Площадь круга и длина окружности
Отмеченные в названии пункта величины рассчитываются с использованием двух простых формул. Они приведены ниже:
- Длина окружности: L = 2*pi*R.
- Площадь круга: S = pi*R2.
В этих формулах pi — это некоторая константа, которая называется числом Пи. Оно является иррациональным, то есть не может быть точно выражено простой дробью. Приблизительно число Пи равно 3,1416.
Как видно из приведенных выражений, чтобы рассчитать площадь и длину достаточно знать только радиус окружности.
Площадь сектора круга и длина его дуги
Перед тем как рассматривать соответствующие формулы, напомним, что угол в геометрии принято выражать двумя основными способами:
- в шестидесятеричных градусах, причем полный оборот вокруг своей оси равен 360o;
- в радианах, которые выражаются в долях числа pi и связаны с градусами следующим равенством: 2*pi = 360o.

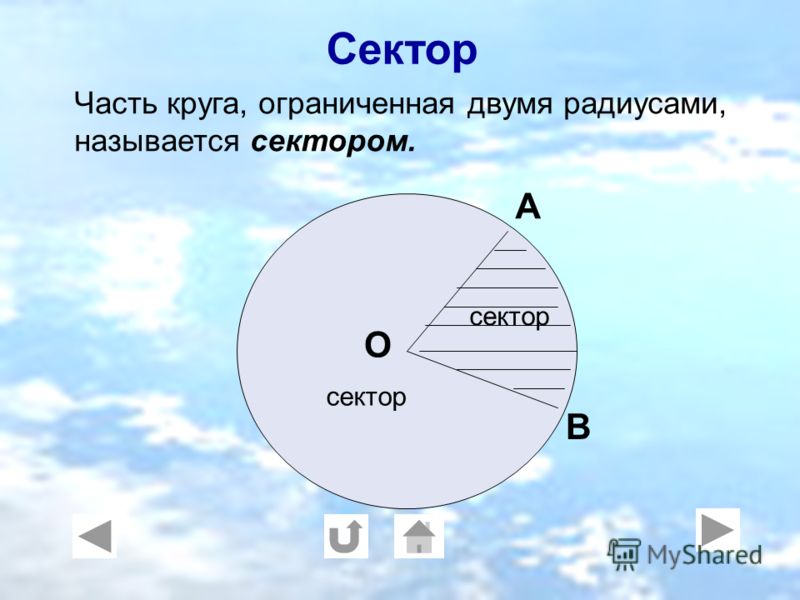
Сектор круга — это фигура, ограниченная тремя линиями: дугой окружности и двумя радиусами, находящимися на концах этой дуги. Пример кругового сектора изображен на фото ниже.
Получив представление о том, что такое сектор для круга, легко понять, как вычислить его площадь и длину соответствующей дуги. Из рисунка выше видно, что дуге сектора соответствует угол θ. Мы знаем, что полная окружность соответствует 2*pi радианам, значит, формула площади кругового сектора примет вид: S1 = S*θ/(2*pi) = pi*R2*θ/(2*pi) = θ*R2/2. Здесь угол θ выражен в радианах. Аналогичная формула площади сектора в случае, если угол θ измеряется в градусах, будет иметь вид: S1 = pi*θ*R2/360.
Длина дуги, образующей сектор, вычисляется по формуле: L1 = θ*2*pi*R/(2*pi) = θ*R. И если θ известен в градусах, тогда: L1 = pi*θ*R/180.
Пример решения задачи
Покажем на примере простой задачи, как пользоваться формулами площади сектора круга и длины его дуги.
Известно, что колесо имеет 12 спиц. Когда колесо делает один полный оборот, то оно преодолевает расстояние 1,5 метра. Чему равна площадь, заключенная между двумя соседними спицами колеса, и чему равна длина дуги между ними?
Как видно из соответствующих формул, чтобы ими пользоваться, необходимо знать две величины: радиус окружности и угол дуги. Радиус можно вычислить, исходя из знания длины окружности колеса, поскольку пройденное им расстояние за один оборот, точно ей соответствует. Имеем: 2*R*pi = 1,5, откуда: R = 1,5/(2*pi) = 0,2387 метра. Угол между ближайшими спицами можно определить, зная их число. Полагая, что все 12 спиц делят равномерно круг на равные сектора, мы получаем 12 одинаковых секторов. Соответственно, угловая мера дуги между двумя спицами равна: θ = 2*pi/12 = pi/6 = 0,5236 радиан.
Мы нашли все необходимые величины, теперь их можно подставить в формулы и посчитать требуемые условием задачи значения. Получаем: S1 = 0,5236*(0,2387)2/2 = 0,0149 м2, или 149 см2; L1 = 0,5236*0,2387 = 0,125 м, или 12,5 см.
Как найти площадь сектора круга: формулы, примеры задач
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Нахождение площади сектора круга
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь сектора круга, а также разберем примеры решения задач для демонстрации их практического применения.
- Определение сектора круга
- Формулы нахождения площади сектора круга
- Через длину дуги и радиус круга
- Через угол сектора (в градусах) и радиус круга
- Через угол сектора (в радианах) и радиус круга
- Примеры задач
Определение сектора круга
Сектор круга – это часть круга, образованная двумя его радиусами и дугой между ними. На рисунке ниже сектор закрашен зеленым цветом.
- AB – дуга сектора;
- R (или r) – радиус круга;
- α – это угол сектора, т.
 е. угол между двумя радиусами. Также его иногда называют центральным углом.
е. угол между двумя радиусами. Также его иногда называют центральным углом.
Формулы нахождения площади сектора круга
Через длину дуги и радиус круга
Площадь (S) сектора круга равняется одной второй произведения длины дуги сектора (L) и радиуса круга (r).
Через угол сектора (в градусах) и радиус круга
Площадь (S) сектора круга равняется площади круга, умноженной на угол сектора в градусах (α°) и деленной на 360°.
Через угол сектора (в радианах) и радиус круга
Площадь (S) сектора круга равняется половине произведения угла сектора в радианах (aрад) и квадрата радиуса круга.
Примеры задач
Задание 1
Дан круг радиусом 6 см. Найдите площадь сектора, если известно, что длина его дуги составляет 15 см.
Решение
Воспользуемся первой формулой, подставив в нее заданные значения:
Задание 2
Найдите угол сектора, если известно, что его площадь равна 78 см2, а радиус круга – 8 см.
Решение
Выведем формулу для нахождения центрального угла из второй формулы, рассмотренной выше:
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Площадь сектора – формула, определение, площадь сектора круга
Площадь сектора круга – это количество пространства, заключенного в пределах границы сектора.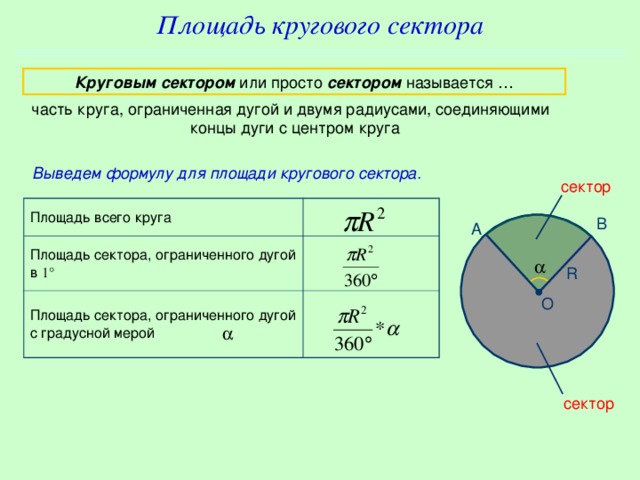 Сектор всегда начинается из центра круга. Сектор круга определяется как часть круга, заключенная между двумя его радиусами и дугой, примыкающей к ним. Полукруг — наиболее распространенный сектор круга, представляющий половину круга. Давайте узнаем больше о площади сектора, ее формуле и о том, как рассчитать площадь сектора, используя радианы и градусы.
Сектор всегда начинается из центра круга. Сектор круга определяется как часть круга, заключенная между двумя его радиусами и дугой, примыкающей к ним. Полукруг — наиболее распространенный сектор круга, представляющий половину круга. Давайте узнаем больше о площади сектора, ее формуле и о том, как рассчитать площадь сектора, используя радианы и градусы.
| 1. | Что такое площадь сектора круга? |
| 2. | Площадь сектора Формула |
| 3. | Площадь сектора в радианах |
| 4. | Часто задаваемые вопросы о районе сектора |
Что такое площадь сектора круга?
Пространство, ограниченное сектором круга, называется площадью сектора. Например, кусок пиццы является примером сектора, представляющего часть пиццы. Существует два типа секторов: второстепенные и крупные секторы. Малый сектор — это сектор, который меньше полукруга, тогда как большой сектор — это сектор, который больше полукруга.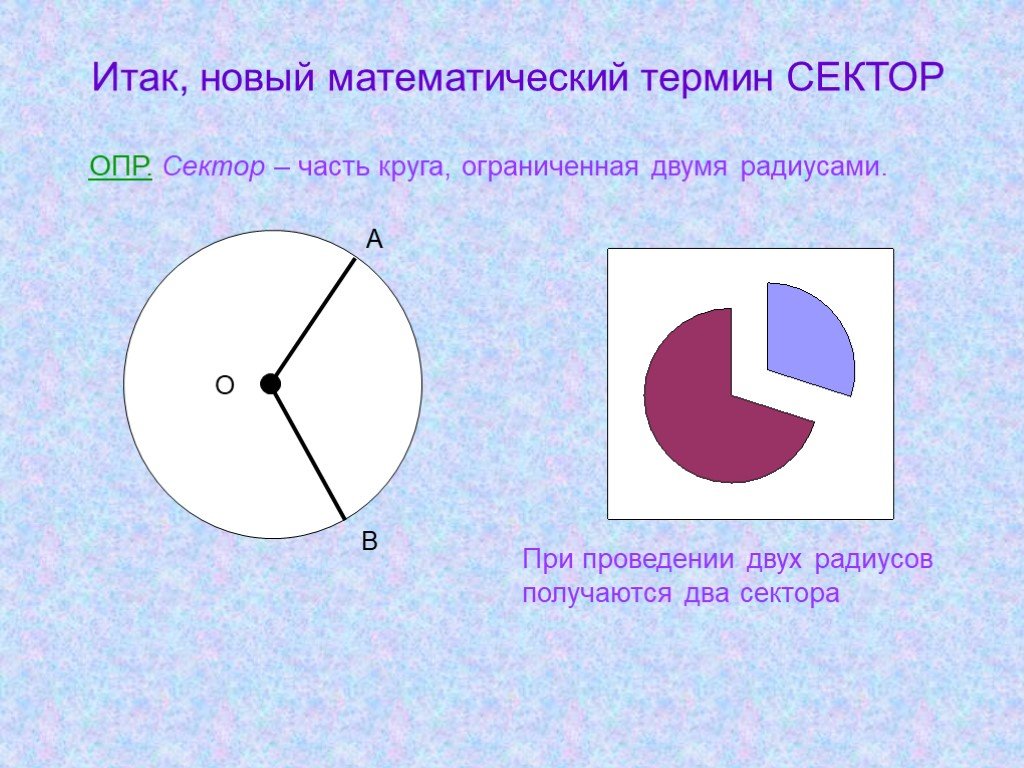
На приведенном ниже рисунке показаны сектора в круге. Заштрихованная область показывает площадь сектора OAPB. Здесь ∠AOB — угол сектора. Следует отметить, что незаштрихованная область также является сектором круга. Таким образом, заштрихованная область — это площадь меньшего сектора, а незаштрихованная область — это площадь большого сектора.
Теперь давайте узнаем о формуле площади сектора и ее выводе.
Определение сектора
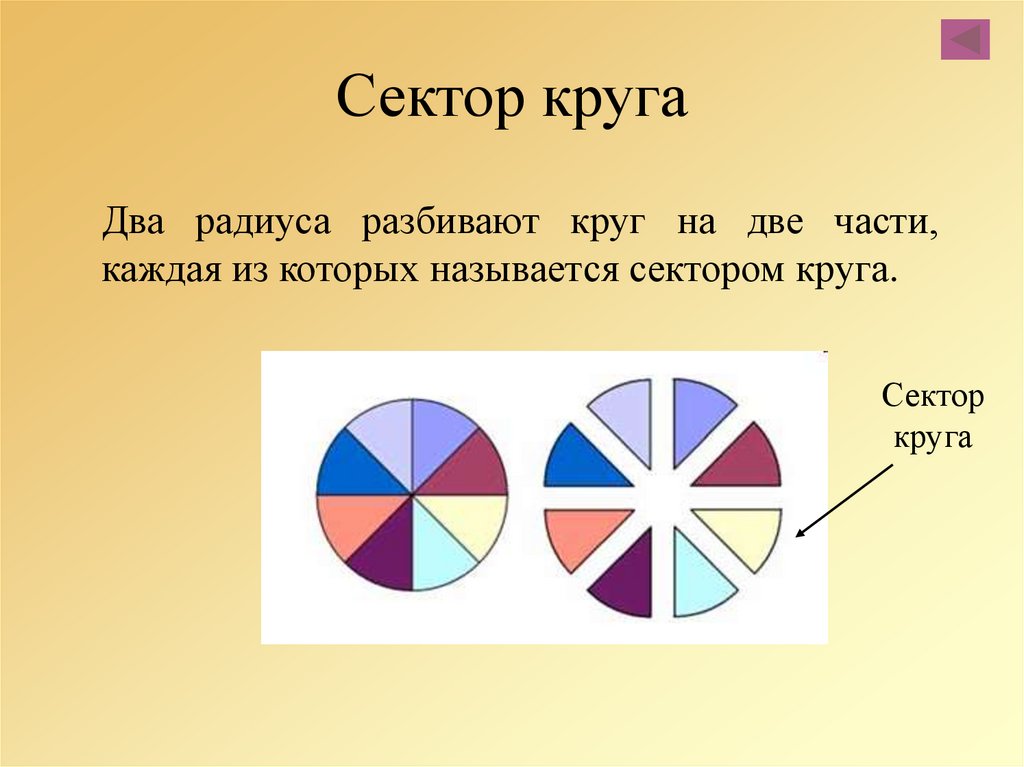
Сектор считается частью круга с двумя радиусами и дугой. Круг разделен на два сектора, а именно: меньший сектор и большой сектор, где меньший сектор является меньшей частью круга, а большая часть является основной частью.
Площадь сектора Формула
Чтобы найти общее пространство, ограниченное сектором, мы используем формулу площади сектора . Площадь сектора можно рассчитать по следующим формулам:
- Площадь сектора круга = (θ/360º) × πr 2 , где θ — угол сектора, образуемый дугой в центре, в градусах, а «r» — радиус круга.

- Площадь сектора круга = 1/2 × r 2 θ, где θ — угол сектора, образуемый дугой в центре, в радианах, а r — радиус круга.
Вывод формулы площади сектора
Применим унитарный метод для вывода формулы площади сектора круга. Мы знаем, что полный круг имеет длину 360º. Площадь круга с углом, измеряющим 360º в центре, равна πr 2 , где r — радиус окружности.
Если угол в центре круга равен 1º, площадь сектора равна πr
- θ — угол, стягиваемый в центре, дается в градусах.
- r — радиус окружности.
Другими словами, πr 2 представляет собой площадь полного круга, а θ/360º говорит нам, какая часть круга покрыта сектором.
Если угол в центре равен θ в радианах, площадь сектора круга = (1/2) × r 2 θ, где
- θ — угол, образуемый в центре , дано в радианах.

- r — радиус окружности.
Следует отметить, что полукруги и квадранты являются особыми видами секторов круга с углами 180° и 90° соответственно.
Площадь сектора в градусах
Воспользуемся этими формулами и на примере научимся вычислять площадь сектора круга, когда стягивающий угол выражается в градусах.
Пример: Окружность разделена на 3 сектора, а центральные углы, образуемые радиусом, составляют 160°, 100° и 100° соответственно. Найдите площади всех трех секторов.
Решение:
Угол, образуемый первым сектором, равен θ = 160°. Следовательно, площадь первого сектора = (θ/360°) × πr
Угол, образуемый вторым сектором, равен θ = 100°. Следовательно, площадь второго сектора = (θ/360°) × πr 2 = (100°/360°) × (22/7) × 6 2 = 5/18 × 22/7 × 36 = 220/7 = 31,43 кв.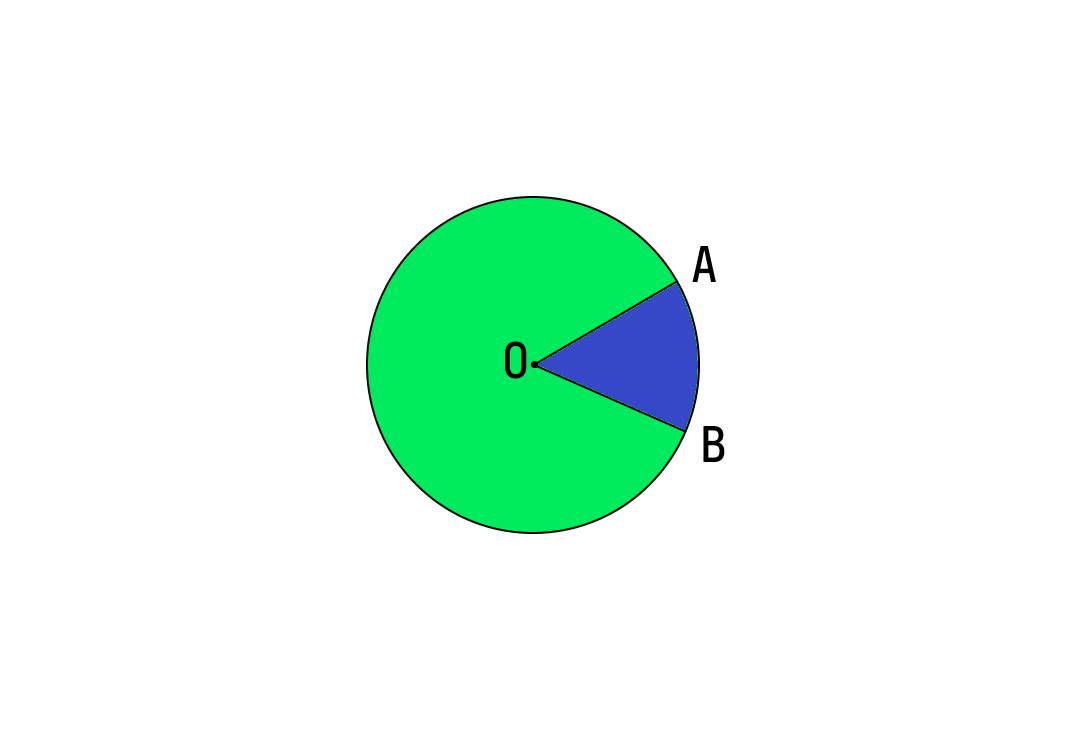
Угол, образуемый третьим сектором, такой же, как угол второго сектора (θ = 100°). Таким образом, площадь второго сектора равна площади третьего сектора. Следовательно, площадь третьего сектора = 31,43 кв.
Площадь сектора в радианах
Если нам нужно найти площадь сектора, когда угол задан в радианах, мы используем формулу Площадь сектора = (1/2) × r 2 θ; где θ — угол, стягиваемый в центре, в радианах, а r — радиус окружности. Итак, давайте разберемся, откуда берется формула. Мы знаем, что формула площади сектора (в градусах) = (θ/360º) × πr 2 , потому что это часть круга. Та же концепция применяется к формуле, когда мы хотим выразить ее в радианах, но нам просто нужно заменить 360° на 2π, потому что 2π (в радианах) = 360°. Это означает, что площадь сектора в радианах = (θ/2π) × πr 2 . При дальнейшем упрощении формулы площади сектора получаем площадь сектора = (θ/2) × r 2 или (1/2) × r 2 θ. Давайте разберемся, как найти площадь сектора в радианах на примере.
Давайте разберемся, как найти площадь сектора в радианах на примере.
Пример: Найдите площадь сектора, если радиус окружности равен 6 единицам, а угол, образуемый в центре = 2π/3
Решение: Дано, радиус = 6 единиц; Угловая мера (θ)= 2π/3
Площадь данного сектора можно рассчитать по формуле Площадь сектора (в радианах) = (θ/2) × r
Следовательно, площадь данного сектора в радианах выражается как 12π квадратных единиц.
Реальный пример площади сектора круга
Одним из наиболее распространенных реальных примеров площади сектора является кусок пиццы. Форма ломтиков круглой пиццы похожа на сектор. Обратите внимание на приведенный ниже рисунок, на котором показана пицца, разделенная на 6 равных ломтиков, где каждый ломтик представляет собой сектор, а радиус пиццы составляет 7 дюймов. Теперь давайте найдем площадь сектора, образованного каждым срезом, используя формулу площади сектора. Следует отметить, что поскольку пицца разделена на 6 равных ломтиков, угол сектора равен 60°. Площадь ломтика пиццы = (θ/360°) × πr 2 = (60°/360°) × (22/7) × 7 2 = 1/6 × 22 × 7 = 77/3 = 25,67 квадратных единиц.
Теперь давайте найдем площадь сектора, образованного каждым срезом, используя формулу площади сектора. Следует отметить, что поскольку пицца разделена на 6 равных ломтиков, угол сектора равен 60°. Площадь ломтика пиццы = (θ/360°) × πr 2 = (60°/360°) × (22/7) × 7 2 = 1/6 × 22 × 7 = 77/3 = 25,67 квадратных единиц.
Советы по области сектора
Вот список нескольких важных моментов, которые помогут решить проблемы области сектора.
- Площадь сектора круга — это дробная часть площади круга.
- Площадь сектора круга радиуса r рассчитывается по формуле Площадь сектора = (θ/360º) × π r 2
- Длина дуги сектора радиуса r может быть рассчитана по формуле Длина дуги сектора = r × θ
☛ Статьи по теме
- Площадь круга
- Дуги и вытянутые углы
- Сегмент круга
- Что такое число Пи?
Площадь сектора Примеры
Пример 1: Если угол сектора круга равен 60°, а радиус круга равен 7 дюймам, какова площадь сектора этого круга?
Решение:
Радиус круга 7 дюймов, угол 60°.

Пример 2: Зонт имеет 8 ребер, расположенных на одинаковом расстоянии друг от друга. Если рассматривать его как плоский круг радиусом 7 единиц, какова будет площадь между двумя последовательными ребрами зонта? (Подсказка: площадь между двумя последовательными ребрами образует сектор круга)
Решение:
Радиус плоского зонта = 7 единиц. В зонте 8 ребер. Так как полный угол круга = 360°, угол каждого сектора зонта = 360/8 = 45°, потому что круг разделен на 8 равных секторов. Таким образом, площадь сектора = (θ/360°) × π r 2 = (45°/360°) × 22/7 × 7 2 = 77/4 = 19,25 квадратных единиц. Следовательно, площадь между двумя последовательными ребрами зонта равна 19,25 кв.
Пример 3: Круг диаметром 2 единицы разделен на 10 равных секторов.
 Сможете ли вы найти площадь каждого сектора круга?
Сможете ли вы найти площадь каждого сектора круга?Решение:
Диаметр окружности равен 2 единицам, следовательно, радиус окружности равен 1 единице. Так как полный угол окружности = 360°, угол каждого сектора окружности равен 360/10 = 36°, потому что полный угол делится на 10 равных частей. Площадь сектора = (θ/360°) × πr 2 = 36°/360° × 22/7 × 1 = 11/35 = 0,314 квадратных единиц. Следовательно, площадь каждого сектора круга составляет 0,314 квадратных единиц.
перейти к слайдуперейти к слайдуперейти к слайду
Как ваш ребенок может освоить математические понятия?
Мастерство математики приходит с практикой и пониманием «почему» за «что». Почувствуйте разницу Cuemath.
Запись на бесплатный пробный урок
Практические вопросы по области сектора
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о площади сектора круга
Какова площадь сектора круга?
Пространство, ограниченное сектором круга, называется площадью сектора круга. Часть окружности, ограниченная двумя радиусами и соответствующей дугой, называется сектором окружности.
Часть окружности, ограниченная двумя радиусами и соответствующей дугой, называется сектором окружности.
Какова формула площади сектора круга?
Две основные формулы, используемые для нахождения Площадь сектора составляет:
- Площадь сектора круга = (θ/360º) × πr 2 , где θ — угол, стягиваемый в центре, в градусах, а r — угол радиус окружности.
- Площадь сектора круга = 1/2 × r 2 θ, где θ — угол, стягиваемый в центре, в радианах, а r — радиус окружности.
Как рассчитать площадь сектора с помощью градусов?
Если угол, образуемый в центре, указан в градусах, площадь сектора можно рассчитать по следующей формуле: площадь сектора круга = (θ/360º) × πr 2 , где θ — угол, образуемый в центре, в градусах, а r — радиус окружности.
Что вы подразумеваете под сектором круга?
Сектор определяется как часть круга, заключенная между двумя его радиусами и дугой, примыкающей к ним. Полукруг — наиболее распространенный сектор круга, представляющий собой половину круга.
Полукруг — наиболее распространенный сектор круга, представляющий собой половину круга.
Что вы подразумеваете под дугой окружности?
Часть кривой или часть окружности окружности называется дугой. Многие объекты имеют кривую форму. Изогнутая часть этих объектов математически называется дугой.
Как вычисляется формула площади сектора круга?
Площадь сектора показывает площадь части площади круга. Мы знаем, что площадь круга рассчитывается по формуле πr 2 . Формула площади сектора круга выводится следующим образом:
- Примените унитарный метод для вывода формулы площади сектора круга.
- Мы знаем, что полный круг имеет длину 360º. Площадь круга с углом, измеряющим 360º в центре, равна πr 2 , где r — радиус окружности.
- Если угол в центре круга равен 1º, площадь сектора равна πr 2 /360º. Таким образом, если угол в центре равен θ, площадь сектора равна площади сектора круга = (θ/360º) × πr 2 , где θ — угол, стягиваемый в центре, указанный в градусов, а r — радиус окружности.

- Другими словами, πr 2 представляет собой площадь полного круга, а θ/360º говорит нам, какая часть круга покрыта сектором.
Как найти площадь сектора с длиной дуги и радиусом?
Площадь сектора можно рассчитать, если известны длина и радиус дуги. Сначала мы вычисляем угол (θ), образуемый дугой, по формуле Длина дуги = (θ/360) × 2πr. Теперь мы уже знаем радиус, а когда известен угол, площадь сектора можно рассчитать по формуле Площадь сектора круга = (θ/360º) × πr 2
Как найти радиус от площади сектора?
Если известна площадь сектора и известен угол (θ), образуемый дугой, радиус можно рассчитать, подставив данные значения в формулу Площадь сектора круга = (θ/360º ) × πr 2 . Например, найдем радиус, если площадь сектора равна 36π, а угол сектора равен 90°. Подставим данные значения в формулу Площадь сектора круга = (θ/360º) × πr 2 , то есть 36π = (90/360) × πr 2 . Итак, значение r 2 = 144, значит r = 12 единиц.
Как найти площадь сектора с точки зрения числа Пи?
Площадь сектора также может быть выражена через пи (π). Например, если радиус окружности равен 4 единицам, а угол, образуемый дугой сектора, равен 90°, найдем площадь сектора через число пи. Площадь сектора = (θ/360º) × πr 2 . Подставляя значения в формулу Площадь сектора = (90/360) × π × 4 2 . Решив это, мы получим площадь как 4π.
Как найти площадь сектора в радианах?
Чтобы найти площадь сектора с центральным углом в радианах, мы используем формулу Площадь сектора = (θ/2) × r 2 ; где θ — угол, стягиваемый в центре, в радианах, а r — радиус окружности. Например, если радиус окружности равен 12 единицам, а угол сектора, образуемый дугой в центре, = 4π/3, найдем площадь сектора. Площадь сектора (в радианах) = (θ/2) × r 2 . Подставляя значения в формулу, получаем Площадь сектора (в радианах) = [4π/(3×2)] × 12 2 = (2π/3) × 144 = 96π. Следовательно, площадь сектора в радианах выражается как 96π квадратных единиц.
Следовательно, площадь сектора в радианах выражается как 96π квадратных единиц.
Как найти площадь сектора без угла?
Если угол сектора не задан, но известны длина дуги и радиус, можно вычислить площадь сектора. Сначала мы находим секторный угол, подставляя заданные значения длины и радиуса дуги в формулу Длина дуги = (θ/360) × 2πr. После вычисления угла мы можем легко найти площадь сектора по формуле Площадь сектора круга = (θ/360º) × πr 2 .
Как найти длину дуги сектора?
Длина дуги — это расстояние вдоль части окружности окружности. Длину дуги окружности можно рассчитать по следующим формулам:
- Длина дуги = θ × r; где θ = центральный угол, образуемый дугой, а r = радиус окружности. Эта формула используется, когда θ выражено в радианах.
- Длина дуги = θ × (π/180) × r; где θ = центральный угол, образуемый дугой, а r = радиус окружности. Эта формула используется, когда θ выражено в градусах.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочий лист по площади
Площадь сектора круга
Содержание
- Сектор круга
- Как найти площадь сектора
- Найдите радиус окружности
- Площадь сектора Формула
- Площадь сектора в радианах
- Площадь сектора круга Примеры
- Длина дуги и площадь сектора
Сектор круга
Каждый раз, когда вы отрезаете кусок от тыквенного пирога, круглого именинного торта или круглой пиццы, вы удаляете сектор. А сектор создан центральным углом, образованным двумя радиусами, и включает область внутри круга от этой центральной точки до самого круга. Часть окружности окружности, ограниченная радиусами, дуга , является частью сектора.
А сектор создан центральным углом, образованным двумя радиусами, и включает область внутри круга от этой центральной точки до самого круга. Часть окружности окружности, ограниченная радиусами, дуга , является частью сектора.
Дуги окружности
Острые центральные углы всегда будут давать малых дуг и малых секторов. Когда центральный угол, образованный двумя радиусами, равен 90°, сектор называется квадрантом (поскольку весь круг состоит из четырех квадрантов или четвертей). Когда два радиуса образуют 180° или половину окружности, сектор называется 9.0055 полукруг и имеет большую дугу .
В отличие от треугольников, границы секторов а не устанавливаются отрезками. Правда, у вас есть два радиуса, образующие центральный угол, но часть окружности, которая составляет третью «сторону», изогнута, поэтому найти площадь сектора немного сложнее, чем найти площадь треугольника.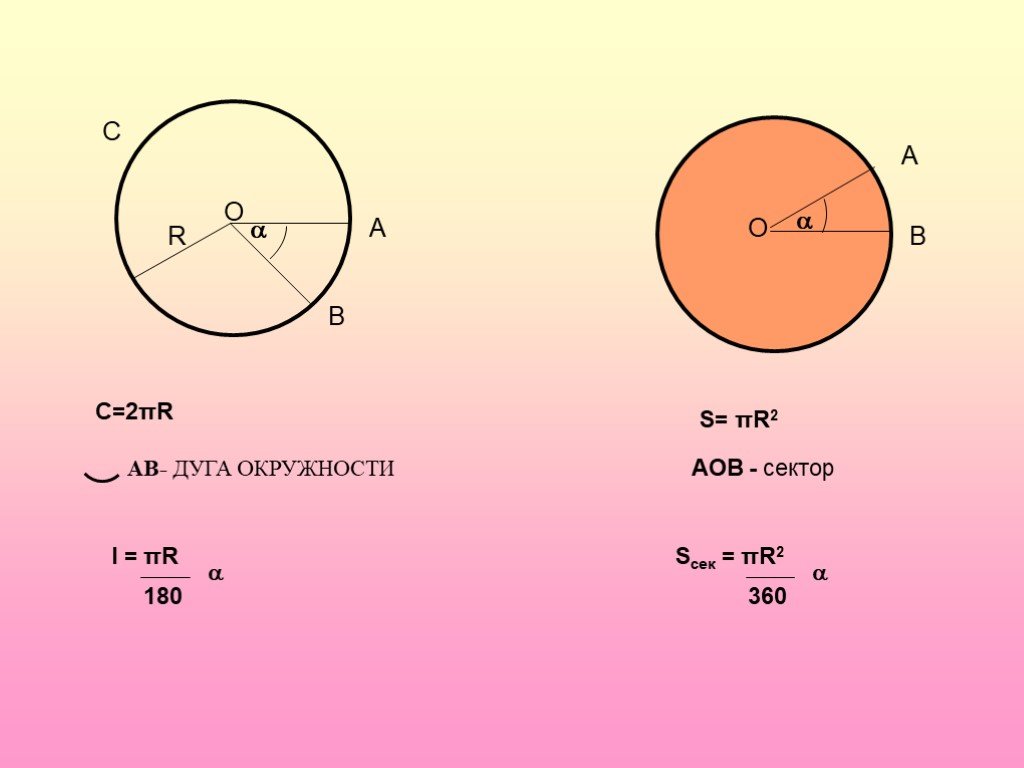 Расстояние вдоль этой изогнутой «стороны» равно длине дуги .
Расстояние вдоль этой изогнутой «стороны» равно длине дуги .
Как найти площадь сектора
Вы не можете найти площадь сектора, если не знаете радиус круга. Однако будьте осторожны; Вы можете найти радиус, если у вас есть диаметр или окружность. Возможно, вам придется сделать небольшую предварительную математику, чтобы получить радиус.
Найдите радиус окружности
При диаметре d окружности радиус r равен:
r=d2
При длине окружности C радиус r равен:
r=C(2π)
Зная радиус, вы получаете длины двух частей сектора. Вам нужно только знать длину дуги или центральный угол в градусах или радианах.
Площадь сектора Формула
Центральный угол позволяет узнать, какую часть или процент всего круга составляет ваш сектор. Квадрант имеет центральный угол 90° и составляет одну четвертую часть всего круга. Центральный угол 45° составляет одну восьмую часть окружности.
Это простые дроби, но что, если ваш центральный угол 9-дюймового тыквенного пирога равен, скажем, 31°?
[вставьте рисунок тыквенного пирога с сектором, разрезанным под углом +/- 31°]
Эта формула поможет вам найти площадь сектора A, если вы знаете центральный угол в градусах, n° и радиус, r, круга:
A = (n°360°) × π × r2
Для вашего тыквенного пирога подключите 31° и 9 дюймов:
A = (31360) × π × 92
A = 21,9126 in2
Площадь сектора в радианах
Если вместо центрального угла в градусах вам дано радиан , вы используете еще более простую формулу.
Чтобы найти площадь A сектора с центральным углом θ радиан и радиусом r:
A = (θ2) × r2
Наше любимое π, кажется, исчезло! На самом деле это не так. Радианы основаны на π (круг равен 2π радианам), поэтому на самом деле вы заменили n°360° на θ2π. Когда в нашей исходной формуле используется θ2π, она упрощается до элегантного (θ2) × r2.
Площадь сектора круга Примеры
У вас есть личная пицца диаметром 30 см. Вы разрезали его на шесть равных частей, так что центральный угол каждой части равен 60°. Какова площадь в квадратных сантиметрах каждого куска?
A = (n°360°) × π × r2
Сначала попробуйте сами, прежде чем смотреть вперед!
A = (60°360°) × π × 152
A = (16) × π × 225
A = 117,8097 см2
Вы не забыли взять половина диаметра найти радиус?
Пример площади сектора в радианах
Предположим, у вас есть сектор с центральным углом 0,8 радиана и радиусом 1,3 метра. Ваша формула:
A = (θ2) × r2
Попробуйте сами, прежде чем смотреть вперед!
A = (0,82) × 1,32
A = 0,676 м2
Длина дуги и площадь сектора
Вы также можете найти площадь сектора по его радиусу и длине дуги.

 Его обычно обозначают буквой D.
Его обычно обозначают буквой D.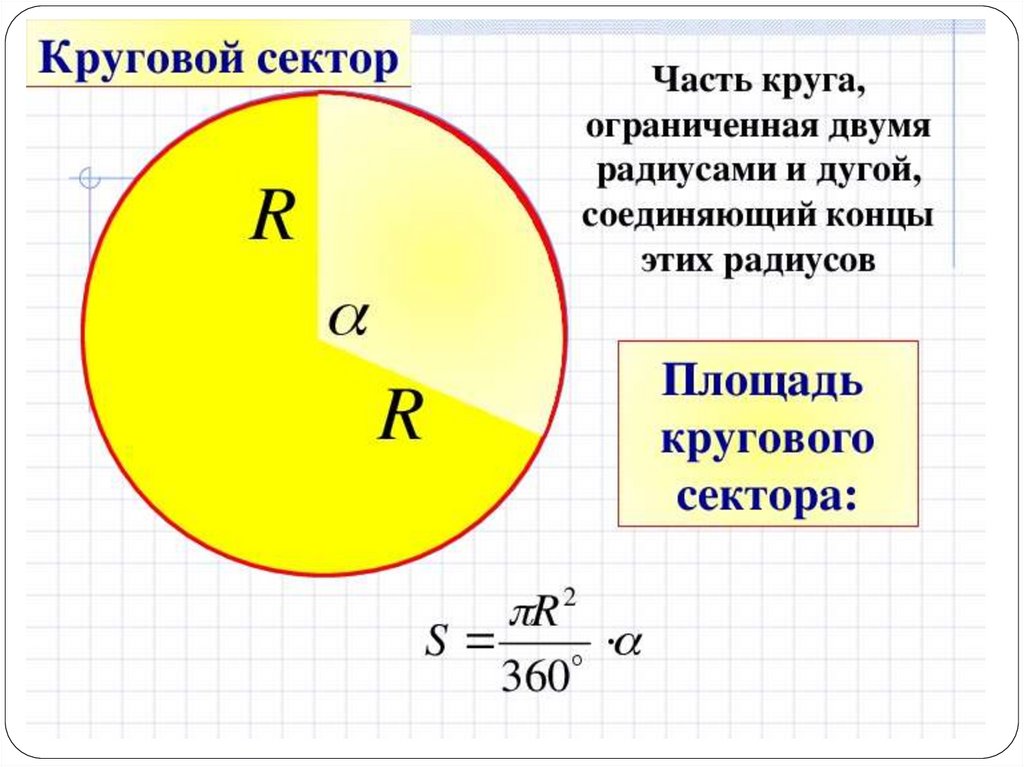
 е. угол между двумя радиусами. Также его иногда называют центральным углом.
е. угол между двумя радиусами. Также его иногда называют центральным углом.

 Сможете ли вы найти площадь каждого сектора круга?
Сможете ли вы найти площадь каждого сектора круга?