Шаблон графика функции y 2×2: Вопрос.ру — «Создайте шаблон параболы Y=x^2 Y=2x^2»

Уроки 1 Функция у=х² «Предмет математика настолько серьезен, что полезно не упустить случая сделать его немного занимательнее»

«Математик, который не является

отчасти поэтом, никогда не достигнет

совершенства в математике».

К. Вейерштрасс

Цели урока:

1.Формировать умения и навыки построения графика квадратичной функции по плану-схеме и с помощью преобразования графиков.

2.Развивать у учащихся умение применять логические операции – сравнение; анализ; развивать и активизировать познавательные процессы – мышление, внимание, восприятие; приобщение учащихся к информационным технологиям;

3.Формировать эстетическую культуру при построении чертежей; умение работать в группе, воспитывать сотрудничество, культуру общения; позволить ощутить учащимся свою значимость при овладении компьютерными программами.

Ход урока:

1.Объяснение нового материала

2. Алгоритм построения графиков квадратичной функции.

3.Преобразование графиков функций.

4.Использование компьютерных программ для построения и преобразования графиков.

5.Итог урока.

Эпиграф к нашему сегодняшнему уроку поощряет нас не останавливаться на достигнутом, а двигаться дальше. Расширяя горизонты своих знаний. Мы начнем наш урок с небольшого видеоряда. Как вы думаете, что объединяет все эти рисунки? Правильно, на каждом из них мы видим форму, напоминающую нам параболу. Сегодня мы продолжим разговор об этой удивительной линии, обобщим уже имеющиеся знания по теме урока, откроем для себя новые свойства параболы.

Графиком какой функции является парабола?

Какая функция называется квадратичной?

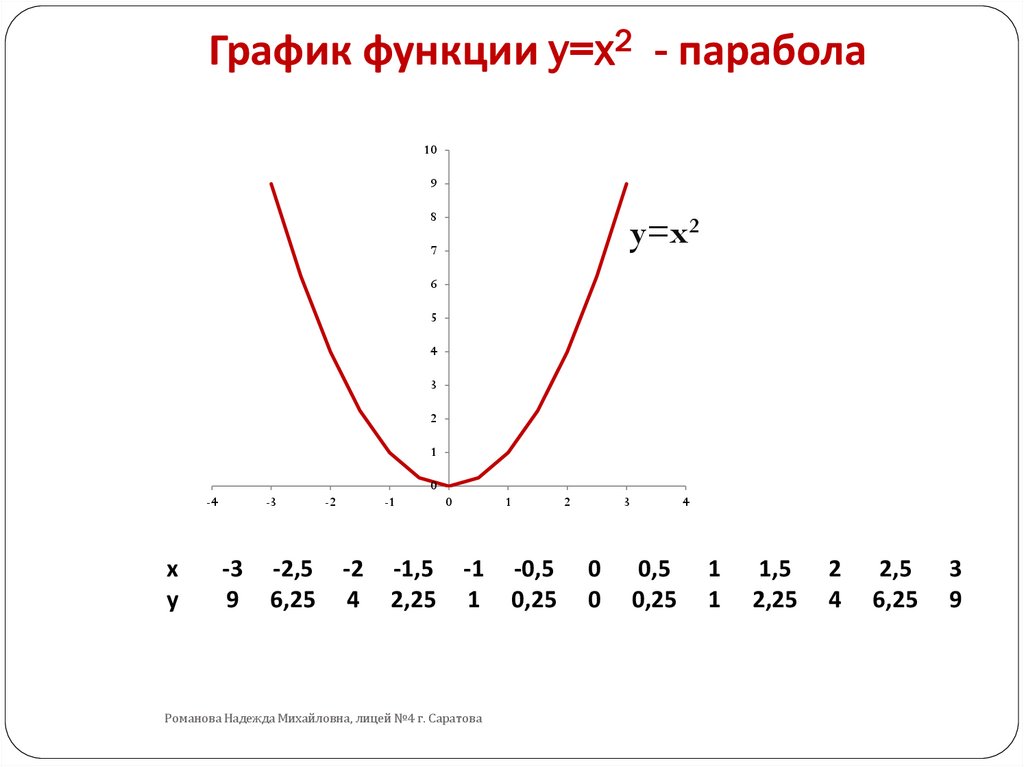
Мы с вами уже рассмотрели частные случаи квадратичной функции, научились строить графики функций у=х², у=ах², у = ах² + в, у =а(х –m)²,

Рассмотрим функции вида у=ах², у = ах² + в, у =а(х –m)², у =а(х –m)²+в.

Пусть первоначально а > 0. ясно, что каждая ордината графика функции у=ах² в а раз больше соответствующей ординаты графика функции у=х². Здесь возможны различные варианты в зависимости от значения а. Если а > 1, то все ординаты графика функции у=х² при умножении на а увеличиваются и сохраняют направление. При 0 1).

Пусть а

у= — ах² симметричен графику у=ах² относительно оси ОХ, т.е. является параболой, ветви которой направлены вниз.

Графики функций у = ах² + в получаются из графиков функций у = ах² параллельным переносом вдоль оси ОУ на в единиц. Если в 0,то сдвиг происходит вверх.

Графики функций у =а(х –m)² получаются из графиков функций у = ах² параллельным переносом вдоль оси ОХ на m единиц. Если m > 0,то сдвиг осуществляется вправо, а если m

Bсе выше перечисленные свойства графиков квадратичной функции нашли свое отражение в следующем стихотворении:

Я есть парабола! Взгляните!

Как я стройна, изящна и горда!

Ведь, если модуль а превысит единицу,

То резко прочь направлюсь я тогда.

А если он поменьше единицы,

То плавно и изящно приближусь я к ОХ,

Ведь существо мое подобно птице,

Я не могу обидеть ось абсцисс.

Мне буква а указ и назиданье:

Лишь только от 0 она по праву руку встанет,

Как лебедь гордая, я крылья вверх стремлю

с огромнейшим желаньем.

А слева от нуля она немилосердна и жестока.

Приходится мне вниз лететь от дорогой оси абсцисс далеко.

А если b побольше 4ас,

То дважды с великою Ох я встречусь.

А если же они равны,

То лишь однажды к абсциссе я прикоснусь заветным поцелуем.

И жаль до слез, что встречи не бывает,

Когда меньше нуля их разность будет.

Да, если солнышко свои лучи моей оси протянет параллельно,

То, отраженные, они не могут жить отдельно

И в фокусе моем сходясь все вместе,

Мне силу дивную дают!»

И римляне бегут, оставив Сиракузы!

И спутник вверх умчался, как шальной.

Красавицы параболы великое искусство

И нам позволит облететь весь шар земной.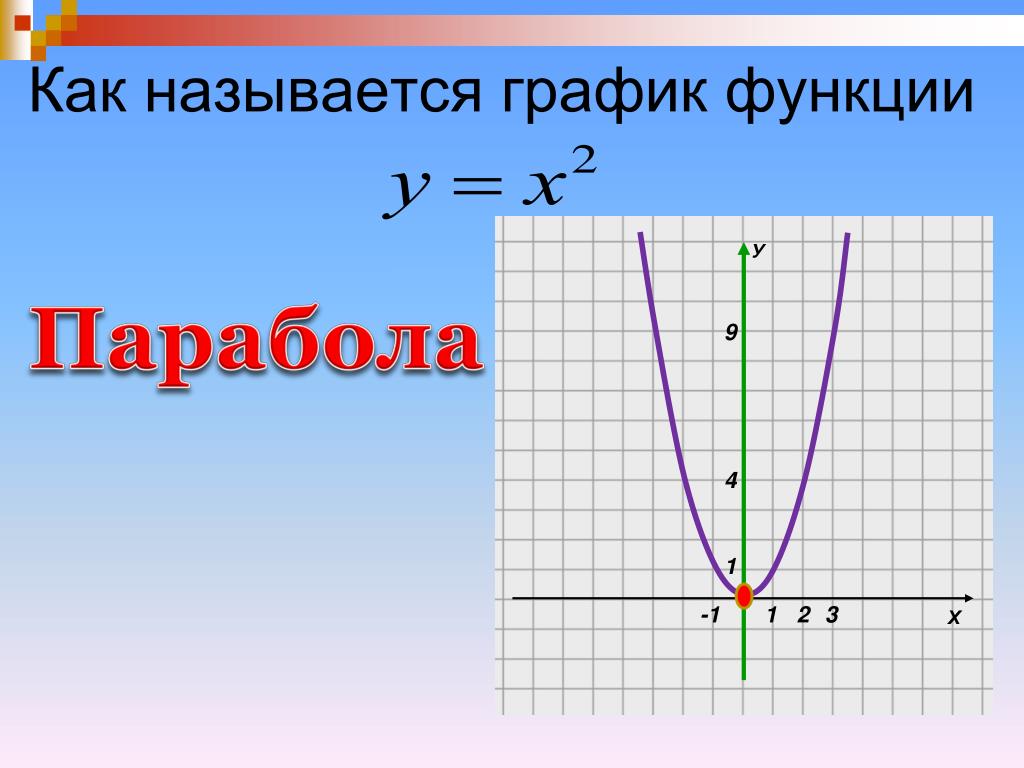

Задания:

Задание1.

Внимательно рассмотрите рисунок. Сравните поведение графиков функций, у которых а = -1, а = 1, а = -2,

а = 2, а = — 0,5, а = 0,5. Чем они похожи? Чем отличаются?

Задание2. Рассмотрим теперь функцию у = ах² + в. Попробуйте догадаться, с графиком какой функции мы будем сравнивать график данной функции.

Для построения графика функции у = ах² + в сравним эту функцию с функцией у=ах². При каждом х значение функции у=ах² отличаются от значений функции у = ах² + в на одно и тоже число в.Геометрически это означает, что каждая точка графика функции у = ах² + в получается из соответствующего графика функции у=ах² сдвигом на в единиц вверх, если в > 0 и вниз, если в

Задание 3. Постройте графики функций: у =2х ²+1 б) у = -2х ² + 2 в) у = 0,5х ² — 1 г) у = 0,5х ² + 4.

Для каждой из функций назовите координаты вершины и укажите направление ветвей.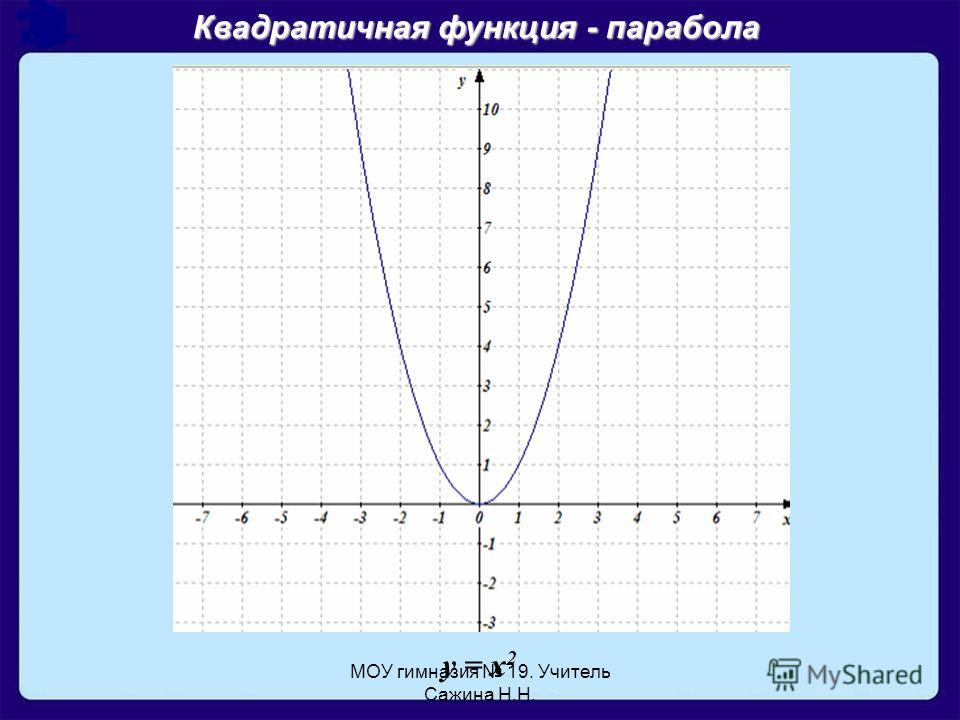

Первый вариант выполняет построение по алгоритму:

Вычисли координаты вершины. Отметь её на координатной плоскости.

Через вершину проведи ось симметрии.

Вычисли и отметь нули функции.

Вычисли координаты дополнительных точек. Отметь их.

Проведи параболу.

Второй вариант выполняет построение с помощью параллельного переноса графиков.

После этого проводится взаимопроверка. Сравните друг с другом полученные графики.

Рассмотрим еще один вид квадратичной функции у =а(х – m)².

Сравнивая функции у=ах² и у =а(х – m)², мы видим, что значение функции у =а(х – m)² при х =хо + m Совпадает со значением функции у=ах² при х = хо. Геометрически это означает, что точка на графике функции у =а(х – m)² с абсциссой х =хо + m имеет одинаковую ординату с точкой графика функции у=ах² , имеющей абсциссу х =хо. Иными словами, график функции у =а(х – m)² получен из графика функции у=ах² параллельным переносом влоль оси абсцисс на m единиц вправо, если. m > 0 и влево, если m

Вершиной параболы у =а(х – m)² является точка (m; о), а осью симметрии – пряиая, проходящая через эту точку, параллельно оси ординат.

Задание 4. Исходя из графика функции у = х², постройте графики функций:

а) у = (х – 2)²+ 3 б) у = (х + 1)² — 2 в) у = (х – 3)² — 1 г) у = (х + 2)² + 4

Задание можно выполнять как на доске и в тетрадях, так и на компьютере, используя любую программу построения графиков или электронные учебники (см Дрофа – Мультимедиа).

Задание 5. По данному графику функции назвать ее уравнение и дать ее краткую характеристику.

Тест

Задание 1.

Какой из графиков соответствует формуле у = -1/2 x²?

Задание 2. Найти область значений функции у=2+1/3 x².

1) [0; )  2) [2; )  3) (-; 2]

Задание 3. В каких координатных четвертях расположен график функции у=0,2(x-3)².

1) I и II    2) II и III    3) I и IV

Задание 4. Какое из чисел {4;6;9}не принадлежит области значений функции

y=2(x-3)²+6?

1) 4    2) 6    3) 9

Задание 5. При каких значениях

x из множества {1;2;3;4} функция y=(x-3)²+5 принимает равные значения?

1) 1 и 2    2) 2 и 3    3) 2 и 4

Тест (для сильных учащихся)
Задание 1. Установите, на каком рисунке изображен график функции у = -0,5 х² — 3

Задание 2. Укажите, на каком рисунке изображен график функции у = (х + 2)² — 4

Задание 3. Определите, на каком рисунке изображен график функции у = 4 — х│х│

Задание 4. Найдите p и q, если точка А(2;-6) является вершиной параболы у = х² + pх + q

1) p = 4 q = 2 2) p = -4 q = -2 3) p = -4 q = 2 4) p = 4 q = -2

Задание 5. Установите, какая из точек А(-2;3), В(4;9), С(-4;11), D(2;-1) принадлежит графику функции у =² — 5

1) С 2) А 3) D 4) В

Задание 6.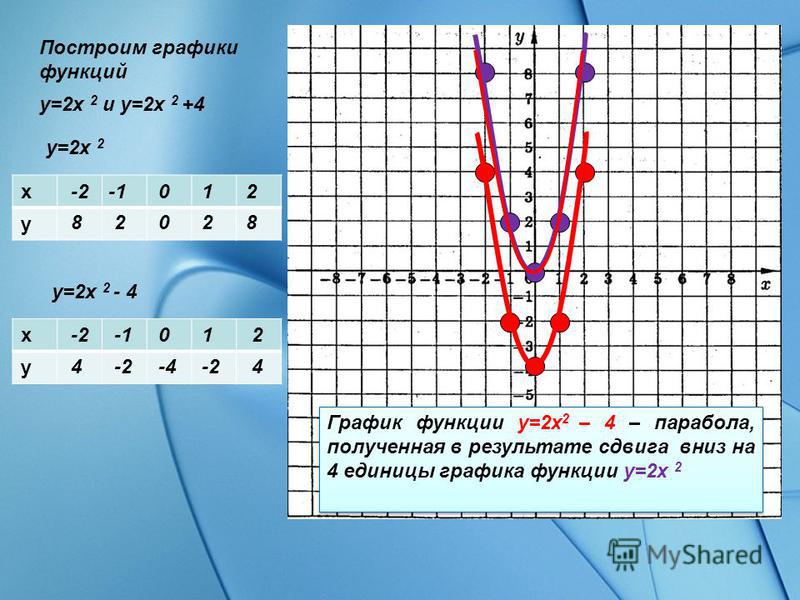 Найдите нули функции у – х()² — 4х

1) 0,2 2) 0,6 3) 6 4) 0

Задание7. Найдите промежуток убывания функции у = (х – 2)² + (х – 1)²

1) (-∞;3] 2) (-∞;2] 3) (-∞;1,5] 4) (-∞;-2]

Задание 8.Найдите наибольшее значение функции, заданной формулой у = -4 х² +7х -3

1) 1/8 2) -1/8 3) — 3/16 4) 1/16

Итог урока.

Урок 7-8. Квадратичная функция и ее график.
«Считать несчастным тот день или тот час,

в который ты не усвоил ничего нового,

ничего не прибавил к своему

образованию».

Ян Амос Коменский

Цели урока:

1.Систематизировать, обобщить и расширить знания учащихся по теме урока.

2.Содействовать развитию математического мышления учащихся.

3.Способствовать развитию творческих способностей учащихся.

Ход урока:

1.Актуализация опорных знаний

2Объяснение нового материала

3Отработка навыков построения графиков квадратичных функций.

4Применение полученных знаний в нестандартной ситуации.

5 Итог урока.

1.Проверка знаний, подготовка учащихся к сознательному усвоению нового материала

Дана функция: y = x² — 4х + 3

Какие способы построения параболы мы уже знаем? (по точкам, с помощью шаблона)

Для того, чтобы воспользоваться шаблоном параболы, что нам нужно знать? (координаты вершины параболы и ось симметрии)

Как можно найти координаты вершины параболы? (воспользуемся методом выделения полного квадрата)

4. Проходит ли ось симметрии данной параболы через точку (2; -1)?

5. Найти нули функции.

6. Вычислить y(0).

7. Вычислить y(4).

Для выполнения задания используем метод выделения полного квадрата: у = х² — 4х +4 – 1, у = (х – 2)² — 1. Координаты вершины: (2;- 1). Ось симметрии х = 2. Ветви направлены вверх. Двое учащихся выполняют задание на боковых досках для последующей проверки.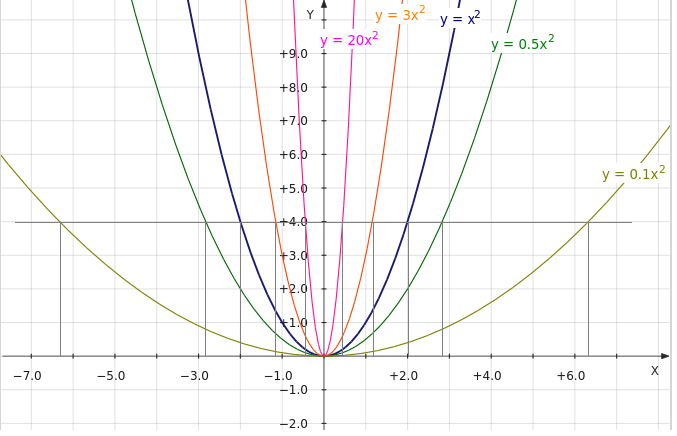

2. Объяснение нового материала

Всегда ли удобно применять метод выделения полного квадрата для нахождения вершины параболы? Обратите внимание на эпиграф к нашему уроку. Сегодня мы познакомимся с универсальным методом построения графика квадратичной функции. Знание этого метода всегда приведет нас к желаемому результату.

Функцию у =ах² + вх + с называют квадратичной, если а, в, с – действительные числа и а не равно 0. для построения графика квадратичной функции воспользуемся методом выделения полного квадрата: ах² + вх + с = а(х² + ) + с = а( х² + 2-) + с = а(х + )² + . Точка с координатами (-;) является вершиной параболы, а прямая х = -, параллельная оси оу, является осью симметрии параболы. При a>0 ветви параболы направлены вверх, при a показывает «крутизну» параболы – чем больше , тем круче поднимаются вверх (опускаются вниз) ее ветви.

График квадратичной функции называется параболой:

a>0 a

Парабола имеет ось симметрии, которая проходит через вершину параболы. Вершина разделяет параболу на две части – ветви параболы. Мы уже знаем, что если в = с = 0, то функция примет вид у=ах² и вершина такой параболы совпадет с началом координат. Так как ах² + вх + с = а(х + )² + , то график квадратичной функции у = ах² + вх + с получается параллельным переносом графика функции у = ах² на вектор р(х₀, у₀), где

х_{0= —}, у₀₌ есть координаты вершины параболы.
У = ах² у = ах² + вх + с

Рассмотрим план построения графика функции: у = ах² + вх + с:

1.Вычисли координаты вершины. Отметь её на координатной плоскости.

2.Через вершину проведи ось симметрии.

3.Вычисли и отметь нули функции.

4.Вычисли координаты дополнительных точек. Отметь их.

5.Проведи параболу.

Отработка навыков построения графиков квадратичных функций.

Задание: построить график функции у = х² + 6х + 5.

1.Найдем координаты вершины х = -3, у= — 4

2. Ось симметрии х = -3

3. Нули функции х = — 5, х = — 1

4.Отмечаем полученные точки на координатной плоскости и проводим через них параболу (иногда требуется найти несколько дополнительных точек).

Для построения графика данной квадратичной функции можно использовать шаблон параболы у=x². Для этого достаточно вычислить координаты вершины параболы, отметить ее на координатной плоскости, провести ось симметрии, определить направление ветвей и, приложив шаблон соответствующей параболы к вершине, построить заданный график.

Задание: используя шаблон параболы y = 2x², построить график функции y = 2х² — 2х +1.

Найдем координаты вершины параболы х = -= . Для того, чтобы найти вторую координату не обязательно запоминать формулу, достаточно подставить х в формулу, задающую функцию: у = 2·- 2·+ 1 = . Координаты вершины параболы (;), ось симметрии х = .

Первичный контроль знаний.

Вариант I

Найдите координаты вершины параболы

Y= — x²-2x+2

А) (-1;3) Б) (1;3) В) (-1;-3) Г) (1;-1)

Укажите график функции y = — x²-2x+2

3. Найдите промежуток убывания функции y = -x²-2x+2

А) (- ;1] Б)[1;+ ) В) (- ;-1] Г) [ -1;+ )

4.Укажите график функции y = (x-3)²+1

Вариант II

Найдите координаты вершины параболы Y = — x²+4x-3

А) (-2;1) Б) (2;1) В) (2;-1) Г) (-2;-1)

Укажите график функции y = — x²+4x-3

3.Найдите промежуток убывания функции y = — x² + 4x -3

А) (- ? ;-2] Б)[-2;+ ? ) В) (- ? ;2] Г) [2;+ ? )

4.Укажите график функции y = (x+2)² +1

Шифры ответов:

1 вариант

Задание	1	2	3	4
Ответ	А	Б	Г	Г

2 вариант

Задание	1	2	3	4
Ответ	Б	В	Г	Б

0>0>1>

Построение графика квадратичной функции — презентация онлайн

Похожие презентации:

Алгоритм построения графика квадратичной функции

Построение графика квадратичной функции

Построение графика квадратичной функции

Построение графика квадратичной функции. (8 класс)

Алгоритм построения графика квадратичной функции

Построение графика квадратичной функции

Построение графика квадратичной функции. (9 класс)

Квадратичная функция её свойства и графики

Квадратичная функция

Построение графиков квадратичной функции, содержащей модуль

1. Построение графика квадратичной функции

16.01.2015

2. Цели:

определение
Квадратичной функцией называется
функция вида y ax 2 bx c ,
где a, b, c – заданные действительные
числа, a 0, x – действительная
переменная.

3. определение

Найдите значение функции
y x 4x
2
при х = 3
y 8 x 2 x 1 при х = -1
2
y 2x 7
2
при х = 0

4. Найдите значение функции

Направление ветвей параболы
y ax 2 bx c
y ax bx c
2

5. Направление ветвей параболы

Х=0
Рис.2
Х = -2
Ось
симметрии
Рис.1

6. Ось симметрии

Найдите точки симметричные
а)
?
2
0
3
6
-6
-4
-2
б)
-2
в)
0
-1
0
г)

7.

Найдите точки симметричныеСамостоятельная работа
Используя шаблон параболы y x 2
постройте графики функций.
y ( x 3) 4
2
y ( x 2) 3
2
y x 2x 2
2

8. Самостоятельная работа Используя шаблон параболы постройте графики функций.

y x 2 2x 2
y ( x 3) 2 4
y ( x 2) 2 3
Используя график функции ответьте на
вопросы:
y ax 2 bx c

10. Используя график функции ответьте на вопросы:

Построить график функции
y x 4x 3
2
1) Найдем координаты вершины параболы
b
x0
2a
y 0 y ( x0 )
4
x0
2
2 *1
y 0 y (2) 2 4 * 2 3 1
2
2; 1

11. Построить график функции

y x 4x 3
2) направление ветвей
2
a=1
a>0
Ветви параболы направлены
вверх

12. 2) направление ветвей

y x 4x 3
3) Найдем нули функции:
2
x 4x 3 0
2
У=0
x1 x 2 4
x1 x 2 3
x1 3,
3;0
x2 1
1;0

13. 3) Найдем нули функции:

y x 4x 3
2
4) ось симметрии
x x0
x 2

14.

4) ось симметрии5) дополнительные точки
0
1
2
3
4
y x 4x 3
2
x
y
0
1
2
3
4
-1
3
0
-1
0
3
7

15. 5) дополнительные точки

6) построение
6) построение
y x 2 4x 3

17. 6) построение

План построения графика
квадратичной функции:
1) Найти координаты вершины
параболы;
2) Определить направление ветвей;
3) Ось симметрии;
4) Найти дополнительные точки;
5) Построение.

18. План построения графика квадратичной функции:

Построить график функции
y x 4x 5
2

19. Построить график функции

y x 2 4x 5

English     Русский Правила

{2}-4ac}}{2a}.

x=\frac{-16±\sqrt{256-4\times 2\left(-y\right)}}{2\times 2}

Квадрат 16.

x=\frac{-16± \sqrt{256-8\left(-y\right)}}{2\times 2}

Умножить -4 на 2.

x=\frac{-16±\sqrt{256+8y}}{2 \times 2}

Умножить -8 раз -y.

x=\frac{-16±\sqrt{8y+256}}{2\times 2}

Прибавьте 256 к 8y.

x=\frac{-16±2\sqrt{2y+64}}{2\times 2}

Извлеките квадратный корень из 256+8y.

x=\frac{-16±2\sqrt{2y+64}}{4}

Умножить 2 раза на 2.

x=\frac{2\sqrt{2y+64}-16}{4}

Теперь решите уравнение x=\frac{-16±2\sqrt{2y+64} {4}, когда ± плюс. Добавьте -16 к 2\sqrt{64+2y}.

x=\frac{\sqrt{2y+64}}{2}-4

Разделить -16+2\sqrt{64+2y} на 4.

x=\frac{-2\sqrt{2y +64}-16}{4}

Теперь решите уравнение x=\frac{-16±2\sqrt{2y+64}}{4}, когда ± минус. Вычтите 2\sqrt{64+2y} из -16.

x=-\frac{\sqrt{2y+64}}{2}-4

Разделить -16-2\sqrt{64+2y} на 4,9{ 2 } — 4 x — 5 = 0

Тригонометрия

4 \sin \theta \cos \theta = 2 \sin \theta

Линейное уравнение

y = 3x + 4

Арифметика 3 0 3 0 9

90

Матрица

\left[ \begin{array} { l l } { 2 } & { 3 } \\ { 5 } & { 4 } \end{array} \right] \left[ \begin{array} { l l l } { 2 } & { 0 } & { 3 } \\ { -1 } & { 1 } & { 5 } \end{массив} \right]

Одновременное уравнение

\left. \begin{cases} { 8x+2y = 46 } \\ { 7x+3y = 47 } \end{cases} \right. 9{2}+2 x-3}

Параболы форм вершин

Сложность построения графика квадратичной функции зависит от формы, в которой вы ее найдете. Мы начнем относительно легко.

f ( x ) = a ( x – h ) ² + k  мы не лжем вам

,

; что есть квадратичная функция. Давай, умножай.

f ( x ) = ось ² + (-2 AH ) x + ( AH ² + K )

H и K K K K K K K K K K K K K K K )

. ( ah ² + k ) также являются константами, которые мы могли бы назвать, скажем, b и c . Видите, вы можете нам доверять, это полностью квадратично.

Когда у вас есть парабола, записанная как f ( x ) = a ( x – h ) ² + k , это вершинная форма . С вершинной формой вы сразу же получаете несколько фрагментов важной информации. Когда вы впервые встречаете кого-то, ваше первое впечатление, как правило, остается с вами. То же самое и с этим уравнением.

Знак a говорит вам, открывается ли парабола вверх или вниз. Если и положительны, он открывается. Если и являются Негативной Нэнси, парабола раскрывается вниз. Вы также знаете, что вершина параболы находится в точке ( ч , к ). Однако будьте осторожны со знаком h .

Sample Problem

Graph the function f ( x ) = ( x – 2) ² – 1. 

The vertex of the parabola is at ( h , k ) = (2, –1). Мы также можем видеть, что парабола открывается вверх. Однако нам нужно еще несколько очков. Мы могли бы составить таблицу и начать подставлять значения x , но обычно есть более простой способ: найти точки пересечения y и x (если они существуют). Начиная с точки пересечения y , которая происходит при x = 0. 

f (0) = (0 – 2) ² – 1 = 4 – 1 = 3 

Прямо на: (0 , 3) — точка на нашей параболе. Теперь перейдите к x -перехватам, которые происходят, когда y = 0, если они есть.

0 = ( х – 2) ² – 1

0 = х ² – 4 х + 4 – 1

0 = x ² – 4 x + 3

Это квадратное уравнение можно разложить на множители.

0 = ( x – 3)( x – 1) 

Таким образом, (1, 0) и (3, 0) также являются точками параболы. Соединив все вместе, мы получаем:

Видишь? Математика умнее, а не сложнее.

Пример задачи

Нарисуйте график функции f ( x ) = -2( x + 1) ² – 2. 

Сразу видно, что вершина находится в (-1, -2) , а парабола направлена ​​вниз. Время выследить нашу г -перехват.

f (0) = -2(0 + 1) ² – 2 = -2(1) – 2 = -4 

Сладкий. Перехват y равен (0, -4). Теперь охотимся за x -перехватами. Некоторые говорят, что использование динамита во время охоты неспортивно. Наверное, они правы.

0 = -2( x + 1) ² – 2 

0 = -2( x ² + 2 x + 1) – 2 

0 = -2 x ² – 4 х — 2 — 2

0 = -2 x ² — 4 x — 4

0 = — x ² — 2 x — 2

. стена. Дискриминант этого уравнения равен:

b ² – 4 ac =(-2) ² – 4(-1)(-2) = 4 – 8 = -4

Отрицательно, поэтому действительных корней у этого уравнения нет. Это означает, что функция никогда не пересечет ось 90 162 x 90 163, поэтому нет x — перехваты. Это имеет смысл, учитывая, что вершина находится в точке (-1, -2), а парабола направлена ​​вниз, поэтому функция не будет двигаться вверх к оси x . Думаю, нам не понадобится этот динамит в конце концов.

Вместо использования x -перехватов мы вставим несколько дополнительных значений x и нанесем их на график.

^{4 -439 9}

x	f ( x )
-3
-4	-20

Мы почти готовы закончить этот график. Однако это будет проще сделать с еще несколькими точками. Помните, что ось симметрии проходит через вершину; теперь мы можем использовать это, чтобы найти еще несколько точек, поскольку у нас есть точки с обеих сторон вершины.

Сравните (0, -4) с вершиной в (-1, -2), например. Это 1 справа по оси x и 2 ниже по оси y . Поскольку функция симметрична, 1 пробел слева от вершины также будет на 2 ниже на y -ось, в точке (-2, -4). Точно так же (-3, -10) — это 2 пробела слева от вершины и 8 вниз, а (-4, -20) — 3 пробела влево и 18 пробелов вниз.

No related posts.