III. Примеры задач с решениями — Схема Горнера
1. Разделить 5x4+5x3+x2−11 на x−1, используя схему Горнера. Решение: Составим таблицу из двух строк: в первой строке запишем коэффициенты многочлена 5x4+5x3+x2−11, расположенные по убыванию степеней переменной x. Заметьте, что данный многочлен не содержит x в первой степени, т.е. коэффициент перед x в первой степени равен 0. Так как мы делим на x−1, то во второй строке запишем единицу: Начнем заполнять пустые ячейки во второй строке. Во вторую ячейку второй строки запишем число 5, просто перенеся его из соответствующей ячейки первой строки: Следующую ячейку заполним по такому принципу: 1⋅5+5=10: Аналогично заполним и четвертую ячейку второй строки: 1⋅10+1=11: Для пятой ячейки получим: 1⋅11+0=11: И, наконец, для последней, шестой ячейки, имеем: 1⋅11+(−11)=0: Задача решена, осталось только записать ответ: Как видите, числа, расположенные во второй строке (между единицей и нулём), есть коэффициенты многочлена, полученного после деления 5x4+5x3+x2−11 на x−1. Можно сформулировать вывод и в такой форме: так как значение многочлена 5x4+5x3+x2−11 при x=1 равно нулю, то единица является корнем многочлена 5x4+5x3+x2−11. 2. Найдите неполное частное, остаток от деления многочлена А(х) = х3 – 2х2 + 2х – 1 на двучлен х – 1. Решение:
Ответ: Q(x) = х2 – х + 1 , R(x) = 0. 3. Вычислите значение многочлена А(х) при х = –1, если А(х) = х3 – 2х – 1. Решение:
Ответ: А(–1)
= 0. 4. Вычислите значение многочлена А(х) при х = 3, неполное частное и остаток, где А(х)= 4х5 – 7х4 + 5х3– 2х + 1. Решение:
Ответ: R(x) = A(3) = 535, Q(x) = 4х4 + 5х3 + 20х2 + 60х +178. 5. Найдите корни уравнения х3 + 4х2 + х – 6 = 0. Решение: Находим
делители свободного члена ±1; ± 2; ± 3; ± 6 Здесь, а = 1 (х – 1 = х – а), а коэффициенты многочлена-делимого равны соответственно
Итак, коэффициенты частного – числа 1, 5, 6, а остаток r = 0. Значит, х3 + 4х2 + х – 6 = (х – 1) (х2 + 5х + 6) = 0 Отсюда: х – 1 = 0 или х2 + 5х + 6 = 0; х = 1, х1 = – 2; х2 = –3. Произведение нескольких выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл. Отсюда находим корни исходного уравнения: \(x_1 = 6, \ x_2 = -3\) – подходят по ОДЗ. Меньший из них \(x = -3\) . Ответ: -3 Задание 20 #1181 2x 4 + 5x 3 — 11x 2 — 20x + 12 = 0 Для начала нужно методом подбора найти один корень. Обычно он является делителем свободного члена. В данном случае делителями числа 1: 2 + 5 — 11 — 20 + 12 = -12 ⇒ число 1 -1: 2 — 5 — 11 + 20 + 12 = 18 ⇒ число -1 не является корнем многочлена 2: 2 ∙ 16 + 5 ∙ 8 — 11 ∙ 4 — 20 ∙ 2 + 12 = 0 ⇒ число 2 является корнем многочлена Мы нашли 1 из корней многочлена. Корнем многочлена является 2, а значит исходный многочлен должен делиться на x — 2 .
В верхней строке выставляются коэффициенты исходного многочлена. В первой ячейке второй строки ставится найденный нами корень 2. Во второй строке пишутся коэффициенты многочлена, который получится в результате деления. Они считаются так:
Последнее число — это остаток от деления. 2x 4 + 5x 3 — 11x 2 — 20x + 12 = (x — 2)(2x 3 + 9x 2 + 7x — 6) Но это еще не конец. Можно попробовать разложить таким же способом многочлен 2x 3 + 9x 2 + 7x — 6. Опять ищем корень среди делителей свободного члена. Делителями числа -6 являются ±1, ±2, ±3, ±6. 1: 2 + 9 + 7 — 6 = 12 ⇒ число 1 не является корнем многочлена -1: -2 + 9 — 7 — 6 = -6 ⇒ число -1 не является корнем многочлена 2: 2 ∙ 8 + 9 ∙ 4 + 7 ∙ 2 — 6 = 60 ⇒ число 2 не является корнем многочлена -2: 2 ∙ (-8) + 9 ∙ 4 + 7 ∙ (-2) — 6 = 0 ⇒ число -2 является корнем многочлена Напишем найденный корень в нашу схему Горнера и начнем заполнять пустые ячейки:
Таким образом мы исходный многочлен разложили на множители: 2x 4 + 5x 3 — 11x 2 — 20x + 12 = (x — 2)(x + 2)(2x 2 + 5x — 3) Многочлен 2x 2 + 5x — 3 тоже можно разложить на множители.
Таким образом мы исходный многочлен разложили на линейные множители: 2x 4 + 5x 3 — 11x 2 — 20x + 12 = (x — 2)(x + 2)(x + 3)(2x — 1) А корнями уравнения являются. Цели:
Тип урока : комбинированный. Оборудование: графопроектор. Наглядность: таблица «Теорема Виета». Ход урока 1. Устный счет а) Чему равен остаток от деления многочлена р n (х) = а n х n + а n-1 х n-1 + … + а 1 х 1 + a 0 на двучлен х-а? б) Сколько корней может иметь кубическое уравнение? в) С помощью чего мы решаем уравнение третьей и четвертой степени? г) Если b четное число в квадратном уравнение, то чему равен Д и х 1 ;х 2 2. Самостоятельная работа (в группах) Составить уравнение, если известны корни (ответы к заданиям закодированы) Используется «Теорема Виета» 1 группа Корни: х 1 = 1; х 2 = -2; х 3 = -3; х 4 = 6 Составить уравнение: B=1 -2-3+6=2; b=-2 с=-2-3+6+6-12-18= -23; с= -23 d=6-12+36-18=12; d= -12 е=1(-2)(-3)6=36 х 4 — 2 х 3 — 23х 2 — 12 х + 36 = 0 (это уравнение решает потом 2 группа на доске) Решение . р = ±1;±2;±3;±4;±6… р 4 (1)=1-2-23-12+36=0 Число 1 удовлетворяет уравнению, следовательно, =1 корень уравнения. По схеме Горнера р 3 (x) = х 3 -х 2 -24x -36 р 3 (-2) = -8 -4 +48 -36=0, х 2 =-2 р 2 (x) = х 2 -3х -18=0 х 3 =-3, х 4 =6 Ответ: 1;-2;-3;6 сумма корней 2 (П) 2 группа Корни: х 1 = -1; х 2 = х 3 =2; х 4 =5 Составить уравнение: B=-1+2+2+5-8; b= -8 с=2(-1)+4+10-2-5+10=15; с=15 D=-4-10+20-10= -4; d=4 е=2(-1)2*5=-20;е=-20 8+15+4х-20=0 (это уравнение решает на доске 3 группа) р = ±1;±2;±4;±5;±10;±20. р 4 (1)=1-8+15+4-20=-8 р 4 (-1)=1+8+15-4-20=0 р 3 (x) = х 3 -9х 2 +24x -20 р 3 (2) = 8 -36+48 -20=0 р 2 (x) = х 2 -7х +10=0 х 1 =2; х 2 =5 Ответ: -1;2;2;5 сумма корней 8(Р) 3 группа Корни: х 1 = -1; х 2 =1; х 3 =-2; х 4 =3 Составить уравнение: В=-1+1-2+3=1;в=-1 с=-1+2-3-2+3-6=-7;с=-7 D=2+6-3-6=-1; d=1 е=-1*1*(-2)*3=6 х 4 — х 3 — 7х 2 + х + 6 = 0 (это уравнение решает потом на доске 4 группа) Решение. р = ±1;±2;±3;±6 р 4 (1)=1-1-7+1+6=0 р 3 (x) = х 3 — 7x -6 р 3 (-1) = -1+7-6=0 р 2 (x) = х 2 -х -6=0; х 1 =-2; х 2 =3 Ответ:-1;1;-2;3 Сумма корней 1(О) 4 группа Корни: х 1 = -2; х 2 =-2; х 3 =-3; х 4 =-3 Составить уравнение: B=-2-2-3+3=-4; b=4 с=4+6-6+6-6-9=-5; с=-5 D=-12+12+18+18=36; d=-36 е=-2*(-2)*(-3)*3=-36;е=-36 х 4 + 4х 3 – 5х 2 – 36х -36 = 0 (это уравнение решает потом 5 группа на доске) Решение. Целые корни ищем среди делителей числа -36 р = ±1;±2;±3… р(1)= 1 + 4-5-36-36 = -72 р 4 (-2) = 16 -32 -20 + 72 -36 = 0 р 3 (х) = х 3 +2х 2 -9х-18 = 0 р 3 (-2)= -8 + 8 + 18-18 = 0 р 2 (х) = х 2 -9 = 0; x=±3 Ответ: -2; -2; -3; 3 Сумма корней-4 (Ф) 5 группа Корни: х 1 = -1; х 2 =-2; х 3 =-3; х 4 =-4 Составить уравнение х 4 + 10х 3 + 35х 2 + 50х + 24 = 0 (это уравнение решает потом 6группа на доске) Решение . р = ±1;±2;±3 р 4 (-1) = 1 -10 + 35 -50 + 24 = 0 р 3 (х) = x- 3 + 9х 2 + 26x+ 24 = 0 p 3 (-2) = -8 + 36-52 + 24 = О р 2 (х) = x 2 + 7x+ 12 = 0 Ответ:-1;-2;-3;-4 сумма-10 (И) 6 группа Корни: х 1 = 1; х 2 = 1; х 3 = -3; х 4 = 8 Составить уравнение B=1+1-3+8=7;b=-7 с=1 -3+8-3+8-24= -13 D=-3-24+8-24= -43; d=43 х 4 — 7х 3 — 13х 2 + 43 x — 24 = 0 (это уравнение решает потом 1 группа на доске) Решение . Целые корни ищем среди делителей числа -24. р 4 (1)=1-7-13+43-24=0 р 3 (1)=1-6-19+24=0 р 2 (x)= х 2 -5x — 24 = 0 х 3 =-3, х 4 =8 Ответ: 1;1;-3;8 сумма 7 (Л) 3. Решение уравнений с параметром 1. Решить уравнение х 3 + 3х 2 + mх — 15 = 0; если один из корней равен (-1) Ответ записать в порядке возрастания R=Р 3 (-1)=-1+3-m-15=0 х 3 + 3х 2 -13х — 15 = 0; -1+3+13-15=0 По условию х 1 = — 1; Д=1+15=16 Р 2 (х) = х 2 +2х-15 = 0 х 2 =-1-4 = -5; х 3 =-1 + 4 = 3; Ответ:- 1;-5; 3 В порядке возрастания: -5;-1;3. 2. Найти все корни многочлена х 3 — 3х 2 + ах — 2а + 6, если остатки от его деления на двучлены х-1 и х +2 равны. Решение: R=Р 3 (1) = Р 3 (-2) Р 3 (1) = 1-3 + а- 2а + 6 = 4-а Р 3 (-2) = -8-12-2а-2а + 6 = -14-4а x 3 -Зх 2 -6х + 12 + 6 = х 3 -Зх 2 -6х + 18 x 2 (x-3)-6(x-3) = 0 (х-3)(х 2 -6) = 0 Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из этих множителей равен нулю, а другой при этом имеет смысл. 2 группа . Корни: -3; -2; 1; 2; 3 группа . Корни: -1; 2; 6; 10; 4 группа . Корни: -3; 2; 2; 5; 5 группа . Корни: -5; -2; 2; 4; 6 группа . Корни: -8; -2; 6; 7. для решения математики. Быстро найти решение математического уравнения в режиме онлайн . Сайт www.сайт позволяет решить уравнение почти любого заданного алгебраического , тригонометрического или трансцендентного уравнения онлайн . Схема Горнера. Корни многочленаЦели урока:
Оборудование: карточки для работы в группах, плакат со схемой Горнера.
Метод обучения: лекция, рассказ, объяснение, выполнение тренировочных упражнений. Форма контроля: проверка задач самостоятельного решения, самостоятельная работа. Ход урока 1. Организационный момент 2. Актуализация знаний учащихся — Какая теорема позволяет определить, является ли число корнем данного уравнения (сформулировать теорему)? Теорема Безу. Остаток от деления многочлена Р(х) на двучлен х-с равен Р(с), число с называют корнем многочлена Р(х), если Р(с)=0. Теорема позволяет, не выполняя операцию деления, определить, является ли данное число корнем многочлена. — Какие утверждения облегчают поиск корней? а) Если старший коэффициент многочлена равен единице, то корни многочлена следует искать среди делителей свободного члена. б) Если сумма коэффициентов многочлена равна 0, то один из корней равен 1.
в)Если сумма коэффициентов стоящих на четных местах, равна сумме коэффициентов, стоящих на нечетных местах, то один из корней равен -1. г) Если все коэффициенты положительны, то корнями многочлена являются отрицательные числа. д) Многочлен нечетной степени имеет хотя бы один действительный корень. 3. Изучение нового материала При решении целых алгебраических уравнений приходиться находить значения корней многочленов. Эту операцию можно существенно упростить, если проводить вычисления по специальному алгоритму, называемому схемой Горнера. Эта схема названа в честь английского ученого Уильяма Джорджа Горнера. Схема Горнера это алгоритм для вычисления частного и остатка от деления многочлена Р(х) на х-с. Кратко, как он устроен.
Пусть дан произвольный многочлен Р(х)=а0хn+ а1хn-1+ …+ аn-1х+ аn. Деление этого многочлена на х-с – это представление его в виде Р(х)=(х-с)g(х) + r(х). Частное g(х)=в0хn-1+ вnхn-2 +…+вn-2х + вn-1, где в0=а0, вn=свn-1 +аn, n=1,2,3,…n-1.
Число, которое после выполнения алгоритма оказывается записанным в правой нижней клетке, и есть остаток от деления многочлена Р(х) на х-с. Например : Разделить многочлен Р(х)= х3-2х+3 на х-2. 1.
2.
3.
4.
Получаем, что х3-2х+3=(х-2) (х2+2х+2) + 7. 4. Закрепление изученного материала Пример 1: Разложите на множители с целыми коэффициентами многочлен Р(х)=2х4-7х3-3х2+5х-1. Решение: Ищем целые корни среди делителей свободного члена -1: 1; -1. Составим таблицу:
X = -1 – корень Р(х)= (х+1) (2х3 -9х2 +6х -1)
Проверим 1/2.
Следовательно, многочлен Р(х) можно представить в виде Р(х)= (х+1) (х-1/2) (х2 -8х +2) = (х+1) (2х -1) (х2 — 4х +1) Пример 2: Решить уравнение 2х4 — 5х3 + 5х2 — 2 = 0 Решение:
Так как сумма коэффициентов многочлена , записанного в левой части уравнения, равна нулю, то один из корней 1.
Получаем Р(х)=(х-1) (2х3 -3х2 =2х +2). Будем искать корни среди делителей свободного члена 2.
Выяснили, что целых корней больше нет.
Итак (х-1) (х+1/2) (2х2 – 4х +4)=0. Далее решаем квадратное уравнение 2х2-4х +4 = 0. Д/4=1-2= -1. Значит это уравнение корней не имеет.
Ответ: 1; -1/2. Пример 3: Решить уравнение 5х4 – 3х3 – 4х2 -3х+ 5 = 0. Решение: Корни данного уравнения будем искать среди делителей свободного члена 5: 1;-1;5;-5. х=1 — корень уравнения, так как сумма коэффициентов равна нулю. Воспользуемся схемой Горнера:
Можно записать (х-1) (5х3 +2х2 -2х-5)=0.
уравнение представим в виде произведения трех множителей: (х-1) (х-1) (5х2 -7х + 5)=0. Решая квадратное уравнение 5х2 -7х+5=0, получили Д=49-100=-51, корней нет. Ответ: 1. Далее работа в парах по карточкам. Карточка 1
Карточка 2
Карточка 3
Карточка 4
5. Проверка знаний при решении в парах осуществляется на уроке путем узнавания способа действия и названия ответа. Домашнее задание: Решите уравнения: а) х4-3х3+4х2-3х+1=0 б) 5х4-36х3+62х2-36х+5=0 в) х4+х3+х+1=4х2 г) х4+2х3-х-2=0
Литература
Уравнения высших степенейСодержание статьи 1. Теорема Виета 2. Теорема Безу 3. Схема Горнера 4. Метод одновременного подбора по коэффициенту при старшей степени и при свободном члене Замечание 1 Уравнения высших степеней — это уравнения, в которых старшая степень при переменной больше либо равна трём. Приравниваем этот многочлен к нулю и находим его корни через дискриминант, они равны $x_{3,4}=-5±\sqrt{19}$. Сообщество экспертов Автор24 Автор этой статьи Дата последнего обновления статьи: 14.03.2022 Реши уравнение х 4. Схема ГорнераСервис для решения уравнений онлайн поможет вам решить любое уравнение. Используя наш сайт, вы получите не просто ответ уравнения, но и увидите подробное решение, то есть пошаговое отображение процесса получения результата. Наш сервис будет полезен старшеклассникам общеобразовательных школ и их родителям. Ученики смогут подготовиться к контрольным, экзаменам, проверить свои знания, а родители – проконтролировать решение математических уравнений своими детьми. Умение решать уравнения – обязательное требование к школьникам. Сервис поможет вам самообучаться и повышать уровень знаний в области математических уравнений. С его помощью вы сможете решить любое уравнение: квадратное, кубическое, иррациональное, тригонометрическое и др. Уравнение с одним неизвестным, которое после раскрытия скобок и приведения подобных членов принимает вид aх + b = 0 , где a и b произвольные числа, называется линейным уравнением с одним неизвестным. Например, все уравнения: 2х + 3= 7 – 0,5х; 0,3х = 0; x/2 + 3 = 1/2 (х – 2) — линейные. Значение неизвестного, обращающее уравнение в верное равенство называется решением или корнем уравнения . Например, если в уравнении 3х + 7 = 13 вместо неизвестного х подставить число 2 , то получим верное равенство 3· 2 +7 = 13. Значит, значение х = 2 есть решение или корень уравнения. А значение х = 3 не обращает уравнение 3х + 7 = 13 в верное равенство, так как 3· 2 +7 ≠ 13. Значит, значение х = 3 не является решением или корнем уравнения. Решение любых линейных уравнений сводится к решению уравнений вида aх + b = 0. Перенесем свободный член из левой части уравнения в правую, изменив при этом знак перед b на противоположный, получим Если a ≠ 0, то х = ‒ b/a . Пример 1. Решите уравнение 3х + 2 =11. Перенесем 2 из левой части уравнения в правую, изменив при этом знак перед 2 на противоположный, получим Выполним вычитание, тогда Чтобы найти х надо разделить произведение на известный множитель, то есть Значит, значение х = 3 является решением или корнем уравнения. Ответ: х = 3 . Если а = 0 и b = 0 , то получим уравнение 0х = 0. Это уравнение имеет бесконечно много решений, так как при умножении любого числа на 0 мы получаем 0,но b тоже равно 0. Решением этого уравнения является любое число. Пример 2. Решите уравнение 5(х – 3) + 2 = 3 (х – 4) + 2х ‒ 1. Раскроем скобки: Приведем подобные члены: Ответ: х — любое число . Если а = 0 и b ≠ 0 , то получим уравнение 0х = — b. Это уравнение решений не имеет, так как при умножении любого числа на 0 мы получаем 0, но b ≠ 0 . Пример 3. Решите уравнение х + 8 = х + 5. Сгруппируем в левой части члены, содержащие неизвестные, а в правой ‒ свободные члены: Приведем подобные члены: Ответ: нет решений. На рисунке 1 изображена схема решения линейного уравнения Составим общую схему решения уравнений с одной переменной. Рассмотрим решение примера 4. Пример 4. Пусть надо решить уравнение 1) Умножим все члены уравнения на наименьшее общее кратное знаменателей, равное 12. 2) После сокращения получим 3) Чтобы отделить члены, содержащие неизвестные и свободные члены, раскроем скобки: 4) Сгруппируем в одной части члены, содержащие неизвестные, а в другой – свободные члены: 5) Приведем подобные члены: 6) Разделим на – 22 , Получим Как видим, корень уравнения равен семи. Вообще такие уравнения можно решать по следующей схеме : а) привести уравнение к целому виду; б) раскрыть скобки; в) сгруппировать члены, содержащие неизвестное, в одной части уравнения, а свободные члены ‒ в другой; г) привести подобные члены; д) решить уравнение вида aх = b,которое получили после приведения подобных членов. Однако эта схема не обязательна для всякого уравнения. При решении многих более простых уравнений приходится начинать не с первого, а со второго (Пример. 2 ), третьего (Пример. 1, 3 ) и даже с пятого этапа, как в примере 5. Пример 5. Решите уравнение 2х = 1/4. Находим неизвестное х = 1/4: 2, Рассмотрим решение некоторых линейных уравнений, встречающихся на основном государственном экзамене. Пример 6. Решите уравнение 2 (х + 3) = 5 – 6х. 2х + 6 = 5 – 6х 2х + 6х = 5 – 6 Ответ: ‒ 0, 125 Пример 7. Решите уравнение – 6 (5 – 3х) = 8х – 7. – 30 + 18х = 8х – 7 18х – 8х = – 7 +30 Ответ: 2,3 Пример 8. Решите уравнение
3(3х – 4) = 4 · 7х + 24 9х – 12 = 28х + 24 9х – 28х = 24 + 12 Пример 9. Найдите f(6), если f (x + 2) = 3 7-х Решение Так как надо найти f(6), а нам известно f (x + 2), Решаем линейное уравнение х + 2 = 6, Если х = 4, тогда Ответ: 27. Если у Вас остались вопросы, есть желание разобраться с решением уравнений более основательно, записывайтесь на мои уроки в РАСПИСАНИИ . Буду рада Вам помочь! Также TutorOnline советует посмотреть новый видеоурок от нашего репетитора Ольги Александровны, который поможет разобраться как с линейными уравнениями, так и с другими. сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна. Предлагаем вам удобный бесплатный онлайн калькулятор для решения квадратных уравнений. Вы сможете быстро получить и разобраться, как они решаются, на понятных примерах. Как решить квадратное уравнение
Для закрепления алгоритма, вот еще несколько показательных примеров решений квадратных уравнений . Пример 1. Решение обычного квадратного уравнения с разными действительными корнями. Для проверки подставим: Пример 2. Решение квадратного уравнения с совпадением действительных корней. Подставим Пример 3. X1=(-В+D 1/2)/2А = (4+6i)/(2*13) = 2/13+3i/13 Вот собственно все возможные случаи решения квадратных уравнений. Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант . Дискриминант
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Выпишем коэффициенты для первого уравнения и найдем дискриминант: Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение: Дискриминант отрицательный, корней нет. Осталось последнее уравнение: Дискриминант равен нулю — корень будет один. Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество. Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много. Корни квадратного уравненияТеперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам: Основная формула корней квадратного уравнения Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D
Первое уравнение: D > 0 ⇒ уравнение имеет два корня. Найдем их: Второе уравнение: D > 0 ⇒ уравнение снова имеет два корня. Найдем их \[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\] Наконец, третье уравнение: D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую: Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок. Неполные квадратные уравненияБывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0. Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его: Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c
/a
) ≥ 0. Достаточно выразить величину x
2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители: Вынесение общего множителя за скобку Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7. 5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу. 4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5. для решения математики. Быстро найти решение математического уравнения в режиме онлайн . Сайт www.сайт позволяет решить уравнение почти любого заданного алгебраического , тригонометрического или трансцендентного уравнения онлайн . X 0 решение. Схема Горнерадля решения математики. Быстро найти решение математического уравнения в режиме онлайн . Сайт www.сайт позволяет решить уравнение почти любого заданного алгебраического , тригонометрического или трансцендентного уравнения онлайн . При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сервис для решения уравнений онлайн поможет вам решить любое уравнение. Используя наш сайт, вы получите не просто ответ уравнения, но и увидите подробное решение, то есть пошаговое отображение процесса получения результата. Наш сервис будет полезен старшеклассникам общеобразовательных школ и их родителям. Ученики смогут подготовиться к контрольным, экзаменам, проверить свои знания, а родители – проконтролировать решение математических уравнений своими детьми. Умение решать уравнения – обязательное требование к школьникам. Сервис поможет вам самообучаться и повышать уровень знаний в области математических уравнений. С его помощью вы сможете решить любое уравнение: квадратное, кубическое, иррациональное, тригонометрическое и др. Польза онлайн сервиса бесценна, ведь кроме верного ответа вы получаете подробное решение каждого уравнения. Преимущества решения уравнений онлайн. Решить любое уравнение онлайн на нашем сайте вы можете абсолютно бесплатно. Сервис полностью автоматический, вам ничего не придется устанавливать на свой компьютер, достаточно будет только ввести данные и программа выдаст решение. 4x 3 — 19x 2 + 19x + 6 = 0 Для начала нужно методом подбора найти один корень. Обычно он является делителем свободного члена. В данном случае делителями числа 6 являются ±1, ±2, ±3, ±6. 1: 4 — 19 + 19 + 6 = 10 ⇒ число 1 -1: -4 — 19 — 19 + 6 = -36 ⇒ число -1 не является корнем многочлена 2: 4 ∙ 8 — 19 ∙ 4 + 19 ∙ 2 + 6 = 0 ⇒ число 2 является корнем многочлена Мы нашли 1 из корней многочлена.
В верхней строке выставляются коэффициенты исходного многочлена. В первой ячейке второй строки ставится найденный нами корень 2. Во второй строке пишутся коэффициенты многочлена, который получится в результате деления. Они считаются так:
Последнее число — это остаток от деления. Таким образом мы исходный многочлен разложили на множители: 4x 3 — 19x 2 + 19x + 6 = (x — 2)(4x 2 — 11x — 3) И теперь, всего лишь, осталось найти корни квадратного уравнения 4x 2 — 11x — 3 = 0 Мы нашли все корни уравнения. Как решать уравнения?В этом разделе мы вспомним (или изучим – уж кому как) самые элементарные уравнения. Итак, что такое уравнение? Говоря человеческим языком, это какое-то математическое выражение, где есть знак равенства и неизвестное. Которое, обычно, обозначается буквой «х» . Решить уравнение — это найти такие значения икса, которые при подстановке в исходное выражение, дадут нам верное тождество. Напомню, что тождество – это выражение, которое не вызывает сомнения даже у человека, абсолютно не отягощенного математическими знаниями. Типа 2=2, 0=0, ab=ab и т. Уравнения бывают всякие (вот удивил, да?). Но всё их бесконечное многообразие можно разбить всего на четыре типа. 4. Все остальные.) Всех остальных, разумеется, больше всего, да…) Сюда входят и кубические, и показательные, и логарифмические, и тригонометрические и всякие другие. С ними мы в соответствующих разделах плотно поработаем. Сразу скажу, что иногда и уравнения первых трёх типов так накрутят, что и не узнаешь их… Ничего. Мы научимся их разматывать. И зачем нам эти четыре типа? А затем, что линейные уравнения решаются одним способом, квадратные другим, дробные рациональные — третьим, а остальные не решаются вовсе! Ну, не то, чтобы уж совсем никак не решаются, это я зря математику обидел.) Просто для них существуют свои специальные приёмы и методы. Но для любых (повторяю — для любых! ) уравнений есть надёжная и безотказная основа для решения. Собственно, решение уравнения и состоит из этих самых преобразований. На 99%. Ответ на вопрос: «Как решать уравнения? » лежит, как раз, в этих преобразованиях. Намёк понятен?) Тождественные преобразования уравнений.В любых уравнениях для нахождения неизвестного надо преобразовать и упростить исходный пример. Причем так, чтобы при смене внешнего вида суть уравнения не менялась. Такие преобразования называются тождественными или равносильными. Отмечу, что эти преобразования относятся именно к уравнениям. В математике ещё имеются тождественные преобразования выражений. Это другая тема. Сейчас мы с вами повторим все-все-все базовые тождественные преобразования уравнений. Базовые потому, что их можно применять к любым уравнениям – линейным, квадратным, дробным, тригонометрическим, показательным, логарифмическим и т. Первое тождественное преобразование: к обеим частям любого уравнения можно прибавить (отнять) любое (но одно и то же!) число или выражение (в том числе и выражение с неизвестным!). Суть уравнения от этого не меняется. Вы, между прочим, постоянно пользовались этим преобразованием, только думали, что переносите какие-то слагаемые из одной части уравнения в другую со сменой знака. Типа: Дело знакомое, переносим двойку вправо, и получаем: На самом деле вы отняли от обеих частей уравнения двойку. Результат получается тот же самый: х+2 — 2 = 3 — 2 Перенос слагаемых влево-вправо со сменой знака есть просто сокращённый вариант первого тождественного преобразования. И зачем нам такие глубокие познания? – спросите вы. В уравнениях низачем. Переносите, ради бога. Только знак не забывайте менять. А вот в неравенствах привычка к переносу может и в тупик поставить…. Второе тождественное преобразование : обе части уравнения можно умножить (разделить) на одно и то же отличное от нуля число или выражение. Понятное дело, х = 2. А вот как вы его нашли? Подбором? Или просто озарило? Чтобы не подбирать и не ждать озарения, нужно понять, что вы просто поделили обе части уравнения на 5. При делении левой части (5х) пятёрка сократилась, остался чистый икс. Чего нам и требовалось. А при делении правой части (10) на пять, получилась, знамо дело, двойка. Вот и всё. Забавно, но эти два (всего два!) тождественных преобразования лежат в основе решения всех уравнений математики. Во как! Имеет смысл посмотреть на примерах, что и как, правда?) Примеры тождественных преобразований уравнений. Основные проблемы.Начнём с первого тождественного преобразования. Перенос влево-вправо. Пример для младшеньких.) Допустим, надо решить вот такое уравнение: 3-2х=5-3х Вспоминаем заклинание: «с иксами — влево, без иксов — вправо!» Это заклинание — инструкция по применению первого тождественного преобразования. 3-2х+3х=5 Так, иксы собрали в кучку. Займёмся числами. Слева стоит тройка. С каким знаком? Ответ «с никаким» не принимается!) Перед тройкой, действительно, ничего не нарисовано. А это значит, что перед тройкой стоит плюс. Так уж математики договорились. Ничего не написано, значит, плюс. Следовательно, в правую часть тройка перенесётся с минусом. Получим: -2х+3х=5-3 Остались сущие пустяки. Слева — привести подобные, справа — посчитать. Сразу получается ответ: В этом примере хватило одного тождественного преобразования. Второе не понадобилось. Ну и ладно.) Пример для старшеньких.) Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.) Можно потренироваться в решении примеров и узнать свой уровень. можно познакомиться с функциями и производными. 2x 4 + 5x 3 — 11x 2 — 20x + 12 = 0 Для начала нужно методом подбора найти один корень. Обычно он является делителем свободного члена. В данном случае делителями числа 12 являются ±1, ±2, ±3, ±4, ±6, ±12. Начнем их подставлять по-очереди: 1: 2 + 5 — 11 — 20 + 12 = -12 ⇒ число 1 -1: 2 — 5 — 11 + 20 + 12 = 18 ⇒ число -1 не является корнем многочлена 2: 2 ∙ 16 + 5 ∙ 8 — 11 ∙ 4 — 20 ∙ 2 + 12 = 0 ⇒ число 2 является корнем многочлена Мы нашли 1 из корней многочлена. Корнем многочлена является 2, а значит исходный многочлен должен делиться на x — 2 . Для того, чтобы выполнить деление многочленов, воспользуемся схемой Горнера:
В верхней строке выставляются коэффициенты исходного многочлена.
Последнее число — это остаток от деления. 2x 4 + 5x 3 — 11x 2 — 20x + 12 = (x — 2)(2x 3 + 9x 2 + 7x — 6) Но это еще не конец. Можно попробовать разложить таким же способом многочлен 2x 3 + 9x 2 + 7x — 6. Опять ищем корень среди делителей свободного члена. Делителями числа -6 являются ±1, ±2, ±3, ±6. 1: 2 + 9 + 7 — 6 = 12 ⇒ число 1 не является корнем многочлена -1: -2 + 9 — 7 — 6 = -6 ⇒ число -1 не является корнем многочлена 2: 2 ∙ 8 + 9 ∙ 4 + 7 ∙ 2 — 6 = 60 ⇒ число 2 не является корнем многочлена -2: 2 ∙ (-8) + 9 ∙ 4 + 7 ∙ (-2) — 6 = 0 ⇒ число -2 является корнем многочлена Напишем найденный корень в нашу схему Горнера и начнем заполнять пустые ячейки:
Таким образом мы исходный многочлен разложили на множители: 2x 4 + 5x 3 — 11x 2 — 20x + 12 = (x — 2)(x + 2)(2x 2 + 5x — 3) Многочлен 2x 2 + 5x — 3 тоже можно разложить на множители.
Таким образом мы исходный многочлен разложили на линейные множители: 2x 4 + 5x 3 — 11x 2 — 20x + 12 = (x — 2)(x + 2)(x + 3)(2x — 1) А корнями уравнения являются. dragonwasrobot.github.io/2015-08-03-an-introduction-to-horner-s-method.md на мастере · dragonwasrobot/dragonwasrobot.github.io · GitHub
предпосылки: Базовые знания Haskell или аналогичного. «Что делает пустыню прекрасной», 1. ВведениеЦель этой записи в блоге — представить метод Хорнера для полиномиальное вычисление и полиномиальное деление, а затем доказать отношения эквивалентности между этими двумя типами приложений. Сообщение в блоге имеет следующую структуру. В разделе
2, мы аргументируем применение
метода Хорнера для полиномиальной оценки, а затем получить его
определение. Рассмотрев полиномиальное вычисление, мы затем приводим доводы в пользу
применение метода Горнера для полиномиального деления и получение его определения
в разделе 3. Наконец, мы формулируем и
доказать отношение эквивалентности между определением полиномиальной оценки
и определение полиномиального деления с использованием метода Хорнера в разделе
4. Пост в блоге завершается
Раздел 5. 92 = (3 \cdot 3)$$, как его промежуточный
полученные результаты. К счастью, мы можем преобразовать формулу многочлена
$$p$$ таким образом, чтобы операции вычисления
показатели степени являются общими для членов. $$ \начать{выравнивать} \tag{1}\label{eq:polynomial-evaluation-horner-example-formula} p(3) &= 7 \cdot (3 \cdot 3 \cdot 3 \cdot 3) + 2 \cdot (3 \cdot 3 \cdot 3) + 5 \cdot (3 \cdot 3) + 4 \cdot (3) + 6 \\ p(3) &= (7 \cdot (3 \cdot 3 \cdot 3) + 2 \cdot (3 \cdot 3) + 5 \cdot (3) + 4) \cdot 3 + 6 \\ p(3) &= ((7 \cdot (3 \cdot 3) + 2 \cdot (3) + 5) \cdot 3 + 4) \cdot 3 + 6 \\ p(3) &= (((7 \cdot 3 + 2) \cdot 3 + 5) \cdot 3 + 4) \cdot 3 + 6, \end{выравнивание} $$ , таким образом удаляя любые избыточные умножения, используемые для оценки экспоненты. Формула \ref{eq:полиномиальная-оценка-хорнера-пример-формула} теперь демонстрирует простую индуктивную структуру, которая добавляет один умножение и одно сложение для каждого члена многочлена $$р$$. В результате теперь мы можем оценить окончательный формула $$p$$, $$ \begin{уравнение} \tag{2}\label{eq:polynomial-evaluation-horner-example-inductive} p(3) = (((7 \cdot 3 + 2) \cdot 3 + 5) \cdot 3 + 4) \cdot 3 + 6, \end{уравнение}, $$ , многократно выполняя умножение и сложение, начиная с самый внутренний набор скобок, $$
\начать{выравнивать}
\tag{3}\label{eq:polynomial-evaluation-horner-example-calculation}
p(3) &= (((7 \cdot 3 + 2) \cdot 3 + 5) \cdot 3 + 4) \cdot 3 + 6 \\
&= ((23 \cdot 3 + 5) \cdot 3 + 4) \cdot 3 + 6 \\
&= (74 \cdot 3 + 4) \cdot 3 + 6 \\
&= 226 \cdot 3 + 6 \\
&= 684. Если сравнить количество операций, выполненных в первом и последнем уравнение Формула \ref{eq:polynomial-evaluation-horner-example-formula}, мы подсчитайте в общей сложности $$14$$ в первом и $$8$$ в последнем. Разница $$6$$ операций точно соответствует количеству умножения, необходимые для вычисления показателей степени в первом уравнение. Таким образом, наше преобразование полиномиальной формулы в ее индуктивная форма, убрала вычислительные накладные расходы на оценку каждый из показателей по порядку. Наконец, даже доказано что количество сложений и умножений, используемых в этом процедуры, действительно являются наименьшим числом, возможным для оценки многочлен. 1 При ближайшем рассмотрении промежуточных результатов Формула \ref{eq:полиномиальная-оценка-хорнера-пример-вычисления}, мы можем разобрать рекурсивную схему подстановки, происходящую под капотом, $$
\начать{выравнивать}
\tag{4}\label{eq:polynomial-evaluation-horner-example-substitution-numbers}
7 &= 7\\
23 &= 7 \cdot 3 + 2\\
74 &= 23 \cdot 3 + 5\\
226 &= 74 \cdot 3 + 4\\
684 &= 226 \cdot 3 + 6. , где каждый промежуточный результат является результатом умножения предыдущий результат на $$3$$ и добавление следующего коэффициента. Если мы назначим промежуточные значения в левой части, $$(7, 23, 74, 226, 684)$$, переменной $$b_i$$ присвоить значение $$3$$ переменной $$k$$ и, наконец, присвоить значения, соответствующие коэффициенты при $$p$$, $$(7, 2, 5, 4, 6)$$, к переменной $$a_i$$, мы можем повторить Формула \ref{eq:полиномиальная-оценка-хорнера-пример-замещения-номера} вот так, $$ \начать{выравнивать} \tag{5}\label{eq:polynomial-evaluation-horner-example-substitution-variables} б_4 &= а_4\\ b_3 &= b_4 \cdot k + a_3\\ b_2 &= b_3 \cdot k + a_2\\ b_1 &= b_2 \cdot k + a_1\\ b_0 &= b_1 \cdot k + a_0. \end{выравнивание} $$ Формула \ref{eq:polynomial-evaluation-horner-example-substitution-variables}
теперь отражает рекурсивно структурированный и легко обобщаемый,
процедура подстановки, где $$b_4 = a_4$$ —
базовый случай, а индуктивный случай определяется в терминах следующего
коэффициент в многочлене и предыдущий промежуточный результат,
$$b_3 = b_4 \cdot k + a_3$$. Мы называем описанную выше процедуру методом Хорнера 2 для полиномиального оценку и формализовать ее в Хаскелл сначала представив многочлен в виде списка целых чисел, {% выделить haskell%} тип Полиномиальный = [Int] {% endhighlight%} , для которого мы определяем процедуру, {% выделить haskell%} hornersPolyEvalAcc :: Polynomial -> Int -> Int -> Int hornersPolyEvalAcc cs x a = case cs of [] -> а (c:cs’) -> пусть a’ = c + x * a в рогахPolyEvalAcc cs’ x a’ {% endhighlight%} , который принимает многочлен, {% выделить haskell%} hornersPolyEval :: Многочлен -> Целое -> Целое hornersPolyEval cs x = hornersPolyEvalAcc cs x 0 {% endhighlight%} 92+4х+6, \end{уравнение*} $$ для $$x = 3$$, передав коэффициенты $$p$$ в виде списка Формализовав метод Хорнера для полиномиальной оценки, поскольку процедуры 3. Полиномиальное деление по методу Горнера Теперь, когда мы использовали метод Хорнера как эффективную процедуру для
оценивая многочлен, используя рекурсивную схему подстановки, мы идем дальше
изучить его использование для полиномиального деления. Согласно определению полиномиальное деление, при делении двух многочленов, $$p$$ и $$d$$, $$\frac{p(x)}{d(x)}$$, где $$d \not= 0$$, результатом является частное, $$q$$, и остаток, $$r$$, удовлетворяющее соотношению, 92+8х+27)+57. \end{уравнение*} $$Если мы рассмотрим промежуточные результаты процедуры, $$(2, 8, 27, 57)$$, т. е. крайние левые значения каждого шага процедуры, можно составить схему рекурсивной подстановки, аналогичную той, что мы видели в случай полиномиальной оценки, $$ \начать{выравнивать*} 2 &= 2\\ 8 &= 2 \cdot 2 + 4\\ 27 &= 8 \cdot 2 + 11\\ 57 &= 27 \cdot 2 + 3. \конец{выравнивание*} $$ , где каждый промежуточный результат равен предыдущему результату умножить на второй член знаменателя, $$x — 2$$, плюс следующий коэффициент. На этот раз мы назначаем промежуточные результаты на слева в переменную $$b_{i-1}$$, последний результат в переменную $$r$$, второй член знаменателя переменной $$k$$, и коэффициенты $$p$$ к переменной $$a_i$$, что дает следующий набор уравнений, $$
\начать{выравнивать*}
б_{2} &= а_3\\
b_{1} &= b_2 \cdot k + a_2\\
b_{0} &= b_1 \cdot k + a_1\\
r &= b_0 \cdot k + a_0. Эти уравнения убедительно свидетельствуют о том, что мы можем разделить $$p$$ с $$d$$, используя тот же рекурсивная процедура замены, как описано в случае оценки, тратя только одно сложение и умножение за член, что снова сводит количество операций к минимуму. Кроме того, мы можем положить схема подстановки выше в табличном формате, аналогичная полиномиальное длинное деление, $$ \begin{уравнение} \tag{7}\label{eq:horner-div-abstract} \начать{массив}{ с | с с с с } & a_3 & a_2 & a_1 & a_0 \\ k & & b_2 \cdot k & b_1 \cdot k & b_0 \cdot k \\ \hline & a_3 & b_2 \cdot k + a_2 & b_1 \cdot k + a_1 & b_0 \cdot k + a_0 \\ & =b_2 & =b_1 & =b_0 & =r \конец{массив} \end{уравнение} $$ , где коэффициенты полинома расположены в верхней строке, второй член знаменателя крайний слева, а коэффициенты полученного частного, $$b_2,b_1,b_0$$, а остаток, $$r$$, в нижней строке таблицы. Формализуем табличное представление в Формула \ref{eq:horner-div-abstract} в виде следующей процедуры, {% выделить haskell%} hornersPolyDivAcc :: Polynomial -> Int -> Int -> Polynomial hornersPolyDivAcc cs x a = case cs of [] -> [] (c:cs’) -> пусть a’ = c + x * a in a’ : (hornersPolyDivAcc cs’ x a’) {% endhighlight%} , который выполняет ту же схему замены, что и в 4. Эквивалентность двух процедур Горнера Из-за сильного сходства между процедурой полиномиального
вычисления и процедуры полиномиального деления, мы
заинтересован в установлении отношения эквивалентности между ними. В качестве
таким образом, заметим, что последний элемент результирующего многочлена {% выделить coq%} forall (cs: многочлен) (x: Int), hornersPolyEval cs x == last $ hornersPolyDiv cs x {% endhighlight%} Доказательство отношения требует, чтобы мы сначала доказали подобное отношение эквивалентности
между основными процедурами {% выделить coq%} forall (cs’: многочлен) (cxa: Int), hornersPolyEvalAcc (c:cs’) x a == пусть а’ = с + х * а в последнем $ hornersPolyDivAcc cs’ x a’ {% endhighlight%} Эквивалентность можно доказать, сначала доказав основную теорему, используя
структурная индукция по многочлену, 5. ЗаключениеВ этом посте мы представили метод Хорнера для многочлена оценка и полиномиальное деление. Кроме того, мы также заявили и доказал отношение эквивалентности между определением Хорнера метод полиномиального вычисления и полиномиального деления. В нашем [следующем посте]({% post_url 2016-04-08-получение-полиномов-Тейлора-с-методом-Хорнера %}), мы покажем, как мы может получить Полиномы Тейлора с использованием Метод Хорнера.
Примеры метода Хорнера. Уравнения в высшей математике. Рациональные корни многочленов. Схема ГорнераСайт «профессиональный репетитор по математике» продолжает серию методических статей по обучению. Публикую описания методов своей работы с наиболее сложными и проблемными темами школьной программы. Данный материал будет полезен учителям и репетиторам по математике, работающим с учащимися 8-11 классов как по обычной программе, так и по программе математических занятий. Репетитор по математике не всегда может объяснить материал, плохо изложенный в учебнике. Гонка за увеличением количества информации приводит лишь к снижению качества ее усвоения и, как следствие, снижению уровня реальных знаний по математике. Но на это никто не обращает внимания. А наших детей заставляют уже в 8 классе изучать то, что мы проходили в институте: теорию вероятностей, решение уравнений высоких степеней и еще что-то. Адаптация материала в книгах для полноценного его восприятия ребенком оставляет желать лучшего и репетитор по математике вынужден как-то с этим бороться. Поговорим о методике преподавания такой специфической темы, как «деление на угол многочлена на многочлен», более известной во взрослой математике как «теорема Безу и схема Горнера». Буквально пару лет назад перед репетитором по математике вопрос не стоял так остро, ведь он не входил в основную школьную программу. Сейчас уважаемые авторы учебника под редакцией Теляковского внесли изменения в последнюю редакцию лучшего, на мой взгляд, учебника и, окончательно испортив его, лишь добавили лишних забот репетитору. А как? Наверное, я бы не стал описывать методику работы с темой, если бы она была правильно представлена в учебниках. Как у нас все происходит? Учебники нужно печатать и продавать. А для этого их нужно регулярно обновлять. Преподаватели вузов жалуются, что дети приходят к ним с пустой головой, без знаний и умений? Растут ли требования к математическим знаниям? Отлично! Удалим часть упражнений, а вместо них вставим темы, изучаемые в других программах. Чем наш учебник хуже? Давайте включим несколько дополнительных глав. Школьники не знают правило деления на угол? Это элементарная математика. И здесь все начинается. Простота темы и качество ее усвоения заключается, прежде всего, в понимании ее логики, а не в том, чтобы по предписанию авторов учебника выполнить определенный набор операций, которые не имеют явной связи друг с другом. В противном случае туман в голове ученику будет обеспечен. Если авторы рассчитывают на относительно сильных студентов (но обучающихся по обычной программе), то не стоит подавать тему в командной форме. Что мы видим в учебнике? Дети, надо делить по этому правилу. Получите многочлен в углу. Таким образом, исходный многочлен будет факторизован. Однако непонятно, почему именно так выбраны члены под углом, зачем их нужно умножать на полином над углом, а потом вычитать из текущего остатка — непонятно. Довожу до сведения репетиторов и учителей математики свое решение задачи, которое практически делает все, что изложено в учебнике, очевидным для ученика. Фактически мы докажем теорему Безу: если число а является корнем многочлена, то этот многочлен можно разложить на множители, один из которых равен х-а, а второй получается из исходного одним из трех способов: путем извлечения линейного множителя с помощью преобразований, деления на угол или по схеме Горнера. Именно с такой формулировкой будет легче работать репетитору по математике. Что такое методология обучения? Прежде всего, это четкий порядок в последовательности объяснений и примеров, на основе которых делаются математические выводы. Эта тема не исключение. Для репетитора по математике очень важно познакомить ребенка с теоремой Безу до того, как будет выполнено деление углов . Важные советы для репетиторов по математике — следуйте инструкциям от начала до конца и не меняйте эту последовательность. Итак, допустим, у нас есть многочлен. Если мы подставим число 1 вместо его x, то значение полинома будет равно нулю. Следовательно, x=1 — его корень. Попробуем разложить на два слагаемых так, чтобы одно из них было произведением линейного выражения и некоторого одночлена, а второе имело бы степень на единицу меньше . То есть представляем его в виде Выбираем моном для красного поля так, чтобы при умножении на старший член он полностью совпадал со старшим членом исходного полинома. Репетитор по математике должен обратить внимание ученика на то, что, подставив единицу в это равенство, мы гарантированно получим в его левой части ноль (поскольку 1 — корень исходного многочлена), а в правильно, очевидно, мы также установим первый член равным нулю. Так что без всякой проверки можно сказать, что единица есть корень «зеленого остатка». Поступим с ним так же, как и с исходным полиномом, извлекая из него тот же линейный множитель . Ученик выбирает для преподавателя моном для красного поля так, чтобы при умножении на старший член линейного выражения он давал старший член разложенного полинома. Вводим его в рамку, сразу раскрываем скобку и выделяем синим цветом то выражение, которое нужно вычесть из расширенного. Проделав эту операцию, получим И, наконец, проделав то же самое с последним остатком окончательно получим Теперь вынесем выражение за скобки и мы столкнемся с разложением исходного многочлена на множители, один из которых «х минус выбранный корень». Чтобы ученик не подумал, что последний «зеленый остаток» случайно разложился на нужные множители, репетитору по математике следует указать на важное свойство всех зеленых остатков – каждый из них имеет корень 1. Так как степени эти вычеты уменьшаются, то какая бы степень исходного многочлена нам не давалась, рано или поздно мы получим линейный «зеленый вычет» с корнем из 1, а значит, он обязательно разложится в произведение на какое-то число и выражение. После такой подготовительной работы репетитору по математике не составит труда объяснить ученику, что происходит при делении угла. Это тот же процесс, только в более короткой и компактной форме, без знаков равенства и без перезаписи одних и тех же выбранных терминов. Слева от угла пишем полином, из которого выделяется линейный множитель, собираем выбранные красные одночлены под углом (теперь становится понятно, почему они должны складываться), чтобы получить «синие многочлены», нужно перемножить «красное» на х-1, а затем вычесть из текущего выбранного так, как это делается при обычном делении чисел в столбик (здесь аналогия с ранее изученным). Полученные «зеленые остатки» подвергают новому отбору и отбору «красных мономов». И так до тех пор, пока не получится нулевой «зеленый остаток». Самое главное, чтобы учащийся понимал дальнейшую судьбу написанных многочленов выше и ниже угла. Очевидно, это скобки, произведение которых равно исходному многочлену. Следующий этап работы репетитора по математике – формулировка теоремы Безу.
Надо сказать, что далеко не все репетиторы по математике показывают ученикам схему горнера, и не все школьные учителя (к счастью для самих репетиторов) так глубоко вникают в тему на уроках. Однако для ученика математического класса я не вижу причин останавливаться на делении в большую сторону. Причем самый удобный и быстрый Техника декомпозиции основана именно на схеме Горнера. Чтобы объяснить ребенку, откуда оно берется, достаточно проследить появление высших коэффициентов в зеленых остатках на примере деления уголком. Становится понятно, что старший коэффициент исходного многочлена сносится в коэффициент первого «красного одночлена», а дальше от второго коэффициента текущего верхнего многочлена вычитал результат умножения текущего коэффициента «красного монома» на . Если в многочлене отсутствует какая-либо степень, то в таблицу принудительно вносится его нулевой коэффициент. В нижнюю строку поочередно вносятся коэффициенты «красных многочленов» по правилу «крючка»: Корень умножается на последний снесенный «красный коэффициент», прибавляется к следующему коэффициенту верхней строки и результат снесен в нижнюю строчку. В последней колонке мы гарантированно получаем наибольший коэффициент последнего «зеленого баланса», то есть ноль. После завершения процесса числа , зажатые между совпавшим корнем и нулевым остатком , оказываются коэффициентами второго (нелинейного) множителя. Поскольку корень а дает ноль в конце нижней строки, то схему Горнера можно использовать для проверки чисел на ранг корня многочлена. Специальная теорема о выборе рационального корня. Все кандидаты на это звание, полученные с его помощью, просто вставляются по очереди слева в схему Горнера. Как только мы получим нуль, тестируемое число будет корнем, а заодно мы получим коэффициенты разложения исходного многочлена на множители. Очень удобно. В заключение хотелось бы отметить, что для точного введения схемы Горнера, а также для практического закрепления темы репетитор по математике должен иметь в своем распоряжении достаточное количество часов. Репетитор, работающий в режиме «раз в неделю», не должен заниматься делением угла. На ЕГЭ по математике и на ГИА по математике вряд ли в первой части когда-нибудь будет уравнение третьей степени, решенное такими средствами. Если репетитор готовит ребенка к ЕГЭ по математике в МГУ, изучение темы становится обязательным. Преподаватели вузов очень любят, в отличие от составителей ЕГЭ, проверять глубину знаний абитуриента. Колпаков Александр Николаевич, репетитор по математике Москва, Строгино слайд 3 Горнер Уильямс Джордж (1786-22 сентября 1837) английский математик. Родился в Бристоле. Учился и работал там, затем в школах Бата. Основные работы по алгебре. В 1819 году опубликовал метод приближенного вычисления действительных корней многочлена, который теперь называется методом Руффини-Хорнера (этот метод был известен китайцам еще в 13 веке). Схема деления многочлена на двучлен x-a названа в честь Горнера. слайд 4 СХЕМА ГОРНЕРАметод деления многочлена n-й степени на линейный двучлен — а, основанный на том, что коэффициенты при неполном частном и остатке r связаны с коэффициентами делимого многочлена и с а по формулам: слайд 5 Расчеты по схеме Горнера занести в таблицу:Пример 1 Разделить Неполное частное х3-х2+3х — 13 и остаток 42=f(-3) . слайд 6 Основным преимуществом этого метода является компактность записи и возможность быстрого деления многочлена на двучлен. Слайд 7 Пример2.Докажем, что многочлен P(x)=x4-6×3+7x-392 делится на x-7, и найдем частное. Решение. По схеме Горнера находим Р(7): Отсюда получаем Р(7)=0, т.е. остаток при делении многочлена на х-7 нуль и, следовательно, многочлен Р(х) кратен (х-7 ). В этом случае числа во второй строке таблицы являются коэффициентами частного от деления Р(х) на (х-7), следовательно, Р(х) = (х-7)(х3+х2+7х +56). Слайд 8 Разложите многочлен на множители x3 — 5×2 — 2x + 16. Этот многочлен имеет целые коэффициенты. Если корнем этого многочлена является целое число, то оно является делителем 16. Таким образом, если данный многочлен имеет целые корни, то это могут быть только числа ±1; ±2; ±4; ±8; ±16. Слайд 9 Полученные числа 1, −3, −8 являются коэффициентами многочлена, который получается делением исходного многочлена на x — 2. Следовательно, результат деления: 1 x2 + (-3)x + (-8) = x2 — 3x — 8. Степень полинома, полученного в результате деления, всегда на 1 меньше степени исходного. Итак: х3 — 5х2 — 2х + 16 = (х — 2)(х2 — 3х — 8). Цели урока:
Оборудование: карточек для работы в группах, плакат со схемой Горнера. Методика обучения: лекция, рассказ, объяснение, выполнение тренировочных упражнений. Форма контроля: задание проверка самостоятельное решение, самостоятельная работа. На занятиях 1. Организационный момент 2. Актуализация знаний учащихся Какая теорема позволяет определить, является ли число корнем заданного уравнения (сформулировать теорему) ? Теорема Безу. Остаток от деления многочлена P(x) на двучлен x-c равен P(c), число c называется корнем многочлена P(x), если P(c)=0. Теорема позволяет, не производя операции деления, определить, является ли данное число корнем многочлена. Какие утверждения облегчают поиск корней? а) Если старший коэффициент многочлена равен единице, то корни многочлена следует искать среди делителей свободного члена. б) Если сумма коэффициентов многочлена равна 0, то один из корней равен 1. в) Если сумма коэффициентов в четных местах равна сумме коэффициентов в нечетных местах, то один из корней равен -1. г) Если все коэффициенты положительные, то корнями многочлена являются отрицательные числа. д) Многочлен нечетной степени имеет хотя бы один действительный корень. 3. Изучение нового материала При решении целых алгебраических уравнений приходится находить значения корней многочленов. Эту операцию можно значительно упростить, если проводить расчеты по специальному алгоритму, называемому схемой Горнера. Эта схема названа в честь английского ученого Уильяма Джорджа Хорнера. Схема Хорнера представляет собой алгоритм вычисления частного и остатка от деления многочлена P(x) на x-c. Кратко, как это работает. Пусть задан произвольный многочлен P(x)=a 0 x n + a 1 x n-1 + …+ a n-1 x+ a n. Деление этого полинома на x-c есть его представление в виде P(x)=(x-c)g(x) + r(x). Частное g(x) = при 0 x n-1 + при n x n-2 + … + при n-2 x + при n-1, где при 0 = a 0, при n = sv n- 1 + n, n=1,2,3,…n-1. Остаток r(x) = St n-1 + a n. Этот метод расчета называется схемой Горнера. Слово «схема» в названии алгоритма связано с тем, что обычно его выполнение формализуется следующим образом.
Число, которое после выполнения алгоритма окажется записанным в правой нижней ячейке, есть остаток от деления многочлена P(x) на x-c. Остальные числа 0 , 1 , 2 ,… нижней строки являются коэффициентами частного. Например: Разделить многочлен Р(х) = х 3 -2х + 3 на х-2. Получаем, что х 3 -2х + 3 = (х-2) (х 2 + 2х + 2) + 7. 4. Закрепление изученного материала Пример 1: Разложить на множители многочлен P(x)=2×4-7x 3 -3x 2 +5x-1 с целыми коэффициентами. Ищем целые корни среди делителей свободного члена -1:1; -один. Составим таблицу: Х = -1 — корень Р(х) = (х + 1) (2х 3 -9х 2 + 6х -1) Проверим 1/2.
Следовательно, полином P(x) можно представить в виде P(x) = (x + 1) (x-1/2) (x 2 -8x +2) = (x + 1) (2x -1) (x 2 — 4x +1) Пример 2: Решить уравнение 2x 4 — 5x 3 + 5x 2 — 2 = 0 Так как сумма коэффициентов многочлена написана слева сторона уравнения равна нулю, то один из корней равен 1.
Получаем Р(х)=(х-1)(2х3-3х2=2х+2). Будем искать корни среди делителей свободного члена 2. Выяснили, что целых корней больше нет. Проверим 1/2; -1/2.
Ответ: 1; -1/2. Пример 3: Решите уравнение 5x 4 — 3x 3 — 4x 2 -3x + 5 = 0. Корни этого уравнения будем искать среди делителей свободного члена 5:1; -1; 5; -5. x=1 является корнем уравнения, так как сумма коэффициентов равна нулю. Воспользуемся схемой Горнера: представим уравнение в виде произведения трех множителей: (х-1) (х-1) (5х 2 -7х + 5) = 0. Решая квадратное уравнение 5х 2 -7х+5= 0, получилось D=49-100=-51, корней нет. Карта 1
Карта 2
Карточка 3
Карточка 4
5. Подведение итогов Проверка знаний при решении в парах проводится на уроке путем узнавания способа действия и названия ответа. Домашнее задание: Решить уравнения: а) х 4 -3х 3 +4х 2 -3х + 1 = 0 б) 5х 4 -36х 3 +62х 2 -36х+5=0 в) х 4 + х 3 + х + 1 = 4 х 2 г) х 4 + 2х 3 -х-2 = 0 Литература
Внимание! Предварительный просмотр слайдов предназначен только для информационных целей и может не отражать весь объем презентации. Если вас заинтересовала эта работа, пожалуйста, скачайте полную версию. Урок типа : Урок усвоения и закрепления начальных знаний. Цель занятия:
Во время занятий 1. Организационный момент. Сообщить тему урока, сформулировать цели. 2. Проверка домашнего задания. 3. Изучение нового материала. Пусть F n (x) = a n x n +a n-1 x n-1 +…+ a 1 x +a 0 — многочлен от x степени n, где a 0 , a 1 ,…,an — заданные числа, a 0 не равен 0. Если многочлен F n (x) разделить с остатком на бином x-a, то частное (неполное частное) есть многочлен Q n-1(x) степени n-1, остаток R есть число, и равенство F n (x)=(x-a) Q n-1 (x) +R. Многочлен F n (x) полностью делится на двучлен (x-a) только в случае R=0. Теорема Безу: Остаток R от деления многочлена F n (x) на бином (x-a) равен значению многочлена F n (x) при x=a, т. Немного истории. Теорема Безу, несмотря на внешнюю простоту и очевидность, является одной из основных теорем теории многочленов. В этой теореме алгебраические свойства многочленов (которые позволяют работать с многочленами как целыми числами) связаны с их функциональными свойствами (которые позволяют рассматривать многочлены как функции). Одним из способов решения уравнений высших степеней является метод факторизации многочлена в левой части уравнения. Расчет коэффициентов полинома и остатка записывается в виде таблицы, которая называется схемой Горнера. Схема Хорнера представляет собой полиномиальный алгоритм деления, написанный для особого случая, когда частное представляет собой двучлен x-a . Хорнер Уильям Джордж (1786 — 1837), английский математик. Основные исследования относятся к теории алгебраических уравнений. Разработал метод приближенного решения уравнений любой степени. В 1819 году он ввел важный для алгебры способ деления многочлена на двучлен х — а (схема Горнера). Вывод общей формулы для схемы Горнера. Деление многочлена f(x) на бином (x-c) с остатком означает нахождение многочлена q(x) и числа r таких, что f(x)=(x-c)q(x)+r Давайте подробно напишите это уравнение: f 0 x n + f 1 x n-1 + f 2 x n-2 + …+f n-1 x + f n =(x-c) (q 0 x n-1 + q 1 x n-2 + q 2 x n-3 +…+ q n-2 x + q n-1)+r Приравнять коэффициенты при одинаковых степенях:
Демонстрация схемы Горнера на примере. Упражнение 1. Используя схему Горнера, разделим многочлен f(x) = x 3 — 5x 2 + 8 с остатком на двучлен x-2.
f(x) = x 3 — 5x 2 + 8 = (x-2) (x 2 -3x-6)-4, где g(x) = (x 2 -3x-6), г = -4 остаток. Разложение многочлена по степеням двучлена. Используя схему Горнера, разложим многочлен f(x)=x 3 +3x 2 -2x+4 по степеням бинома (x+2). В результате должно получиться разложение f (x) = x 3 +3x 2 -2x+4 = (x+2)(x 2 +x-4)+12 = (x+2)((x -1)(х+ 2)-2)+12 = (((1*(х+2)-3)(х+2)-2)(х+2))+12 = (х+2) 3 — 3(x+2 ) 2 -2(x+2)+12 Схема Горнера часто используется при решении уравнений третьей, четвертой и более высоких степеней, когда удобно разложить многочлен в двучлен x-a. Например, число 2 является корнем многочлена F 3 (x)=3x 3 -2x-20, так как F 3 (2)=0. это означает. Что факторизация этого многочлена содержит множитель x-2. F 3 (x)=3x 3 -2x-20=(x-2)(3x 2 +6x+10). Любой многочлен F n (x) степени n 1 может иметь не более n действительных корней. Любой целочисленный корень уравнения с целыми коэффициентами является делителем его свободного члена. Если старший коэффициент уравнения равен 1, то все уравнения с рациональными корнями, если они существуют, являются целыми. Закрепление изученного материала. Для закрепления нового материала учащимся предлагается выполнить номера из учебника 2.41 и 2.42 (стр. 65). (2 ученика решают у доски, а остальные, решив, сверяют задания в тетради с ответами на доске). Подведение итогов. Поняв устройство и принцип работы схемы Горнера, ее можно использовать и на уроках информатики, когда рассматривается вопрос о переводе целых чисел из десятичных в двоичные и наоборот. Перевод из одной системы счисления в другую основан на следующей общей теореме Теорема. Для перевода целого числа Ар из р -арной системы счисления в основную систему счисления d необходимо Ар последовательно делить с остатком на число d , записанное в той же р -арной системе счисления, до тех пор, пока полученное частное становится равным нулю. Тогда остаток от деления будет d -цифровые цифры Ad , начиная с младшего разряда до старшего разряда. Все действия необходимо производить в p -арная система счисления. Для человека это правило удобно только тогда, когда р = 10, т.е. при переводе из десятичной системы. Что же касается компьютера, то ему, наоборот, «удобнее» производить расчеты в двоичной системе. Домашнее задание. Есть две задачи, которые нужно выполнить. 1-й. Используя схему Горнера, разделите многочлен f(x)=2x 5 -x 4 -3x 3 +x-3 на двучлен (x-3). 2-й. Найдите целые корни многочлена f(x) = x 4 -2x 3 +2x 2 -x-6. (Учитывая, что любой целый корень уравнения с целыми коэффициентами является делителем его свободного члена) Литература.
Классическая китайская версия метода ГорнераКлассическая китайская версия метода Хорнера Дональд Б. Вагнер По методу Хорнера см. напр. Rees & Sparks 1967: 294–297, а также многочисленные страницы во всемирной паутине. Хорнер (1819) представил процедуру аппроксимации корней любой бесконечно дифференцируемой функции, но современные описания «метода Горнера» рассматривают только случай полиномиальных функций.
О китайской версии метода Хорнера см., в частности, Chemla 1994; также Wang & Needham 1955; Лам Лей Йонг 1970; 1977: 195–196, 251–285; 1986 год; Либбрехт 1973: 175–191; Марцлофф 1997: 221–249; Шен и др. 1999: 175–195, 204–226; Чемла и Го 2004: 322–335, 363–379. Классические китайские математики и вычислители регулярно извлекали числовые корни многочленов с помощью метода, который по сути такой же, как «метод Хорнера», который иногда преподается в современных школах и колледжах. Определяется первая цифра корня, корни уравнения уменьшаются на значение этой цифры (операция, которая представляет собой замену переменной), определяется следующая цифра, и этот шаг повторяется до тех пор, пока не будет достигнута желаемая точность. В этой статье я подробно опишу алгоритм. Корреспондент бросил мне вызов, спросив, действительно ли можно использовать метод, не зная заранее результата. Ответ оказывается положительным, но с некоторыми осложнениями. Историки, имеющие дело с ранними математическими текстами, обычно выражают свое понимание текста, используя уравнения в современных обозначениях. Это обеспечивает ясную и точную помощь читателям. В этой статье я пошел еще дальше: я выражаю классические китайские алгоритмы с помощью компьютерных программ, написанных на языке программирования Basic. Я бы никогда не рекомендовал Basic для серьезного программирования. Однако это настолько просто, что читатели, изучившие программирование на любом языке, поймут приведенные здесь программы. В Приложении 1 я собрал большую выборку многочленов, решенных в китайских текстах с 7 по 14 века. Xiaotong 王孝通, 7 век н.э. Об этой книге см., в частности, Lim & Wagner (2013a; 2013b; 2017). Название книги Ван Сяотуна можно приблизительно перевести как Продолжение древней математики . Он подарил его императору примерно в 628 году нашей эры. Он включает 19 задач по объемной или планиметрии, требующих численного решения одного или нескольких многочленов. Это 25 кубиков и два квадратика. В дальнейшем будут рассматриваться только кубические уравнения — квадратичные уравнения можно решить путем небольшой модификации алгоритма для кубических уравнений. Все кубики Ван Сяотуна имеют форму .
Оказывается, есть довольно простой метод решения таких уравнений на счетной доске. Сначала определяется общее кратное D числителей; в этом случае D = 89. Тогда коэффициенты преобразуются в неправильные дроби, в которых знаменатель a равно D , знаменатель числа b равен D 2 , а знаменатель числа c равен D 3 Затем знаменатели отбрасываются и полученное уравнение решается методом, приведенным выше, x 3 + 1550 x 2 + 784 193 x = 45 322 445 728 Найденный корень 1157 делится на 9.0069 D для получения положительного корня из (4), x = 13. Эта процедура сводится к замене переменной y = Dx . В Приложении 3 приведена базовая программа для решения кубических уравнений, в которых дроби рассматриваются, как описано здесь. В более поздних текстах класс рассматриваемых многочленов намного шире, и особенно в « Siyuan yujian » Чжу Шицзе (1303 г. н.э.) они кажутся совершенно общими, с произвольной степенью и как с положительными, так и с отрицательными коэффициентами. Они имеют общий вид и алгоритм уменьшения корней многочлена этой формы на значение следующей цифры, d , соответствующий (3) выше, может быть записан на Basic, для m=0 до n–1 для i=n–1 до шага m –1 a(i) = a(i) + d*a(i+1) (5) следующий я следующий м Это достаточно просто сделать на счетной доске, но выбрать цифру d уже не так просто, как с кубиками Ван Сяотуна. В этом случае можно было оценить верхнюю границу для одного корня и перейти оттуда к правильной цифре. В общем случае у досовременного калькулятора, по-видимому, не было простого способа оценить верхнюю границу для корней, и, кроме того, самый большой корень может быть не тем, который он ищет. Следующая задача калькулятора состоит в том, чтобы определить, после уменьшения корней на d с помощью (5), является ли d слишком большим или маленьким. В Базовой программе, приведенной в Приложении 4, используется следующая процедура. Программа запрашивает значение d , которое, как известно, больше первой цифры нужного корня, но меньше любого старшего корня. Он уменьшает корни на это значение и сохраняет знак постоянного коэффициента, a 0 . С этого момента, если уменьшение на d не приводит к тому, что знак a 0 отличается от сохраненного знака, d слишком велико. Выполняется процедура, аналогичная процедуре для кубиков Ван Сяотуна, с поиском цифр до | и 0 | меньше некоторого заданного ε. Программа в Приложение 4 не является полным решением проблемы. х 4 – 26 х 3 – 467 х 2 + 8300 х , корни которого равны 24 и
26.8323. Учитывая это уравнение в качестве входных данных, программа неверно сообщает, что оно не имеет положительных действительных корней. Это не означает, что человек-калькулятор не мог найти эти корни. Это означает только то, что я недостаточно хороший программист. Из Приложения 1 видно, что в одной книге Цинь Цзюшао « Шушу цзючжан 數書九章» некоторые корни многочленов даны с дробной частью. Например, в книге корень многочлена х 2 + 82 655 х – 2 269 810 000 = 0 дается как 21 742 10 426 / 126 140 2108704 = 5,26 140 212604 = 5,26 140 212604; правильный корень 21 742,082655, так что это очень хорошее приближение. , затем Я могу добавить, что это приближение эквивалентно предположению, что F является приблизительно линейным в интервале (0,1), , так что . уравнения, для которых приближение Цинь Цзюшао не годится, например, делая p n очень большими, но в случаях, рассмотренных в Шушу jiuzhang это довольно хорошее приближение. Чемла, Каринэ и Го Шучунь. 2004. Les neuf chapitres: Le classique mathématique de la China ancienne et ses commentaires . Париж: Дюно. Чемла, Карин. 1982. Étude du livre «Reflets des mesures du cercle sur la mer» . Неопубликованная диссертация, Парижский университет XIII. Чемла, Карин. 1994. «Сходства между китайскими и арабскими математическими сочинениями: (I) извлечение корня». Го Шучунь 郭书春 и др. (2006). Нефритовое зеркало четырех неизвестных . Шэньян, Ляонинское образовательное издательство / Ляонин Цзяоюй Чубаньше. Horner, WG 1819. «Новый метод решения числовых уравнений всех порядков методом непрерывного приближения». Философские труды Лондонского королевского общества 109: 308–335. www.jstor.org/stable/107508 Лам Лей-Йонг [Лан Лиронг 蓝丽蓉]. 1970. «Геометрическая основа древнекитайского метода извлечения квадратного корня». Исида 61.1: 92–102. www.jstor.org/stable/229151 Лам Лей-Йонг [Лан Лиронг 蓝丽蓉]. 1977. Критическое исследование Ян Хуэй Суан Фа, китайского математического трактата XIII века . Сингапур: Издательство Сингапурского университета. Лам Лей-Йонг [Лан Лиронг 蓝丽蓉]. 1986. «Развитие полиномиальных уравнений в традиционном Китае». Математическая смесь (Сингапурское математическое общество) 14. Либбрехт, Ульрих. 1973. Китайская математика в тринадцатом веке: Шу-шу чиу-чан из Цинь Цзю-шао . (Научная серия Массачусетского технологического института Восточной Азии, 1). Факты. репр. Минеола, Нью-Йорк: Довер, 2005. .
Лим, Тина Су Лин и Дональд Б. Вагнер. 2013а. «Платформа и пандус Великого астролога: четыре задачи по объемной геометрии из «Продолжения древней математики» Ван Сяотуна (7 век нашей эры)». История математики 40.1: 3–35. www.sciencedirect.com/science/article/pii/S0315086012000596 Лим, Тина Су Лин и Дональд Б. Вагнер. 2013б. «Ван Сяотун о прямоугольных треугольниках: шесть задач из «Продолжения древней математики» (7 век н.э.)». Наука, техника и медицина Восточной Азии 37: 12–35. Опубликовано в 2016 г. www.eastm.org/index.php/journal/article/view/648/562 Лим, Тина Су Лин и Дональд Б. Вагнер. 2017. Продолжение древней математики: Цзигу суаньцзин Ван Сяотуна, алгебра и геометрия в Китае VII века . Мартцлофф, Жан-Клод. 1997. История китайской математики . тр. Стивен С. Уилсон. Берлин / Гейдельберг: Springer-Verlag. «Исправленное второе издание», 2006 г. Ориг. Histoire des mathémathiques chinoises , Paris: Masson, 1987. Нидхэм, Джозеф и Ван Линг 王鈴. 1959. Наука и цивилизация в Китае , том. 3: Математика и науки о небе и земле. Кембридж: Издательство Кембриджского университета. Цянь Баокун 錢寶琮. 1932. Zhongguo suanxue shi 中國算學史 上卷 («История китайской математики, часть 1, Чянь Бао-цзун»). (Голи Чжунъян Яньцзююань Лиши Юян Яньцзюсуо Данкан 國立中央研究院歷史語言研究所 單刊甲種之六, A.6). Бэйпин: Academia Sinica. www.scribd.com/doc/285715053 Рис, Пол К. и Фред В. Спаркс. 1967. Колледж алгебры . 5-е изд. Нью-Йорк: Макгроу-Хилл. Шен Каншен 沈康身, Джон Н. Кроссли и Энтони В.-К. Лун. 1999. Девять глав по математическому искусству: Companion and comment . Сивин, Натан. 2009. Предоставление времен года: китайская астрономическая реформа 1280 года с изучением ее многих измерений и переводом ее записей 授时曆叢考. (Источники и исследования по истории математики и физических наук). Нью-Йорк: Спрингер. «Натан Сивин, в сотрудничестве с покойным Киёси Ябуути (藪內清) и Сигеру Накаяма (中山茂)». www.springer.com/gp/book/9780387789552 Ван Лин 王鈴 и Джозеф Нидхэм. 1955. «Метод Хорнера в китайской математике: его истоки в процедурах извлечения корней династии Хань». Тунг Пао 43.5: 345–401. www.jstor.org/stable/4527405 Полином выглядит так: «Решение» означает нахождение «корней» . … «корень» (или «ноль») — это место, где функция равна нулю Проверим: Как мы решаем многочлены? Это зависит от степени ! Первый шаг при решении многочлена — найти его степень. Степень многочлена с одной переменной равна … … наибольшему показателю этой переменной. Зная степень, мы также можем дать многочлену имя: Итак, теперь мы знаем степень, как решить? Так что нам делать с теми, которые мы не можем решить? Попробуйте решить их по частям! Если мы найдем один корень, мы можем тогда уменьшить многочлен на одну степень (пример ниже), и этого может быть достаточно, чтобы решить весь многочлен. Вот несколько основных способов поиска корней. Мы можем решить с помощью базовой алгебры: 2x+1 является линейным полиномом: 1 +1 — прямая Линейная, поэтому корень один. Решите с помощью алгебры: «Корень» — это когда y равно нулю: 2x+1 = 0 Вычтите 1 из обеих частей: 2x = −1 Разделите обе части на 2: x = −1/2 Вот и решение: x = −1/2 (вы также можете увидеть это на графике) Мы также можем решать квадратичные многочлены, используя базовую алгебру (прочитайте эту страницу для объяснения). Всегда полезно проверить, можем ли мы сделать простое разложение на множители: Это кубическое… но подождите… мы можем разложить » х»: х 3 +2x 2 −x = x(x 2 +2x−1) Теперь у нас есть один корень (x=0), а то, что осталось, является квадратичным, что мы можем точно решить. Или мы можем заметить знакомую закономерность: Опять же, это куб. x 3 −8 = x 3 −2 3 7 x Таким образом, мы можем превратить его в следующее: x 3 −8 = (x−2)(x 2 +2x+4) Существует корень при x=2, потому что: (2−2)(2 2 +2×2+4) = (0) (2 2 +2×2+4) Затем мы можем решить квадратное уравнение x 2 +2x+4 и мы закончим Нарисуйте полином и посмотрите, где он пересекает ось x. Графики — хороший способ найти приблизительные ответы, и нам также может повезти, и мы найдем точный ответ. Осторожно: прежде чем прыгать и строить графики, вы должны действительно знать, как ведут себя полиномы, чтобы найти все возможные ответы! Полезно знать: Когда многочлен факторизуется следующим образом: f(x) = (x−a)(x−b)(x−c). Тогда a , b, c и т. д. — это корней ! Итак, Линейные Факторы и Корни связаны, зная одно, мы можем найти другое. (Подробности см. в Теореме о факторах.) Мы видим «(x−3)», и это означает, что 3 является корнем (или «нулем») функции. Уверен? Итак, поставим 3 вместо x: f(x) = (3 3 +2·3 2 )(3−3) f(3) = (3 3 +2·3 2 )(0) Да! f(3)=0, поэтому 3 — это корень. Нашли корень? Проверьте это! Просто поставьте корень вместо «х»: многочлен должен быть равен нулю. Многочлен степени 3, и решить его может быть сложно. Итак, давайте сначала построим ее: Кривая пересекает ось x в трех точках, и одна из них может находиться в точке 2 . f(2) = 2(2) 3 −(2) 2 −7(2)+2 Да! f(2)=0 , значит, мы нашли корень! Как насчет того, где она пересекается около −1,8 : f(−1,8) = 2(−1,8) 3 −(−1,8) 91−2,096 2(−2,096 2 Нет, это не равно нулю, поэтому −1,8 не будет корнем (но может быть близко!) Но мы открыли один корень, и мы можем использовать это для упрощения полинома, как здесь 2)=0 является корнем … это означает, что мы также знаем множитель: (x−2) должно быть множителем 2x 3 −x 2 −7x+2 Далее, разделите 2x 3 −x 2 −7x+2 на (x−2), используя полиномиальное длинное деление, чтобы найти: 2x 3 −x 2 −7x+2 = (x−2)(2x 2 +3x−1) Итак, теперь мы можем решить 2x 2 +3x−1 как квадратное уравнение и будем знать все корни. Последний пример показал, насколько полезно найти только один корень. Помните: Если мы найдем один корень, мы можем уменьшить многочлен на одну степень и этого может быть достаточно, чтобы решить весь многочлен. При попытке найти корни, как далеко влево и вправо от нуля мы должны идти? Есть способ сказать, и нужно сделать несколько вычислений, но это все простая арифметика. Прочтите Bounds on Zeros для получения подробной информации. Существует простой способ узнать, сколько существует корней . Основная теорема алгебры гласит: Многочлен степени n … Итак: количество корней = степень многочлена . Степень равна 3 (поскольку наибольший показатель степени равен 3), поэтому: Имеется 3 корней. Да, действительно, некоторые корни могут быть комплексными числами (т.е. иметь мнимую часть), поэтому они не будут отображаться как простое «пересечение оси x» на графике. Но есть интересный факт: Комплексные корни всегда идут парами ! Таким образом, мы либо получаем без комплексных корней , либо 2 комплексных корней, либо 4 и т. д. Никогда нечетное число. Это означает, что мы автоматически знаем это: Существует также особый способ узнать, сколько корней отрицательных или положительных , называемый Правилом знаков, о котором вы можете прочитать. Иногда множитель появляется более одного раза. Мы называем это Множественность : Множественность — это то, как часто определенный корень является частью факторинга. Это можно было бы записать более длинным образом: f(x) = (x−5)(x−5)(x−5 )(x+7)(x−1)(x−1) (x−5) используется 3 раза, поэтому корень «5» имеет кратность 3 , аналогично (x+7) встречается один раз и (x−1) появляется дважды. Итак: В: Почему это полезно? Когда мы видим такой множитель, как (x-r) n , «n» — это кратность, а Мы можем видеть это на этом графике: (x−2) имеет четную кратность , поэтому он просто касается оси в точке x=2 (x−4) имеет нечетную кратность , поэтому он пересекает ось в точке x=4 Вот так: Предположим, у меня есть многочлен
a n x n + a n-1 x n-1 + …
+ а 1 x + a 0 и точка
x * , при котором я хотел оценить этот полином. Теперь наша ближайшая цель состоит в том, чтобы просто подставить точку прямо в многочлен, чтобы получить
a n (x * ) n + a n-1 (x * ) n-1 + … + a 1 (x * ) + a 0 и далее прорабатываем очевидным образом: повышаем
х * в энной степени и умножить на n , затем возводим x * в (n-1)-ю степень и умножаем на n-1 ,
и так далее, добавляя их все вместе в конце. Хотя кажется, что работы много. Мы могли бы быть более эффективными, если бы работали наоборот: то есть, начиная с
x * и кэширование промежуточных степеней x * по мере продвижения вверх. Как оказалось, есть — мы можем использовать Правило Хорнера ! Правило Хорнера не только более эффективно, чем любой из вышеперечисленных подходов, но и фактически является оптимальным алгоритмом для вычисления полиномов: то есть мы можем математически доказать, что любое другое правило для вычисления полиномов может не лучше, чем алгоритм Хорнера. Правило. Итак, давайте рассмотрим, как работает это правило, и напишем код Java, чтобы проверить его! [Мы вернулись с SICP сообщения в блоге об упражнениях! Это вдохновлено упражнением 2.34.] В целях сравнения давайте быстро рассмотрим способы, которыми мы в противном случае вычислили бы многочлен. Начнем с самого очевидного способа: Здесь мы используем результат как переменную для хранения промежуточных ответов каждый раз. Итак, например, предположим, что у нас есть многочлен
5x 4 + 2x 3 – 3x 2 + x – 7, и нам нужно значение многочлена в точке x=3. Мы бы работали так: Я написал это в более «математической» форме здесь, но обратите внимание, что мы, по сути, работаем через описанный выше набор шагов. Мы вычисляем каждое из условий (и каждую из степеней x = 3) отдельно и суммируем их по мере прохождения. Мы могли бы легко написать код Java для этого, верно? В методе calculatePolynomial() мы начинаем с n-го члена многочлена и определяем значение этого члена. Чтобы мы могли сравнить каждый из полиномиальных методов оценки, которые мы рассмотрим, мы также определили некоторые статические переменные totalAdditions и totalMultiplications для отслеживания этих операций при выполнении программы. Они обновляются в цикле, и мы отобразим значения этих переменных в выводе в конце. 92 + x — 7 По крайней мере, мы получили правильный ответ. Но мы делаем довольно много умножений для такого маленького многочлена! В общем, вычисление полинома n-й степени таким образом означает, что мы в конечном итоге делаем n сложений и (0 + 1 + 2
+ … + n) умножения (поскольку для получения
a i x i мы умножаем x на себя (i-1) раз, а затем умножаем на i коэффициент, чтобы получить i умножений для этого шага.) Это видно по количеству сложений и умножений, которые мы имели как для обработанного решения, так и для вывода нашей программы (у нас есть дополнительное сложение, отображаемое в программу, так как мы добавили самый первый член к результату, который изначально равен 0. Таким образом, мы можем резюмировать эффективность этой схемы полиномиальных вычислений как следует: Здесь легко увидеть, что число умножений будет расти квадратично по мере увеличения степени многочлена. Хотя, конечно, мы можем добиться большего. Как мы упоминали ранее, мы уже можем повысить эффективность вычислений, заметив, что мы вычисляем много одинаковых степеней x для каждого члена. Рассмотрим пример с многочленом 5x 4 + 2x 3 – 3x 2 + x – 7. Здесь мы вычисляем x 2 три раза помноженное на , так как мы вычислили бы x 2 , поскольку мы вычисляли x 3 и x 4 ! Таким образом, один из способов добиться улучшения состоит в том, чтобы кэшировать эти промежуточные степени x. Наш новый набор шагов выглядит так: Итак, вы можете видеть, что мы храним x 2 , чтобы мы могли использовать его для получения x 3 , которые мы сохраняем, чтобы помочь нам получить x 4 , и так далее. Если бы мы выполнили наш пример вручную, используя этот метод, мы бы получили следующую работу: И, конечно же, это легко трансформируется в другую небольшую программу, которую мы можем использовать для вычисления многочленов: Мы также используем переменную powerOfX, чтобы сохранить предыдущий член x, чтобы мы могли использовать его для вычисления следующего члена многочлена. Это должно работать, чтобы уменьшить количество умножений, которые мы в конечном итоге делаем. Когда мы запускаем код, вывод выглядит следующим образом: java Polynomial2 92 + x — 7 Таким образом, с помощью этого нового метода нам удалось уменьшить количество умножений! И поскольку мы присвоили коэффициенту a 0 вместо того, чтобы прибавлять его к 0, на этот раз у нас было только 4 добавления. Вычисление полинома n-й степени таким способом всегда требует n сложений и 2 + 2 + … + 2 = 2n умножений: Это лучше — по крайней мере, количество умножений, которые нам нужно сделать, теперь растет линейно со степенью многочлена. Мы можем еще больше уменьшить количество умножений. Учтите, что мы всегда можем переписать многочлен следующим эквивалентным образом: Это основная идея правила Хорнера , названного в честь математика Уильяма Джорджа Хорнера. По сути, мы начинаем с коэффициента a n , умножаем его на x и добавляем коэффициент a n-1 . Затем мы умножаем весь этот результат на x и прибавляем н-2 коэффициент. Затем мы снова умножаем все на x и добавляем коэффициент a n-3 и так далее для остальных членов полинома. Вы можете видеть, что, работая таким образом, мы должны получить правильные степени x: , и аналогично вплоть до члена a 1 , который умножается на x один раз. Алгоритм вычислений точно отражает этот процесс: Вот и весь алгоритм! (Он даже выглядит красивее, чем другие алгоритмы, которые у нас были выше. В качестве примера, если бы нам нужно было работать с нашим полиномиальным примером вручную, мы бы сделали следующее: И этот алгоритм достаточно легко преобразовать в работающий код Java. Итак, теперь у нас есть 4 сложения и 4 умножения, и это хорошо! В заключение этого сообщения в блоге мы можем отметить, что вычисление полинома n-й степени с помощью правила Хорнера всегда требует только n сложений и умножений: И на самом деле, это лучшее, что мы можем сделать. Математик Александр Островский доказал в 1954 году, что правило Горнера использует оптимальное количество сложений, а другой математик Виктор Пан доказал в 1954 году. Заполните пропущенные выражения, чтобы завершить следующие определения
некоторых основных операций манипулирования списками в виде накоплений: Процедура накопления Вычисление многочлена от $x$ при заданном значении x можно сформулировать
как накопление. Вычисляем многочлен с использованием известного алгоритма под названием Правило Хорнера , которое структурирует
вычисление как Другими словами, мы начинаем с $a_n$, умножаем на $x$, добавляем $a_{n-1}$,
умножаем на $x$ и так далее, пока не достигнем $a_0$. Заполните следующий шаблон, чтобы создать процедуру, которая оценивает
многочлен по правилу Горнера. Предположим, что коэффициенты
полинома расположены в последовательности от $a_0$ до $a_n$. 95$ при $x=2$ вы бы оценили Переопределить Используя процедуру, аналогичную Процедура Предположим, мы представляем вектор $\boldsymbol v=(v_i)$ как последовательность
числа и матрицы $\boldsymbol m=(m_{ij})$ как последовательности
векторы (строки матрицы). Например, матрица представлен как последовательность Мы можем определить скалярный продукт как Заполните пропущенные выражения в следующих процедурах для
вычисление других матричных операций. Процедура Каковы значения Назовите свойство, которому должно удовлетворять |
Естественно, что так как степень исходного многочлена 5x4+5x3+x2−11 равнялась четырём, то степень полученного многочлена 5x3+10x2+11x+11 на единицу меньше, т.е. равна трём. Последнее число во второй строке (ноль) означает остаток от деления многочлена 5x4+5x3+x2−11 на x−1. 
2 —
3x — 18 = 0\)
. Корни \(x_1 = 6,\ x_2 = -3\)
, тогда окончательно \
Для того, чтобы выполнить деление многочленов, воспользуемся схемой Горнера:
Если он равен 0, значит мы все верно посчитали.
Для этого можно решить квадратное уравнение через дискриминант , а можно поискать корень среди делителей числа -3. Так или иначе, мы придем к выводу, что корнем этого многочлена является число -3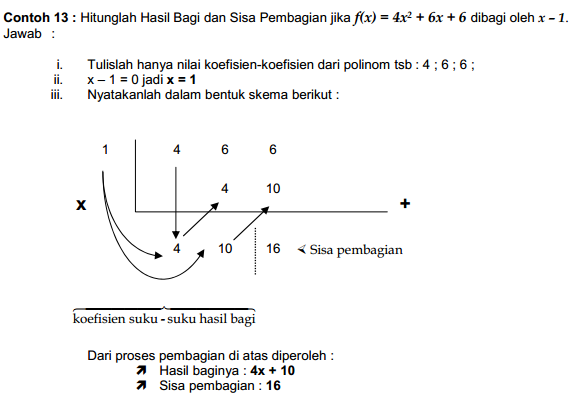 
Целые корни ищем среди делителей числа 36. 
Целые корни ищем среди делителей числа 6. 
Целые корни ищем среди делителей числа 24. 
(Ь Н Ы)
При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.
сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения.
Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.
Остаток r(х)= свn-1 +аn . Этот метод вычисления и называется схемой Горнера. Слово « схема» в названии алгоритма связана с тем, что обычно его выполнение оформляют следующим образом. Сначала рисуют таблицу 2(n+2). В левой нижней клетке записывают число с, а в верхней строке коэффициенты многочлена Р(х). При этом левую верхнюю клетку оставляют пустой.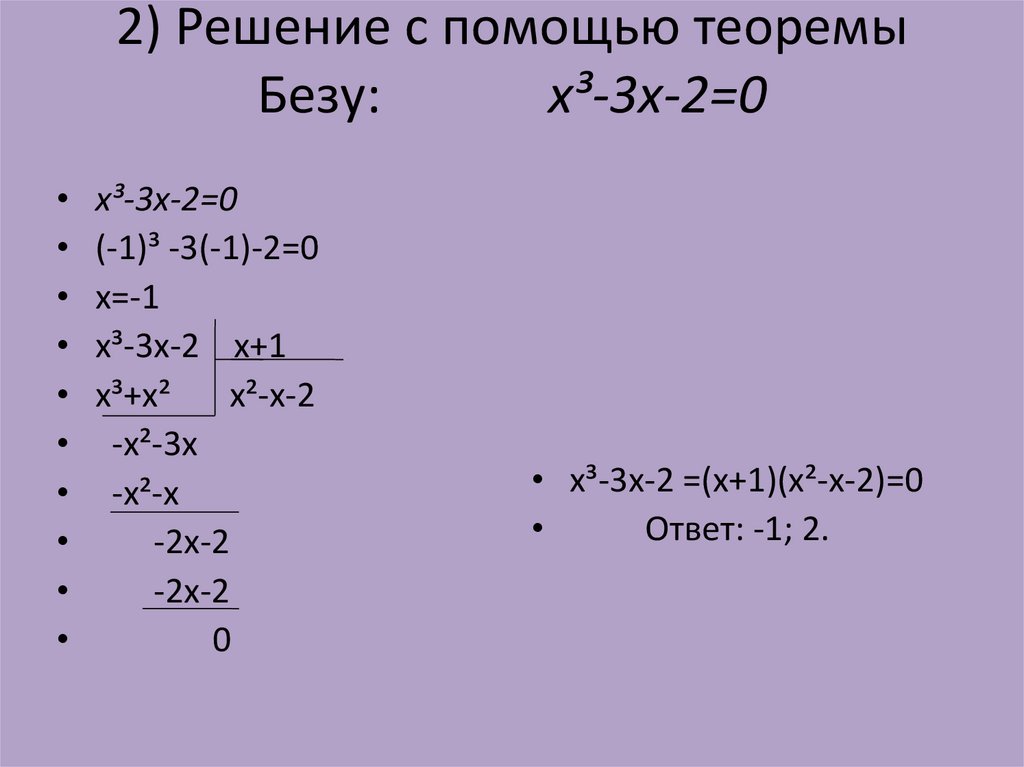
Другие числа в0, в1, в2,… нижней строки являются коэффициентами частного.
Воспользуемся схемой Горнера: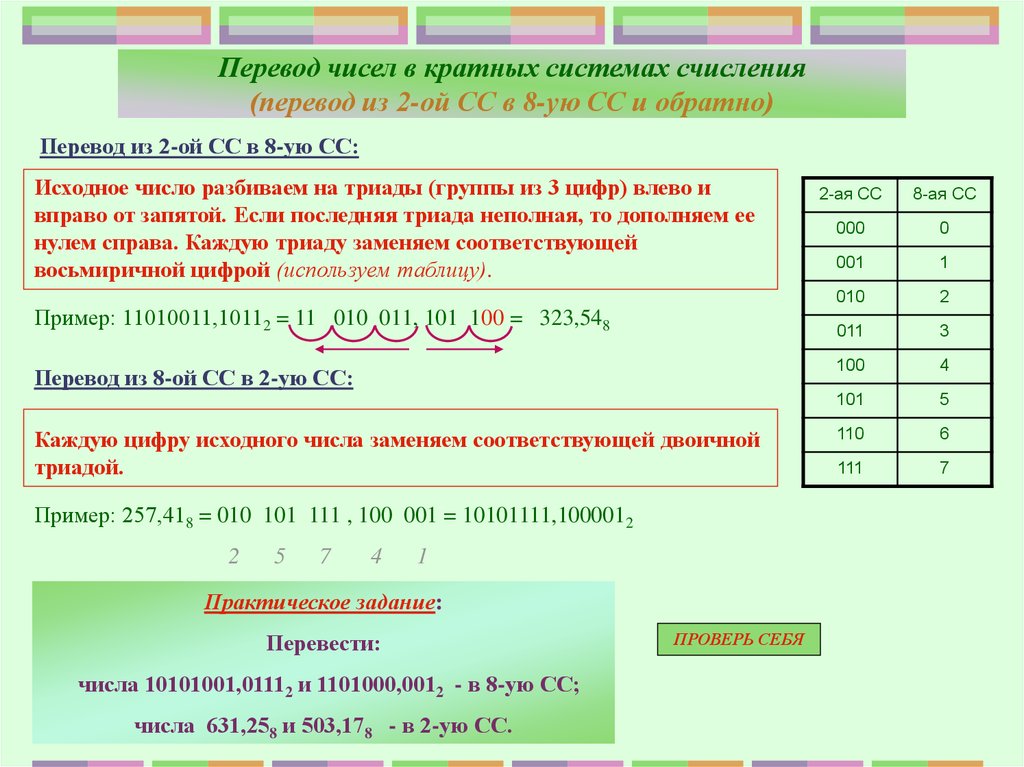
Проверим 1/2; -1/2.
Для 5х3 +2х2 -2х-5=0 х=1 также является корнем и
Подведение итогов 
2+10x+6$.
Польза онлайн сервиса бесценна, ведь кроме верного ответа вы получаете подробное решение каждого уравнения. Преимущества решения уравнений онлайн. Решить любое уравнение онлайн на нашем сайте вы можете абсолютно бесплатно. Сервис полностью автоматический, вам ничего не придется устанавливать на свой компьютер, достаточно будет только ввести данные и программа выдаст решение. Любые ошибки в расчетах или опечатки исключены. С нами решить любое уравнение онлайн очень просто, поэтому обязательно используйте наш сайт для решения любых видов уравнений. Вам необходимо только ввести данные и расчет будет выполнен за считанные секунды. Программа работает самостоятельно, без человеческого участия, а вы получаете точный и подробный ответ. Решение уравнения в общем виде. В таком уравнении переменные коэффициенты и искомые корни связаны между собой. Старшая степень переменной определяет порядок такого уравнения. Исходя из этого, для уравнений используют различные методы и теоремы для нахождения решений.
2-4ac. Если дискриминант меньше нуля, то уравнение не имеет действительных корней (корни находятся из поля комплексных чисел), если равен нулю, то у уравнения один действительный корень, и если дискриминант больше нуля, то уравнение имеет два действительных корня, которые находятся по формуле: D= -b+-sqrt/2а. Для решения квадратного уравнения онлайн вам достаточно ввести коэффициенты такого уравнения (целые числа, дроби или десятичные значения). При наличии знаков вычитания в уравнении необходимо поставить минус перед соответствующими членами уравнения. Решить квадратное уравнение онлайн можно и в зависимости от параметра, то есть переменных в коэффициентах уравнения. С этой задачей отлично справляется наш онлайн сервис по нахождению общих решений. Линейные уравнения. Для решения линейных уравнений (или системы уравнений) на практике используются четыре основных метода. Опишем каждый метод подробно. Метод подстановки. Решение уравнений методом подстановки требует выразить одну переменную через остальные.
После этого выражение подставляется в другие уравнения системы. Отсюда и название метода решения, то есть вместо переменной подставляется ее выражение через остальные переменные. На практике метод требует сложных вычислений, хотя и простой в понимании, поэтому решение такого уравнения онлайн поможет сэкономить время и облегчить вычисления. Вам достаточно указать количество неизвестных в уравнении и заполнить данные от линейных уравнений, далее сервис сделает расчет. Метод Гаусса. В основе метода простейшие преобразования системы с целью прийти к равносильной системе треугольного вида. Из нее поочередно определяются неизвестные. На практике требуется решить такое уравнение онлайн с подробным описанием, благодаря чему вы хорошо усвоите метод Гаусса для решения систем линейных уравнений. Запишите в правильном формате систему линейных уравнений и учтите количество неизвестных, чтобы безошибочно выполнить решение системы. Метод Крамера. Этим методом решаются системы уравнений в случаях, когда у системы единственное решение.
Главное математическое действие здесь – это вычисление матричных определителей. Решение уравнений методом Крамера проводится в режиме онлайн, результат вы получаете мгновенно с полным и подробным описанием. Достаточно лишь заполнить систему коэффициентами и выбрать количество неизвестных переменных. Матричный метод. Этот метод заключается в собрании коэффициентов при неизвестных в матрицу А, неизвестных – в столбец Х, а свободных членов в столбец В. Таким образом система линейных уравнений сводится к матричному уравнению вида АхХ=В. У этого уравнения единственное решение только если определитель матрицы А отличен от нуля, иначе у системы нет решений, либо бесконечное количество решений. Решение уравнений матричным методом заключается в нахождении обратной матрицы А.
Cегодня разберёмся, как эти линейные уравнения решать.
Привести квадратное уравнение к общему виду: 
Уравнение становиться линейным.
Решение квадратного уравнения с комплексными корнями. 
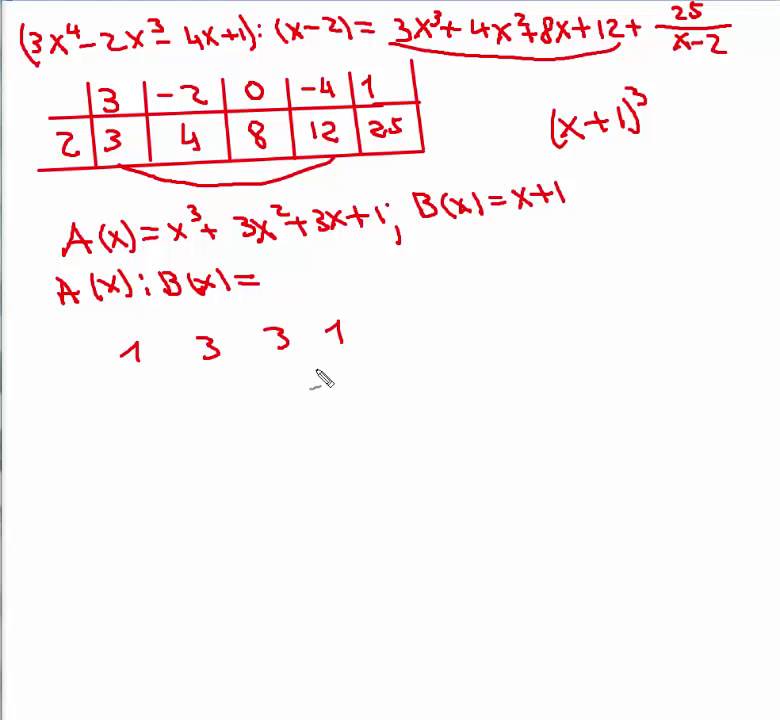
Если отрицательное — корней не будет вообще.
При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.
сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения.
Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.
Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн .
Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.
Любые ошибки в расчетах или опечатки исключены. С нами решить любое уравнение онлайн очень просто, поэтому обязательно используйте наш сайт для решения любых видов уравнений. Вам необходимо только ввести данные и расчет будет выполнен за считанные секунды. Программа работает самостоятельно, без человеческого участия, а вы получаете точный и подробный ответ. Решение уравнения в общем виде. В таком уравнении переменные коэффициенты и искомые корни связаны между собой. Старшая степень переменной определяет порядок такого уравнения. Исходя из этого, для уравнений используют различные методы и теоремы для нахождения решений. Решение уравнений данного типа означает нахождение искомых корней в общем виде. Наш сервис позволяет решить даже самое сложное алгебраическое уравнение онлайн. Вы можете получить как общее решение уравнения, так и частное для указанных вами числовых значений коэффициентов. Для решения алгебраического уравнения на сайте достаточно корректно заполнить всего два поля: левую и правую части заданного уравнения.
2-4ac. Если дискриминант меньше нуля, то уравнение не имеет действительных корней (корни находятся из поля комплексных чисел), если равен нулю, то у уравнения один действительный корень, и если дискриминант больше нуля, то уравнение имеет два действительных корня, которые находятся по формуле: D= -b+-sqrt/2а. Для решения квадратного уравнения онлайн вам достаточно ввести коэффициенты такого уравнения (целые числа, дроби или десятичные значения). При наличии знаков вычитания в уравнении необходимо поставить минус перед соответствующими членами уравнения. Решить квадратное уравнение онлайн можно и в зависимости от параметра, то есть переменных в коэффициентах уравнения. С этой задачей отлично справляется наш онлайн сервис по нахождению общих решений. Линейные уравнения. Для решения линейных уравнений (или системы уравнений) на практике используются четыре основных метода. Опишем каждый метод подробно. Метод подстановки. Решение уравнений методом подстановки требует выразить одну переменную через остальные.
После этого выражение подставляется в другие уравнения системы. Отсюда и название метода решения, то есть вместо переменной подставляется ее выражение через остальные переменные. На практике метод требует сложных вычислений, хотя и простой в понимании, поэтому решение такого уравнения онлайн поможет сэкономить время и облегчить вычисления. Вам достаточно указать количество неизвестных в уравнении и заполнить данные от линейных уравнений, далее сервис сделает расчет. Метод Гаусса. В основе метода простейшие преобразования системы с целью прийти к равносильной системе треугольного вида. Из нее поочередно определяются неизвестные. На практике требуется решить такое уравнение онлайн с подробным описанием, благодаря чему вы хорошо усвоите метод Гаусса для решения систем линейных уравнений. Запишите в правильном формате систему линейных уравнений и учтите количество неизвестных, чтобы безошибочно выполнить решение системы. Метод Крамера. Этим методом решаются системы уравнений в случаях, когда у системы единственное решение.
Главное математическое действие здесь – это вычисление матричных определителей. Решение уравнений методом Крамера проводится в режиме онлайн, результат вы получаете мгновенно с полным и подробным описанием. Достаточно лишь заполнить систему коэффициентами и выбрать количество неизвестных переменных. Матричный метод. Этот метод заключается в собрании коэффициентов при неизвестных в матрицу А, неизвестных – в столбец Х, а свободных членов в столбец В. Таким образом система линейных уравнений сводится к матричному уравнению вида АхХ=В. У этого уравнения единственное решение только если определитель матрицы А отличен от нуля, иначе у системы нет решений, либо бесконечное количество решений. Решение уравнений матричным методом заключается в нахождении обратной матрицы А.
Корнем многочлена является 2, а значит исходный многочлен должен делиться на x — 2 . Для того, чтобы выполнить деление многочленов, воспользуемся схемой Горнера:
Если он равен 0, значит мы все верно посчитали.
д. Так как решать уравнения? Давайте разберёмся.
Работает везде и всегда. Эта основа — Звучит страшно, но штука очень простая. И очень (очень!) важная.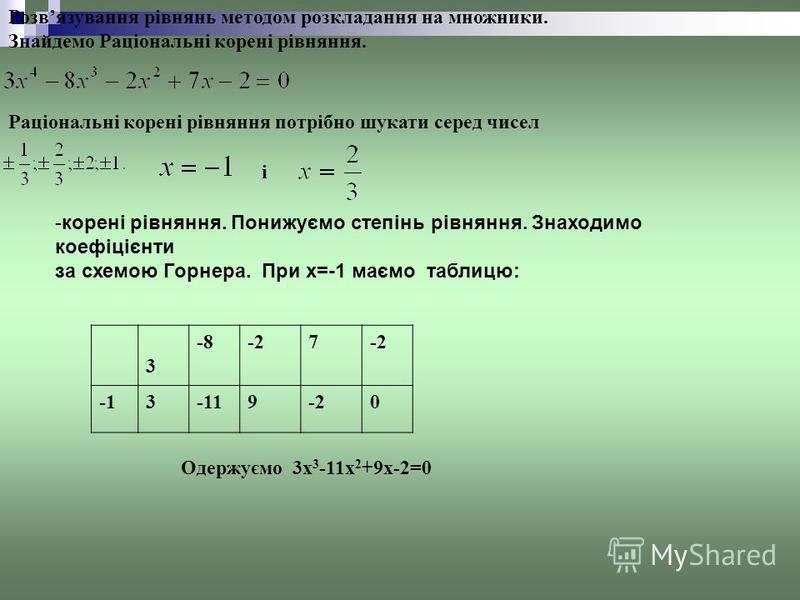
д. и т.п.
Здесь уже появляется понятное ограничение: на ноль умножать глупо, а делить и вовсе нельзя. Это преобразование вы используете, когда решаете что-нибудь крутое, типа
) Какое выражение с иксом у нас справа? 3х ? Ответ неверный! Справа у нас — 3х ! Минус три икс! Стало быть, при переносе влево, знак поменяется на плюс. Получится:
Тестирование с мгновенной проверкой. Учимся — с интересом!)
В первой ячейке второй строки ставится найденный нами корень 2. Во второй строке пишутся коэффициенты многочлена, который получится в результате деления. Они считаются так:
Если он равен 0, значит мы все верно посчитали.
Для этого можно решить квадратное уравнение через дискриминант , а можно поискать корень среди делителей числа -3. Так или иначе, мы придем к выводу, что корнем этого многочлена является число -3 
..» 
На самом деле, поскольку число
умножения на $$3$$ уменьшается на
$$1$$ для каждого члена, мы можем вложить умножения
по срокам вроде так,
\end{выравнивание}
$$
\end{выравнивание}
$$
Процедура завершается
когда он достигает последнего члена многочлена
$$p$$, где $$b_0 = b_1 \cdot k +
a_0$$ — результат вычисления $$p(k)$$.
Наконец, мы определяем процедуру-оболочку,
\конец{выравнивание*}
$$
Точно так же мы определяем функцию-оболочку, 92 + 11x + 3$$ с биномом $$d(x) =
x — 2$$, мы бы передали список 
4 Между прочим, приведенная выше теорема
также доказывает специфичную для реализации версию
теорема о полиномиальном остатке.
Хорнера. ↩
К сожалению, таких тем становится все больше, а ошибки изложения вслед за авторами методичек допускаются массово. Это касается не только начинающих репетиторов по математике и репетиторов по совместительству (тьюторов – студентов и преподавателей вузов), но и опытных преподавателей, репетиторов – профессионалов, репетиторов с опытом и квалификацией. Далеко не все репетиторы математики обладают талантом грамотного корректора шероховатостей школьных учебников. Не все также понимают, что эти исправления (или дополнения) необходимы. Лишь немногие занимаются адаптацией материала для его качественного восприятия детьми. К сожалению, прошли те времена, когда учителя математики вместе с методистами и авторами публикаций массово обсуждали каждую букву учебника. В прошлом, прежде чем в школах был введен учебник, проводились серьезные анализы и исследования результатов обучения. Пришло время дилетантов, стремящихся сделать учебники универсальными, подгоняя их под стандарты сильных математических классов.
Учителя школ и классов, не имеющих статуса математических, ориентируясь на нововведения авторов, стали чаще включать в свои уроки дополнительные параграфы, а любознательные дети, разглядывая красивые страницы своего учебника по математике, все чаще задают Воспитатель: «Что это за деление углом? Мы проходим через это? Как разделить угол? От таких прямых вопросов никуда не деться. Воспитатель должен что-то сказать ребенку.
Мы должны сделать такой абзац необязательным, озаглавив его «для тех, кто хочет знать больше». Репетиторы против? И какое нам дело до репетиторов вообще? Методисты и школьные учителя тоже против? Не будем усложнять материал и рассмотрим самую простую его часть.
И самое главное, непонятно, почему выбранные мономы нужно добавлять в конце и почему получившиеся скобки будут разложением исходного многочлена. Любой грамотный математик поставит жирный знак вопроса над объяснениями, которые даются в учебнике.
Это очень важно! Лучший способ понять это на конкретном примере. Возьмем некоторый многочлен с выбранным корнем и покажем прием его факторизации с помощью знакомого ученику 7-го класса метода тождественных преобразований. При соответствующих сопроводительных пояснениях, акцентах и подсказках репетитора по математике вполне возможно передать материал без каких-либо общематематических выкладок, произвольных коэффициентов и степеней.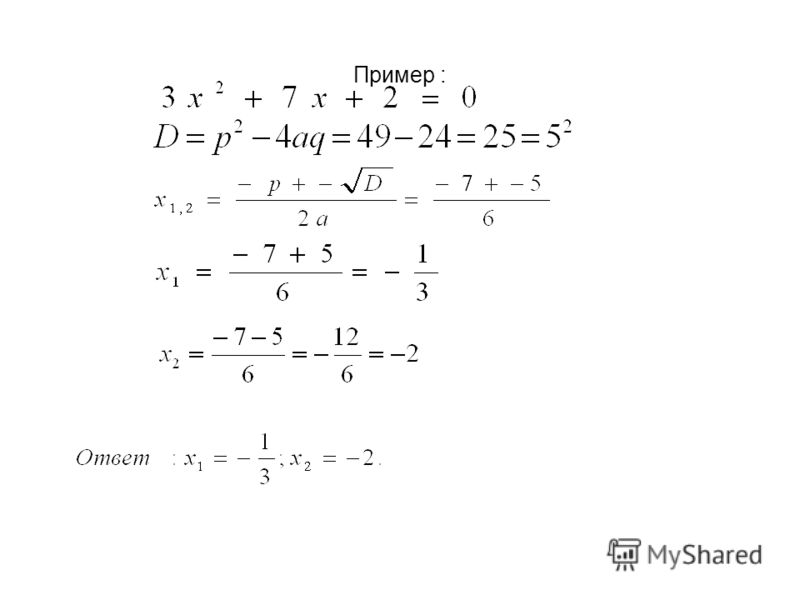
Если ученик не самый слабый, то ему вполне по силам дать репетитору по математике нужное выражение: . Воспитателя нужно сразу попросить вставить его в красную коробку и показать, что будет, когда их откроют. Лучше всего этот виртуальный временный многочлен подписать под стрелками (под фото), выделив его каким-нибудь цветом, например, синим. Это поможет вам выбрать слагаемое для красного поля, называемое остатком от выборки. Я бы посоветовал репетиторам указать здесь, что этот остаток можно найти вычитанием. Выполнив эту операцию, получим:
Репетитор по математике рисует перед учеником две клетки и просит заполнить их слева направо.
На самом деле его формулировка при таком подходе воспитателя становится очевидной: если число а является корнем многочлена, то его можно разложить на множители, один из которых, а другой получается из исходного в одном из трех способы:
Таким образом, вы можете добавить результат умножения на . Акцентировав внимание ученика на специфике действий с коэффициентами, репетитор по математике может показать, как обычно выполняются эти действия, не записывая сами переменные. Для этого удобно ввести корень и коэффициенты исходного многочлена в порядке старшинства в следующую таблицу:
По сути, схема Горнера — это еще одна форма записи метода группировки, хотя, в отличие от последней, она совершенно не описательная. Ответ (факторизация) здесь получается сам собой, и мы не видим самого процесса его получения. Мы не будем заниматься строгим обоснованием схемы Горнера, а лишь покажем, как она работает.
Непосредственной проверкой убеждаемся, что корнем этого многочлена является число 2, т. е. x3 — 5×2 — 2x + 16 = (x — 2)Q(x), где Q(x) — многочлен второго степень
Таблица первой розыгрыша 2(n+2). В нижнюю левую ячейку записывается число c, а в верхнюю строчку — коэффициенты многочлена P(x). При этом верхняя левая ячейка остается пустой.
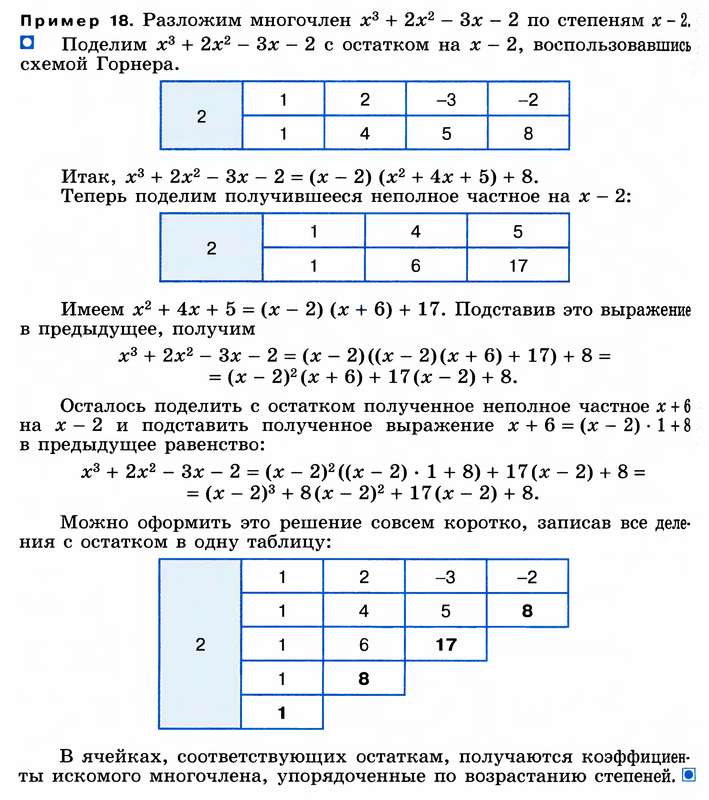Воспользуемся схемой Горнера:
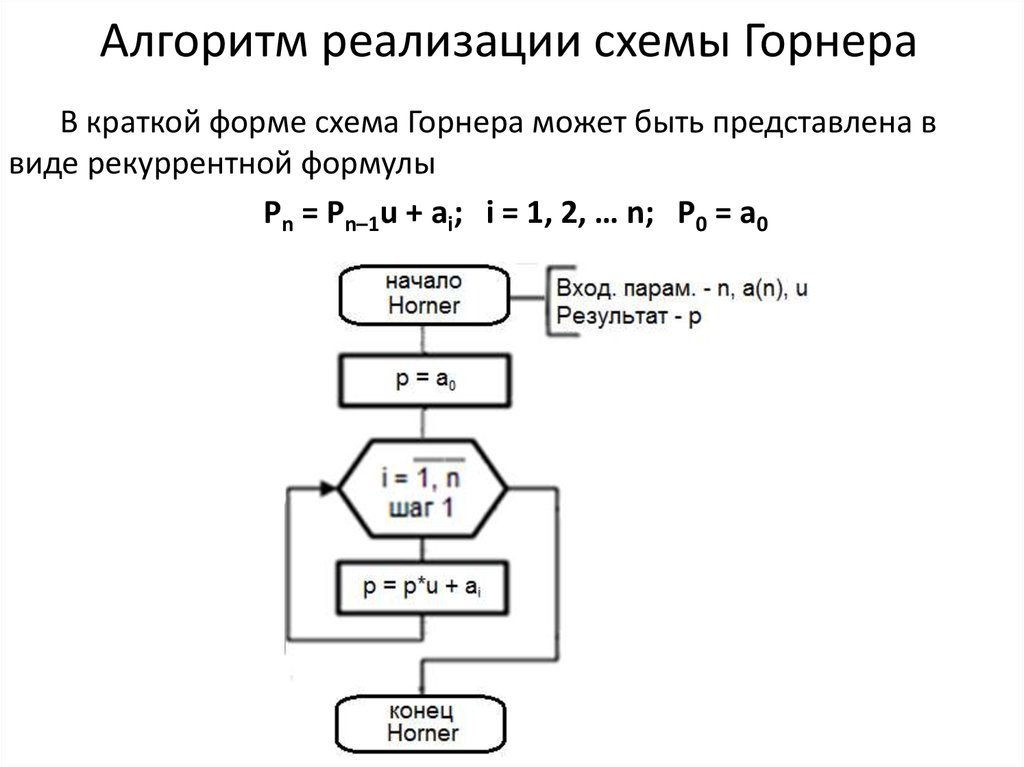Совершенствовать навыки применения схемы Горнера для разложения многочлена по степеням и деления многочлена на двучлен.
е. R= P n (a).
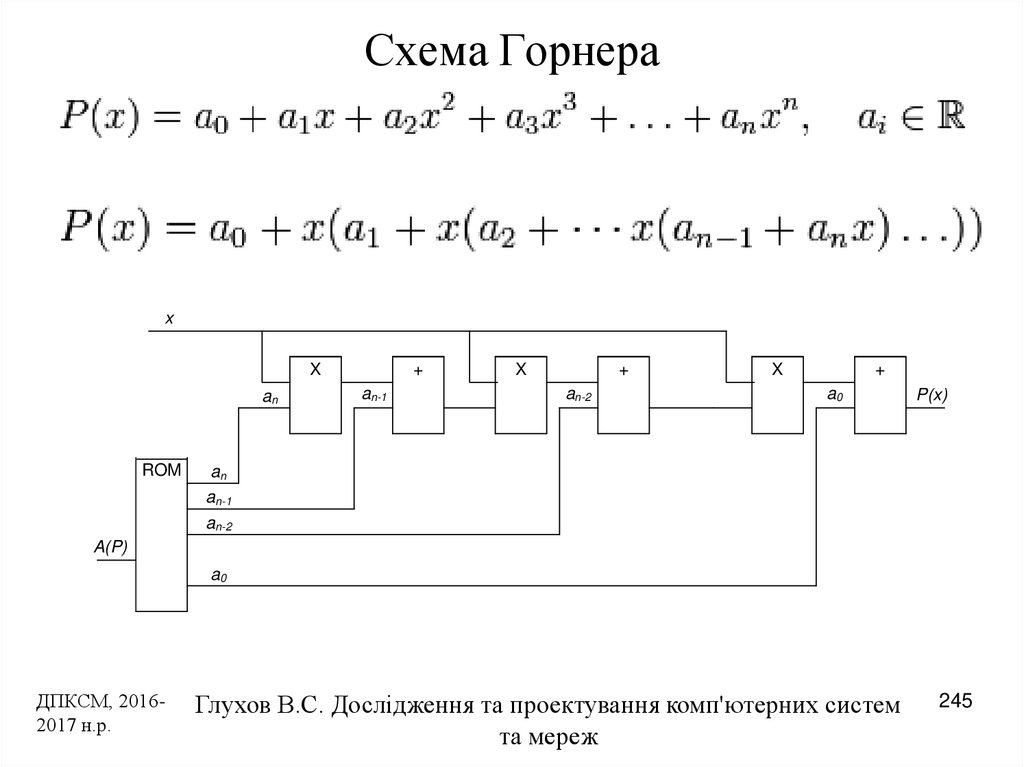Номер a называется корень полинома F n (x) = f 0 x n + f 1 x n-1 + f 2 x n-2 + …+f n-1 x + f n, если x=a значение многочлена F n (x) равно нулю: F n (a)=0, т.е. если многочлен делится нацело на двучлен x-a.
Поэтому для преобразования «2 в 10» используется последовательное деление на десять в двоичной системе, а «10 в 2» — сложение степеней десяти. Для оптимизации расчетов процедуры «10 в 2» в компьютере используется экономичная вычислительная схема Хорнера.
достиг. Операция проводится на бумаге в западном варианте, в китайском — счетными стержнями, разложенными на столе.
Можно увидеть, что некоторые из более ранних книг включают только определенные классы полиномов, в то время как более поздние кажутся неограниченными в степени полинома или использовании положительных и отрицательных коэффициентов. Самая ранняя из них, , продолжение древней математики Ван Сяотуна, , включает ограниченный класс полиномов, что делает алгоритм их численного решения довольно простым. Алгоритм для этого класса будет рассмотрен здесь первым.
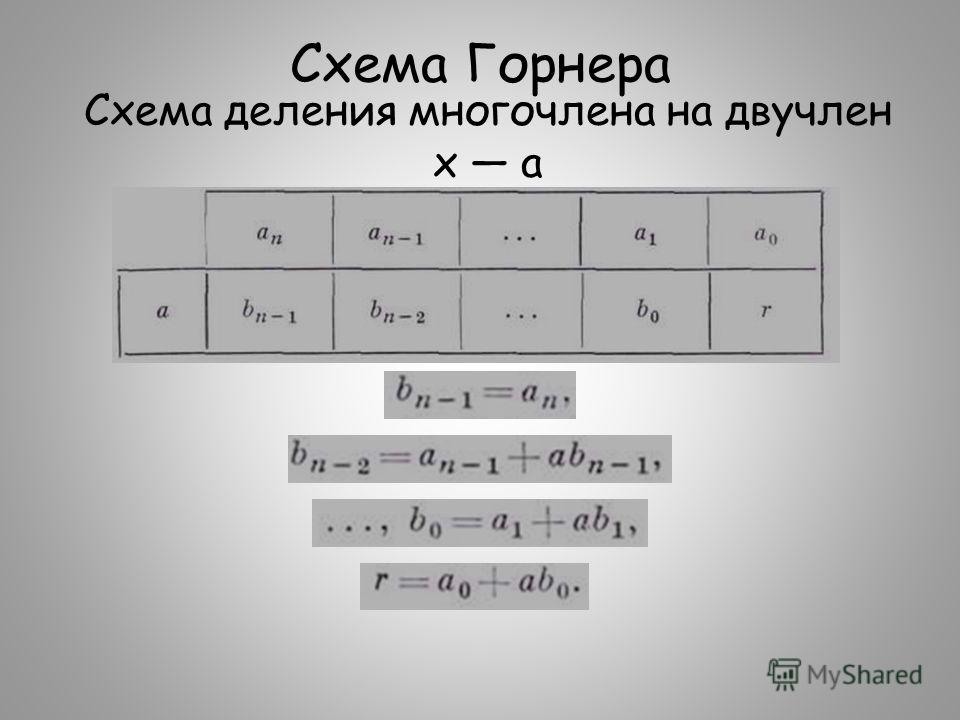707067070707070706707067070706706706706706706706706706706706707070707070707070707070 гг. 2 – d 3 (2)
0069 д до а 
Как с этим справились? В некоторых случаях знаменатели дробей являются делителями степеней десяти, и это не проблематично. Например, в задаче 17,
Таким образом, калькулятор должен иметь возможность начать с грубой оценки желаемого корня.
Если многочлен имеет два корня с одинаковой первой цифрой и одинаковым порядком величины, он не сможет найти ни один из корней. В Приложении 1 есть один такой случай: Siyuan yujian имеет уравнение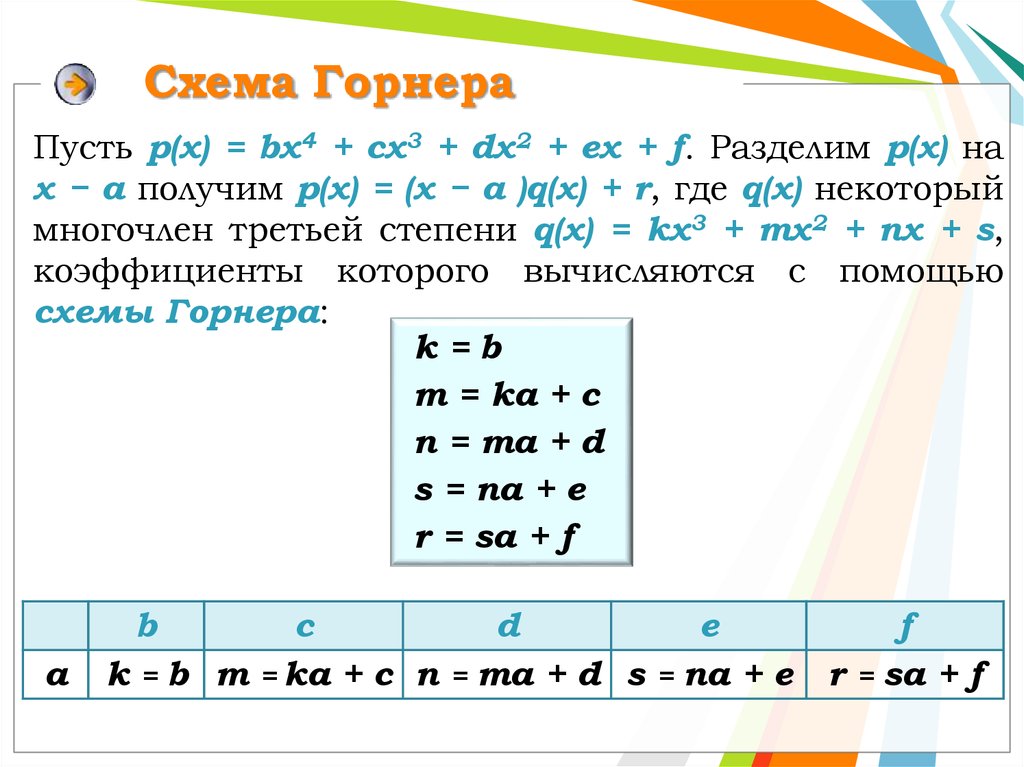
Либбрехт (1973: 198) объясняет, что приближение Цинь Цзюшао таково: 
Арабские науки и философия 4: 207–266. journals.cambridge.org/abstract_S0957423
1: 9–34.
Копенгаген: NIAS Press. Предстоит.
Оксфорд / Пекин: издательство Оксфордского университета / издательство Science Press. books.google.dk/books?id=eiTJHRGTG6YC
..
..
.. но это также «разность двух кубов»:
..
Мы можем легко проверить, просто поставьте «2» вместо «x»: