Помогите решить / разобраться (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
Посмотреть правила форума
| artcert |
| ||
28/04/16 |
| ||
| |||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| artcert |
| ||
28/04/16 |
| ||
| |||
| svv |
| |||
23/07/08 |
| |||
| ||||
| artcert |
| ||
28/04/16 |
| ||
| |||
| svv |
| |||
23/07/08 |
| |||
| ||||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
| artcert |
| ||
28/04/16 |
| ||
| |||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| artcert |
| ||
28/04/16 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 10 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Найти площадь поверхности сферы онлайн
Пример решили: 3293 раза Сегодня решили: 0 раз
Введите радиус сферы
Радиус R
Вычисление площади поверхности сферы
Скачать решение в PDF
Порекомендуйте наш сервис друзьям
Вконтакте
Одноклассники
Google+
Сфера (шаровая поверхность) – геометрическое тело, ограниченное сферической поверхностью,
все точки которого находятся на равном расстоянии от центра. 2 $$
2 $$
Попробуйте другие сервисы
Найти площадь треугольника
Найти площадь поверхности параллелепипеда
Найти площадь поверхности куба
Найти площадь ромба
Найти площадь кругового сектора
Площадь сферы. Объем шара. Как найти площадь и объем шара Что такое площадь поверхности шара
Имея при себе всего одну формулу и зная изначально, чему равен диаметр или радиус, можно с лёгкостью вычислить площадь поверхности шара. Формула будет иметь вид S =4πR2 , где число «пи» умножается на 4, затем на радиус шара в квадратной степени. Но перед непосредственными вычислениями следует сразу разобраться в терминах.
Трактовка значений
Это следует знать:
- Шар – геометрический объект, получившийся в результате вращательных полукруговых движений вокруг центра.
 Любая точка поверхности шара находится на одинаковом расстоянии от центра.
Любая точка поверхности шара находится на одинаковом расстоянии от центра. - Сфера – не то же самое, что шар. Если тот является объёмным объектом и включает в себя внутреннее пространство, то сфера – это лишь поверхность данного объекта и имеет только свою площадь. Иными словами – нельзя сказать, что сфера имеет такой-то объём, в отличие от шара.
- Число «пи» — это постоянное число, равное отношению длины окружности к её диаметру. В сокращённом виде его принято обозначать числом, равным 3,14. Но на самом деле, после тройки идёт больше тысячи цифр!
- Радиус шара равен ½ его диаметру . Точный диаметр можно вычислить с использованием нескольких плоских и ровных предметов. Нужно лишь зажать шар между этими предметами, которые зажимают шар и расположены перпендикулярно друг к другу, а затем измерить получившийся диаметр.
- Квадратная степень обозначается в виде двойки и означает то, что это число надо умножить на само себя один раз.
 Если бы степень числа была в виде тройки, то умножать на само себя нужно было бы два раза. Записав выражение на бумаге, можно понять, почему используются именно двойка и тройка, а не единица и двойка.
Если бы степень числа была в виде тройки, то умножать на само себя нужно было бы два раза. Записав выражение на бумаге, можно понять, почему используются именно двойка и тройка, а не единица и двойка. - Объём – величина, обозначающая размер в пространстве, занимающее объектом. От диаметра зависит объём шара. Формула будет равна четырём трети, умноженным на число «пи» и вновь умноженным на его радиус в кубе.
- Площадь – величина, обозначающая размер поверхности объекта, но не внутреннего пространства.
Занимательные факты
Это интересно:
- У числа «пи» есть собственные фан-клубы по всему миру. Члены общества пытаются запомнить как можно больше знаков из этого числа, а также пытаются разгадать вселенские тайны, сокрытые в числе.
- Площадь суши Земли составляет всего 29,2 % от её общей поверхности. Точное число площади сложно назвать из-за неравномерного рельефа Земли, такие как впадины и горы.
- Знания о формуле площади шара можно применять и в быту.
 Также этими знаниями можно подавлять соперника в споре.
Также этими знаниями можно подавлять соперника в споре.
Продемонстрировав объём своих знаний в области геометрии, можно изначально заставить вас уважать, а ремонтникам и продавцам можно дать понять, что вас просто так не обмануть.
Применение формулы
Рассмотрим на примере, как вычислить площадь круглого шара , диаметр которого равен 50 см. Следуя формуле, нужно 50 разделить на два (чтобы получить радиус), возвести полученное число в квадрат и умножить всё это дело сначала на 4, затем на 3,14. В итоге получим число в 7 850 квадратных сантиметров.
Формула вычисления площади применяется не только среди учителей в школе и научных сотрудников в лаборатории. Данная формула может пригодиться обычному маляру. Ведь если шар большой, а краски мало, то возникает вопрос – хватит ли ему этой смеси, чтобы покрасить весь объект. И это далеко не единственный бытовой случай, где может пригодиться формула.
Формула вычисления объёма может пригодиться и строительной бригаде, что делает ремонт. И неважно, какой это объект – промышленное здание, небольшой дом или обычная квартира. Этим и отличаются профессионалы – они умеют применять свои знания на практике.
И неважно, какой это объект – промышленное здание, небольшой дом или обычная квартира. Этим и отличаются профессионалы – они умеют применять свои знания на практике.
Но как быть, если не представляется возможным измерить объект? Такой вопрос может возникнуть в случае огромных размеров объекта или его недосягаемости. В этом случае могут помочь электронные технологии, в основе работы которых лежит сканирование пространства определёнными частотами и лазерами. С современными технологиями необязательно знать все формулы наизусть. Достаточно иметь подключение к интернету и зайти на любой онлайн-калькулятор.
Принято считать, что первый, кто нашёл и вывел формулу объёма и площади шара, был Архимед . Это величайший древнегреческий учёный, живший за 300 лет до нашей эры. Он был не только математиком, но и физиком, и инженером. Он один из первых людей, кто попытался «оцифровать» окружающий нас мир. Его теоремы и труды используются по сей день.
Именно Архимед определил границы числа «пи» и обозначил их, не имея никаких современных гаджетов. Сам Архимед очень гордился найденной формулой, с помощью которой вычисляется объём шара. Его потомки в честь этого изобразили на его могильном камне цилиндр и шар.
Сам Архимед очень гордился найденной формулой, с помощью которой вычисляется объём шара. Его потомки в честь этого изобразили на его могильном камне цилиндр и шар.
Если бы каким-то чудом он переродился в наше время, то он сразу же смог бы преобразить этот мир и вывести его на новый уровень.
Видео
На примере этого видео вам будет легко понять, как найти площадь поверхности шара.
Многие из нас любят играть в футбол или, по крайней мере, почти каждый из нас слышал про эту знаменитую спортивную игру. Всем известно, что в футбол играют мячом.
Если спросить прохожего, форму какой геометрической фигуры имеет мяч, то часть людей скажут, что форму шара, а часть, что формы сферы. Так кто же из них прав? И в чем разница между сферой и шаром?
Важно!
Шар — это пространственное тело. Внутри шар чем-либо заполнен. Поэтому у шара можно найти объем.
Примеры шара в жизни: арбуз и стальной шарик.
Шар и сфера, подобно кругу и окружности, имеют центр, радиус и диаметр.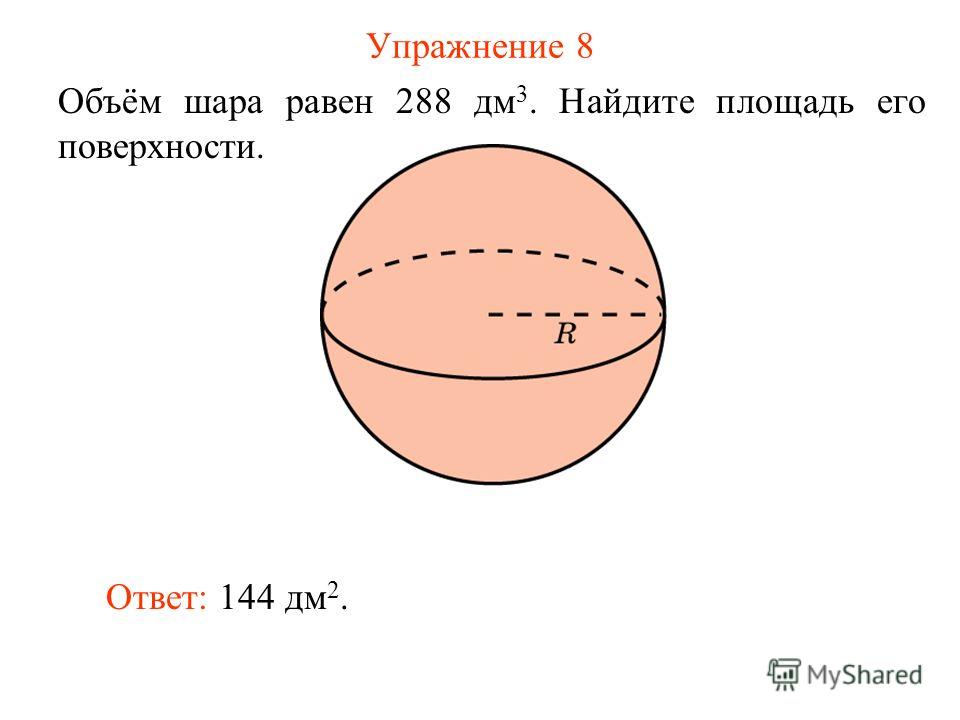
Важно!
Сфера — поверхность шара. У сферы можно найти площадь поверхности.
Примеры сферы в жизни: волейбольный мяч и шарик для игры в настольный теннис.
Как найти площадь сферы
Запомните!
Формула площади сферы: S = 4π R 2
Для того, чтобы найти площадь сферы, необходимо вспомнить,
что такое степень числа .
Зная определение степени,
можно записать формулу площади сферы следующим образом.
S = 4π
R 2 =
4π
R · R;
Закрепим полученные знания и решим задачу на площадь сферы.
Зубарева 6 класс. Номер 692(а)
Условие задачи:
- Вычислите площадь сферы, если её радиус равен 1 =
3 ·
=
=
/ (4 · 3)
= ) =
= ) =
= = = = 1 - R 3 = 1
- R = 1 м
Важно!
Уважаемые родители!
При окончательном расчете радиуса
не надо заставлять ребенка считать кубический корень. Учащиеся
6-го класса еще не проходили и не знают определение корней в математике. 2\approx314
S
=
π
⋅
D
2
=
π
⋅
1
0
2
≈
3
1
4
(см. кв.)
2\approx314
S
=
π
⋅
D
2
=
π
⋅
1
0
2
≈
3
1
4
(см. кв.)
Ответ: 314 см. кв.
Определение.
Сфера (поверхность шара ) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).
Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение.
Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).
Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение. Радиус сферы (шара) (R) — это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).
Определение. Диаметр сферы (шара) (D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.
Формула. Объём шара :
| V = | 4 | π R 3 = | 1 | π D 3 |
| 3 | 6 |
Формула. Площадь поверхности сферы через радиус или диаметр:
S = 4π R 2 = π D 2
Уравнение сферы
1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат :
x 2 + y 2 + z 2 = R 2
2. Уравнение сферы с радиусом R и центром в точке с координатами (x 0 , y 0 , z 0) в декартовой системе координат :
(x — x 0) 2 + (y — y 0) 2 + (z — z 0) 2 = R 2
Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.
Основные свойства сферы и шара
1. Все точки сферы одинаково удалены от центра.
2. Любое сечение сферы плоскостью является окружностью.
3. Любое сечение шара плоскостью есть кругом.
4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.
5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.
6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.
7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.
8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются , а в плоскости пересечения образуется круг.
Секущая, хорда, секущая плоскость сферы и их свойства
Определение. Секущая сферы — это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.
Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.
Определение. Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).
Определение. Секущая плоскость — это плоскость, которая пересекает сферу.
Определение. Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сеченме образует соответственно большую окружность и большой круг . Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).
Любая хорда, проходящая через центр сферы (шара) является диаметром.
Хорда является отрезком секущей прямой.
Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:
d
Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:
m
Местом сечения секущей плоскости на сфере всегда будет малая окружность , а на шаре местом сечения будет малый круг . Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r
такого круга можно найти по формуле:
Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r
такого круга можно найти по формуле:
r = √R 2 — m 2 ,
Где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.
Определение. Полусфера (полушар) — это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.
Касательная, касательная плоскость к сфере и их свойства
Определение. Касательная к сфере — это прямая, которая касается сферы только в одной точке.
Определение. Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.
Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения
Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.
Определение. Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h
называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.
Высотой сегмента h
называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.
Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:
S = 2π Rh
Расчет объемной теплоты сгорания газа
Электропроводность воды, или что такое кондуктометрия
Как найти площадь поверхности шара? – Обзоры Вики
А формула для площади поверхности сферы радиуса R такова: 4 * Пи * Р2.
Какова формула площади поверхности? переменные:
| Формула площади поверхности | Значение площади поверхности |
|---|---|
| SA = 2B + Ph | Найдите площадь каждого лица. Сложите все области. |
| SA = B + 12sP | Найдите площадь каждого лица. Сложите все области. Сложите все области. |
| СА=2B+2u03c0rh | Найдите площадь основания, умноженную на 2, затем добавьте площади к площадям прямоугольника, равным длине окружности, умноженной на высоту. |
• 17 сентября 2020 г.
Что такое формула шара? Ответ: Уравнение сферы в стандартной форме имеет вид x2 + у2 + г2 = г2. Посмотрим, как это получается. Пояснение: Пусть A (a, b, c) будет неподвижной точкой в пространстве, r будет положительным вещественным числом и P (x, y, z) будет движущейся точкой, такой что AP = r будет константой.
Во-вторых Что такое ДПС и ВСТ сферы? Площадь поверхности (TSA) = CSA = 4πr2. Полусфера: Площадь изогнутой поверхности (CSA) = 2 π r2. Общая площадь поверхности = TSA = 3 π r2.
Что является основанием шара?
Правый конус — это конус, вершина которого находится непосредственно над центром основания. имеет круглая основа который соединен с единственной точкой (называемой вершиной). Сфера — это трехмерное твердое тело, состоящее из всех точек, находящихся на одинаковом расстоянии от данного центра.
Сфера — это трехмерное твердое тело, состоящее из всех точек, находящихся на одинаковом расстоянии от данного центра.
…
Площадь поверхности конуса.
| s 2 | = | + × π |
|---|---|---|
| s | = | + × |
то сколько поверхностей у шара? Сфера – это три объемный объект круглой формы. В отличие от других трехмерных фигур, сфера не имеет ни вершин, ни краев.
…
Сфера.
| 1. | Определение сферы |
|---|---|
| 4. | Разница между кругом и сферой |
| 5 . | Площадь поверхности сферы |
| 6. | Объем сферы |
| 7. | Часто задаваемые вопросы о Сфере |
LSA и TSA сферы одинаковы? сфера имеет только одну поверхность, то есть изогнутую, а не плоскую. Так, площадь криволинейной поверхности и общая площадь поверхности сферы одинаковы… … Итак, криволинейная поверхность и общая площадь поверхности в случае полушария — это 2 разные области.
Сколько поверхностей у шара?
Сфера – это три объемный объект круглой формы. В отличие от других трехмерных фигур, сфера не имеет ни вершин, ни краев. Все точки на поверхности сферы равноудалены от ее центра.
…
Сфера.
| 1. | Определение сферы |
|---|---|
| 5 . | Площадь поверхности сферы |
| 6. | Объем сферы |
| 7. | Часто задаваемые вопросы о Сфере |
Является ли сфера кругом? Определение круга и сферы
Круг — это двухмерная фигура, тогда как Сфера — это трехмерный объект. У круга все точки находятся на одинаковом расстоянии от центра по плоскости, тогда как в сфере все точки равноудалены от центра по любой из осей.
Сфера — это призма?
Призмы представляют собой многогранники или объекты с несколькими плоскими гранями. У призмы не может быть изогнутой стороны, поэтому такие объекты, как цилиндр, конус или сфера, не являются призмами.
Каковы размеры сферы? Сфера представляет собой трехмерный объект круглой формы.
…
Формулы сферы.
| Диаметр сферы | Д = 2р , где r — радиус |
|---|---|
| Площадь поверхности сферы | СА = 4πr 2 Квадратные единицы |
| Объем сферы | V = 4/3πr 3 Кубические единицы |
Что такое сферическая математика?
сфера, в геометрии, множество всех точек в трехмерном пространстве, лежащих на одинаковом расстоянии (радиусе) от данной точки (центра), или результат вращения круга вокруг одного из его диаметров. Компоненты и свойства сферы аналогичны свойствам круга.
Шар — это сфера?
A шар сферический; он имеет форму сферы — трехмерной версии двухмерного круга.
Как можно найти площадь поверхности сферы, объяснив это с помощью изображений? Чтобы найти площадь поверхности шара, используйте формула (4πr2), где r = радиус окружности.
Чему равна площадь боковой поверхности шара? Площадь боковой поверхности шара определяется выражением 4πr2 4πr 2 где r — радиус сферы. Следовательно, площадь криволинейной поверхности (CSA) полушария определяется выражением 2πr2 2 π r 2 , где r — радиус сферы, частью которой является полушарие.
Как найти площадь поверхности сферы без радиуса?
Что такое сфера Бьюс? Совершенно симметричный трехмерный объект круглой формы. является Сферой. Линия, соединяющая центр с границей, называется радиусом квадрата. Вы найдете точку, равноудаленную от любой точки на поверхности сферы. … Это вдвое больше длины радиуса сферы.
Браслет — это сфера?
Сфера — это круглая твердая фигура, по своей поверхности каждая точка которой равноудалена от ее центра. Это объемная фигура, состоящая из объема.
…
| Circle | Sphere | |
|---|---|---|
| Общие примеры | Браслеты и шины. | Теннисные мячи и планеты. |
Что такое сфера в географии? Сфера (от греческого σφαῖρα — sphaira, «шар, шар») — это геометрический объект, являющийся трехмерным аналогом двумерного круга. … В географии Землю часто представляют как сферу, а небесная сфера является важным понятием в астрономии.
Как называется трехмерный объект?
кубический, прямоугольная призма, сфера, конус и цилиндр — это основные трехмерные формы, которые мы видим вокруг себя.
Как называется вытянутый треугольник? В геометрии, треугольная призма — трехсторонняя призма; это многогранник, состоящий из треугольного основания, переведенной копии и трех граней, соединяющих соответствующие стороны.
Как называется треугольник в 3D?
Собственно это и называется треугольная призма. В квадратной пирамиде все грани, являющиеся треугольниками, сходятся в одной точке. В треугольной призме у вас есть две противоположные стороны, которые являются треугольниками. Вы увидите все это в разных ориентациях.
В треугольной призме у вас есть две противоположные стороны, которые являются треугольниками. Вы увидите все это в разных ориентациях.
Из каких частей состоит шар?
Элементами сферы являются:
- Центр — это внутренняя точка, равноудаленная от любой точки сферы.
- Радиус — это расстояние от центра до точки сферы.
- Хорда — это отрезок, соединяющий любые две точки поверхности.
- Диаметр – это хорда, проходящая через центр.
Что такое сфера с примером?
Определение сферы — это форма шара, поверхность которой находится на одинаковом расстоянии от центра во всех точках или на уровне общества. Примером сферы является глобус. Примером сферы является высшая корка или те, кто находится в высших слоях общества.
Площадь большого круга шара равна
Научись решать задачи ЕГЭ за пару минут!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2013-12-16
Если в условии речь идёт о единичном кубе, то это означает, что ребро этого куба равно единице; если речь идёт о единичной сфере, то это означает, что её радиус равен единице. Формулы площади и объёма шара смотрите здесь.
Формулы площади и объёма шара смотрите здесь.
Площадь большого круга шара равна 17. Найдите площадь поверхности шара.
Мы знаем, что площадь поверхности шара находится по формул:
Необходимо найти радиус шара. Площадь осевого сечения (больший круг) равна 17. Из формулы площади круга можем найти его радиус.
Радиус большого круга является радиусом шара. Таким образом:
*Можно было сразу без данных вычислений сделать вывод, что площадь поверхности шара в 4 раза больше площади поверхности большого круга.
Ответ: 48
Во сколько раз увеличится площадь поверхности шара, если его радиус увеличить в три раза?
Запишем площадь поверхности исходного шара:
Площадь поверхности шара с радиусом втрое большим равна:
Таким образом, площадь поверхности шара увеличится в 9 раз.
Ответ: 9
Во сколько раз увеличится объем шара, если его радиус увеличить в шесть раз?
Объем шара находится по формуле:
При увеличении радиуса в шесть раз его объём будет:
Таким образом, объем шара увеличится в 216 раз.
Ответ: 216
Объем одного шара в 216 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Формула объёма шара:
Формула площади поверхности шара:
Пусть объёмы шаров соответственно равны:
Из условия следует, что:
То есть, мы установили, что радиус первого больше радиуса второго в 6 раз. Если радиус шара уменьшить в 6 раз, то площадь поверхности шара изменится следующим образом:
То есть она уменьшится в 36 раз.
Ещё один вариант рассуждения.
Объемы шаров (а так же их радиусов) соотносятся как:
То есть радиус одного шара в 6 раза больше другого.
Формула площади поверхности шара:
Если радиус одного шара увеличить в 6 раз, то площадь поверхности изменится следующим образом:
То есть она увеличится в 36 раз. Таким образом, площадь поверхности первого шара больше площади поверхности второго в 36 раз.
Ответ: 36
27073. Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара.
Что необходимо отметить сразу же? Это то, что радиус цилиндра равен радиусу шара и высота цилиндра равна двум его радиусам.
Площадь поверхности шара находится по формуле:
То есть нам нужно найти радиус шара. Это можно сделать из формулы площади поверхности цилиндра:
*Как уже сказано, высота цилиндра равна двум радиусам, значит:
Как вы догадываетесь, сам радиус можно и не вычислять, и в формулу площади поверхности шара подставить лR2:
Ответ: 12
27105. Объем прямоугольного параллелепипеда, описанного около сферы, равен 216. Найдите радиус сферы.
Параллелепипед описанный около сферы является кубом. Формула объёма куба имеет вид:
Ребро данного куба равно диаметру сферы. Найдём его:
Таким образом, радиус сферы равен трём.
Ответ: 3
27126. В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на Пи.
В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на Пи.
Ребро куба равно диаметру шара. Значит радиус шара равен 1,5. Вычислим объём шара:
Результат разделим на Пи и запишем ответ.
Ответ: 4,5
27059. Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
Посмотреть решение
27072. Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза?
Посмотреть решение
27097. Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
Посмотреть решение
27125. Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов.
Посмотреть решение
27162. Объем одного шара в 27 раз больше объема другого. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Посмотреть решение
27163. Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.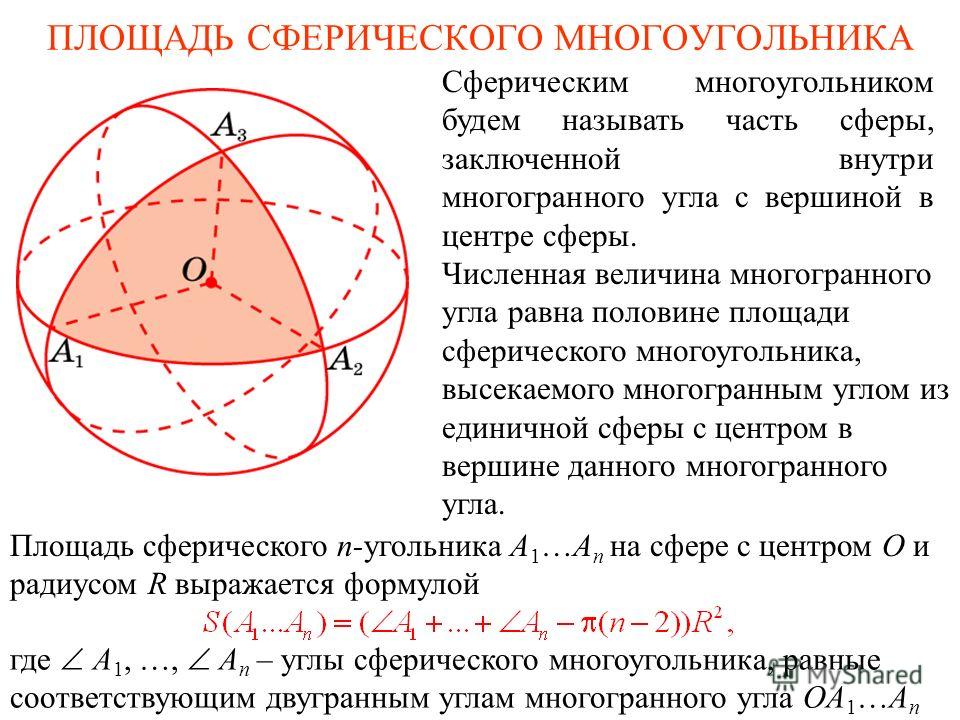
Посмотреть решение
27174. Объем шара равен 288Пи. Найдите площадь его поверхности, деленную на Пи.
Посмотреть решение
27043. Прямоугольный параллелепипед описан около сферы радиуса 1. Найдите его объем.
Посмотреть решение
27067. Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
Посмотреть решение
27127. Около куба с ребром равным корню из трёх описан шар. Найдите объем этого шара, деленный на Пи.
Посмотреть решение
Как видим, требуется знание формул и немножко логики. В будущем также будем рассматривать стереометрические задачи, не пропустите! На этом всё. Успеха Вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Стереометрия ШАР | ЕГЭ-№2Объём
Подготовка к ОГЭ по математике. Полный курс!
Полный Видеокурс по РУССКОМУ ЯЗЫКУ!
ПРЕМИУМ-КУРС по математике на 100 баллов!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Подготовка школьников к ЕГЭ (Справочник по математике — Стереометрия
| Справочник по математике | Геометрия (Стереометрия) | Сферы и шары |
| Шар, сфера и их части |
| Площади сферы и ее частей. Объемы шара и его частей |
Шар, сфера и их части
Введем следующие определения, связанные с шаром, сферой и их частями.
Определение 1. Сферой с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O равно r (рис. 1).
Определение 2. Шаром с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O не превосходит r (рис. 1).
1).
Рис.1
Таким образом, сфера с центром в точке O и радиусом r является поверхностью шара с центром в точке O и радиусом r.
Замечание. Радиусом сферы (радиусом шара) называют отрезок, соединяющий любую точку сферы с центром сферы. Длину этого отрезка также часто называют радиусом сферы (радиусом шара).
Определение 3. Сферическим поясом (шаровым поясом) называют часть сферы, заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).
Определение 4. Шаровым слоем называют часть шара, заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).
Рис.2
Окружности, ограничивающие сферический пояс, называют основаниями сферического пояса.
Расстояние между плоскостями Расстояние между плоскостями оснований сферического пояса называют высотой сферического пояса.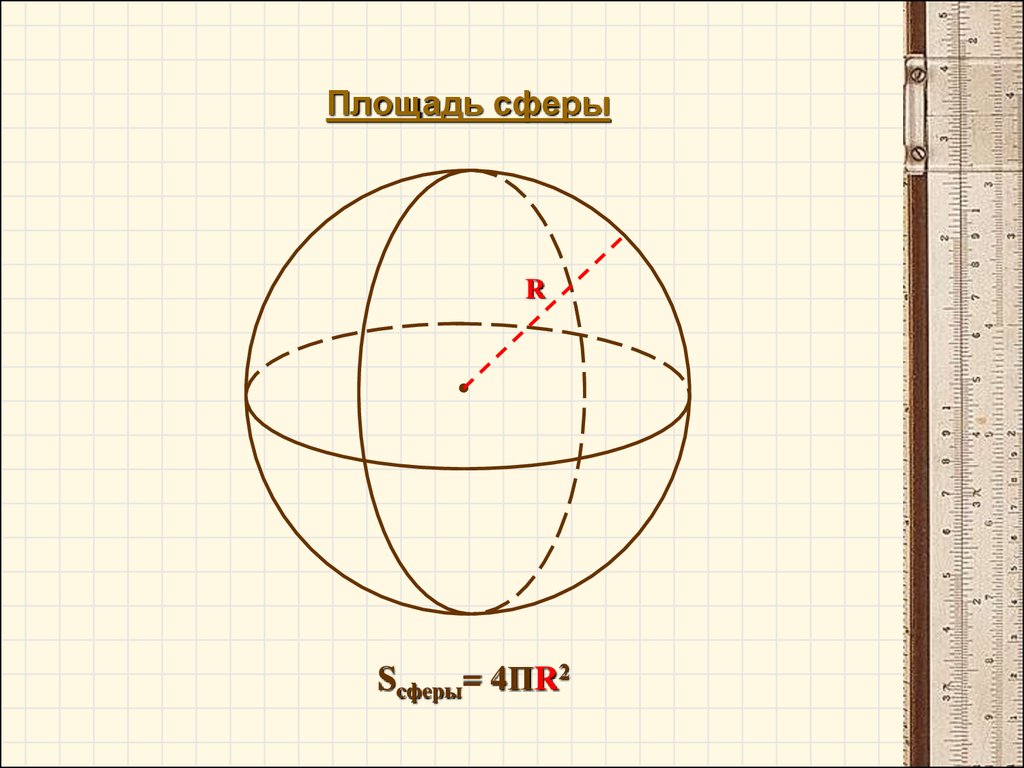
Из определений 3 и 4 следует, что шаровой слой ограничен сферическим поясом и двумя кругами, плоскости которых параллельны параллельны между собой. Эти круги называют основаниями шарового слоя.
Высотой шарового слоя называют расстояние между плоскостями расстояние между плоскостями оснований шарового слоя.
Определение 5. Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость (рис. 3).
Определение 6. Шаровым сегментом называют каждую из двух частей, на которые делит шар пересекающая ее плоскость (рис. 3).
Рис.3
Из определений 3 и 5 следут, что сферический сегмент представляет собой сферический пояс, у которого одна из плоскостей оснований касается сферы (рис. 4). Высоту такого сферического пояса и называют высотой сферического сегмента.
Соответственно, шаровой сегмент – это шаровой слой, у которого одна из плоскостей оснований касается шара (рис. 4). Высоту такого шарового слоя называют высотой шарового сегмента.
4). Высоту такого шарового слоя называют высотой шарового сегмента.
Рис.4
По той же причине всю сферу можно рассматривать как сферический пояс, у которого обе плоскости оснований касаются сферы (рис. 5). Соответственно, весь шар – это шаровой слой, у которого обе плоскости оснований касаются шара (рис. 5).
Рис.5
Определение 7. Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы (рис. 6).
Рис.6
Высотой шарового сектора называют высоту его сферического сегмента.
Замечание. Шаровой сектор состоит из шарового сегмента и конуса с общим основанием. Вершиной конуса является центр сферы.
Площади сферы и ее частей.
 Объемы шара и его частей
Объемы шара и его частейВ следующей таблице приведены формулы, позволяющие вычислить объем шара и объемы его частей, а также площадь сферы и площади ее частей.
| Фигура | Рисунок | Формула | Описание |
| Сфера | S = 4πr2, где | Площадь сферы | |
| Шар | где | Объем шара | |
| Сферический пояс | S = 2πrh, где Площадь сферического пояса не зависит от радиусов r1 и r2 ! | Площадь сферического пояса | |
| Шаровой слой | где | Объем шарового слоя | |
| Сферический сегмент | S = 2πrh, где | Площадь сферического сегмента | |
| Шаровой сегмент | где | Объем шарового сегмента | |
| Шаровой сектор | где | Объем шарового сектора |
| Сфера |
Площадь сферы: S = 4πr2, где |
| Шар |
Объем шара: где |
| Сферический пояс |
Площадь сферического пояса: S = 2πrh, где Площадь сферического пояса не зависит от радиусов r1 и r2 ! |
| Шаровой слой |
Объем шарового слоя: где |
| Сферический сегмент |
Площадь сферического сегмента: S = 2πrh, где |
| Шаровой сегмент |
Объем шарового сегмента: где |
| Шаровой сектор |
Объем шарового сектора: где |
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
Площадь поверхности сферы
Площадь поверхности сферы — это площадь, занимаемая изогнутой поверхностью сферы. Круглые формы принимают форму сферы, если рассматривать их как трехмерные структуры. Например, глобус или футбольный мяч. Давайте узнаем о формуле площади поверхности сферы и о том, как рассчитать площадь поверхности сферы в этом уроке.
Круглые формы принимают форму сферы, если рассматривать их как трехмерные структуры. Например, глобус или футбольный мяч. Давайте узнаем о формуле площади поверхности сферы и о том, как рассчитать площадь поверхности сферы в этом уроке.
| 1. | Какова площадь поверхности сферы? |
| 2. | Получение площади поверхности сферы |
| 3. | Формула площади поверхности сферы |
| 4. | Как рассчитать площадь поверхности сферы? |
| 5. | Часто задаваемые вопросы о площади поверхности сферы |
Какова площадь поверхности сферы?
Площадь, покрытая внешней поверхностью сферы, называется площадью поверхности сферы. Сфера – это трехмерная форма круга. Разница между сферой и кругом заключается в том, что круг представляет собой 2-мерную форму (2D-форму), тогда как сфера представляет собой 3-мерную форму. Площадь поверхности сферы выражается в квадратных единицах. Обратите внимание на сферу, приведенную ниже, которая показывает центр, радиус и диаметр сферы.
Площадь поверхности сферы выражается в квадратных единицах. Обратите внимание на сферу, приведенную ниже, которая показывает центр, радиус и диаметр сферы.
Определение сферы
Сфера представляет собой трехмерный объект круглой формы без вершин и краев. Важными аспектами этой формы являются радиус, диаметр, окружность и объем.
Вывод площади поверхности сферы
Сфера имеет круглую форму, поэтому, чтобы найти площадь ее поверхности, мы соотносим ее с изогнутой формой, например с цилиндром. Цилиндр — это форма, которая имеет криволинейную поверхность наряду с плоскими поверхностями. Теперь, если радиус цилиндра такой же, как радиус сферы, это означает, что сфера может идеально вписаться в цилиндр. Это означает, что высота цилиндра равна высоте сферы. Таким образом, эту высоту также можно назвать диаметром сферы. Поэтому этот факт был доказан великим математиком Архимедом, что если радиус цилиндра и сферы равен r, то площадь поверхности сферы равна площади боковой поверхности цилиндра.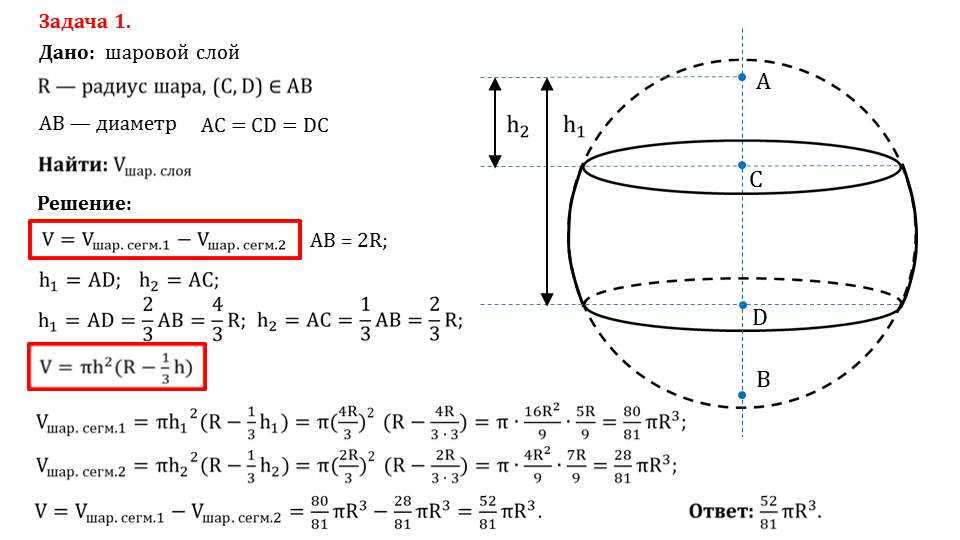
Следовательно, соотношение между площадью поверхности сферы и площадью боковой поверхности цилиндра определяется как:
Площадь поверхности сферы = Площадь боковой поверхности цилиндра
Площадь боковой поверхности цилиндра = 2πrh, где ‘ r — радиус, а h — высота цилиндра. Теперь высоту цилиндра также можно назвать диаметром сферы, потому что мы предполагаем, что эта сфера идеально помещается в цилиндре. Следовательно, можно сказать, что высота цилиндра = диаметру сферы = 2r. Итак, в формуле площадь поверхности Сферы = 2πrh; «h» можно заменить диаметром, то есть 2r. Следовательно, площадь поверхности сферы равна 2πrh = 2πr(2r) = 4πr 2
Формула площади поверхности сферы
Формула площади поверхности сферы зависит от радиуса сферы. Если радиус сферы равен r, а площадь поверхности сферы равна S. Тогда площадь поверхности сферы выражается как:
Площадь поверхности сферы = 4πr
2 ; где «r» — радиус сферы. В пересчете на диаметр площадь поверхности сферы выражается как S = 4π(d/2) 2
где d — диаметр сферы.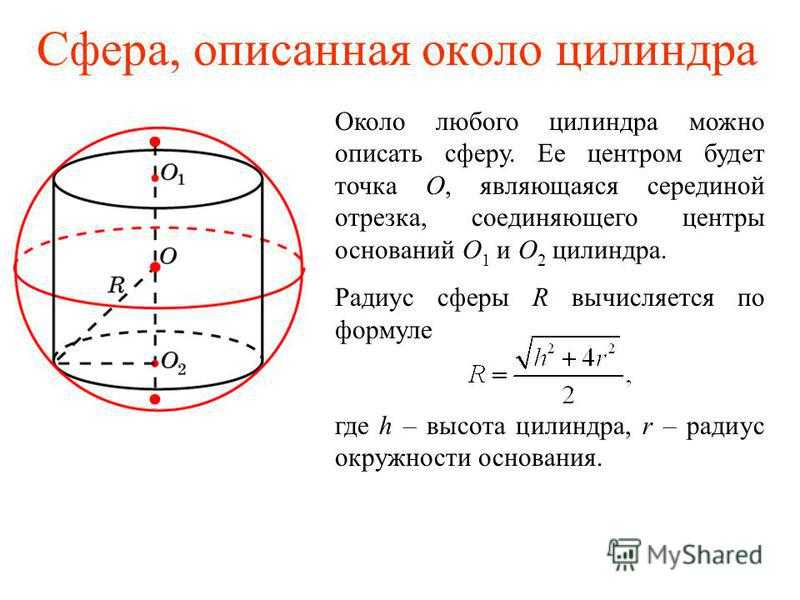
Как рассчитать площадь поверхности сферы?
Площадь поверхности шара – это пространство, занимаемое его поверхностью. Площадь поверхности сферы можно рассчитать по формуле площади поверхности сферы. Шаги для расчета площади поверхности сферы приведены ниже.
Давайте рассмотрим пример, чтобы узнать, как рассчитать площадь поверхности сферы, используя ее формулу.
Пример: Найдите площадь поверхности сферического шара с радиусом 9 дюймов.
- Шаг 1: Обратите внимание на радиус сферы. Здесь радиус шара равен 9 дюймам.
- Шаг 2: Как мы знаем, площадь поверхности сферы = 4πr 2 , поэтому после подстановки значения r = 9 мы получаем площадь поверхности сферы = 4πr 2 = 4 × 3,14 × 9 2 = 4 х 3,14 х 81 = 1017,36
- Шаг 3: Следовательно, площадь поверхности сферы равна 1017,36 в 2
Площадь криволинейной поверхности сферы
Площадь криволинейной поверхности сферы — это общая площадь поверхности сферы, поскольку сфера имеет только одну изогнутую поверхность.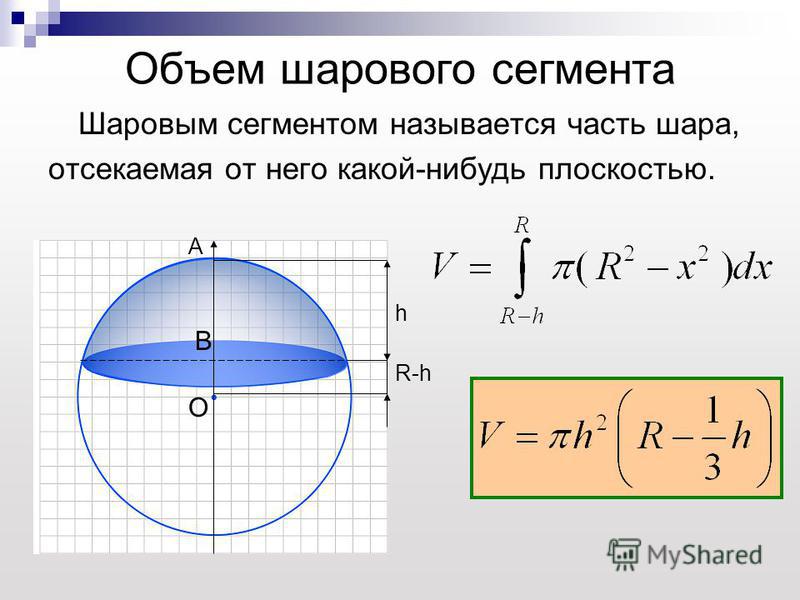 Поскольку у сферы нет плоской поверхности, площадь криволинейной поверхности сферы равна общей площади поверхности сферы. Следовательно, формула площади криволинейной поверхности сферы выражается как Площадь криволинейной поверхности сферы = 4πr 2 ; где «r» — радиус сферы.
Поскольку у сферы нет плоской поверхности, площадь криволинейной поверхности сферы равна общей площади поверхности сферы. Следовательно, формула площади криволинейной поверхности сферы выражается как Площадь криволинейной поверхности сферы = 4πr 2 ; где «r» — радиус сферы.
☛ Связанные статьи
- Площадь поверхности куба
- Площадь поверхности прямоугольного параллелепипеда
- Площадь поверхности призмы
- Площадь поверхности конуса
- Разница между площадью и площадью поверхности
Площадь поверхности сферы Примеры
Пример 1: Если радиус сферы равен 20 футам, найдите площадь ее поверхности. (Используйте π = 3,14).
Решение: Дано, радиус ‘r’ сферы = 20 футов.Площадь поверхности сферы = 4πr 2 = 4 × π × 20 2 = 5024 фута 2
∴ Площадь поверхности сферы 5024 фута 2 9
Пример 2: Найдите площадь поверхности сферы, если ее радиус равен 6 единицам.

Решение: Дано, радиус ‘r’ = 6 единиц. Итак, подставим значение r = 6 единиц
⇒ Площадь поверхности сферы = 4πr 2 = 4 × π × 6 2 = 4 × 3,14 × 36 = 452,16 ед. 2
∴
Пример 3: Укажите истинное или ложное значение.
а.) Сфера представляет собой трехмерную форму круга.
b.) Площадь криволинейной поверхности сферы – это общая площадь поверхности сферы, поскольку у сферы есть только одна криволинейная поверхность.
Решение:
а.) Верно, сфера — это трехмерная форма круга.
b.) Правда, площадь криволинейной поверхности сферы равна общей площади поверхности сферы, потому что у сферы есть только одна изогнутая поверхность.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.
Записаться на бесплатный пробный урок
Практические вопросы по площади поверхности сферы
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о площади поверхности сферы
Что такое площадь поверхности сферы в математике?
Площадь поверхности сферы — это общая площадь, которая покрыта ее внешней поверхностью. Площадь поверхности сферы всегда выражается в квадратных единицах. Формула площади поверхности сферы зависит от радиуса и диаметра сферы. Это математически выражается как 4πr 2 ; где «r» — радиус сферы.
Почему площадь поверхности сферы в 4 раза больше площади круга?
Нить, полностью покрывающая площадь поверхности сферы, может полностью покрыть площадь поверхности ровно четырех кругов. Таким образом, вы можете проверить, что площадь поверхности сферы в четыре раза больше площади круга. Когда мы пишем формулу площади поверхности сферы, мы пишем площадь поверхности сферы = 4πr 2 = 4(πr 2 ) = 4 × площадь круга.
Сколько сторон и вершин у сферы?
Сфера — это трехмерная фигура, круглая, как круг. Следовательно, у него нет ни сторон, ни вершин, ни граней.
Есть ли у сферы бесконечные грани?
Нет, у шара нет лица. Грань — это плоская поверхность, а сфера не имеет плоской поверхности. Это делает сферу безликой трехмерной формой (3D-формой).
Что такое площадь криволинейной поверхности и общая площадь поверхности сферы?
Сфера имеет только одну поверхность, и она изогнута. Поскольку у сферы нет плоской поверхности, площадь криволинейной поверхности сферы равна общей площади поверхности сферы, которая равна 4πr 2 .
☛Также проверьте:
- Формулы площади поверхности
- Геометрические формулы
- Формулы измерения
Что такое площадь поверхности сферической формулы в терминах диаметра?
Формула площади поверхности сферы в пересчете на диаметр определяется как πD 2 , где «D» — диаметр сферы. Он дает отношение между площадью поверхности сферы и диаметром сферы.
Он дает отношение между площадью поверхности сферы и диаметром сферы.
Как рассчитать площадь поверхности сферы по объему?
Площадь поверхности сферы можно легко рассчитать с помощью объема сферы. В этом случае мы должны знать значение радиуса сферы. Радиус сферы можно рассчитать по формуле объема сферы, то есть Объем сферы = 4/3 × πr 3 . Отсюда можно вычислить радиус и затем подставить его значение в формулу площади поверхности. Мы знаем, что площадь поверхности сферы = 4πr 2 . Другой способ следить за этим заключается в следующем. Из формулы объема мы можем вывести, что r 3 = 3V/4π или r = (3V/4π) 1/3 . После этого мы можем подставить значение r в формулу площади поверхности сферы.
Что такое Калькулятор площади поверхности сферы?
Калькулятор площади поверхности сферы — это онлайн-инструмент для детей, облегчающий их расчеты. Это созданный системой инструмент, в котором формула площади поверхности предустановлена, все, что нам нужно сделать, это ввести значение заданных параметров, таких как радиус, и мы получим площадь поверхности сферы. Попробуйте калькулятор площади поверхности сферы от Cuemath и получите ответы за несколько секунд.
Попробуйте калькулятор площади поверхности сферы от Cuemath и получите ответы за несколько секунд.
Как изменится площадь поверхности сферы при уменьшении радиуса вдвое?
Площадь поверхности сферы увеличивается на одну четвертую, когда радиус уменьшается вдвое, потому что r становится r/2. Так как площадь поверхности сферы = 4πr 2 , то, если мы заменим «r» на r/2, формула станет 4π(r/2) 2 = πr 2 , что составляет одну четвертую от площадь поверхности. Таким образом, площадь поверхности сферы становится одной четвертой, как только ее радиус уменьшается вдвое.
Как изменится площадь поверхности сферы при утроении радиуса?
Площадь поверхности сферы становится равной 36πr 2 , когда радиус увеличивается втрое, потому что ‘r’ становится 3r’. Мы знаем, что площадь поверхности сферы = 4πr 2 , поэтому, если мы заменим «r» на 3r, мы получим формулу: площадь поверхности = 4π(3r) 2 = 4π × 9r 2 = 36πr 2
Площадь поверхности сферы
Ворранат Пакорнрат,
Абхинит Гоэль,
Тадеуш Абий,
а также
92 } \, dt . A=2π∫aby(dtdy)2+(dtdx)2dt.
A=2π∫aby(dtdy)2+(dtdx)2dt.
Мы можем получить сферу, вращая полукруг вокруг оси xxx. Этот круг можно параметризовать как x(t)=rcos(t)x(t)=r\cos(t) x(t)=rcos(t) и y(t)=rsin(t)y(t ) = r\sin(t) y(t)=rsin(t) для 0≤t≤π0 \leq t \leq \pi 0≤t≤π. Отсюда получаем
dxdt=-rsin(t),dydt=rcos(t). \frac{dx}{dt} = -r\sin(t), \quad \frac{dy}{dt} = r\cos(t) .dtdx=−rsin(t),dtdy=rcos(t ).
Подстановка в наши уравнения площади поверхности дает 92. \_\квадрат \end{align} A=2π∫0πrsin(t)(−rsin(t))2+(rcos(t))2 dt=2π∫0πrsin(t)r2(sin(t)2 +cos(t)2) dt=2π∫0πr2sin(t) dt=2πr2∫0πsin(t) dt=4πr2. □
Теорема Архимеда о шляпной коробке
Теорема Архимеда о шляпной коробке утверждает, что для любого сечения сферы ее боковая поверхность будет равна поверхности цилиндра той же высоты, что и сечение, и того же радиуса сферы.
Напомним наш последний раздел доказательства.
После вращения полукруга вокруг оси xxx мы получим площадь поверхности сферы, и если мы вырежем только частичный участок с параллельными основаниями, новая площадь поверхности будет продемонстрирована на изображении ниже:
На изображении площадь боковой поверхности сечения окрашена в голубой цвет с двумя круглыми основаниями разного радиуса. Чтобы лучше визуализировать высоту секции, эта секция будет повернута на 90 градусов, как показано ниже:
Теперь внутри сечения есть 2 переменных угла, ∠a\угол a∠a и ∠b\угол b∠b, которые появляются как интегральные границы сечения сечения.
9яркий] \\ &= (2\pi r)r\big[\cos (a) — \cos (b)\big] . \end{align}A′=2πr2∫absin(t) dt=2πr2[−cos(t)∣ab]=(2πr)r[cos(a)−cos(b)].Рассматривая прямоугольные треугольники с радиусом rrr (жирный красный цвет) на изображении, очевидно, что rrr является стороной гипотенузы для обоих. В результате вертикальные стороны можно рассчитать как r×cos(a)r\times \cos (a)r×cos(a) и r×cos(b)r\times \cos (b)r× cos(b) для левого и правого треугольников соответственно.
Следовательно, высота сечения равна h=(r×cos(a))−(r×cos(b))=r[cos(a)−cos(b)]h = \big( r\times \cos (a)\big) — \big(r\times \cos (b)\big) = r\big[\cos (a) — \cos (b)\big]h=(r× cos(a))−(r×cos(b))=r[cos(a)−cos(b)].
Подстановка этого члена в предыдущее уравнение дает
A′=(2πr)r[cos(a)−cos(b)]=2πrh.A’ = (2\pi r)r\big[\cos (a) — \cos (b)\big ] = 2\pi правая сторона. A′=(2πr)r[cos(a)−cos(b)]=2πrh.
Ясно, что это формула боковой поверхности цилиндра с радиусом rrr и высотой hhh!
Это означает, что площадь боковой поверхности сечения сферы равна площади боковой поверхности цилиндра с радиусом rrr и высотой h,h,h, как показано на рисунке, и это верно для любого уровня вовлеченной сферы. □_\квадрат□
Ломтик помидора Ломтик огурца Каждый срез обоих видов имеет одинаковую площадь боковой поверхности. Неточно, в зависимости от уровня огранки
Сферический помидор и цилиндрическая часть огурца имеют одинаковую высоту и радиус.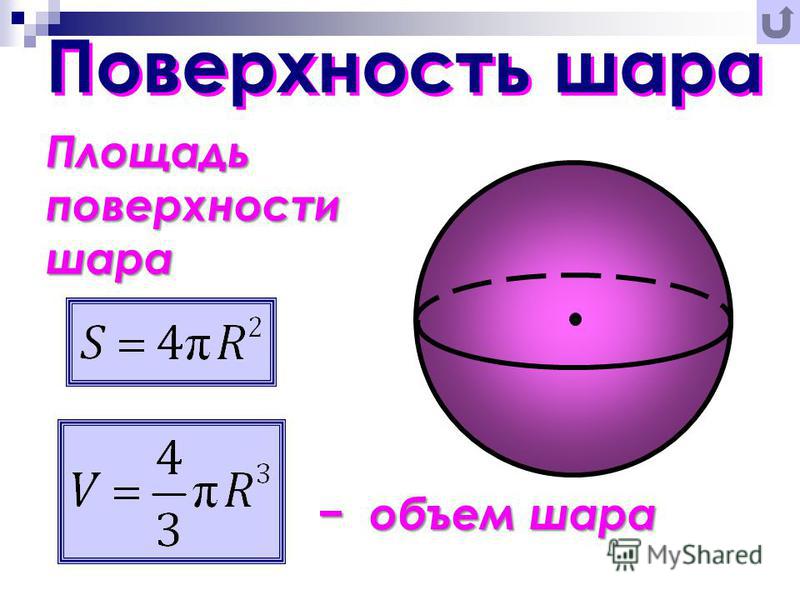 Затем их нарезают ломтиками одинаковой толщины, как показано выше.
Затем их нарезают ломтиками одинаковой толщины, как показано выше.
Сравнивая каждого ломтика обоих видов, какой из ломтиков будет иметь большую площадь боковой поверхности кожуры?
Дыня плюс тарелка Оба варианта имеют одинаковую площадь поверхности. Не хватает информации Синий купол
Маленький зеленый кружок вписан в часть большого синего круга, касаясь средней хорды, как показано вверху слева. Затем графики вращаются вокруг оси yyy, чтобы получить три фигуры: синий купол, зеленую сферическую дыню и красную сервировочную тарелку.
Какой из следующих вариантов будет иметь большую площадь поверхности?
I. Синий купол
II. Дыня плюс тарелка
Магазин сладостей продает конфеты 2-х разных форм: сферический шар и купол. Куполообразная форма представляет собой сферическое сечение большей сферы с высотой hhh и радиусом основания R,R,R, как показано выше, в то время как конфетный шар имеет радиус rrr с 2r=R+h3r = R + h3r=R+h .
Куполообразная форма представляет собой сферическое сечение большей сферы с высотой hhh и радиусом основания R,R,R, как показано выше, в то время как конфетный шар имеет радиус rrr с 2r=R+h3r = R + h3r=R+h .
Если обе формы имеют одинаковую общую площадь поверхности, каково отношение Rh\frac{R}{h}hR? 93 V=34πr3 для объема сферы радиусом r,r,r, вы знаете, что радиус арбуза равен r=6 см.r=6 \text{ см}.r=6 см. Поскольку вы разрезаете арбуз на две точные половинки, вы можете подумать, что площадь поверхности половины арбуза также равна половине площади поверхности всего арбуза. Однако это мышление ошибочно.
Как показано на диаграмме выше, площадь поверхности половинки арбуза больше половины площади поверхности целого арбуза на площадь поперечного сечения A.A.A. Таким образом, площадь поверхности половинки арбуза равна (половина площади поверхности арбуза) + (площадь A).\text{(половина площади поверхности арбуза)} + \text{(площадь A)}. 2 = 108 \pi. \ _\квадрат21×4π×62+π×62=108π. □
9{\frac{1}{3}}231
2 = 108 \pi. \ _\квадрат21×4π×62+π×62=108π. □
9{\frac{1}{3}}231
Диаметр сплошного металлического прямоугольного цилиндра равен его высоте. После вырезания из этого цилиндра максимально возможной твердой сферы SSS оставшийся материал переделывается, чтобы сформировать твердую сферу Q.Q.Q.
Каково отношение радиуса сферы SSS к радиусу сферы Q?Q?Q?
Процитировать как: Площадь поверхности сферы. Brilliant.org . Извлекаются из https://brilliant.org/wiki/площадь-поверхность-сфера/
Площадь поверхности сферы
Площадь поверхности сферы — это площадь, занимаемая изогнутой поверхностью этой сферы. В геометрии сфера — это трехмерная твердая фигура круглой формы, каждая точка на ее поверхности равноудалена от ее центра. Например, глобус, мяч и так далее. Расстояние между любой точкой на поверхности сферы и ее центром называется «радиусом сферы». Сфера — это трехмерная фигура, определенная в трех измерениях, т.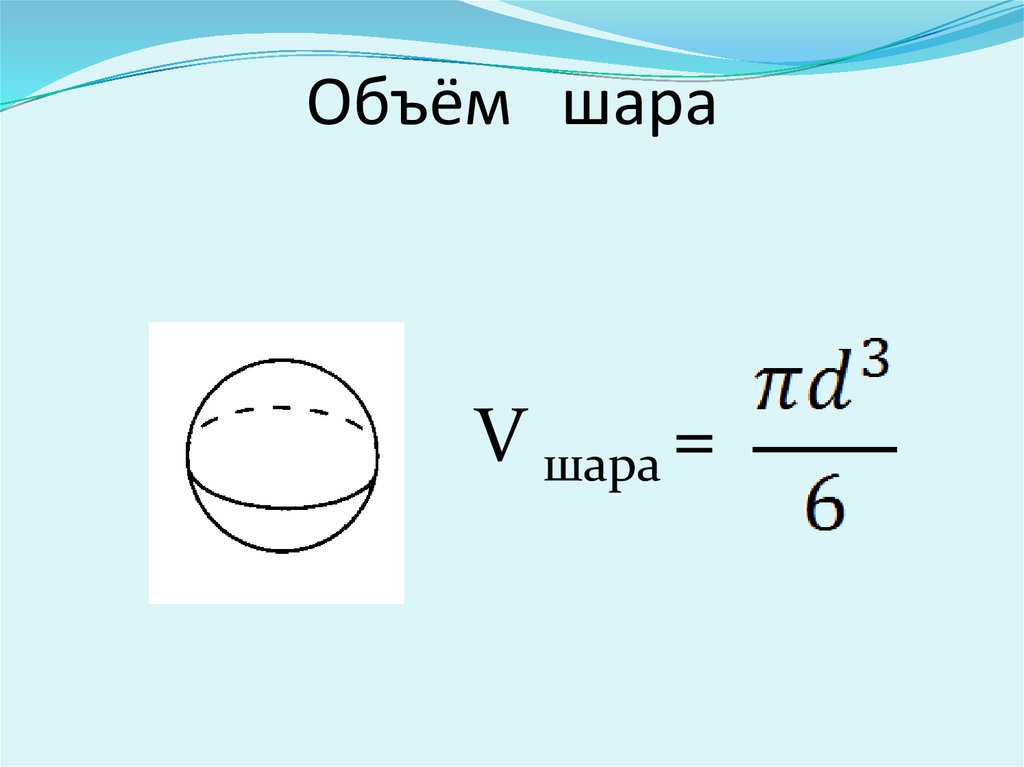 е. по оси x, оси y и оси z, тогда как круг — это двумерная форма, определенная на плоскости.
е. по оси x, оси y и оси z, тогда как круг — это двумерная форма, определенная на плоскости.
Какова площадь поверхности сферы?
Площадь поверхности сферы — это область, покрытая внешней поверхностью в трехмерном пространстве. Можно сказать, что сфера — это трехмерная форма круга. Формула площади поверхности сферы выражается в пи (π) и радиусе.
Площадь поверхности сферы = 4πr 2 квадратных единиц
Где r = радиус сферы.
Площадь поверхности сферы Формула
Площадь поверхности сферы рассчитывается с использованием радиуса сферы. Если площадь поверхности сферы равна S, а радиус равен r, то формула площади поверхности сферы будет следующей:
Площадь поверхности сферы = 4πr 2
вместо радиуса дан диаметр сферы, формула примет вид:
Площадь поверхности сферы = πd 2
Вычисление площади поверхности сферы
Площадь, занимаемая поверхностью сферы в космосе, является площадью поверхности сферы. Мы знаем, что сфера имеет круглую форму, поэтому, чтобы вычислить площадь ее поверхности, мы можем соединить ее с изогнутой формой, например с цилиндром. Цилиндр — это трехмерная фигура, имеющая криволинейную поверхность с двумя плоскими поверхностями по бокам. Считаем, что радиус сферы и радиус цилиндра одинаковы. Таким образом, сфера может идеально вписаться в цилиндр. Следовательно, высота шара равна высоте цилиндра, т. е. диаметру шара. Этот факт доказал математик Архимед, что площадь поверхности шара радиуса «r» равна площади боковой поверхности цилиндра радиуса «r». Следовательно,
Мы знаем, что сфера имеет круглую форму, поэтому, чтобы вычислить площадь ее поверхности, мы можем соединить ее с изогнутой формой, например с цилиндром. Цилиндр — это трехмерная фигура, имеющая криволинейную поверхность с двумя плоскими поверхностями по бокам. Считаем, что радиус сферы и радиус цилиндра одинаковы. Таким образом, сфера может идеально вписаться в цилиндр. Следовательно, высота шара равна высоте цилиндра, т. е. диаметру шара. Этот факт доказал математик Архимед, что площадь поверхности шара радиуса «r» равна площади боковой поверхности цилиндра радиуса «r». Следовательно,
Площадь поверхности сферы = Площадь боковой поверхности цилиндра
Мы знаем, что,
Площадь боковой поверхности цилиндра = 2πrh,
Где r – радиус цилиндра, а h – его высота.
Мы предположили, что сфера идеально помещается в цилиндр. Значит, высота цилиндра равна диаметру шара.
Высота цилиндра (h) = диаметр сферы (d) = 2r (где r — радиус)
Следовательно,
Площадь поверхности сферы = Площадь боковой поверхности цилиндра = 2πrh
Площадь поверхности сферы = 2πr × (2r) = 4πr 2
Следовательно,
Площадь поверхности сферы = 4πr 2 квадратных единиц
Где r = радиус сферы
Как найти площадь поверхности сферы
Площадь поверхности сферы — это просто площадь, занимаемая ее поверхностью. Давайте рассмотрим пример, чтобы увидеть, как определить площадь поверхности сферы, используя ее формулу.
Давайте рассмотрим пример, чтобы увидеть, как определить площадь поверхности сферы, используя ее формулу.
Пример: Найдите площадь поверхности сферы радиусом 7 см.
Шаг 1: Обратите внимание на радиус данной сферы. Здесь радиус сферы равен 47 см.
Шаг 2: Мы знаем, что площадь поверхности сферы = 4πr 2 . Итак, подставляем значение заданного радиуса в уравнение = 4 × (3,14) × (7) 2 = 616 см 2 .
Шаг 3: Следовательно, площадь поверхности сферы равна 616 квадратных см.
Площадь изогнутой поверхности сферы
Сфера имеет только одну изогнутую поверхность. Следовательно, площадь криволинейной поверхности сферы равна общей площади поверхности сферы, которая равна площади поверхности сферы в целом. Таким образом, можно с уверенностью сказать, что площадь криволинейной поверхности сферы = 4πr0114
Решенные примеры площади поверхности сферы
Пример 1: Вычислите общую площадь поверхности сферы радиусом 15 см. (Возьмем π = 3,14)
(Возьмем π = 3,14)
Решение:
Учитывая, что радиус сферы = 15 см
Мы знаем, что общая площадь поверхности сферы = 4 π r 2 квадратных единиц
5 = 9 4 × (3,14) × (15)
2= 2826 см 2
Следовательно, общая площадь поверхности шара равна 2826 см 2 .
Пример 2. Рассчитайте диаметр сферы, площадь поверхности которой составляет 616 квадратных дюймов. (Возьмем π = 22/7)
Решение:
Учитывая, площадь криволинейной поверхности сферы = 616 кв. в
Мы знаем,
Общая площадь поверхности сферы = 4 π r 2 квадратные единицы
⇒ 4 π R 2 = 616
⇒ 4 × (22/7) × R 2 = 616
⇒ R 2 = (616 × 7)/(4 × R 2 = (616 × 7)/(4 × 22) = 49
⇒ r = √49 = 7 in
Мы знаем, что диаметр = 2 × радиус = 2 × 7 = 14 дюймов
Следовательно, диаметр сферы равен 14 дюймам.
Пример 3: Найдите стоимость, необходимую для покраски шара в форме сферы с радиусом 10 см. Стоимость покраски шара 4 ₨ за квадратный сантиметр. (Возьмем π = 3,14)
Решение:
Учитывая, что радиус шара = 10 см
Мы знаем, что,
Площадь поверхности сферы = 4 π r 2 квадратных единиц
= 4 × (3,14) × (10) 2
= 1256 квадратных см
Таким образом, общая стоимость покраски шара = 4 × 1256 = ₨ 5024/-
5
5 Пример 4: Найдите площадь поверхности шара диаметром 21 см. (Возьмем π = 22/7)
Решение:
Учитывая, что диаметр сферы равен 21 см
Мы знаем, что
диаметр = 2 × r радиус
⇒ 2 × 2 = 10,5 смТеперь площадь поверхности сферы = 4 π r 2 квадратных единиц
= 4 × (22/7) × (10,5)
= 1386 кв. см
Следовательно, общая площадь поверхности сферы = 1386 кв.
см
Пример 5. Найдите отношение площадей поверхностей двух сфер, радиусы которых относятся как 4:3. (Возьмем π = 22/7)
Решение:
Учитывая, что отношение между радиусами двух сфер = 4:3
Мы знаем, что
Площадь поверхности сферы = 4 π r 2
Из уравнения можно сказать, что площадь поверхности сферы прямо пропорциональна квадрату ее радиуса.
Area ∝ (radius) 2
⇒ A 1 /A 2 = (r 1 ) 2 /(r 2 ) 2
⇒ A 1 / A 2 = (4) 2 / (3) 2 = 16/9
Следовательно, отношение между полными площадями данных двух сфер составляет 16:9..
Пример 6: Найдите отношение радиусов двух сфер, когда их площади относятся как 25:121. (Возьмем π = 22/7)
Решение:
Учитывая, что отношение между полными площадями поверхностей двух сфер = 25:121
Мы знаем, что,
Общая площадь поверхности сферы = 4 π r 2
Из уравнения можно сказать, что площадь поверхности сферы прямо пропорциональна квадрату ее радиуса.
Area ∝ (radius) 2 ⇒ radius ∝ √Area
⇒ r 1 /r 2 = √A 1 /√A 2
⇒ r 1 /r 2 = √25/√121 = 5/11
Следовательно, отношение радиусов данных двух сфер равно 5:11.
Часто задаваемые вопросы о площади поверхности сферы
Вопрос 1: Как найти площадь поверхности сферы?
Ответ:
Площадь поверхности сферы находится по формуле
Площадь поверхности = 4πr 2
Где r — радиус сферы.
Вопрос 2: Какова площадь поверхности полушария?
Ответ:
Площадь поверхности полушария равна сумме половины площади поверхности сферы и площади основания, то есть
S.A. = 2πr 2 + πr 2
Площадь поверхности полушария = 3πr 2
Вопрос 3: Какова площадь боковой поверхности шара?
Ответ:
Площадь боковой поверхности равна площади поверхности сферы, которая равна площади криволинейной поверхности сферы.
Площадь поверхности сферы: формула, расчет, единицы
- Написано Мадхуримой Дасом
- Последнее изменение 19-07-2022
- Автор Мадхурима дас
- Последнее изменение 19-07-2022
Сумма площадей, занимаемых поверхностью объекта, является площадью поверхности. Трехмерная форма обычно представляет собой твердое тело с глубиной и высотой. Сфера, с другой стороны, представляет собой трехмерную форму, в которой каждая точка на ее поверхности находится на равном расстоянии от центра. Метод интегрирования можно использовать для вычисления площади поверхности сферы. Площадь поверхности сферы равна четырехкратному произведению \(\pi \left( {pi} \right)\) на квадрат радиуса. Размер сферы, то есть радиус сферы, определяет 9{\text{2}}}\) и т. д.
Математика — сложный предмет. Для учащихся важно усвоить эти основные понятия математики. Они могут освоить предмет с регулярной практикой. В этой статье давайте подробно разберемся во всем, что касается площади поверхности сферы.
Давайте разберем сферу на примере. Рассмотрим баскетбол. Какой формы баскетбольный мяч? Это круг? Нет. Мы не можем сказать, что баскетбольный мяч имеет форму круга.
Но в баскетболе есть соединение круга. Как? Попробуйте вращать круг вдоль любого из его диаметров. Вы видите, что выходит?
Изучение концепций экзамена на Embibe
Разве он не похож по форме на баскетбольный мяч? Да, это так. Баскетбольный мяч — это трехмерная фигура, полученная при вращении круга по любому из его диаметров. Баскетбольный мяч имеет форму сферы.
Что такое определение сферы?
Круг — это двумерная фигура, которую можно легко нарисовать на листе бумаги.
С другой стороны, сфера — это трехмерная форма, подобная форме футбольного или баскетбольного мяча. Три оси координат, ось x, ось y и ось z используются для определения формы сферы. Как и круг, сфера также имеет центральную точку. Каждая точка на поверхности сферы равноудалена от ее центра. Это фиксированное расстояние от центра до любой точки на окружности сферы называется радиусом сферы. Размер сферы определяется радиусом сферы.
Каковы свойства сферы?
- Сфера — симметричная трехмерная фигура.
- Все точки на поверхности сферы равноудалены от начала координат или центра.
- Не имеет вершин и ребер.
- Имеет только одну изогнутую поверхность.
Каковы примеры сферы?
Мы можем видеть множество сферических объектов вокруг себя. В эту категорию попадают футбольные, баскетбольные и другие спортивные мячи.
Какие есть типы сфер?
Есть два типа сфер.
- Сплошная сфера
- Полая сфера
Сплошная сфера:
Твердая сфера — это трехмерный объект, имеющий форму сферы и заполненный материалом, из которого он состоит.
Например, шарики представляют собой твердые сферы.
Полая сфера:
Полая сфера — это сфера, имеющая только внешнюю сферическую границу и ничем не заполненная внутри.
Для простоты понимания рассмотрим шарик мороженого.
Что такое площадь поверхности?
Объем космического пространства, покрывающего трехмерную форму, известен как площадь поверхности. Площади любой трехмерной геометрической фигуры можно разделить на три типа. Это:
- Площадь изогнутой поверхности
- Площадь боковой поверхности
- Общая площадь поверхности
Площадь изогнутой поверхности
Площадь криволинейной поверхности — это площадь всех криволинейных областей твердого тела.
Площадь боковой поверхности
Площадь боковой поверхности – это площадь всех граней, кроме верхней и нижней граней или оснований.
Общая площадь поверхности
Общая площадь поверхности — это площадь всех граней (включая верхнюю и нижнюю грани) твердотельного объекта.
Что вы понимаете под площадью поверхности сферы?
Сфера — трехмерная геометрическая фигура идеально круглой формы. Вокруг нас так много сферических объектов. Архимед вывел формулу площади поверхности более двух тысяч лет назад. Площадь поверхности сферы описывается как количество квадратных единиц, необходимых для покрытия поверхности сферы.
Площадь поверхности сферы — это площадь ее криволинейной поверхности, поскольку нет разницы между площадью криволинейной поверхности и общей площадью поверхности сферы.
Значение \(\pi \)
Постоянный член \(\pi \) (pi) используется в формуле площади круга. \(\pi \) — постоянный член, также известный как постоянная Архимеда. Один из способов определить π состоит в том, что это отношение длины окружности к ее диаметру. Это иррациональное число, значение которого равно \(3,141592}\)
где \(d\) — диаметр сферы.Что такое полушарие?
Возьмите сферический лимон и разрежьте его на две половинки.
Два кусочка лимона, которые у нас есть сейчас, представляют собой не что иное, как два полушария. Полушарие – это точная половина шара. По сути, два одинаковых полушария составляют сферу. Точно так же мы можем взять пример с половинкой арбуза.
Какова формула площади поверхности полушария?
Полусфера — это трехмерная фигура, равная половине сферы. Площадь поверхности полушария можно разделить на два типа. 92}\)
Если сравнить две сферы разного размера, то сфера большего радиуса будет иметь большую площадь поверхности.Здесь розовая сфера имеет радиус \(1\,{\text{м}}\), а синяя сфера имеет радиус \(2\,{\text{м}}{\текст {.}}\) Так как синяя сфера имеет больший радиус, площадь поверхности синей сферы будет больше, чем у розовой сферы.
Каковы единицы площади поверхности сферы?
Единицей радиуса сферы могут быть любые единицы длины, такие как \({\text{мм}},\,{\text{см}},\,{\text{м}},\) и т. д. Поскольку в формуле площади поверхности сферы радиус возводится в квадрат, единица измерения также должна быть возведена в квадрат.
2}\) 92}\)
Мы можем найти радиус сферы из площади поверхности сферы как \(r = \sqrt {\frac{A}{{4\pi}}} \)
Итак, радиус данная сфера \ (r = \ sqrt {\ frac {{201}} {{4 \ times 3,14}}} \, {\ rm {m}} \) \ (= \ sqrt {16,003 \,} \, {\ text{m}}\)
\(\примерно 4\,{\text{m}}\)В . 4 . Какова общая площадь поверхности твердого полусферического объекта радиусом \(2\,{\text{см}}\) , учитывая \(\pi = \frac{{22}}{7}.\) 92}\).
Это также можно получить с помощью интегрального исчисления.Q.3. Что такое CSA и TSA сферы?
Ответ: Площадь криволинейной поверхности (CSA) и общая площадь поверхности (TSA) одинаковы для сферы, поскольку сфера не имеет плоской поверхности.Q.4. Чему равен объем и площадь поверхности шара?
Ответ: Объем сферы – это количество пространства, которое она содержит.3}\) 92}\), где \(r\) — радиус.
Учеба в Эмбибе
Embibe предоставляет платформу для бесплатной отработки вопросов K-12. Максимально используйте эти учебные материалы и освойте предмет. Найдите ниже практические вопросы по математике для 8, 9, 10, 11 и 12 классов. Ссылки приведены ниже:
Из этой статьи мы узнали о формуле сферы и полушария, чтобы найти площадь поверхности, а также их примеры. Мы надеемся, что эта подробная статья о Поверхности Сферы окажется вам полезной. Если у вас есть какие-либо вопросы, пожалуйста, свяжитесь с нами через поле для комментариев ниже, и мы свяжемся с вами как можно скорее. 9Формула 24πR2. Я имею в виду внутреннее ощущение связи между площадью поверхности сферы и этими четырьмя кругами.
Но почему?!?
Как было бы прекрасно, если бы произошло какое-то изменение перспективы, показывающее, как вы можете красиво и идеально разместить эти четыре круга на поверхности сферы?
Ничто не может быть настолько простым, поскольку кривизна поверхности сферы отличается от кривизны плоской плоскости, поэтому попытки обмотать сферу бумагой на самом деле не работают.
Удачи.
Тем не менее, я хотел бы показать вам два способа представления площади поверхности сферы, которые удовлетворительным образом связывают ее с четырьмя окружностями одинакового радиуса.
Первый — классический. Это одна из настоящих жемчужин геометрии, которую должны испытать все студенты.
Вторая линия рассуждений принадлежит мне и проводит более прямую линию между сферой и ее тенью.
И, наконец, я расскажу, почему это четырехчастное отношение не уникально для сфер, а вместо этого является частным случаем гораздо более общего факта для всех выпуклых форм в 3D.
Первый подход
Начиная с высоты птичьего полета, идея первого подхода состоит в том, чтобы показать, что площадь поверхности сферы такая же, как площадь цилиндра с таким же радиусом и той же высотой, что и у сферы. .
Или, скорее, цилиндр без верха и низа, который можно назвать «этикеткой» этого цилиндра.
Мы можем развернуть этикетку, чтобы увидеть, что это на самом деле простой прямоугольник.
24πR2.
Но в духе математической игривости приятно посмотреть, как в это вписываются четыре круга с радиусом RRR. Идея состоит в том, что вы можете развернуть каждый круг в треугольник, не изменяя его площадь, и красиво разместить их на нашей развернутой этикетке цилиндра. Подробнее об этом чуть позже.
Более насущный вопрос, почему сфера может быть связана с цилиндром. Эта анимация уже дает представление о том, как она работает:
Идея состоит в том, чтобы аппроксимировать площадь сферы множеством крошечных прямоугольников, покрывающих ее. Мы покажем, что если вы спроецируете эти маленькие прямоугольники прямо наружу, как если бы отбрасывали тень от маленьких источников света, расположенных на оси Z, проекция каждого прямоугольника на цилиндр в конечном итоге будет иметь ту же площадь, что и исходный прямоугольник.
Площадь каждого маленького прямоугольника на сфере равна площади его проекции на цилиндр.
Но с чего бы это? Что ж, здесь действуют два конкурирующих эффекта.
С одной стороны, поскольку этот прямоугольник проецируется наружу, его ширина будет увеличиваться.
Проецируемый прямоугольник шире исходного.
Для прямоугольников, направленных к полюсам, эта ширина немного масштабируется, поскольку они проецируются на большее расстояние. Для тех, кто ближе к экватору, меньше.
Разница в ширине больше на полюсах.
Но, с другой стороны, поскольку эти прямоугольники наклонены по отношению к направлению z, во время этой проекции высота каждого такого прямоугольника будет уменьшена. Представьте себе, что вы держите какой-нибудь плоский предмет и смотрите на его тень. Когда вы меняете ориентацию этого объекта, тень выглядит более или менее сплющенной под некоторыми углами.
Эти прямоугольники, обращенные к полюсам, сильно наклонены таким образом, поэтому их высота сильно сжимается. Для тех, кто ближе к экватору, меньше.
Разница в высоте также более велика на полюсах.
Выяснится, что эти два эффекта — растяжение по ширине и сжатие по высоте — прекрасно компенсируют друг друга.
В качестве грубого наброска, не могли бы вы согласиться, что это очень красивый способ рассуждения? Конечно, суть здесь в том, чтобы показать, почему эти два конкурирующих эффекта на каждом прямоугольнике идеально компенсируются. В некотором смысле детали, раскрывающие это, так же красивы, как и уменьшенная структура полного аргумента.
Растягивание по ширине
При решении любых математических задач никогда не помешает начать с присвоения имен вещам. Допустим, радиус сферы равен RRR. Кроме того, сосредоточившись на одном конкретном прямоугольнике, давайте назовем расстояние между нашим прямоугольником и осью Z ddd.
Это поперечное сечение сферы показывает, как мы маркируем вещи.
Вы можете с полным правом пожаловаться на то, что это расстояние ddd немного неоднозначно в зависимости от того, с какой точки прямоугольника вы начинаете, но для все более и более мелких прямоугольников эта неоднозначность будет незначительной. И мельче и мельче — это как раз то время, когда это приближение с помощью прямоугольников в любом случае приближается к истинной площади поверхности.
Чтобы выбрать произвольный стандарт, скажем, ddd — это расстояние от нижней части прямоугольника до оси Z.
Чтобы подумать о проецировании на цилиндр, представьте себе два подобных треугольника.
Первый делит основание с прямоугольником на сфере. Второй — это увеличенная версия этого, увеличенная так, что он едва достигает цилиндра, что означает, что его длинная сторона теперь имеет длину RRR. Таким образом, отношение их оснований, то есть насколько расширяется ширина нашего прямоугольника, равно Rd\frac{R}{d}dR.
Сплющивание высоты
Что насчет высоты? Как именно это уменьшается по мере того, как мы проектируем?
Чтобы понять это, давайте начнем с того, что сосредоточим внимание на этом двухмерном поперечном сечении:
Затем, чтобы подумать о проекции, давайте увеличим масштаб и создадим маленький прямоугольный треугольник, как показано ниже:
Наш прямоугольный треугольник гипотенуза вдоль исходного прямоугольника и один из его катетов вдоль проекции этого прямоугольника на цилиндр.
Совет от профессионала: Каждый раз, когда вы занимаетесь геометрией с кругами или сферами, помните о том, что все, что касается окружности, перпендикулярно радиусу, проведенному к этой точке касания. Удивительно, насколько полезным может быть один маленький факт.
Как только мы нарисуем эту радиальную линию вместе с расстоянием ddd, у нас получится еще один прямоугольный треугольник.
Часто в геометрии мне нравится представлять себе настройку параметров установки и представлять, как меняются соответствующие формы; это помогает делать предположения о том, какие существуют отношения.
В этом случае можно предположить, что два нарисованных мною треугольника подобны друг другу, поскольку их формы меняются согласованно друг с другом.
Это действительно так, но, как всегда, не верьте мне на слово, посмотрите, сможете ли вы обосновать это для себя.
Подобные треугольники
Опять же, никогда не помешает дать вещам больше имен.
Назовем эти углы α\alphaα и β\betaβ:
Поскольку это прямоугольный треугольник, вы знаете, что α+β+90°=180°\alpha + \beta + 90\градус = 180\градусα+β+90°=180°. Теперь увеличим масштаб нашего маленького треугольника и посмотрим, сможем ли мы вычислить его углы:
У вас есть 90°+β+(какой-то угол)90\градус + \beta + \text{(какой-то угол)}90°+β +(некоторый угол), образующий прямую. Так что этот маленький угол должен быть α\alphaα. Это позволяет нам заполнить еще несколько значений, показывая, что этот маленький треугольник имеет те же углы α\alphaα и β\betaβ, что и большой.
Так что они действительно похожи.
Глубоко в сорняках иногда легко забыть, зачем мы это делаем. Мы хотим знать, насколько высота нашего прямоугольника-сферы сжимается во время проекции, что является отношением гипотенузы к катету справа. По сходству с большим треугольником это отношение равно Rd\frac{R}{d}dR.
Действительно, когда этот прямоугольник проецируется наружу на цилиндр, эффект увеличения ширины полностью компенсируется тем, насколько высота сжимается из-за наклона.
Теперь, если вы действительно мыслите критически, вы, возможно, все еще не удовлетворены тем, что это показывает, что площадь поверхности сферы равна площади этой метки цилиндра. В конце концов, эти маленькие прямоугольники всего лишь 90 452 аппроксимируют 90 453 соответствующих площадей.
Идея состоит в том, что это приближение становится все ближе и ближе к истинному значению для все более и более тонких покрытий. Поскольку для любого конкретного покрытия прямоугольники сферы имеют ту же площадь, что и прямоугольники цилиндра, любые значения, к которым приближается каждая из этих двух серий приближений, должны быть фактически одинаковыми.
По мере того, как вы углубляетесь в философию и спрашиваете, что именно мы подразумеваем под площадью поверхности, эти виды прямоугольных аппроксимаций не просто помогают в нашем наборе инструментов для решения задач, они в конечном итоге служат способом строгого определения площади гладких криволинейных поверхностей. хотя часто требуется некоторый уход.
Этот вид рассуждений по сути является исчислением, просто изложенным без жаргона. На самом деле, я думаю, что подобные аккуратные геометрические рассуждения, для понимания которых не требуется никаких знаний в области математического анализа, могут послужить отличным способом подвести итоги для новых студентов, изучающих математику, чтобы у них были основные идеи, прежде чем они увидят определения, которые делают их точными ( а не наоборот).
Эти геометрические рассуждения являются отличной подготовкой к пониманию исчисления.
Соединение с кругами
Если вам не терпится увидеть прямое соединение с четырьмя кругами, есть хороший способ развернуть эти круги в треугольники. Если это то, чего вы раньше не видели, я более подробно расскажу о том, почему это работает, в первом уроке серии исчислений.
Основная идея состоит в том, чтобы связать тонкие концентрические кольца круга с горизонтальными срезами этого треугольника.
Каждый круг разворачивается таким образом, что тонкое кольцо круга соответствует тонкой линии треугольника.
Поскольку окружность каждого такого кольца увеличивается линейно пропорционально радиусу, всегда равному 2πr2\pi r2πr, когда вы развернете их все и выровняете, их концы образуют прямую линию (в отличие от какой-то криволинейной линии). форма), что дает вам треугольник с основанием 2πr2\pi r2πr и высотой rrr.
И четыре из этих развернутых кругов вписываются в наш прямоугольник, который в некотором смысле является развернутой версией поверхности сферы.
Второй подход
Тем не менее, вы можете задаться вопросом, есть ли способ напрямую связать сферу с окружностью того же радиуса, вместо того, чтобы проходить через посредника в виде цилиндра.
Если вы готовы засучить рукава и использовать немного тригонометрии, на самом деле можно провести эту более прямую связь.
Я глубоко убежден, что лучший способ по-настоящему выучить математику — это решать задачи самостоятельно, что немного лицемерно исходить из канала, состоящего в основном из лекций.
Итак, давайте попробуем здесь что-то немного другое и представим доказательство в виде строго управляемой последовательности упражнений. Да, я знаю, что это менее весело, и это означает, что вам придется вытащить бумагу, чтобы выполнить какую-то работу, но я гарантирую, что таким образом вы получите больше пользы.
Обзор решения
На высоком уровне подход будет состоять в том, чтобы разрезать сферу на множество тонких колец, параллельных плоскости xy.
Сравним площадь этих колец с площадью их теней на плоскости xy.
Тени всех колец в верхней полусфере образуют идеальный круг.
Все тени колец от верхней полусферы составляют круг того же радиуса, что и сфера. Основная идея будет заключаться в том, чтобы показать соответствие между этими кольцевыми тенями и каждым вторым кольцом на сфере.
Здесь мы смотрим на каждое второе кольцо сферы. Вашей целью будет найти соответствие между показанными здесь чередующимися кольцами и тенями колец верхнего полушария, показанными выше.
Режим испытаний здесь заключается в том, чтобы перестать читать сейчас и попытаться предсказать, как это может произойти.
Мы обозначим каждое из этих колец на основе угла θ\thetaθ между осью z и линией, идущей к кольцу из центра сферы.
Каждое кольцо будет идентифицировано соответствующим ему углом θ\thetaθ.
Итак, θ\thetaθ находится в диапазоне от 0 до 180 градусов, или от 000 до π\piπ радиан. А изменение угла от одного кольца к следующему назовем dθd \thetadθ, значит, толщина одного из этих колец будет RdθR \mathop{d\theta}Rdθ, где RRR — радиус сферы.
Хорошо, структурированное время тренировки. Мы облегчимся с разминкой.
Вопрос 1
Какова длина окружности внутреннего края этого кольца с точки зрения RRR и θ\thetaθ?
Окружность кольца зависит от его радиуса. Радиус кольца — это расстояние от оси Z до самого кольца, которое я буду называть строчными буквами rrr. (Обратите внимание, что нам , а не , говоря о радиусе сферы, которую мы называем заглавной RRR.
)
rrr можно найти с помощью некоторой тригонометрии, основанной на прямоугольном треугольнике:
Мы знаем, что sin(θ)=rR\sin( \theta) = \frac{r}{R}sin(θ)=Rr, , что означает, что r=Rsin(θ)r = R\sin(\theta)r=Rsin(θ).
Теперь, когда у нас есть радиус кольца, найти его длину окружности — просто умножить на 2π2\pi2π.
Длина окружности равна 2πRsin(θ)2\pi R\sin(\theta)2πRsin(θ). 92 \sin(\theta) \mathop{d\theta}2πR2sin(θ)dθ для кольца под углом θ\thetaθ.
Вопрос 2
Какова площадь тени одного из этих колец на плоскости xy? Выразите свой ответ в терминах RRR, θ\thetaθ и dθ\mathop{d \theta}dθ.
(Подсказка: вспомните похожие прямоугольные треугольники, использованные в доказательстве проекции на цилиндр.)
Вспомните исходное доказательство проекции на цилиндр. Помните, как высота прямоугольника уменьшалась, когда он проецировался на цилиндр, а степень сжатия зависела от того, насколько был наклонен прямоугольник?
Здесь очень похожая история.
Когда кольцо проецируется вниз на плоскость xy, его толщина будет уменьшаться, и это сжатие будет зависеть от угла θ\thetaθ. Мы создадим два одинаковых прямоугольных треугольника, которые должны показаться вам знакомыми:
Фактор сжатия, который мы пытаемся найти, — это отношение толщины тени к толщине кольца. С точки зрения угла θ\thetaθ в нашем маленьком треугольнике, это ShadowRing=adjacenthypotenuse\frac{\text{Shadow}}{\text{Ring}} = \frac{\text{adjacent}}{\text{гипотенуза} }RingShadow=hypotenuseadjacent, или cos(θ)\cos(\theta)cos(θ). 92 \sin(\theta)\cos(\theta) \mathop{d\theta}4πR2sin(θ)cos(θ)dθ?
Первоначальный обзор проблемы дает подсказку, которая помогает устранить некоторые догадки, которые в противном случае могли бы быть связаны с попыткой найти подходящее кольцо:
«Основная идея будет заключаться в том, чтобы показать соответствие между этими тенями колец верхнее полушарие] и каждое второе кольцо на сфере».
Таким образом, разумным соответствием могло бы быть соединение каждого кольца в точке θ\thetaθ с кольцом в точке 2θ2\theta2θ.
Это позволяет нам покрыть чередующиеся кольца по всей сфере, как было сказано выше. 92 \sin(\theta)\cos(\theta) \mathop{d\theta}4πR2sin(θ)cos(θ)dθ, что действительно вдвое превышает площадь тени кольца θ\thetaθ.
Следовательно, соответствие между тенью кольца θ\thetaθ и кольцом 2θ2\theta2θ обладает именно тем свойством, которое мы ищем.
Вопрос 4
Я с самого начала сказал, что существует соответствие между всеми тенями северного полушария, образующими круг радиуса RRR, и любым другим кольцом на сфере. Используйте свой ответ на последний вопрос, чтобы точно объяснить, что это за соответствие.
Каждая тень соответствует одному из чередующихся колец сферы. Особое свойство этого соответствия, изложенное в вопросе 3, состоит в том, что соответствующее кольцо имеет площадь, вдвое превышающую площадь тени.
Это означает, что чередующиеся кольца имеют общую площадь, в два раза превышающую общую площадь теней.
Вопрос 5
Принеси домой.
Почему это означает, что площадь круга составляет ровно ¼ площади поверхности сферы, особенно когда мы рассматриваем все более и более тонкие кольца? 924πR2.
Более общая формула тени
И, наконец, было бы упущением не упомянуть вкратце тот факт, что площадь поверхности сферы является частным случаем гораздо более общего факта: если взять любую выпуклую форму , и посмотрите на среднюю площадь всех его теней, усредненную по всем возможным ориентациям в трехмерном пространстве, площадь поверхности твердого тела будет точно в 4 раза больше средней площади тени.
Почему это так? Я оставлю эти подробности на другой день.
Заметили ошибку? Отправьте исправление на Github
Особая благодарность тем, кто ниже, за поддержку оригинального видео, стоящего за этим постом, и текущим покровителям за финансирование текущих проектов. Если вы найдете эти уроки ценными, рассмотрите возможность присоединиться.
1stViewMathsAdam MielsAdrian RobinsonAlan SteinAlex DodgeAlex FriederAlexis OlsonAli YahyaAlvaro Begue-AguadoAlvin KhaledAnalysis HeroAndreas NautschAndrew BuseyAndrew FosterAndy PetschAnkalagonAnthony VdovitchenkoAntonio JuarezArt IanuzziArthur ZeyAwooBen GrangerBernd SingBob SandersonBoris VeselinovichBrad WeiersBrian SlettenBrian Staroselskybrian tiger chowBrice GowerBritt SelvitelleBritton FinleyBrooks RybaBurt HumburgChandra SripadaCharles SoutherlandChris ConnettChristian CooperChristian KaiserChristian MercatChristopher LortonClark GaebelClaudio CorbettaConvenienceShoutCooper JonesDan DavisonDanger DaiDave BDave Kesterdave nicponskiDavid ClarkDavid GowDavid HouseDavid J WuDelton DingDerek G MillerDevarsh DesaiDevin ScottDheeraj NarasimhaeaglleElliot WinklerEric KoslowEric YoungeEryq OuithaqueueEurghSireAweEvan MiyazonoEvan PhillipsFederico LebronFlorian ChudigiewitschFlorian RagwitzGiovanni FilippiGokcen EraslanGordon GouldGrahamGregory HopperGuy CobbGünther Köckera ndlHal HildebrandHamid Reza ZaheriHenry ReichIaroslav TymchenkoIsaac ShamieJJacob MagnusonJacob WallingfordJaewon JungJake Vartuli — SchonbergJameel SyedJames GolabJames HughesJan PijpersJason HiseJayne GabrieleJeff LinseJeff StraathofJerry LingJohn C.
VeseyJohn GriffithJohn HaleyJohn ShaughnessyJohn V WertheimJonathan EppeleJonathan WilsonJono ForbesJordan ScalesJoseph John CoxJoseph KellyJoshua TobkinJuan BenetJulian PulgarinKai-Siang AngKanan GillKaustuv DeBiswasKeith SmithKenneth LarsenKevin NorrisKevin OrrKrishanu SankarKristoff KieferKyle BegovichKyle HooksL0j1kLee Burnettelevav ferber tasLinh TranLockLuc RitchieLudwig SchubertLukas -krtek.net- NovyLukas BiewaldMagister MugitMagnus DahlströmMagnus LysfjordmakkostyaManne MoquistManuel GarciaMarcus KöhlerMark B BahuMark JobesMarkus PerssonMartin Sergio H. FaesterMathew BramsonMathias JanssonMatt LangfordMatt ParlmerMatt RovetoMatt RussellMatthew CockeMaurício CollaresMayank M. MehrotraMert ÖzMichael FaustMichael HardelMichael Kohle rMikael NordvallMike DourMike DussaultMikkoMrSneakyMrTorrezMustafa MahdiMárton VaitkusNathan JessurunNenad VitorovicNero LiNicanNiklas BuschmannOctavian VoicuOliver SteeleOmar Zrienotavio goodPatch KesslerPeter EhrnstromPeter McinerneyPeterCxyPsylenceQinghong ShiQuantopianRabidCamelRandy C.
WillRandy TrueRichard BarthelRichard BurgmannRichard ComishRipta PasayRish KundaliaRobert DavisRobert TeedRobert van der TuukRoobieRoy LarsonRyan AtallahRyan WilliamsSandy WilbournScott Walter, Ph.D.Sean BarrettSean GallagherSebastian BraunertShahbaz ShaikhsidwillSindre Reino TrosterudsoekulSolara570Song GaoStephen Michael HartleySteve CohenSteven SolowayStevie MetkeSundar SubbarayanTed SuzmanThomas Peter BerntsenTim RobinsonTina LeTino AdamsTlasTobias ChristiansenTyler HerrmannVValentin Mayer-EichbergerValeriy SkobelevVictor CastilloVictor KostyukVictor LeeVladyslav KurmazXavier BernardYana ChernobilskyYaw EtseYinYangBalance.AsiaYixiu ZhaoYu JunZach CardwellZachary Elliott噗噗兔
Площадь поверхности сферы: формула, вывод
Жасмин Гровер
Старший специалист по контенту | Обновлено 5 апреля 2022 г.
Площадь поверхности сферы — это площадь, покрытая внешней поверхностью сферы. Площадь поверхности объекта равна сумме площадей, покрытых его поверхностью.
Объект с глубиной и высотой образует трехмерную форму . Сфера представляет собой трехмерную форму с равномерно распределенными точками на ее площади. Площадь поверхности сферы можно рассчитать с помощью метод интеграции .
Содержание
- Что такое площадь поверхности сферы?
- Формула площади поверхности сферы
- Вывод площади поверхности сферы
- Как найти площадь поверхности сферы
- Площадь Сферы
- Hater Artember Speem of Sphere Speader of Sphere
- Late Laster At Speephere Speance Speance Speance Speance Spean
- Общая площадь поверхности сферы
- Вещи, чтобы запомнить
- Вопросы для образцов
Ключевые термины: Радиус, диаметр, сфера, круг, область, объем, объем, ополатчик.
Площадь поверхности цилиндра
Что такое площадь поверхности сферы?
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Сфера — это объект, каждая точка на круглой поверхности которого равна фиксированному центру сферы. Радиус — это расстояние между центром и поверхностью. Площадь, занимаемая криволинейной поверхностью сферы, называется площадью ее поверхности. Оба круг и сфера имеют круглую форму. Ключевое различие между ними заключается в том, что сфера — это трехмерная фигура, поскольку она имеет объем, тогда как круг — двумерная фигура. Единицей площади поверхности сферы являются квадратные единицы.
Сфера
Формула площади поверхности сферы
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Сфера представляет собой трехмерный объект, напоминающий круг и имеющий круглую форму. Площадь поверхности каждого трехмерного объекта можно разделить на три категории. Это так:
- Площадь изогнутой поверхности
- Площадь боковой поверхности
- Общая площадь поверхности
Формула для расчета площади поверхности сферы может использоваться для вычисления площади поверхности сферы.
Предположим, что это сфера радиуса «r». Площадь «a» сферы может затем быть определена по формуле:
A = 4πr 2
Деривация поверхностной площади на площади поверхностной площадь
.0042
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Поскольку сфера имеет круглую форму, мы соединяем ее с параболой , такой как цилиндр , чтобы вычислить площадь ее поверхности. Цилиндр — это фигура с криволинейной поверхностью, имеющей плоские поверхности с обеих сторон. Когда радиус цилиндра и радиус сферы одинаковы, сфера может точно вписаться в цилиндр. Это означает, что высота цилиндра равна диаметру сферы. В результате Архимед показал, что когда радиус цилиндра и сферы равен «r», площадь поверхности сферы равна боковой площади цилиндра.
Таким образом,
Площадь поверхности сферы = площадь боковой поверхности A цилиндра
Здесь
Площадь латеральной поверхности a Cynlid радиус цилиндра и h = высота цилиндра
Теперь предположим, что сфера идеально помещается в цилиндр, поэтому высота цилиндра также является диаметром цилиндра
Высота цилиндра = диаметр сферы = 2r
Итак,
Площадь поверхности сферы = 2πrh
Теперь в площади поверхности сферы мы можем заменить h на 2r (потому что высота цилиндра = диаметру сферы = 2r )
Итак, площадь поверхности сферы = 2πrh = 2πr(2r) = 4πr 2
Отсюда
A = 4πr 2
Здесь r – радиус сферы.
Как найти площадь поверхности сферы
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Давайте рассмотрим этот пример, чтобы увидеть, как использовать формулу для определения площади поверхности сферы.
Пример: Найдите площадь поверхности сферы радиусом 6 см.
Шаг 1: Обратите внимание на заданный радиус сферы. Здесь радиус сферы равен 6 см.
Шаг 2: Теперь мы знаем, что площадь поверхности сферы = 4πr 2 , поэтому, подставляя значения в данную формулу, мы получаем 4 × 3,14 × 6 × 6 = 452,16
Шаг 3: Таким образом, площадь поверхности сферы равна 452,16 см2
Площадь криволинейной поверхности сферы криволинейная площадь поверхности. Поскольку сфера имеет только одну кривую поверхность, площадь ее криволинейной поверхности равна общей площади поверхности. Итак,
Площадь криволинейной поверхности сферы = Общая площадь поверхности сферы = 4πr 2
Площадь боковой поверхности сферы
[Щелкните здесь, чтобы просмотреть примеры вопросов]
Площадь боковой поверхности включает все области, кроме основания (т.
е. верх и низ).
Нам не нужны точные верхние и нижние части в форме сферы. Таким образом, площадь боковой поверхности шара равна общей площади поверхности шара. Таким образом,
Площадь боковой поверхности сферы = Общая площадь поверхности сферы = 4πr 2
Общая площадь поверхности сферы
Общая площадь поверхности твердого тела равна сумме его сторон, верха и низа. Сфера не имеет сторон. Таким образом, он рассчитывается как 4πr2.
Общая площадь поверхности сферы = 4πr 2
Что следует помнить
- Сфера — это объект, каждая точка на круглой поверхности которого равна фиксированному центру сферы.
- Общая площадь поверхности, площадь боковой поверхности и площадь криволинейной поверхности сферы равны, т. е. 4πr 2 .
- Объем сферы радиуса «r» можно определить по формуле V = 4/3 πr3
- Радиус сферы — это расстояние между центром сферы и любой точкой на поверхности сферы.
Обозначается буквой «р». Итак, г = d/2.
- Диаметр сферы — это самая длинная линия в центре сферы, которая касается обоих концов сферы. Диаметр в два раза больше радиуса сферы. Обозначается буквой «д». Итак, д = 2р.
Примеры вопросов
Вопросы. Если площадь поверхности шара 314 см 2 , то найдите диаметр шара. (2 балла)
Ответ. дано,
Площадь поверхности сферы = 314 см 2
Следовательно, 4πr 2 = 314
R 2 = 314/4π
R 2 = 314/(4 × 314. )
r 2 = 314/12,56
r 2 = 25
r = 5
r = d/2
Итак, d = 10
Таким образом, диаметр сферы равен 10 см.
Вопросы. Рассчитайте стоимость покраски футбольного мяча в форме шара с радиусом 7 см. Если стоимость росписи футбольного мяча составляет 2,5 рупии за квадратный сантиметр. (Предположим, что π = 22/7) (2 балла)
Ответ.
Мы знаем, что
Площадь поверхности шара = 4πr 2
Итак, 4 × 22/7 × 7 × 7 = 616 см 2
Итак, площадь футбольного мяча равна 616 см 2
Теперь стоимость покраски футбольного мяча составляет 2,5 × 616 = 1540 индийских рупий
Ques. Сколько квадратных километров составляет площадь суши, если три четверти поверхности мира покрыты водой, если предположить, что земля имеет сферическую форму с радиусом 6370 км? (2 балла)
Ответ. (6370) 2
= 127527400 км 2
Вопрос. Найдите площадь поверхности шара диаметром 8 см. (2 балла)
Ответ. Дано,
Диаметр сферы = 8 см
Итак, радиус = 8/2 = 4 см
Мы знаем, что,
Площадь поверхности сферы = 4πr 2
= 4 × 22/ 7 × 4 × 4
= 201,14 см 2
Зав. Вычислите объем сферы с 154 см 2 площади поверхности.
(3 балла)
Отв. дано,
Площадь поверхности сферы = 154 см 2
Мы знаем, что,
Площадь поверхности сферы = 4πr 2
SO, 4πr 2 = 154 CM 2
.4 × 22/7 × r 2 = 154
r 2 = 49/4
r = 3,5
Теперь объем сферы = 4/3πr 3
7 х 3,5 х 3,5 х 3,5
= 179,66 см3
Итак, объем шара равен 179,66 см 3 .
Вопросы. Один ладу радиусом 5 см принадлежит лавочнику. Сколько ладу радиусом 2,5 см можно сделать из одного и того же материала? (3 балла)
Отв. Объем ладду радиусом 5 см (V 1 ) = 4/3 × 22/7 × (5) 3
= 11000/21 см 3
Кроме того, объем ладду радиусом 2,5 см (V2) = 4/3πr 3
= 4/3 × 22/7 × (2,5) 3 см 3
= 1375/21 см 3
Следовательно,
Число радиусов может быть равно 2
.
V 1 /V 2 = 11000/1375 = 8
Запросы. Диаметр Луны составляет около четверти диаметра Земли. Рассчитайте отношение их площадей к поверхности. (3 балла)
Отв. Диаметр Луны = 1/4 диаметра Земли
Пусть радиус Земли на км
Тогда радиус Луны = (r/4) км
Теперь площадь поверхности Земли = 4πr 2
Площадь поверхности Луны = 4π(r/4) 2
= 4π × (1 /16) r 2 = (1/4) × πr 2
Отношение площади поверхности Луны и Земли = (1/4) × πr 2 : 4πr 2 = (1/4) : 4 = 1/16
Вопрос. Когда воздух накачивается в сферический шар, его радиус увеличивается с 7 см до 14 см. Рассчитайте соотношение площадей поверхности воздушного шара в обоих сценариях. (4 балла)
Ответ. Радиус сферического шара изначально, r1 = 7 см сферический шар после накачки воздуха, r 2 = 14 см
Площадь поверхности шара после накачки воздуха = 4πr2
= 4 × π × (14) 2
= 4 × π × 196
Соотношение двух сценариев = Площадь поверхности баллона до накачивания воздуха / Площадь поверхности баллона после накачивания воздуха
= 4 × π × 49 : 4 x π × 196
= 1:4
Отношение площадей поверхности шара в двух сценариях = 1 : 4
Вопрос.

 Подскажите, пожалуйста, литературу, где есть подробный вывод формулы элемента площади поверхности сферы и площади сферы. Конкретно интересует вопрос, откуда в формуле для элемента поверхности множитель (для сферы единичного радиуса)?
Подскажите, пожалуйста, литературу, где есть подробный вывод формулы элемента площади поверхности сферы и площади сферы. Конкретно интересует вопрос, откуда в формуле для элемента поверхности множитель (для сферы единичного радиуса)?
 ..азимутальном угле.
..азимутальном угле.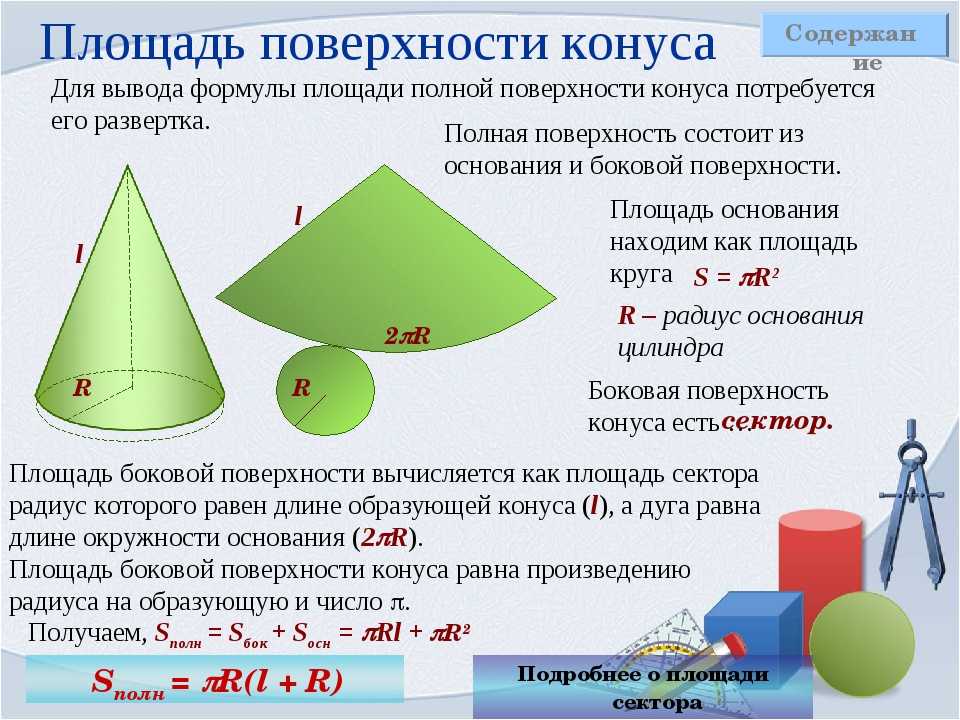 04.2016, 16:24
04.2016, 16:24  Привёл наглядный пример.
Привёл наглядный пример. С другой стороны, . Значит, .
С другой стороны, . Значит, .
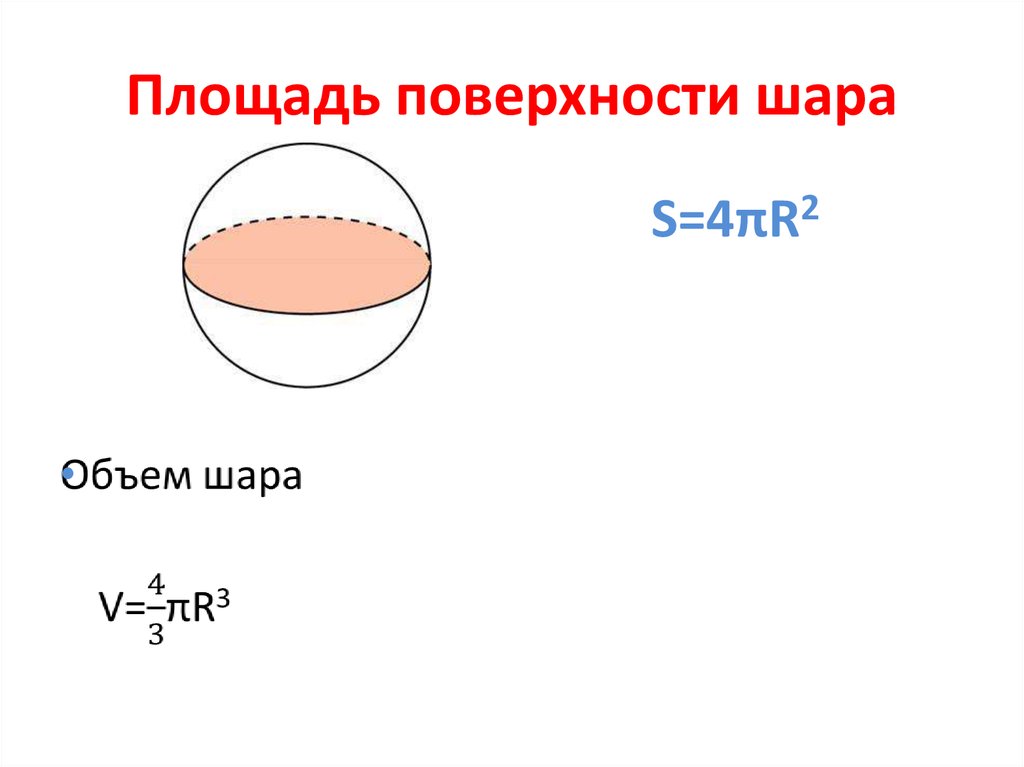
 04.2016, 18:19
04.2016, 18:19  Любая точка поверхности шара находится на одинаковом расстоянии от центра.
Любая точка поверхности шара находится на одинаковом расстоянии от центра. Если бы степень числа была в виде тройки, то умножать на само себя нужно было бы два раза. Записав выражение на бумаге, можно понять, почему используются именно двойка и тройка, а не единица и двойка.
Если бы степень числа была в виде тройки, то умножать на само себя нужно было бы два раза. Записав выражение на бумаге, можно понять, почему используются именно двойка и тройка, а не единица и двойка. Также этими знаниями можно подавлять соперника в споре.
Также этими знаниями можно подавлять соперника в споре.

 После вращения полукруга вокруг оси xxx мы получим площадь поверхности сферы, и если мы вырежем только частичный участок с параллельными основаниями, новая площадь поверхности будет продемонстрирована на изображении ниже:
После вращения полукруга вокруг оси xxx мы получим площадь поверхности сферы, и если мы вырежем только частичный участок с параллельными основаниями, новая площадь поверхности будет продемонстрирована на изображении ниже: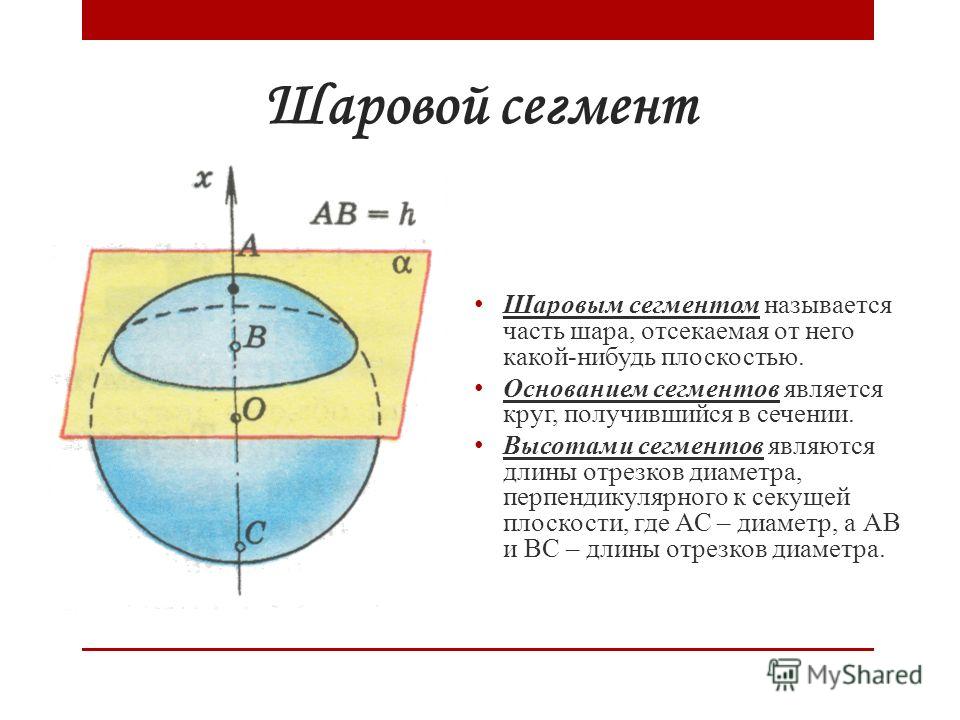

 см
см


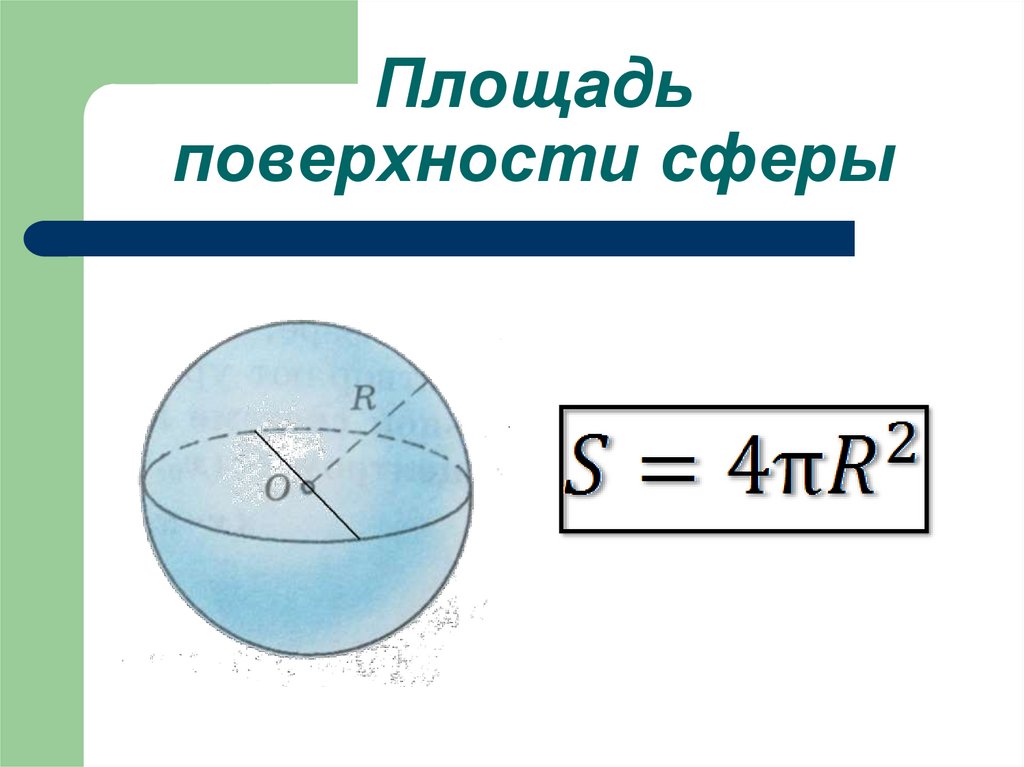 С другой стороны, сфера — это трехмерная форма, подобная форме футбольного или баскетбольного мяча. Три оси координат, ось x, ось y и ось z используются для определения формы сферы. Как и круг, сфера также имеет центральную точку. Каждая точка на поверхности сферы равноудалена от ее центра. Это фиксированное расстояние от центра до любой точки на окружности сферы называется радиусом сферы. Размер сферы определяется радиусом сферы.
С другой стороны, сфера — это трехмерная форма, подобная форме футбольного или баскетбольного мяча. Три оси координат, ось x, ось y и ось z используются для определения формы сферы. Как и круг, сфера также имеет центральную точку. Каждая точка на поверхности сферы равноудалена от ее центра. Это фиксированное расстояние от центра до любой точки на окружности сферы называется радиусом сферы. Размер сферы определяется радиусом сферы. Например, шарики представляют собой твердые сферы.
Например, шарики представляют собой твердые сферы.

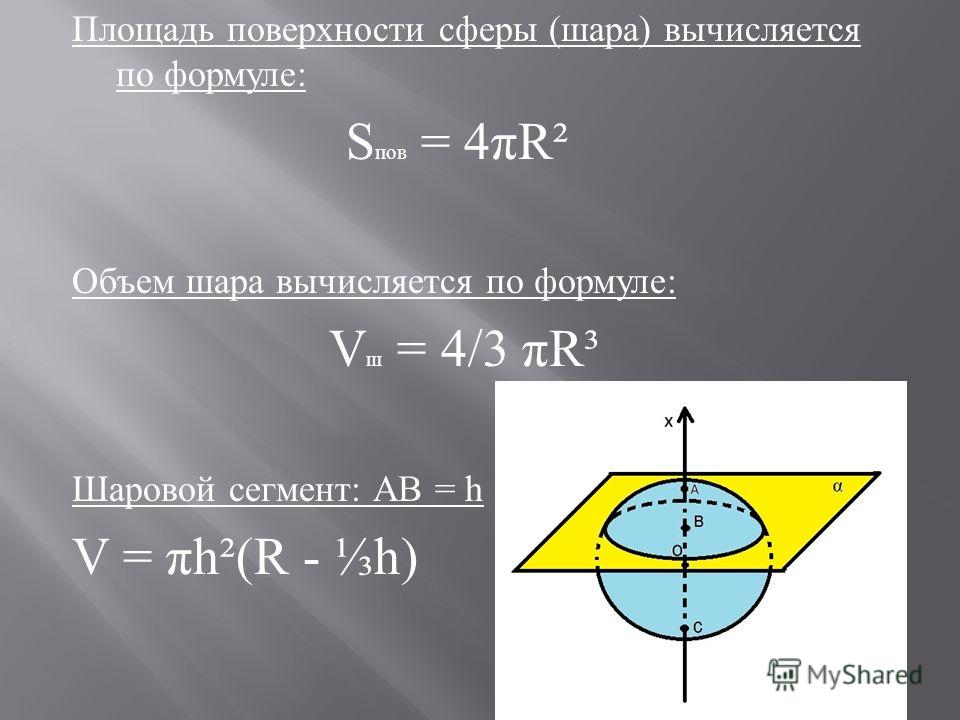 2}\) 92}\)
2}\) 92}\)  3}\) 92}\), где \(r\) — радиус.
3}\) 92}\), где \(r\) — радиус.
 24πR2.
24πR2. С одной стороны, поскольку этот прямоугольник проецируется наружу, его ширина будет увеличиваться.
С одной стороны, поскольку этот прямоугольник проецируется наружу, его ширина будет увеличиваться.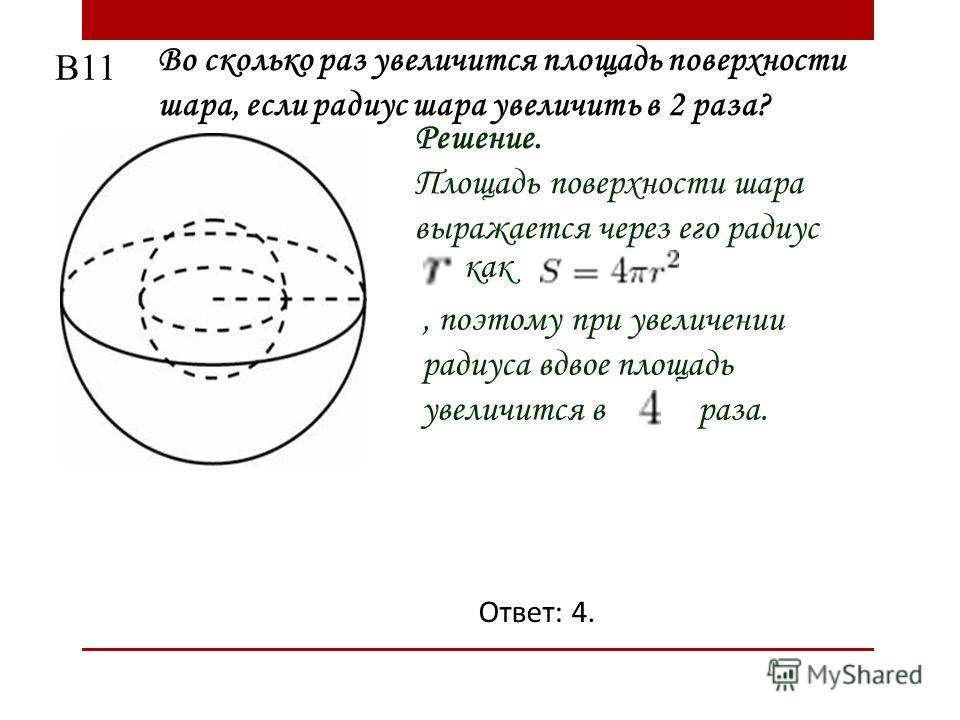
 Чтобы выбрать произвольный стандарт, скажем, ddd — это расстояние от нижней части прямоугольника до оси Z.
Чтобы выбрать произвольный стандарт, скажем, ddd — это расстояние от нижней части прямоугольника до оси Z.
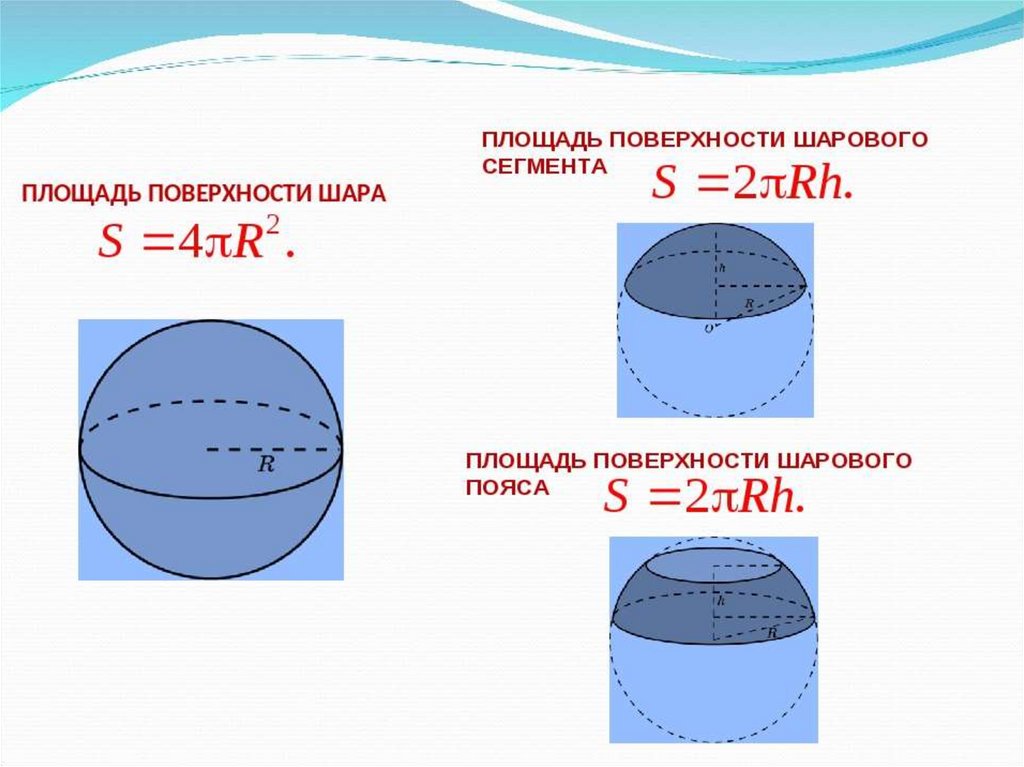 Назовем эти углы α\alphaα и β\betaβ:
Назовем эти углы α\alphaα и β\betaβ: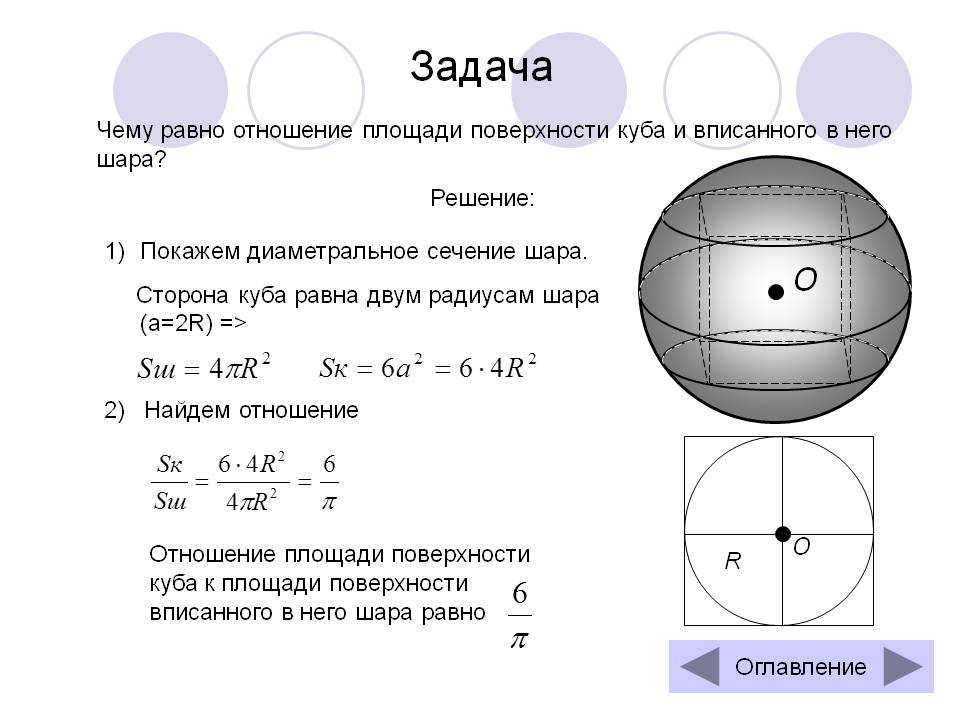


 Итак, давайте попробуем здесь что-то немного другое и представим доказательство в виде строго управляемой последовательности упражнений. Да, я знаю, что это менее весело, и это означает, что вам придется вытащить бумагу, чтобы выполнить какую-то работу, но я гарантирую, что таким образом вы получите больше пользы.
Итак, давайте попробуем здесь что-то немного другое и представим доказательство в виде строго управляемой последовательности упражнений. Да, я знаю, что это менее весело, и это означает, что вам придется вытащить бумагу, чтобы выполнить какую-то работу, но я гарантирую, что таким образом вы получите больше пользы.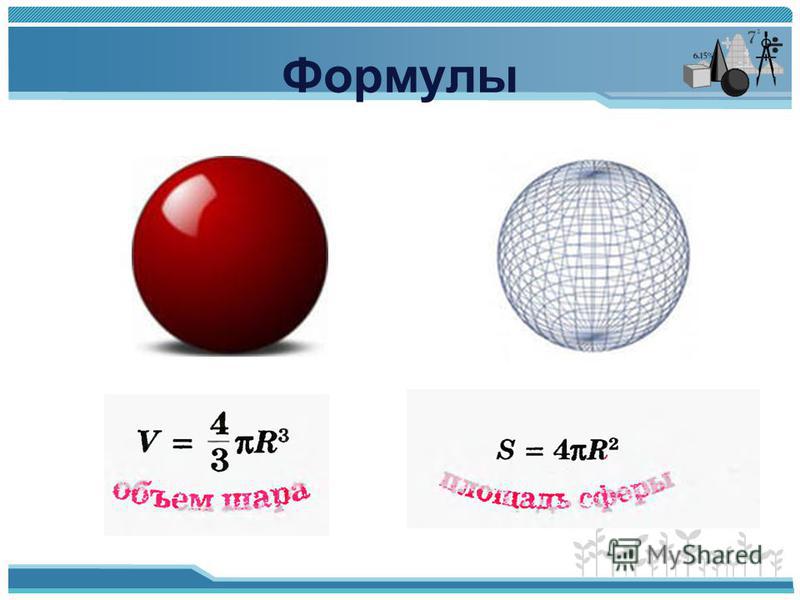
 )
)
 Это позволяет нам покрыть чередующиеся кольца по всей сфере, как было сказано выше. 92 \sin(\theta)\cos(\theta) \mathop{d\theta}4πR2sin(θ)cos(θ)dθ, что действительно вдвое превышает площадь тени кольца θ\thetaθ.
Это позволяет нам покрыть чередующиеся кольца по всей сфере, как было сказано выше. 92 \sin(\theta)\cos(\theta) \mathop{d\theta}4πR2sin(θ)cos(θ)dθ, что действительно вдвое превышает площадь тени кольца θ\thetaθ. Почему это означает, что площадь круга составляет ровно ¼ площади поверхности сферы, особенно когда мы рассматриваем все более и более тонкие кольца? 924πR2.
Почему это означает, что площадь круга составляет ровно ¼ площади поверхности сферы, особенно когда мы рассматриваем все более и более тонкие кольца? 924πR2.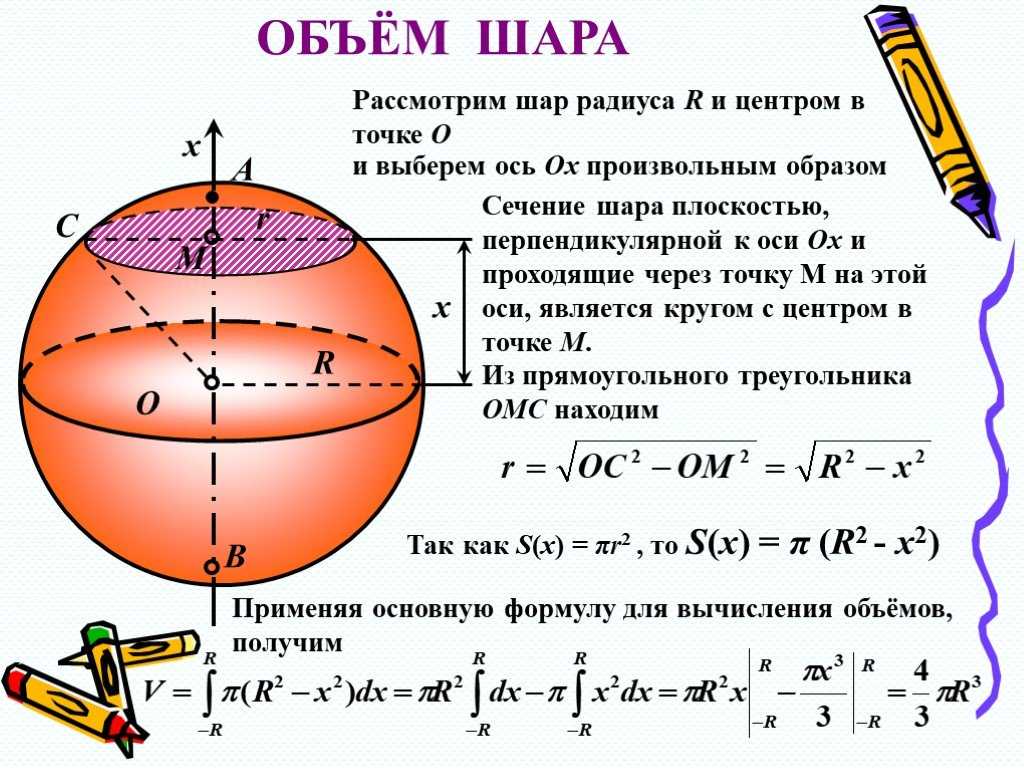 VeseyJohn GriffithJohn HaleyJohn ShaughnessyJohn V WertheimJonathan EppeleJonathan WilsonJono ForbesJordan ScalesJoseph John CoxJoseph KellyJoshua TobkinJuan BenetJulian PulgarinKai-Siang AngKanan GillKaustuv DeBiswasKeith SmithKenneth LarsenKevin NorrisKevin OrrKrishanu SankarKristoff KieferKyle BegovichKyle HooksL0j1kLee Burnettelevav ferber tasLinh TranLockLuc RitchieLudwig SchubertLukas -krtek.net- NovyLukas BiewaldMagister MugitMagnus DahlströmMagnus LysfjordmakkostyaManne MoquistManuel GarciaMarcus KöhlerMark B BahuMark JobesMarkus PerssonMartin Sergio H. FaesterMathew BramsonMathias JanssonMatt LangfordMatt ParlmerMatt RovetoMatt RussellMatthew CockeMaurício CollaresMayank M. MehrotraMert ÖzMichael FaustMichael HardelMichael Kohle rMikael NordvallMike DourMike DussaultMikkoMrSneakyMrTorrezMustafa MahdiMárton VaitkusNathan JessurunNenad VitorovicNero LiNicanNiklas BuschmannOctavian VoicuOliver SteeleOmar Zrienotavio goodPatch KesslerPeter EhrnstromPeter McinerneyPeterCxyPsylenceQinghong ShiQuantopianRabidCamelRandy C.
VeseyJohn GriffithJohn HaleyJohn ShaughnessyJohn V WertheimJonathan EppeleJonathan WilsonJono ForbesJordan ScalesJoseph John CoxJoseph KellyJoshua TobkinJuan BenetJulian PulgarinKai-Siang AngKanan GillKaustuv DeBiswasKeith SmithKenneth LarsenKevin NorrisKevin OrrKrishanu SankarKristoff KieferKyle BegovichKyle HooksL0j1kLee Burnettelevav ferber tasLinh TranLockLuc RitchieLudwig SchubertLukas -krtek.net- NovyLukas BiewaldMagister MugitMagnus DahlströmMagnus LysfjordmakkostyaManne MoquistManuel GarciaMarcus KöhlerMark B BahuMark JobesMarkus PerssonMartin Sergio H. FaesterMathew BramsonMathias JanssonMatt LangfordMatt ParlmerMatt RovetoMatt RussellMatthew CockeMaurício CollaresMayank M. MehrotraMert ÖzMichael FaustMichael HardelMichael Kohle rMikael NordvallMike DourMike DussaultMikkoMrSneakyMrTorrezMustafa MahdiMárton VaitkusNathan JessurunNenad VitorovicNero LiNicanNiklas BuschmannOctavian VoicuOliver SteeleOmar Zrienotavio goodPatch KesslerPeter EhrnstromPeter McinerneyPeterCxyPsylenceQinghong ShiQuantopianRabidCamelRandy C. WillRandy TrueRichard BarthelRichard BurgmannRichard ComishRipta PasayRish KundaliaRobert DavisRobert TeedRobert van der TuukRoobieRoy LarsonRyan AtallahRyan WilliamsSandy WilbournScott Walter, Ph.D.Sean BarrettSean GallagherSebastian BraunertShahbaz ShaikhsidwillSindre Reino TrosterudsoekulSolara570Song GaoStephen Michael HartleySteve CohenSteven SolowayStevie MetkeSundar SubbarayanTed SuzmanThomas Peter BerntsenTim RobinsonTina LeTino AdamsTlasTobias ChristiansenTyler HerrmannVValentin Mayer-EichbergerValeriy SkobelevVictor CastilloVictor KostyukVictor LeeVladyslav KurmazXavier BernardYana ChernobilskyYaw EtseYinYangBalance.AsiaYixiu ZhaoYu JunZach CardwellZachary Elliott噗噗兔
WillRandy TrueRichard BarthelRichard BurgmannRichard ComishRipta PasayRish KundaliaRobert DavisRobert TeedRobert van der TuukRoobieRoy LarsonRyan AtallahRyan WilliamsSandy WilbournScott Walter, Ph.D.Sean BarrettSean GallagherSebastian BraunertShahbaz ShaikhsidwillSindre Reino TrosterudsoekulSolara570Song GaoStephen Michael HartleySteve CohenSteven SolowayStevie MetkeSundar SubbarayanTed SuzmanThomas Peter BerntsenTim RobinsonTina LeTino AdamsTlasTobias ChristiansenTyler HerrmannVValentin Mayer-EichbergerValeriy SkobelevVictor CastilloVictor KostyukVictor LeeVladyslav KurmazXavier BernardYana ChernobilskyYaw EtseYinYangBalance.AsiaYixiu ZhaoYu JunZach CardwellZachary Elliott噗噗兔 Объект с глубиной и высотой образует трехмерную форму . Сфера представляет собой трехмерную форму с равномерно распределенными точками на ее площади. Площадь поверхности сферы можно рассчитать с помощью метод интеграции .
Объект с глубиной и высотой образует трехмерную форму . Сфера представляет собой трехмерную форму с равномерно распределенными точками на ее площади. Площадь поверхности сферы можно рассчитать с помощью метод интеграции . Площадь поверхности цилиндра
Площадь поверхности цилиндра