«Почему принято считать, что в окружности 360 градусов, а не 100 или 1000?» — Яндекс Кью
ПопулярноеСообщества
Стать экспертом Кью
Математика
Коринец Э.
·
81,8 K
ОтветитьУточнитьВиктор Брыксин
92
пенсионер · 24 июл 2021
Я уже высказывался, что число 360 возникает из попыток древних построить календарь. Но, как заметили многие авторы, число 360 удобно делимо на равные доли: и пополам, и на три, и на четыре, и на пять, и на шесть, и т.д. Количество вариантов деления большое, поэтому удовлетворялись разнообразные потребности практики. Число 360 не могло быть не популярным. Геометрическая особенность состоит в том, что окружность легко делится циркулем и пополам, и на три, и на четыре, и на шесть. Я, думаю, что древние умели это делать и сопоставляли числовые свойства и геометрические. Деление дуги окружности пополам простая процедура, способствовавшая дроблению этой шкалы. Так что возникновение 360 равномерных засечек по периметру диска, т.е. появление угловой единицы градус было вполне естественным. Я затрудняюсь с ответом, когда появилась процедура деления окружности на пять равных частей, но она не столь существенна для построения упомянутой шкалы.
Я, думаю, что древние умели это делать и сопоставляли числовые свойства и геометрические. Деление дуги окружности пополам простая процедура, способствовавшая дроблению этой шкалы. Так что возникновение 360 равномерных засечек по периметру диска, т.е. появление угловой единицы градус было вполне естественным. Я затрудняюсь с ответом, когда появилась процедура деления окружности на пять равных частей, но она не столь существенна для построения упомянутой шкалы.
Комментировать ответ…Комментировать…
Виктор Брыксин
92
пенсионер · 1 мар 2021
В древние времена на месте нынешних Сирии и Ирака, в междуречье Тигра и Евфрата существовало государство Месопотамия. Там возникла 60-ричная система исчисления, задолго до появления римских и арабских цифр. Пробег минутной стрелки в современных часах (60 минут за 1 час) это отголосок того времени. Я думаю, что 360 угловых единиц (градусов) возникли из временных.
Комментировать ответ…Комментировать…
Алферьевский Сергей
3
Механик, точные науки · 2 сент 2020
В древности, без компьютеров и графопостраителей сложно было поделить круг более, чем на 360 частей ручками и с примитивными чертежными приспособлениями. Вот и взяли по мах.
Сколько дней в году, так же, у разных народов по разному было, кто как придумал.
В мореходстве круг 32 румба.
Не хватает градусов, есть минута, а там еще секунда и тд.
Комментировать ответ…Комментировать…
Дмитрий Даймон
4
инженер-хитротехник, «специалист по мягкому металлу, по хлебу и по салу» (с) · 5 сент 2020
Одно время была попытка ввести «правильные» числа, и появились «грады». При этом прямой угол был равен ста градам, а окружность, соответственно, четырем сотням. Но, как показала практика, не прижилось.
Но, как показала практика, не прижилось.
А еще окружность меряется в радианах, и тогда она «два пи»
Комментировать ответ…Комментировать…
Первый
Владимир Сивохин
16
28 мар 2020
Диск Солнца с восхода до заката укладывается на небосклоне в определённое время года на определённой широте 180 раз.Ночью — тоже ( от заката до рассвета). Отсюда один угловой градус — это одна «денежка» Солнца; прямой угол — это Солнце в полдень = 90 градусов, всё остальное — от деления 180 (или 360 ) градусов.
Александр Новиков
21 июля 2020
солнце в полночь?
Комментировать ответ…Комментировать…
Первый
Владимир В.
-8
3 янв 2020
Всё, что касается замкнутых циклов, (кругов, окружностей) пришло из математики.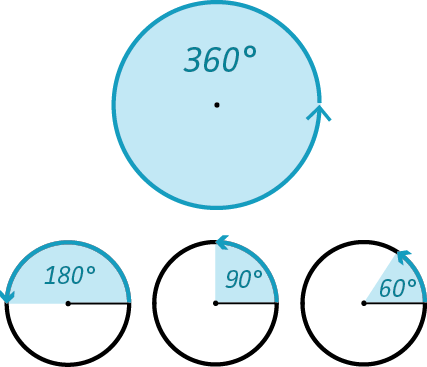 Круг делили пополам, половинки ещё пополам, и так далее. Самую мелкую часть назвали градус или 1/360 часть.
Круг делили пополам, половинки ещё пополам, и так далее. Самую мелкую часть назвали градус или 1/360 часть.
Ирек Галеев
3 января 2020
Интересно, а как календарь составляли, если в году 365 суток и недели разбить по 5 дней нельзя было? Пробовал так… Читать дальше
Комментировать ответ…Комментировать…
Иван Григорьевич Стрельников
2
5 авг 2020
Оборот Земли вокруг Солнца до известной катастрофы составлял 360 дней. Круг был разделён на 9 (девять) сроков или 40 (четырдцать) недель по 9 дней. Срок = сърок = сорок!!! 14 — это четырнадцать 4+10, 40 — это четырдцать 4 * 10. До сих пор мы поминаем покойника в неделю (9=девять дней) и в срок (40=четырдцать) дней. Потом дней стало 365,25. 41+40+41+40+41+40+41+40+41=365… Читать далее
lavzariu
5 августа 2020
А есть еще административный календарь, вспомните 10 дней на рассмотрение челобитной царю, 100 дней восхождения на. .. Читать дальше
.. Читать дальше
Комментировать ответ…Комментировать…
lavzariu
-2
хххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххх… · 18 июл 2020
360 легко делить, но тяжело считать. В свою очередь, 1000 легко считать, но тяжело делить по-справедливости. В шумерские времена, справедливо разделить, был вопрос жизни и смерти. Сейчас все наоборот: точный расчет решает все!.
Отсюда вывод; надо переходить на новое летоисчисление, которое будет включать в себя и все старые (мертвые) календари!.
Комментировать ответ…Комментировать…
Владимир Брунбендер
2
28 мая 2020
У древних шумеров на каждой руке было по 6 пальцев, поэтому они применяли 12-ричную систему счисления. Сутки они разделили на 2 части (день — ночь), каждую часть по 12 часов. Окружность при помощи циркуля легко разделить на 3 равные части. Если каждую часть разделить на 120, то как раз и получится 360.
Окружность при помощи циркуля легко разделить на 3 равные части. Если каждую часть разделить на 120, то как раз и получится 360.
Комментировать ответ…Комментировать…
Первый
Анатолий Е.
5
7 мая 2020
Градус,это «Два шага», вот и получается что в » в горизонт суток» помещается 720 проекций солнечных дисков.720 разделить на 2 (два шага) получаем 360.
Комментировать ответ…Комментировать…
|
5 сервисов для оценки компетенций сотрудников
Метод «360 градусов» — способ оценки сотрудников. Он помогает определить их сильные стороны, зоны роста и показывает, в каком направлении развиваться, чтобы принести максимальную пользу компании.
Он помогает определить их сильные стороны, зоны роста и показывает, в каком направлении развиваться, чтобы принести максимальную пользу компании.
Обычно оценка выглядит как опрос — мнением о сотруднике делятся его руководители, коллеги и подчинённые. После HR-департамент или отдел обучения обрабатывает ответы и делает выводы. Например, насколько специалист соответствует должности и можно ли включить его в кадровый резерв.
Специальные сервисы помогают оценить сотрудников быстрее: сами собирают обратную связь и сохраняют анонимность ответов, анализируют данные и показывают результаты в наглядных отчётах.
В материале 5 онлайн-сервисов для оценки персонала по модели «360 градусов», которые чаще всего ищут в поисковиках. Все сервисы работают через интернет. Чтобы начать оценку, достаточно создать аккаунт. Рассказываем, как они устроены и чем отличаются.
Как проходит оценка «360 градусов»
iSpring Learn
Пробный доступ: 14 дней сразу после регистрации
В Реестре отечественного ПО: да
Мобильное приложение: да
Техподдержка: по телефону и почте круглосуточно
Подробнее: на сайте
Для оценки есть готовая модель компетенций по шести направлениям: «Аналитическое мышление», «Вовлечённость», «Коммуникации и взаимодействие», «Лидерство», «Мотивация и развитие» и «Навыки переговоров».
Создать свою модель компетенций под каждую должность поможет визуальный редактор — знать HTML не обязательно, достаточно прописать компетенции и указать, по какой шкале их оценивать. Например, от 1 до 5 или 1 до 10 баллов. В результате получается готовый опросник для оценки сотрудников. В начале опроса можно поставить инструкцию, чтобы объяснить респондентам, сколько времени займёт опрос и как корректно давать обратную связь.
Для оценки в сервисе есть два типа вопросов: закрытые и открытые. В закрытых респонденты выбирают один вариант ответа. В открытых — могут оставить развёрнутый комментарий. Он попадёт в финальный отчёт по сотруднику.
Опросник адаптируется под размер экрана. Для оформления можно использовать готовый шаблон или сделать опросник в корпоративном стиле. Например, добавить обложку, изменить цвет кнопок.
Чтобы начать оценку, вручную вносить данные сотрудников не нужно. Пользователей можно загрузить Excel-списком или перенести данные из кадровой системы — для этого у сервиса есть интеграция с Битрикс24, 1С, E-Staff.
iSpring Learn автоматизирует часть работы: назначает опрос, напоминает о сроках тем, кто забыл, собирает данные и составляет отчёты.
Аналитика в сервисе показывает сильные стороны и зоны роста оцениваемого сотрудника. Новые результаты можно сравнить с предыдущими, чтобы увидеть прогресс, или сопоставить с показателями другого специалиста компании. Ещё можно посмотреть, как оценивают сотрудника отдельно подчинённые, коллеги, руководители и насколько их мнение отличается.
Есть общий рейтинг по всем сотрудникам — сразу видно самых перспективных. Отчёты можно выгрузить на компьютер в XLSX-формате.
Оценка «360 градусов» — одна из возможностей iSpring Learn. Также через сервис можно проводить вебинары, создавать учебные курсы со статьями, видеороликами и тренажёрами и проверять знания сотрудников при помощи онлайн-тестов.
В начале опроса можно разместить инструкцию с общими правилами, если в компании проводят оценку впервые
В отчёте по сотруднику видно, какие компетенции западают и в каком направлении ему стоит развиваться
Радар компетенций покажет, что о сотруднике думаю подчинённые, коллеги и руководители
В iSpring Learn можно сопоставить результаты специалиста с портретом идеального сотрудника компании. Например, чтобы взвешенно принять решение о повышении
Например, чтобы взвешенно принять решение о повышении
Wakeup
Пробный доступ: бессрочный
В Реестре отечественного ПО: нет
Мобильное приложение: нет
Техподдержка: работает всю неделю по почте с 9 до 18
Подробнее: на сайте
Сервис разработала команда Максима Батырева — бизнес-тренера и автора бестселлеров «45 татуировок менеджера» и «45 татуировок продавана».
Здесь есть 9 готовых компетенций, которые подходят для оценки топ-менеджеров. В их числе делегирование, постановка задач, планирование и мотивация сотрудников. Компетенции можно изменить или добавить новые в онлайн-редакторе.
Для оценки Wakeup использует пятибалльную шкалу. Её нельзя изменить. Добавить открытые вопросы и настроить опросник в фирменном стиле тоже не получится.
Чтобы запустить оценку, сотрудников и респондентов придётся добавить в сервис вручную: указать имя, должность, отдел и почту, на которую пришлют приглашение.
Аналитика показывает, как сотрудника оценило окружение и каким он видит себя сам. В отдельном отчёте по сотруднику видно, какие компетенции западают и что о нём думают отдельно коллеги, подчинённые и руководство.
В сервисе есть 9 готовых компетенций для оценки сотрудников
Wakeup автоматически разошлёт приглашения на оценку и проверит результаты
Так выглядит сводный учёт по оцениваемому сотруднику в Wakeup
Детальный отчёт, в котором видно, какие компетенции западают
StartExam
Пробный доступ: 14 дней после разговора с менеджером
В Реестре отечественного ПО: да
Мобильное приложение: нет
Техподдержка: по почте круглосуточно
Подробнее: на сайте
Компания проводит оценку «360 градусов» на внутренней платформе под ключ. Для работы нужен список респондентов и оцениваемых, модель компетенций, а также шкала для оценки.
Команда StartExam берёт на себя техническую часть: переносит модель компетенций на платформу, собирает опрос и оформляет в фирменном стиле компании, готовит инструкции и рассылки с просьбой оценить сотрудников, анализирует информацию и составляет отчёты. В среднем это занимает 3–4 недели. Отредактировать модель компетенций или заменить респондентов самостоятельно не получится — только через провайдера.
В среднем это занимает 3–4 недели. Отредактировать модель компетенций или заменить респондентов самостоятельно не получится — только через провайдера.
Во время оценки заказчик получает доступ к личному кабинету, в котором видит, кто прошёл опрос, а кто ещё не приступал.
Данные с аналитикой приходят на почту спустя 2–3 дня после оценки. Сводный отчёт даёт общую картину по всем оцениваемым сотрудникам — видно, кто соответствует должности, а кто нет.
Отчёт по сотруднику покажет, насколько его компетенции не дотягивают до стандарта и над чем стоит поработать в первую очередь.
Оценка сотрудников через StartExam в среднем занимает 3–4 недели
Так выглядит список респондентов и оцениваемых, которых просят предоставить в StartExam для запуска оценки
Сводный отчёт помогает сравнить сотрудников между собой
Персональный отчёт даёт детальную картину по конкретному сотруднику: какие навыки западают, над чем стоит поработать прежде всего, каким специалист видит себя и насколько это совпадает с мнением окружающих. В среднем отчёт занимает 20 страниц
В среднем отчёт занимает 20 страниц
Proaction
Пробный доступ: 2 дня после разговора с менеджером
В Реестре отечественного ПО: да
Мобильное приложение: нет
Техподдержка: по почте в будние дни
Подробнее: на сайте
Для оценки персонала есть два способа: создать опрос на основе модели компетенций компании или использовать готовые шаблоны. Доступны наборы вопросов по трём направлениям: «Личные качества», «Оценка руководителя», «Голос внутреннего клиента». Всего в них входит 15 компетенций. В том числе «Лояльность», «Бизнес-видение», «Желание развиваться», «Внимание к деталям».
Работа в сервисе частично автоматизирована. Например, можно загрузить данные сотрудников Ecxel-списком — Proaction сам создаст аккаунты, вышлет приглашение для оценки, напомнит о сроках и проверит результаты. Таким же образом можно добавить в сервис модель компетенций, которую используют в компании, чтобы не создавать самому.
Сервис показывает информацию как по всем оцениваемым сотрудникам, так и по каждому в отдельности. По отчётам видно, кто соответствует профилю должности, а кто нет и какие компетенции западают.
Для руководителя есть краткий отчёт. Кроме данных о сильных сторонах и пробелах работника, здесь есть рекомендации, какие задачи ему стоит поручать, а с какими лучше подождать.
Ещё одна особенность сервиса — он показывает, когда сотрудники отвечали неискренне, намеренно занижая или завышая оценку. Такие оценки можно убрать из общей статистики, чтобы получить объективную картину.
По отчёту руководителя понятно, над какими качествами и навыками стоит поработать сотруднику, а какие проблемы он даже не осознаёт. Также здесь есть рекомендации, как специалисту стать лучше.
Анализ расхождения показывает, насколько представление сотрудника о себе отличается от мнения окружения
Как и в других сервисах, здесь есть радар компетенций, который показывает, как сотрудника оценивают подчинённые, коллеги и руководители
Сервис показывает, кто намеренно занизил или завысил оценку во время опроса. Определить такие оценки можно по статусу «Не достоверно»
Определить такие оценки можно по статусу «Не достоверно»
Yva.ai
Пробный доступ: нет
В Реестре отечественного ПО: нет
Мобильное приложение: нет
Техподдержка: по почте в будние дни
Подробнее: на сайте
Чтобы проверить квалификацию команды, вместо классического «360 градусов» сервис проводит пульс-опросы. Это серия коротких вопросов о компании и коллегах, на которые сотрудники отвечают раз в неделю. По словам разработчиков, опрос занимает минуту.
Для оценки можно придумать свои вопросы или использовать банк готовых. В него входит 105 калиброванных вопросов. Из них сервис еженедельно назначает сотрудникам в случайном порядке 5–10 заданий. Опрос можно пройти с компьютера или телефона.
Yva.ai автоматически анализирует ответы и соберёт отдельные отчёты для руководителей и команды. В личном кабинете сотрудники видят, насколько полезным его считают коллеги, за какие черты ценят и какие видят проблемы. Здесь же показано, к какой группе они относятся. Например, входят в топ-10 инноваторов, продвигающих в компании сильные идеи.
Здесь же показано, к какой группе они относятся. Например, входят в топ-10 инноваторов, продвигающих в компании сильные идеи.
Руководители видят компетенции каждого сотрудника, его уровень выгорания и вовлечённости в работу. Особенность сервиса в том, что он показывает, как меняются показатели каждого работника в динамике, — от недели к неделе — есть ли у него прогресс или он устал и близок к увольнению.
По словам разработчиков, сервис измеряет больше 100 метрик. Например, находит скрытых лидеров, показывает, насколько сотрудник доволен работой, что ему не нравится в компании или насколько он близок к выгоранию
В сервисе есть закрытые и открытые вопросы, в которых сотрудники могут поделиться мнением и написать, что их тревожит
В личном кабинете сотрудник может посмотреть, что думают о нём коллеги, какие навыки важно развивать и насколько его ценят в команде
Оценка 360 градусов: преимущества, недостатки и процесс осуществления
Преимущества оценки на 360 градусов
Создает самосознание
360 градусная обратная связь дает сотрудникам возможность для самоанализа. Поскольку это целостный процесс, люди лучше понимают свои сильные и слабые стороны, что мотивирует их к самосовершенствованию. Такого рода процесс обратной связи в дальнейшем приводит к повышению квалификации, дисциплины, что снижает их истощение. Логика проста: если человек получает одну и ту же обратную связь от нескольких человек, он/она с большей вероятностью будет действовать в соответствии с ней.
Поскольку это целостный процесс, люди лучше понимают свои сильные и слабые стороны, что мотивирует их к самосовершенствованию. Такого рода процесс обратной связи в дальнейшем приводит к повышению квалификации, дисциплины, что снижает их истощение. Логика проста: если человек получает одну и ту же обратную связь от нескольких человек, он/она с большей вероятностью будет действовать в соответствии с ней.
Повышает прозрачность на рабочем месте
Это одно из очевидных преимуществ такого процесса обратной связи. Когда мы говорим об оценке один на один, обзор более асимметричен, чем вы думаете. Это оставляет достаточно места для ошибочных суждений и неправильных решений, которые могут повлиять на производительность и снизить доходы.
Совокупность знаний
Одним из менее известных преимуществ этого метода оценки эффективности является то, что он предоставляет вам обширные данные о ваших сотрудниках.
Когда оценка на 360 градусов используется правильно и эффективно, у вас есть прочная основа, на которой можно основывать свою политику в области управления и подбора персонала. Кроме того, инвестирование в систему обратной связи на 360 градусов помогает отслеживать улучшения, особенно в более гибких областях, таких как дисциплина, мотивация, лидерство и т.д.
Кроме того, инвестирование в систему обратной связи на 360 градусов помогает отслеживать улучшения, особенно в более гибких областях, таких как дисциплина, мотивация, лидерство и т.д.
Понимание сотрудников
Руководители смогут проанализировать soft skills специалиста и как человек вписывается в команду в других аспектах, которые не всегда связаны с проектом. Это еще больше повысит вовлеченность и производительность труда.
Надлежащая подготовка
Легче обучать своих новых сотрудников, когда у вас есть представление о качествах, которые делают команду успешной. Это, на самом деле, одно из самых важных преимуществ метода обратной связи на 360 градусов. Данные, которые вы получаете от менеджеров, коллег, подчиненных или даже клиентов, могут указать на пробелы в наборах навыков, необходимых в вашей отрасли.
Недостатки оценки на 360 градусов
Восприимчив к нечестным отзывам
Это, вероятно, самый вопиющий и очевидный недостаток метода оценки эффективности 360 градусов. Если ваши сотрудники не доверяют вашей системе, то вы, скорее всего, получите нечестные отзывы. Люди, как правило, начнут давать отзывы, которые вам нравится слышать, что сделает систему бесполезной.
Если ваши сотрудники не доверяют вашей системе, то вы, скорее всего, получите нечестные отзывы. Люди, как правило, начнут давать отзывы, которые вам нравится слышать, что сделает систему бесполезной.
Кроме того, предположим, что сотрудники знают, что данные могут быть использованы для проверки эффективности, в этом случае они могут предоставить ложные данные, чтобы преуменьшить значение других или принять коллективные меры для лучшего анализа.
Эффективно, но медленно
Нет никаких сомнений в том, что эта система оценки эффективна, но большинство менеджеров согласятся с тем, что она работает медленно. Человек, получающий письмо, обычно откладывает отзыв до последнего, или может даже забыть об этом. Другие, кто ценит важность обратной связи, как правило, в конечном итоге переоценивают рейтинг, что еще больше задерживает оценку.
Подозрительная и недоверчивая обстановка
Поскольку представленные обзоры, как правило, авторитетны, это создает обстановку подозрений в отношении защиты данных.![]() Это заставляет людей дважды подумать, прежде чем отправлять отзывы.
Это заставляет людей дважды подумать, прежде чем отправлять отзывы.
Кроме того, если лидер или руководство не реагируют на обратную связь, сотрудники могут посчитать, что это бессмысленное занятие, что приведет к тому, что сотрудники не будут воспринимать опросы всерьез и нарушат подотчетность руководителя.
Поэтому крайне важно, чтобы при внедрении системы оценки на 360 градусов вы действовали на основе полученных данных и получили результат, который удовлетворит всех.
Как провести оценку на 360 градусов?
1. Определите цель
Оценка 360 градусов лучше всего подходит для организаций, где все в основном зависит от кросс-функциональных способностей команды. В отличие от других обзоров, вам необходимо определить цель, ради которой вы стремитесь собрать значимые отзывы от всех, с кем вы связаны.
Здесь целью оценки может быть что угодно, например:
- Понимание масштабов взаимодействия между членами команды
- Поиск лазеек, которые могут возникнуть в любой точке контакта или во время функционирования.

- Повысить эффективность работы подразделений друг с другом.
- Для получения непредвзятого мнения о сотрудниках от всех, с кем они контактировали.
- Предоставление значимых и действенных комментариев для них, чтобы улучшить их возможности со всех сторон.
- Аттестация персонала.
- Список целей будет варьироваться в зависимости от требований, поэтому, если вы думаете начать с подбор персонала с данного метода, подумайте, зачем вам это нужно.
2. Определение компетенций
Процесс метода оценки очень эффективен, когда вы хотите, чтобы ваши сотрудники получили общее представление об их работе как ценных членов команды. Чтобы упростить процесс, вам необходимо определить основные компетенции, на которые вы хотите рассчитывать, принимая во внимание отзывы различных команд.
Все компетенции, которые вы определяете, должны напрямую относиться к должностной роли сотрудников и касаться задач организации.
3. Курирование соответствующей анкеты
Для обратной связи на 360 градусов вам нужно выбрать правильные вопросы для всех, кто участвует в этом процессе. Эти вопросы имеют решающее значение для того, чтобы помочь вам определить области, в которых сотрудники преуспевают, и проблемы, требующие немедленного внимания.
Кроме того, поскольку вы будете получать отзывы от нескольких членов команды, вам необходимо оценить вопросы с их точки зрения. Например, если вы собираете информацию о работе маркетолога от методиста, которые тесно сотрудничают друг с другом, попробуйте получить последнюю точку зрения и наоборот.
4. Сохранение конфиденциальности
Основной мотив опросов сотрудников состоит в том, чтобы помочь им понять свои сильные стороны и поработать над своими слабостями. И на протяжении всего процесса личность участников и их взгляды должны оставаться конфиденциальными, чтобы обеспечить эффективность оценки.
Какие вопросы задавать?
Многие менеджеры согласны с тем, что обратная связь на 360 является полезным инструментом для программ вовлечения сотрудников, наставничества, периодов проверки сотрудников и улучшает опыт сотрудников; но когда приходит время задавать вопросы, появляется застой. Открытый вопрос, в котором спрашивается мнение о работе сотрудника как хороший, так и плохой – бесполезен. Это даст вам только неорганизованные и хаотичные данные.
Открытый вопрос, в котором спрашивается мнение о работе сотрудника как хороший, так и плохой – бесполезен. Это даст вам только неорганизованные и хаотичные данные.
Каждая организация обладает уникальными характеристиками, особой культурой и широким спектром потребностей в лидерстве. Важно иметь в виду, что каждому сотруднику нужна обратная связь в разных областях, чтобы она была полезной.
Оценка 360 градусов – Как и зачем проводить? Все тонкости за 15 минут на понятных примерах
6. Цели и границы применимости метода 360 градусов.
Цель оценки — помочь коллеге (подчиненному, руководителю) увидеть свои сильные и слабые стороны, чтобы после усилить «провисающие компетенции» или более уверенно пользоваться своими сильными сторонами.
6.1. Какие задачи может решить организация с помощью оценки 360:
а. Лучше спланировать обучение сотрудников.
Например, понять, какие именно тренинги действительно нужны участникам кадрового резерва.
б. Повысить эффективность сотрудников за счет повышения самооценки.
Например, человек несправедливо считает, что у него нет лидерских задатков и не рискует брать на себя ответственность за проекты. После признания коллегами лидерских качеств, он может обрести уверенность в себе и браться за более ответственные задачи.
в. Подобрать проектную команду, выявить сотрудников, способных работать над сложными проектами.
г. Повысить эффективность руководителей, устранить конфликты.
Пример.
Руководитель дал подчиненному более высокие оценки по методу 360, чем все остальные. С помощью дополнительных проверок руководитель выяснил, что переоценивал деловые качества сотрудника в силу личной приязни, давая ему несправедливые преференции перед более компетентными сотрудниками, и что коллектив демотивирован наличием «любимчика» и часть сотрудников собирались сменить работу.
Руководитель начал принимать более взвешенные решения и давать всем равные возможности. Психологический климат исправился, всех сотрудников удалось сохранить.
Психологический климат исправился, всех сотрудников удалось сохранить.
Другой пример.
Менеджера нижнего звена включили в кадровый резерв для подготовки на более высокую управленческую должность.
Для составления плана индивидуального развития провели опрос по методу 360 градусов.
В числе прочего были вопросы, связанные с развитием и поддержкой подчиненных. Сам менеджер, его коллеги и руководители высоко оценили его качества в этой области.
Мнение подчиненных стало неожиданностью для «резервиста»: почти все подчиненные выбрали варианты «мой руководитель никогда не поддерживает мои инициативы и начинания», «руководитель никогда не защищает меня перед руководством».
HR-специалист обсудил результаты с «резервистом». Выяснилось, что оцениваемый менеджер применял на практике популярную установку «защищай своих сотрудников перед остальными отделами и начальством, отстаивай их интересы, но с самими сотрудниками будь строг и требователен». На всех совещаниях он пробивал хорошие условия, возможности, льготы, «зеленый свет» для своих подчиненных. А в личном общении с этими подчиненными крайне редко хвалил их и не озвучивал предпринятые в их интересах шаги; зато не упускал возможности сделать замечание, выговор за малейшие недоработки.
А в личном общении с этими подчиненными крайне редко хвалил их и не озвучивал предпринятые в их интересах шаги; зато не упускал возможности сделать замечание, выговор за малейшие недоработки.
В итоге сотрудники видели в нем лишь «придирчивого начальника», а результаты его усилий считали просто благоприятным стечением обстоятельств.
Менеджер был очень расстроен и согласился, что необходимо изменить сценарий общения с подчиненными. В его программу развития включили несколько целевых коммуникативных тренингов. Спустя полгода повторный опрос 360 показал гораздо более позитивное отношение подчиненных; KPI группы под его руководством за это время повысился на 16%.
Третий пример (приводила Светлана Иванова на одном из вебинаров).
Подчиненные и коллеги поставили руководителю среднего звена высокие оценки; вышестоящие руководители оценили деловые качества этой дамы низко.
HR-эксперту удалось «вытащить на поверхность» важную психологическую установку этой сотрудницы: она очень не любила людей, «заискивающих перед начальством», «подлизывающихся». В связи с этим с руководителями она часто разговаривала резко, с оттенком грубости, что отрицательно влияло на её профессиональный имидж. С коллегами и подчиненными, в то же время, она вела себя корректно.
В связи с этим с руководителями она часто разговаривала резко, с оттенком грубости, что отрицательно влияло на её профессиональный имидж. С коллегами и подчиненными, в то же время, она вела себя корректно.
С помощью тренингов удалось устранить эту особенность поведения сотрудницы, что положительно повлияло на её карьеру.
6.2. Для каких целей НЕ ПОДХОДИТ оценка 360:
а. Отбор в кадровый резерв.
б. Оценка для принятия решений о кадровых перестановках, изменении оплаты труда.
в. Аттестация.
Для перечисленных целей нужно использовать объективные методы оценки: экзамены для оценки профессиональных навыков (hard skills), тестирование, ассессмент для оценки «надпрофессиональных» навыков (soft skills).
Применяя метод оценки 360 для кадровых перестановок, оценивающий получает недостоверные данные, потому что сотрудники начинают искажать ответы:
✓завышают оценки, пытаясь помочь коллеге продвинуться по службе или сохранить работу,
✓ занижают оценки, мешая коллеге, к которому нет симпатий, продвинуться по службе,
✓ занижают оценки, сводя личные счеты,
✓ завышают оценки по просьбе коллеги, чтобы тому подняли зарплату.
Результаты оценки становятся недостоверными.
почему круг разделён на 360 градусов — Спрашивалка
ЯМ
Якоб Михель
почему круг разделён на 360 градусов круг градус
390
53
0
Ответы
ДК
Дарья Калиниченко
Казалось бы, какая связь между рассветом и количеством градусов в окружности? Самая прямая.
Дело в том, что солнечный диск преодолевает на небе расстояние, равное его диаметру — ровно за 4 минуты. Сегодня специально проверил по секундомеру.
60 разделить на 4 минуты = 15 диаметров в час.
15 умножить на 24 часа = 360 диаметров в сутки.
Итого, полный круг по небу равняется 360 диаметров солнечного диска. То есть, те самые 360°.
А угловой диаметр солнца, соответственно, равняется 1°.
Всё очень просто, не так ли?
Кстати, становится понятным и сам значок градуса — ° — это, типа, маленькое Солнце.
0
ДБ
Дима Бавыкин
необязательно на 360градусов, можно раделить в градах и радианах разделить круг.1 радиан = (1/2π) оборота = 180/π градусов = 200/π градов., следовательно если в градах то будет поделен на 400 градов., а вообще можно еще поделить на минуты секунды декаграда сантиграды,,,,вообщем вариантов разделить круг много))))
0
АР
Александр Реутов
По приблизительному количеству дней в году. См. древнюю астрологию.
0
Евгений Фед
потому, что ктото так придумал и все этому верят
0
Ядолов
Не знаю. А у артиллеристрв круг разделён на 60 д.у.
А у артиллеристрв круг разделён на 60 д.у.
0
Валентина Бульгак
В центре круга 4 прямых угла по 90 градусов.
0
Smail Of Smail
Обломов был прав -Две за мало три замного!
0
ПВ
Павел Выходцев
да..странно..на 3 по 120 градусов многова то
0
Василий Млозняк
потому что он разделен на 360 градусов
0
ЯМ
Якоб Михель
??????????
1
Марина Климовская
почему я подумала про 365 дней в году?
0
Минзиля Имайкина
по одному градусу на каждый день
0
НТ
Нина Трубина
пополам то получится 180градусов
0
Алла( Allaja) Бакланова
наверное, так учились считать. ..
..
0
Татьяна Юрьевич
попробуй разделить по другому.
0
GK
Grey Kostja
так удобней было разделить его
0
GK
Grey Kostja
так удобней было разделить его
0
Анастасия Ковалёва
поому что больше не убралось
0
АК
Айман Кулатаева
оо боже я далеко от этого
0
Ирина Сычева
я не математик, я филолог
0
Николай Насонов
он круглый и360 градусев
0
Следующая страница
Другие вопросы
Подскажите пожалуйста как избавить себя от сверх наглости? мне нужно чувство скромности
Что делать, чтоб девушка моя сделала мне минет?
,,Гы ! —вот имеННо —ТЫ !! (( Сколько ? ,накусала,, за ПРАЗДНИКИ !! —фото можешЪ СПОКОЙНО тут выложить ? а
подскажите пожалуста где можно скачать полные игры для телефона
почему когда чубайс сказал вам брать заводы вы отдали их директором и их детям? так вам коммунисты посоветовали ?
Почему современное общество имбицилов считает, что девушкам нужно уступать, а мужчинам можно в душу срать и отбирать всё?
Девушка на работе/учебе, в чем плюсы и минусы?
составь словарь к еме «осень»или»зима»
У меня wi-fi Dlink DWA-125 Не могу подключиться Помогите. Он показывает восклицательный знак и всё
Он показывает восклицательный знак и всё
почему извержение вулкана становится в одном случае стихийным бедствием, а в других редким запоминающимся зрелищем?
,,Хъм ! вам ? тоже часто говорятЪЪ —(( Роешся как ,,свиня,, в —АПЕЛЬСИНАХЪ !! Доброго Утра ! ЗЛОдейчики всем вам.
что означает видеть себя во сне длинными волосами
как качать с хабов?!.. пользователей вижу а их файлы не открываются…. может я что то ненастроил?
К чему это приснилось? См. внутри
Разве использовать кого-то ради своих целей, сидеть на шее хорошо? Любовь настоящая бескорыстна, любящие всё делят пополам
Почему круг имеет 360 градусов?
Вы когда-нибудь задумывались о том, как странно, что круг имеет 360 градусов? На первый взгляд кажется, что выбранное число было довольно случайным — почему бы не 100, или 500, или 720 градусов? Был ли это действительно случайный выбор? Или на самом деле была какая-то веская причина, по которой 360 было выбрано как количество делений в круге?
Сегодня мы узнаем, что на это действительно была веская причина. Что это было? Мы не совсем уверены. Но у нас есть несколько неплохих идей. И именно об этих идеях мы и поговорим.
Что это было? Мы не совсем уверены. Но у нас есть несколько неплохих идей. И именно об этих идеях мы и поговорим.
Когда и где 360 градусов
Как вы, наверное, знаете, в наши дни мы, люди, любим делить круг на 360 клиньев в форме пирога. Каждый из этих клиньев содержит угол при вершине, и мы говорим, что величина этого угла равна 1 градусу. Как вы, наверное, знаете, градусы — не единственный способ измерения углов. Углы также измеряются в радианах, а иногда (очень редко) они даже измеряются в непонятных военных единицах, называемых градианами (поэтому на многих калькуляторах есть кнопки «град град»).
Хотя мы точно не знаем, почему была выбрана конвенция 360 градусов (подробнее об этом через минуту), мы приблизительно знаем, когда и где все это началось. По крайней мере, мы знаем, что это произошло давным-давно — как 4 или 5 тысяч лет назад с вавилонянами, греками и, возможно, другими, даже более древними группами.
Что касается вопроса о , почему было выбрано 360 градусов, вот что, по нашему мнению, произошло…
Причина №1: Продолжительность года
Даже если в данный момент вы совершенно не представляете, почему существуют 360 градусов по кругу, держу пари, что если вы остановитесь и подумаете несколько минут, вы сможете найти одну возможность. Если после этих нескольких минут вы все еще не уверены, подумайте, где еще вы видели в своей жизни число, близкое к 360. И если вы все еще застряли после этого, подумайте о Солнце… Земле… орбитах… и календарях.
Если после этих нескольких минут вы все еще не уверены, подумайте, где еще вы видели в своей жизни число, близкое к 360. И если вы все еще застряли после этого, подумайте о Солнце… Земле… орбитах… и календарях.
Понятно?
Вы можете заключить, что Солнце проходит около 1/360 пути по этому кругу каждый день.
Земля обращается вокруг Солнца за один год. А в году всего чуть больше 365 дней. Это означает, что Земля вращается вокруг своей оси чуть более 365 раз в год. И это означает, что каждый день кажется, что Солнце проходит около 1/365 пути по огромному кругу, спроецированному на небо, которое простирается вокруг Земли (так называемая эклиптика). Если бы вы жили несколько тысячелетий назад и у вас не было современных инструментов для точной регистрации положения объектов на небе, вы могли бы сделать вывод, что Солнце каждый день проходит около 1/360 пути по этому кругу, а это именно то, что древние сделали астрономы. И тогда они сделали скачок и решили разделить этот круг на небе — и все круги — на 360 четных частей, чтобы Солнце проходило через 1 часть в день. Каждая из этих частей была названа 1 градусом, что дало нам представление о том, что круг содержит 360 градусов.
Каждая из этих частей была названа 1 градусом, что дало нам представление о том, что круг содержит 360 градусов.
Логично, правда? И учитывая, что древние вавилонский и персидский календари были основаны на 360-дневном году, кажется вероятным, что это простое астрономическое наблюдение является причиной того, что круг содержит 360 градусов.
Причина №2: Вавилоняне и числа с основанием 60
Но это не конец истории. Потому что есть и другие разумные идеи относительно происхождения соглашения 360 градусов. Как мы видели ранее, вавилоняне пользовались 360-дневным календарем. И, как оказалось, вавилоняне также использовали систему счисления с основанием 60 (называемую шестидесятеричной системой счисления). Точно так же, как мы используем 10 различных символов для представления чисел в нашей десятичной системе с основанием 10, древние вавилоняне использовали 60 символов для представления чисел.
Какое это имеет значение? Что ж, 60 x 6 = 360. Это означает, что 360 — это хорошее четное число, кратное числу в вавилонской системе (что имело бы такое же эстетическое значение для их мозгов, как и четное число, кратное 10, для нашего). Но это еще не все. Вавилоняне знали о равносторонних треугольниках. И они знали, что если вы расположите 6 таких равносторонних треугольников определенным образом так, чтобы край одного был выровнен поверх края следующего, последний в конечном итоге снова встретится с первым. Другими словами, общий угол, образованный 6 такими равносторонними треугольниками, будет таким же, как угол вокруг окружности. Учитывая, что вавилоняне использовали число 60 в качестве основы для счисления, они решили, что каждый из углов равностороннего треугольника будет равен 60 градусам. Таким образом, если вы умножите эти 60 градусов на 6 равносторонних треугольников, которые в совокупности образуют что-то вроде круга, вы получите 6 х 60 = 360 градусов. И таким образом, 360 градусов по кругу.
Но это еще не все. Вавилоняне знали о равносторонних треугольниках. И они знали, что если вы расположите 6 таких равносторонних треугольников определенным образом так, чтобы край одного был выровнен поверх края следующего, последний в конечном итоге снова встретится с первым. Другими словами, общий угол, образованный 6 такими равносторонними треугольниками, будет таким же, как угол вокруг окружности. Учитывая, что вавилоняне использовали число 60 в качестве основы для счисления, они решили, что каждый из углов равностороннего треугольника будет равен 60 градусам. Таким образом, если вы умножите эти 60 градусов на 6 равносторонних треугольников, которые в совокупности образуют что-то вроде круга, вы получите 6 х 60 = 360 градусов. И таким образом, 360 градусов по кругу.
Вот и все.
Причина № 3: множество факторов числа 360
Но это еще не конец истории… потому что есть еще одна причина любить число 360. А именно, оно делится без остатка на 2, 3, 4, 5, 6, 8. , 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120 и 180. Это множество факторов!
Это множество факторов!
И это делает 360 действительно удобным числом, потому что это означает, что мы можем разделить круг на 2, 3, 4, 5, 6, 8, 9, 10, 12 и так далее четных частей. Это делает решение проблем вручную — что, заметьте, было единственным способом решить проблемы тысячи лет назад — намного проще.
Хотя это само по себе не кажется достаточной причиной, чтобы склонить людей определять круг как имеющий 360 градусов, это определенно не помешало бы. И вполне возможно, что комбинация всех трех причин (а возможно, и других) в конечном итоге привела нас к определению степени, которым мы пользуемся до сих пор.
Подведение итогов
Хорошо, это все древняя математика, на которую у нас есть время на сегодня.
Чтобы получить больше удовольствия от математики, ознакомьтесь с моей книгой The Math Dude’s Quick and Dirty Guide to Algebra . И не забудьте стать поклонником The Math Dude на Facebook, где вы найдете множество отличных материалов по математике, публикуемых в течение недели. Если вы есть в Твиттере, подпишитесь на меня и там.
Если вы есть в Твиттере, подпишитесь на меня и там.
До встречи в следующий раз, это Джейсон Маршалл с «Быстрыми и грязными советами чувака-математика, чтобы сделать математику проще». Спасибо за внимание, любители математики!
Изображение Земли и Солнца от Shutterstock.
Полный круг | История Сегодня
В школе мы знаем, что в круге 360 градусов, но откуда эти 360 взялись? Когда указывается, что вавилоняне считали по основанию 60, а не по основанию 10, как мы, люди часто спрашивают, есть ли связь. Короткий ответ: нет. Более длинный ответ связан с вавилонской астрономией.
Как и другие древние народы, месопотамцы наблюдали за изменением положения солнца, луны и пяти видимых планет (Меркурия, Венеры, Марса, Юпитера и Сатурна) на фоне звезд на небе. До 2000 г. до н.э. писец в южном городе Урук, говоря о празднике богини Инанны, дал понять, что, как и Венера, она может быть как утренней, так и вечерней звездой, в зависимости от того, появляется ли она до восхода солнца или после захода солнца. Для них Венера была единым объектом, и они наблюдали ее изменение положения вместе с другими планетами и Луной. Все эти положения лежат на одном и том же большом круге, называемом эклиптикой, определяемом видимым движением солнца, наблюдаемого с земли в течение года. Причина, по которой Луна и планеты находятся на эклиптике, заключается в том, что, с точки зрения Земли, плоскость Солнечной системы встречается с небесным сводом по большому кругу, так что все они появляются именно там.
Для них Венера была единым объектом, и они наблюдали ее изменение положения вместе с другими планетами и Луной. Все эти положения лежат на одном и том же большом круге, называемом эклиптикой, определяемом видимым движением солнца, наблюдаемого с земли в течение года. Причина, по которой Луна и планеты находятся на эклиптике, заключается в том, что, с точки зрения Земли, плоскость Солнечной системы встречается с небесным сводом по большому кругу, так что все они появляются именно там.
Для точной записи их движений необходимы две вещи: фиксированный календарь и метод записи положений на эклиптике. Календари сложны. Фазы луны составляли ритм в жизни всех древних культур, и для жителей Месопотамии было естественным основывать свой календарь на месяцах, которые начинались вечером первого полумесяца на закате. При хорошей видимости лунный месяц длится 29 или 30 дней, и примерно к 500 г. до н.э. вавилоняне открыли схему определения начала каждого месяца. Это использовало 19-годовой цикл: 19 лет — это почти ровно 235 лунных месяцев, и схема работает на семь длинных лет (из 13 месяцев) и 12 коротких лет (из 12 месяцев). Это привело к фиксированному методу чередования длинных и коротких лет, который до сих пор используется в еврейском календаре и во всем христианском году в зависимости от даты Пасхи.
Это привело к фиксированному методу чередования длинных и коротких лет, который до сих пор используется в еврейском календаре и во всем христианском году в зависимости от даты Пасхи.
Записи, которые помогли им открыть этот цикл, появились в середине восьмого века до нашей эры, когда вавилонские астрономы записывали ночные наблюдения в то, что мы сейчас называем «астрономическими дневниками». Они продолжаются до конца клинописных исследований в первом веке нашей эры, что дало восемьсот лет астрономических записей: потрясающее достижение, намного более продолжительное, чем что-либо в Европе по сей день. Это способствовало большим успехам, особенно их открытию так называемых циклов Сароса для предсказания затмений. Каждый из них представляет собой цикл из 223 лунных месяцев, увековеченный в течение более чем 1000 лет. Сегодня действуют циклы Сароса, впервые увиденные в восьмом и девятом веках. Они остаются основой для предсказания затмений и подробно публикуются на веб-сайте НАСА.
Астрономы Вавилона использовали циклы Сароса к концу седьмого века до нашей эры. Им нужен был только лунный календарь, чтобы следить за ними, но для более сложной работы на Луне и планетах им нужен был постоянный, не лунный календарь. Поэтому они приняли старую идею административного календаря, использовавшуюся когда-то в третьем тысячелетии: 12 месяцев по 30 дней в году, что составляет 360-дневный цикл. Этот «идеальный календарь» вновь появляется во втором тысячелетии до нашей эры в вавилонских Семи Скрижалях Творения , в котором говорится, что бог Мардук «установил по три звезды на двенадцать месяцев». Эти тройки звезд соответствовали 12 частям эклиптики, по одной на каждый идеальный месяц из 30 дней, но это был идеализированный календарь, не используемый в повседневной жизни.
12 равных делений года также применяются для дня от заката до заката, разделенного на 12 беру . Например, в Эпосе о Гильгамеше , написанном во втором тысячелетии до нашей эры, наш герой мчится наперегонки с солнцем в Книге IX, и нам рассказывают, как он прогрессирует в каждом 9-м тысячелетии до нашей эры. 0013 beru , в итоге выходит прямо впереди. Как и в случае с идеальным месяцем, beru был разделен на 30 равных частей, называемых uš , что дает 360 uš за 24-часовой период. Таким образом, каждый составлял четыре минуты в современных терминах. Использовались также дроби от х : например, в астрономических дневниках мы находим случай, когда первое появление Луны было видно в течение 3 ¾ четверти х (15 минут).
0013 beru , в итоге выходит прямо впереди. Как и в случае с идеальным месяцем, beru был разделен на 30 равных частей, называемых uš , что дает 360 uš за 24-часовой период. Таким образом, каждый составлял четыре минуты в современных терминах. Использовались также дроби от х : например, в астрономических дневниках мы находим случай, когда первое появление Луны было видно в течение 3 ¾ четверти х (15 минут).
Для этих дневников важна точная запись времени, а также положения луны и планет. В пятом веке до нашей эры была разработана схема, которую можно было разбить на мелкие детали: эклиптика была разделена на 12 равных частей, каждая из которых была разделена на 30 более мелких частей (также называемых 9).0013 uš ), что в сумме дает 360 uš . Для большей точности число и было разбито на 60 делений. Каждую из 12 частей они обозначили созвездием звезд и, когда греки взяли за вавилонские результаты, они сохранили эти созвездия, но дали им греческие имена — Близнецы, Рак и Лев — большинство из которых имели те же значения, что и в Вавилонии.
По мере развития греческой геометрии возникло понятие угла как величины — например, сложение углов треугольника дает то же самое, что и два прямых угла — но в евклидовом Элементы (ок. 300 г. до н.э.) нет другой единицы измерения, кроме прямого угла. Затем, во втором веке до нашей эры, греческий астроном Гиппарх Родосский начал применять геометрию к вавилонской астрономии. Ему нужен был метод измерения углов, и он, естественно, следовал вавилонскому делению эклиптики на 360 градусов, точно так же деля окружность. Итак, хотя углы пришли от греков, 360 градусов пришли из вавилонской астрономии.
Марк Ронан — почетный профессор математики Университетского колледжа Лондона.
60 секунд и 360 градусов. Учебник по шестидесятеричной системе… | Хесус Наджера
Учебник по системе Sexagemisal (Base-60)
Первоначально опубликовано на https://www.setzeus.com/public-blog-post/60-seconds-360-grades Задумывались ли вы, почему в минуте/часе 60 секунд/минут? Или почему мы решили, что круг это ровно 360 градусов? Для любопытных кошек это, вероятно, обычное размышление, которое в тот или иной момент пробудило ваш интерес — наша система нумерации последовательно охватывает около десяти цифр (0–9). ), кроме для нескольких, разовых концепций, зачем это?
), кроме для нескольких, разовых концепций, зачем это?
Короткий ответ: история тесно связывает распространение времени и степеней с периодом, когда безраздельно властвовала шестидесятеричная система счисления с основанием 60. Более длинный ответ — эта статья, где мы сначала представим базовую систему нумерации, а затем постепенно введем вавилонский стандарт, который остается актуальным.
Базовая система представляет собой фиксированное количество различных цифр или комбинацию цифр, разрешенных в рамках определенной системы нумерации. Универсальная система счисления, с которой вы лучше всего знакомы, известна как 9.0108 десятичная система . Префикс «dec» относится к девяти цифрам, которые составляют нашу систему счисления: 0 — 9. Однако в математике, вместо десятичной системы, мы просто ссылаемся на этот стандарт нумерации как по основанию-10. Хотя это немного выходит за рамки этой статьи, большинство историков математики предполагают, что основная причина, по которой многие общества пришли к десятичной системе, заключается в том, что у нас есть 10 пальцев для счета. Повторим, это известно как основание 10, потому что система счисления «обертывается» один раз старшей цифрой (9).) Был достигнут.
Повторим, это известно как основание 10, потому что система счисления «обертывается» один раз старшей цифрой (9).) Был достигнут.
В любом случае, главное: десятичная система счисления / база-10 — это , а не единственная существующая система счисления (база). На самом деле, вполне вероятно, что вы наткнулись хотя бы на одну из следующих распространенных баз:
Именно эта последняя базовая система, шестидесятеричная базовая система, является темой du jour . Мы быстро объясним, как это работает, а затем погрузимся в историю того, почему он был создан в первую очередь. Хотя мы рассмотрим доказательства, общепризнано, что ни один универсальный ответ не согласован, по крайней мере, на данный момент — мы рассматриваем только теорий , стоящих за принятием этой мощной оставшейся базовой системы.
Как видно из приведенной выше таблицы, шестидесятеричная система — это древняя система счисления, которая определяется шестьюдесятью различными цифрами и более известна как с основанием 60 . По причинам, которые мы вскоре рассмотрим, основание 60 возникло в древнем Шумере в 3-м тысячелетии до нашей эры в Месопотамии (современный южный Ирак). Вскоре после этого он был передан древним вавилонянам и, в конечном итоге, всем соседним народам.
По причинам, которые мы вскоре рассмотрим, основание 60 возникло в древнем Шумере в 3-м тысячелетии до нашей эры в Месопотамии (современный южный Ирак). Вскоре после этого он был передан древним вавилонянам и, в конечном итоге, всем соседним народам.
Сейчас это трудно понять, но тогда система с основанием 60 была значительным прорывом в нумерации; тот факт, что он остается актуальным в современном повседневном применении, нельзя упускать из виду. Как следует из названия статьи, основание-60 — это система нумерации , используемая всякий раз, когда люди указывают время или ссылаются на градусы окружности.
Он заметно отличается тем, как он «переполняется» от 59 до 0, в отличие от нашей стандартной системы с основанием 10. В следующей таблице, найденной в вавилонских артефактах, указано, что вертикальный клин (V) представляет 1, а горизонтальный клин (<) представляет 10 — он десятичный, пока не достигнет 59.:
Вавилонские клинописные числительные Главной ошибкой в вавилонской системе, описанной выше, было отсутствие нуля — из-за этой ошибки 1 и 60 нельзя было различить по внешнему виду. Отличать их от контекста было неудобно, поэтому вскоре после этого был изобретен знак для пробела.
Отличать их от контекста было неудобно, поэтому вскоре после этого был изобретен знак для пробела.
Второй пример, немного хронологически более ранний, чем таблица выше, следующая сетка показывает древние месопотамские единицы времени. Один год делится на 12×30 = 360 дней, а один день делится на 12×30 = 360 частей. В этом примере они фактически используют base-360 — это было прямо перед принятием базы 60, но все еще служит примером наших корней обозначений.
Первоначально опубликовано на https://www.setzeus.com/public-blog-post/60-seconds-360-degreesУ шумеров было 12 часов в сутках, но в какой-то момент это время было изменено на 24 часа. В любом случае, это одно из самых ранних сохранившихся писаний древнего общества, в котором для обозначения времени использовалась ранняя шестидесятеричная система.
Удовлетворяя наше любопытство, будет справедливо спросить , почему эта базовая система вообще существовала или откуда она взялась. В отличие от десятичной системы, которую почти повсеместно приписывают удобству наших десяти цифр (пальцев), шестидесятеричная система немного более загадочна; за этим принятием стоит множество конкурирующих теорий, ниже мы рассмотрим четыре распространенные гипотезы.
Теория № 1 — Слияние культур
Одна из теорий, с которыми я столкнулся во время исследования, выглядит следующим образом:
Наиболее распространенная теория гласит, что два более ранних народа объединились 7 и образовали шумеров. Предположительно, одна группа основывала свою систему счисления на 5, а другая на 12. Когда две группы торговали вместе, они разработали систему, основанную на 60, чтобы обе могли ее понять.
К сожалению, мне не удалось проверить вышеприведенное утверждение из достоверного исторического источника. Многие статьи приписывают цитату одному выпуску «USA Today», но похоже, что указанный выпуск исчез. Основная логика, лежащая в основе этого культурного слияния, заключающаяся в том, что шумеры пришли к Base-60 просто потому, что две предшествующие культуры использовали Base-5 и Base-12, кажется слишком удобной без дополнительных доказательств. Надеюсь, теперь понятно, почему это просто теории.
Теория № 2 — 60 — это очень сложное число
К счастью, мы не первые, кто копается в анналах истории математики в поисках ответа на вопрос о росте числа с основанием 60. Известно, что самая популярная из предложенных гипотез была выдвинута неким Феоном Александрийским. Где-то лет ок. 335 — ок. 405, он пришел к выводу, что шумеры ценили и принимали основание 60, потому что оно имеет много делителей. Конечно, с учетом 12 делителей у него, безусловно, есть большое количество: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60. Есть много положительных качеств при выборе числа. с большим количеством делителей — в том числе и с тем, что легко сократить дробь со знаменателем на 60. Для дальнейшего доказательства того, что это, вероятно, был преднамеренный выбор, взгляните на следующую таблицу, в которой показаны первые 120 чисел с цифрами их делителей по оси Y:
Известно, что самая популярная из предложенных гипотез была выдвинута неким Феоном Александрийским. Где-то лет ок. 335 — ок. 405, он пришел к выводу, что шумеры ценили и принимали основание 60, потому что оно имеет много делителей. Конечно, с учетом 12 делителей у него, безусловно, есть большое количество: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60. Есть много положительных качеств при выборе числа. с большим количеством делителей — в том числе и с тем, что легко сократить дробь со знаменателем на 60. Для дальнейшего доказательства того, что это, вероятно, был преднамеренный выбор, взгляните на следующую таблицу, в которой показаны первые 120 чисел с цифрами их делителей по оси Y:
Положительное целое число, у которого больше делителей, чем у любого меньшего положительного целого числа, например 60, называется сильносоставным числом (HCN). HCN выступает за единицу измерения из-за его делимости. Как мы уже выяснили, соотношение между месопотамскими единицами измерения либо является делителем, либо кратным 60. системы счисления, среди ученых и историков существует высокий консенсус относительно того, почему она превратилась в наиболее широко принятую систему счисления — главным образом потому, что считать до 10 на пальцах обеих рук — врожденное свойство. Следуя тому же ходу мысли, третья гипотеза пытается оправдать месопотамскую шестидесятеричную систему с помощью аналогичной логики: система, полученная из счета с помощью наших цифр.
системы счисления, среди ученых и историков существует высокий консенсус относительно того, почему она превратилась в наиболее широко принятую систему счисления — главным образом потому, что считать до 10 на пальцах обеих рук — врожденное свойство. Следуя тому же ходу мысли, третья гипотеза пытается оправдать месопотамскую шестидесятеричную систему с помощью аналогичной логики: система, полученная из счета с помощью наших цифр.
Легко представить, что система счисления с основанием 10 или 5 возникла из счета пальцев одной руки, но как, черт возьми, можно считать по 12? Как оказалось, это неортодоксально, но вполне возможно сосчитать до 12 на одной руке. Фактически, историк Жорж Ифра утверждает, что система нумерации из двенадцати частей, как и связанная с ней система нумерации из шестидесяти частей, восходит к давно установленному и широко используемому методу счета по пальцам. Как он выразился, это:
Метод двенадцатеричного счета по пальцам Использовался в Индии, Индокитае, Пакистане, Афганистане, Иране, Турции, Ираке, Сирии и Египте.
в один момент времени. Так как же на пальцах можно сосчитать до 12? И как это связано с шестидесятеричной системой счисления по основанию?
Не обращая внимания на большой палец, рассмотрите четыре пальца на левой руке, особенно три части, разделенные нашими двумя суставами. Используя наши правая рука, начиная с большого пальца, мы считаем эти три сустава на каждом пальце, чтобы получить 12. Каждый раз, когда вы достигаете 12, перемещайте свой «счетный палец» на правой руке (от большого пальца к указательному к среднему). …) и продолжайте считать.
Как это соответствует стандарту шестидесятеричный (Base-60)? Считая до 12 на левой руке пятью чередующимися указательными инструментами (наша правая рука).
Стоит отметить, что никакие прямые письменные свидетельства не подтверждают эту теорию, это просто предположение, основанное на соседних культурах. И в каком-то смысле это, конечно, непрактичный метод подсчета, но действительно правдоподобно, что эта смешанная функция подсчета пальцев использовалась в качестве компаса, чтобы установить ограничение системы счисления на 60.
Теория №4 — 60 имеет астрономическое значение
Окончательная версия теории, представленная здесь, предлагает астрономический двигатель в качестве основной опоры для принятия. Ключ к ответу на вопрос, почему у шумеров была шестидесятеричная система, лежит в их календарной системе: лунно-солнечном календаре.
Многие соседние города-государства Месопотамии, такие как Ур, Урук и Лагаш, использовали похожий лунно-солнечный календарь. Все расположено недалеко от береговой линии Персидского залива, скорее всего, это не случайно. Геологическая теория здесь предполагает, что все они считали лунные циклы важными из-за приливных колебаний, вызванных гравитационным притяжением Луны. Это означало сильную расстановку приоритетов и адаптацию календаря Lunisolar. Поскольку фаза Луны меняется каждые 30 дней (точнее, 29.53), 30 или 29 дней должны составлять 1 месяц.
Это соответствует графику Шумера, представленному выше. Кроме того, из этой таблицы видно, что они уже отметили год как 360 дней.
При необходимости связать месяцы с годами и по-прежнему согласовываться со всеми вышеперечисленными причинами, будет небольшой скачок сказать, что 60 точно соответствует этому ответу как наименьшее общее кратное 12 и 30.
Мы живем в эпоху, которая сейчас компилируется. с достижениями новаторов и ученых на протяжении столетий, мы принимаем это как должное, но мы полностью отделены от понимания того, что находится под капотом. Интернет прочно вошёл в нашу жизнь, но мало кто может объяснить, как он работает; миллионы людей летают каждый божий день, но менее одного пассажира за поездку, вероятно, могут объяснить физику аэродинамики и турбулентности.
Наши отношения со временем и углами ничем не отличаются. Это своеобразная аномалия, что обе концепции используют систему счисления с основанием 60, немного отличающуюся от остальной части нашего математического языка; и все же это настолько переплетенная часть нашей природы, что мы теперь принимаем это как должное, не понимая почему.
Ну, по крайней мере, теперь вы можете: система счисления с основанием 60 является стандартом, который восходит к 3-му тысячелетию (до н.э.). Почему он был принят в первую очередь? Подтвержденного ответа нет, но четыре разные теории указывают на сочетание причин.
Интуитивное руководство по углам, градусам и радианам – BetterExplained
Очевидно, что круги должны иметь 360 градусов. Верно?
Неправильно. У большинства из нас есть , понятия не имею, , почему в круге 360 градусов. Мы запоминаем магическое число как «размер круга» и приводим себя в замешательство при изучении высшей математики или физики с их так называемыми «радианами».
«Радианы упрощают математику!» эксперты говорят без простой причины, почему (дискуссии, связанные с рядами Тейлора, непросты). Сегодня мы раскроем, что такое радианы на самом деле, и интуитивно понимаем, почему они облегчают математику.
Откуда берутся степени?
До чисел и языка у нас были звезды.
Древние цивилизации использовали астрономию для обозначения времен года, предсказания будущего и умилостивления богов (принося человеческие жертвы, им лучше быть вовремя ).
Какое отношение это имеет к углам? Ну, дружище, загадай мне вот что: не странно ли, что в круге 360 градусов, а в году 365 дней? И не странно ли, что созвездия кружатся по небу в течение года?
В отличие от пиратов, держу пари, вы, сухопутные бабы, не можете определять времена года по ночному небу. Вот Большой Ковш (Большая Медведица), вид из Нью-Йорка в 2008 году (попробуйте любой город):
Созвездия совершают круг каждый день (видео). Если смотреть в одно и то же время каждый день (в полночь), они также будут делать круг в течение всего года. Вот теория о том, как появились степени:
- Люди заметили, что созвездия совершают полный круг каждый год
- Каждый день они немного отклонялись («на градус»)
- Поскольку в году примерно 360 дней, окружность имеет 360 градусов
Но, но… почему бы не 365 градусов по кругу?
Дайте им слабину: у них было солнечных часов , и они не знали, что год должен иметь удобные 365,242199 градусов, как у вас.
360 достаточно близко для работы в правительстве. Он хорошо вписывается в вавилонскую систему счисления с основанием 60 и хорошо делится (на 2, 3, 4, 6, 10, 12, 15, 30, 45, 9).0… ну вы поняли).
Основание математики на Солнце кажется совершенно разумным
Земле повезло: ~360 — большое количество дней в году. Но это кажется произвольным: на Марсе у нас было бы около 680 градусов по окружности для более длинного марсианского года. А в некоторых частях Европы использовали градианы, когда вы делите круг на 400 частей.
Многие объяснения заканчиваются здесь словами: «Ну, степень произвольна, но нам нужно выбрать какое-то число ». Не здесь: мы увидим, что вся предпосылка степени задом наперед .
Правило радианов, градусы Слюни
Градус — это то, на сколько мне, наблюдателю, нужно наклонить голову, чтобы увидеть вас, движущегося. Это немного эгоистично, тебе не кажется?
Предположим, вы увидели, как ваш друг бежит по большой дорожке:
«Эй, Билл, как далеко ты ушел?»
«Ну, у меня был очень хороший темп, думаю, я пробежал 6 или 7 миль…»
«Офигеть.
Как далеко я повернул голову, чтобы увидеть, как ты двигаешься?
«Что?»
«Я буду использовать для вас короткие слова. Я в середине пути. Вы бегали вокруг. Насколько… сильно… я… повернул… голову?
«Придурок».
Эгоистично, да? Вот как мы занимаемся математикой! Мы пишем уравнения в терминах «Эй, как далеко я повернул голову, чтобы увидеть, что планета/маятник/колесо двигаются?». Бьюсь об заклад, вы никогда не задумывались о чувствах, надеждах и мечтах маятника.
Считаете ли вы, что уравнения физики должны быть упрощены для движущегося или наблюдателя?
Радианы: бескорыстный выбор
Большая часть физики (и жизни!) связана с выходом из системы отсчета и взглядом на вещи с точки зрения другого человека. Вместо того, чтобы задаваться вопросом, как далеко мы наклонили голову, подумайте, как далеко продвинулся другой человек .
Градусы измеряют углы тем, насколько сильно мы наклонили голову.
Радианы измеряют углы по пройденному расстоянию .
Но абсолютное расстояние не так полезно, поскольку 10 миль — это разное количество кругов в зависимости от трассы. Итак, мы делим на радиус, чтобы получить нормализованный угол:
Вы часто будете видеть это как
или угол в радианах (тета) это длина дуги (s), деленная на радиус (r).
Окружность имеет 360 градусов или 2pi радиан — полный оборот равен 2 * pi * r / r. Таким образом, радиан составляет около 360/(2 * пи) или 57,3 градуса.
Теперь не уподобляйтесь мне, запоминая эту мысль «Отлично, еще один юнит. 57,3 градуса — это так странно». Потому что это странно, когда ты все еще думаешь о себе!
Перемещение на 1 радиан (единицу) — это совершенно нормальное расстояние. Иными словами, наша идея «чистого, 9Угол 0 градусов» означает, что движок проходит очень нечистых единиц pi/2. Подумайте об этом — «Эй, Билл, ты можешь пробежать для меня 90 градусов? Это что? О, да, с вашей точки зрения, это пи/2 мили».
Странность двусторонняя.
Радианы — это чуткий способ заниматься математикой — переход от наклона головы к точке зрения движущегося.
Что в имени?
Радианы — это количество расстояний в терминах «единиц радиуса», и я думаю, что «радиан» является сокращением для этого понятия.
Строго говоря, радианы — это просто числа, такие как 1,5 или 73, и не имеют единиц измерения (в расчете «радианы = пройденное расстояние / радиус» мы видим, что длина делится на длину, поэтому любые единицы измерения отменяются).
Но с практической точки зрения мы не математические роботы, и полезно думать о радианах как о «расстоянии», пройденном по единичному кругу.
Использование радианов
Я все еще привыкаю думать в радианах. Но мы довольно часто сталкиваемся с понятием «расстояние движителя»:
При измерении определенных скоростей вращения мы используем «обороты в минуту», а не «градусы в секунду». Это сдвиг в сторону точки отсчета двигающегося («Сколько кругов он прошел?») и в сторону от произвольной градусной меры.
Когда спутник вращается вокруг Земли, мы понимаем его скорость в «милях в час», а не в «градусах в час». Теперь разделите на расстояние до спутника, и вы получите орбитальную скорость в радианах в час.
Синус, эта замечательная функция, определяется через радиан как
Эта формула работает только тогда, когда x в радианах! Почему? Что ж, синус в основном связан с пройденным расстоянием , а не с наклоном головы. Но мы оставим это обсуждение на другой день.
Радиан Пример 1: Колеса автобуса
Давайте рассмотрим реальный пример: у вас есть автобус с колесами радиусом 2 метра (это автобус-монстр). Я скажу, как быстро крутятся колеса, а вы скажете, как быстро движется автобус. Готовый?
«Колеса поворачиваются на 2000 градусов в секунду». Вы могли бы подумать:
- Хорошо, колеса вращаются со скоростью 2000 градусов в секунду. Это означает, что он делает 2000/360 или 5 и 5/9 оборотов в секунду.
Окружность = 2 * pi * r, значит, она движется, гм, 2 * 3,14 * 5 и 5/9… где мой калькулятор…
Хорошо. А теперь представьте себе машину с колесами радиусом 2 метра (тоже монстр). «Колеса автомобиля вращаются со скоростью 6 радиан в секунду». Вы могли бы подумать:
- Радианы — это расстояние вдоль единичной окружности — мы просто масштабируем по реальному радиусу, чтобы увидеть, как далеко мы продвинулись. 6 * 2 = 12 метров в секунду. Следующий вопрос.
Вау, в машине разобраться было проще, чем в автобусе! Никаких сумасшедших формул, никакого числа пи — просто умножить на , чтобы преобразовать скорость вращения в линейную скорость. Все потому, что радианы говорят в терминах движителя.
Обратное тоже легко. Предположим, вы едете со скоростью 90 футов в секунду по шоссе (60 миль в час) на своих 24-дюймовых ободах (радиус 1 фут). Как быстро вращаются колеса?
Итак, 90 футов в секунду / 1 фут радиуса = 90 радиан в секунду.
Это было легко.
Я подозреваю, что рэперы поют о 24-дюймовых дисках именно по этой причине.
Радиан Пример 2: sin(x)
Время для более мощного примера. Исчисление связано со многими вещами, и одна из них — это то, что происходит, когда числа становятся очень большими или очень маленькими.
Выберите количество градусов (x) и введите sin(x) в свой калькулятор:
Когда вы сделаете x маленьким, например, 0,01, sin(x) тоже уменьшится. А отношение sin(x)/x примерно равно 0,017 — что это значит? Еще более странно, что значит умножать или делить на степень? У вас могут быть квадратные или кубические градусы?
Радианцы спешат на помощь! Зная, что они относятся к пройденному расстоянию (это не просто отношение!), мы можем интерпретировать уравнение следующим образом:
- x — это расстояние, которое вы прошли по окружности
.- sin(x) — это то, как высоко вы находитесь на круге
Таким образом, sin(x)/x — это отношение того, насколько высоко вы находитесь, к тому, как далеко вы зашли: количество энергии, направленной «вверх».
Если вы двигаетесь вертикально, это соотношение равно 100%. Если вы двигаетесь горизонтально, это соотношение равно 0%.
Когда что-то движется на небольшую величину, например, от 0 до 1 градуса с нашей точки зрения, это в основном движется прямо вверх. Если вы перейдете еще на меньшую величину, от 0 до 0,00001 градуса, это будет , а на самом деле идет прямо вверх. Пройденное расстояние (x) очень близко к высоте (sin(x)).
По мере уменьшения x отношение приближается к 100 % — больше движения прямо вверх. Радианы помогают нам интуитивно понять, почему sin(x)/x приближается к 1, когда x становится крошечным. Мы просто немного подталкиваем в вертикальном направлении. Кстати, это также объясняет, почему sin(x) ~ x для малых чисел.
Конечно, вы можете строго доказать это с помощью исчисления, но интуиция в радианах поможет вам понять это.
Помните, что эти соотношения работают только при измерении углов в радианах. С градусами вы сравниваете свой рост на окружности (sin(x)) с тем, как далеко некоторый наблюдатель наклонил голову (x градусов), и это быстро становится уродливым.
Так в чем смысл?
Степени имеют свое место: в нашей собственной жизни мы являемся фокусом и хотим видеть, как вещи влияют на нас. Как сильно я наклоняю свой телескоп, крутлю сноуборд или поворачиваю руль?
С законами природы мы наблюдатель, описывающий движение других. Радианцы о них, а не о нас. Мне потребовалось много лет, чтобы понять, что:
- Градусов произвольные , потому что они основаны на солнце (365 дней ~ 360 градусов), но они назад , потому что они с точки зрения наблюдателя.
- Поскольку радианы выражены в терминах движителя, уравнения «встают на место». Преобразование скорости вращения в линейную легко, и такие идеи, как sin(x)/x, имеют смысл.
Равные углы можно рассматривать с нескольких точек зрения, а понимание радиан делает математические и физические уравнения более интуитивными. Счастливая математика.
Другие сообщения из этой серии
- Наглядное интуитивное руководство по воображаемым числам
- Интуитивная арифметика с комплексными числами
- Понимание того, почему сложное умножение работает
- Интуитивное руководство по углам, градусам и радианам
- Интуитивное понимание формулы Эйлера
- Интерактивное руководство по преобразованию Фурье
- Интуитивное руководство по свертке
- Интуитивное понимание синусоиды
- Интуитивное руководство по линейной алгебре
- Интуиция программиста для умножения матриц
- Мнимое умножение против мнимых показателей
- Интуитивное руководство по гиперболическим функциям
Угол 360 градусов – объяснение и примеры
Угол 360 градусов или полный угол – это мера внутреннего угла окружности.

В радианах полный угол равен $2\pi$ радианам.
$360$ Углы в градусах играют важную роль в математике, включая геометрию и тригонометрию, а также в естественных науках, включая астрономию и физику. Они также важны в инженерии, архитектуре и дизайне.
Прежде чем перейти к этому разделу, просмотрите углы и типы углов.
В этом разделе рассматриваются:
- Что такое угол 360 градусов?
- Угол 360 градусов против нулевого угла
- Определение угла 360 градусов
- Примеры полного угла
Что такое угол 360 градусов?
Угол в 360$ градусов — это полный оборот или «полный угол». Это также мера внутреннего угла окружности и сумма внутренних углов четырехугольника.
В радианах полный угол равен $2\pi$ радианам.
Поворот объекта на $360$ градусов возвращает его в исходное положение и первоначальную ориентацию.
Угол 360 градусов и нулевой угол
Угол 360 градусов и нулевой угол могут выглядеть одинаково. Это связано с тем, что если объект поворачивается на ноль градусов или на $360$ градусов, конечный результат будет таким же.
Процесс отличается. В одном случае ничего не сдвинулось. В другом случае объект совершил полный круг.
Однако из-за этого факта тригонометрические функции являются $2\pi$ циклическими. То есть их значения повторяются через каждые $2\pi$ или $360$ градусов. То есть свойства угла в 360$ будут такими же, как и у угла в 0$.
Угол 360 градусов Определение
Угол $360$ градусов — это полный оборот. Он равен $2\pi$ радианам или внутреннему углу окружности.
Примеры полного угла
Наиболее классическим примером полного угла является единичный круг.
Это круг радиусом один с центром в начале координат. Такой круг имеет длину окружности $2\pi$, а длина дуги любого участка окружности равна длине радиана.
Эти круги используются в тригонометрии, потому что в этом круге легко нарисовать прямоугольные треугольники, которые имеют простые размеры, что упрощает поиск тригонометрических соотношений.
Суммарный угол единичной окружности равен $360$ градусам. При работе с углами, превышающими $360$, отношения находятся путем вычитания $360$ градусов или $2\pi$ радиан столько раз, сколько необходимо, пока не получится число $k$, большее или равное $0$ и меньшее, чем $360. $. Тогда отношение для начального угла равно отношению при $k$.
Примеры
В этом разделе рассматриваются распространенные примеры задач на полные углы и их пошаговые решения.
Пример 1
Докажите, что сумма внутренних углов четырехугольника равна $360$ градусов.
Решение
Есть несколько способов сделать это. Один из способов заключается в том, чтобы узнать, что сумма внутренних углов треугольника равна $180$ градусам или мере прямой линии.
Этот факт известен с древности и может быть доказан без измерения углов. На самом деле, у Евклида есть доказательство этого факта в его элементах в предложении 32.
Но если соединить два треугольника, получится четырехугольник.
Следовательно, сумма внутренних углов четырехугольника должна быть равна сумме внутренних углов двух треугольников. То есть сумма внутренних углов должна быть равна мере двух прямых.
Но две прямые — это полный угол. Следовательно, внутренний угол четырехугольника равен $360$ градусам или $2\pi$ радианам.
Пример 2
Найдите угол, который больше или равен $0$ градусов и меньше $360$, что эквивалентно $567$ градусам. Классифицируйте этот угол.
Решение
Полный угол и угол, равный нулю градусов, лежат на одной прямой и указывают в одном направлении. В этот момент углы сбрасываются. Следовательно, угол $360$ действует так же, как угол $0$. Точно так же угол в 361$ градус обладает теми же свойствами, что и угол в 1$ градус.
Таким образом, чтобы найти угол с теми же свойствами, нужно многократно вычитать из угла $360$ градусов или $3\pi$, пока разница не станет числом от $0$ до $360$.
В этом случае $567-360 = 207$.
Таким образом, угол с мерой $567$ градусов будет иметь те же свойства, что и рефлекторный угол $207$ градусов.
Пример 3
Аналоговые часы показывают 4 часа. Какое время будет после того, как минутная стрелка сделает оборот на 360 долларов? На сколько градусов повернется часовая стрелка за это же время?
Решение
Когда минутная стрелка делает поворот на 360$ градусов, она возвращается в исходное положение. Поскольку начальное время было 4 часа, минутная стрелка начиналась с двенадцати. После поворота он вернется на двенадцать.
Когда минутная стрелка делает полный оборот за сутки, это означает, что прошел один час. Таким образом, часовая стрелка переместится из положения, находящегося прямо на четвёрке, прямо на пятерке. Это означает, что часовая стрелка переместится на $\frac{1}{12}$-й круг. В градусах это $\frac{360}{12} = 30$ градусов. В радианах это $\frac{2\pi}{12} = \frac{\pi}{6}$ радиан.
Пример 4
Круг имеет радиус $4$.
Найдите длину отрезка окружности, длина дуги которого равна $360$ градусов.
Решение
Длина дуги отрезка — это длина окружности окружности, заключенной под заданным углом, образованным центром окружности и двумя радиусами.
Длина дуги $360$ градусов означает, что угол, образованный двумя радиусами, является полным углом. Но это также полный внутренний угол круга. Следовательно, длина отрезка окружности, содержащегося в этом угле, равна полной окружности.
Длина окружности этого круга равна $8\times\pi = 8\pi$.
Пример 5
Покажите, что сумма внутреннего угла и соответствующего ему внешнего угла в многоугольнике составляет полный угол.
Решение
Внутренний угол многоугольника равен наименьшему из двух возможных углов. Другой угол, который будет углом рефлекса, представляет собой тот же угол, измеренный в противоположном направлении (по часовой стрелке или против часовой стрелки).
Эти два угла вместе образуют круг.
Следовательно, их угловая мера составляет $360$ градусов или $2\pi$ радиан, то же, что и полный угол.
Другие примеры и пояснения
- Докажите, что если к треугольнику добавить четырехугольник так, что две прямые четырехугольника лежат на одной линии с двумя линиями сторон треугольника, а другая сторона четырехугольника равна третья сторона, то новая фигура представляет собой треугольник.
- Часовая стрелка на часах поворачивается на $360$ градусов. Что такое новое время и на сколько градусов повернулась минутная стрелка?
Ключ ответа
- Треугольник и четырехугольник с одной общей стороной образуют фигуру с $3+4-2 = 5$ сторонами и углами. Суммарная мера его внутреннего угла составит $540$ градусов.
Однако этот пятиугольник имеет два прямых угла, потому что две стороны четырехугольника лежат на одной линии с двумя сторонами треугольника. Каждый прямой угол в многоугольнике фактически уменьшает его на одну сторону. В этом случае общее количество сторон будет $5-2 = 3$.Следовательно, полученная фигура будет треугольником.
- Если часовая стрелка повернется на $360$ градусов, значит, прошло двенадцать часов. Это означает, что время то же самое, но изменилось время AM или PM. Например, если начальное время было 8:00, новое время — 20:00.
Поскольку минутная стрелка совершает оборот на $360$ один раз в час, она сделала оборот на $360 \× 12 = 4320$ градусов.Иллюстрации/математические объекты, созданные с помощью GeoGebra.
Plus 360 Degrees GmbH
Вы любите печенье?
🍪 Мы используем файлы cookie, чтобы обеспечить вам максимальное удобство на нашем веб-сайте. Узнать больше — Принять — Отклонить
3D Meister Planner
3D Meister Planner — самый простой в мире 3D-планировщик! Это современное приложение, использующее весь потенциал современных веб-технологий за счет использования аппаратного ускорения и параллельных вычислений. Пользователи могут легко выбирать из множества вариантов, одновременно имея возможность легко реализовать их с помощью существующих баз данных продуктов.
Для получения дополнительной информации, пожалуйста, посетите наши веб-сайты продуктов и свяжитесь с нами!
Посетите проект
Realtime 3D Experts
Plus 360 Degrees — отмеченная наградами студия из Берлина, Германия. Он был основан 3D-художником и дизайнером продуктов Делией Отетеа, а также многопрофильным художником и веб-разработчиком Иваном Морено с целью создания специализированных высококачественных 3D-опытов в реальном времени для брендов и агентств. Наша команда имеет опыт создания контента и ресурсов для реалистичных 3D-приложений, видеоигр и инсталляций с использованием широкого спектра методов и инструментов.
Наши самые известные разработки — это конфигураторы транспортных средств, где пользователи могут исследовать и настраивать их под любым углом. Помимо разработки новых решений для автомобильной промышленности, мы также обслуживаем аэрокосмическую промышленность, архитектуру, моду и промышленный дизайн.
Над облаками
Над облаками — дань уважения Земле.
Это видео в реальном времени, которое отправляет пользователя в путешествие над землей по разным местам по всему миру. Он призван вдохновить каждого из нас, объединить нас и заставить осознать, что есть только один дом – Земля. Сделано в WebGL, доступно с компьютеров и мобильных устройств.
Посетите проект
Тщательно построенный
Мы можем справиться со всеми аспектами интерактивного 3D-проекта; от концепции до дизайна и разработки. Мы разрабатываем и создаем пользовательский интерфейс с учетом имиджа наших клиентов, целевых групп и платформ распространения. Мы ищем союз искусства и перформанса, зная, что для достижения наилучшего результата они всегда должны идти рука об руку. Наши клиенты всегда получат от этого максимум пользы.
Мы никогда не стоим на месте. Для того, чтобы мы могли предложить нашим клиентам новейшие и самые передовые решения, мы постоянно находимся в состоянии исследований и разработок. Вот почему мы всегда расширяем границы современных технологий, а также тестируем различные методы предоставления привлекательного контента конечным пользователям.
О любви
О любви — это метафора двух людей, которые находят друг друга, и этапов, которые они проходят в своей связи. Все начинается с бурной жизни свиданий и поиска подходящего партнера. Затем представлена прелюдия, ведущая к первому поцелую. Затем эти двое соединяются и проходят фазу увлечения, и, в конце концов, они начинают путешествие того, как мы все оказались здесь — создавая новую жизнь.
Посетите проект
Признание
Наши работы были представлены на известных международных мероприятиях, таких как SIGGRAPH WebGL BOF, 3DWebFest, Временная выставка Музея дизайна MOOD, Неделя дизайна в Будапеште, Фестиваль архитектуры и дизайна интерьера Мумбаи — FOAID, Международный промышленный дизайн в Шэньчжэне Ярмарка — SZIDF, среди прочих мероприятий. Он также был опубликован в книгах по дизайну, книгах по компьютерному программированию и научных статьях по трехмерной компьютерной графике и интерактивным методам.
Мы имеем честь быть награжденными и проинтервьюированы международными организациями дизайна, такими как A Prime Design Award and Competition, Adobe Design Achievement Award и FWA, будучи Иваном FWA Hero.
Иван поделился на всемирно известной JSConfEU своими творческими, художественными и техническими процессами в создании фотореалистичной компьютерной графики в реальном времени.
uxcars
UXCARS — это лучшая веб-платформа для визуализации автомобилей, которая революционизирует онлайн-опыт, позволяя пользователям исследовать, настраивать, делиться и играть с самой большой коллекцией интерактивных 3D-автомобилей, ускоряя процесс принятия решений. Целью проекта является предоставление наилучших визуальных и эффективных результатов пользователям, которые либо ищут свою следующую покупку, либо автолюбителям, которые хотят настроить свой текущий автомобиль.
Посетите проект
Наши клиенты
На протяжении многих лет мы имеем удовольствие работать с клиентами из различных отраслей, такими как The Boeing Company, Alcar Holding, RPA, ACME DC, Isabella Wren, Sommer, Sistemi Moderni и другими. Если вы хотите стать нашим следующим партнером, не стесняйтесь обращаться к нам!
Car Visualizer Classics
Car Visualizer Classics был создан как продолжение первого Car Visualizer и, как видно из названия, представляет коллекцию классических автомобилей.
Благодаря усовершенствованию методов разработки это более совершенный визуализатор транспортных средств, к которому можно получить доступ с множества устройств.
Посетите проект
Кросс-платформенный
Наша внутренняя платформа позволяет использовать конфигураторы на нескольких носителях распространения контента; киоск, настольный компьютер, ноутбук, планшет и мобильный телефон, а также видеопроекция и большие установки. Наша команда использует возможности WebGL для развертывания приложений для самых разных компьютеров и устройств.
«Лучше и быстрее» — один из наших девизов. Мы всегда нацелены на предоставление самых привлекательных и высокопроизводительных приложений. После многих лет доработки и полировки созданный нами конвейер позволяет нам создавать живой контент с очень эффективным временем обработки.
Годы создания контента для различных носителей научили нас важности внимания к мельчайшим деталям. Это то, что отличает нас.
Автомобильный визуализатор
Автомобильный визуализатор был новаторским проектом в области онлайновых 3D-презентаций в реальном времени.




 Проделаем ту же операцию необходимое число раз. Затем положим размеченную таким образом верёвку поверх нарисованной на земле окружности (узелки соответствуют меткам, которые оставил бы на земле катящийся диск в первом способе построения). В данном случае при вычерчивании окружности можно обойтись без рулетки: радиус R окружности получим, отложив на верёвке диаметр диска n/2 раз (при нечётном n придётся добавить длину радиуса).
Проделаем ту же операцию необходимое число раз. Затем положим размеченную таким образом верёвку поверх нарисованной на земле окружности (узелки соответствуют меткам, которые оставил бы на земле катящийся диск в первом способе построения). В данном случае при вычерчивании окружности можно обойтись без рулетки: радиус R окружности получим, отложив на верёвке диаметр диска n/2 раз (при нечётном n придётся добавить длину радиуса). Первые оценки. Проблема соизмеримости длины окружности с ее диаметром. Бесконечные ряды, произведения и другие выражения для π. Сходимость и ее качество. Выражения, содержащие π. Последовательности, быстро сходящиеся к π. Современные методы вычисления π, использование компьютеров. Об иррациональности и трансцендентности π и некоторых других чисел. Предварительных знаний для понимания курса не требуется.
Первые оценки. Проблема соизмеримости длины окружности с ее диаметром. Бесконечные ряды, произведения и другие выражения для π. Сходимость и ее качество. Выражения, содержащие π. Последовательности, быстро сходящиеся к π. Современные методы вычисления π, использование компьютеров. Об иррациональности и трансцендентности π и некоторых других чисел. Предварительных знаний для понимания курса не требуется. И дети, и взрослые читатели часто сожалели, что там были только математические задачи, — ведь и все естествознание заслуживает столь же активного, творческого к себе отношения. Теперь я отвечаю на эти пожелания — следуя скорее Яну Амосу Каменскому, чем современным педагогам, то есть всегда стремясь быть понятным читателю, не имеющему предварительных знаний (но столь же любознательному, как большинство подростков).
И дети, и взрослые читатели часто сожалели, что там были только математические задачи, — ведь и все естествознание заслуживает столь же активного, творческого к себе отношения. Теперь я отвечаю на эти пожелания — следуя скорее Яну Амосу Каменскому, чем современным педагогам, то есть всегда стремясь быть понятным читателю, не имеющему предварительных знаний (но столь же любознательному, как большинство подростков). В конце концов, вы ведь учили математику в школе!
В конце концов, вы ведь учили математику в школе! Но не зря ли мы тратим время? Чем может помочь геометрия в жизни? Измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться.
Но не зря ли мы тратим время? Чем может помочь геометрия в жизни? Измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться. Рассмотрены задачи «о ходе коня» и «о восьми ферзях», которыми занимались великие математики Эйлер и Гаусс. Дано математическое освещение некоторых чисто шахматных вопросов — геометрические свойства шахматной доски, математика шахматных турниров, система коэффициентов Эло.
Рассмотрены задачи «о ходе коня» и «о восьми ферзях», которыми занимались великие математики Эйлер и Гаусс. Дано математическое освещение некоторых чисто шахматных вопросов — геометрические свойства шахматной доски, математика шахматных турниров, система коэффициентов Эло.