4)Биномиальный ряд.
Разложим в ряд Маклорена функцию f(x)=(1+x)m, где m любое целое постоянное число. Непосредственная оценка остаточного члена и тут затруднена. Поступим следующим образом. Заметим, что функция f(x)=(1+x)m удовлетворяет дифференциальному уравнению (1+x)f'(x)=(m)f(x) (*), и условию f(0)=1. Найдем степенной ряд, сумма которого S(x) удовлетворяет уравнению (*) и условию S(0)=1: (5). Подставим в (*) получим . Приравняем коэффициенты при одинаковых степенях x:a1=m;a1+2a2=ma1; …;nan+(n+1)an+1=man. Отсюда найдем — это биномиальные коэффициенты. Подставляя их в формулу (5), получим:
(6).
Если m целое
положительное число, то сумма (6)
обрывается, т.к. начиная с члена содержащего
xm+1 все
коэффициенты равны нулю. При других m
имеется бесконечный ряд. Определим его
радиус сходимости:
,,.
Ряд (6) сходится при |x|<1. Получили, что в (-1;1) ряд (6) представляет функцию S(x), удовлетворяющую дифференциальному уравнению (*) и условиюS(0)=1. Но дифференциальному уравнению может удовлетворять только одна функция с таким условием, потому S(x)=(1+x)m в (-1;1). Итак:
(7).
Это и есть биноминальный ряд. При m целом положительным он обрывается и дает формулу бинома Ньютона.
5)Функция f(x)=arctg(x).
Рассмотрим ряд: сходится в (-1;1). Проинтегрируем на [0;x], |x|<1. Получим:
(8).
Можно доказать, что (4) верно на [-1,1].
Если дана функции (1) и нужно вычислить ее приближенное
значение при некотором х, то достаточно
взять сумму нескольких ее первых членов
f(x)»Sn(x).
Сколько первых членов нужно взять, чтобы
обеспечить точность вычисления, на этот
вопрос дает ответ оценка остатка ряда
|r n(x)|.
Если ряд типа Лейбница, то |rn(x)|£|an+1xn+1|. Отсюда находим n, начинаяс которого rn(x) не превосходит заданной точности. Если ряд другой, то применяют мажорируемый ряд (обычно геометрическую прогрессию) сумму остатка которой можно оценить легче.
Примеры:
1)Вычислить число е сточностью до 7 знаков.
Т.к. , то при x=1 имеем: Оценим |rn|.
.
Итак, . Должно быть ; видно, что при n=10 это уже есть. Поэтому достаточно взять 11 первых членов:
.
2) Вычисление логарифмов чисел.
Если х принадлежит (-1;1), то (1). если заменитьх на -х, то (2) также справедливо в (-1;1).(1) и(2) применяются для вычисления ln чисел между 0 и 2. Как вычислить логарифмылюбых чисел? Сходящиеся ряды можно вычитать. Из (1) вычтем (2), получим:
(3)
верно в (-1;1). Всякое положительное
число t можно представить в виде при хÎ(-1;1):
t-t×x=1+x,
,
потому можно вычислять:
Всякое положительное
число t можно представить в виде при хÎ(-1;1):
t-t×x=1+x,
,
потому можно вычислять:
.
3) Вычисление корней.
Надо с большой точностью вычислить . Допустим известно некоторое приближенное значение этого корня »b, тогда a»bn, , где a-небольшая величина: ½a½<1. Тогда
. Разлагая в биномиальный ряд, получим с любой точностью.
Пример: Поэтому
Вычисление интегралов.
=
Выбирая нужное число членов полученного знакочередующегося ряда, мы и найдем значение данного интеграла с заданной точностью.
Степенные ряды
применяются к вычислению пределов
(раскрытию неопределенности), к
приближенному решению дифференциальных
уравнений и т. п.
п.
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации — обмен информацией между организацией и её внешней средой… Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь… История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации… Интересное: Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений… Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными. Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 4 из 4 1. Имеем ; , и по формуле (5.2) получаем . (5.3) Областью сходимости этого степенного ряда является интервал . 2. Имеем: , , , , , откуда , , , , и т.д. Очевидно, что производные четного порядка , а нечетного порядка , , и по формуле (5.2) имеем (5.4) Область сходимости ряда . 3. . Рассматривая аналогично функции , получим: (5.5) Область сходимости ряда . 4. , где – любое действительное число. Имеем , , , , …, , … При : , , , , …, и по формуле (5.2) получаем (5.6) Найдем интервал сходимости ряда: Ряд, составленный из модулей , исследуем с помощью признака Даламбера: . Следовательно, интервал сходимости ряда . На концах интервала при сходимость ряда зависит от конкретных значений . Ряд (5.6) называется биномиальным. Если – целое положительное число, то биномиальный ряд представляет формулу бинома Ньютона, так как при сомножитель равен нулю, следовательно, -йчлен ряда и все последующие равны нулю, т. Выпишем некоторые разложения функции при различных . : , (5.7) Если в это разложение подставить вместо , получим: (5.8) : , (5.9) : , (5.10) 5. . Получить разложение для этой функции, непосредственно вычисляя коэффициенты с помощью производных, не очень просто, поэтому мы воспользуемся разложением (5.7) и свойством 2) степенных рядов. Интегрируя почленно равенство (5.7) в интервале , где , с учетом того, что , получим (5.11) Область сходимости ряда (после выяснения сходимости на концах интервала) есть . 6. Проделаем то же самое, что и в предыдущем случае, воспользовавшись разложением (5.8): (5.12) Область сходимости ряда . 7. Воспользуемся разложением (5.10), подставив в него вместо : Интегрируя в интервале , где , получаем: (5.13) Область сходимости ряда Можно доказать, что ряды, приведенные в формулах (5. При разложении более сложных функций часто используют готовые разложения (5.3) – (5.13). Примеры 1) Разложить в ряд Маклорена функцию Решение. Воспользуемся известной тригонометрической формулой Разложим в ряд Маклорена функцию , заменяя в разложении (5.5) на : Тогда Это и есть разложение в ряд Маклорена функции . Очевидно, что оно справедливо при любом . 2) Разложить в ряд Тейлора по степеням функцию Решение. Преобразуем данную функцию так, чтобы можно было воспользоваться разложением (5.7): Полученное разложение справедливо, когда . Отсюда получаем или . Применение рядов в приближенных вычислениях Степенные ряды имеют самые разнообразные приложения. С их помощью вычисляют с заданной степенью точности значения функций, определенных интегралов, которые являются «не берущимися» или слишком сложными для вычислений, интегрируются дифференциальные уравнения. Примеры I. Вычислить приближенно с точностью до 0,0001: а) Решение. Для вычисления запишем ряд (5.3) при , принадлежащем области сходимости : Взяв первые пять членов разложения, на основании следствия из теоремы Лейбница для сходящегося знакочередующегося ряда, мы допустим погрешность , не превышающую первого отброшенного члена (по абсолютной величине), т.е. . Итак, б) Решение. Воспользуемся разложением (5.11), подставив в него , входящее в область сходимости : Так как данный числовой ряд не является знакопеременным, то о погрешности нельзя судить по величине первого отбрасываемого члена. Если в качестве взять сумму первых трех членов, мы допустим погрешность (здесь мы учли, что сумма сходящегося геометрического ряда в скобках равна ) Итак, в) Решение. Для вычисления запишем ряд (5.4) при , принадлежащем области сходимости : (необходимо взять два члена, так как при этом погрешность ). . II. Вычислить приближенно с точностью до 0,001 следующие интегралы: a) Решение. Так как интеграл «не берущийся», «точное» интегрирование здесь невозможно. Воспользуемся разложением (5.4). Разделив обе части на , получим , причем ряд сходится при всех значениях . Интегрируя почленно, получим: Возьмем первые три члена разложения, т.к. . Итак, б) Решение. Заменив на в разложении (5.3), получим: . Умножая полученный ряд на : , и почленно интегрируя в интервале , принадлежащем интервалу сходимости ряда , имеем: При этом . Итак, . Задачи Разложить в ряд Маклорена следующие функции, указав промежутки сходимости полученных рядов. 86. 87. 88. 89. 90. 91. 92. Разложить в ряд Тейлора следующие функции и найти область сходимости полученного ряда. 93. по степеням 94 по степеням 95. 96. по степеням 97. по степеням 98. по степеням Вычислить приближенно с точностью до 0,0001: 99. 100. 101. 102. 103. 104. Вычислить приближенно, взяв первые два члена разложения в ряд подынтегральной функции, и оценить допущенные при этом погрешности: 105. 106. Ответы В задачах1, 3, 6, 7, 8, 9, 10, 12, 13, 15, 17, 18, 19, 21, 22, 23, 31, 32, 33, 34, 35, 37, 38, 42, 43, 44 – ряды сходятся. В задачах 2, 4, 5, 11, 14, 16, 20, 24, 25, 26, 27, 28, 29, 30, 36, 39, 40, и 41 – ряды расходятся. В задачах 45, 46, 47, 49, 50, 51, 55 – ряды абсолютно сходятся. В задачах 48, 53, 54, 57 – ряды сходятся условно. В задачах 52, 56, 58, 59 – ряды расходятся. 60.(-1;1],61.[-1/2;1/2),62.{0},63.(-1/3;1/3],64.(-1;1),65.[0;2],66.[-10;10),67.(-∞;∞), 68.(-7;-1), 69. [-4;4), 70. 86. 87. 88. 89. 90. 91. 92. 93. 94. 95. 96. 97. 98. 99. 100. 101. 102. 103. 104. 105. 106. .
Оглавление §1. Основные понятия. 4 §2. Признаки сходимости знакопостоянных рядов. 7 §3. Признаки сходимости знакопеременных рядов. 22 §4. Степенные ряды.. 27 §5. Ряды Маклорена и Тейлора. 32 §6. Применение рядов в приближенных вычислениях. 39 Ответы.. 43 Подписано в печать 2012 г. Формат 60´84/16. Бумага писчая. Отпечатано на ризографе.
Московский государственный университет тонких химических технологий им. М.В.Ломоносова Издательско-полиграфический центр 117571, Москва, просп. Вернадского, 86.
* Напомним, что степенью степенного выражения называется наибольшая из степеней входящих в него слагаемых, само это слагаемое называется старшим, а его коэффициент называется старшим коэффициентом. Например, у степенного выражения старшее слагаемое имеет степень 1,5, а старший коэффициент равен 5. ⇐ Предыдущая1234 Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим. |
Биномиальный ряд и функция — Статистика Как сделать
Последовательность и ряд >
Биномиальный ряд является разновидностью ряда Маклорена для степенной функции f(x) = (1 + x) m . Расширение ряда можно найти по формуле: «Биномиальный ряд» назван так потому, что это ряд — сумма членов в последовательности (например, 1 + 2 + 3). ), а это «бином» — две величины (от латинского binomius , что означает «два имени»). Два термина заключены в круглые скобки. Например, (a + b) и (1 + x) являются биномами. Когда эти величины возводятся в степень и расширяются, мы получаем биномиальное разложение : Как только вы превысите четвертую степень, алгебра станет утомительной. Формула расширения биномиального ряда также может использоваться для упрощения более сложных функций. Σ в формуле — это обозначение суммирования, что в основном означает «сложить все». (m k) — биномиальный коэффициент, равный m! / (к! (м – к)!), где ! символ — факториал. Пример вопроса: Выразите следующую функцию в виде биномиального ряда: Решение : Шаг 1 Вычислите первые несколько значений биномиального коэффициента (m k). Это не дает большой подсказки, поэтому давайте продолжим с третьим и четвертым членами: Возникает закономерность, поэтому мы можем обобщить расширение для любого «k» до: Примечание : Если вы не видите шаблона, продолжайте поиск коэффициентов, пока не увидите! Образец почти всегда появляется после третьего или четвертого биномиального коэффициента, поэтому, если к тому времени у вас его нет, вернитесь и проверьте свою алгебру. Шаг 2: Запишите решение. Все, что вам здесь нужно сделать, это записать члены, рассчитанные на шаге 1 (показаны желтыми прямоугольниками), а затем соответствующую степень x (синие прямоугольники). Критерий соотношения можно использовать, чтобы показать, что ряд сходится для абсолютных значений x меньше 1, |x| < 1 (к ожидаемой сумме (1 + x) k ) и расходится при |x| > 1. Забавный факт: формула биномиального ряда высечена на надгробии Ньютона (по его просьбе) в Вестминстерском аббатстве (Nitecki, стр. 367). Термин «биномиальная функция» может означать несколько разных вещей: Биномиальная функция «А» — это функция с двумя членами (Dick & Patton, 1992). Примеры: Биномиальная функция – это особая функция вида: f m (x) = (1 + x) m Где «m» — действительное число. Если m положителен, функция является полиномиальной функцией. В исчислении используются другие формы биномиальных функций. Например, в виде степенного ряда биномиальная функция определяется для любого действительного числа α: (1 + t) α = e α log (+ t) В теории вероятности и статистике функцию биномиальной вероятности иногда называют просто 9.0027 биномиальная функция . Общая форма биномиальной функции вероятности: вероятность отказа, определенная для множества {0,…,N). «Успехи» и «Неудачи» определяются тем, какой эксперимент вы проводите, а не успехом или неудачей всего эксперимента. Например, если вы пытаетесь найти вероятность того, что вы вытащите красный шар из банки с красными и черными шарами, вашим «успехом» будет вытаскивание красного шара, а «неудачей» будет вытаскивание черного. Биномиальные функции используются в программном обеспечении для расчета биномиальных вероятностей. Например, в R dbinom(x,n,p) находит количество успешных попыток для определенного количества испытаний. Гипергеометрическая функция Гаусса (иногда называемая гипергеометрической функцией Эйлера-Гаусса или «гипергеометрическим уравнением») представляет собой специальную функцию, определяемую рядом: Где: Поскольку функция определяется рядом, ее иногда называют гипергеометрическим рядом . Аналогичная функция, конфлюэнтная гипергеометрическая функция, обозначается через F (a; b; z). Функция также может быть представлена интегралами: Вычисление любых гипергеометрических функций, кроме простейших, затруднено, особенно когда все параметры сложные. Функция представляет собой аналитическую функцию, которая генерирует более сложные комбинаторные числа, обобщающие биномиальный ряд. Функция предоставляет информацию об отношениях между комбинаторными числами и их ростом. Многие специальные функции могут быть выражены в гипергеометрических терминах. Решения в замкнутой форме линейных дифференциальных уравнений с полиномиальными коэффициентами можно много раз определить в терминах гипергеометрической функции Гаусса. Функция гипергеометрической функции Гаусса возникает во многих практических областях, таких как: Bolton, W. (2000). Математика для инженеров. Новизна.
Биномиальный ряд против биномиального расширения
 Вам не нужно вычислять их полностью: есть своего рода ярлык. Формула дает разложение любого биномиального ряда , но вам все равно придется поработать с алгеброй, чтобы разложить его на самом деле.
Вам не нужно вычислять их полностью: есть своего рода ярлык. Формула дает разложение любого биномиального ряда , но вам все равно придется поработать с алгеброй, чтобы разложить его на самом деле. Выражение функции в виде биномиального ряда
Обратите внимание, что квадратный корень в знаменателе можно переписать с помощью алгебры как степень (до -½), поэтому мы можем используйте формулу с переписанной функцией (1 + x) -½  Здесь вы ищете шаблон для некоторого произвольного значения «k». Итак, вам придется работать с алгеброй, пока вы не сможете четко увидеть закономерность. Первые два значения расширения:
Здесь вы ищете шаблон для некоторого произвольного значения «k». Итак, вам придется работать с алгеброй, пока вы не сможете четко увидеть закономерность. Первые два значения расширения: Сходимость биномиального ряда
 Кроме того, радиус сходимости равен R = 1, если только показатель степени (k) не является целым положительным числом.
Кроме того, радиус сходимости равен R = 1, если только показатель степени (k) не является целым положительным числом. 1. Биномиальная функция двух членов

2.
Биномиальная функция Биномиальная функция вероятности

Использование в математическом программном обеспечении
Вычисление
 Частично это связано с проблемами отмены и ошибки округления.
Частично это связано с проблемами отмены и ошибки округления. Для чего используется гипергеометрическая функция Гаусса?

Ссылки
Дик, Т. и Паттон, К. Исчисление, Том 1. Издательство PWS-Kent Publishing Company.
Фарахманд, А. 11.10 Подробнее о серии Тейлора; Биномиальный ряд. Получено 22 сентября 2020 г. с: https://math.berkeley.edu/~arash/notes/07_01.pdf
Gonzalez-Zugast, J. (2011). Биномиальный ряд. Получено 23 сентября 2020 г. с: http://faculty.uml.edu/jennifer_gonzalezzugasti/Calculus%20II%20Video%20Lectures/documents/9..10.1TheBinomialSeries.pdf
Nagy, G. Биномиальные функции и ряды Тейлора (раздел 10.10). Получено 19 декабря 2019 г. с: https://users.math.msu.edu/users/gnagy/teaching/12-spring/mth233/L35-133.pdf
Nitecki, Z. (2009). Исчисление деконструировано. Второй курс исчисления для первого года обучения.
Олив, Дж. (2003). Математика: руководство по выживанию для студентов: рабочая тетрадь для самопомощи для студентов, изучающих естественные науки и инженерные науки. Издательство Кембриджского университета.

 ..
..
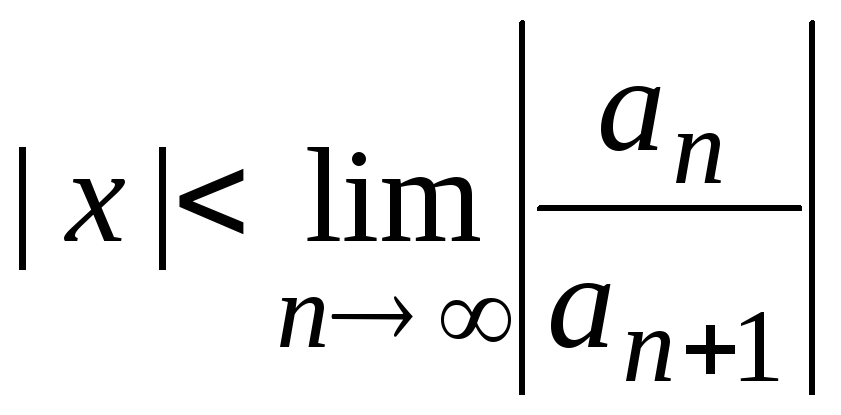
 3) – (5.13), сходятся к функциям, для которых они составлены.
3) – (5.13), сходятся к функциям, для которых они составлены.
 Итак,
Итак, по степеням
по степеням (-2;2), 71. , 72. [1;3), 73. (-1/3;1/3), 74. (-∞;∞), 75. [-1;1], 76. [-1;1), 77. (1;5], 78. (-1/4;1/4), 79. (-1/3;1/3), 80. (-3;1], 81. (-1;1], 82. (-∞;∞), 83. , 84. , 85. [-1/e;1/e),
(-2;2), 71. , 72. [1;3), 73. (-1/3;1/3), 74. (-∞;∞), 75. [-1;1], 76. [-1;1), 77. (1;5], 78. (-1/4;1/4), 79. (-1/3;1/3), 80. (-3;1], 81. (-1;1], 82. (-∞;∞), 83. , 84. , 85. [-1/e;1/e), Уч. изд. листов 2.
Уч. изд. листов 2.  ..
..