Сходимость степенного ряда: Интервал сходимости степенного ряда

Сходимость степенного ряда с примерами решения

Содержание:

 

1. Радиус сходимости и круг сходимости степенного ряда

Степенным рядом называется ряд

где — коэффициенты степенного ряда.

 Областью сходимости степенного ряда называется совокупность тех значений х, при которых степенной ряд (14.1) сходится.

Число R — такое, что при ряд (14.1) сходится, а при — расходится, называется радиусом сходимости степенного ряда.

Интервал называется интервалом сходимости степенного ряда. При ряд может как сходиться, так и расходиться.

Радиус сходимости степенного ряда может быть найден по формуле:

Формула (14.2) применима, если, начиная с некоторого номера , все

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Высшая математика: лекции, формулы, теоремы, примеры задач с решением

Для степенного ряда вида

радиус сходимости находится по формуле (14. 2), а интервал сходимости из условия , т.е. имеет вид:

Пример с решением 1:

Найти области сходимости степенных рядов:

Решение:

а) Найдем радиус сходимости ряда по формуле (14.2): т.е. интервал сходимости ряда

Теперь выясним поведение ряда на концах интервала сходимости.

Возможно вам будут полезны данные страницы:

Найдите координаты точки пересечения графиков

Найти область сходимости ряда: пример решения

Геометрическое распределение

Экстремум функции

На левом конце при — данный степенной ряд принимает вид этот ряд сходится по признаку Лейбница (см. §13.3, п. 4). На правом конце при

нический ряд (§ 13.2, п. 3) при у которого все члены с четными номерами равны нулю. Так как , то этот ряд сходится.

Следует отметить, что сходимость ряда на левом конце интервала сходимости при — могла быть установлена с помощью достаточного признака сходимости знакопеременного ряда, так как ряд, составленный из абсолютных величин его членов, т.е. ряд сходится. Итак, область сходимости данного ряда

Обращаем внимание на то, что при исследовании сходимости степенного ряда на концах интервала сходимости в ситуации, когда получаемый ряд — с положительными членами, применять признак Даламбера не имеет смысла, так как при этом всегда будем получать с нерешенным вопросом о сходимости ряда: в этом случае рекомендуется рассматривать другие признаки сходимости (например, признак сравнения, интегральный, необходимый признаки и т.д.)

б) Найдем радиус сходимости по формуле (14.2):

т.е область сходимости ряда

в) Задачу можно решать аналогично предыдущим. Решение упрощается, если заметить, что при

т.е. необходимый признак сходимости не выполняется, и ряд расходится.

Итак, область сходимости ряда состоит из одной точки х = 0.

г) Найдем радиус сходимости по формуле (14.2)

Для нахождения предела заменим бесконечно малые величины

при им эквивалентными

получим В соответствии с п. 4 интервал сходимости находится из условия , или (1; 3).

Теперь выясним поведение ряда на концах интервала сходимости. На левом конце при х = 1 данный ряд принимает вид

при любом натуральном ).

Так как при любом есть сходящийся обобщенный гармонический ряд при , то по признаку сравнения данный ряд сходится.

На правом конце при степенной ряд принимает вид , т.е. является знакочередующимся рядом и по достаточному признаку сходимости знакопеременного (а значит, и знакочередующегося) ряда сходится, так как сходится ряд, составленный из абсолютных величин его членов, т.е. ряд . Итак, область сходимости данного ряда [I; 3].

д) Выпишем несколько первых членов ряда:

Очевидно, что находить радиус сходимости по формуле (14. 2) в данном случае не представляется возможным, так как коэффициенты ряда (14.1) и т.д. равны нулю. Поэтому применим непосредственно признак Даламбера. Данный ряд будет абсолютно сходиться, если и расходиться, если Поэтому найдем Следовательно, ряд сходится при или на интервале Исследуем сходимость на концах интервала сходимости.

При ряд принимает вид п~ -I (-1/ = 1 f (-1Г = _lf 1 _ 1+1

„=1 п 3″-’ п з1 2 3

Этот ряд сходится по признаку Лейбница (§ 13.3).

При ряд принимает вид расходящийся

гармонический ряд. Итак, область сходимости ряда [-1/3; 1/3).

е) Так как члены ряда, стоящие на нечетных местах, отсутствуют, т.е. коэффициенты ряда и т.д., то формулу (14.2) для нахождения радиуса сходимости использовать нельзя. Можно применить непосредственно признак Даламбера, как это делалось в примере в п. д). Но в данном случае удобнее сделать замену Тогда ряд примет вид Область сходимости этого ряда получена в п. а): Возвращаясь к переменной х, получим откуда т. е. область сходимости ряда

Радиус сходимости и круг сходимости степенного ряда

Определение 1. Функциональные ряды вида

где — заданные комплексные числа, — комплексное переменное, называются степенными рядами. Числа называются коэффициентами степенного ряда (33.1).

Предполагая, что коэффициенты ряда и число фиксированы, будем исследовать поведение ряда (33.1) при различных .

Если в ряде (33.1) выполнить замену переменного, положив , то получим ряд

Очевидно, что исследование сходимости ряда (33.1) эквивалентно исследованию сходимости ряда (33.2), поэтому в дальнейшем будем рассматривать ряды вида (33.2), используя, как правило, для обозначения переменной букву , а не

ТЕОРЕМА 1 (первая теорема Абеля). Если степенной ряд сходится при , то он сходится, и притом абсолютно, при любом , для которого

Доказательство. Пусть ряд

сходится. Тогда его n-й член стремится к нулю при

(см. п. 30.1), поэтому последовательность ограничена, т. е. существует такая постоянная , что

В силу этого, для n-го члена ряда (33.3) имеет место оценка Если (рис. 9), то ряд являясь суммой геометрической прогрессии со знаменателем сходится. Поэтому, согласно признаку сравнения (см. п. 30.5), сходится и ряд а это означает абсолютную сходимость ряда (33.3) при

СЛЕДСТВИЕ. Если степенной ряд (33.3) расходится при , то он расходится и при всяком , для которого

Действительно, если и ряд (33.4) расходится, то расходится и ряд (33.3), так как если бы он сходился, то, в силу доказанного, сходился бы и ряд (33.4).

Неравенство задает на комплексной плоскости С замкнутый круг радиуса R с центром в точке

Определение 2. Пусть задан ряд . Если R — неотрицателъное число или обладает тем свойством, что при всех z, для которых ряд (33.3) сходится, а при всех z, для которых , ряд (33.3) расходится, то R называется радиусом сходимости степенного ряда (33. 3).

Множество точек , для которых , называется кругом сходимости ряда (33.3).

Если , то круг сходимости вырождается в точку, а если , то круг сходимости совпадает со всей комплексной плоскостью С.

ТЕОРЕМА 2. У всякого степенного ряда (33.3) существует радиус сходимости R. Внутри круга сходимости, т. е. при любом , для которого ряд (33.3) сходится абсолютно. На любом круге , где г фиксировано и , ряд (33.3) сходится равномерно.

Доказательство. Обозначим через А множество всех неотрицательных чисел х, в которых ряд сходится. При х = 0 этот ряд заведомо сходится, поэтому множество А не пусто и, следовательно, имеет конечную или бесконечную верхнюю грань. Пусть sup А = R. Покажем, что R — радиус сходимости ряда (33.3). Действительно, пусть и Согласно определению верхней грани, существует такое , что (см. определение 4′ в п. 3.4). В силу определения множества А, для указанного х ряд (33.5) сходится, поэтому, согласно первой теореме Абеля, в выбранной точке г сходится абсолютно ряд Если , то выберем такое действительное число х, что ; тогда снова, в силу определения множества А, ряд (33.

5) в такой точке х расходится — она лежит на действительной оси правее всех точек, в которых ряд (33.5) сходится. Поэтому, согласно следствию из первой теоремы Абеля, для выбранного z расходится и ряд

Итак, действительно, R является радиусом сходимости ряда (33.3).

Если теперь , то, по доказанному, ряд (33.3) при z = г абсолютно сходится, т. е. сходится числовой ряд А так как для любой точки круга (рис. 10)

то, согласно признаку Вейерштрасса (см. п. 32.3), на этом круге ряд (33.3) сходится равномерно. □

Таким образом, областью сходимости всякого степенного ряда является всегда «круг», т. е. обычный круг, исключая, быть может, некоторое множество точек ограничивающей его окружности (будем для краткости называть ее границей круга сходимости), в которых он может расходиться.

Пример с решением 2:

Подчеркнем, что радиус сходимости степенного ряда (33.3) обладает следующим свойством: для каждого числа z такого, что , указанный ряд абсолютно сходится, а для каждого z такого, что , он просто, а следовательно, и подавно абсолютно расходится (расходится ряд, составленный из абсолютных величин членов данного ряда). Это следует, очевидно, из определения радиуса сходимости и теоремы 2.

Члены степенного ряда являются непрерывными функциями и, как было показано, на всяком круге, лежащем вместе со своей границей внутри круга сходимости, степенной ряд сходится равномерно, поэтому его сумма непрерывна на всяком указанном круге. Очевидно, что для любой точки z круга сходимости, |z| < R, можно подобрать круг, содержащий эту точку и лежащий вместе с границей в круге сходимости (достаточно взять его радиус г таким, что |z| < г < R), поэтому степенной ряд непрерывен в каждой точке г, лежащей внутри его круга сходимости: |z| < R. Рассмотрим теперь случай, когда степенной ряд сходится в точке , лежащей на границе его круга сходимости. Отметим, что случай может быть сведен к случаю z = R простой заменой переменного

ТЕОРЕМА 3 (вторая теорема Абеля). Если R — радиус сходимости ряда и этот ряд сходится при то он сходится равномерно на отрезке [0, R] действительной оси.

СЛЕДСТВИЕ. Если степенной ряд (33.3) сходится при z = R, то его сумма непрерывна на отрезке [0, /?] действительной оси.

Доказательство. Пусть Представим ряд Члены ряда

не зависят от х, поэтому его сходимость означает и его равномерную сходимость. Последовательность же ограничена

на отрезке , ее члены неотрицательны: и она убывает в каждой точке (при она не строго убывает, точнее, является стационарной). Поэтому, в силу признака Абеля равномерной сходимости рядов (см. теорему 7 в п. 32.3), ряд (33.3) равномерно сходится на отрезке .

Следствие вытекает из того, что сумма равномерно сходящегося ряда непрерывных функций является также непрерывной функцией.

Все сказанное с помощью преобразования типа , (— новая переменная, фиксировано) переносится и на общие степенные ряды вида (33.1). В частности, областью сходимости такого степенного ряда всегда является круг вида , конечно, как и выше, с точностью до точек ограничивающей его окружности. Этот круг называется кругом сходимости (ряда (33.1)), aR — его радиусом сходимости.

Пример с решением 3:

Радиус сходимости равен нулю, т. е. этот ряд сходится только при

Действительно, исследуя абсолютную сходимость этого ряда по признаку Даламбера, при любом получим

Таким образом, рассматриваемый ряд не сходится абсолютно при любом ; отсюда, в силу следствия из первой теоремы Абеля, он расходится при любом .

Пример с решением 4:

Радиус сходимости ряда равен , так как было показано (см. п. 32.1), что этот ряд сходится при любом .

Пример с решением 5:

Сумма бесконечной геометрической прогрессии

сходится при и расходится при . Поэтому ее радиус сходимости R = 1. Отметим, что во всех точках границы круга сходимости, т. е. во всех точках окружности , ряд (33.6) расходится, так как для общего члена ряда имеем следовательно, он не стремится к нулю при .

Пример с решением 6:

Ряд

сходится при , так как при выполнении этого условия

При ряд (33. 7) расходится, поскольку в этом случае т. е. не выполняется необходимое условие сходимости ряда. Радиус сходимости ряда (33.7), как и ряда (33.6), равен единице, однако в каждой точке границы круга сходимости ряд (33.7), в отличие от ряда (33.6), сходится.

Пример с решением 7:

Ряд имеет радиус сходимости R = 1.

Действительно, применив признак Даламбера для определения z, при которых ряд абсолютно сходится (расходится), получим

и, следовательно, при данный ряд сходится, причем абсолютно, а при он расходится. При получается расходящийся гармонический ряд , а при z = -1 — сходящийся ряд (см. и. 30.3 и 30.9). Таким образом, в этом п = О П

примере на границе круга сходимости есть точки, в которых ряд сходится, и точки, в которых он расходится.

Таким образом, область сходимости степенного ряда не совпадает, вообще говоря, с его кругом сходимости, а состоит из внутренности этого круга, т. е. множества , и, быть может, еще из некоторого множества точек, лежащих на его границе.

Из рассмотренных примеров видно, что иногда радиус сходимости R степенного ряда находится с помощью признака Даламбера сходимости рядов с положительными членами .

Действительно, справедливо следующее утверждение: если существует предел

В самом деле, если число R определено этой формулой и то

поэтому ряд (33.3) для такого z сходится (и притом абсолютно).

Если же и, следовательно, ряд (33.3) абсолютно расходится. Таким образом, R действительно является радиусом сходимости ряда (33.3).

Аналогично можно найти величину радиуса сходимости R и с помощью признака Коши (см. теорему 9 в п. 30.6), если только существует предел (конечный или бесконечный) . В этом случае

Действительно, если число R задается этой формулой и если , то

и поэтому ряд (33.3) сходится. Если же , то и, следовательно, ряд (33.3) абсолютно не сходится.

Таким образом, R является радиусом сходимости ряда (33.3).

Затруднения при использовании таких методов определения радиуса сходимости степенного ряда могут возникнуть, например, уже в том случае, когда в рассматриваемом ряде имеются коэффициенты со сколь угодно большими номерами, равные нулю. Тогда можно попробовать применить один из этих методов, предварительно перенумеровав подряд все члены ряда с отличными от нуля коэффициентами (отчего его сходимость и сумма в случае, если он сходится, не изменяются).

Поясним сказанное на примере. Пусть требуется определить радиус сходимости ряда Признак Даламбера неприменим для определения сходимости этого ряда, так как отношение не имеет смысла

для четных номеров п. Не дает ответа здесь и признак Коши, поскольку нетрудно проверить, что здесь предел не существует.

Однако если положить , и записать данный ряд в виде

,

то, исследовав абсолютную сходимость этого ряда с помощью признака Даламбера, получим

Отсюда следует, что рассматриваемый ряд абсолютно сходится, когда , т. е. когда , и абсолютно расходится, когда . Таким образом, радиус сходимости этого степенного ряда равен 1.

Подчеркнем, что с помощью признака Даламбера и признака Коши можно найти радиус сходимости не для произвольного степенного ряда, а лишь для такого, у которого существуют указанные выше пределы (быть может, после новой нумерации членов).

Глава 95. Степенные ряды. Область сходимости

В курсе математического анализа изучаются последовательности и ряды, членами которых являются не числа, а функции, определенные на некотором множестве. Такие функциональные последовательности и ряды широко применяются в различных приложениях для анализа и приближенных вычислений. Мы ограничимся рассмотрением степенных рядов.

Определение: Функциональный ряд вида

(9.5.1)

Называется Степенным рядом. Постоянные числа называются Коэффициентами степенного ряда (9.5.1).

При разных значениях переменной мы получим разные числовые ряды, которые могут быть сходящимися или расходящимися. Особый интерес представляет множество значений , при которых ряд (9.5.1) сходится, оно называется Областью сходимости степенного ряда.

Очевидно, что частичная сумма степенного ряда представляет собой Функцию переменной . Стало быть, последовательность частичных сумм является Функциональной последовательностью и сумма ряда (9.5.1) является Функцией переменной : .

Теорема: (Теорема Абеля). Если степенной ряд (9.5.1) Сходится при и , то он Абсолютно сходится при всех , таких, что . Если ряд (9.5.1) Расходится при , то он Расходится И при всех , удовлетворяющих неравенству .

Теорема Абеля примечательна утверждением, что если степенной ряд (9.5.1) сходится при , то он сходится абсолютно всюду на отрезке . Если же – точка расходимости ряда, то он расходится везде вне интервала .

Отсюда следует основополагающая в теории степенных рядов Теорема.

Теорема: Если степенной ряд (9.5.1) Сходится не только при , то существует такое положительное число (возможно, и бесконечное), что ряд Абсолютно сходится в интервале и Расходится везде вне этого интервала.

Число и интервал называются соответственно Радиусом сходимости и интервалом сходимости степенного ряда. Всякий степенной ряд имеет свой радиус сходимости . При вопрос о сходимости должен рассматриваться конкретно для каждого ряда.

Способ определения радиуса сходимости степенного ряда (9.5.1) указывает следующая Теорема.

Теорема

Если для степенного ряда (9.5.1) существует Предел

,

(9.5.2)

То Радиус сходимости этого ряда определяется формулой .

Заметим, что если предел (9.5.2) равен нулю, то степенной ряд сходится на всей числовой прямой, т. е. .

Рассмотрим примеры на Определение радиуса сходимости степенного ряда.

Пример

Определить радиус сходимости ряда .

Решение

Согласно Теореме 3, радиус сходимости этого ряда определяется по формуле , т. е. данный ряд Абсолютно сходится на всей числовой оси.

Пример

Определить радиус сходимости ряда , .

Решение

Радиус сходимости находим . Радиус сходимости данного ряда . Выясним вопрос о сходимости ряда в точке . При подстановке в степенной ряд значения , получим числовой ряд , который имеет различный характер сходимости в зависимости от .

А) при ряд сходится Условно на отрезке как знакопеременный ряд, а на интервале он сходится Абсолютно (т. к. и ряд сходится как сумма геометрической прогрессии со знаменателем ).

Б) При ряд сходится Абсолютно на отрезке .

Пример

Определить радиус сходимости ряда , .

Решение

Получаем: . При получаем, что необходимое условие сходимости числового ряда не соблюдается. Следовательно, данный ряд сходится абсолютно на интервале как сумма геометрической прогрессии со знаменателем меньше единицы.

Пример

Определить радиус сходимости ряда .

Решение

Радиус сходимости ряда: Следовательно, данный ряд сходится лишь в точке .

Свойства степенных рядов

Вообще говоря, сумма степенного ряда является функцией от переменной .

.

(9.5.3)

Пусть интервал сходимости этого ряда . Тогда говорят, что функция может быть разложена в степенной ряд на интервале .

Степенные ряды обладают рядом свойств; два из них мы приведем без доказательства.

Степенной ряд можно Дифференцировать почленно на промежутке его сходимости, так что

(9.5.4)

1. При этом интервал сходимости ряда (9.5.4) тот же, что и ряда (9.5.3). Таким же образом можно вычислить производные любого порядка.

2. Степенной ряд можно Интегрировать почленно в интервале его сходимости , т. е. .

Замечание

Из свойства 1 следует, что сумма степенного ряда непрерывна на интервале его сходимости.

< Предыдущая		Следующая >

п} =\lim_{n\to\infty} |x|{|a_{n+1}|\over |a_n|} = |x|\lim_{n\to\infty} {|a_{n+1}|\over |a_n|} =L|x|, $$ при условии, что $\ds \lim |a_{n+1}|/|a_n|$ существует. Затем серия сходится, если $L|x|1/L$. Только два значения $x=\pm1/L$ требуют дальнейшего изучение. Таким образом, ряд определенно будет определять функцию на интервал $(-1/L,1/L)$ и, возможно, распространится на один или оба также конечные точки. Заслуживают упоминания два частных случая: если $L=0$, то предел равен $0$ независимо от того, какое значение принимает $x$, поэтому ряд сходится для всех $x$ и функция определена для всех действительных чисел. Если $L=\infty$, то для любого ненулевого значения $x$ предел бесконечен, поэтому ряд сходится только при $x=0$. Стоимость $1/L$ называется 9п \ над п (п + 1)} $ (отвечать)

Серия Power: определение, пример и сходимость

Последовательность и серия >

Содержание:

• Определение серии Power
• Интеграция серии Power
• Формальная серия Power

Степенной ряд , который подобен многочлену бесконечной степени, может быть записан в нескольких различных формах. Базовая форма, суммирование, начинающееся с n = 0:

Простой пример:

В некоторых ситуациях может потребоваться исключить первый член или первые несколько терминов (например, n = 0 или n = {0, 1, 2}). Когда это происходит, игнорируемые члены помещаются перед суммой. Например, вот как выглядит ряд, если убрать первые два члена:

Почему эти ряды полезны?

Эти ряды очень полезны, потому что они дают нам возможность представлять трансцендентные функции (например, экспоненциальные функции или логарифмические функции) по-другому. Эта альтернативная форма облегчает исследование поведения функции при малых или больших изменениях одной из независимых переменных (Cockett & Doggett, 2003).

Сходимость степенных рядов

Эти ряды могут сходиться везде или в одной точке x . Интервал, в котором она сходится, называется интервалом сходимости. Например, ряд
1 + x + x ² + … + x ⁿ + …
представляет собой геометрический ряд с фиксированным значением x, который для интервала сходимости (-1, 1) дает в сумме

.
Вне (-1, 1) ряд расходится.

Степенной ряд также может иметь комплексные значения в форме:

Где (z – z ₀ ) – ряд «сил». Сходимость комплекснозначного степенного ряда определяется сходимостью вещественного ряда

Где w устанавливается равным w = (z – z ₀ ) (Уайльд, 2006).

Интегрирование силовых рядов

Интегрирование — это относительно простая процедура представления интегрированной функции в виде суммы эквивалентного ряда.

Интеграция особенно полезна для функций, которые не так просто заменить обычным суммированием. Шаг интеграции обеспечивает взаимозаменяемость от функции к суммированию. Можно найти степенной ряд, представляющий поведение этой функции, особенно для функций с одной переменной, которые имеют непрерывность в заданной области значений x .

Стремление найти степенной ряд для сложных функций широко распространено в области дифференциальных уравнений.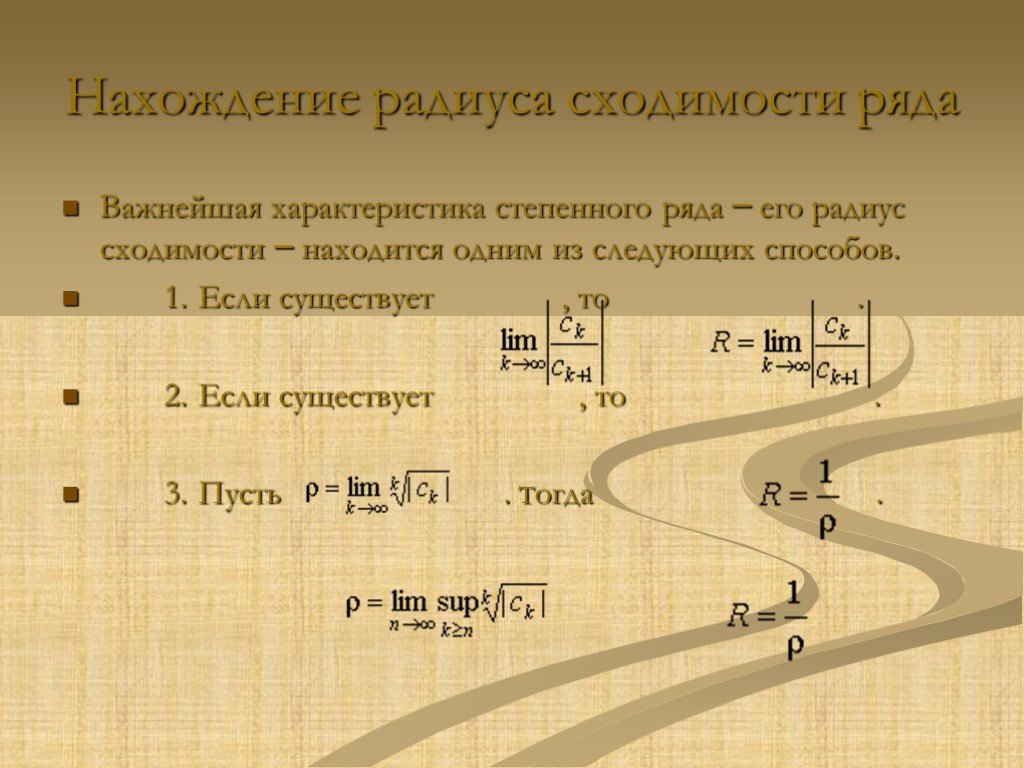 Математики используют подобные методы для представления решений дифференциального уравнения в виде степенного ряда (Ливитт, Дж. А.).

Процедура проверки

Доказательство интеграции для любой заданной серии должно показать, что интеграция затрагивает все термины в этой серии; Ряд может иметь интегральную оценку для каждого члена. Распределение интегрального состояния можно записать следующим образом:

Пусть обобщенный степенной ряд сходится в ограниченной области x значений (также известной как радиус сходимости). Ограниченная область имеет длину R , которая действует как радиус x значений , что заставляет ряды сходиться.

Поскольку функция f(x) представляет собой ряд и сходится в ограниченной области, f(x) является непрерывной функцией и может быть представлена ​​в виде разделимых членов.

Поскольку f(x) можно вычислить в пределах |x| < R, мы можем переписать f(x) = a ₀ + a ₁ x + a ₂ x ² +…+ a _n x ⁿ

3 Интеграл от обеих сторон уравнения заставляют интегрирование каждого члена через свойство распределения интегралов .

В качестве примера определенных интегралов допустимый интервал общего степенного ряда ограничен длиной значений x, которые сходятся f(x). Установка закрытого интервала [0, z] , где [0, z] находится в пределах |x| < ℝ создает интегральную формулу степенного ряда:

Пусть z = x для более простого представления:

Где C — константа, которая оценивается, если задано начальное значение для соответствующего х значение .

Поскольку каждый член в пределах f(x) может быть интегрирован для получения сходящегося значения, сумма всех интегрированных членов представляет собой общую интеграцию степенного ряда. Это свойство интеграции в степенном ряду справедливо для интервалов x , которые существуют исключительно в радиусе сходимости ряда.

Выбор значения за пределами этого радиуса приводит к результатам суммирования, которые содержат добавленные дубликаты, неопределенности и саму бесконечность.

Интегральное преобразование степенных рядов

Один из методов, который можно использовать для интегрирования степенных рядов, заключается в том, что функции не распознаются из типичных преобразований степенных рядов. Примером может быть следующее:

Для F(x) = ln(2-x), найти эквивалентный степенной ряд

Сначала функция натурального логарифма не упоминается в списке степенных рядов эквивалентности. Вместо этого можно видеть, что если F(x) найти свою производную, возникает функция общего степенного ряда и с ним можно работать.

Шаг 1 : Найдите первую производную данной функции и перепишите F(x) в интегральной форме.

Шаг 2 : Распознайте функциональный шаблон, который можно напрямую заменить обычным степенным рядом.

Шаг 3 : Решите интеграл и упорядочите члены.

Где C — постоянное значение, которое изменяется в зависимости от выбранного значения x, которое подставляется.

Интегральный трюк для интеграции степенных рядов

Интегрирование степенных рядов также можно использовать для нахождения расширения для заданного интеграла вместо заданной функции. Давайте возьмем другую версию приведенного выше примера и присоединим ее к определенному интегралу:

Найдите разложение в степенной ряд для G(x):

Шаг 1 : Преобразуйте внутреннюю функцию ) в степенной ряд; Вы будете брать интеграл от этой функции.

Внутренняя функция ln(1 + t) должна быть представлена ​​в виде степенного ряда и в ее разделимых терминах.

Шаг 2 : Замените во внутренней функции степенной ряд и вычислите определенный интеграл.

Где, опять же, C — постоянное значение, определяемое для выбранного значения x, которое должно находиться в пределах радиуса сходимости в расчетном ряду.

Формальный степенной ряд (или формальный ряд ) имеет вид (Tao, 2016):

Где:

• a = действительное число, где ряд находится в центре,
• c _n = коэффициент ряда,
• c ₀ , c ₁ , … = последовательность действительных чисел (не зависящая от x).

Обратите внимание, что последовательность не может зависеть от x , чтобы ряд был формальным степенным рядом. Например:

• Формальный ряд : n! (х – 3) ^п
• Неформальная серия : 3 ^х (х – 3) ⁿ (коэффициент 3 ^х зависит от х).

Не предполагается, что формальный ряд сходится (хотя это может быть), и «x» не присваивается никакого значения. Формальный ряд был разработан, чтобы обойти вопрос сходимости и упростить анализ.

Ссылки

Henrici, P. (1988). «Определение и алгебраические свойства формальных рядов». §1.2 в Прикладном и вычислительном комплексном анализе, Vol. 1: Power Series-Integration-Conformal Mapping-Location of Zeros. Нью-Йорк: Wiley, стр. 9.-13, 1988.
Benestad, C. et al. (2015). P. Серия, Математика 121 Исчисление II. Получено 3 января 2020 г. с: https://mathcs.clarku.edu/~ma121/powerseries.pdf
Cockett, M. & Doggett, G. (2003). Математика для химиков, том 2: серия P., комплексные числа и линейная алгебра (учебные тексты по химии), 1-е издание. Королевское химическое общество.
Ливитт, Джей А. «Методы и применение P. Series». Американское математическое общество , том. 20, 1996 г., стр. 46–52., https://www.ams.org/journals/mcom/19.66-20-093/S0025-5718-1966-0187402-4/S0025-5718-1966-0187402-4.pdf.
Тао, Т. (2016). Анализ I: Третье издание (тексты и литература по математике), 1-е изд. Издание 2016 года. Книжное агентство Индостана.
Уайльд, И. (2006). Конспект лекций по комплексному анализу. Издательство Имперского колледжа.
Уилф, Х. (1994). Генерирующая функционалология, 2-е изд. Нью-Йорк: Академическая пресса.

УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Мощный ряд: определение, пример и сходимость» из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/power-series/

————————————————— ————————-

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.