Симметрия относительно оси х: Что значит симметрично относительно оси. Урок математики

Содержание

параллельный перенос, симметрия относительно осей координат

Видеоурок 1: Преобразование графиков функций. Параллельный перенос вдоль осей координат

Видеоурок 2: Преобразования графиков функций. Симметрия относительно осей координат

Лекция: Преобразования графиков: параллельный перенос, симметрия относительно осей координат

Существует ряд основных простейших функций, вид которых нам известен. Но, когда функция видоизменяется, тяжело понять, каким образом изменится её график. Сейчас мы с вами разберемся, каким образом происходит преобразование графиков в зависимости от заданной функции.

1. Симметричные функции:

Итак, если мы имеем функцию, которая имеет противоположный знак, то получим следующее преобразование.

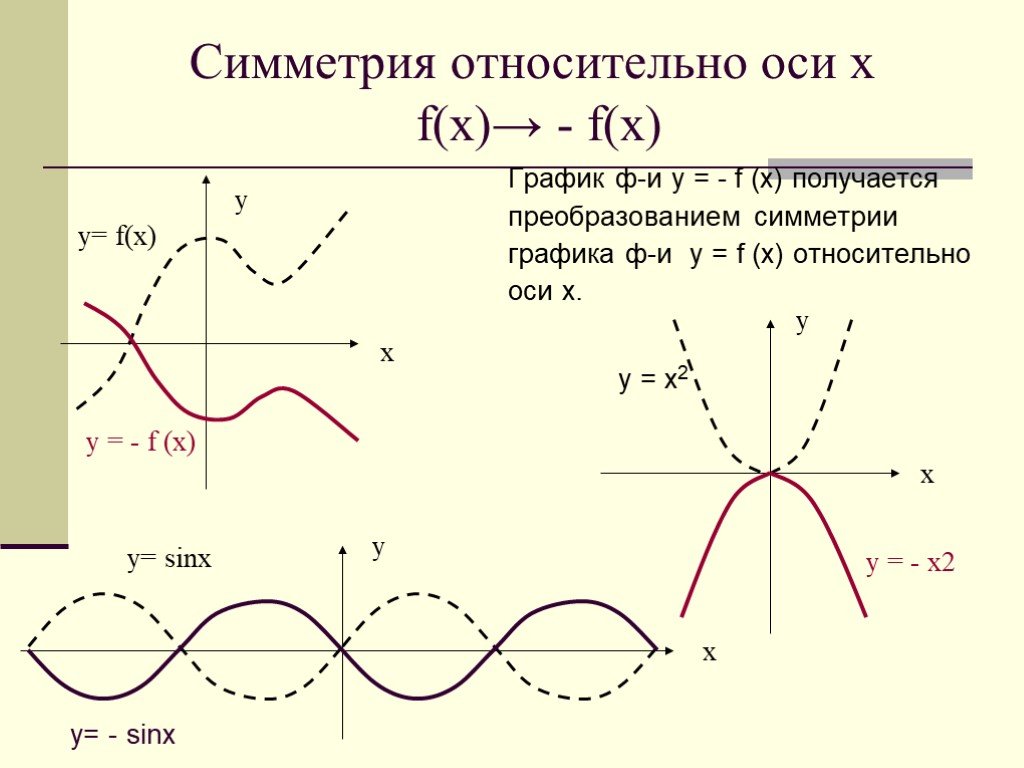
y = f(x) => y = -f(x)

Получим график, симметричный относительно оси ОХ.

Не трудно заменить, что для те же значений «х», будет противоположное значение «у».

Ниже Вы можете ознакомиться с примерами подобных преобразований для квадратичной, показательной и тригонометрической функции:

2. Преобразование функции для противоположного значения аргумента: y = f(x) => y = f(-x)

Получим график, симметричный относительно оси ОУ. Не трудно заменить, что для те же значений «у», будет противоположное значение «х».

Ниже Вы можете ознакомиться с примерами подобных преобразований для некоторых функций:

Обратите внимание, график квадратичной функции остается неизменным, поскольку при возведении отрицательного аргумента в квадрат, получится то же значение функции.

3. Параллельный перенос

Если в аргументе происходит сдвиг на некоторое число, то говорят о параллельном переносе по оси ОХ: y = f(x) => y = f(x — а)

Если число вычитают, то перенос происходит вправо по оси ОХ, если перед числом стоит знак плюс, то график переносится влево по оси ОХ.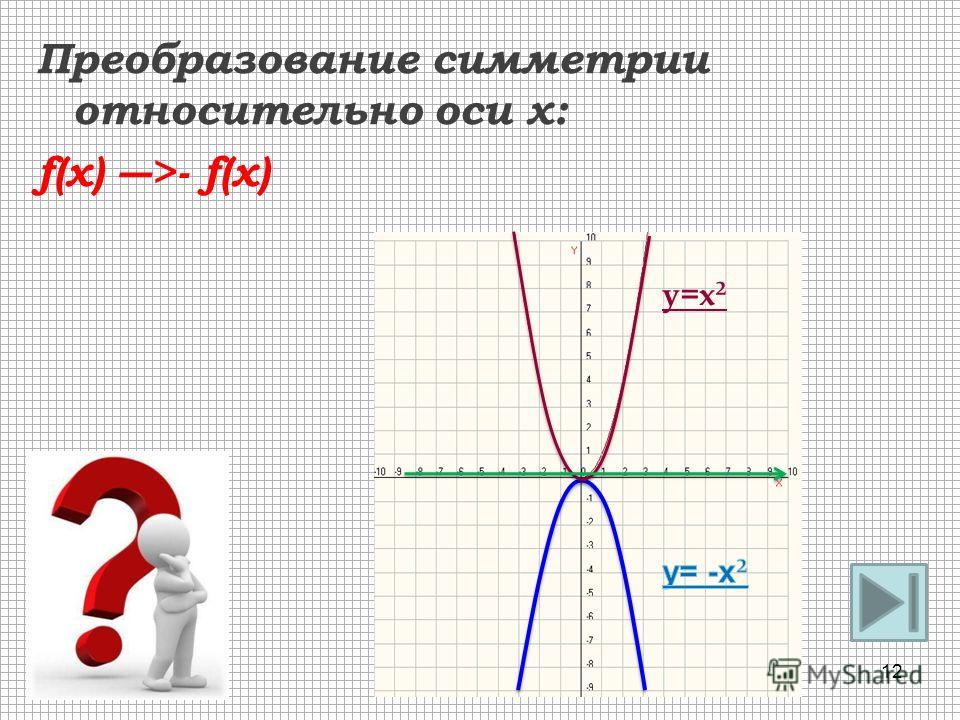

Примеры:

Перенос по оси ОУ происходит в том случае, когда: y = f(x) => y = f(x) — b.

Примеры переноса по оси ОУ:

4. Растяжение/сжатие

Если некоторая функция умножается на целое число y = f(x) => y = f(аx), то график сжимается. Если функция умножается на дробное число, то график растягивается.

Обратите внимание: при изменении значения «х» при растяжении и сжатии значения «у» не изменяется.

Растяжение и сжатие по оси ОУ происходит в том случае, если y = f(x) => y = kf(x).

Если данный коэффициент будет дробным, то график сжимается, если целым, то растягивается:

Обратите внимание: при изменении значения «у» при растяжении и сжатии значения «х» не изменяется.

Примеры:

2.3 Характерные химические свойства простых веществ неметаллов: водорода, галогенов, кислорода, серы, азота, фосфора, углерода, кремния

2 Характерные химические свойства и получение простых веществ — металлов: щелочных, щелочноземельных, алюминия; переходных элементов (меди, цинка, хрома, железа)

1.2.4 Общая характеристика неметаллов IVA – VIIA групп в связи с их положением в Периодической системе химических элементов Д.И.Менделеева и особенностями строения их атомов

3.3.3 Квадратичная функция, её график

1.2.1 Возникновение государственности у восточных славян. Князья и дружина. Вечевые порядки. Принятие христианства

Вконтакте
Сайт

1.2: Графики и симметрия — Математика LibreTexts

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 226

Ларри Грин
Общественный колледж Лейк-Тахо

Симметрия (геометрия)

Определение: Симметричный относительно оси y

Мы говорим, что граф является симметричным относительно оси y , если для каждой точки \((a,b)\) на на графике также есть точка \((-a,b)\) на графике; следовательно \[f(x,y) = f(-x,y). \]

Визуально мы видим, что ось y действует как зеркало для графика. Мы продемонстрируем несколько функций для проверки симметрии графически с помощью графического калькулятора.

Определение: Симметричный относительно оси x

Мы говорим, что граф является симметричным относительно оси x , если для каждой точки \((a,b)\) на графике также существует точка \((a,-b)\) на графике; следовательно \[f(x,y) = f(x,-y).\]

Визуально мы видим, что ось x действует как зеркало для графика. Мы продемонстрируем несколько функций для проверки симметрии графически с помощью графического калькулятора.

Определение: Симметрия относительно начала координат

Говорят, что граф симметричен относительно начала координат, если для каждой точки \((a,b)\) на графике существует также точка \((-a,-b)\) на графике ; следовательно \[f(x,y) = f(-x,-y).\]

Визуально мы имеем, что для данной точки \(P\) на графике, если мы проводим отрезок \(PQ\) через \(P\) и начало координат такое, что начало координат является серединой \(PQ\), то \(Q\) также находится на графике.

Мы воспользуемся графическим калькулятором для проверки всех трех симметрий.

Симметрия (алгебра)

Симметрия по оси x

Чтобы алгебраически проверить, симметричен ли график относительно оси x, мы заменяем все \(y\) на \(-y\) и посмотрим, получим ли мы эквивалентное выражение.

Пример \(\PageIndex{1}\)

Для

\[x — 2y = 5 \]

мы заменяем на

\[ x — 2(-y) = 5.\]

Упрощение мы получаем

\[x+2y=5.\]

Что не эквивалентно исходному выражению. Так 92+ x — 2\]

Решение

Мы устанавливаем \(x = 0\), чтобы получить:

\[y = 0 + 0 — 2 = -2.\]

Следовательно, точка пересечения y равна в \((0,-2)\).

Авторы и авторство

Эта страница под названием 1.2: Графики и симметрия распространяется по незаявленной лицензии, ее автором, ремиксом и/или куратором был Ларри Грин.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или Страница
Автор
Ларри Грин
Показать страницу TOC
нет
Теги
1. симметрия относительно начала координат
2. симметрия относительно оси x
3. симметрия относительно оси Y

Как проверить симметрию

Этот урок научит вас проверять симметрию. Вы можете проверить график отношения на симметрию относительно оси x, оси y и начала координат. В этом уроке мы подтвердим симметрию алгебраически.

Тест на симметрию относительно оси x.

График отношения симметричен относительно оси X, если для каждая точка (x, y) на графике, точка (x, -y) также находится на графике. Чтобы проверить симметрию относительно оси x, просто замените y на -y и посмотрите, получится ли по-прежнему то же уравнение. Если вы получите такое же уравнение, то график симметричен относительно оси x.

Пример #1:

является ли x = 3y ⁴ — 2 симметричным относительно оси x?

Замените y на -y в уравнении.

X = 3(-y) ⁴ — 2

X = 3y ⁴ — 2

Поскольку замена y на -y дает то же уравнение, уравнение x = 3y ⁴ — 2 симметрично с относительно оси x.

Тест на симметрию относительно оси Y.

График отношения симметричен относительно оси y, если для каждая точка (x, y) на графике, точка (-x, y) также находится на графике.
Чтобы проверить симметрию относительно оси Y, просто замените x на -x и посмотрите, получится ли по-прежнему то же уравнение. Если вы получите такое же уравнение, то график симметричен относительно оси Y.

Пример #2:

является ли y = 5x ² + 4 симметричным относительно оси x?

Замените x на -x в уравнении.

Y = 5(-x) ² + 4

Y = 5x ² + 4

Поскольку замена x на -x дает то же уравнение, уравнение y = 5x ² + 4 симметрично с относительно оси Y.

Тест на симметрию относительно начала координат.

График отношения симметричен относительно начала координат, если для каждая точка (x, y) на графике, точка (-x, -y) также находится на графике.
Чтобы проверить симметрию относительно начала координат, просто замените x на -x и y
на -y и посмотрите, получится ли по-прежнему то же уравнение. Если вы получите такое же уравнение, то график симметричен относительно начала координат.