Руководство для начинающих по линейному программированию и симплексному алгоритму | Хенни де Хардер | Январь 2023 г.
Ферма с кукурузой. Натюрморт от Dall-E 2.Решение широкого круга задач оптимизации
Линейное программирование — мощный инструмент. Он находит применение в самых разных областях, включая инженерное дело, финансы и исследования операций. Линейное программирование использовалось для решения таких разнообразных задач, как планирование рейсов авиакомпаний и проектирование производственных процессов. В этом сообщении блога мы рассмотрим основы линейного программирования и то, как его можно использовать для решения практических задач.
Линейное программирование (ЛП) — это метод математической оптимизации. Он используется для поиска оптимального решения задач, связанных с несколькими переменными и ограничениями. Представляя ограничения и целевую функцию задачи в виде системы линейных уравнений и неравенств, алгоритмы линейного программирования могут систематически искать пространство решений и находить решения, которые максимизируют или минимизируют заданную цель.
Сначала приведу простой пример. Затем мы углубимся в симплекс-алгоритм, который используется в фоновом режиме для быстрого поиска оптимального решения задач LP.
Предположим, у фермера есть 120 акров земли, на которых он выращивает две культуры: пшеницу и кукурузу. Для пшеницы требуется 2 акра земли на тонну, а для кукурузы требуется 1 акр земли на тонну. Фермер хочет максимизировать прибыль от урожая, которая составляет 100 евро за тонну пшеницы и 150 евро за тонну кукурузы. У фермера также есть ограничение в 50 тонн пшеницы и 40 тонн кукурузы, которые можно произвести.
Чтобы решить эту задачу с помощью линейного программирования, нам сначала нужно определить переменные решения, то есть количество пшеницы и кукурузы, которое фермер будет выращивать. Мы будем использовать переменные w и c для представления количества тонн пшеницы и кукурузы соответственно.
Далее нам нужно написать целевую функцию, которая представляет собой прибыль, которую фермер хочет максимизировать.
В этом случае целевая функция:
Затем нам нужно записать ограничения, которые представляют пределы количества пшеницы и кукурузы, которые могут быть произведены. Ограничения:
Первые два ограничения представляют ограничения на общее количество тонн пшеницы и кукурузы, которое может быть произведено. Третье ограничение представляет собой ограничение на общее количество доступной земли.
Чтобы решить эту задачу, мы можем использовать симплекс-алгоритм или другой метод линейного программирования, чтобы найти значения w и c , которые максимизируют целевую функцию с учетом ограничений. В этом случае оптимальным решением будет выращивание 40 тонн пшеницы и 40 тонн кукурузы, что принесет прибыль в размере 10 000 евро.
Это простой пример, иллюстрирующий основные этапы решения задачи линейного программирования. На практике линейное программирование используется для решения гораздо более сложных задач с большим количеством переменных и ограничений.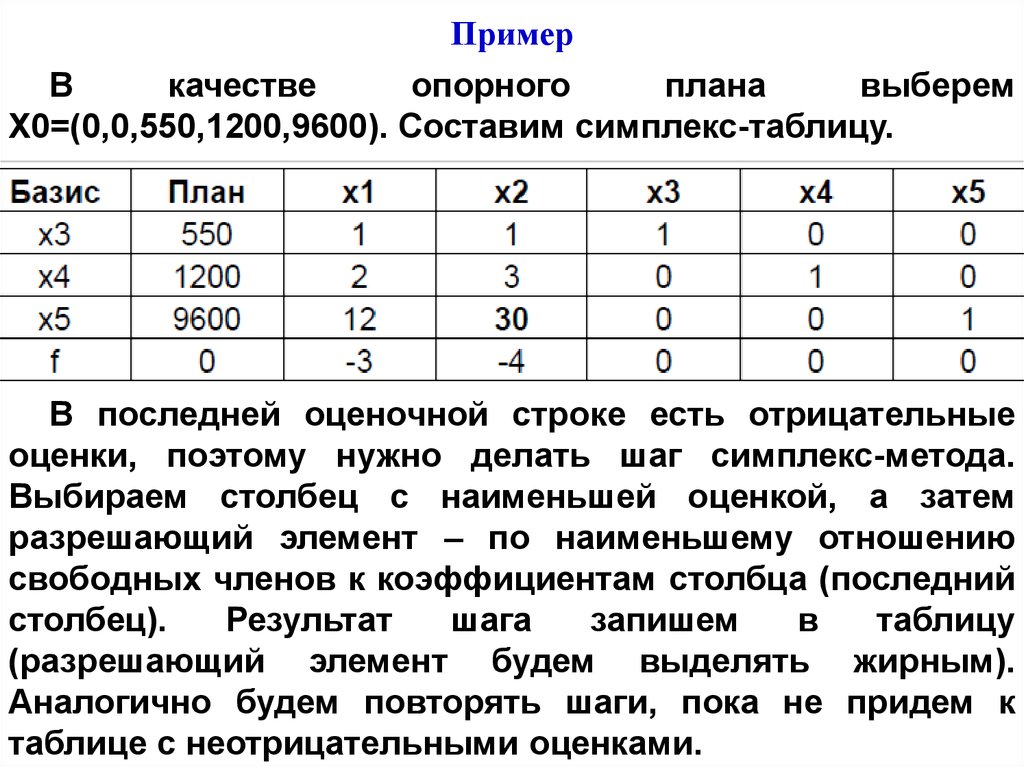
Ниже визуализация проблемы:
Визуализация линейного программирования. Изображение автора.Серая область называется допустимой областью. Каждая точка области содержит допустимое решение. Область ограничена ограничениями.
Фундаментальная теорема линейного программирования утверждает, что максимумы приходятся на углы области. Это важная информация, которую использует симплексный алгоритм.
Симплекс-алгоритм — широко используемый метод решения задач линейного программирования. Он был разработан Джорджем Данцигом в 1947. Интуиция, лежащая в основе алгоритма, состоит в том, чтобы систематически «ходить» из угла в угол в допустимом пространстве области. Когда оптимальное решение найдено, процесс останавливается.
Симплекс-алгоритм — это итеративный процесс, основанный на математических вычислениях и логических рассуждениях для поиска оптимального решения задачи линейного программирования. Он эффективен и надежен, а также используется в смешанном целочисленном программировании (после ослабления ограничений).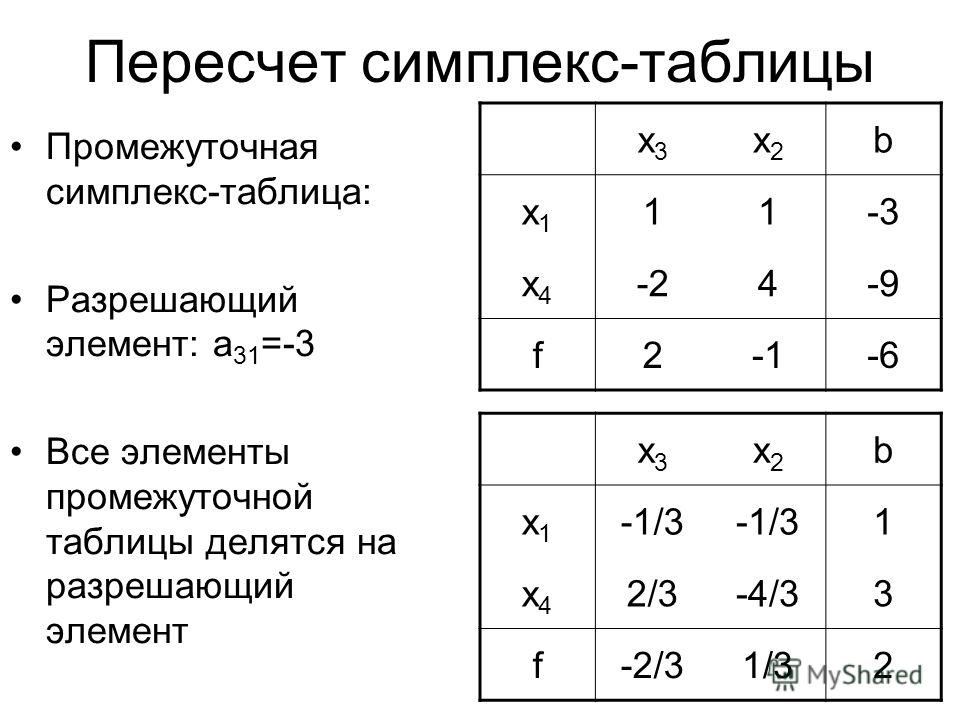
Основные шаги симплексного алгоритма следующие:
- Преобразование ограничений задачи линейного программирования в систему линейных уравнений стандартной формы.
- Найдите базовое допустимое решение, установив некоторые переменные равными нулю и найдя оставшиеся переменные.
- Протестируйте базовое допустимое решение, чтобы убедиться, что оно оптимально. Если это так, алгоритм завершен. Если нет, алгоритм выбирает переменную для входа в базис и соответствующим образом обновляет базовое допустимое решение.
- Повторяйте шаг 3, пока не будет найдено оптимальное решение.
Давайте пройдемся по шагам один за другим на примере пшеницы и кукурузы.
Шаг 1. Преобразовать ограничения задачи линейного программирования в систему линейных уравнений стандартной формы.
Первый шаг — переписать ограничения и цель в стандартной форме:
В стандартной форме знаки «меньше чем» заменяются знаками равенства, и к каждому ограничению добавляется резервная переменная (s1, s2, s3).
Таким образом, значение меньше чем сохраняется, потому что переменные резерва могут принимать только положительные значения.
Часто для облегчения чтения задачи используется таблица. Таблица — это таблица, в которую мы записываем коэффициенты. Столбец представляет собой переменную, а строка — ограничение. В этом случае нижняя строка содержит коэффициенты цели. Последний столбец содержит значения в правой части уравнений. Мы используем стандартную форму для создания таблицы:
Таблица для задачи о кукурузе и пшенице. Каждое ограничение и цель представлены в строках, а столбцы представляют переменные. Значения являются коэффициентами. Изображение автора. Шаг 2. Найдите базовое допустимое решение, установив некоторые переменные равными нулю и найдя оставшиеся переменные.
Теперь, когда у нас есть таблица, мы можем использовать ее для поиска базового допустимого решения. Базовое допустимое решение — это решение, удовлетворяющее всем ограничениям и лежащее в вершине.
Мы можем легко обнаружить один из таблицы.
В таблице есть два типа переменных: основных переменных и неосновных переменных . Базовые переменные имеют только одну ненулевую запись, а неосновные переменные имеют более одной ненулевой записи. 9Базис 0017 содержит все основные переменные. Если мы посмотрим на текущее состояние таблицы, то в основе лежат переменные slack s₁ , s₂ и s₃ . Переменные w и c не являются базовыми и равны нулю. Текущее базовое допустимое решение имеет следующие значения: с₁ = 50, с₂ = 40, с₃ = 120, Z = 0, w = 0 и c = 05 и основные переменные. Изображение автора.
Это решение соответствует следующей угловой точке:
Начальная точка симплексного алгоритма. Изображение автора. Шаг 3. Проверьте базовое допустимое решение, чтобы убедиться, что оно оптимально. Если это так, алгоритм завершен. Если нет, алгоритм выбирает переменную для входа в базис и соответствующим образом обновляет базовое допустимое решение.
Проверить, является ли базовое допустимое решение оптимальным, можно, взглянув на целевую строку в таблице. Поскольку это задача максимизации, мы можем улучшить ее, удалив отрицательные коэффициенты. Мы больше не сможем улучшаться, если все отрицательные значения исчезнут. В нижнем ряду отрицательные значения, поэтому возможно улучшение, а оптимальное решение пока не найдено.
Теперь нам нужно выбрать переменную для входа в базу. Чтобы выбрать входящую переменную, возьмите наименьший коэффициент в целевом ряду. В нашем случае это -150, что соответствует c. Это входящая переменная. Затем нам нужно выбрать строку для выполнения исключения Гаусса. Это делается путем деления значений RHS на коэффициенты c . Итак, в нашем случае мы получили 40/1=40 для второй строки и 120/1=120 для третьей строки. Наименьшее значение — 40, поэтому используется вторая строка.
Теперь мы можем стереть таблицу строкой 2, чтобы включить c в базисе:
Новое целевое значение равно 6000, а переменные в базе — c , с₁ и с₃ , равные 40, 50 и 80 соответственно. Мы перешли к новой угловой точке, следующему базовому допустимому решению:
Теперь мы перешли к следующему допустимому решению (нижний правый угол). Изображение автора. Шаг 4. Повторяйте шаг 3, пока не будет найдено оптимальное решение.
Оптимальное решение не найдено, так как в целевой строке таблицы отрицательное значение. Итак, давайте повторим шаг 3: вводимая переменная w , потому что она имеет самый низкий коэффициент в целевой строке. Строка, которую мы должны использовать для исключения Гаусса, — это строка 3, потому что 80/2 < 50/1. После сокращения строки таблица выглядит следующим образом:
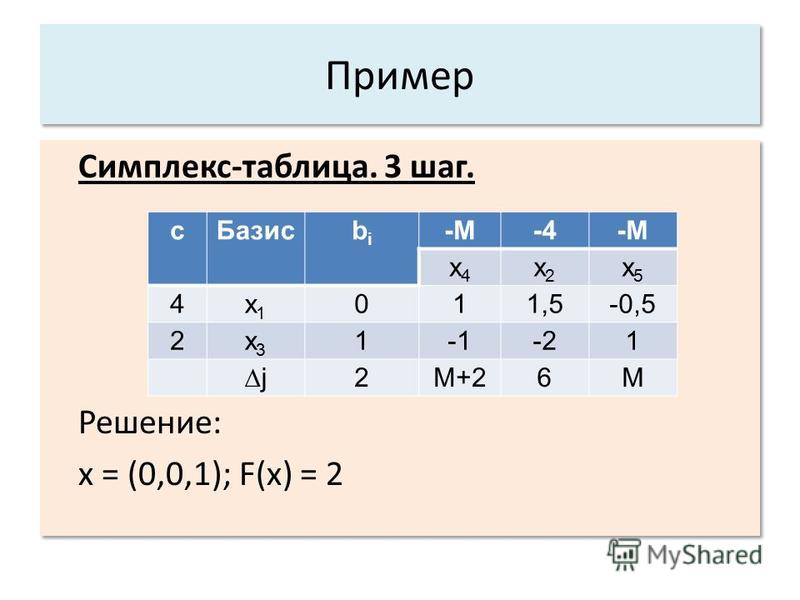Изображение автора.Базисными переменными являются w , c и s₁ с соответствующими значениями 40, 40 и 10 соответственно. Значение Z (цель) равно 10000. Это как раз оптимальное решение, которое у нас было в начале. В нижней строке нет отрицательных записей, так что это оптимальное решение. Шагов, которые мы сделали:
Шагов, которые мы сделали при решении задачи с симплекс-алгоритмом. Начиная снизу слева, делая два шага, чтобы закончить на оптимальном решении. Изображение автора.Это простой пример работы симплексного алгоритма. Он используется для решения более сложных задач, чем та, которую мы здесь обсуждали.
Линейное программирование — это инструмент, который может помочь отдельным лицам и организациям максимально эффективно использовать свои ресурсы и достигать своих целей. Независимо от того, являетесь ли вы владельцем бизнеса, пытающимся максимизировать прибыль, исследователем, стремящимся оптимизировать сложный процесс, или студентом, изучающим методы оптимизации, линейное программирование предлагает широкий спектр приложений и возможностей для роста.
Поняв принципы линейного программирования и симплекс-алгоритм, вы сможете сделать первый шаг к решению множества задач оптимизации и принятию обоснованных решений, которые могут иметь долгосрочные последствия.
При применении этих методов на практике вам не нужно реализовывать алгоритм, потому что это сделает за вас программное обеспечение для оптимизации.
Симплекс-алгоритм также применяется в смешанном целочисленном программировании, где ослабление ограничений делает возможным применение алгоритма. Если вы хотите узнать больше, вы можете прочитать статьи ниже.
Как справиться с проблемами оптимизации?
Простые примеры с решениями и кодом.
по направлению datascience.com
Эвристика математической оптимизации, которую должен знать каждый специалист по данным
Локальный поиск, генетические алгоритмы и многое другое.
в направлении datascience.com
Симплексный метод решения LPP (с примерами)
РЕКЛАМА:
После прочтения этой статьи вы узнаете о:- 1.
Введение в симплекс-метод 2. Принцип симплекс-метода 3. Вычислительная процедура 4. Блок-схема.
Симплексный метод, также называемый симплексным методом или симплексным алгоритмом, был разработан Г.Б. Данцег, американский математик. Симплекс-метод подходит для решения задач линейного программирования с большим количеством переменных. Метод посредством итеративного процесса постепенно приближается и в конечном итоге достигает максимального или минимального значения целевой функции.
Принцип симплекс-метода :ОБЪЯВЛЕНИЙ:
Не удалось получить графическое решение задачи ЛП с более чем двумя переменными. По этим причинам была разработана математическая итерационная процедура, известная как «симплексный метод». Симплекс-метод применим к любой задаче, которую можно сформулировать в терминах линейной целевой функции с учетом набора линейных ограничений.
Симплекс-метод предоставляет алгоритм, основанный на фундаментальной теореме линейного программирования.
В нем говорится, что «оптимальное решение задачи линейного программирования, если оно существует, всегда находится в одной из угловых точек пространства допустимых решений».
Симплекс-метод представляет собой систематический алгоритм, состоящий из перехода от одного базового допустимого решения к другому в заданном порядке таким образом, чтобы значение целевой функции улучшалось. Процедура прыжка из вершины в вершину повторяется. Симплекс-алгоритм представляет собой итеративную процедуру решения задач LP.
Состоит из:
РЕКЛАМА:
(i) Наличие пробного базового допустимого решения уравнения ограничений,
(ii) Проверка оптимальности решения,
(iii) Улучшение первого пробного решения путем повторения процесса до получения оптимального решения.
Вычислительная процедура симплекс-метода :Вычислительный аспект симплексной процедуры лучше всего пояснить на простом примере.
РЕКЛАМА:
Пример 1:
Рассмотрим задачу линейного программирования:
Увеличить z = 3x 1 + 2x 2
С учетом x 1 + x 2 , ≤ 4
РЕКЛАМА:
x 1 – x 2 , ≤ 2
x 1 , x 2 , ≥ 4
< 2 x v x 2 > 0
Решение:
РЕКЛАМА:
Шаги симплексного алгоритма следующие:
Шаг 1:
Формулировка математической модели:
(i) Сформулируйте математическую модель данного LPP.
(ii) Если целевая функция имеет тип минимизации, то преобразовать ее в функцию максимизации с помощью следующего соотношения
Уменьшить Z = – Увеличить Z*
Когда Z* = -Z
(iii) Убедитесь, что все значения b i [все правые константы ограничений] положительны. Если нет, его можно изменить на положительное значение, умножив обе стороны ограничений на -1.
В этом примере все b i (константы стороны высоты) уже положительны.
(iv) Затем преобразуйте ограничения неравенства в уравнение, введя переменную неотрицательного резерва или излишка. Коэффициенты резервных или избыточных переменных равны нулю в целевой функции.
В этом примере ограничения неравенства «≤» необходимы только резервные переменные s 1 и s 2 .
Поэтому данная задача теперь становится:
Шаг 2:
Настройте начальное решение.
Запишите коэффициенты всех переменных в данном LPP в табличной форме, как показано в таблице ниже, чтобы получить начальное базовое допустимое решение.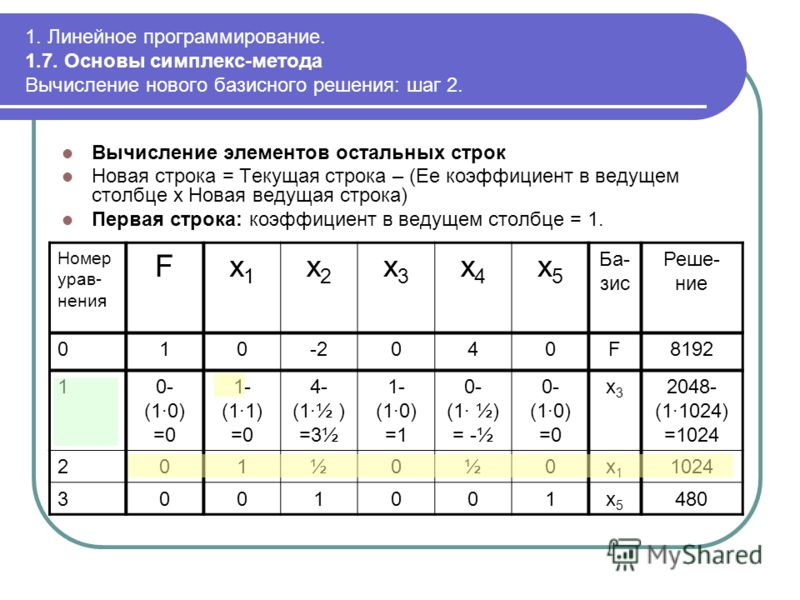
х В = В -1 В
В первой строке таблицы указаны коэффициенты c j переменных в целевой функции, которые остаются одинаковыми в последующих таблицах. Эти значения представляют затраты или прибыль на единицу целевой функции каждой из переменных.
Вторая строка содержит заголовки основных столбцов простой таблицы. Столбец C B дает коэффициенты текущих базовых переменных в целевой функции. Столбец x B дает текущие значения соответствующих переменных в базисе.
Числа a ij представляют скорость, с которой ресурс (i-1, 2-m) потребляется каждой единицей деятельности j (j = 1,2… n).
Значения z j представляют собой величину, на которую значение целевой функции Z уменьшится или увеличится, если к новому решению добавить одну единицу данной переменной.
Следует помнить, что значения неосновных переменных всегда равны нулю на каждой итерации.
Итак, x 1 = x 2 = 0 здесь, столбец x B дает значения основных переменных в первом столбце.
Так 5, = 4, с 2 = 2, здесь; Полное начальное допустимое решение можно сразу прочитать из таблицы 2 как s 1 = 4, s 2 , x, = 0, x 2 = 0 и значение целевой функции равно нулю.
Шаг 3:
Тест на оптимальность:
Теперь приступим к проверке базовой допустимости на оптимальность по приведенным ниже правилам. Это делается путем вычисления «чистой оценки» D j для переменной x j по формуле
Тест на оптимальность :
(i) Если все Δ j ≥ 0, тестируемое решение будет оптимальным.
(ii) Если хотя бы один Δ j отрицательный, тестируемое решение не является оптимальным, тогда переходите к улучшению решения на шаге 4.
(iii) Если соответствует наиболее отрицательному Δ j , все элементы столбца X j отрицательны или равны нулю (≤ 0), то тестируемое решение будет неограниченным
Применяя это правило для проверки оптимальности начального базового допустимого решения, можно заметить, что Δ 1 и Δ 2 оба отрицательны.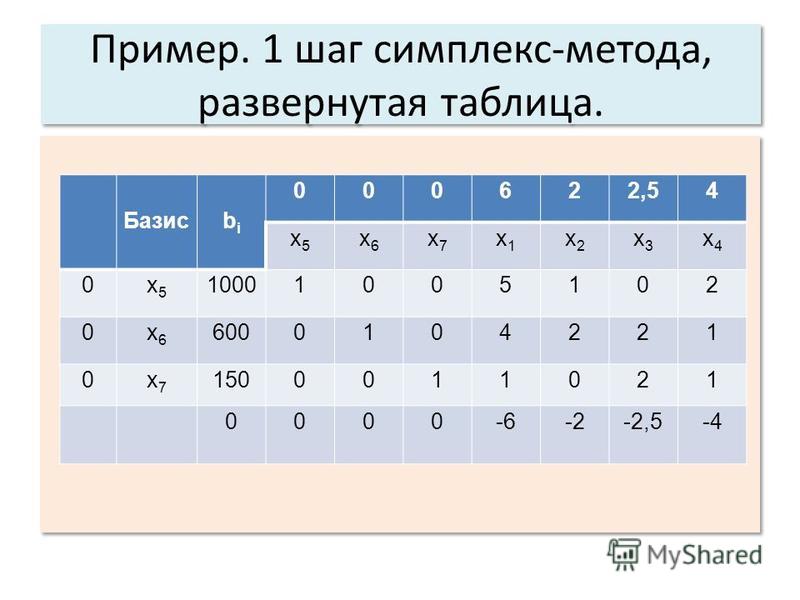
Следовательно, перейдите к улучшению этого решения на шаге 4.
Шаг 4:
Чтобы улучшить это базовое допустимое решение, вектор или, входящий в базисную матрицу, и вектор, который должен быть удален из базисной матрицы, определяются по следующим правилам, такие векторы обычно называются «входящий вектор» и «исходящий вектор» соответственно. .
«Входящий вектор»:
Входящий вектор X k всегда выбирается в соответствии с самым отрицательным значением Δ j . (скажем, Δ k ). Здесь Δ k = Mix (Δ 1 , Δ 2 ) = Min [ – 3, -2] = – 3 = Δ.
Следовательно, k = 1 и вектор-столбец x 1 должны войти в базовую матрицу. Столбец x 1 отмечен стрелкой вверх (↑).
«Исходящий вектор»:
Исходящий вектор β r выбирается в соответствии с минимальным отношением элементов X B к соответствующим положительным элементам заданного входящего вектора X К .
Это правило называется правилом минимального отношения. В математической форме это правило записывается как
Сравнивая обе части этого уравнения, r = 2, поэтому вектор B 2 , отмеченный направленной вниз стрелкой (↓), должен быть удален из базовой матрицы.
Теперь начальная таблица (2) изменена на таблицу (3)
Шаг 5:
Для того, чтобы поставить B 2 на место входящего вектора X1 = единица должна занимать отмеченную «□» позицию и ноль во всех остальных местах X 1 . Если число в отмеченной позиции «□» отлично от единицы, разделите все элементы этой строки на «ключевой элемент» (элемент на пересечении стрелки минимального отношения ( ←) и стрелки входящего вектора (↑) называется ключевой элемент). Затем вычтите соответствующие множители этой новой строки из других оставшихся строк, чтобы получить ноль в оставшейся позиции столбца X 1 .
Таким образом, процесс может быть усилен простым матричным преобразованием следующим образом:
Матрица промежуточных коэффициентов:
Таблица 4:
Теперь создайте улучшенную простую таблицу следующим образом:
Из этой таблицы улучшенное базовое допустимое решение читается как:
х 1 = 2, х 2 = 0, с 1 = 2 , с 2 = 0
Улучшенное значение Z = 6
Таким образом, оптимальное решение получается как
x B = 3, x 2 = 1, макс.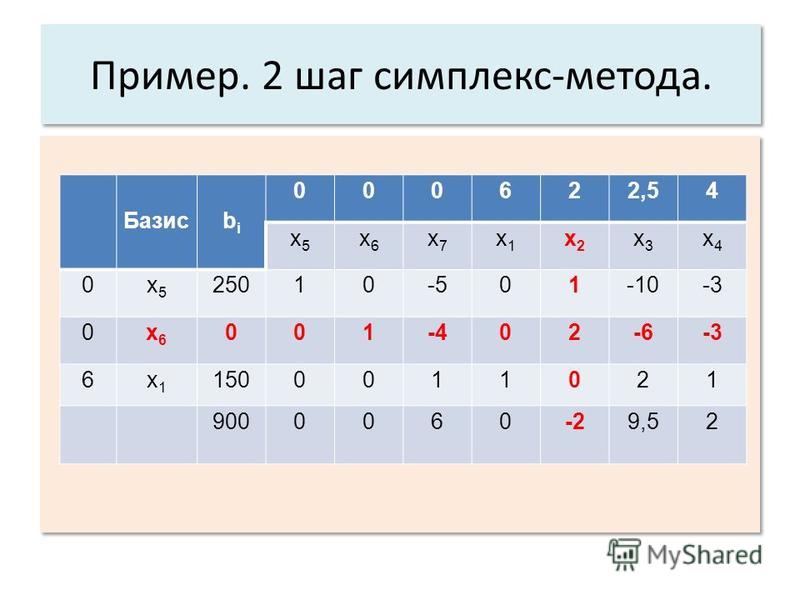
z = 11
Шаг 6:
Теперь повторяйте шаги с 3 по 5 по мере необходимости, пока не будет получено оптимальное решение в таблице 5.
Δ k = самое отрицательное Δ j = – 5 = Δ 2
. . . k = 2 и, следовательно, X 2 должен быть входным вектором (Ключевой столбец) По минимальному коэффициенту отношения
Так как отрицательный коэффициент не учитывается, то второй коэффициент не учитывается.
Поскольку первое отношение минимально, удалите первый вектор p, сформируйте базовую матрицу. Следовательно, ключевой элемент равен 2.
Развертывая первую строку по ключевым элементам 2, матрица промежуточных коэффициентов получается как
Это решение, читаемое из этой таблицы, равно x 1 = 3, x 2 = 2, S 1 , = 0, S 2 = 0 и Z = 11,
Также с помощью формулы Δ j = C B X j – C j убедитесь, что все Δ j неотрицательны.