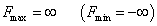Симплекс-метод решения задачи линейного программирования в Excel
Рассмотрим решение задачи линейного программирования с помощью симплекс-метода в Excel на примере
Целевая функция имеет вид
Z = 35∙x1+25∙x2+10∙x3+20∙x4→ max
Ограничения, записанные в виде системы линейных уравнений
4∙x1+1∙x2+2∙x3+0∙x4 ≤ 120
1∙x1+3∙x2+1∙x3+1∙x4 ≤ 160∙
2∙x1+1∙x2+1∙x3+3∙x4 ≤ 130
x1, x2, x3, x4 ≥ 0 – целые
Теперь данную задачу для решения запишем в Excel

В ячейке E4 вставим формулу
=A4*A5+B4*B5+C4*C5+D4*D5
Для ячейки E7, E8 и E9 формула будет иметь вид
=$A$4*A7+$B$4*B7+$C$4*C7+$D$4*D7
=$A$4*A8+$B$4*B8+$C$4*C8+$D$4*D8
=$A$4*A9+$B$4*B9+$C$4*C9+$D$4*D9
Также можно воспользоваться формулой:
=СУММПРОИЗВ(A4:D4;A7:D7)
На вкладке данные переходим в Поиск решения
Выбираем ячейку с целевой функцией, ставим галочку максимум, далее выбираем ячейки изменяемых переменных ($A$4:$D$4) и добавляем ограничения при помощи кнопки Добавить. Также ставим галочку переменные без ограничений неотрицательные, выбираем, выбираем метод решения – симплекс-метод решения линейных задач.



Можно также перейти в параметры и настроить точность.
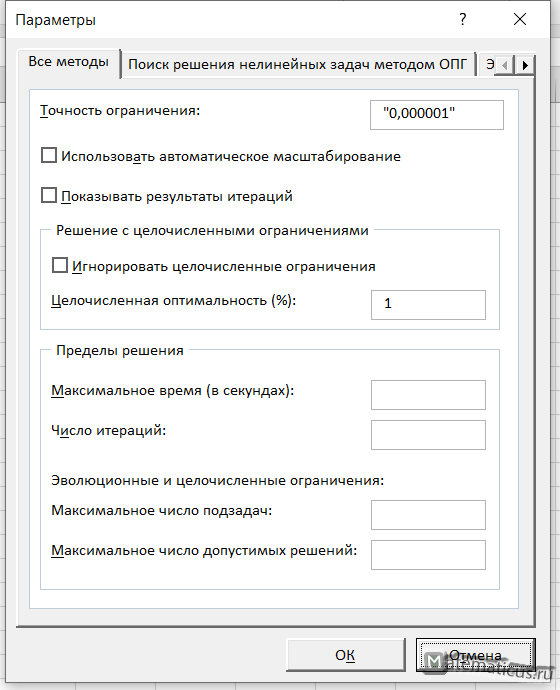
Итак, нажимаем Найти решение, появляется окно результаты поиска решений, выбираем сохранить найденное решение.

В итоги получили решения задачи
Z=2015
x1=19; x2=42; x3=0; x4=15

Подробный разбор симплекс-метода / Habr
Пролог
Недавно появилась необходимость создать с нуля программу, реализующую алгоритм симплекс-метода. Но в ходе решения я столкнулся с проблемой: в интернете не так уж много ресурсов, на которых можно посмотреть подробный теоретический разбор алгоритма (его обоснование: почему мы делаем те или иные шаги) и советы по практической реализации — непосредственно, алгоритм. Тогда я дал себе обещание — как только завершу задачу, напишу свой пост на эту тему. Об этом, собственно, и поговорим.
Замечание. Пост будет написан достаточно формальным языком, но будет снабжен комментариями, которые должны внести некоторую ясность. Такой формат позволит сохранить научный подход и при этом, возможно, поможет некоторым в изучении данного вопроса.
§1. Постановка задачи линейного программирования
Определение: Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств.
Общая задача линейного программирования (далее – ЛП) имеет вид:
§2. Каноническая форма задачи ЛП
Каноническая форма задачи ЛП:
Замечание: Любая задача ЛП сводится к канонической.
Алгоритм перехода от произвольной задачи ЛП к канонической форме:
- Неравенства с отрицательными $inline$b_i$inline$ умножаем на (-1).
- Если неравенство вида (≤), то к левой части добавляем $inline$s_i$inline$ – добавочную переменную, и получаем равенство.
- Если неравенство вида (≥), то из левой части вычитаем $inline$s_i$inline$, и получаем равенство.
- Делаем замену переменных:
- Если $inline$x_i ≤ 0$inline$, то $inline$x_i’= -x_i ≥ 0$inline$
- Если $inline$x_i$inline$ — любой, то $inline$x_i= x_i’ — x_i»$inline$, где $inline$x_i’, x_i»≥ 0$inline$
Замечание: Будем нумеровать $inline$s_i$inline$ по номеру неравенства, в которое мы его добавили.
Замечание: $inline$s_i$inline$ ≥0.
§3. Угловые точки. Базисные/свободные переменные. Базисные решения
Определение: Точка $inline$Х ∈ D$inline$ называется угловой точкой, если представление$inline$ Х= αХ^1+ (1-α) Х^2,где Х^1,Х^2 ∈D;0< α<1 $inline$ возможно только при $inline$Х^1=Х^2 $inline$.
Иными словами, невозможно найти две точки в области, интервал проходящий через которые содержит $inline$Х$inline$ (т.е. $inline$Х$inline$ – не внутренняя точка).
Графический способ решения задачи ЛП показывает, что нахождение оптимального решения ассоциируется с угловой точкой. Это является основной концепцией при разработке симплекс-метода.
Определение: Пусть есть система m уравнений и n неизвестных (m < n). Разделим переменные на два множества: (n-m) переменные положим равными нулю, а остальные m переменных определяются решением системы исходных уравнений. Если это решение единственно, то тогда ненулевые m переменных называют базисными; нулевые (n-m) переменных – свободными (небазисными), а соответствующие результирующие значения переменных называют базисным решением.
§4. Симплекс-метод
Симплекс-метод позволяет эффективно найти оптимальное решение, избегая простой перебор всех возможных угловых точек. Основной принцип метода: вычисления начинаются с какого-то «стартового» базисного решения, а затем ведется поиск решений, «улучшающих» значение целевой функции. Это возможно только в том случае, если возрастание какой-то переменной приведет к увеличению значения функционала.
- Задача должна иметь каноническую форму.
- У задачи должен быть явно выделенный базис.
Определение: Явно выделенным базисом будем называть вектора вида:$inline$(..0100..)^T, (..010..)^T,(..0010..)^T…$inline$, т.е. только одна координата вектора ненулевая и равна 1.
Замечание: Базисный вектор имеет размерность (m*1), где m – количество уравнений в системе ограничений.
Для удобства вычислений и наглядности обычно пользуются симплекс-таблицами:
- В первой строке указывают «наименование» всех переменных.
- В первом столбце указывают номера базисных переменных, а в последней ячейке – букву Z (это строка функционала).
- В «середине таблицы» указывают коэффициенты матрицы ограничений — aij.
- Последний столбец – вектор правых частей соответствующих уравнений системы ограничений.
- Крайняя правая ячейка – значение целевой функции. На первой итерации ее полагают равной 0.
Замечание: Базис – переменные, коэффициенты в матрице ограничений при которых образуют базисные вектора.
Замечание: Если ограничения в исходной задаче представлены неравенствами вида ≤, то при приведении задачи к канонической форме, введенные дополнительные переменные образуют начальное базисное решение.
Замечание: Коэффициенты в строке функционала берутся со знаком “-”.
Алгоритм симплекс-метода:
1. Выбираем переменную, которую будем вводить в базис. Это делается в соответствии с указанным ранее принципом: мы должны выбрать переменную, возрастание которой приведет к росту функционала. Выбор происходит по следующему правилу:
- Если задача на минимум – выбираем максимальный положительный элемент в последней строке.
- Если задача на максимум – выбираем минимальный отрицательный.
Такой выбор, действительно, соответствует упомянутому выше принципу: если задача на минимум, то чем большее число вычитаем – тем быстрее убывает функционал; для максимума наоборот – чем большее число добавляем, тем быстрее функционал растет.
Замечание: Хотя мы и берем минимальное отрицательное число в задаче на максимум, этот коэффициент показывает направление роста функционала, т.к. строка функционала в симплекс-таблице взята со знаком “-”. Аналогичная ситуация с минимизацией.
Определение: Столбец симплекс-таблицы, отвечающий выбранному коэффициенту, называется ведущим столбцом.
2. Выбираем переменную, которую будем вводить в базис. Для этого нужно определить, какая из базисных переменных быстрее всего обратится в нуль при росте новой базисной переменной. Алгебраически это делается так:
- Вектор правых частей почленно делится на ведущий столбец
- Среди полученных значений выбирают минимальное положительное (отрицательные и нулевые ответы не рассматривают)
Определение: Такая строка называется ведущей строкой и отвечает переменной, которую нужно вывести из базиса.
Замечание: Фактически, мы выражаем старые базисные переменные из каждого уравнения системы ограничений через остальные переменные и смотрим, в каком уравнении возрастание новой базисной переменной быстрее всего даст 0. Попадание в такую ситуацию означает, что мы «наткнулись» на новую вершину. Именно поэтому нулевые и отрицательные элементы не рассматриваются, т.к. получение такого результата означает, что выбор такой новой базисной переменной будет уводить нас из области, вне которой решений не существует.
3. Ищем элемент, стоящий на пересечении ведущих строки и столбца.
Определение: Такой элемент называется ведущим элементом.
4. Вместо исключаемой переменной в первом столбце (с названиями базисных переменных) записываем название переменной, которую мы вводим в базис.
5. Далее начинается процесс вычисления нового базисного решения. Он происходит с помощью метода Жордана-Гаусса.
- Новая Ведущая строка = Старая ведущая строка / Ведущий элемент
- Новая строка = Новая строка – Коэффициент строки в ведущем столбце * Новая Ведущая строка
Замечание: Преобразование такого вида направлено на введение выбранной переменной в базис, т.е. представление ведущего столбца в виде базисного вектора.
6. После этого проверяем условие оптимальности. Если полученное решение неоптимально – повторяем весь процесс снова.
§5. Интерпретация результата работы симплекс-метода
1. Оптимальность
Условие оптимальности полученного решения:
- Если задача на максимум – в строке функционала нет отрицательных коэффициентов (т.е. при любом изменении переменных значение итогового функционала расти не будет).
- Если задача на минимум – в строке функционала нет положительных коэффициентов (т.е. при любом изменении переменных значение итогового функционала уменьшаться не будет).
2. Неограниченность функционала
Однако, стоит отметить, что заданный функционал может не и достигать максимума/минимума в заданной области. Алгебраический признак этого можно сформулировать следующим образом:
При выборе ведущей строки (исключаемой переменной) результат почленного деления вектора правых частей на ведущий столбец содержит только нулевые и отрицательные значения.
Фактически, это значит, что какой бы рост мы не задавали новой базисной переменной, мы никогда не найдем новую вершину. А значит, наша функция не ограничена на множестве допустимых решений.
3. Альтернативные решения
При нахождении оптимального решения возможен еще один вариант – есть альтернативные решения (другая угловая точка, дающая то же самое значение функционала).
Алгебраический признак существования альтернативы:
После достижения оптимального решения имеются нулевые коэффициенты при свободных переменных в строке функционала.
Это значит, что при росте соответствующей переменной с нулевым коэффициентом значение функционала не изменится и новое базисное решение будет также давать оптимум функционала.
Эпилог
Данная статья направлена на более глубокое понимание теоретической части. В замечаниях и пояснениях здесь можно получить ответы на вопросы, которые обычно опускают при изучении этого метода и принимают априори. Однако, надо понимать, что многие методы численной оптимизации основаны на симплекс-методе (например, метод Гомори, М-Метод) и без фундаментального понимания вряд ли получится сильно продвинуться в дальнейшем изучении и применении всех алгоритмов этого класса. Чуть позже напишу статью о практической реализации симплекс-метода, а также несколько статей о Методе искусственных переменных (М-Метод), Методе Гомори и Методе ветвей и границ.
Спасибо за внимание!
P.S.
Если уже сейчас Вы мучаетесь с реализацией симплекс-метода, советую почитать книгу А. Таха Введение в исследование операций — там все неплохо разобрано и в теории, и на примерах; а также посмотрите примеры решения задач matburo.ru — это поможет с реализацией в коде.
Решение симплекс методом задачи ЛП: пример и алгоритм
Симплекс метод — это метод последовательного перехода от одного базисного решения (вершины многогранника решений) системы ограничений задачи линейного программирования к другому базисному решению до тех пор, пока функция цели не примет оптимального значения (максимума или минимума).
Симплекс метод был предложен американским математиком Р.Данцигом в 1947 году, с тех пор для нужд промышленности этим методом нередко решаются задачи линейного программирования с тысячами переменных и ограничений.
Перед тем, как перейти к алгоритму симплекс метода, несколько определений.
Всякое неотрицательное решение системы ограничений называется допустимым решением.
Пусть имеется система m ограничений с n переменными (m n).
Допустимым базисным решением является решение, содержащее m неотрицательных основных (базисных) переменных и n — m неосновных. (небазисных, или свободных) переменных. Неосновные переменные в базисном решении равны нулю, основные же переменные, как правило, отличны от нуля, то есть являются положительными числами.
Любые m переменных системы m линейных уравнений с n переменными называются основными, если определитель из коэффициентов при них отличен от нуля. Тогда остальные n — m переменных называются неосновными (или свободными).
Алгоритм симплекс метода
- Шаг 1. Привести задачу линейного программирования к канонической форме. Для этого перенести свободные члены в правые части (если среди этих свободных членов окажутся отрицательные, то соответствующее уравнение или неравенство умножить на — 1) и в каждое ограничение ввести дополнительные переменные (со знаком «плюс», если в исходном неравенстве знак «меньше или равно», и со знаком «минус», если «больше или равно»).
- Шаг 2. Если в полученной системе m уравнений, то m переменных принять за основные, выразить основные переменные через неосновные и найти соответствующее базисное решение. Если найденное базисное решение окажется допустимым, перейти к допустимому базисному решению.
- Шаг 3. Выразить функцию цели через неосновные переменные допустимого базисного решения. Если отыскивается максимум (минимум) линейной формы и в её выражении нет неосновных переменных с отрицательными (положительными) коэффициентами, то критерий оптимальности выполнен и полученное базисное решение является оптимальным — решение окончено. Если при нахождении максимума (минимума) линейной формы в её выражении имеется одна или несколько неосновных переменных с отрицательными (положительными) коэффициентами, перейти к новому базисному решению.
- Шаг 4. Из неосновных переменных, входящих в линейную форму с отрицательными (положительными) коэффициентами, выбирают ту, которой соответствует наибольший (по модулю) коэффициент, и переводят её в основные. Переход к шагу 2.
Важные условия
- Если допустимое базисное решение даёт оптимум линейной формы (критерий оптимальности выполнен), а в выражении линейной формы через неосновные переменные отсутствует хотя бы одна из них, то полученное оптимальное решение — не единственное.
- Если в выражении линейной формы имеется неосновная переменная
с отрицательным коэффициентом в случае её максимизации (с положительным — в случае
минимизации), а во все уравнения системы ограничений этого шага указанная переменная
входит также с отрицательными коэффициентами или отсутствует, то линейная форма не ограничена
при данной системе ограничений. В этом случае её максимальное (минимальное)
значение записывают в виде

Путём построения симплексных таблиц решить задачу линейного программирования намного проще, чем путём алгебраических преобразований, который показан в следующем параграфе. Симплексные таблицы очень наглядны. Существует несколько разновидностей правил работы с симплексными таблицами. Мы разберём правило, которое чаще всего называется правилом ведущего столбца и ведущей строки.
Будет нелишним открыть в новом окне пособие Действия с дробями: их, дробей в задачах на симплекс-метод, мягко говоря, хватает.
Пример. Найти максимум функции 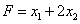 при ограничениях
при ограничениях
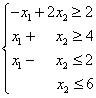
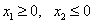
Решение.
Вводим добавочные неотрицательные переменные
 и сводим
данную систему неравенств к эквивалентной ей системе уравнений
и сводим
данную систему неравенств к эквивалентной ей системе уравнений
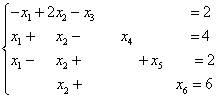
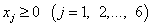 .
.
Это было сделано с соблюдением следующего правила: если в первоначальном ограничении знак «меньше или равно», то добавочную переменную нужно прибавлять, а если «больше или равно», то добавочную переменную нужно отнимать.
Введённые добавочные переменные принимаем за основные (базисные). Тогда 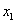 и
и
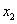 —
неосновные (свободные) переменные.
—
неосновные (свободные) переменные.
Выразив основные (базисные) переменные через неосновные (свободные), получим
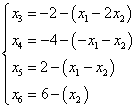
Функцию цели также выразим через неосновные (свободные) переменные:
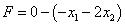
Из коэффициентов при переменных (неизвестных) построим первую симплексную таблицу.
| Таблица 1 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X1 | X2 | |||
| X3 | -2 | 1 | -2 | |
| X4 | -4 | -1 | -1 | |
| X5 | 2 | 1 | -1 | |
| X6 | 6 | 0 | 1 | |
| F | 0 | -1 | -2 | |
Последнюю строку таблицы, в которой записаны функция цели и коэффициенты при свободных переменных в ней, будем называть в индексной строкой.
Полученное решение не оптимально, так как в индексной строке коэффициенты при свободных переменных отрицательны. То есть оптимальным будет то решение, в котором коэффициенты при свободных переменных в индексной строке будут больше или равны нулю.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Для перехода к следующей таблице найдём наибольшее (по модулю) из чисел
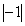 и
и
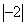 . Это число 2. Поэтому
ведущий столбец — тот столбец, в котором записано
. Это число 2. Поэтому
ведущий столбец — тот столбец, в котором записано 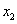
Для определения ведущей строки находим минимум отношений свободных членов к элементам ведущего столбца, причём если в числителе положительное число, а в знаменателе отрицательное, отношение считается равным бесконечности.
Итак,
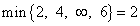 .
.
Поэтому ведущая строка — та, в которой записано 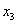
Ведущим элементом, таким образом, является -2.
Составляем вторую симплексную таблицу.
Новый базисный элемент 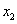 вписываем первой строкой, а столбец, в котором стояло
вписываем первой строкой, а столбец, в котором стояло 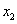 ,
вписываем новую свободную переменную
,
вписываем новую свободную переменную 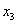
Заполняем первую строку. Для этого все числа, стоящие в ведущей строке таблицы 1, делим на ведущий элемент и записываем в соответствующий столбец первой строки таблицы 2, кроме числа, стоящего в ведущем столбце, куда записывается величина, обратная ведущему элементу (то есть, единица, делённая на ведущий элемент).
Заполняем столбец вспомогательных коэффициентов. Для этого числа ведущего столбца таблицы 1, кроме ведущего элемента, записываем с противоположными знаками в графу вспомогательных коэффициентов таблицы 2.
| Таблица 2 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X1 | X3 | |||
| X2 | 1 | -1/2 | -1/2 | |
| X4 | -3 | -3/2 | -1/2 | 1 |
| X5 | 3 | 1/2 | -1/2 | 1 |
| X6 | 5 | 1/2 | 1/2 | -1 |
| F | 2 | -2 | -1 | 2 |
Кто ещё не открыл в новом окне пособие Действия с дробями, может сделать это сейчас, поскольку самое время.
Для получения остальных строк таблицы 2 числа, уже стоящие в первой строке этой таблицы, умножаем на вспомогательный коэффициент, стоящий в заполняемой строке, и к результату прибавляем число из таблицы 1, стоящее в той же строке при соответствующей переменной.
Например, для получения свободного члена второй строки число 1 умножаем на 1 и прибавляем
из таблицы 1 число -4. Получаем -3. Коэффициент при 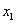 во второй строке находим так же:
во второй строке находим так же: 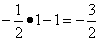 .
Так как в предыдущей таблице отсутствует столбец с новой свободной переменной
.
Так как в предыдущей таблице отсутствует столбец с новой свободной переменной 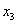 ,
то коэффициент второй строки в столбце новой свободной переменной
,
то коэффициент второй строки в столбце новой свободной переменной 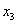 будет
будет 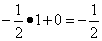 (то есть из таблицы
1 прибавляем 0, так как в таблице 1 столбец с
(то есть из таблицы
1 прибавляем 0, так как в таблице 1 столбец с 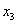 отсутствует).
отсутствует).
Так же заполняется и индексная строка:
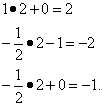
Полученное таким образом решение вновь не оптимально, так как в индексной строке коэффициенты при свободных переменных вновь отрицательны.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Для перехода к следующей симплексной таблице найдём наибольшее (по модулю) из чисел
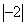 и
и
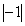 , то есть, модулей
коэффициентов в индексной строке. Это число 2. Поэтому
ведущий столбец — тот столбец, в котором записано
, то есть, модулей
коэффициентов в индексной строке. Это число 2. Поэтому
ведущий столбец — тот столбец, в котором записано 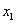 .
.
Для поиска ведущей строки найдём минимум отношений свободных членов к элементам ведущей строки. Получаем:
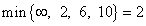 .
.
Следовательно, ведущая строка — та, в которой записано 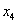 ,
а ведущим элементом является -3/2.
,
а ведущим элементом является -3/2.
Составляем третью симплексную таблицу
Новую базисную переменную 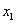 записываем первой строкой. В столбец, в котором было
записываем первой строкой. В столбец, в котором было 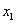 ,
вписываем новую свободную переменную
,
вписываем новую свободную переменную 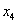 .
.
Первая строка:
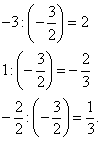
Вспомогательные коэффициенты:
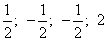
| Таблица 3 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X4 | X3 | |||
| X1 | 2 | -2/3 | 1/3 | |
| X2 | 2 | -1/3 | -1/3 | 1/2 |
| X5 | 2 | 1/3 | -2/3 | -1/2 |
| X6 | 4 | 1/3 | 1/3 | -1/2 |
| F | 6 | -4/3 | -1/3 | 2 |
Вычисление остальных строк на примере второй строки:
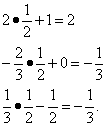
Полученное решение вновь не оптимальное, поскольку коэффициенты при свободных неизвестных в индексной строке вновь отрицательные.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Для перехода к четвёртой симплексной таблице найдём наибольшее из чисел
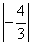 и
и
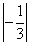 . Это число
. Это число
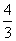 .
.
Следовательно, ведущий столбец — тот, в котором записано 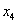 .
.
Для нахождения ведущей строки найдём минимум модулей отношений свободных членов к элементам ведущего столбца:
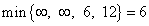 .
.
Поэтому ведущая строка — та, в которой записано 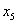 ,
а ведущий элемент 1/3.
,
а ведущий элемент 1/3.
В четвёртой симплексной таблице новую базисную переменную
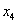 записываем первой строкой.
В столбец, где было
записываем первой строкой.
В столбец, где было 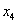 , записываем
новую свободную переменную
, записываем
новую свободную переменную 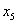 .
.
Первая строка:
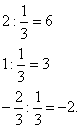
Вспомогательные коэффициенты:
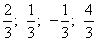 .
.
| Таблица 4 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X5 | X3 | |||
| X4 | 6 | 3 | -2 | |
| X1 | 6 | 2 | -1 | 2/3 |
| X2 | 4 | 1 | -1 | 1/3 |
| X6 | 2 | -1 | 1 | -1/3 |
| F | 14 | 4 | -3 | 4/3 |
Вычисление остальных строк на примере второй строки:
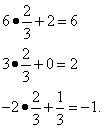
Полученное решение так же не оптимально, но оно уже лучше предыдущих, так как один из коэффициентов при свободных переменных в индексной строке неотрицателено.
Для улучшения плана перейдём к следующей симплексной таблице.
Найдём наибольшее из чисел 4 и 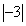 .
Это число 4. Следовательно, ведущий столбец
.
Это число 4. Следовательно, ведущий столбец 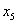 .
.
Для нахождения ведущей строки найдём
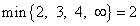 .
.
Следовательно, ведущая строка — та, в которой записано 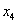 .
Но
.
Но 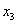 и
и
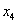 уже были вместе среди
свободных переменных. Поэтому для перевода очередной переменной из свободных в базисные выбираем другой
ведущий столбец — тот, в котором записано
уже были вместе среди
свободных переменных. Поэтому для перевода очередной переменной из свободных в базисные выбираем другой
ведущий столбец — тот, в котором записано 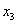 .
.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Для нахождения ведущей строки найдём
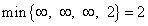 .
.
Следовательно, ключевая строка —
та, в которой записано 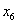 ,
а ведущий элемент 1.
,
а ведущий элемент 1.
В пятой симплексной таблице новую базисную переменную
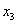 записываем первой строкой.
В столбец, где было
записываем первой строкой.
В столбец, где было 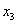 , записываем
новую свободную переменную
, записываем
новую свободную переменную 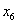 .
.
Первая строка:
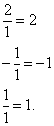
Вспомогательные коэффициенты:
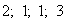 .
.
| Таблица 5 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X5 | X6 | |||
| X3 | 2 | -1 | 1 | |
| X4 | 10 | 2 | ||
| X1 | 8 | 1 | ||
| X2 | 6 | 1 | ||
| F | 20 | 1 | 3 | 3 |
Попробуем сразу узнать, не является ли решение оптимальным. Поэтому для остальных строк вычислим только свободные члены (чтобы узнать значения базисных переменных при равенстве свободных переменных нулю) и коэффициенты при свободных переменных в индексной строке.
Свободные члены:
— во второй строке 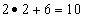 ;
;
— в третьей строке 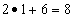 ;
;
— в четвёртой строке 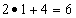 .
.
Индексная строка:
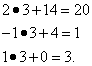
Смотрим в симплексную таблицу 5. Видим, что получено оптимальное решение, так как коэффициенты при свободных неизвестных в индексной строке неотрицательны.
Ответ:
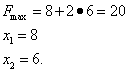
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс методом.

Решим алгебраическими преобразованиями тот же пример, что и в предыдущем параграфе.
Следует отметить, что при решении этой разновидностью симплекс метода лучше не записывать функцию
цели в виде 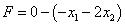 ,
так как при этом легко запутаться в знаках. Но в этом случае пункт алгоритма, определяющий критерий
оптимальности, будет модифицирован следующим образом.
,
так как при этом легко запутаться в знаках. Но в этом случае пункт алгоритма, определяющий критерий
оптимальности, будет модифицирован следующим образом.
Если отыскивается максимум (минимум) линейной формы и в её выражении нет неосновных переменных с положительными (отрицательными) коэффициентами, то критерий оптимальности выполнен и полученное базисное решение является оптимальным — решение окончено. Если при нахождении максимума (минимума) линейной формы в её выражении имеется одна или несколько неосновных переменных с положительными (отрицательными) коэффициентами, перейти к новому базисному решению.
Пример. Найти максимум функции 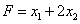 при ограничениях
при ограничениях
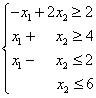
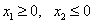
Решение.
Шаг I. Вводим добавочные неотрицательные переменные
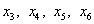 и сводим
данную систему неравенств к эквивалентной ей системе уравнений
и сводим
данную систему неравенств к эквивалентной ей системе уравнений
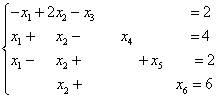
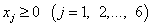 .
.
Введённые добавочные переменные принимаем за основные, так как в
этом случае базисное решение системы легко находится. Тогда 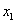 и
и
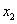 —
неосновные переменные.
—
неосновные переменные.
Выразив основные переменные через неосновные, получим
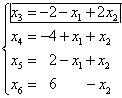
Следовательно, данному разбиению переменных на основные и неосновные
соответствует базисное решение 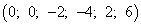 ,
которое является недопустимым (две переменные отрицательны), а поэтому оно не оптимальное.
От этого базисного решения перейдём к улучшенному.
,
которое является недопустимым (две переменные отрицательны), а поэтому оно не оптимальное.
От этого базисного решения перейдём к улучшенному.
Чтобы решить, какую переменную следует перевести из неосновных в
основные, рассмотрим любое из двух имеющихся уравнений последней системы с отрицательными
свободными членами, например второе. Оно показывает, что в основные переменные можно
перевести 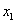 и
и
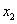 , так как
в этом уравнении они имеют положительные коэффициенты (следовательно, при их
увеличении, а это произойдёт, если переведём любую из них в основные переменные,
переменная
, так как
в этом уравнении они имеют положительные коэффициенты (следовательно, при их
увеличении, а это произойдёт, если переведём любую из них в основные переменные,
переменная 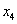 увеличится).
увеличится).
Попробуем перевести в основные переменную 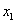 .
Чтобы установить, какую переменную следует перевести из основные в неосновные, найдём
абсолютную величину наименьшего отношения свободных членов системы к коэффициентам
при
.
Чтобы установить, какую переменную следует перевести из основные в неосновные, найдём
абсолютную величину наименьшего отношения свободных членов системы к коэффициентам
при 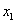 . Имеем
. Имеем
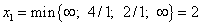 . Оно
получено из третьего уравнения, показывающего, что в неосновные нужно перевести
переменную
. Оно
получено из третьего уравнения, показывающего, что в неосновные нужно перевести
переменную 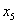 ,
которая в исходном базисном решении положительна. Следовательно, полученное базисное
решение, как и исходное, содержит две отрицательные компоненты, т. е. при переходе к такому
базисному решению улучшения не произойдёт.
,
которая в исходном базисном решении положительна. Следовательно, полученное базисное
решение, как и исходное, содержит две отрицательные компоненты, т. е. при переходе к такому
базисному решению улучшения не произойдёт.
Если же перевести в основные переменную 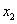 ,
то наименьшее отношение свободных членов к коэффициентам при
,
то наименьшее отношение свободных членов к коэффициентам при 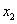 составит
составит 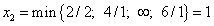 .
Оно получено из первого уравнения, в котором свободный член отрицателен. Следовательно,
переводя
.
Оно получено из первого уравнения, в котором свободный член отрицателен. Следовательно,
переводя 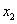 в
основные, а
в
основные, а 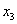 в неосновные переменные, мы получим базисное решение, в котором число отрицательных
компонент на единицу меньше, чем в исходном. Поэтому остановимся на этой возможности:
переводим
в неосновные переменные, мы получим базисное решение, в котором число отрицательных
компонент на единицу меньше, чем в исходном. Поэтому остановимся на этой возможности:
переводим 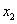 в основные, а
в основные, а 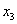 в неосновные переменные. Поэтому в приведённой выше системе уравнений выделенным оказалось
первое уравнение.
в неосновные переменные. Поэтому в приведённой выше системе уравнений выделенным оказалось
первое уравнение.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Шаг II.
Основные переменные 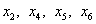 ,
неосновные переменные
,
неосновные переменные 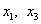 .
.
Выразим новые основные переменные через новые неосновные, начиная с выделенного на шаге I уравнения. В результате получим
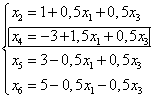
Следовательно, имеем новое базисное решение 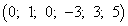 ,
которое также является недопустимым, а поэтому не оптимальным. Но в нём, как мы и
предвидели, только одна переменная отрицательна (а именно
,
которое также является недопустимым, а поэтому не оптимальным. Но в нём, как мы и
предвидели, только одна переменная отрицательна (а именно 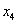 ).
).
От полученного базисного решения необходимо перейти к другому.
Рассмотрим уравнение с отрицательным свободным членом, т. е. второе уравнение. Оно
показывает, что в основные переменные можно перевести 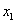 и
и
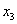 . Переведём в
основные переменные
. Переведём в
основные переменные 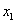 .
Найдём наименьшее из абсолютных величин отношений свободных членов системы к
коэффициентам при
.
Найдём наименьшее из абсолютных величин отношений свободных членов системы к
коэффициентам при 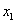 .
Имеем
.
Имеем 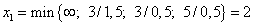 .
Значит, в неосновные переменные нужно перенести
.
Значит, в неосновные переменные нужно перенести 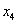 .
Так как наименьшее отношение получено из второго уравнения, то его выделяем. В новом
базисном решении уже не окажется отрицательных компонент, т. е. оно является
допустимым.
.
Так как наименьшее отношение получено из второго уравнения, то его выделяем. В новом
базисном решении уже не окажется отрицательных компонент, т. е. оно является
допустимым.
В особых случаях решение завершается на II шаге: это, например, случаи, когда максимум целевой функции — бесконечность и когда система не имеет ни одного решения.
Шаг III.
Основные переменные: 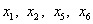 ,
неосновные переменные:
,
неосновные переменные: 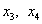 .
Выразив основные переменные через неосновные, получим
.
Выразив основные переменные через неосновные, получим
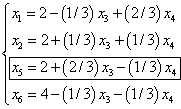
Новое базисное решение имеет вид 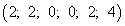 .
Является ли оно оптимальным, можно установить, если выразить линейную форму через
неосновные переменные рассматриваемого базисного решения. Сделав это, получим
.
Является ли оно оптимальным, можно установить, если выразить линейную форму через
неосновные переменные рассматриваемого базисного решения. Сделав это, получим
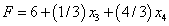 . Так как
мы ищем максимум линейной формы, а нашли лишь одно допустимое решение, то продолжим перебор.
. Так как
мы ищем максимум линейной формы, а нашли лишь одно допустимое решение, то продолжим перебор.
Переводим в число основных переменную 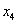 ,
имеющую больший положительный коэффициент. Находим
,
имеющую больший положительный коэффициент. Находим 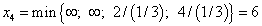 .
Это наименьшее отношение получено из третьего уравнения системы, поэтому его выделяем.
Оно показывает, что при
.
Это наименьшее отношение получено из третьего уравнения системы, поэтому его выделяем.
Оно показывает, что при 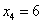 переменная
переменная 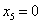 и поэтому перейдёт в число неосновных.
и поэтому перейдёт в число неосновных.
В некотором особом случае решение завершается на III шаге: это случай, когда оптимальное решение — не единственное.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Шаг IV.
Основные переменные: 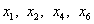 ,
неосновные переменные:
,
неосновные переменные: 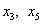 .
Выразив основные переменные через неосновные, получим
.
Выразив основные переменные через неосновные, получим
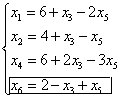
Линейная форма, выраженная через те же неосновные переменные, примет
вид 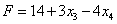 . Продолжим перебор для поиска максимума.
. Продолжим перебор для поиска максимума.
Увеличение линейной формы возможно при переходе к новому базисному
решению, в котором переменная 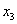 является основной. Находим
является основной. Находим 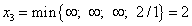 .
Это наименьшее отношение получено из четвёртого уравнения системы и показывает, что
при
.
Это наименьшее отношение получено из четвёртого уравнения системы и показывает, что
при 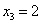 переменная
переменная 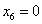 и
переходит в число неосновных.
и
переходит в число неосновных.
Шаг V.
Основные переменные: 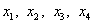 ,
неосновные переменные:
,
неосновные переменные: 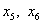 .
Выразив основные переменные через неосновные, получим
.
Выразив основные переменные через неосновные, получим
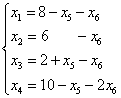
Линейная форма, выраженная через неосновные переменные нового
базисного решения, имеет вид 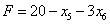 .
Критерий оптимальности для случая максимизации линейной формы выполнен. Следовательно,
базисное решение
.
Критерий оптимальности для случая максимизации линейной формы выполнен. Следовательно,
базисное решение 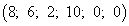 является оптимальным, а максимум линейной формы
является оптимальным, а максимум линейной формы 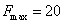
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Начало темы «Линейное программирование»
Продолжение темы «Линейное программирование»
Поделиться с друзьями
Решение задачи линейного программирования графическим методом, симплекс-методом и через «Поиск решения» в Excel ЗАДАНИЕ. кг сырья первого типа, a
Лабораторная работа 1
 Лабораторная работа 1 Решение задач линейного программирования графическим методом с использованием MS Excel Цель работы решить задачу линейного программирования графическим методом, с использованием надстройки
Лабораторная работа 1 Решение задач линейного программирования графическим методом с использованием MS Excel Цель работы решить задачу линейного программирования графическим методом, с использованием надстройки
Линейное программирование
 Линейное программирование Задача 1… 2 Задача 2… 3 Задача 3… 5 Задача 4… 7 Задача 5… 10 Задача 6… 12 Задача 7… 15 Задача 8… 19 Задача 9… 21 Задача 10… 24 Задача 11… 27 Задача 1. Составить
Линейное программирование Задача 1… 2 Задача 2… 3 Задача 3… 5 Задача 4… 7 Задача 5… 10 Задача 6… 12 Задача 7… 15 Задача 8… 19 Задача 9… 21 Задача 10… 24 Задача 11… 27 Задача 1. Составить
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
 Исследование операций Определение Операция — мероприятие, направленное на достижение некоторой цели, допускающее несколько возможностей и их управление Определение Исследование операций совокупность математических
Исследование операций Определение Операция — мероприятие, направленное на достижение некоторой цели, допускающее несколько возможностей и их управление Определение Исследование операций совокупность математических
Практическая работа 5.4.
 Практическая работа 5.4. Решение задачи об оптимальном распределении ресурсов при выпуске продукции с использованием процедуры «Поиск решения» Microsoft Excel Цель работы. Выполнив эту работу, Вы научитесь:
Практическая работа 5.4. Решение задачи об оптимальном распределении ресурсов при выпуске продукции с использованием процедуры «Поиск решения» Microsoft Excel Цель работы. Выполнив эту работу, Вы научитесь:
Экономико-математические методы и модели.
 ИНСТИТУТ МИРОВОЙ ЭКОНОМИКИ И ИНФОРМАТИЗАЦИИ НЕГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ Экономико-математические методы и модели. МОСКВА — 00 Практические задания
ИНСТИТУТ МИРОВОЙ ЭКОНОМИКИ И ИНФОРМАТИЗАЦИИ НЕГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ Экономико-математические методы и модели. МОСКВА — 00 Практические задания
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
 Краткая теория для выполнения контрольной работы по дисциплине ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ Составление штатного расписания Пусть известно, что в штате больницы состоит 6 санитарок, 8 медсестер, 10 врачей,
Краткая теория для выполнения контрольной работы по дисциплине ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ Составление штатного расписания Пусть известно, что в штате больницы состоит 6 санитарок, 8 медсестер, 10 врачей,
изделия j-го вида i 1,
 Лабораторная работа 4 Тема работы: Решение задачи об оптимальном распределении ресурсов при выпуске продукции с использованием процедуры Поиск решения Microsoft Excel. Цель работы: Научиться использовать
Лабораторная работа 4 Тема работы: Решение задачи об оптимальном распределении ресурсов при выпуске продукции с использованием процедуры Поиск решения Microsoft Excel. Цель работы: Научиться использовать
определяется матрицей A.
 Задание.Мебельная фабрика планирует выпуск двух видов продукции А и Б. Спрос на продукцию не определен, однако можно предполагать, что он может принимать одно из трех состояний (I, II и III). В зависимости
Задание.Мебельная фабрика планирует выпуск двух видов продукции А и Б. Спрос на продукцию не определен, однако можно предполагать, что он может принимать одно из трех состояний (I, II и III). В зависимости
Графическое решение задачи
 На приобретение машин для участка выделены 30 т.р. Производственная площадь участка — 70 м 2. Можно закупить машины двух видов: стоимостью 3 т.р. и 5 т.р. олее дорогая машина требует для установки 12 м
На приобретение машин для участка выделены 30 т.р. Производственная площадь участка — 70 м 2. Можно закупить машины двух видов: стоимостью 3 т.р. и 5 т.р. олее дорогая машина требует для установки 12 м
Контрольная работа. F=6*x 1 +3*х 2, (3)
 Контрольная работа Задача 5 На предприятии имеется сырье видов 1, 2, 3 Из него можно изготавливать изделия типов А и В Пусть запасы видов сырья на предприятии составляют b 1, b 2, b 3 ед соответственно,
Контрольная работа Задача 5 На предприятии имеется сырье видов 1, 2, 3 Из него можно изготавливать изделия типов А и В Пусть запасы видов сырья на предприятии составляют b 1, b 2, b 3 ед соответственно,
ГУМРФ им. адмирала С.О. Макарова. х х
 Постановка задачи Для перевозки изделий, состоящи из дву контейнеров А и В, у компании «Транзит» имеются три транспортны средства разны типов, возможности которы приведены в таблице. Перевозка дву различны
Постановка задачи Для перевозки изделий, состоящи из дву контейнеров А и В, у компании «Транзит» имеются три транспортны средства разны типов, возможности которы приведены в таблице. Перевозка дву различны
Графическое решение задачи
 Решить задачу линейного программирования, где 3x12x2 8 x14x2 10 x1 0 x 2 0 LX3x14x2 max а) геометрическим способом, б) перебором базисных решений, в) симплекс-методом. Графическое решение задачи L X 3×14
Решить задачу линейного программирования, где 3x12x2 8 x14x2 10 x1 0 x 2 0 LX3x14x2 max а) геометрическим способом, б) перебором базисных решений, в) симплекс-методом. Графическое решение задачи L X 3×14
Адрес: г. Воронеж ул. Мичурина, 1, ауд. 124
 Министерство сельского хозяйства РФ Воронежский государственный аграрный университет им. К.Д. Глинки Кафедра информационного обеспечения и моделирования агроэкономических систем Контактная информация:
Министерство сельского хозяйства РФ Воронежский государственный аграрный университет им. К.Д. Глинки Кафедра информационного обеспечения и моделирования агроэкономических систем Контактная информация:
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
 МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Ижевский государственный технический университет кафедра САПР МЕТОДИЧЕСКИЕ УКАЗАНИЯ к проведению практических занятий по дисциплине «Системный анализ» на тему
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Ижевский государственный технический университет кафедра САПР МЕТОДИЧЕСКИЕ УКАЗАНИЯ к проведению практических занятий по дисциплине «Системный анализ» на тему
АЛГОРИТМ СИМПЛЕКС-МЕТОДА
 АЛГОРИТМ СИМПЛЕКС-МЕТОДА Прежде всего нужно знать, что симплекс-метод является универсальным методом решения задач линейного программирования (ЗЛП) в том смысле, что он позволяет решать ЗЛП с любым количеством
АЛГОРИТМ СИМПЛЕКС-МЕТОДА Прежде всего нужно знать, что симплекс-метод является универсальным методом решения задач линейного программирования (ЗЛП) в том смысле, что он позволяет решать ЗЛП с любым количеством
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
 Учреждение образования «Полоцкий государственный университет» МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ к практической подготовке по дисциплине «Высшая математика: Математическое программирование» для студентов заочного
Учреждение образования «Полоцкий государственный университет» МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ к практической подготовке по дисциплине «Высшая математика: Математическое программирование» для студентов заочного
Решение задач исследования операций
 Федеральное агентство по образованию Белгородский государственный технологический университет им. В. Г. Шухова Г. Л. Окунева, А. В. Борзенков, С. В. Рябцева Решение задач исследования операций Учебное
Федеральное агентство по образованию Белгородский государственный технологический университет им. В. Г. Шухова Г. Л. Окунева, А. В. Борзенков, С. В. Рябцева Решение задач исследования операций Учебное
МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ЭКОНОМИКЕ
 МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ КЕМЕРОВСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ ПИЩЕВОЙ ПРОМЫШЛЕННОСТИ Г.С. Ветрова, Л.А. Яковлева МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ЭКОНОМИКЕ Учебное пособие для студентов экономических
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ КЕМЕРОВСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ ПИЩЕВОЙ ПРОМЫШЛЕННОСТИ Г.С. Ветрова, Л.А. Яковлева МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ЭКОНОМИКЕ Учебное пособие для студентов экономических
Лабораторный практикум
 МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное общеобразовательное учреждение высшего профессионального образования «Российский экономический университет имени
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное общеобразовательное учреждение высшего профессионального образования «Российский экономический университет имени
Линейная алгебра
 Линейная алгебра 08.12.2012 Линейные модели в экономике Линейное программирование Линейная алгебра (лекция 13) 08.12.2012 2 / 25 Задача линейного программирования: F (x 1, x 2,…, x n ) = n c j x j max(min),
Линейная алгебра 08.12.2012 Линейные модели в экономике Линейное программирование Линейная алгебра (лекция 13) 08.12.2012 2 / 25 Задача линейного программирования: F (x 1, x 2,…, x n ) = n c j x j max(min),
1.1. Инструмент подбор параметра
 Excel 2007. Анализ «что-если» 1. Подбор параметра 1.1. Инструмент подбор параметра 2. Создание сценариев для анализов «что-если» 2.1. Создание сценария 2.2. Просмотр сценария 2.3. Создание итогового отчета
Excel 2007. Анализ «что-если» 1. Подбор параметра 1.1. Инструмент подбор параметра 2. Создание сценариев для анализов «что-если» 2.1. Создание сценария 2.2. Просмотр сценария 2.3. Создание итогового отчета
Симплекс метод онлайн
Данный онлайн калькулятор решает задачу линейного программирования симплекс методом. Дается подробное решение с пояснениями. Для решения задачи линейного программирования задайте количество ограничений и количество переменных. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить». Теоретическую часть смотрите в статье: Решение задачи линейного программирования. Симплекс метод.
| Количество ограничений: m= | 1234567891011121314151617181920 |
| Количество переменных : n= | 1234567891011121314151617181920 |
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Симплекс метод
Симплекс метод − это метод решения задачи линейного программирования (ЗЛП). Суть метода заключается в нахождении начального допустимого плана, и в последующем улучшении плана до достижения максимального (или минимального) значения целевой функции в данном выпуклом многогранном множестве или выяснения неразрешимости задачи. Подробнее в статье: Решение задачи линейного программирования. Симплекс метод.
Примеры решения ЗЛП симплекс методом
Пример 1. Решить следующую задачу линейного программирования:
Р е ш е н и е. Матрица коэффициентов  системы уравнений имеет вид:
системы уравнений имеет вид:
 |
Правая часть ограничений системы уравнений имеет вид:
 |
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последняя строка — это целевая функция, умноженная на −1. Последние три векторы столбцы обазуют базис в трехмерном пространствое. Следовательно базисные переменные  , а свободные переменные
, а свободные переменные  :
:
 |
Запишем текущий опорный план:
 |
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-3), следовательно в базис входит вектор x2. Определяем, какой вектор выходит из базиса. Для этого вычисляем  при
при  . min(40:6, 28:2)=20/3 соответствует строке 1. Из базиса выходит вектор x3. Сделаем исключение Гаусса для столбца x2, учитывая, что ведущий элемент соответствует строке 1. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 2, 3, 4 со строкой 1, умноженной на -1/3, 1/6, 1/2, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
. min(40:6, 28:2)=20/3 соответствует строке 1. Из базиса выходит вектор x3. Сделаем исключение Гаусса для столбца x2, учитывая, что ведущий элемент соответствует строке 1. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 2, 3, 4 со строкой 1, умноженной на -1/3, 1/6, 1/2, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
 |
Запишем текущий опорный план:
 |
Данный опорный план не является оптимальным, так как в последней строке есть отрицательный элемент (-3), следовательно в базис входит вектор x1. Определяем, какой вектор выходит из базиса. Для этого вычисляем  при
при  . min(44/3:11/3, 62/3:5/3)=4 соответствует строке 2. Из базиса выходит вектор x4. Сделаем исключение Гаусса для столбца x1, учитывая, что ведущий элемент соответствует строке 2. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 1, 3, 4 со строкой 2, умноженной на 1/11, -5/11, 9/11, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
. min(44/3:11/3, 62/3:5/3)=4 соответствует строке 2. Из базиса выходит вектор x4. Сделаем исключение Гаусса для столбца x1, учитывая, что ведущий элемент соответствует строке 2. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 1, 3, 4 со строкой 2, умноженной на 1/11, -5/11, 9/11, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
Запишем текущий опорный план:
 |
Текущий опорный план является оптимальным, так как в строках 4 под переменными  нет отрицательных элементов.
нет отрицательных элементов.
Решение можно записать так: 

 .
.
Значение целевой функции в данной точке: F(X)=
 .
.
Пример 2. Найти максимум функции
 |
при условиях
Р е ш е н и е. Матрица коэффициентов  системы уравнений имеет вид:
системы уравнений имеет вид:
 |
Правая часть ограничений системы уравнений имеет вид:
 |
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последняя строка — это целевая функция, умноженная на −1:
 |
Базисные векторы x4, x3, следовательно, все элементы в столбцах x4, x3, ниже горизонтальной линии должны быть нулевыми.
Обнулим все элементы столбца x4, кроме ведущего элемента. Для этого сложим строку 3 со строкой 1, умноженной на 4. Обнулим все элементы столбца x3, кроме ведущего элемента. Для этого сложим строку 3 со строкой 2, умноженной на 1.
Симплекс таблица примет вид:
Запишем текущий опорный план:
Данный опорный план не является оптимальным, так как в последней строке есть отрицательный элемент (-11), следовательно в базис входит вектор x2. Определяем, какой вектор выходит из базиса. Для этого вычисляем  при
при  . Все
. Все  следовательно целевая функция неограничена сверху. Т.е. задача линейного программирования неразрешима.
следовательно целевая функция неограничена сверху. Т.е. задача линейного программирования неразрешима.
Примеры решения ЗЛП методом искусственного базиса
Пример 1. Найти максимум функции
при условиях
Р е ш е н и е. Так как количество базисных векторов должен быть 3, то добавляем искусственное переменное, а в целевую функцию добавляем это переменное, умноженное на −M, где M, очень большое число:
Матрица коэффициентов  системы уравнений имеет вид:
системы уравнений имеет вид:
Правая часть ограничений системы уравнений имеет вид:
 |
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последние две строки − это целевая функция, умноженная на −1 и разделенная на две части. Последняя строка − строка с исскуственными переменными:
Базисные векторы  следовательно, все элементы в столбцах
следовательно, все элементы в столбцах  ниже горизонтальной линии должны быть нулевыми.
ниже горизонтальной линии должны быть нулевыми.
Обнулим все элементы столбца  кроме ведущего элемента. Для этого сложим строку 5 со строкой 3, умноженной на -1.
кроме ведущего элемента. Для этого сложим строку 5 со строкой 3, умноженной на -1.
Симплекс таблица примет вид:
Запишем текущий опорный план:
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-5), следовательно в базис входит вектор  Определяем, какой вектор выходит из базиса. Для этого вычисляем
Определяем, какой вектор выходит из базиса. Для этого вычисляем  при
при 
 соответствует строке 3. Из базиса выходит вектор
соответствует строке 3. Из базиса выходит вектор  Сделаем исключение Гаусса для столбца
Сделаем исключение Гаусса для столбца  учитывая, что ведущий элемент соответствует строке 3. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строку 5 со строкой 3, умноженной на 1. Далее делим строку с ведущим элементом на ведущий элемент.
учитывая, что ведущий элемент соответствует строке 3. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строку 5 со строкой 3, умноженной на 1. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
Запишем текущий опорный план:
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-3), следовательно в базис входит вектор  Определяем, какой вектор выходит из базиса. Для этого вычисляем
Определяем, какой вектор выходит из базиса. Для этого вычисляем  при
при 
 соответствует строке 1. Из базиса выходит вектор x2. Сделаем исключение Гаусса для столбца x1, учитывая, что ведущий элемент соответствует строке 1. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 2, 3, 4 со строкой 1, умноженной на 3/2, -1/10, 3/2, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
соответствует строке 1. Из базиса выходит вектор x2. Сделаем исключение Гаусса для столбца x1, учитывая, что ведущий элемент соответствует строке 1. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 2, 3, 4 со строкой 1, умноженной на 3/2, -1/10, 3/2, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
Запишем текущий опорный план:
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-13/2), следовательно в базис входит вектор x3. Определяем, какой вектор выходит из базиса. Для этого вычисляем  при
при 
 соответствует строке 3. Из базиса выходит вектор x5. Сделаем исключение Гаусса для столбца x3, учитывая, что ведущий элемент соответствует строке 3. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 1, 2, 4 со строкой 3, умноженной на 5/3, 25/9, 65/9, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
соответствует строке 3. Из базиса выходит вектор x5. Сделаем исключение Гаусса для столбца x3, учитывая, что ведущий элемент соответствует строке 3. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 1, 2, 4 со строкой 3, умноженной на 5/3, 25/9, 65/9, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
Запишем текущий опорный план:
Текущий опорный план является оптимальным, так как в строках 4−5 под переменными  нет отрицательных элементов.
нет отрицательных элементов.
Решение исходной задачи можно записать так:
  . . |
Значение целевой функции в данной точке:
  . . |
Пример 2. Найти оптимальный план задачи линейного программирования:
Р е ш е н и е. Так как количество базисных векторов должен быть 3, то добавляем искусственные переменные, а в целевую функцию добавляем эти переменные, умноженные на −M, где M, очень большое число:
Матрица коэффициентов  системы уравнений имеет вид:
системы уравнений имеет вид:
Правая часть ограничений системы уравнений имеет вид:
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последние две строки − это целевая функция, умноженная на −1 и разделенная на две части. Последняя строка − строка с исскуственными переменными:
Базисные векторы x4, x5, x6, следовательно, все элементы в столбцах x4, x5, x6, ниже горизонтальной линии должны быть нулевыми.
Обнулим все элементы столбца x4, кроме ведущего элемента. Для этого сложим строку 4 со строкой 1, умноженной на -1. Обнулим все элементы столбца x5, кроме ведущего элемента. Для этого сложим строку 5 со строкой 2, умноженной на -1. Обнулим все элементы столбца x6, кроме ведущего элемента. Для этого сложим строку 5 со строкой 3, умноженной на -1.
Симплекс таблица примет вид:
Запишем текущий опорный план:
В строке 5 элементы, соответствующие переменным x1, x2, x3, x4, x5, x6 неотрицательны, а число находящийся в пересечении данной строки и столбца x0 отрицательнo. Тогда исходная задача не имеет опорного плана. Следовательно она неразрешима.
Пример — Табличный симплекс метод
Необходимо решить задачу линейного программирования.
Целевая функция:
2x 1+5x2+3x3+8x4 →min
Ограничивающие условия:
3x1+6x2-4x3+x4≤12
4x1-13x2+10x3+5x4≥6
3x1+7x2+x3≥1
Приведем систему ограничений к каноническому виду, для этого необходимо перейти от неравенств к равенствам, с добавлением дополнительных переменных.
Так как наша задача — задача минимизации, то нам необходимо преобразовать ее к задаче на поиск максимума. Для этого изменим знаки коэффициентов целевой функции на противоположные. Элементы первого неравенства записываем без изменений, добавив в него дополнительную переменную x5 и изменив знак «≤» на «=». Т. к. второе и третье неравенства имеют знаки «≥» необходимо поменять знаки их коэффициентов на противоположные и внести в них дополнительные переменные x6 и x7 соответственно. В результате получем эквивалентную задачу:
3x1+6x2-4x3+x4+x5=12
-4x1+13x2-10x3-5x4+x6=-6
-3x1-7x2-x3+x7=-1
Переходим к формированию исходной симплекс таблицы. В строку F таблицы заносятся коэффициенты целевой функции с противоположным знаком.
x1 | x2 | x3 | x4 | Своб член | |
| F | 2 | 5 | 3 | 8 | |
| X5 | 3 | 6 | -4 | 1 | 12 |
| X6 | -4 | 13 | -10 | -5 | -6 |
| X7 | -3 | -7 | -1 | -1 |
В составленой нами таблице имеются отрицательные элементы в столбце свободных членов, находим среди них максимальный по модулю — это элемент: -6, он задает ведущую строку — X6. В этой строке так же находим максимальный по модулю отрицательный элемент: -10 он находится в столбце X3 который будет ведущим столбцом. Переменная в ведущей строке исключается из базиса, а переменная соответсвующая ведущему столцу включается в базис. Пересчитаем симплекс-таблицу:
| X1 | X2 | X6 | X4 | Своб член | |
| F | 0.8 | 8.9 | 0.3 | 6.5 | -1.8 |
| X5 | 4.6 | 0.8 | -0.4 | 3 | 14.4 |
| X3 | 0.4 | -1.3 | -0.1 | 0.5 | 0.6 |
| X7 | -2.6 | -8.3 | -0.1 | 0.5 | -0.4 |
В составленой нами таблице имеются отрицательные элементы в столбце свободных членов, находим среди них максимальный по модулю — это элемент: -0.4, он задает ведущую строку — X7. В этой строке так же находим максимальный по модулю отрицательный элемент: -8.3 он находится в столбце X2 который будет ведущим столбцом. Переменная в ведущей строке исключается из базиса, а переменная соответсвующая ведущему столцу включается в базис. Пересчитаем симплекс-таблицу:
| X1 | X7 | X6 | X4 | Своб член | |
| F | -1.988 | 1.072 | 0.193 | 7.036 | -2.229 |
| X5 | 4.349 | 0.096 | -0.41 | 3.048 | 14.361 |
| X3 | 0.807 | -0.157 | -0.084 | 0.422 | 0.663 |
| X2 | 0.313 | -0.12 | 0.012 | -0.06 | 0.048 |
Так как в столбце свободных членов нет отрицательных элементов, то найдено допустимое решение.В строке F имеются отрицательные элементы, это означает что полученое решение не оптимально. Определим ведущий столбец. Для этого найдем в строке F максимальный по модулю отрицательный элемент — это -1.988 Ведущей строкой будет та для которой отношение свободного члена к соответствующему элементу ведущего столбца минимально. Ведущей строкой является X2, а ведущий элемент: 0.313.
| X2 | X7 | X6 | X4 | Своб член | |
| F | 6.351 | 0.31 | 0.269 | 6.655 | -1.924 |
| X5 | -13.895 | 1.763 | -0.577 | 3.882 | 13.694 |
| X3 | -2.578 | 0.152 | -0.115 | 0.577 | 0.539 |
| X1 | 3.195 | -0.383 | 0.038 | -0.192 | 0.153 |
Так как в строке F нет отрицательных элементов, то
найдено оптимальное решение. Так как исходной задачей был поиск минимума, то оптимальным решением будет свободный член строки F, взятый с противоположным знаком. F=1.924
при значениях переменных равных: x3=0.539, x1=0.153. Переменные x2 и x4 не входят в базис, поэтому x2=0 x4=0.
Симплекс-метод — Википедия
- Не путать с «симплекс-методом» — методом оптимизации произвольной функции. См. Метод Нелдера — Мида
Симплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве.
Сущность метода: построение базисных решений, на которых монотонно убывает линейный функционал, до ситуации, когда выполняются необходимые условия локальной оптимальности.
В работе Л. В. Канторовича «Математические методы организации и планирования производства» (1939) были впервые изложены принципы новой отрасли математики, которая позднее получила название линейного программирования.[1]
Исторически общая задача линейного программирования была впервые поставлена в 1947 году Джорджем Бернардом Данцигом, Маршаллом Вудом и их сотрудниками в департаменте военно-воздушных сил США. В то время эта группа занималась исследованием возможности использования математических и смежных с ними методов для военных задач и проблем планирования. В дальнейшем для развития этих идей в ВВС была организована исследовательская группа под названием Project SCOOP. Первое успешное решение задачи линейного программирования на ЭВМ SEAC было проведено в январе 1952 года[2].
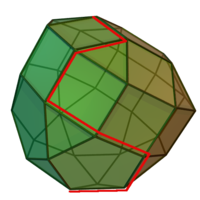 Переход от одной вершины к другой
Переход от одной вершины к другойЗадача линейного программирования состоит в том, что необходимо максимизировать или минимизировать некоторый линейный функционал на многомерном пространстве при заданных линейных ограничениях.
Заметим, что каждое из линейных неравенств на переменные ограничивает полупространство в соответствующем линейном пространстве. В результате все неравенства ограничивают некоторый выпуклый многогранник (возможно, бесконечный), называемый также полиэдральным комплексом. Уравнение W(x) = c, где W(x) — максимизируемый (или минимизируемый) линейный функционал, порождает гиперплоскость L(c). Зависимость от c порождает семейство параллельных гиперплоскостей. Тогда экстремальная задача приобретает следующую формулировку — требуется найти такое наибольшее c, что гиперплоскость L(c) пересекает многогранник хотя бы в одной точке. Заметим, что пересечение оптимальной гиперплоскости и многогранника будет содержать хотя бы одну вершину, причём, их будет более одной, если пересечение содержит ребро или k-мерную грань. Поэтому максимум функционала можно искать в вершинах многогранника. Принцип симплекс-метода состоит в том, что выбирается одна из вершин многогранника, после чего начинается движение по его рёбрам от вершины к вершине в сторону увеличения значения функционала. Когда переход по ребру из текущей вершины в другую вершину с более высоким значением функционала невозможен, считается, что оптимальное значение c найдено.
Последовательность вычислений симплекс-методом можно разделить на две основные фазы:
- нахождение исходной вершины множества допустимых решений,
- последовательный переход от одной вершины к другой, ведущий к оптимизации значения целевой функции.
При этом в некоторых случаях исходное решение очевидно или его определение не требует сложных вычислений, например, когда все ограничения представлены неравенствами вида «меньше или равно» (тогда нулевой вектор совершенно точно является допустимым решением, хотя и, скорее всего, далеко не самым оптимальным). В таких задачах первую фазу симплекс-метода можно вообще не проводить. Симплекс-метод, соответственно, делится на однофазный и двухфазный.
Усиленная постановка задачи[править | править код]
Рассмотрим следующую задачу линейного программирования:
- cTx→max,Ax⩽b,x⩾0,b⩾0.{\displaystyle c^{T}x\to \max ,Ax\leqslant b,x\geqslant 0,b\geqslant 0.}
Теперь поставим эту задачу в эквивалентной усиленной форме. Необходимо максимизировать Z, где:
- [1−cT00AE][Zxxs]=[0b],x,xs⩾0{\displaystyle {\begin{bmatrix}1&-c^{T}&0\\0&A&E\end{bmatrix}}{\begin{bmatrix}Z\\x\\x_{s}\end{bmatrix}}={\begin{bmatrix}0\\b\end{bmatrix}},x,x_{s}\geqslant 0}
Здесь x — переменные из исходного линейного функционала, xs — новые переменные, дополняющие старые таким образом, что неравенство переходит в равенство, c — коэффициенты исходного линейного функционала, Z — переменная, которую необходимо максимизировать. Полупространства x⩾0{\displaystyle x\geqslant 0} и xs⩾0{\displaystyle x_{s}\geqslant 0} в пересечении образуют многогранник, представляющий множество допустимых решений. Разница между числом переменных и уравнений даёт нам число степеней свободы. Проще говоря, если мы рассматриваем вершину многогранника, то это число рёбер, по которым мы можем продолжать движение. Тогда мы можем присвоить этому числу переменных значение 0 и назвать их «небазисными». Остальные переменные при этом будут вычисляться однозначно и называться «базисными». Сам же набор этих переменных называется базисом. Полученная точка будет вершиной в пересечении соответствующих небазисным переменным гиперплоскостей. Для того, чтобы найти т. н. начальное допустимое решение (вершину, из которой мы начнём движение), присвоим всем изначальным переменным x значение 0 и будем их считать небазисными, а все новые будем считать базисными. При этом начальное допустимое решение вычисляется однозначно : xsi=bi{\displaystyle \mathbf {x} _{si}=\mathbf {b} _{i}}.
Алгоритм[править | править код]
Теперь приведём шаги алгоритма. На каждом шаге мы будем менять множества базисных и небазисных векторов (двигаться по рёбрам), и матрица будет иметь следующий вид:
- [1cBTB−1A−cTcBTB−10B−1AB−1][Zxxs]=[cBTB−1bB−1b],{\displaystyle {\begin{bmatrix}1&c_{B}^{T}B^{-1}A-c^{T}&c_{B}^{T}B^{-1}\\0&B^{-1}A&B^{-1}\end{bmatrix}}{\begin{bmatrix}Z\\x\\x_{s}\end{bmatrix}}={\begin{bmatrix}c_{B}^{T}B^{-1}b\\B^{-1}b\end{bmatrix}},}
где cB{\displaystyle c_{B}} — коэффициенты вектора c{\displaystyle c}, соответствующие базисным переменным (переменным xs{\displaystyle x_{s}} соответствуют 0), B{\displaystyle B} — столбцы [AE]{\displaystyle [\mathbf {A} \mathbf {E} ]}, соответствующие базисным переменным. Матрицу, образованную оставшимися столбцами обозначим D{\displaystyle D}. Почему матрица будет иметь такой вид поясним в описании шагов алгоритма.
Первый шаг.
Выбираем начальное допустимое значение, как указано выше. На первом шаге B{\displaystyle B} — единичная матрица, так как базисными переменными являются xs{\displaystyle x_{s}}. cB{\displaystyle c_{B}} — нулевой вектор по тем же причинам.
Второй шаг
Покажем, что в выражении (cBTB−1A−cT)x+(cBTB−1)xs{\displaystyle (c_{B}^{T}B^{-1}A-c^{T})x+(c_{B}^{T}B^{-1})x_{s}} только небазисные переменные имеют ненулевой коэффициент. Заметим, что из выражения Ax+xs=b{\displaystyle Ax+x_{s}=b} базисные переменные однозначно выражаются через небазисные, так как число базисных переменных равно числу уравнений. Пусть x′{\displaystyle x’} — базисные, а x″{\displaystyle x»} — небазисные переменные на данной итерации. Уравнение Ax+xs=b{\displaystyle Ax+x_{s}=b} можно переписать, как Bx′+Dx″=b{\displaystyle Bx’+Dx»=b}. Умножим его на B−1{\displaystyle B^{-1}} слева: x′+B−1Dx″=B−1b{\displaystyle x’+B^{-1}Dx»=B^{-1}b}. Таким образом мы выразили базисные переменные через небазисные, и в выражении B−1Ax+B−1xs{\displaystyle B^{-1}Ax+B^{-1}x_{s}}, эквивалентному левой части равенства, все базисные переменные имеют единичные коэффициенты. Поэтому, если прибавить к равенству Z−cTx=0{\displaystyle Z-c^{T}x=0} равенство cBTB−1Ax+cBTB−1xs{\displaystyle c_{B}^{T}B^{-1}Ax+c_{B}^{T}B^{-1}x_{s}}, то в полученном равенстве все базисные переменные будут иметь нулевой коэффициент — все базисные переменные вида x сократятся, а базисные переменные вида xs не войдут в выражение cBTB−1xs{\displaystyle c_{B}^{T}B^{-1}x_{s}}.
Выберем ребро, по которому мы будем перемещаться. Поскольку мы хотим максимизировать Z, то необходимо выбрать переменную, которая будет более всех уменьшать выражение
(cBTB−1A−cT)x+(cBTB−1)xs{\displaystyle (c_{B}^{T}B^{-1}A-c^{T})x+(c_{B}^{T}B^{-1})x_{s}}.
Для этого выберем переменную, которая имеет наибольший по модулю отрицательный коэффициент[3]. Если таких переменных нет, то есть все коэффициенты этого выражения неотрицательны, то мы пришли в искомую вершину и нашли оптимальное решение. В противном случае начнём увеличивать эту небазисную переменную, то есть перемещаться по соответствующему ей ребру. Эту переменную назовём входящей.
Третий шаг
Теперь необходимо понять, какая базисная переменная первой обратится в ноль по мере увеличения входящей переменной. Для этого достаточно рассмотреть систему:
- [B−1AB−1][xxs]=B−1b{\displaystyle {\begin{bmatrix}B^{-1}A&B^{-1}\end{bmatrix}}{\begin{bmatrix}x\\x_{s}\end{bmatrix}}=B^{-1}b}
При фиксированных значениях небазисных переменных система однозначно разрешима относительно базисных, поэтому мы можем определить, какая из базисных переменных первой достигнет нуля при увеличении входящей. Эту переменную назовем выходящей. Это будет означать, что мы натолкнулись на новую вершину. Теперь входящую и выходящую переменную поменяем местами — входящая «войдёт» в базисную, а выходящая из них «выйдет» в небазисные. Теперь перепишем матрицу B и вектор cB в соответствии с новыми наборами базисных и небазисных переменных, после чего вернёмся ко второму шагу. x»
Поскольку число вершин конечно, то алгоритм однажды закончится. Найденная вершина будет являться оптимальным решением.
Причины использования[править | править код]
Если в условии задачи линейного программирования не все ограничения представлены неравенствами типа «≤», то далеко не всегда нулевой вектор будет допустимым решением. Однако каждая итерация симплекс-метода является переходом от одной вершины к другой, и если неизвестно ни одной вершины, алгоритм вообще не может быть начат.
Процесс нахождения исходной вершины не сильно отличается от однофазного симплекс-метода, однако может в итоге оказаться сложнее, чем дальнейшая оптимизация.
Модификация ограничений[править | править код]
Все ограничения задачи модифицируются согласно следующим правилам:
- ограничения типа «≤» переводятся на равенства созданием дополнительной переменной с коэффициентом «+1». Эта модификация проводится и в однофазном симплекс-методе, дополнительные переменные в дальнейшем используются как исходный базис.
- ограничения типа «≥» дополняются одной переменной с коэффициентом «−1». Поскольку такая переменная из-за отрицательного коэффициента не может быть использована в исходном базисе, необходимо создать ещё одну, вспомогательную, переменную. Вспомогательные переменные всегда создаются с коэффициентом «+1».
- ограничения типа «=» дополняются одной вспомогательной переменной.
Соответственно, будет создано некоторое количество дополнительных и вспомогательных переменных. В исходный базис выбираются дополнительные переменные с коэффициентом «+1» и все вспомогательные. Осторожно: решение, которому соответствует этот базис, не является допустимым.
Различия между дополнительными и вспомогательными переменными[править | править код]
Несмотря на то, что и дополнительные, и вспомогательные переменные создаются искусственно и используются для создания исходного базиса, их значения в решении сильно отличаются:
- дополнительные переменные сообщают, насколько соответствующее им ограничение «недоиспользовано». Значение дополнительной переменной, равное нулю, соответствует равенству значений правых и левых частей ограничения.
- вспомогательные переменные сообщают, насколько данное условие далеко от допустимого (относительно конкретного ограничения). Если значение вспомогательной переменной больше нуля, то данное решение не выполняет определённое ограничение, а значит не является допустимым.
То есть ненулевое значение дополнительной переменной может (но не должно) сигнализировать о неоптимальности решения. Ненулевое значение вспомогательной переменной сигнализирует о недопустимости решения.
Фазы решения[править | править код]
После того, как было модифицировано условие, создаётся вспомогательная целевая функция. Если вспомогательные переменные были обозначены, как yi{\displaystyle y_{i}}, i∈{1,…,k}{\displaystyle i\in \left\{1,\dots ,k\right\}}, то вспомогательную функцию определим, как
После этого проводится обыкновенный симплекс-метод относительно вспомогательной целевой функции. Поскольку все вспомогательные переменные увеличивают значение z′{\displaystyle z’}, в ходе алгоритма они будут поочерёдно выводится из базиса, при этом после каждого перехода новое решение будет всё ближе к множеству допустимых решений.
Когда будет найдено оптимальное значение вспомогательной целевой функции, могут возникнуть две ситуации:
- оптимальное значение z′{\displaystyle z’} больше нуля. Это значит, что как минимум одна из вспомогательных переменных осталась в базисе. В таком случае можно сделать вывод, что допустимых решений данной задачи линейного программирования не существует.
- оптимальное значение z′{\displaystyle z’} равно нулю. Это означает, что все вспомогательные переменные были выведены из базиса, и текущее решение является допустимым.
Во втором случае мы имеем допустимый базис, или, иначе говоря, исходное допустимое решение. Можно проводить дальнейшую оптимизацию с учётом исходной целевой функции, при этом уже не обращая внимания на вспомогательные переменные. Это и является второй фазой решения.
В модифицированном методе матрица
[1cBTB−1A−cTcBTB−10B−1AB−1]{\displaystyle {\begin{bmatrix}1&c_{B}^{T}B^{-1}A-c^{T}&c_{B}^{T}B^{-1}\\0&B^{-1}A&B^{-1}\end{bmatrix}}}
не пересчитывается, хранится и пересчитывается только матрица B−1{\displaystyle B^{-1}}. В остальном алгоритм похож на вышеописанный.
1. Вычисляем двойственные переменные d=cBTB−1{\displaystyle d=c_{B}^{T}B^{-1}}
2. Проверка оптимальности. cBTB−1A−cT{\displaystyle c_{B}^{T}B^{-1}A-c^{T}} преобразуется в dTA−cT{\displaystyle d^{T}A-c^{T}}.
Проверка заключается в вычислении dTAn−cn{\displaystyle d^{T}A_{n}-c_{n}} для всех столбцов n∈N{\displaystyle n\in N}. Столбец со значением < 0 можно вводить в базис.
Часто выбирают минимальное значение, но для этого нужно перебрать все столбцы.
Чаще выбирают значение, меньшее некоторого заданного значения −ε{\displaystyle -\varepsilon }
Если такого столбца не обнаружится, за ε{\displaystyle \varepsilon } принимается максимальное найденное абсолютное значение и соответствующий столбец AJ{\displaystyle A_{J}} вводится в базис.
3. Определение выводимого.
Пусть AJ{\displaystyle A_{J}} — вводимый столбец, соответствующий переменной xJ{\displaystyle x_{J}} Базисный план — это решение системы ABp=b{\displaystyle A_{B}p=b} Увеличиваем ABp+ϑAJ=b{\displaystyle A_{B}p+\vartheta A_{J}=b}.
Умножим слева на B−1{\displaystyle B^{-1}}, то есть B−1ABp+ϑB−1AJ=B−1b{\displaystyle B^{-1}A_{B}p+\vartheta B^{-1}A_{J}=B^{-1}b}.
Здесь B−1b{\displaystyle B^{-1}b} — базисный план, q=B−1AJ{\displaystyle q=B^{-1}A_{J}} — разложение вводимого столбца по базису.
Находим максимальное значение ϑ{\displaystyle \vartheta }, при котором все значения не отрицательны. Если ϑ{\displaystyle \vartheta } может быть взято как угодно велико, решение не ограничено. В противном случае один из элементов выйдет на нулевое значение. Выводим соответствующий столбец из базиса.
4. Пересчет опорного(базисного) плана.
Вычисляем новый опорный план по уже приведенной формуле x=p+ϑB−1AJ{\displaystyle x=p+\vartheta B^{-1}A_{J}} с найденным значением ϑ{\displaystyle \vartheta }.
5. Пересчитываем обратную к базисной B−1{\displaystyle B^{-1}}.
Пусть B−1AF{\displaystyle B^{-1}A_{F}} — выводимый столбец.
Матрица B представима в виде [BGAF]{\displaystyle [B_{G}A_{F}]}
где BG{\displaystyle B_{G}} — базисная матрица без выводимого столбца.
После замены столбца базисная матрица будет иметь вид [BGAJ]{\displaystyle [B_{G}A_{J}]}
Нам нужно найти матрицу B1{\displaystyle B_{1}}, такую что
[BG,AJ]B1−1=E{\displaystyle [B_{G},A_{J}]B_{1}^{-1}=E} => [B−1BGB1−1,B−1AJ]=B−1{\displaystyle [B^{-1}B_{G}B_{1}^{-1},B^{-1}A_{J}]=B^{-1}} => [B−1BG,q]B1−1=B−1{\displaystyle [B^{-1}B_{G},q]B_{1}^{-1}=B^{-1}} =>
[Eq′0qf]B1−1=B−1{\displaystyle {\begin{bmatrix}E&q’\\0&q_{f}\end{bmatrix}}B_{1}^{-1}=B^{-1}}
Откуда B1−1=[E−q′/qf01/qf]B−1{\displaystyle B_{1}^{-1}={\begin{bmatrix}E&-q’/q_{f}\\0&1/q_{f}\end{bmatrix}}B^{-1}}
Замечание.
При пересчете матрицы B−1{\displaystyle B^{-1}} накапливаются ошибки округления. Во избежание получения больших ошибок время от времени матрица пересчитывается полностью. Этот процесс называется «повторением».
Мультипликативный вариант симплекс-метода[править | править код]
В мультипликативном варианте матрица B−1{\displaystyle B^{-1}} не хранится, хранятся лишь множители [E−q′/qf01/qf]{\displaystyle {\begin{bmatrix}E&-q’/q_{f}\\0&1/q_{f}\end{bmatrix}}}
При решении экономических задач часто матрица ограничений разреженная, в таком случае мультипликативный вариант получает дополнительные преимущества — можно хранить мультипликаторы в сжатом виде (не хранить нули).
Во избежание накопления ошибок округления может использоваться LU-разложение матрицы.
При подавляющем числе ограничений типа «неравенство» может быть использован метод переменного базиса. [4]
Метод основан на том, что базисная матрица может быть представлена в виде
[AB0AEE]{\displaystyle {\begin{bmatrix}A_{B}&0\\A_{E}&E\end{bmatrix}}}
Обратная к ней имеет вид
[AB−10−AB−1AEE]{\displaystyle {\begin{bmatrix}A_{B}^{-1}&0\\-A_{B}^{-1}A_{E}&E\end{bmatrix}}}
При относительно небольших размерах матрицы AB−1{\displaystyle A_{B}^{-1}} остальная часть матрицы может не храниться.
Таким подходом удается решить задачи с десятками миллионов строк ограничений (например, из теории игр).
Для реализации двойственного метода необходимо перейти от задачи на минимум к задаче на максимум (или наоборот) путём транспонирования матрицы коэффициентов. При переходе от задачи на минимум целевая функция примет вид:
g=∑i=1nbiyi→max{\displaystyle g=\sum _{i=1}^{n}b_{i}y_{i}\to max}
при ограничениях
∑i=1naijyi≤cj{\displaystyle \sum _{i=1}^{n}a_{ij}y_{i}\leq c_{j}}.
Теорема двойственности. Если из пары двойственных задач одна обладает оптимальным планом, то и другая имеет решение, причем экстремальные значения линейных функций этих задач равны.
Если линейная функция одной из задач не ограничена, то другая не имеет решения.
Симплекс-метод удивительно эффективен на практике, но в 1972 Кли и Минти [5] привели пример, в котором симплекс-метод перебирал все вершины симплекса, что показывает экспоненциальную сходимость метода в худшем случае. С тех пор для каждого варианта метода был найден пример, на котором метод вел себя исключительно плохо.
Наблюдения и анализ эффективности метода в практических приложениях привело к развитию других способов измерения эффективности.
Симплекс-метод имеет среднюю полиномиальную сходимость при широком выборе распределения значений в случайных матрицах.[6][7]
Вычислительная эффективность оценивается обычно при помощи двух параметров:
1) Числа итераций, необходимого для получения решения;
2) Затрат машинного времени.
В результате численных экспериментов получены результаты:
1) Число итераций при решении задач линейного программирования в стандартной форме с M{\displaystyle M} ограничениями и N{\displaystyle N} переменными заключено между M{\displaystyle M} и 3M{\displaystyle 3M}. Среднее число итераций 2M{\displaystyle 2M}. Верхняя граница числа итераций равна 2M+N{\displaystyle 2M+N}.
2) Требуемое машинное время пропорционально M3{\displaystyle M^{3}}.
Число ограничений больше влияет на вычислительную эффективность, чем число переменных, поэтому при формулировке задач линейного программирования нужно стремиться к уменьшению числа ограничений пусть даже путём роста числа переменных.
Одной из наиболее трудоёмких процедур в симплекс-методе является поиск вводимого в базис столбца Для лучшей сходимости, казалось бы, нужно выбирать переменную с наилучшей невязкой, но для этого нужен полный просмотр, то есть нужно умножить столбец двойственных переменных (которые иногда называются теневыми ценами) на все столбцы матрицы[8]. Такой подход хорошо работает для небольших задач, которые решаются вручную. Более того, строгое соблюдение правила выбора максимальной по модулю невязки может оказаться неоптимальным с точки зрения общего количества итераций, необходимых для получения экстремума. Максимальный выигрыш на одной итерации может привести к медленному убыванию значения целевой функции на последующих шагах и, следовательно, замедлить процесс решения задачи[9].
При больших матрицах ограничений процедура поиска вводимой переменной начинает отнимать много времени и часто делаются попытки избежать просмотра всех столбцов матрицы, для чего могут применяться такие методы:
- Барьер. Как только невязка переменной будет достаточно сильно отличаться от нуля (превосходит некоторой величины, называемой барьером), переменную вводят в базис. Если все невязки оказались меньше барьера, в качестве вводимой выбирается переменная с наименьшей невязкой, сам же барьер уменьшается по некоторому правилу (например, половина наименьшей невязки). Барьер часто используется со следующим приёмом. Близкий подход описан в книге Муртафа, см. раздел 3.6.2. Частичное оценивание книги[10].
- Циклический просмотр. Поиск вводимой переменной начинается с позиции, следующей за введённой на предыдущей итерации переменной.
- Групповой отбор (В книге Муртафа этот приём называется многократным оцениванием. См. раздел 3.6.3. Многократное оценивание[11].) При поиске вводимой переменной отбирается не одна переменная, а несколько кандидатов. На следующих итерациях просмотр осуществляется только среди отобранных кандидатов, при этом кандидат может из списка вычёркиваться.
- Назначение весов. Переменным назначаются веса. См. раздел 3.6.4 Метод оценивания в системе DEVEX Муртафа[12].
- Поиск наиболее крутого ребра Гольдфарба и Рида. См. раздел 3.6.5 Метод оценивания с поиском наиболее крутого ребра в книге Муртафа[13].
Возможны и другие приёмы, такие как правило Заде.
- ↑ Канторович Л. В. Математические методы организации планирования производства // Издание Ленинградского государственного университета. — Ленинград, 1939.
- ↑ С. Гасс. Линейное программирование (методы и приложения). — Москва: Государственное издательство физико-математической литературы, 1961. — (Физико-математическая библиотека инженера).
- ↑ Такая рекомендация часто встречается в учебниках, но не всегда верна. См. раздел #Методы повышения эффективности