Чему равна градусная мера угла – . .

Что такое градусная мера угла? Свойства углов. Как узнать меру угла

Математика, геометрия – многим эти науки, как, впрочем, и большинство других точных, даются крайне тяжело. Людям трудно разобраться в формулах и странной терминологии. Что скрывается под этим странным понятием?

Определение

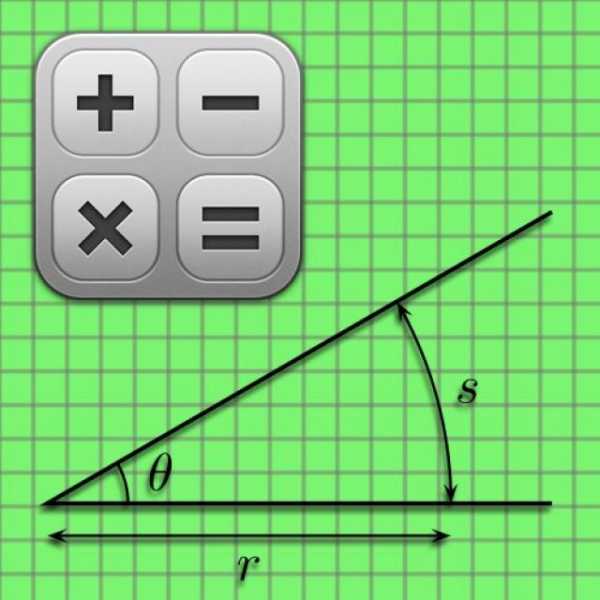
Для начала, нужно рассмотреть просто меру угла. В этом поможет изображение луча и прямой линии. Сначала нужно провести, например, горизонтальную прямую линию. Затем от её первой точки проводится луч, не параллельный прямой. Таким образом, между прямой и лучом появляется некоторое расстояние, небольшой угол. Мера угла – это размер этого самого поворота луча.

Это понятие обозначает определенное цифровое значение, которое будет больше нуля. Оно выражается в градусах, а также его составных частях, то есть минутах и секундах. То количество градусов, которое поместится в угол между лучом и прямой, и будет градусной мерой.

Свойства углов

• Абсолютно каждый угол будет иметь определённую градусную меру.
• Если он полностью развернут, то число будет равняться 180 градусам.
• Для нахождения градусной меры рассматривается сумма всех углов, которые разбил луч.
• С помощью любого луча можно создать полуплоскость, в которой реально сделать угол. Он будет иметь градусную меру, величина которой будет менее 180, и такой угол может быть лишь один.

Как узнать меру угла?

Как правило, минимальной градусной мерой является 1 градус, который составит 1/180 от развернутого угла. Однако иногда нельзя получить настолько четкую цифру. В этих случаях применяют секунды и минуты.

При их нахождении значение можно перевести в градусы, таким образом получится доля градуса. Иногда применяют дробные числа, вроде 80,7 градуса.

Также важно запомнить ключевые величины. Прямой угол всегда будет равняться 90 градусам. Если мера больше, то он будет считаться тупым, а если меньше, то острым.

topkin.ru

Что такое градусная мера угла?

Добрый вечер! Помочь Вам понять что такое градусная мера угла — не составит труда. Только читайте внимательно!
Градусная мера угла — это такая величина, которая показывает сколько градусов, минут и секунд находится между сторонами (чаще всего — двумя) угла. Немало важным будет прояснить значение термина градус, которое происходит от латинского слова со значением деления шкалы, ступени ( а в нашем понятии это преобразовалось в более понятное значение — единица измерения в геометрии, которая используется для плоских углов). У градуса есть постоянный символ, которым он обозначается это  вверху справа у числового значения угла.
Существуют определённый свойства угла (можно сказать аксиомы, которые не требуют доказательства, а могут спокойно использоваться при решении задач:

1. Каждый угол имеет определенную градусную меру, которая больше нуля. А развернутый угол равен   .
2. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
3. От любого луча в заданную плоскость можно отложить только один угол с заданной градусной мерой, меньшей ,

Например. Нам дан луч , который делит угол на 2 угла.Найдите угол , если , а . Начинаем рассуждать. Угол, который надо найти состоит из двух углов, на которые его поделил луч, то есть: 

Ответ: 

ru.solverbook.com

Радианная и градусная мера угла

Здесь рассматриваем задачи Proc32 — Proc33 из задачника Абрамяна: описание функций преобразования углов из градусов в радианы и наоборот.

Так что такое радианная мера угла? Рассмотрим некоторую окружность радиуса R с центром в точке О. Поскольку окружность делится на 360 градусов, а длина окружности равна 2πR, то на 1 градус приходится длина дуги равная 2πR/360 = πR/180. Тогда

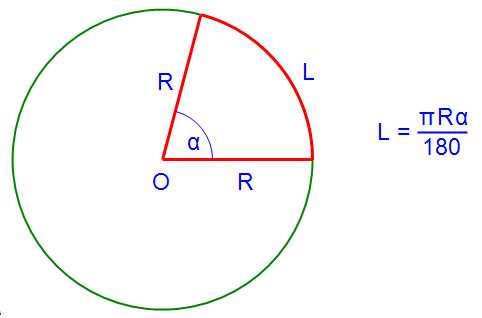
В этом смысле очень интересна ситуация, когда длина дуги L равна радиусу окружности R. Каков при этом угол дуги? Вспоминая предыдущую формулу для вычисления длины дуги, имеем: πRα/180 = R, откуда πα/180 = 1, а отсюда получаем α = 180/π.

Итак, если длина дуги равна радиусу окружности, то соответствующий угол равен 180/π. Этот угол называется радианом (Rad):

1 Rad = 180/π градуса.

Таким образом,

π радианов = 180°, а 1° = π/180 радиана.

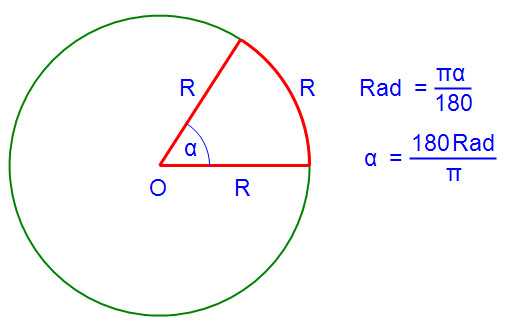
Радианная мера угла – это такая мера угла, при которой за 1 Rad принимается угол дуги, равной радиусу этой дуги. Поскольку 1 радиану соответствует длина дуги равная радиусу, то отсюда следует такой вывод:

Например, если длина дуги равна 1.5R, то радианная мера угла этой дуги равна 1.5; если длина дуги равна 0.25R, то радианная мера равна 0.25; для дуги длиной 2πR (вся окружность) радианная мера равна 2π и т.д. Вообще, для дуги длиной L угол в радианах равен L/R, где R – радиус.

Радиан – это очень удобный способ измерения углов, поскольку вместо самих углов мы можем оперировать коэффициентами отношений длин дуг и их радиусов. В высшей математике во всех тригонометрических функциях используется только радианная мера.

Proc32. Описать функцию DegToRad(D) вещественного типа, находящую величину угла в радианах, если дана его величина D в градусах (D — вещественное число, 0 ≤ D < 360). Воспользоваться следующим соотношением: 180° = π радианов. В качестве значения π использовать 3.14. С помощью функции DegToRad перевести из градусов в радианы пять данных углов.

Код Pascal

1  
2  
3  
4  
5  
6  
7  
8  
9  
10  
11  
12  
13  
14  
15  
16  
17  
18  
19  
20  
21  
22  
23  
24  
25  
26  
27  
28  
29  

{ Функция возвращает величину угла в радианах,
если дана его величина D в градусах 
(D — вещественное число, 0 ≤ D < 360) }
function DegToRad(D: real): real;
const
  pi = 3.14; { <-- Число "пи" }
begin
  DegToRad := pi * D / 180
end;

  { Основная программа }

const
  n: byte = 5; { <-- количество углов для ввода }

var
  D, R: real; { <-- градусы, радианы }
  i: byte;

begin
  for i := 1 

  

  
to n do begin
    write('Угол в градусах: ');
    readln(D);
    { Вызываем функцию вычисления угла в радианах: }
    R := DegToRad(D);
    writeln(' угол в радианах: ', R:0:2);
    writeln
  end
end.

Сравните задачу Proc32 с задачей Begin29.

Proc33. Описать функцию RadToDeg(R) вещественного типа, находящую величину угла в градусах, если дана его величина R в радианах (R — вещественное число, 0 ≤ R < 2·π). Воспользоваться следующим соотношением: 180° = π радианов. В качестве значения π использовать 3.14. С помощью функции RadToDeg перевести из радианов в градусы пять данных углов.

Код Pascal

1  
2  
3  
4  
5  
6  
7  
8  
9  
10  
11  
12  
13  
14  
15  
16  
17  
18  
19  
20  
21  
22  
23  
24  
25  
26  
27  
28  

{ Функция возвращает величину угла в градусах, если дана его 
величина R в радианах (R — вещественное число, 0 ≤ R < 2·π) }
function RadToDeg(R: real): real;
const
  pi = 3.14;
begin
  RadToDeg := 180 * R / pi
end;

  { Основная программа }

const
  n: byte = 5; { <-- количество углов для ввода }

var
  R, D: real; { <-- радианы, градусы }
  count: byte;

begin
  for count := 1 to n do begin
    write('Угол в радианах: ');
    readln(R);
    { Вызываем функцию для вычисления угла в градусах: }
    D := RadToDeg(R);
    writeln(' угол в градусах: ', D:0:2);
    writeln
  end
end.

Сравните задачу Proc33 с задачей Begin30.

progmatem.ru

Объясните пожалуйста, что такое радианная мера угла?

так же, как длина в футах или метрах, так угол и в радианах, и в градусах… просто другие единицы.

угол равный 1 радиану или, что то же самое, дуга окружности, длина которой равна радиусу этой окружности. Кроме радианной меры угла существует также градусная мера угла, которой является угол в 1 градус. Радиан — от латинского слова radius — спица в колесе, луч. Если продумать еще раз определение угла в 1 радиан, то становится понятно, что в качестве единицы измерения в данном случае используется радиус окружности.

Радианная мера угла — угол равный 1 радиану или, что то же самое, дуга окружности, длина которой равна радиусу этой окружности

радиальная мера угла, это угол заключенный между двух радиусов, одной и той же окружности. За единицу принят радиан, угол между двумя радиусами, стягивающими дугу окружности, длинной равной радиусу

угол равный 1 радиану, дуга окружности, длина которой равна радиусу. угол в 360гр = 2п радиан 180 = п рад 90 = п/2 рад 60 =п/3 рад 45 = п/4 рад 30 = п/6 рад

Это в пи. 180 град = пи радиан, 90 градусов = пи/2 радиан и т. д.

1 Радиан- это центральный угол, длина дуги которого рравна радиусу окружности. К примеру, n- это количество градусов и n=90градусов =&gt; n=(Пи * 90)/180

touch.otvet.mail.ru

Как найти градусную меру угла

completerepair.ru