Sin 2 a cos 2 a: 1- sin 2 a — cos 2 a упростить выражение

Основное Тригонометрическое Тождество — Доказательство

Связь между sin и cos одного угла

Вы уже наверняка знаете, что тождественный — это равный. 

Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция. 

Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:

Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.

Равенство tg²α + 1 = 1/cos²α и равенство 1 + сtg²α + 1 = 1/sin²α выводят из основного тождества, разделив обе части на sin²α и cos²α.

В результате деления получаем:

Поэтому основному тригонометрическому тождеству уделяется максимум внимания.

Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая. 

sin²α + cos²α = 1

Сумма квадратов синуса и косинуса одного угла тождественно равна единице.

Чтобы доказать тождество, обратимся к теме единичной окружности. 

Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.

Докажем тождество sin²α + cos²α = 1

1. Итак, нам известны координаты точки A (1; 0).

   Произвольный угол α, тогда cos α = x0 = ОB.



2. Если развернуть точку A на угол α, то точка A становится на место точки A₁.


3. По определениям:
   • Синус угла (sin α) — это отношение противолежащего катета к гипотенузе. 
   • Косинус угла (cos α) — это отношение прилежащего катета к гипотенузе.
   Это значит, что точка A₁ получает координаты cos α, sin α.


4. Опускаем перпендикулярную прямую A₁B на x0 из точки A₁.

   Образовался прямоугольный треугольник OA₁B.

   |A₁B| = |у|

   |OB| = |x|.



5. Гипотенуза OA₁ имеет значение, равное радиусу единичной окружности.

   |OA₁| = 1.



6. Применяя полученное выражение, записываем равенство по теореме Пифагора, поскольку получившийся угол — прямой:

   |A₁B|² + |OB|² = |OA₁|².



7. Записываем в виде: |y|² + |x|² = 1².

   Это значит, что y² + x² = 1.
   sin угла α = y
   cos угла α = x



8. Вставляем данные угла вместо координат точек:

   OB = cos α
   

   A₁B = sin α
   A₁O = 1



9. Получаем основное тригонометрическое тождество: sin²α + cos²α = 1.
   Что и требовалось доказать. 

Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:

• sin α = ±
• cos α = ±

Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.

Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.

 

Тангенс и котангенс через синус и косинус

Немного вводных:

• Синус угла  — это ордината y.
• Косинус угла  — это абсцисса x.
• Тангенс угла  — это отношение ординаты к абсциссе. 
• Котангенс угла — это отношение абсциссы к ординате.

Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.

• tg α =
• ctg α =

Исходя из определений:

Это позволяет сделать вывод, что тригонометрические тождества 

задаются sin и cos углов.

Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.

Отдельно стоит обратить внимание на то, что тригонометрические тождества

верны для всех углов α, значения которых вписываются в диапазон. 

• Например,  выражение применимо для любого угла α, не равного + π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.

Выражение

применимо для любого угла α, не равного π * z, где z — это любое целое число. 

Связь между тангенсом и котангенсом

Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
 

• Тождество записывается в следующем виде:
  tg α * ctg α = 1.

Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.

Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.

tg α * ctg α = 1.

 

1. По определению:

   tg α = y/x

   ctg α = x/y


2. Отсюда следует, что tg α * ctg α = y/x * x/y = 1


3. Преобразовываем выражение, подставляем  и ,
   получаем:

Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.

Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.

Какие, какие числа?🤯

Взаимно обратные числа — это два числа, произведение которых равно 1.

 

 

Тангенс и косинус, котангенс и синус

Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла  — с синусом.

Эта связь становится очевидна, если взглянуть на тождества:
 

• tg²α + 1 =

Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.

• 1 + ctg²α =

Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.

Вывести оба этих тождества можно из основного тригонометрического тождества:
sin²α + cos²α = 1.
 

 

1. Для этого нужно поделить обе части тождества на cos²α, где косинус не равен нулю.


2. В результате деления получаем формулу tg²α + 1 =


3. Если обе части основного тригонометрического  тождества sin²α + cos²α = 1 разделить на  sin²α, где синус не равен нулю, то получим тождество:
   1 + ctg²α = .  


4. Отсюда можно сделать вывод, что тригонометрическое тождество tg²α + 1 = применимо для любого угла α, не равного + π + z, где z — это любое целое число.


5. А тригонометрическое тождество 1 + ctg²α = применимо для любого угла, не равного π * z, где z — это любое целое число. 

Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами. 

Основные тригонометрические тождества

1	sin2α + cos2α = 1
2
3
4	tgα * ctgα = 1
5	tg2α + 1 =
6	1 + ctg2α =

Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.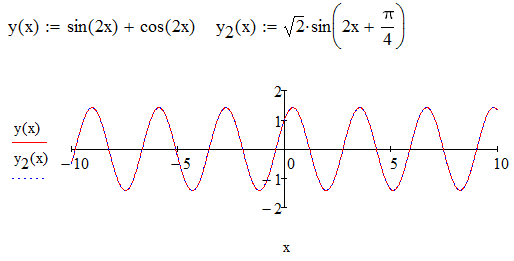

Примеры решения задач

Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.

Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.

Как решаем:

 

1. Чтобы решить задачу, необходимы следующие тригонометрические тождества:



2. Выражаем cos α из тригонометрической единицы:



3. Далее подставляем значения sin α:



4. Вычисляем:



5. Нам известны значения sin α и cos α, поэтому можно легко найти тангенс, используя формулу:



6. Таким же образом, используя формулу, вычисляем значение котангенса:

Ответ:

Задачка 2. Найдите значение cos α,
если:

Как решаем: 

 

1. Чтобы решить задачу, необходимы следующие тригонометрические тождества:



2. Выражаем cos α из тригонометрической единицы:



3. Далее подставляем значения sin α:



4. Вычисляем:
   


5. То же самое проделываем со вторым значение sin α

   Подставляем значения sin α:



6. Вычисляем:

Ответ:

Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.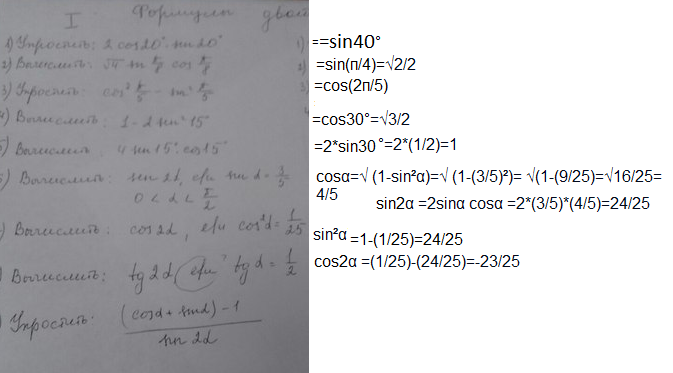

Алгебра любит практику — как можно больше практики. Чтобы натренироваться в решении задачек и накачать математический бицепс, записывайте вашего ребенка на бесплатный вводный урок математики в онлайн-школу Skysmart.

У нас есть все для эффективных и веселых занятий: опытные преподаватели, интересные задачки, интерактивный формат и внушительная порция вдохновения и поддержки!

формулы cos, sin, tg, ctg

Основные формулы тригонометрии — это формулы, устанавливающие связи между основными тригонометрическими функциями. Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных формул можно решить практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь сами формулы, а не их вывод, которому будут посвящены отдельные статьи.

Основные тождества тригонометрии

Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.

Тригонометрические тождества

sin2a+cos2a=1tgα=sinαcosα, ctgα=cosαsinαtgα·ctgα=1tg2α+1=1cos2α, ctg2α+1=1sin2α

Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).

Формулы приведения

Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.

Формулы приведения

sinα+2πz=sinα, cosα+2πz=cosαtgα+2πz=tgα, ctgα+2πz=ctgαsin-α+2πz=-sinα, cos-α+2πz=cosαtg-α+2πz=-tgα, ctg-α+2πz=-ctgαsinπ2+α+2πz=cosα, cosπ2+α+2πz=-sinαtgπ2+α+2πz=-ctgα, ctgπ2+α+2πz=-tgαsinπ2-α+2πz=cosα, cosπ2-α+2πz=sinαtgπ2-α+2πz=ctgα, ctgπ2-α+2πz=tgαsinπ+α+2πz=-sinα, cosπ+α+2πz=-cosαtgπ+α+2πz=tgα, ctgπ+α+2πz=ctgαsinπ-α+2πz=sinα, cosπ-α+2πz=-cosαtgπ-α+2πz=-tgα, ctgπ-α+2πz=-ctgαsin3π2+α+2πz=-cosα, cos3π2+α+2πz=sinαtg3π2+α+2πz=-ctgα, ctg3π2+α+2πz=-tgαsin3π2-α+2πz=-cosα, cos3π2-α+2πz=-sinαtg3π2-α+2πz=ctgα, ctg3π2-α+2πz=tgα

Формулы приведения являются следствием периодичности тригонометрических функций.

Тригонометрические формулы сложения

Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.

Тригонометрические формулы сложения

sinα±β=sinα·cosβ±cosα·sinβcosα+β=cosα·cosβ-sinα·sinβcosα-β=cosα·cosβ+sinα·sinβtgα±β=tgα±tgβ1±tgα·tgβctgα±β=-1±ctgα·ctgβctgα±ctgβ

На основе формул сложения выводятся тригонометрические формулы кратного угла. 

Формулы кратного угла: двойного, тройного и т.д.

Формулы двойного и тройного угла

sin2α=2·sinα·cosαcos2α=cos2α-sin2α, cos2α=1-2sin2α, cos2α=2cos2α-1tg2α=2·tgα1-tg2α сtg2α=сtg2α-12·сtgα sin3α=3sinα·cos2α-sin3α, sin3α=3sinα-4sin3αcos3α=cos3α-3sin2α·cosα, cos3α=-3cosα+4cos3αtg3α=3tgα-tg3α1-3tg2αctg3α=ctg3α-3ctgα3ctg2α-1

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Формулы половинного угла

Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.

Формулы половинного угла

sin2α2=1-cosα2cos2α2=1+cosα2tg2α2=1-cosα1+cosαctg2α2=1+cosα1-cosα

Формулы понижения степени

Формулы понижения степени

sin2α=1-cos2α2cos2α=1+cos2α2sin3α=3sinα-sin3α4cos3α=3cosα+cos3α4sin4α=3-4cos2α+cos4α8cos4α=3+4cos2α+cos4α8

Часто при расчетах действовать с громоздктми степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:

Общий вид формул понижения степени

для четных n

sinnα=Cn2n2n+12n-1∑k=0n2-1(-1)n2-k·Ckn·cos((n-2k)α)cosnα=Cn2n2n+12n-1∑k=0n2-1Ckn·cos((n-2k)α)

для нечетных n

sinnα=12n-1∑k=0n-12(-1)n-12-k·Ckn·sin((n-2k)α)cosnα=12n-1∑k=0n-12Ckn·cos((n-2k)α)

Сумма и разность тригонометрических функций

Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.

Сумма и разность тригонометрических функций

sinα+sinβ=2sinα+β2·cosα-β2sinα-sinβ=2sinα-β2·cosα+β2cosα+cosβ=2cosα+β2·cosα-β2cosα-cosβ=-2sinα+β2·sinα-β2, cosα-cosβ=2sinα+β2·sinβ-α2

Произведение тригонометрических функций

Если формулы суммы и разности функций позволяют перейти к их произведению, то формулы произведения тригонометрических функций осуществляют обратный переход — от произведения к сумме. Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.

Формулы произведения тригонометрических функций

sinα·sinβ=12·(cos(α-β)-cos(α+β))cosα·cosβ=12·(cos(α-β)+cos(α+β))sinα·cosβ=12·(sin(α-β)+sin(α+β))

Универсальная тригонометрическая подстановка

Все основные тригонометрические функции — синус, косинус, тангенс и котангенс, — могут быть выражены через тангенс половинного угла. 

Универсальная тригонометрическая подстановка

sinα=2tgα21+tg2α2cosα=1-tg2α21+tg2α2tgα=2tgα21-tg2α2ctgα=1-tg2α22tgα2

Решить уравнение sin^2(x/2)-cos^2(x/2)=cos2x

  Здравствуете, Дорогие друзья! В этой статье мы разберём очередной пример, где  требуется решить тригонометрическое уравнение и найти корни принадлежащие заданному отрезку. Способов определения корней, которые принадлежат отрезку несколько.

Кому-то понятнее определять их по тригонометрической окружности, кому-то используя числовую ось. Здесь представлено два алгебраических способа. Каждый из них уже рассматрен отдельно: один в этой статье, другой здесь. Эти способы позволяют найти корни посредством алгебраических вычислений (без построения тригонометрической окружности или числовой оси).

Тригонометрические уравнения, которые будут на ЕГЭ по математике, не требуют ни каких «глубоких» умений в их преобразовании, достаточно знать основные формулы и иметь навык их использования.

Ещё раз отмчу, что для решения подобных заданий  необходимо в совершенстве владеть методикой решения простейших тригонометрических уравнений; знать табличные значения тригонометрических функций углов от 0 до 90 градусов; знать формулы приведения; уметь проводить преобразования, используя тригонометрические формулы; переводить радианы в градусы и обратно. 

Дано уравнение:

а) Решите уравнение.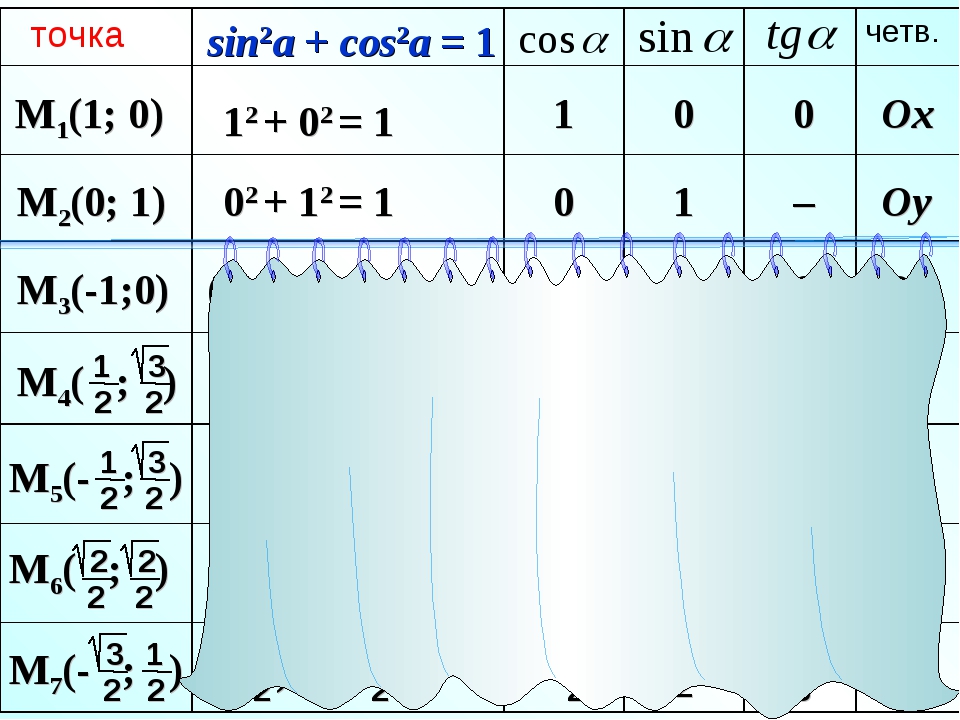
б) Укажите корни уравнения, принадлежащие отрезку.

Решение:

а) Преобразуем уравнение (и левую и правую часть по формуле косинуса двойного аргумента):

Произведём замену переменной: пусть cos x = t.

Получили квадратное уравнение  2t² + t – 1 = 0.

Решим его, получим  простейшие тригонометрические уравнения:

Изобразим корни на тригонометрической окружности:

 

б) Первый способ:

Переведём  радианы в  градусы. Так как Пи  радиан это 180 градусов, то отрезок

в градусах будет выглядеть следующим образом: [– 270⁰; 540⁰].

Определим  корни. Суть подхода: берём произвольные коэффициенты k и подставляем в каждый из корней, далее вычисляем и смотрим – принадлежат ли полученные корни заданному  интервалу. Если принадлежат, то отмечаем их как верный ответ.

Ещё раз запишем все полученные (в пункте а) корни:

При k = 0:

При k = 1:

При k = 2:

 

При k = – 1:

При k = – 2:

Таким образом, отрезку [– 270⁰; 540⁰]  принадлежат корни:

– 180⁰; – 60⁰; 60⁰; 180⁰; 300⁰;  420⁰  и 540⁰

в радианах это

Вопрос: какие «произвольные» коэффициенты k брать?

В пределах от –3 до 3, так как границы заданного интервала в подобных типовых заданиях ЕГЭ обычно лежат «недалеко» от нуля.

Данный способ совершенным назвать нельзя. Но он, безусловно, позволяет находить верное решение. Важно перебрать необходимые значения k и убедиться, что получены все корни принадлежащие данному отрезку.

Для чего углы мы переводили из радианной меры в градусную?

Многим  наиболее «понятна» работа с углами в градусной мере.

 

Второй способ:

Суть его заключается в следующем:

1.    Берём один из корней.

2.    Составляем неравенство (корень принадлежит указанному интервалу).

3.    Решаем это неравенство.

4.    Находим коэффициент(ы) k

5.    Подставляем найденный коэффициент(ты) обратно в этот корень, и затем вычисляем.

И так поступаем с каждым корнем (полученным в пункте а).

Первый корень:

Решаем неравенство:

Так как число k целое, то значит    k₁ = 0    k₂ = 1

Вычисляем корни, принадлежащие интервалу:

Следующий корень:

Решаем неравенство:

Так как число k целое, то значит    k₁ = 0    k₂ = 1

Вычисляем корни, принадлежащие интервалу:

Следующий корень:

Решаем неравенство:

Так как число k целое, то значит    k₁ = – 1,    k₂ = 0,      k₃ = 1

Вычисляем корни принадлежащие интервалу:

Всего получили семь корней:

Ответ:

тригонометрических отождествлений.

Темы по тригонометрии.

Темы | Дом

20

Взаимные идентичности

Тангенс и котангенс

Пифагорейские тождества

Формулы суммы и разности

Формулы двойного угла

Формулы полууглов

Произведений суммой

Суммы как произведения

ИДЕНТИЧНОСТЬ — ЭТО РАВЕНСТВО, которое истинно для любого значения переменной.(Уравнение — это равенство, которое верно только для определенных значений переменной.)

В алгебре, например, у нас есть это тождество:

( x + 5) ( x — 5) = x ² — 25.

Значение идентичности состоит в том, что при вычислении мы можем заменить любой член другим. Мы используем идентичность, чтобы придать выражению более удобную форму. В исчислении и во всех его приложениях центральное значение имеют тригонометрические тождества.

На этой странице мы представим основные личности. У студента не будет лучшего способа практиковать алгебру, чем доказывать их. Ссылки на доказательства приведены ниже.

Взаимные идентичности

sin θ	=	1 csc θ		csc θ	=	1 sin θ
cos θ	=	1 сек θ		сек θ	=	1 cos θ
tan θ	=	1 детская кроватка θ		детская кроватка θ	=	1 tan θ

Проба

Опять же, при вычислении мы можем заменить любой член идентичности другим.Итак, если мы видим «sin θ», то мы можем, если захотим, заменить

»

это с «

1 csc θ

«; и симметрично, если мы увидим»

1 csc θ

«,

, тогда мы можем заменить его на «sin θ».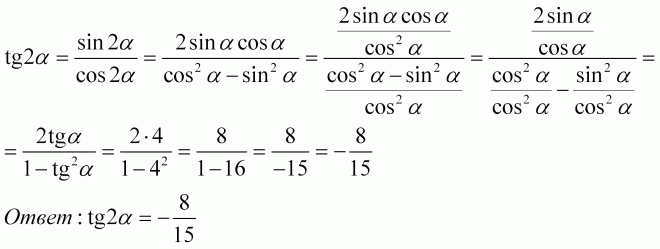

Проблема 1. Что означает утверждение, что csc θ является обратной величиной
sin θ?

Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).

Это означает, что их продукт 1.

sin θ csc θ = 1.

Урок 5 алгебры.

Задача 2. Оценить

tan 30 ° csc 30 ° cot 30 °.

tan 30 ° csc 30 ° cot 30 °	=	tan 30 ° cot 30 ° csc 30 °
	=	1 · csc 30 °
	=	2.

Тема 4.

Тангенс и котангенс

тангенс угла θ =

sin θ cos θ

детская кроватка θ =

cos θ sin θ

Проба

Пример 1. Покажите: tan θ cos θ = sin θ.

Решение: Проблема означает, что мы должны написать левую часть, а затем показать с помощью подстановок и алгебры, что мы можем преобразовать ее, чтобы она выглядела как правая часть.

Начинаем:

Мы подошли к правой стороне.

Пифагорейские тождества

а)	sin 2 θ + cos 2 θ	=	1.
б)	1 + загар 2 θ	=	сек 2 θ
в)	1 + детская кроватка 2 θ	=	csc 2 θ
a ‘)	sin 2 θ	=	1 — cos 2 θ.
	cos 2 θ	=	1 — sin 2 θ.

Они называются тождествами Пифагора, потому что, как мы увидим в их доказательстве, они являются тригонометрической версией теоремы Пифагора.

Два идентификатора, помеченные как ‘) — «а-простое число» — просто разные версии а).Первый показывает, как мы можем выразить sin θ через cos θ; второй показывает, как мы можем выразить cos θ через sin θ.

Примечание: sin ² θ — «синус-квадрат тета» — означает (sin θ) ² .

Задача 3. Треугольник 3-4-5 прямоугольный.

а) Почему?

Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).

Он удовлетворяет теореме Пифагора.

б) Оцените следующее:

sin 2 θ

=

16 25

cos 2 θ

=

9 25

sin 2 θ + cos 2 θ

=

1.

Пример 2. Показать:

Это то, что мы хотели показать.

Формулы суммы и разности

sin (α + β)	=	sin α cos β + cos α sin β
sin (α — β)	=	sin α cos β — cos α sin β
cos (α + β)	=	cos α cos β — sin α sin β
cos (α — β)	=	cos α cos β + sin α sin β

Примечание: В формулах синуса + или — слева также + или — справа.Но в формулах косинуса + слева становится — справа; и наоборот.

Поскольку эти тождества доказываются непосредственно из геометрии, от студента обычно не требуется усваивать доказательство. Однако все последующие тождества основаны на этих формулах суммы и разности. Студент обязательно должен их знать.

Вот доказательство формул суммы.

Пример 3. Оценить sin 15 °.

Решение.	sin 15 °
				Формулы
				Темы 4 и 5

Пример 4.Доказательство:

Это то, что мы хотели доказать.

Формулы двойного угла

Проба

Существует три версии cos 2α. Первый — с точки зрения обоих cos α и sin α. Второй — только по cos α. Третий — только с точки зрения sin α

Пример 5. Показать: sin 2α

Это то, что мы хотели доказать.

Пример 6. Показать:

Решение.

грех x

— согласно предыдущему тождеству с α =.

Формулы полууглов

Следующие ниже формулы половинного угла являются инверсией формул двойного угла, поскольку α составляет половину от 2α.

Знак плюс или минус зависит от квадранта. Под корнем косинус имеет знак +; синус, знак -.

Проба

.

Пример 7. Вычислить cos

π 8

.

.

Пример 8. Вывести идентификатор для tan

α 2

.

при делении числителя и знаменателя на cos α.

Произведений суммой

а)	sin α cos β		=	½ [sin (α + β) + sin (α — β)]
б)	cos α sin β		=	½ [sin (α + β) — sin (α — β)]
в)	cos α cos β		=	½ [cos (α + β) + cos (α — β)]
г)	sin α sin β		=	−½ [cos (α + β) — cos (α — β)]

Проба

Суммы как произведения

д)	sin A + sin B	=	2 sin ½ ( A + B ) cos ½ ( A — B )
е)	sin A — sin B	=	2 sin ½ ( A — B ) cos ½ ( A + B )
г)	cos A + cos B	=	2 cos ½ ( A + B ) cos ½ ( A — B )
ч)	cos A — cos B	=	−2 sin ½ ( A + B ) sin ½ ( A — B )

В доказательствах ученик увидит, что тождества с e) по h) являются инверсиями соответственно от a) до d), которые доказываются в первую очередь.Тождество f) используется для доказательства одной из основных теорем исчисления, а именно о производной sin x .

Учащийся не должен пытаться запомнить эти личности. Достаточно попрактиковаться в их доказательствах — и увидеть, что они исходят из формул суммы и разности.

Темы | Дом

---

Авторские права © 2021 Лоуренс Спектор

Вопросы или комментарии?

Электронная почта: themathpage @ яндекс.com

Тригонометрические идентичности

Тригонометрические идентичности

(Математика | Триггер | Личности)

sin (тета) = кондиционер	csc (theta) = 1 / sin (theta) = c / a
cos (тета) = b / c	сек (тета) = 1 / cos (тета) = c / b
загар (тета) = грех (тета) / соз (тета) = а / б	кроватка (тета) = 1 / загар (тета) = b / a

---

sin (-x) = -sin (x)
csc (-x) = -csc (x)
cos (-x) = cos (x)
sec (-x) = sec (x)
tan (-x ) = -tan (x)
детская кроватка (-x) = -cot (x)

sin ^ 2 (x) + cos ^ 2 (x) = 1	загар ^ 2 (x) + 1 = сек ^ 2 (x)	детская кроватка ^ 2 (x) + 1 = csc ^ 2 (x)
sin (x y) = sin x cos y cos х грех у
cos (x y) = cos x уютный грех х грех у

загар (x y) = (загар х загар у) / (1 загар х загар у)

sin (2x) = 2 sin x cos x

cos (2x) = cos ^{^ 2} (x) — sin ^{^ 2} (x) = 2 cos ^{^ 2} (x) — 1 = 1-2 грех ^{^ 2} (x)

загар (2x) = 2 загар (x) / (1 — загар ^{^ 2} (x))

sin ^{^ 2} (x) = 1/2 — 1/2 cos (2x)

cos ^{^ 2} (x) = 1/2 + 1/2 cos (2x)

sin x — грех y = 2 sin ((x — y) / 2) cos ((x + y) / 2)

cos x — cos y = -2 sin ((x — y) / 2) sin ((x + y) / 2)

Триггерная таблица общих углов

угол	0	30	45	60	90
sin ^ 2 (а)	0/4	1/4	2/4	3/4	4/4
cos ^ 2 (а)	4/4	3/4	2/4	1/4	0/4
загар ^ 2 (а)	0/4	1/3	2/2	3/1	4/0

---

Данный треугольник abc с углами A, B, C; a противоположно A, b напротив B, c напротив C:

a / sin (A) = b / sin (B) = c / sin (C) (Закон Синусов)

c ^ 2 = a ^ 2 + b ^ 2 — 2ab cos (C) b ^ 2 = a ^ 2 + c ^ 2 — 2ac cos (B) a ^ 2 = b ^ 2 + c ^ 2 — 2bc cos (A)

(Закон косинусов)

(a — b) / (a ​​+ b) = tan [(A-B) / 2] / tan [(A + B) / 2] (Закон касательных)

Как доказать sin ^ 2x + cos ^ 2x = 1? + Пример

Формула для круга с центром в начале координат:

# х ^ 2 + у ^ 2 = г ^ 2 #

То есть, расстояние от начала координат до любой точки # (x, y) # на окружности равно радиусу # r # окружности.4 / 2,7-0,01) = 0 [-2,5, 2,5, -1,25, 1,25]}

Пусть угол в начале координат будет тета (# theta #).

Теперь по тригонометрии.

Для угла # theta # в прямоугольном треугольнике триггерная функция #sin theta # представляет собой отношение # «противоположная сторона» / «гипотенуза» #. В нашем случае длина стороны, противоположной # theta #, является координатой # y # нашей точки # (x, y) #, а гипотенуза — нашим радиусом # r #. Итак:

#sin theta = «opp» / «hyp» = y / r «» <=> «» y = rsintheta #

Аналогично, #cos theta # — это отношение координаты # x # в # (x, y) # к радиусу # r #:

#cos theta = «adj» / «hyp» = x / r «» <=> «» x = rcostheta #

Итак, у нас есть # x = rcostheta # и # y = rsintheta #.2 тета = 1 #

И все. Это действительно все, что нужно сделать. Так же, как расстояние между началом координат и любой точкой # (x, y) # на окружности должно быть радиусом окружности, сумма квадратов значений для #sin theta # и #cos theta # должна быть 1 для любого угла #theta. #.

Найдите sin 2x, cos 2x и tan 2x, если tan x = 3/4 и x оканчивается в квадранте III.

Вопрос:

Найдите {eq} \ sin 2x, \ cos 2x, {/ eq} и {eq} \ tan 2x {/ eq}, если {eq} \ tan x = \ frac {3} {4} {/ eq} и {eq} x {/ eq} оканчивается в квадранте III.2 (x)} \ [0,3 см] \ pm \ frac {\ sqrt {5}} {4} & = \ sec (x) \\ [0,3 см] — \ frac {\ sqrt {5}} {4} & = \ sec (x) & \ left [\ text {Angle} x \ text {находится в квадранте III, поэтому секанс отрицательный} \ right] \\ [0,3 см] \ sec (x) & = — \ frac {\ sqrt {5}} {4} \ end {align} \\ $$

Отсюда мы можем найти {eq} \ cos x {/ экв}.

$$ \ begin {align} \ cos x & = \ frac {1} {\ sec x} \\ [0,3 см] & = \ frac {1} {- \ frac {\ sqrt {5}} {4}} \\ [0,3 см] & = 1 \ times — \ frac {4} {\ sqrt {5}} \\ [0,3 см] \ cos x & = — \ frac {4} {\ sqrt {5}} \\ [0.3см] \ end {align} \\ $$

Также решите относительно {eq} \ sin x {/ экв}.

$$ \ begin {align} \ tan x & = \ frac {\ sin x} {\ cos x} \\ [0,3 см] \ frac {3} {4} \ times — \ frac {4} {\ sqrt {5}} & = \ frac {\ sin x} {- \ frac {4} {\ sqrt {5}}} \ times — \ frac {4} {\ sqrt {5}} \\ [0,3 см] — \ frac {3} {\ sqrt {5}} & = \ sin x \\ [0,3 см] \ sin x & = — \ frac {3} {\ sqrt {5}} \ end {align} \\ $$

Теперь мы можем решить для {eq} \ sin 2x, \ cos 2x, {/ eq} и {eq} \ tan 2x {/ экв}.

$$ \ begin {align} \ sin 2x & = 2 \ sin x \ cos x \\ [0.2 \ [0,3 см] & = \ frac {16} {5} — \ frac {9} {5} \\ [0,3 см] \ cos 2x & = \ boxed {\ color {blue} {\ frac {7} {5}}} \\ [1 см] \ tan 2x & = \ frac {\ sin 2x} {\ cos 2x} \\ [0,3 см] & = \ frac {\ frac {24} {5}} {\ frac {7} {5}} \\ [0,3 см] & = \ frac {24} {5} \ times \ frac {5} {7} \\ [0,3 см] \ tan 2x & = \ boxed {\ color {blue} {\ frac {24} {7}}} \\ [1 см] \ end {align}

$

Тригонометрических идентичностей

Возможно, сначала вы захотите прочитать о тригонометрии!

Прямой треугольник

Тригонометрические тождества — это уравнения, которые верны для прямоугольных треугольников. (Если это не прямоугольный треугольник, перейдите на страницу «Треугольники».)

Каждая сторона прямоугольного треугольника имеет имя:

Соседний всегда находится рядом с углом

И Напротив находится напротив угла

Мы скоро будем играть со всеми видами функций, но помните, что все возвращается к этому простому треугольнику с:

• Угол θ
• Гипотенуза
• Соседний
• напротив

Синус, косинус и тангенс

Три основных функции в тригонометрии — это синус, косинус и тангенс.

Это всего лишь длины одной стороны делится на другой

Для прямоугольного треугольника с углом θ :

Функция синуса:	sin ( θ ) = Противоположно / Гипотенуза
Функция косинуса:	cos ( θ ) = Соседний / Гипотенуза
Касательная функция:	tan ( θ ) = напротив / рядом

Для заданного угла θ каждое отношение остается неизменным
независимо от того, насколько большой или малый треугольник

Когда мы разделим синус на косинус, получим:

sin (θ) cos (θ) = Противоположно / Гипотенуза Соседний / Гипотенуза = Противоположно Соседний = tan (θ)

Итак, мы можем сказать:

Это наш первый Тригонометрический идентификатор .

Косеканс, секанс и котангенс

Мы также можем разделить «наоборот» (например, Соседний / Противоположный вместо Противоположный / Соседний ):

Косекансная функция:	csc ( θ ) = Гипотенуза / Напротив
Секущая функция:	сек ( θ ) = Гипотенуза / Соседний
Функция котангенса:	детская кроватка ( θ ) = рядом / напротив

Пример: когда Противоположность = 2 и Гипотенуза = 4, тогда

sin (θ) = 2/4 и csc (θ) = 4/2

На основании всего, что мы можем сказать:

грех (θ) = 1 / csc (θ)

cos (θ) = 1 / сек (θ)

загар (θ) = 1 / детская кроватка (θ)

И наоборот:

csc (θ) = 1 / sin (θ)

сек (θ) = 1 / cos (θ)

детская кроватка (θ) = 1 / tan (θ)

А еще у нас есть:

детская кроватка (θ) = cos (θ) / sin (θ)

Теорема Пифагора

Следующие тригонометрические тождества мы начнем с теоремы Пифагора:

Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат a плюс квадрат b равен квадрату c: a 2 + b 2 = c 2

Если разделить на c ² , получим

а ² с ² + б ² с ² знак равно в ² в ²

Это можно упростить до:

( a c ) ² + ( б c ) ² = 1

Итак, a / c — это Противоположно / Гипотенуза , что составляет sin (θ)

И b / c — это Соседний / Гипотенуза , что составляет cos (θ)

Так (a / c) ² + (b / c) ² = 1 также можно записать:

Примечание:

• sin ² θ означает найти синус θ, , затем возвести результат в квадрат и
• sin θ ² означает возводить в квадрат θ, затем выполняет синусоидальную функцию

Пример: 32 °

Использование только 4 десятичных разряда :

• sin (32 °) = 0.5299 …
• cos (32 °) = 0,8480 …

Теперь посчитаем sin ² θ + cos ² θ :

0,5299 ² + 0,8480 ²
= 0,2808 … + 0,7191 …
= 0,9999 …

Мы очень близки к 1, используя всего 4 десятичных знака. Попробуйте это на вашем калькуляторе , и вы получите лучшие результаты!

Связанные идентификационные данные включают:

sin ² θ = 1 — cos ² θ
cos ² θ = 1 — sin ² θ
tan ² θ + 1 = sec ² θ
tan ² θ = sec ² θ — 1
детская кроватка ² θ + 1 = csc ² θ
детская кроватка ² θ = csc ² θ — 1

Как вы их помните? Упомянутые до сих пор личности можно запомнить , используя одну хитроумную диаграмму под названием Magic Hexagon:

Но подождите… Это еще не все!

Есть еще много идентификаторов … вот некоторые из наиболее полезных:

Идентичности с противоположными углами

грех (−θ) = −sin (θ)

cos (−θ) = cos (θ)

тангенс (-θ) = -тан (θ)

Double Angle Identities

Half Angle Identities

Обратите внимание, что «±» означает, что это может быть или один , в зависимости от значения θ / 2

Тождества суммы углов и разностей

Обратите внимание, что это означает, что вы можете использовать плюс или минус, а средство — использовать противоположный знак.

sin (A B) = sin (A) cos (B) cos (A) sin (B)

cos (A B) = cos (A) cos (B) sin (A) sin (B)

загар (A B) = загар (A) загар (B) 1 загар (A) загар (B)

детская кроватка (A B) = детская кроватка (A) детская кроватка (B) 1 детская кроватка (B) детская кроватка (A)

Треугольники

Существуют также идентичности треугольников, которые применяются ко всем треугольникам (а не только к прямоугольным треугольникам). 2x в новой форме, которая означает то же самое.

Мы делаем упор на умножение скобок, и поэтому убираем дробь из путь.

Мы видим, что члены cos2x сокращаются, упрощая, таким образом, выражение.

Следовательно, это упрощенное выражение. Иногда по математике вы ползаете выбраться из дыры только для того, чтобы упасть в другую. У нас все еще есть cos в квадрате термин, который вызовет некоторые трудности.

Напомним выражение [4], которое мы сделали ранее, как показано выше.

Если мы умножим углы на 2 с обеих сторон, то уравнение останется сбалансированный, однако, он дает нам квадрат в квадрате 2x для замены.

Я предпочитаю, чтобы это было написано вот так. Теперь мы можем заменить cos в квадрате 2x в нашем предыдущем уравнении [5], как показано ниже.

На этом этапе мы заменяем и упрощаем.

Мы вспоминаем нашу исходную задачу интеграции, и теперь мы можем записать ее в другая форма, как показано на правой стороне.

Мы можем интегрировать каждый термин отдельно, как показано на правой стороне. Хотя первый член на правой стороне, который является константой, легко интегрируется, второй член потребуется еще немного подумать.Поэтому мы фокусируем наше внимание на интеграции второй член, как показано ниже красным.

Мы сосредотачиваемся на интеграции cos4x и получаем ответ, показанный красным. Теперь мы можем подставим эту часть решения в нашу исходную задачу интеграции как показано ниже.

Следовательно, это решение, где C — постоянная интегрирования.

3. Формулы двойных углов

М. Борна

Формулы двойного угла могут быть весьма полезны, когда нам понадобится позднее упростить сложные тригонометрические выражения.

При использовании этих формул лучше помнить, откуда они берутся, чем пытаться запоминать настоящие формулы. Так вы поймете это лучше и сможете меньше загромождать память.

Синус двойного угла

sin 2 α = 2 sin α cos α

Доказательство

Вспомните из последнего раздела синус суммы двух углов:

sin ( α + β ) = sin α cos β + cos α sin β

Мы будем использовать это, чтобы получить синус двойного угла.

Если взять левую сторону (LHS):

sin ( α + β )

и заменяя β на α , получаем:

sin ( α + β ) = sin ( α + α ) = sin 2 α

Рассмотрим RHS:

sin α cos β + cos α sin β

Поскольку мы заменили β в LHS на α , нам нужно сделать то же самое с правой стороны.Делаем так, и получаем:

sin α cos α + cos α sin α = 2 sin α cos α

Объединяя наши результаты для LHS и RHS, мы получаем важный результат:

sin 2 α = 2 sin α cos α

Этот результат называется синусом двойного угла. Это полезно для упрощения выражений позже.

Косинус двойного угла

Используя аналогичный процесс, мы получаем косинус двойного угла по формуле :

cos 2 α = cos ² α — sin ² α

Доказательство

На этот раз мы начнем с косинуса суммы двух углов:

cos ( α + β ) = cos α cos β — sin α sin β ,

и еще раз замените β на α как на левой, так и на правой стороне, как показано ниже:

LHS = cos ( α + α ) = cos (2 α )

RHS = cos α cos α — sin α sin α = cos ² α — sin ² α

Различные формы результата двойного угла косинуса

Используя результат sin ² α + cos ² α = 1 (который мы нашли в тригонометрических идентичностях), мы можем записать правую часть приведенной выше формулы как:

cos ² α — sin ² α

= (1 — sin ² α ) — sin ² α

= 1− 2sin ² α

Аналогичным образом мы можем заменить (1 — cos ² α ) на sin ² α в нашу правую часть и получить:

cos ² α — sin ² α

= cos ² α — (1 — cos ² α )

= 2cos ² α — 1

Резюме — Косинус двойного угла

Следующие значения имеют эквивалентное значение, и мы можем использовать то, что нам нравится, в зависимости от ситуации:

cos 2α = cos ² α — sin ² α

cos 2α = 1− 2 sin ² α

cos 2α = 2 cos ² α — 1

Пример 1

Найдите cos 60 °, используя функции 30 °. 2`

`= 1-2 (144/169)`

`= (169-288) / 169`

`= (- 119) / 169`

Обратите внимание, что мы не нашли сначала значение x с помощью калькулятора, а затем нашли требуемое значение.Если бы мы сделали это, мы бы не нашли точное значение и упустили бы удовольствие увидеть формулу двойного угла в действии 🙂

Упражнения

1. Не находя «x», найдите точное значение «sin 2x» , если «cos x = 4/5» (в квадранте I).

Ответ

Мы понимаем, что нам нужно использовать треугольник 3-4-5 (из-за 4 и 5 в вопросе).

Мы можем использовать нашу формулу для синуса двойного угла, чтобы найти необходимое значение:

`sin 2x = 2 sin x cos x`

`= 2 (3/5) (4/5)`

`= 24/25`

2.2x`

`=» RHS «`

.

No related posts.