Sin 2 п 3: Mathway | Популярные задачи

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значение
cos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )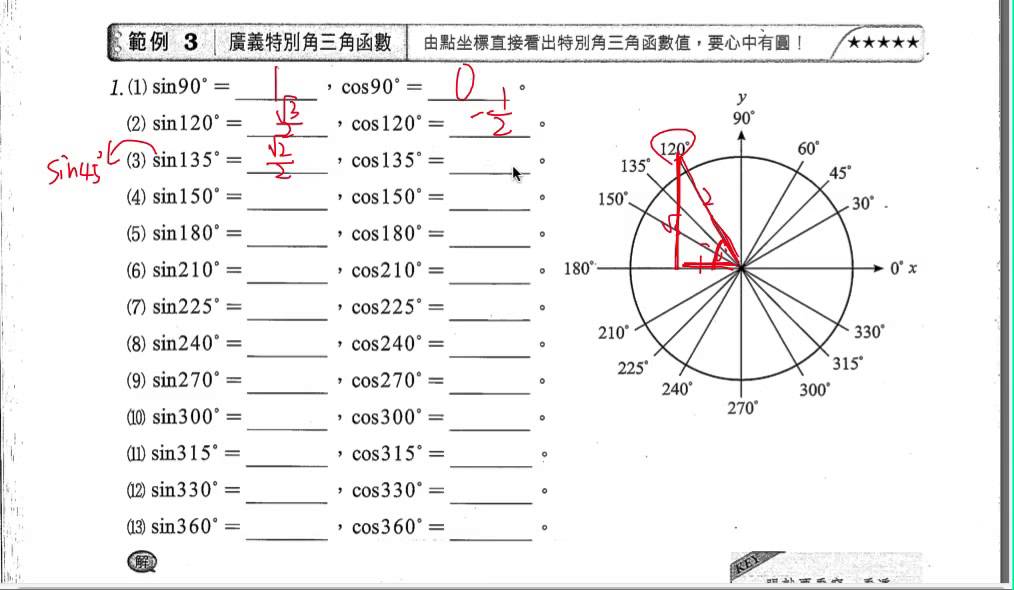
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )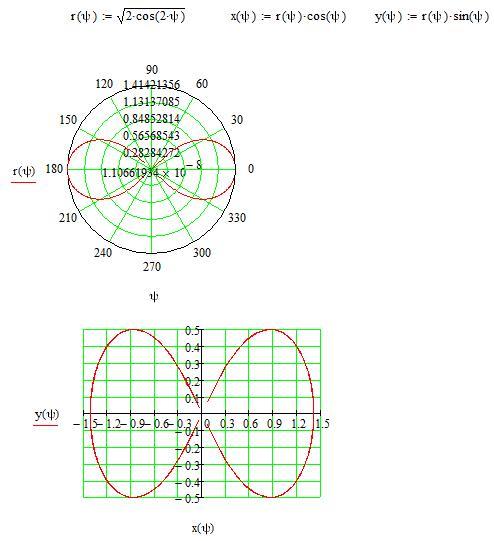
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )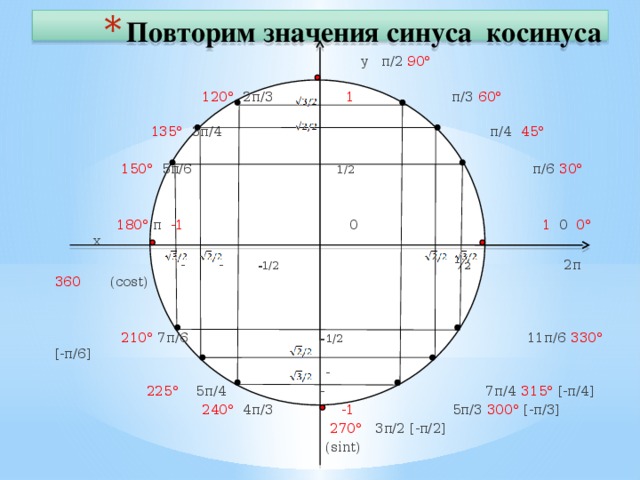
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74
Найти точное значение		tan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81
Найти точное значение		sin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )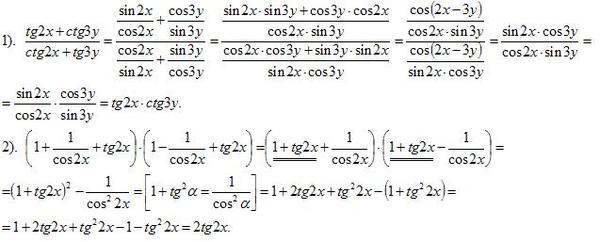
87Найти точное значение
sin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Аренда и прокат Divinity: Original Sin 2

Божественный мертв. Наступает Пустота. А внутри вас просыпаются доселе неведомые силы. Битва за божественность началась. Выбирайте мудро и хорошо подумайте, кому доверять: в эти непростые времена тьма может таиться в каждом сердце. Изучите продуманную систему тактических сражений и играйте вместе с тремя другими игроками. Но помните, что богом сможет стать лишь один из вас.

Divinity: Original Sin 2. Definitive Edition – это новейшее и самое полное издание знаменитой ролевой игры. Нелинейная захватывающая история спасения мира, многогранная пошаговая боевая система и продвинутый искусственный интеллект придутся по душе ветеранам серии Divinity, а поклонники классических ролевых игр по достоинству оценят невероятную свободу и многообразие возможностей для импровизации и экспериментов вне привычных рамок видеоигр.

Divinity: Original Sin 2 провозглашает максимальную свободу в обширном открытом мире, поощряет импровизацию и творческий подход и предлагает нарушать любые правила. Здесь вы можете пуститься в путешествие в любом направлении, пообщаться с каждым встречным (живым, мертвым или вовсе не человеком) и взаимодействовать с чем угодно настолько свободно, как никогда еще не бывало прежде.

Особенности игры Divinity. Original Sin II:

Вы можете играть за любого из шести уникальных персонажей – и у каждого своя история и свои задачи. Или попробуйте создать собственного героя. Каким он будет? Эльфом, поедающим плоть собратьев? Царственным ящером? Мертвецом, восставшим из могилы? Окружающий мир всегда реагирует на вас в зависимости от вашего выбора.

Собирайте отряд и развивайте отношения со спутниками. Вас ждет бесклассовая система развития на базе двухсот с лишним навыков и заклинаний и целая дюжина различных школ. В огромном мире, полном тайн и приключений, первое прохождение станет лишь началом изучения всех возможностей игры!

Расправляйтесь с врагами в тактических пошаговых сражениях, используя силы стихий и их сочетания. Превратите в свое оружие само поле боя! Занимайте господствующую высоту, чтобы получить преимущество, и загоняйте врагов в ловушки.

Отправляйтесь куда угодно, говорите с кем угодно, используйте что угодно – в Ривеллоне свобода для странствий и экспериментов не ограничена ничем! Вы можете убить любого неигрового персонажа, можете поговорить со всеми животными… и даже у призраков найдутся свои секреты. Доверьтесь своему воображению и изучите бесчисленные возможности взаимодействия с игровым миром.

Исследуйте обширный мир Ривеллона в одиночку или в компании. Принять участие в грандиозном приключении по сети могут до 4 игроков одновременно, присоединяясь или уходя в любой момент. Или позовите друга в гости и отправляйтесь в путешествие вдвоем в режиме разделения экрана!

Играя с друзьями, вы можете начать соперничество или, напротив, объединить силы для достижения общей цели. Новая система отношений обеспечивает более тонкое взаимодействие между персонажами, ведь каждый участник похода преследует собственные цели. Вы можете выполнять личные цели своих спутников, чтобы поддержать их ради благого дела, или побороться за право самим прокладывать свой путь.

* : 0 < q < s, \; |р| < \min(t,1/2)\big\} \leq \max(0,3st - 1/2). \qquad{(4)} $$ Если выполняется (4), то его можно использовать для оценки всего интеграла; Я предоставляю читателю проверить, сходится ли полученный интеграл. Итак, давайте рассмотрим случаи, когда (4) не работает.

Зафиксируем $s > 1$ и $t > 0$, и пусть $D_{s,t} = (-s,s)\times(-t,t)$. Если $D_{s,t}$ содержит два линейно независимых элемента из $\Lambda$, то $D$ содержит фундаментальную область для $\Lambda$, скажем, $F$; у нас есть $$ 1 + 2N_{s,t} = \#(\Lambda\cap D_{s,t}) = \sum_{\mathbf x\in\Lambda\cap D_{s,t}} m(\mathbf x + F ) = m \ left (\ bigcup _ {\ mathbf x \ in \ Lambda \ cap D_ {s, t}} (\ mathbf x + F) \ right) \leq m(2D_{s,t}) = 4st, $$ откуда следует выполнение (4). Аналогично, если $D_{s,t}\cap\Lambda = \{\mathbf 0\}$, то выполняется (4). 92 \geq \max(1,3st — 1/2) \geq 2st, $$ поэтому $q|r| = д|д\пи — р| \leq 1/2$. Теперь из известной теоремы следует, что $p/q$ сходится к $\pi$, т. е. $(q,p) = (q_n,p_n)$ для некоторого $n\in\mathbb N$. Итак, если мы позволим $$ \Lambda_c = \{(k q_n, k(q_n\pi — p_n)) : n,k\in\mathbb N\} $$ тогда $$ N_{s,t} = \#(\Lambda_c\cap D_{s,t}). $$ Другими словами, вклад в подынтегральную функцию (3) вносят только точки, происходящие из $\Lambda_c$. 2}\cdot $$ Отсюда следует, что (1) сходится тогда и только тогда, когда сходится (2).

Если это доказательство слишком техническое, чтобы следовать ему, я попытаюсь обобщить основные идеи: Прежде всего, любое рациональное число $p/q$, не сходящееся с $\pi$, должно удовлетворять $q|q \пи — р| > 1/2$ (это общеизвестный факт). Самого по себе этого факта недостаточно, чтобы гарантировать, что члены, исходящие от несходящихся, не приведут к расходимости ряда (2), поскольку в конечном итоге вы сравниваете его с гармоническим рядом, который (едва ли) расходится. Но это всего лишь самая грубая оценка: наиболее рациональных чисел $p/q$ будут удовлетворять $q|q\pi — p| \гг 1$. Поскольку (2) включает суммирование по всех $q$, будет много «усреднения», и поэтому «всплески», возникающие при малом $q|q\pi — p|$, будут размыты. в долгосрочной перспективе. Чтобы формализовать это, вам нужно поговорить о решетках и фундаментальных областях — в основном идея состоит в том, что количество точек пересечения решетки с выпуклой центрально-симметричной областью примерно такое же, как площадь области, за исключением некоторых исключительных случаев.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *