Лучший ответ по мнению автора
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
задача для 5 класса. После строительства дома осталось некоторое количество плиток. Их можно использовать для выкладывания прямоугольной площадки на
После строительства дома осталось некоторое количество плиток. Их можно использовать для выкладывания прямоугольной площадки на
ответы майл ру помогите решить задачу какое наименьшее количество карандашей надо прибавить к 146 уже имеющимя карандашам, чтобы получившееся
Решено
В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.75 . Найдите АС.
Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площад
Решено
в зоопарке живут крокодилы и страусы. В сумме у них 40 голов и 94 ноги. Сколько там крокодилов и страусов?Пользуйтесь нашим приложением
Чему равен интеграл sin x dx
Обновлено: 14.09.2022
Словами это читается так: интеграл от синуса равен сумме отрицательного косинуса и произвольной постоянной. \pi = -\cos \pi + \cos 0 = -(-1) + 1 = 1+1=2 $$
\pi = -\cos \pi + \cos 0 = -(-1) + 1 = 1+1=2 $$
Решение определённых интегралов
Калькулятор предоставляет ПОДРОБНОЕ решение определённых интегралов.
Этот калькулятор находит решение определенного интеграла от функции f(x) с данными верхними и нижними пределами.
Примеры
С применением степени
(квадрат и куб) и дроби
С применением синуса и косинуса
Гиберболические синус и косинус
Гиберболические тангенс и котангенс
Гиберболические арксинус и арккосинус
Гиберболические арктангенс и арккотангенс
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке): absolute(x) Абсолютное значение x
(модуль x или |x|) arccos(x) Функция — арккосинус от x arccosh(x) Арккосинус гиперболический от x arcsin(x) Арксинус от x arcsinh(x) Арксинус гиперболический от x arctg(x) Функция — арктангенс от x arctgh(x) Арктангенс гиперболический от x exp(x) Функция — экспонента от x (что и e^x) log(x) or ln(x) Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) sin(x) Функция — Синус от x cos(x) Функция — Косинус от x sinh(x) Функция — Синус гиперболический от x cosh(x) Функция — Косинус гиперболический от x sqrt(x) Функция — квадратный корень из x sqr(x) или x^2 Функция — Квадрат x ctg(x) Функция — Котангенс от x arcctg(x) Функция — Арккотангенс от x arcctgh(x) Функция — Гиперболический арккотангенс от x tg(x) Функция — Тангенс от x tgh(x) Функция — Тангенс гиперболический от x cbrt(x) Функция — кубический корень из x gamma(x) Гамма-функция LambertW(x) Функция Ламберта x! или factorial(x) Факториал от x
В выражениях можно применять следующие операции: Действительные числа вводить в виде 7. 3 — возведение в степень x + 7 — сложение x — 6 — вычитание 15/7 — дробь
3 — возведение в степень x + 7 — сложение x — 6 — вычитание 15/7 — дробь
Другие функции: asec(x) Функция — арксеканс от x acsc(x) Функция — арккосеканс от x sec(x) Функция — секанс от x csc(x) Функция — косеканс от x floor(x) Функция — округление x в меньшую сторону (пример floor(4.5)==4.0) ceiling(x) Функция — округление x в большую сторону (пример ceiling(4.5)==5.0) sign(x) Функция — Знак x erf(x) Функция ошибок (или интеграл вероятности) laplace(x) Функция Лапласа asech(x) Функция — гиперболический арксеканс от x csch(x) Функция — гиперболический косеканс от x sech(x) Функция — гиперболический секанс от x acsch(x) Функция — гиперболический арккосеканс от x
Постоянные: pi Число «Пи», которое примерно равно
3.14159.. e Число e — основание натурального логарифма, примерно равно
2,7183.. i Комплексная единица oo Символ бесконечности — знак для бесконечности
Вычислите интеграл (подробно и по шагам, пожалуйста) ∫sinx dx вычисляется без проблем, а вот с удвоенным получается не пойми что.
 -8
-8Является ли пара чисел (2; — 1) решением уравнения 2х + 5 = -3? Yonduur narueung
1) Из города выехал мотоцикл и двигался со скоростью 40 км/ч. Через полчаса вслед за ним выехал автомобиль со скоростью 60 км/ч. Через сколько времени … после своего выезда из города автомобиль догонит мо- тоцикл? . 2)Нержавеющая сталь является сплавом железа, хрома и никеля. Лист та- кой стали содержит 15% хрома. 0.5% никеля, а железа — на 2,78 кг бо- лыше, чем хрома. Найдите массу листа. Io nonor ero 060-
1 задача)В первой цистерне в три раза больше бензина, чем во второй. Когда из первой цистерны взяли 400 л бензина, а со второй 800 л, оказалось, что в … первый , цистерне бензина стало в 8 раз больше, чем во второй: Сколько бензина было в каждой цистерна сначала?
. Сумма двух чисел равна 52,7, одно из них в 2,4 раза больше другого. Найдите большее из этих чисел. иста
СРОЧНО 50БАЛООВ3sin²x+4sinxcosx+con²x=0[tex]\pi — arctg \frac [/tex][tex]arctg \frac [/tex][tex] \frac [/tex][tex]arctg \frac [/tex]1>
В зависимости от параметра a найдите количество решений уравнения x^2-8|x|=a^2-20
Читайте также:
- Как дюпать в игре scum
- Лучше может быть только что нибудь светлое будущее например
- Кеншин патруль как сделать
- Divinity original sin бутылка клубящейся грязи где
- Рация эрика 315 как пользоваться
Интеграл от sin 2x и интеграл от sin 2 x имеют разные значения. Чтобы найти интеграл sin 2 x, мы используем формулу cos 2x и метод подстановки, тогда как мы используем только метод подстановки, чтобы найти интеграл sin 2x.
Чтобы найти интеграл sin 2 x, мы используем формулу cos 2x и метод подстановки, тогда как мы используем только метод подстановки, чтобы найти интеграл sin 2x.
Определим разницу между интегралом sin 2x и интегралом sin 2 x, найдя их значения соответствующими методами, а также решим некоторые задачи, связанные с этими интегралами. 92x
Чему равен интеграл от Sin 2x dx?
Интеграл от sin 2x обозначается ∫ sin 2x dx, а его значение равно -(cos 2x) / 2 + C , , где «C» — постоянная интегрирования. Для доказательства воспользуемся интегрированием методом подстановки. Для этого предположим, что 2x = u. Тогда 2 dx = du (или) dx = du/2. Подставляя эти значения в интеграл ∫ sin 2x dx,
∫ sin 2x dx = ∫ sin u (du/2)
= (1/2) ∫ sin u du
Мы знаем, что интеграл от sin x равен -cos x + C. Таким образом,
= (1/2) (-cos u) + C
Подставляя u = 2x здесь,
∫ sin 2x dx = -(cos 2x) / 2 + C
Это интеграл формулы sin 2x.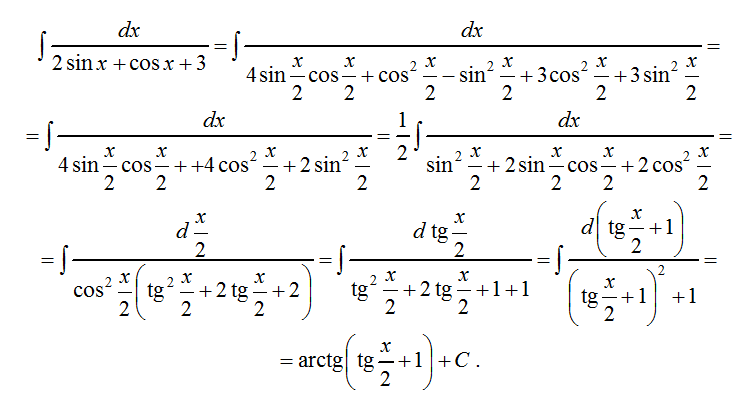
Определенный интеграл от греха 2x
Определенный интеграл — это неопределенный интеграл с некоторыми нижними и верхними границами. По основной теореме математического анализа, чтобы вычислить определенный интеграл, мы подставляем верхнюю и нижнюю границы в значение неопределенного интеграла, а затем вычитаем их в том же порядке. При вычислении определенного интеграла константой интегрирования можно пренебречь. Вычислим здесь некоторые определенные интегралы от интеграла sin 2x dx. 92x Использование формулы двойного угла для cos
Чтобы найти интеграл от sin 2 x, мы используем формулу двойного угла для cos. Одна из формул cos 2x: cos 2x = 1 — 2 sin 2 x. Решая это для sin 2 x, мы получаем sin 2 x = (1 — cos 2x) / 2. Мы используем это, чтобы найти ∫ sin 2 x dx. Тогда мы получаем
∫ sin 2 x dx = ∫ (1 — cos 2x) / 2 dx
= (1/2) ∫ (1 — cos 2x) dx
= (1/2) ∫ 1 dx — (1/2) ∫ cos 2x dx
92x Используя интегрирование по частям Мы знаем, что можем записать sin 2 x как sin x · sin x.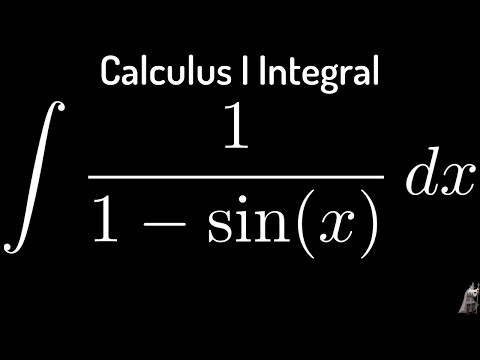 Чтобы найти интеграл произведения, мы можем использовать интегрирование по частям.
Чтобы найти интеграл произведения, мы можем использовать интегрирование по частям.
∫ sin 2 x dx = ∫ sin x · sin x dx = ∫ u dv
Здесь u = sin x и dv = sin x dx.
Тогда du = cos x dx и v = -cos x.
По формуле интегрирования по частям
∫ sin 2 x dx = (-1/2) (2 sin x cos x) + ∫ cos 2 x dx
По формуле двойного угла sin, 2 sin x cos x = sin 2x и тригонометрическое тождество, cos 2 x = 1 — sin 2 x. Итак,
∫ sin 2 x dx = (-1/2) sin 2x + ∫ (1 — sin 2 x) dx
∫ sin 2 x dx = (-1/2) sin 2x + ∫ 1 dx — ∫ sin 2 x dx
∫ sin 2 x dx + ∫ sin 2 x dx = (-1/2) sin 2x + x + C₁ 9{\pi}\)
= [π/2 — (sin 2π)/4] — [0 — (sin 0)/4]
= π/2 — 0/4
= π/2
Следовательно, интеграл от sin 2 x от 0 до π равен π/2.
Важные примечания, относящиеся к интегралу от Sin 2x и интегралу от Sin 2 x:
- ∫ sin 2x dx = -(cos 2x)/2 + C
- ∫ sin 2 x dx = x/2 — (sin 2x)/4 + C
Темы, относящиеся к интегралу Sin 2 x и интегралу Sin 2x: 93x дх? ∫ sin 3 x dx = ∫ sin 2 x sin x dx = ∫ (1 — cos 2 x) sin x dx. Чтобы найти ∫ sin 3x dx, пусть 3x = u. Тогда 3 дх = ду. Отсюда dx = du/3. Тогда приведенный выше интеграл принимает вид ∫ sin u (1/3) du = (1/3) (-cos u) + C = (-1/3) cos (3x) + C. 92x дх? Нет, значения этих двух интегралов НЕ совпадают. Имеем В старшей школе интеграция была одной из самых страшных тем в математике. В этой статье подробно объясняется интеграл от sin 2 (x). На самом деле темы интеграции и дифференциации идут рука об руку. Слово «интеграция» означает «интегрировать», то есть «присоединяться». Дифференцировать означает разбить функцию на бесконечно малые части. Наоборот, интеграция — это как раз обратное. На самом деле требуется соединение этих бесконечно малых частей, чтобы сформировать исходную функцию. Для интеграла от sin 2 (x) функция интегрирования может быть записана как: I = 9×0000 2 ∫003sin dx ____(1) Ясно, что мы не можем решить этот интеграл с помощью какой-либо прямой формулы. Итак, чтобы решить это, мы должны использовать тригонометрическое тождество половинного угла ∫sin 2 (x). Теперь, как мы все знаем, тригонометрическое тождество половинного угла sin 2 (x) = (1 – cos 2x) / 2. Таким образом, уравнение____(1) можно переписать как: I = ∫ (1 – cos 2x) / 2 dx, Или, I = 1/2 ( ∫ (1 – cos 2x) dx, Или, I = 1/2 ∫ 1 dx – 1/2 ∫ cos 2x dx, Следовательно, первая часть интеграла решается очень легко. Но , для второй части интеграла необходимо применить формулу интегрирования Также необходимо использовать формулу интегрирования: ∫ cos kx dx= (sin kx / k) + c Далее, используя эта формула, мы имеем, 9или * (sin 2x) + c, (где «c» — константа). Таким образом, ясно, что интеграл от sin 2 (x) равен x/2 – 1/4 * (sin 2x) + c. Мы должны проинтегрировать ∫ sin 2 x . Далее мы разбили шаги интеграла от sin 2 (x) чтобы вы лучше поняли. Для sin 2 (x) мы будем использовать формулу двойного угла cos : переставить так, чтобы получилось sin 2 (x) подлежащее: sin 2 (x) = 1/2(1 – cos(2x)) Теперь вы можете переписать интегрирование: ∫sin 2 (x) dx = ∫ 1 / 2(1 – cos(2x)) dx Тогда мы используем правило сумм (правило распределения) ∫ f(x) + g(x) dx= ∫ f(x) dx + ∫ g(x) dx. Таким образом, мы получаем ∫ (1 / 2) dx − ∫ ( cos 2x/2 ) dx. Затем используем правило «интегрирования константы»: ∫ a dx = ax + c ; где «с» — константа. Так как 1/2 является константой, мы можем убрать ее из интегрирования, чтобы упростить вычисление. Следовательно, мы получим x / 2 − ∫ ( cos 2x ) / 2 dx. Следуя этому, мы можем использовать константное правило: ∫ a f(x) dx = a ∫ f(x) dx. 1 / 2 x ∫(1 – cos(2x)) dx = 1/2 x (x – 1/2sin(2x)) + C На самом деле очень важно, что поскольку это не определенный интеграл, мы должны добавить константу C в конце интегрирования. Теперь, упростив приведенное выше уравнение, мы получим окончательный ответ: ∫sin 2 (x) dx = 1/2X – 1/4 sin(2x) + C. Теперь найдем интеграл sin 2 (x) другим методом. Теперь найдем интеграл от ∫sin 2 (X) dx по частям. However, we shall use this formula for the same: ∫ 𝑢′( 𝑥) 𝑣( 𝑥) 𝑑𝑥 = 𝑢( 𝑥) 𝑣( .0003 2 (x) dx как ∫ sin(x) sin(x) dx. ∫ sin(𝑥) sin(𝑥) 𝑑𝑥 = −cos(𝑥) sin(𝑥) − ∫ (−cos(𝑥)) cos(𝑥) 𝑑𝑥 Если мы снова применим интегрирование по частям к самому правому выражению, мы получим, ∫ sin 2 (x) dx = ∫ sin 2 (x) dx, что не очень полезно. Однако настоящий трюк состоит в том, чтобы переписать ∫cos 2 (x) dx на втором шаге как 1− ∫ sin 2 (x) . Тогда мы получим ∫ sin 2 (x)dx. Теперь все, что нам нужно сделать, это передать ∫sin 2 (x) dx из правой части в левую часть уравнения: 2 ∫sin 2 (x) dx = − cos(𝑥) sin(𝑥) + 𝑥 + 𝐶 ∫sin 2 (x) dx = 1 / 2 (𝑥 − cos(𝑥) sin(𝑥)) + 𝐶____(2). Мы знаем, что sin 2x = 2 sin(x) cos(x). Следовательно, cos(x) sin(x) = (sin 2x) / 2. Итак, если мы подставим это значение cos(x) sin(x) в уравнение ___(2), Мы получим : ∫ sin 2 (x) dx = x / 2 – (sin 2x) / 4 + C. Итак, мы должны писать C/2, а не C, но это все равно просто неопределенная константа, поэтому, как это принято, мы переименовываем C/2 в C, чтобы получить результат в обычном виде. Теперь мы перейдем к нахождению определенного интеграла от sin 2 (x), когда верхний предел (b) = π и нижний предел (a) = 0 . Таким образом, это можно записать как: I = ∫sin 2 (x) dx от 0 до π Далее, мы можем просто записать это как: ∫sin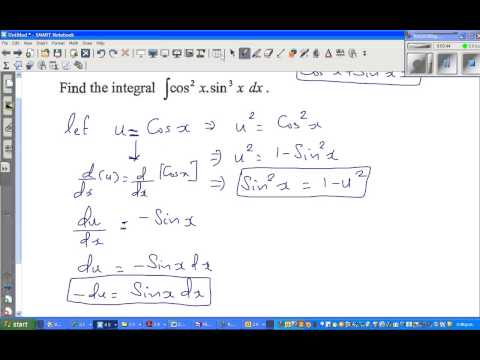 Подставим cos x = u. Тогда -sin x dx = du. Тогда приведенный выше интеграл принимает вид ∫ (1 — u 2 ) (- du) = -u + u 3 /3 + C. Подставив сюда u = sin x, ∫ sin 3 x dx = -cos x + cos 3 x/3 + C.
Подставим cos x = u. Тогда -sin x dx = du. Тогда приведенный выше интеграл принимает вид ∫ (1 — u 2 ) (- du) = -u + u 3 /3 + C. Подставив сюда u = sin x, ∫ sin 3 x dx = -cos x + cos 3 x/3 + C. Чему равен интеграл от Sin 3x dx?
Мэтуэй | Популярные проблемы
1 Найти производную — d/dx натуральное бревно х 2 Оцените интеграл 92) 21 Оценить интеграл интеграл от 0 до 1 кубического корня из 1+7x относительно x 22 Найти производную — d/dx грех(2x) 23 Найти производную — d/dx 9(3x) по отношению к x 41 Оценить интеграл интеграл от cos(2x) по x 42 Найти производную — d/dx 1/(корень квадратный из х) 43 Оцените интеграл 9бесконечность 45 Найти производную — d/dx х/2 46 Найти производную — d/dx -cos(x) 47 Найти производную — d/dx грех(3x) 92+1 68 Оценить интеграл интеграл от sin(x) по x 69 Найти производную — d/dx угловой синус(х) 70 ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х 85 Найти производную — d/dx лог х 86 Найти производную — d/dx арктан(х) 87 Найти производную — d/dx бревно натуральное 5х92 Интеграл от sin2(x) — метод, результат и все объяснение

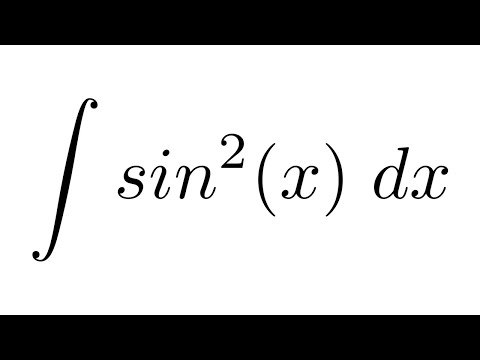
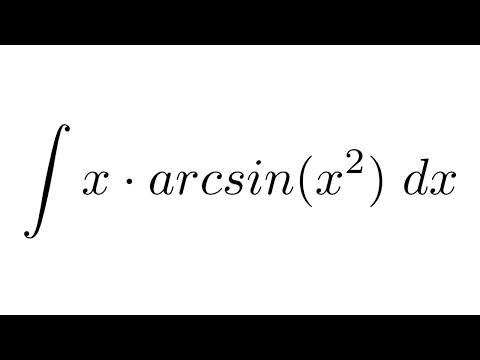

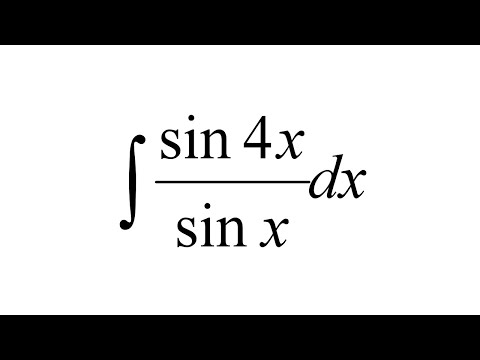
Как мы обсуждали чуть позже: есть два типа интегрирования —
определенное и неопределенное . Решите интеграл I = ∫sin
2 (x) dx от 0 до π . 2 (x
3) dx от 0 до π = ∫(1−cos2x) / 2) dx от 0 до π.

Однако это написано, потому что ( ∵ sin 2 (x) = (1−cos 2x) / 2).
= 1 / 2 [∫dx от 0 до π – ∫cos ( 2x ) dx от 0 до π]
= 1/2 [ x− (sin 2x) / 2
= 1/2 [ (π −0) − (sin 2π − sin 0) / 2]
= π / 2,
Таким образом, определенный интеграл от ∫ sin 2 (x) dx в пределах от 0 до π равен π / 2,
. Интеграл от sin 2 (x) Wolfram:Wolfram — еще один онлайн-калькулятор, вычисляющий интеграл от функций. Итак, очевидно, вы можете найти интеграл от sin 2 (x) и на нем.
Вольфрамовый калькулятор исключительно хорош. Это потому, что он не только с легкостью отображает результат, но и отображает график. Он даже отображает расширенную форму, альтернативную форму и разложение интеграла в ряд.
Подводя итог, можно сказать, что это может быть очень полезным инструментом для всех студентов, которые хотят углубиться в конкретный интеграл и выяснить его природу в деталях.
Здесь мы также предоставляем вам ссылку для доступа к этому замечательному калькулятору:
Wolfram
Типы интеграции:Интеграцию можно разделить на два типа:
- Определенный интеграл.
- Неопределенный интеграл.
- Первый тип интеграла — это определенный интеграл .
Это в основном интегрирование по фиксированному пределу. Изначально задаются две границы лимита – верхняя граница и нижняя граница.
Число «а», стоящее под знаком интеграла, называется нижний предел интеграла и число «b» вверху знака интеграла называется верхним пределом интеграла. Кроме того, несмотря на то, что a и b были заданы как интервал, нижний предел не обязательно должен быть меньше верхнего предела. В совокупности мы часто будем называть a и b интервалом интегрирования .
Далее приведены правила решения определенных интегралов:0051 неопределенные интегралы .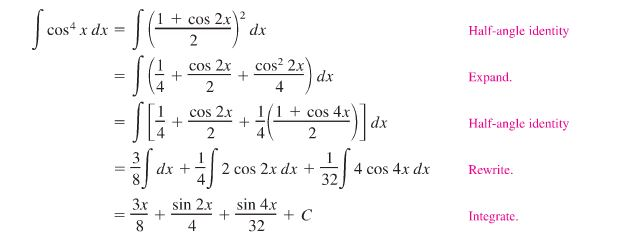
Неопределенный интеграл, иногда называемый первообразной, от функции f ( x ), обозначаемой как
). Поскольку производная константы равна нулю, неопределенный интеграл не уникален. Однако процесс нахождения неопределенного интеграла называется интегрированием. Интеграл от sin 2x:Интеграл от sin 2x можно обозначить как:
∫ sin (2x) dx_____( 3)
Однако это интегрирование решается очень просто. Вы можете использовать метод подстановки интегрирования, чтобы решить эту проблему.
Также значение этого будет -(cos 2x) / 2 + C, где «C» — постоянная интегрирования.
Теперь, продолжая интегрирование подстановкой,
Теперь предположим, что 2x = u.
Полностью дифференцирующий,
2 dx = du.
Следовательно, dx = du/2.
Теперь мы должны подставить это значение dx в интеграл sin 2x, то есть
уравнение ___(3), мы получим,
∫ sin 2x dx = ∫ sin u (du/2)
= (1/2) ∫ sin u du
Однако мы знаем, что интеграл от sin x равен -cos x + C.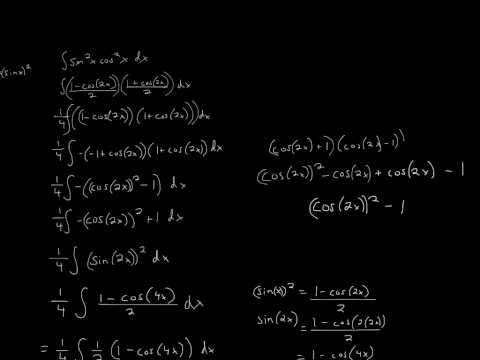 Таким образом, последнюю строку можно записать так:
Таким образом, последнюю строку можно записать так:
= (1/2) [(- cos и) + С].
Теперь, подставив сюда u = 2x,
∫ sin 2x dx = -(cos 2x) / 2 + C1, где C1 = C / 2.
Итак, это интеграл формулы sin 2x.
Интеграл sin 2 (x) Часто задаваемые вопросы: 1. С чем интегрируется sin 2 (x)?Ответ: Интеграл от sin 2 x равен x / 2 – (sin 2x) / 4 + c.
2. Почему важно записать постоянную интегрирования в неопределенном интеграле от sin 2 (x)?Ответ: Если F(x) является первообразной функции f(x), то есть F'(x)= f(x),
Тогда G(x) = F(x) + C (где C — любая константа) также является первообразной f(x),
Так как G'(x) = [F(x) + C]’= F'(х) = f(х).
Следовательно, существует семейство функций (отличающихся только константой), являющихся первообразными функции f(x).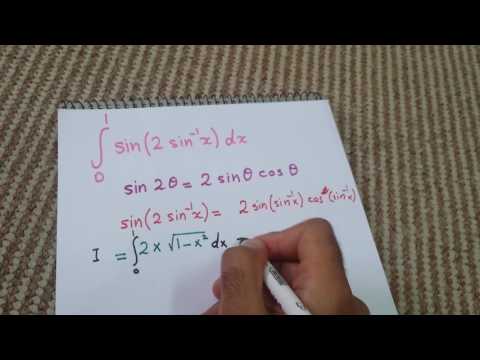 Итак, чтобы включить все первообразные f(x), константа интегрирования C используется для неопределенных интегралов. Важность C заключается в том, что он позволяет нам выразить общую форму первообразных.
Итак, чтобы включить все первообразные f(x), константа интегрирования C используется для неопределенных интегралов. Важность C заключается в том, что он позволяет нам выразить общую форму первообразных.
Ответ: В общем, форма определенного интеграла: верхний предел интегрирования за вычетом той же первообразной, оцененной на нижнем пределе интегрирования. Поскольку константы интегрирования одинаковы для обеих частей этой разности, они игнорируются при вычислении определенного интеграла, поскольку они вычитаются и дают нуль. Двигаясь дальше и помня об этом, выберите постоянную интегрирования равной нулю для всех определенных интегралов. 92 раза? («sin Square x»)
Содержание
Что такое интеграл от Sin²x? Это похоже на поиск обратной производной. В этом смысле интегрирования являются антипроизводными. Интеграция — это добавление частей, чтобы найти целое.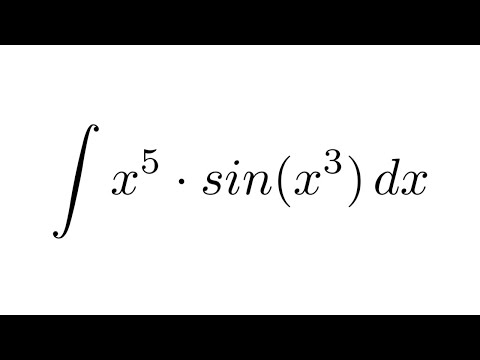 Вся пицца интегрирована, а кусочки — это отдельные функции, которые можно интегрировать. Предположим, что f(x) — любая функция, а f′(x) — ее производная. Интегрирование f′(x) по dx равно
Вся пицца интегрирована, а кусочки — это отдельные функции, которые можно интегрировать. Предположим, что f(x) — любая функция, а f′(x) — ее производная. Интегрирование f′(x) по dx равно
$$∫ f′(x) dx = f(x) + C.$$
Интегралы можно выразить двумя способами. Интегралы от неопределенной функции — это интегралы от функции, когда нет предела интегрированию. Они содержат произвольную константу. Определенные интегралы: интеграл функции с пределами интегрирования. Интервал интегрирования имеет два значения. Нижняя граница одна, а верхняя граница другая. Постоянной интеграции нет.
Интеграл sin²xИнтеграция sin²(x) невозможна, поэтому мы должны преобразовать его в другую форму, что мы можем легко сделать, используя триггерные тождества. Интегрирование квадрата греха будет основано на понятии двойных углов cos.
Интеграл от sin²x $$sin²(x)$$
$$cos(2x) = 1 – 2sin²(x)$$ [Из тригонометрических тождеств двойного угла cos]
$$sin²(x) = (1/2)(1 – cos(2x)$$
Интегрируем с обеих сторон
$$∫sin²(x)dx = ∫(1/2)(1 – cos(2x) dx$$
$$= 1/2 × (x – 1/2sin(2x)) + C$$
Таким образом, $$∫sin2(x) dx = (1/2)x – (1/4)sin(2x) + C$$
Следовательно, окончательный интеграл от sin2x равен $$(1/2)x – (1/4)sin(2x) + C$$
Пошаговое руководство по нахождению интеграла от sin²x $$∫sin²(x)dx$$
• Использовать тождества Пифагора: $$sin²x=1/2−cos2x/2$$
$$∫(1/2−cos2x/2)dx$$
• Использовать сумму Правило: $$∫f(x)+g(x)dx=∫f(x)dx+∫g(x)dx. $$
$$
$$∫(1/2)dx−∫(cos2x/2)dx$ $
• Используйте это правило: $$∫adx=ax+C$$
$$x/2−∫(cos2x/2)dx$$
• Используйте правило постоянного коэффициента: $$∫cf(x)dx=c ∫f(x)dx.$$
$$x/2−1/2∫(cos2x)dx$$
Пусть u=2x, du=2dx, тогда , dx= (1/2) du
• Использование u и выше, перепишите $$∫cos2xdx$$.
$$∫(cosu)/2du$$
• Используйте правило постоянного коэффициента: $$∫cf(x)dx=c∫f(x)dx.$$
• Используйте тригонометрическое интегрирование: интеграл cosu равен sinu.
$$(sinu)/2$$
• Подставьте u=2x обратно в исходный интеграл.
$$sin2x/2$$
• Интеграл следует переписать после завершения подстановки.
$$x/2−sin2x/4$$
• Добавить константу.
$$x/2−sin2x/4+C$$ Как интегрировать sin2x?
Итак, теперь мы должны проинтегрировать sin 2x
$$∫sin 2x dx = ½ ∫2 × sin(2x) dx (i)$$
Предположим, что u = 2x. Тогда du = 2dx.
Мы знаем, что $$∫sin x = − cos x + C$$
Следовательно, после подстановки уравнение (i) принимает вид
$$∫sin 2x dx = ½ ∫sin(u) du$$
$ $∫sin 2x dx = ½ (– cos u du) + C$$
$$∫sin 2x dx = −½ cos(2x) + C$$
Таким образом, $$∫sin 2xdx = −½ cos ( 2x) + C$$
Чему может быть равен sin 2x? Формула Sin2x — еще одна формула двойного угла. С помощью этой формулы мы можем найти синус угла, значение которого удвоилось. Мы знаем, что грех — это одно из основных тригонометрических соотношений, определяющих длину стороны, противоположной углу и гипотенузе в прямоугольном треугольнике. С использованием основных тригонометрических формул существует множество формул, связанных с sin 2x. Диапазон функции sin равен [-1, 1], поэтому диапазон sin2x также равен [-1, 1].
С помощью этой формулы мы можем найти синус угла, значение которого удвоилось. Мы знаем, что грех — это одно из основных тригонометрических соотношений, определяющих длину стороны, противоположной углу и гипотенузе в прямоугольном треугольнике. С использованием основных тригонометрических формул существует множество формул, связанных с sin 2x. Диапазон функции sin равен [-1, 1], поэтому диапазон sin2x также равен [-1, 1].
Sin 2x — тождество двойного угла для синуса в тригонометрии. Угловые отношения изучаются в тригонометрии путем сравнения углов и сторон прямоугольных треугольников. Есть две простые формулы для sin 2x:
$$sin(2x) = 2 sin x cos x$$ (в терминах sin и cos)
$$sin(2x) = (2tan x)/(1 + tan2x)$$ (в терминах tan)
Это основные формулы sin 2x. Но мы можем записать эту формулу только в терминах sin x (или) cos x, используя тригонометрическое тождество sin2x + cos2x = 1. Их
$$sin 2x = 2 √(1 – cos2x) cos x$$ (формула sin 2x через cos)
$$sin 2x = 2 sin x √(1 – sin2x)$$ (формула sin 2x в с точки зрения греха)
Почему sin 2pi 0? Чтобы найти значение sin 2pi, давайте сначала вспомним функцию синуса для различных стандартных углов из тригонометрической таблицы. sin 0 = 0, sin π/6 = 1/2, sin π/4 = √2/2, sin π/3 = √3/2 и sin π/2 = 1. Эта таблица не содержит значения грех 2пи. Здесь будут использованы различные методы, чтобы найти, что sin 2pi равен 0. Также будет приведено несколько примеров, иллюстрирующих, как это работает.
sin 0 = 0, sin π/6 = 1/2, sin π/4 = √2/2, sin π/3 = √3/2 и sin π/2 = 1. Эта таблица не содержит значения грех 2пи. Здесь будут использованы различные методы, чтобы найти, что sin 2pi равен 0. Также будет приведено несколько примеров, иллюстрирующих, как это работает.
Sin числа 2pi равен 0, т. е. sin 2π = 0. Используя тригонометрическую таблицу, мы можем найти тригонометрические отношения стандартных углов 0, π/6, π/4, π/3 и π/2. Эта таблица не дает нам значения sin 2pi. Тригонометрические отношения нестандартных углов чаще всего находятся с использованием опорных углов и квадранта, в котором лежит угол. 2pi также можно найти таким образом. Можно использовать несколько других методов, чтобы найти значение sin 2pi, в том числе
- Используя формулу двойного угла
- Использование опорного угла
- Использование единичной окружности
Мы докажем, что sin 2π = 0 в каждом из этих методов.
Синус числа 2pi равен 0.
Синус числа 2pi Используя формулу двойного угла
Мы можем найти значение sin числа 2pi, используя формулу синуса двойного угла: sin 2x = 2 sin x cos x. Поскольку мы должны определить значение sin(2π), мы должны заменить x = π в приведенной выше формуле. Это дает нам:
Поскольку мы должны определить значение sin(2π), мы должны заменить x = π в приведенной выше формуле. Это дает нам:
sin 2π = 2 sin π cos π -(1)
Так как угол π также является нестандартным углом, мы находим значения sin π и cos π по формулам суммы и разности. Тогда мы получаем
sin π = sin (π/2 + π/2) = sin π/2 cos π/2 + cos π/2 sin π/2 = (1)(0) + (0)(1) = 0
cos π = cos (π/2 + π/2) = cos π/2 cos π/2 – sin π/2 sin π/2 = (0)(0) – (1)(1) = -1
Подставьте эти значения в (1),
sin 2π = 2 (0) (-1) = 0
Следовательно, sin 2pi = 0.
Sin 2pi Использование опорных углов
Когда мы конвертируем 2π в градусы, мы получаем 360°. 360° лежит в интервале [0°, 360°], поэтому сам его котерминальный угол является опорным углом. Если мы вычтем из него 360 °, мы найдем котерминальный угол. Если мы разделим 360° на 360°, то получим 0°. Следовательно, котерминальный угол 360° равен 0°. Кроме того, 360° означает один полный оборот, поэтому он приходится либо на первый квадрант, либо на четвертый квадрант. Итак, рассмотрим оба случая.
Итак, рассмотрим оба случая.
- Первый квадрант: Мы знаем, что в первом квадранте грех положителен.
Тогда sin 360° = + sin 0° = 0 (поскольку sin 0° = 0) - Четвертый квадрант: Мы знаем, что в четвертом квадранте грех отрицателен.
Тогда sin 360° = – sin 0° = 0 (поскольку sin 0° = 0)
В обоих случаях sin 360° = sin 2π = 0,
Следовательно, sin 2π = 0,
Синус 2pi Используя единичный круг
Прежде чем найти значение sin 2pi.
- Единичная окружность — это окружность радиусом с центром в начале координат.
- Точка на единичной окружности соответствует углу.
- Угол образован линией, соединяющей начало координат и точку с положительным направлением оси x против часовой стрелки.
- Если P(x, y) соответствует некоторому углу θ, то x = cos θ и y = sin θ. Другими словами, синус угла представляет собой координату y точки.

Окружность 0° на единичной окружности состоит из 2π, что составляет всего 360° и представляет собой один полный оборот, так что это не что иное, как угол между осью x и ею самой. Точка единичного круга (1, 0) также находится на оси x, поэтому мы знаем, что 0° соответствует той же точке. Таким образом,
sin 2π = sin 0° = координата y (1, 0) = 0.
Следовательно, sin 2π = 0.
Что такое формула cos2x? Связь между углом и его сторонами объясняется тригонометрическими отношениями угла в прямоугольном треугольнике. Так что же означает cos2x? Помимо формулы косинуса 2х или косинуса 2х, существует также формула двойного угла или формула косинуса 2х. В формуле есть двойной угол, поэтому она называется формулой двойного угла. Он управляется этими тригонометрическими функциями суммы и разности двух чисел (углов) и соответствующими выражениями. Теперь, когда мы понимаем, что такое формула cos 2x, мы можем перейти к изучению тригонометрии и формулы cos2x.
Теперь, если вам интересно, что такое формула cos2x, позвольте мне сказать вам, что у нас есть формула 5 cos x.
- Тригонометрическая формула $$cos2x = Cos²x – Sin²x$$
- Тригонометрическая формула $$cos2x = 1 – 2Sin²x$$
- Тригонометрическая формула $$cos2x = 2Cos²x – 1$$
- Тригонометрическая формула $$cos2x = (1−tan²x)/(1+tan²x)$$
- Тригонометрическая формула $$cos2x = (Cos²x−Sin²x)/(Cos²x+Sin²x)$$
17.2: Неоднородные линейные уравнения — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2627
- Гилберт Странг и Эдвин «Джед» Герман
- OpenStax
Цели обучения
- Напишите общее решение неоднородного дифференциального уравнения.

- Решите неоднородное дифференциальное уравнение методом неопределенных коэффициентов.
- Решить неоднородное дифференциальное уравнение методом вариации параметров.
В этом разделе мы рассмотрим, как решать неоднородные дифференциальные уравнения. Терминология и методы отличаются от тех, которые мы использовали для однородных уравнений, поэтому давайте начнем с определения некоторых новых терминов.
Общее решение неоднородного линейного уравнения
Рассмотрим неоднородное линейное дифференциальное уравнение
\[a_2(x)y″+a_1(x)y′+a_0(x)y=r(x). \nonumber \]
Соответствующее однородное уравнение
\[a_2(x)y″+a_1(x)y′+a_0(x)y=0 \nonumber \]
называется дополнительным уравнением . Мы увидим, что решение дополнительного уравнения является важным шагом в решении неоднородного дифференциального уравнения.
Определение: частное решение
Решение \(y_p(x)\) дифференциального уравнения, которое не содержит произвольных констант, называется частным решением уравнения.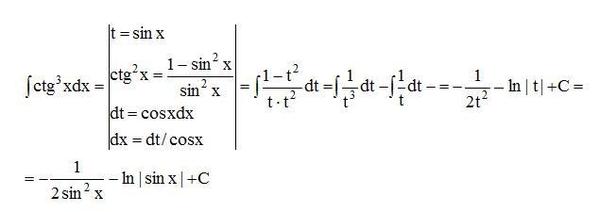
ОБЩЕЕ РЕШЕНИЕ НЕОДНОРОДНОГО УРАВНЕНИЯ
Пусть \(y_p(x)\) любое частное решение неоднородного линейного дифференциального уравнения
\[a_2(x)y″+a_1(x)y′+a_0(x )у=г(х). \nonumber \]
Также пусть \(c_1y_1(x)+c_2y_2(x)\) обозначает общее решение дополнительного уравнения. Затем общее решение неоднородного уравнения задается выражением
\[y(x)=c_1y_1(x)+c_2y_2(x)+y_p(x). \nonumber \]
Доказательство
Чтобы доказать, что \(y(x)\) является общим решением, мы должны сначала показать, что оно является решением дифференциального уравнения, и, во-вторых, что любое решение дифференциального уравнения может быть записано в виде форма. Подставив \(y(x)\) в дифференциальное уравнение, мы получим
\[\begin{align*}a_2(x)y″+a_1(x)y′+a_0(x)y &=a_2(x )(c_1y_1+c_2y_2+y_p)″+a_1(x)(c_1y_1+c_2y_2+y_p)′ \\ &\;\;\;\; +a_0(x)(c_1y_1+c_2y_2+y_p) \\[4pt] &=[a_2(x)(c_1y_1+c_2y_2)″+a_1(x)(c_1y_1+c_2y_2)′+a_0(x)(c_1y_1+c_2y_2 )] \\ &\;\;\;\; +a_2(x)y_p″+a_1(x)y_p′+a_0(x)y_p \\[4pt] &=0+r(x) \\[4pt] &=r(x).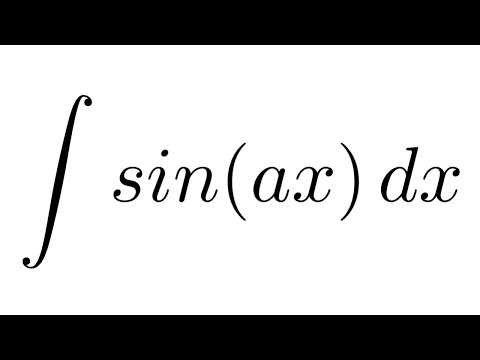 \end{выравнивание*}\]
\end{выравнивание*}\]
Итак, \(y(x)\) является решением.
Теперь пусть \(z(x)\) будет любым решением \(a_2(x)y»+a_1(x)y’+a_0(x)y=r(x).\) Тогда
\[\ begin{align*}a_2(x)(z−y_p)″+a_1(x)(z−y_p)′+a_0(x)(z−y_p) &=(a_2(x)z″+a_1 (x)z′+a_0(x)z) \\ &\;\;\;\;−(a_2(x)y_p″+a_1(x)y_p′+a_0(x)y_p) \\[4pt] &=r(x)−r(x) \\[4pt] &=0, \end{align*}\]
, поэтому \(z(x)−y_p(x)\) является решением дополнительной уравнение. Но \(c_1y_1(x)+c_2y_2(x)\) является общим решением дополнительного уравнения, поэтому существуют константы \(c_1\) и \(c_2\), такие что
\[z(x)−y_p(x)=c_1y_1(x)+c_2y_2(x). \nonumber \]
Отсюда мы видим, что
\[z(x)=c_1y_1(x)+c_2y_2(x)+y_p(x). \nonumber \]
Пример \(\PageIndex{1}\): проверка общего решения
Учитывая, что \(y_p(x)=x\) является частным решением дифференциального уравнения \(y″+y= x,\) запишите общее решение и проверьте, убедившись, что решение удовлетворяет уравнению.
Решение
Дополнительным уравнением является \(y″+y=0,\), которое имеет общее решение \(c_1 \cos x+c_2 \sin x.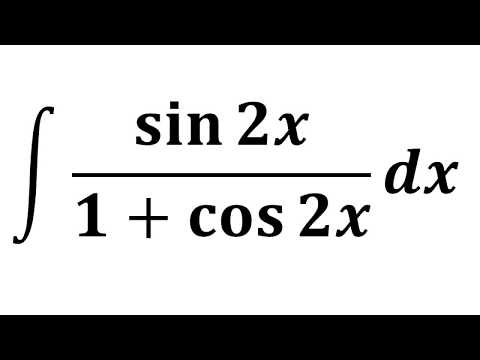 \) Итак, общее решение неоднородного уравнения
\) Итак, общее решение неоднородного уравнения
\[y(x)=c_1 \cos x+c_2 \sin x+x. \nonumber \]
Чтобы убедиться, что это решение, подставьте его в дифференциальное уравнение. У нас есть
\[y′(x)=−c_1 \sin x+c_2 \cos x+1 \nonumber \]
и
\[y″(x)=−c_1 \cos x−c_2 \sin Икс. \nonumber \]
Затем
\[\begin{align*} y″(x)+y(x) &=−c_1 \cos x−c_2 \sin x+c_1 \cos x+c_2 \sin x+ x \\[4pt] &=x.\end{align*} \nonumber \]
Итак, \(y(x)\) является решением \(y″+y=x\). 9{4x}−2\)
В предыдущем разделе мы научились решать однородные уравнения с постоянными коэффициентами. Поэтому для неоднородных уравнений вида \(ay″+by′+cy=r(x)\) мы уже знаем, как решать дополнительное уравнение, и задача сводится к нахождению частного решения неоднородного уравнения. Рассмотрим теперь для этого два приема: метод неопределенных коэффициентов и метод вариации параметров.
Неопределенные коэффициенты
Метод неопределенных коэффициентов включает обоснованные предположения о форме конкретного решения на основе формы \(r(x)\).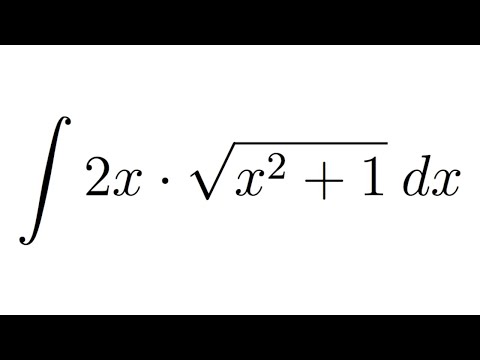 Когда мы берем производные полиномов, показательных функций, синусов и косинусов, мы получаем многочлены, показательные функции, синусы и косинусы. Поэтому, когда \(r(x)\) имеет одну из этих форм, возможно, что решение неоднородного дифференциального уравнения может принять ту же форму. Давайте посмотрим на несколько примеров, чтобы увидеть, как это работает. 9{−3x}\). Поскольку \(r(x)=3x\), конкретное решение может иметь вид \(y_p(x)=Ax+B\). Если это так, то мы имеем \(y_p′(x)=A\) и \(y_p″(x)=0\). Чтобы \(y_p\) было решением дифференциального уравнения, мы должны найти такие значения для \(A\) и \(B\), что
Когда мы берем производные полиномов, показательных функций, синусов и косинусов, мы получаем многочлены, показательные функции, синусы и косинусы. Поэтому, когда \(r(x)\) имеет одну из этих форм, возможно, что решение неоднородного дифференциального уравнения может принять ту же форму. Давайте посмотрим на несколько примеров, чтобы увидеть, как это работает. 9{−3x}\). Поскольку \(r(x)=3x\), конкретное решение может иметь вид \(y_p(x)=Ax+B\). Если это так, то мы имеем \(y_p′(x)=A\) и \(y_p″(x)=0\). Чтобы \(y_p\) было решением дифференциального уравнения, мы должны найти такие значения для \(A\) и \(B\), что
\[\begin{align*} y″+4y′+3y &=3x \\[4pt] 0+4(A)+3(Ax+B) &=3x \\[4pt] 3Ax+(4A+3B) &=3x. \nonumber \end{align*} \nonumber \]
Приравняв коэффициенты подобных членов, получим
\[\begin{align*} 3A &=3 \\ 4A+3B &=0. \end{align*} \nonumber \] 9{−3x}+x−\frac{4}{3}. \nonumber \]
В примере \(\PageIndex{2}\) обратите внимание, что хотя \(r(x)\) не включает постоянный член, нам необходимо было включить постоянный член в наше предположение . Если бы мы приняли решение в виде \(y_p=Ax\) (без постоянного члена), мы бы не смогли найти решение. (Проверьте это!) Если функция \(r(x)\) является полиномом, наше предположение о конкретном решении должно быть полиномом той же степени, и оно должно включать все члены более низкого порядка, независимо от того, являются ли они присутствует в \(r(x)\). 9{2t}+ \sin t+ \cos t \)
Если бы мы приняли решение в виде \(y_p=Ax\) (без постоянного члена), мы бы не смогли найти решение. (Проверьте это!) Если функция \(r(x)\) является полиномом, наше предположение о конкретном решении должно быть полиномом той же степени, и оно должно включать все члены более низкого порядка, независимо от того, являются ли они присутствует в \(r(x)\). 9{2t}+ \sin t+ \cos t \)
В предыдущей контрольной точке \(r(x)\) включала как синус, так и косинус. Однако, даже если \(r(x)\) включает только синус или только косинус, в предположении должны присутствовать оба члена. Метод неопределенных коэффициентов также работает с произведениями многочленов, экспонент, синусов и косинусов. Некоторые ключевые формы \(r(x)\) и соответствующие предположения для \(y_p(x)\) приведены в таблице \(\PageIndex{1}\).
СТРАТЕГИЯ РЕШЕНИЯ ЗАДАЧ: МЕТОД НЕОПРЕДЕЛЕННЫХ КОЭФФИЦИЕНТОВ
- Решите дополнительное уравнение и запишите общее решение.
- Основываясь на форме \(r(x)\), сделайте начальное предположение для \(y_p(x)\).
- Проверить, является ли какой-либо член предположения для \(y_p(x)\) решением дополнительного уравнения. Если это так, умножьте предположение на \(x). Повторяйте этот шаг до тех пор, пока в \(y_p(x)\) не останется членов, которые решают дополнительное уравнение.
- Подставьте \(y_p(x)\) в дифференциальное уравнение и приравняйте одинаковые члены, чтобы найти значения неизвестных коэффициентов в \(y_p(x)\).
- Сложите общее решение дополнительного уравнения и только что найденное частное решение, чтобы получить общее решение неоднородного уравнения.

Пример \(\PageIndex{3}\): Решение неоднородных уравнений
Найдите общие решения следующих дифференциальных уравнений.
9229{−3x}\)(шаг 1). Основываясь на форме \(r(x)=−6 \cos 3x,\), наше начальное предположение для конкретного решения: \(y_p(x)=A \cos 3x+B \sin 3x\) (шаг 2) . Ни одно из условий в \(y_p(x)\) не решает дополнительное уравнение, так что это правильное предположение (шаг 3).Теперь мы хотим найти значения для \(A\) и \(B,\), поэтому подставим \(y_p\) в дифференциальное уравнение. У нас есть
\[y_p′(x)=−3A \sin 3x+3B \cos 3x \text{ и } y_p″(x)=−9A \cos 3x−9B \sin 3x, \nonumber \]
поэтому мы хотим найти значения \(A\) и \(B\) такие, что 92+Bt\) (шаг 3). Проверяя это новое предположение, мы видим, что ни одно из условий в \(y_p(t)\) не решает дополнительное уравнение, поэтому это верное предположение (снова шаг 3). Теперь нам нужно найти значения для \(A\) и \(B,\), поэтому мы подставляем \(y_p\) в дифференциальное уравнение. У нас есть \(y_p′(t)=2At+B\) и \(y_p″(t)=2A\), поэтому мы хотим найти такие значения AA и BB, что
У нас есть \(y_p′(t)=2At+B\) и \(y_p″(t)=2A\), поэтому мы хотим найти такие значения AA и BB, что\[\begin{align*}y″−3y′ &=−12t \\[4pt] 2A−3(2At+B) &=−12t \\[4pt] −6At+(2A−3B) &=− 12т. \конец{выравнивание*}\]
Следовательно, 9{2t}−5 \cos 2t+ \sin 2t\)Изменение параметров
Иногда \(r(x)\) не является комбинацией полиномов, экспонент или синусов и косинусов. В этом случае метод неопределенных коэффициентов не работает, и приходится использовать другой подход для нахождения частного решения дифференциального уравнения. Мы используем подход, называемый методом вариации параметров .
Чтобы немного упростить наши расчеты, мы разделим дифференциальное уравнение на \(a,\), чтобы получить старший коэффициент, равный 1. Тогда дифференциальное уравнение будет иметь вид
\[y″+py′+qy=r(x), \nonumber \]
где \(p\) и \(q\) — константы.
Если общее решение дополнительного уравнения имеет вид \(c_1y_1(x)+c_2y_2(x)\), мы будем искать частное решение вида
\[y_p(x)=u( х)у_1(х)+v(х)у_2(х).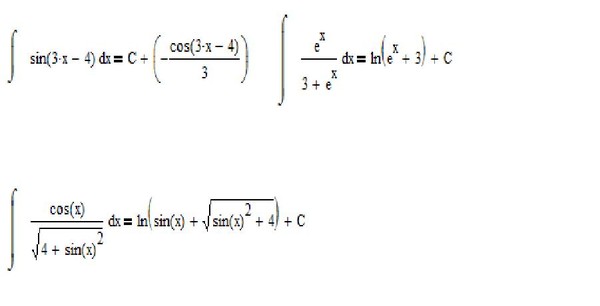 \nonumber \]
\nonumber \]
В этом случае мы используем два линейно независимых решения дополнительного уравнения для формирования нашего частного решения. Однако мы предполагаем, что коэффициенты являются функциями \(x\), а не константами. Мы хотим найти функции \(u(x)\) и \(v(x)\) такие, что \(y_p(x)\) удовлетворяет дифференциальному уравнению. У нас есть
\[\begin{align*}y_p &=uy_1+vy_2 \\[4pt] y_p′ &=u′y_1+uy_1′+v′y_2+vy_2′ \\[4pt] y_p″ &=(u′ y_1+v′y_2)′+u′y_1′+uy_1″+v′y_2′+vy_2″. \end{align*}\]
Подставляя в дифференциальное уравнение, получаем
\[\begin{align*}y_p″+py_p′+qy_p &=[(u′y_1+v′y_2)′+u ′y_1′+uy_1″+v′y_2′+vy_2″] \\ &\;\;\;\;+p[u′y_1+uy_1′+v′y_2+vy_2′]+q[uy_1+vy_2] \\[4pt] &=u[y_1″+p_y1′+qy_1]+v[y_2″+py_2′+qy_2] \\ &\;\;\;\; +(u′y_1+v′y_2)′+p(u′y_1+v′y_2)+(u′y_1′+v′y_2′). \end{выравнивание*}\]
Обратите внимание, что \(y_1\) и \(y_2\) являются решениями дополнительного уравнения, поэтому первые два члена равны нулю. Таким образом, имеем
\[(u′y_1+v′y_2)′+p(u′y_1+v′y_2)+(u′y_1′+v′y_2′)=r(x).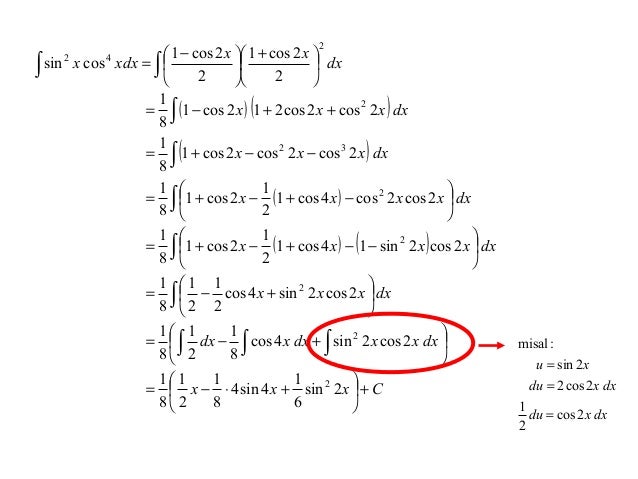 \nonumber \]
\nonumber \]
Если мы упростим это уравнение, наложив дополнительное условие \(u′y_1+v′y_2=0\), первые два члена равны нулю, и это сводится к \(u′y_1′+v′ y_2′=r(x)\). Итак, с этим дополнительным условием мы имеем систему двух уравнений с двумя неизвестными:
\[\begin{align*} u′y_1+v′y_2 &= 0 \\[4pt] u′y_1′+v′ у_2′ &=г(х). \end{выравнивание*}\]
Решение этой системы дает нам \(u′\) и \(v′\), которые мы можем интегрировать, чтобы найти \(u\) и \(v\).
Тогда \(y_p(x)=u(x)y_1(x)+v(x)y_2(x)\) является частным решением дифференциального уравнения. Решение этой системы уравнений иногда бывает сложной задачей, поэтому давайте воспользуемся этой возможностью, чтобы рассмотреть правило Крамера, которое позволяет нам решать систему уравнений с помощью определителей.
ПРАВИЛО: ПРАВИЛО КРАМЕРА
Система уравнений
\[\begin{align*} a_1z_1+b_1z_2 &=r_1 \\[4pt] a_2z_1+b_2z_2 &=r_2 \end{align*}\]
имеет единственное решение тогда и только тогда, когда определитель коэффициентов отличен от нуля. В этом случае решение имеет вид
В этом случае решение имеет вид
\[z_1=\dfrac{\begin{array}{|ll|}r_1 b_1 \\ r_2 b_2 \end{array}}{\begin{array}{|ll| }a_1 b_1 \\ a_2 b_2 \end{массив}} \; \; \; \; \; \текст{и} \; \; \; \; \; z_2 = \dfrac{\begin{array}{|ll|}a_1 r_1 \\ a_2 r_2 \end{array}}{\begin{array}{|ll|}a_1 b_1 \\ a_2 b_2 \end{array}} . \label{cramer} \]
Пример \(\PageIndex{4}\): использование правила Крамера 92}\),\( z_2=\frac{2x+2}{11x}\)
СТРАТЕГИЯ РЕШЕНИЯ ЗАДАЧИ: МЕТОД ВАРИАЦИИ ПАРАМЕТРОВ
- Решите дополнительное уравнение и запишите общее решение \[c_1y_1(x)+c_2y_2(x). \номер\]
- Используйте правило Крамера или другой подходящий метод, чтобы найти функции \(u′(x)\) и \(v′(x)\), удовлетворяющие \[\begin{align*} u′y_1+v′y_2 &=0 \ \[4pt] u′y_1′+v′y_2′ &=r(x). \конец{выравнивание*}\]
- Интегрируйте \(u′\) и \(v′\), чтобы найти \(u(x)\) и \(v(x)\). Тогда \(y_p(x)=u(x)y_1(x)+v(x)y_2(x)\) является частным решением уравнения.
 3 x \номер\] 9т \лн|т| \)
3 x \номер\] 9т \лн|т| \)Ключевые понятия
- Чтобы решить неоднородное линейное дифференциальное уравнение второго порядка, сначала найдите общее решение дополнительного уравнения, а затем найдите частное решение неоднородного уравнения.
- Пусть \(y_p(x)\) — любое частное решение неоднородного линейного дифференциального уравнения \[a_2(x)y»+a_1(x)y’+a_0(x)y=r(x), \nonumber \] и пусть \(c_1y_1(x)+c_2y_2(x)\) обозначает общее решение дополнительного уравнения. Тогда общее решение неоднородного уравнения определяется выражением \[y(x)=c_1y_1(x)+c_2y_2(x)+y_p(x). \номер\]
- Если \(r(x)\) является комбинацией многочленов, показательных функций, синусов и косинусов, используйте метод неопределенных коэффициентов, чтобы найти конкретное решение. Чтобы использовать этот метод, примите решение в той же форме, что и \(r(x)\), при необходимости умножая на x , пока предполагаемое решение не станет линейно независимым от общего решения дополнительного уравнения.
 Затем подставьте предполагаемое решение в дифференциальное уравнение, чтобы найти значения для коэффициентов.
Затем подставьте предполагаемое решение в дифференциальное уравнение, чтобы найти значения для коэффициентов. - Когда \(r(x)\) является , а не комбинацией многочленов, экспоненциальных функций или синусов и косинусов, используйте метод вариации параметров, чтобы найти конкретное решение. Этот метод включает использование правила Крамера или другого подходящего метода для поиска функций и \(v′(x)\), удовлетворяющих \[\begin{align*}u′y_1+v′y_2 &=0 \\[4pt] u′y_1 ′+v′y_2′ &=r(x). \end{align*}\] Тогда \(y_p(x)=u(x)y_1(x)+v(x)y_2(x)\) является частным решением дифференциального уравнения.
Ключевые уравнения
- Дополнительное уравнение
\(a_2(x)y″+a_1(x)y′+a_0(x)y=0\) - Общее решение неоднородного линейного дифференциального уравнения
\(y(x)=c_1y_1(x)+c_2y_2(x)+y_p(x)\)
Глоссарий
- дополнительное уравнение
- для неоднородного линейного дифференциального уравнения \(a+2(x)y″+a_1(x)y′+a_0(x)y=r(x),\) ассоциированное однородное уравнение, называемое дополнительным уравнением , это \(a_2(x)y»+a_1(x)y’+a_0(x)y=0\)
- метод неопределенных коэффициентов
- метод, который включает в себя предположение о форме конкретного решения, а затем вычисление коэффициентов в предположении
- метод варьирования параметров
- метод, заключающийся в поиске частных решений в виде \(y_p(x)=u(x)y_1(x)+v(x)y_2(x)\), где \(y_1\) и \(y_2\ ) являются линейно независимыми решениями дополнительных уравнений, а затем решают систему уравнений, чтобы найти \(u(x)\) и \(v(x)\) г.

- частный раствор
- решение \(y_p(x)\) дифференциального уравнения, которое не содержит произвольных констант
Эта страница под названием 17.2: Неоднородные линейные уравнения распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Странгом и Эдвином «Джедом» Херманом (OpenStax) через исходный контент, который был отредактирован. к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- ОпенСтакс
- Лицензия
- CC BY-NC-SA
- 9Версия лицензии 1954 г.
- 4,0

- Программа ООР или издатель
- ОпенСтакс
- Показать страницу Оглавление
- нет
- Теги
- автор @ Эдвин «Джед» Герман
- автор@Гилберт Странг
- дополнительное уравнение
- Правило Крамера
- метод неопределенных коэффициентов
- метод изменения параметров
- частный раствор
- источник@https://openstax.org/details/books/calculus-volume-1
Решения Balbharati для математики и статистики 2 (Искусство и наука) 12-й стандарт HSC Maharashtra State Board, глава 3 — Бессрочная интеграция [Последнее издание] 92x)dx`
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.
 1 | Вопрос 2.06 | Страница 102
1 | Вопрос 2.06 | Страница 102Вычислите следующие интегралы: `int sinx/(1 + sinx)dx`
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.1 | Вопрос 2.07 | Страница 102
Вычислите следующие интегралы: `int tanx/(sec x + tan x)dx`
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.1 | Вопрос 2.08 | Страница 102
Вычислите следующие интегралы: `int sqrt(1 + sin 2x) dx`
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.1 | Вопрос 2.09| Страница 102
Вычислите следующие интегралы: `intsqrt(1 — cos 2x)dx`
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.1 | Вопрос 2.1 | Страница 102
Вычислите следующие интегралы: `int sin 4x cos 3x dx`
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.1 | Вопрос 3.01 | Страница 102
Вычислите следующие интегралы: `int x/(x + 2).dx`
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.1 | Вопрос 3.02 | Страница 102
Вычислите следующие интегралы: `int(4x + 3)/(2x + 1).dx`
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.
 1 | Вопрос 3.03 | Страница 102
1 | Вопрос 3.03 | Страница 102Вычислить следующие интегралы: `int(5x + 2)/(3x — 4).dx`
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.1 | Вопрос 3.04 | Страница 102
Вычислить следующие интегралы: `int(x — 2)/sqrt(x + 5).dx`
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.1 | Вопрос 3.05 | Страница 102
Вычислите следующие интегралы: `int (2x — 7)/sqrt(4x — 1).dx`
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.1 | Вопрос 3.06 | Страница 102 9-11)`
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.2 (A) | Вопрос 1.11 | Страница 110
Интегрируйте следующие функции по отношению к x : x 9 .sec 2 (x 10 )
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.2 (A) | Вопрос 1.12 | Страница 110
Интегрируйте следующие функции по отношению к x : e 3logx (x 4 + 1) –1
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.2 (A) | Вопрос 1.13 | Страница 110
Интегрируйте следующие функции по отношению к x : `sqrt(tanx)/(sinx.
 cosx)` 93 — 1)`
cosx)` 93 — 1)`ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.2 (A) | Вопрос 1.25 | Страница 110
Интегрируйте следующие функции по отношению к x : `(1)/(x.logx.log(logx)`.
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.2 (A) | Q 2.01 | Страница 110
Интегрируем следующие функции относительно x : `(cos3x — cos4x) /(sin3x + sin4x)`
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.2 (A) | Q 2.02 | Страница 110
Интегрируем следующие функции относительно x : `cosx/sin(x — a)`
ПРОСМОТР РЕШЕНИЯ 9(2x) — 5)`
ПРОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.2 (A) | Вопрос 2.1 | Страница 110
Интегрируйте следующие функции по отношению к x : cos 8 xcotx
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.2 (A) | Вопрос 2.11 | Страница 110
Интегрируйте следующие функции по отношению к x : tan 5 x
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.2 (A) | Вопрос 2.12 | Страница 110
Интегрируйте следующие функции по отношению к x : cos 7 x
ПОСМОТРЕТЬ РЕШЕНИЕ 92 — 5).
 dx`
dx`ПОКАЗАТЬ РЕШЕНИЕ
Упражнение 3.2 (B) | Вопрос 1.07 |
Вычислите следующее: `int sqrt((9 + x)/(9 — x)).dx`
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.2 (B) | Вопрос 1.08 |
Вычислите следующее: `int sqrt((2 + x)/(2 — x)).dx`
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.2 (B) | Вопрос 1.09 |
Вычислите следующее: `int sqrt((10 + x)/(10 — x)).dx`
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.2 (B) | Вопрос 1.1 | Страница 123 92x).dx`
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.2 (B) | Вопрос 1.2 |
Вычислите следующее: `int sinx/(sin 3x).dx`
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.2 (B) | Вопрос 2.1 | Страница 123
Интегрируйте следующие функции по отношению к x : `int (1)/(3 + 2sinx).dx`
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.2 (B) | Вопрос 2.2 | Страница 123
Интегрируйте следующие функции по отношению к x : `int (1)/(4 — 5cosx).dx`
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.2 (B) | Вопрос 2.
 3 | Страница 123
3 | Страница 123Интегрировать следующие функции с.р.т. x : `int (1)/(2 + cosx — sinx).dx`
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.2 (B) | Вопрос 2.4 | Страница 123
Интегрируйте следующие функции по отношению к x : `int (1)/(3 + 2sin x — cosx)dx`
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.2 (B) | Вопрос 2.5 | Страница 123
Интегрируйте следующие функции по отношению к x : `int (1)/(3 — 2cos 2x).dx`
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.2 (B) | Вопрос 2.6 | Страница 123
Интегрируйте следующие функции по отношению к x : `int (1)/(2sin 2x — 3)dx`
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.2 (B) | Вопрос 2.7 | Страница 123
Интегрируйте следующие функции по отношению к x : `int (1)/(3 + 2 sin2x + 4cos 2x).dx`
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.2 (B) | Вопрос 2.8 | Страница 123
Интегрируйте следующие функции по отношению к x : `int (1)/(cosx — sinx).dx`
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.
 (2x).sin3x` 92x)`
(2x).sin3x` 92x)`ПРОСМОТР РЕШЕНИЯ
Упражнение 3.4 | Вопрос 1.18 | Страница 145
Интегрируйте следующее w.r.t. x : `(1)/(sinx + sin2x)`
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.4 | Вопрос 1.19 | Страница 145
Интегрируйте следующее w.r.t. x : `(1)/(2sinx + sin2x)`
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.4 | Вопрос 1.2 | Страница 145
Интегрируйте следующее w.r.t. x : `(1)/(sin2x + cosx)`
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.4 | Вопрос 1.21 | Страница 145 95)*dx` =
ПОСМОТРЕТЬ РЕШЕНИЕ
Разное Упражнение 3 | Вопрос 1.03 |
Выберите правильные варианты из предложенных:
`int (log (3x))/(xlog (9x))*dx` =
log (3x) – log (9x) + c·
log (x) – (log 3) · log (log 9x) + c
log 9 – (log x) · log (log 3x) + c
log (x) + (журнал 3) · журнал (лог 9x) + c
ПОСМОТРЕТЬ РЕШЕНИЕ 92) + c`
`x cot (x/2) + c`
`- x детская кроватка (x/2) + c`
`кроватка (x/2) + c`
`x коричневый (x/2) + c`
`x/(2)[sin (log x) — cos (log x) ] + c`
`x/(2)[sin (log x) + cos (log x)] + c`
`x/(2)[cos (log x) — sin (log x) x)] + c`
`x/(4)[cos (log x) — sin (log x)] + c`
92*dx` =`x/(1 + log x) + c`
x(1 + log x) + c
`x/(1 + log x) + c`
`x/(1 — log x) + c`
x cos (log x) + c
sin (log x) + c
cos (log x) + c
x sin (log x) + c
tan x – x + c
+x
2
загар x + c
x – загар x + c
– x – кроватка x + c
ПОСМОТРЕТЬ РЕШЕНИЕ
Разное Упражнение 3 | Вопрос 2.7 | Страница 150
Проинтегрируйте следующее по соответствующей переменной: cos 3x cos 2x cos x
ПОСМОТРЕТЬ РЕШЕНИЕ
Разное Упражнение 3 | Вопрос 2.

ПРОСМОТРЕТЬ РЕШЕНИЕ
Разное Упражнение 3 | Вопрос 1. 06 | Страница 148
06 | Страница 148
Выберите правильные варианты из предложенных:
`int (x-sinx)/(1 — cosx)*dx` =
ПРОСМОТР РЕШЕНИЯ
Разное Упражнение 3 | Вопрос 1.07 | Страница 148 9-x + c`
ПРОСМОТР РЕШЕНИЯ
Разное Упражнение 3 | Вопрос 1.12 |
Выберите правильные варианты из предложенных:
`int sin (log x)*dx` =
ПРОСМОТР РЕШЕНИЯ
Разное Упражнение 3 | Вопрос 1. 18 | Страница 150
18 | Страница 150
Выберите правильные варианты из предложенных:
`int [sin (log x) + cos (log x)]*dx` =
ПРОСМОТР РЕШЕНИЯ
Разное Упражнение 3 | Вопрос 1.19 | Страница 150
Выберите правильные варианты из предложенных:
`int (cos2x — 1)/(cos2x + 1)*dx` =

 04.17
04.17

 3 x \номер\] 9т \лн|т| \)
3 x \номер\] 9т \лн|т| \) Затем подставьте предполагаемое решение в дифференциальное уравнение, чтобы найти значения для коэффициентов.
Затем подставьте предполагаемое решение в дифференциальное уравнение, чтобы найти значения для коэффициентов.

 1 | Вопрос 2.06 | Страница 102
1 | Вопрос 2.06 | Страница 102 1 | Вопрос 3.03 | Страница 102
1 | Вопрос 3.03 | Страница 102 cosx)` 93 — 1)`
cosx)` 93 — 1)` dx`
dx` 3 | Страница 123
3 | Страница 123 (2x).sin3x` 92x)`
(2x).sin3x` 92x)`