| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град.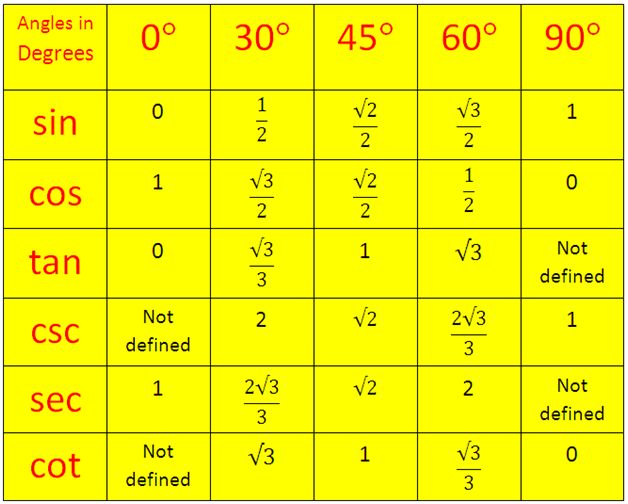 ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.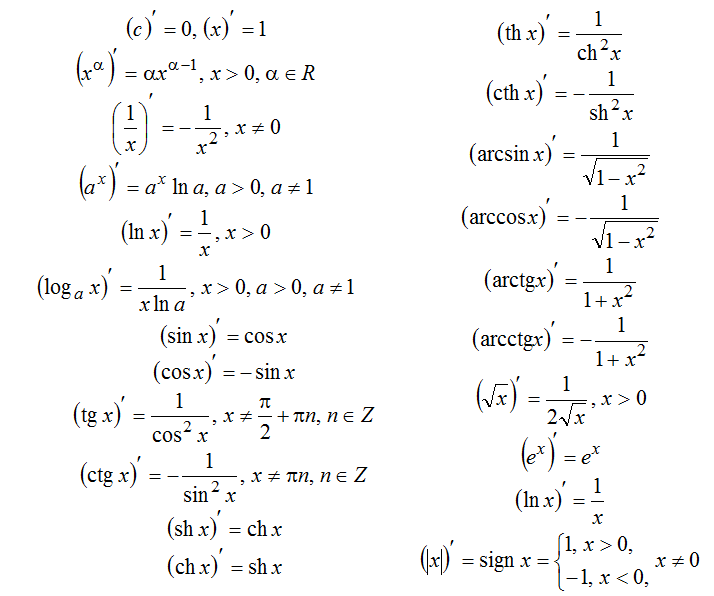 ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | cos(150 град. ) | ||
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.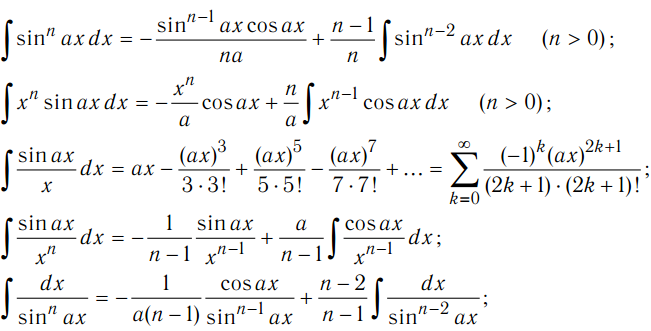 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град.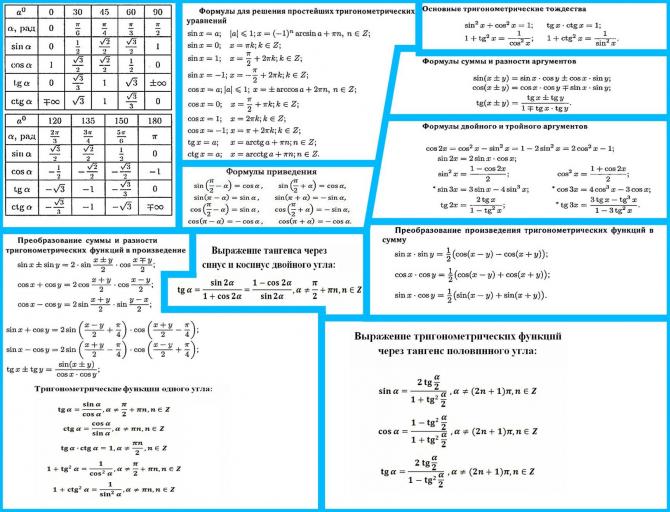 ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Решение простейших тригонометрических уравнений. Уравнения sin t = a — АЛГЕБРА — Уроки для 10 классов — конспекты уроков — План урока — Конспект урока — Планы уроков
УРОК 21
Тема.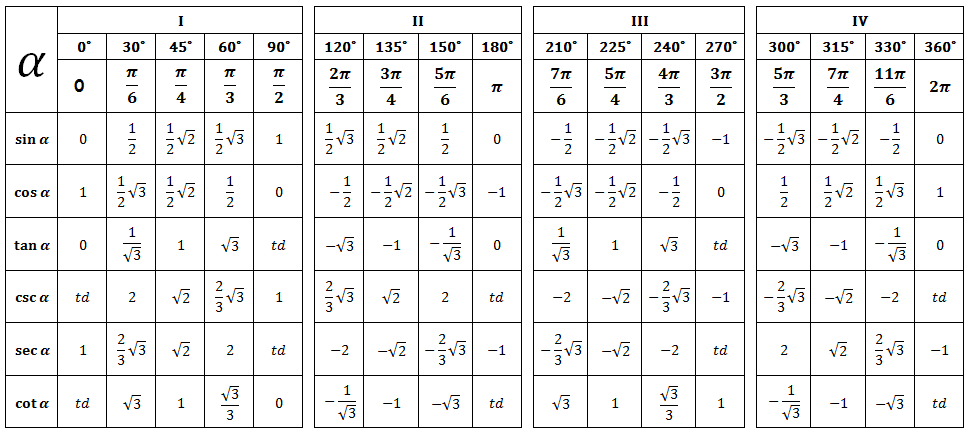 Решение простейших тригонометрических уравнений. Уравнения sin t = а
Решение простейших тригонометрических уравнений. Уравнения sin t = а
Цель урока: усвоение учащимися вывода и применения формул для корней уравнения sin t = а.
Оборудование: Таблица «Уравнения sin t = а».
И. Проверка домашнего задания
1. Ответы на вопросы, возникшие при выполнении домашних заданий.
2. Самостоятельная работа.
Вариант 1
Решите уравнение:
а) 2cos = . (3 балла)
б) 2cos2x + cos x — 1 = 0. (3 балла)
в) 4cos x = 4 — sin x. (3 балла)
г) sin 3x sin x — cos 3x cos x = . (3 балла)
Вариант 2
Решите уравнение :
а) 2 cos = . (3 балла)
б) 2cos2x — cosx — 1 = 0. (3 балла)
в) 8 sin2х + cosx + 1 = 0. (3 балла)
г) sin2 — cos2 = 1. (3 балла)
Ответ:
B-1. a)±+4πn, nZ; б) ±+2πn и π+2πn, nZ; в)2πn, nZ; г) ±+πn,nZ.
В-2. a) ±+, nZ; б) 2πn и ±+2πn, nZ; в) n+2πn, nZ; г) 4πn, nZ.
a) ±+, nZ; б) 2πn и ±+2πn, nZ; в) n+2πn, nZ; г) 4πn, nZ.
II. Сообщение темы урока
III. Восприятия и осознания материала о решения уравнения sin t = a
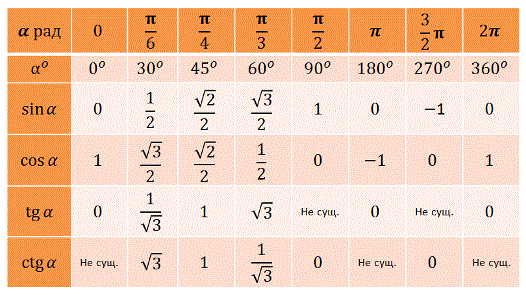
Демонстрируется таблица 9.
Объяснение учителя
1) Если |а| > 1, то уравнение не имеет решений, поскольку |sin x| 1 для любого t.
2) Если |а| 1, то, учитывая, что sin t — ордината точки Рt единичного круга, имеем: ординату, равную а, имеют две точки единичного круга (на оси OY откладываем число а и через эту точку проведем прямую, перпендикулярную оси ординат (рис. 123), которая пересечет окружность в двух токах — и ):
t1 = arcsin a + 2πn, nZ,
t2 = n — arcsin а + 2πn, nZ.
Эти две формулы можно записать в виде одной формулы:
t = (-1)k arcsin a + nk, kZ (1)
Нетрудно убедиться, что при парном k = 2π имеем:
t1 = (-1)2n arcsin а + 2πn или t1 = arcsin a + 2πn, nZ;
при нечетном k = 2n + 1 имеем:
t2 = (-1)2n+1 arcsin а + (2n + 1)n;
t2 = — arcsin а + 2πn + n;
t2 = n — arcsin a + 2πn, nZ.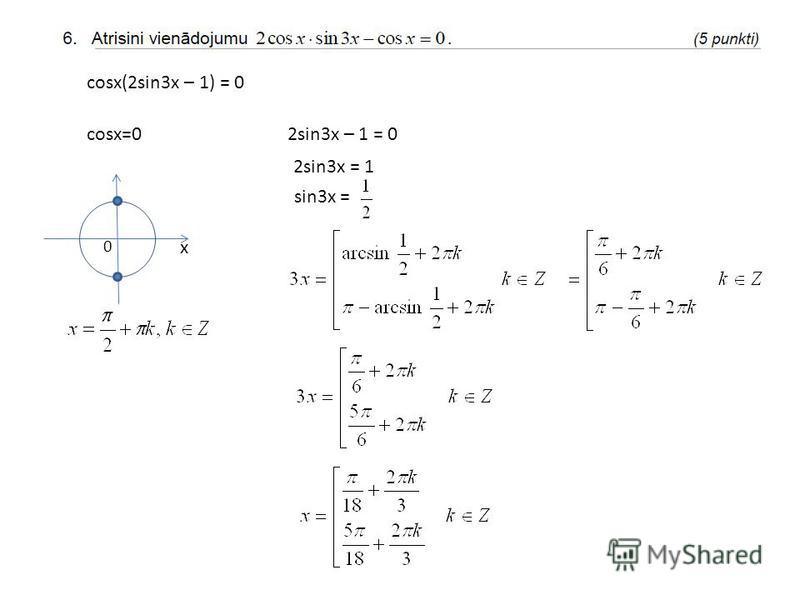
3) Если а = 1, то, учитывая то, что sint — это ордината точки Pt (единичного круга, имеем: ординату, равную 1, точка Рt образована из точки Р0(1;0) поворотом на угол + 2πn, nZ.
Следовательно, t = + 2πn, nZ. Если а = -1, то t = — + 2πn, nZ.
4) Если а = 0, имеем t = 0 + πn; t = πn, nZ.
Рассмотрим примеры.
Пример 1. Решите уравнение sinx = .
Решение
Согласно формуле (1) имеем: х = (-1)n arcsin + πn, nZ.
Поскольку arcsin = , то х = (-1)n + πn, nZ.
Ответ: (-1)n + πn, nZ.
Пример 2. Решите уравнение sin х = — .
Решение
Согласно формуле (1) имеем: х = (-1)n arcsin + πn, nZ.
Поскольку arcsin = — , то х =(-1)n ·+ πn, nZ; х = (-1)n+1 + πn, nZ.
Ответ: (-1)n+1 + πn, nZ.
Пример 3. Решите уравнение sin x = — 1.
Решение
Согласно формуле (1) имеем: х = (-1)n arcsin(- 1) + πn, nZ.
Значение arcsin(-1) найдем с помощью микрокалькулятора:
arcsin(- 1) 0,427, тогда х (-1)n · 0,427 + πn, nZ.
Ответ: (-1)n · arcsin(-1) + πn (-1)n · 0,427 + πn, nZ.
IV. Осмысление изученного материала
Комментируемое выполнения упражнений
Решите уравнение.
1. a) 2sin x — 1 = 0; б) 2sin = — 1; в) 2sin = — ; г) 2sin = .
Ответ: а) (-1)n + πn, nZ; б) (-1)n+1+ 2πn, nZ; в) +(-1) n+1+, nZ; г) +(-1)n+1 + 4πn, nZ.
2. a) sin 3x cos x — cos 3x sin х = ;
б) sin 2x cos 2x = — ;
в) sin cos — cossin= ;
г) cos 2x sin 3x + sin 2x cos 3x = 1.
Ответ: а) (-1)n + , nZ; б) (-1)n+1 + , nZ; в) (-1)n+3 πn, nZ; г) +, nZ.
3. а) (2sin x — 1)(3sin x + 1) = 0; б) (4sin 3х — 1)(2sin х + 3) = 0.
Ответ: а) (-1)n+ πn и (-1)n+1arcsin + πn, nZ; б) (-1)n +, nZ.
Таблица 9
V.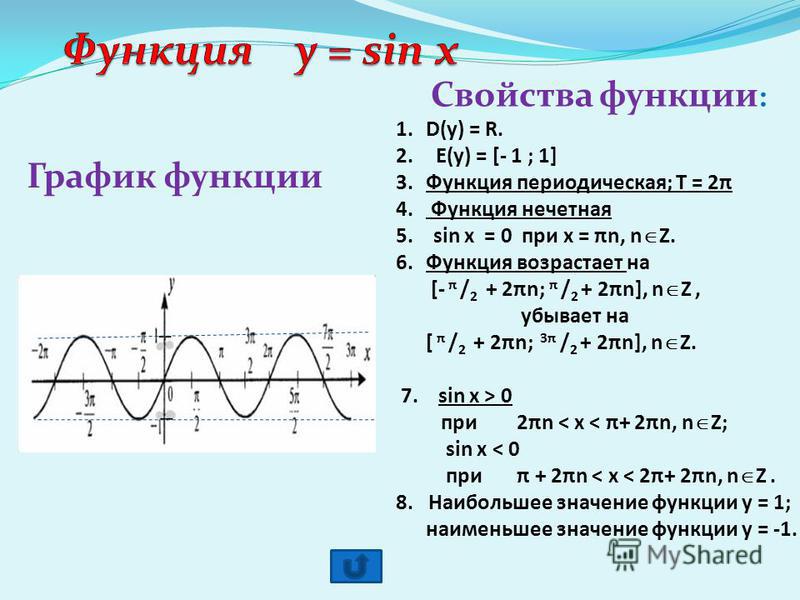 Подведение итогов урока
Подведение итогов урока
VI. Домашнее задание
Раздел II § 2 (1). Вопросы и задания для повторения раздела II № 13-15. Упражнения№ 1 (6; 7; 8; 14; 17; 18), № 2 (3).
| Назад | Содержание | Вперед |
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт.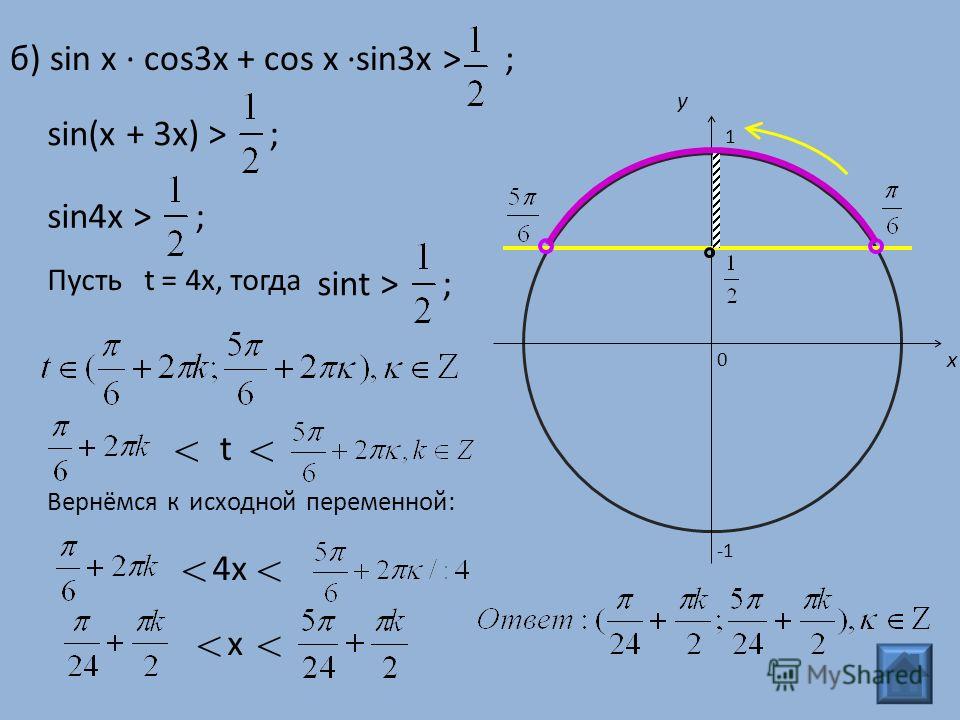 )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Синусоидальная функция — исчисление
Эта статья о конкретной функции от подмножества действительных чисел до действительных чисел.В статье представлена информация о функции, включая ее домен, диапазон и ключевые данные, относящиеся к построению графиков, дифференцированию и интегрированию.
Посмотреть полный список конкретных функций на этой вики
Для функций, включающих углы (тригонометрические функции, обратные тригонометрические функции и т. д.), мы следуем соглашению, согласно которому все углы измеряются в радианах. Так, например, угол измеряется как .
Содержание
- 1 Определение
- 2 Ключевые данные
- 3 личности
- 4 График
- 5 Дифференциация
- 5.1 Первая производная
- 6 Интеграция
- 6.1 Первая первообразная: стандартный метод
- 6.2 Первая первообразная: использование формулы тройного угла
- 6.3 Повторная антидифференцировка
- 7 Серия Power и серия Taylor
- 7.1 Расчет степенного ряда
Определение
Эта функция, обозначенная , определяется как композиция функции куба и функции синуса. В явном виде это карта:
В явном виде это карта:
Для краткости мы пишем или .
Ключевые данные
| Товар | Значение |
|---|---|
| Домен по умолчанию | все действительные числа, т. е. все |
| диапазон | закрытый интервал, т. е. абсолютное максимальное значение: 1, абсолютное минимальное значение: -1 |
| период | , т. е. |
| локальные максимальные значения и точки достижения | Все локальные максимальные значения равны 1, и они достигаются во всех точках формы, где изменяется над целыми числами. |
| локальные минимальные значения и точки достижения | Все локальные минимальные значения равны -1, и они достигаются во всех точках формы, где изменяется над целыми числами. |
| точек перегиба (обе координаты) | Все точки вида , а также точки вида где где варьируется в целых числах. |
| производная | |
| вторая производная | |
| первообразная | |
| важные симметрии | нечетная функция (следует из того, что композиция нечетных функций является нечетной, и тот факт, что функция куба и функция синуса нечетны) полуоборотная симметрия относительно всех точек формы зеркальная симметрия относительно всех прямых.  |
Тождества
У нас есть тождество:
График
Вот базовый график, построенный на интервале:
Вот более крупный план, построенный на интервале . Толстые черные точки соответствуют локальным экстремальным значениям, а толстые красные точки соответствуют точкам перегиба.
Дифференциация
Первая производная
Чтобы дифференцировать один раз, мы используем цепное правило дифференцирования. В явном виде мы рассматриваем функцию как составную часть функции куба и функции синуса, поэтому функция куба является внешней функцией , а функция синуса является внутренней функцией .
Получаем:
[ПОКАЗАТЬ БОЛЬШЕ]
Интегрирование
Первая первообразная: стандартный метод
Перепишем и затем проинтегрируем по u-подстановке где . Явно:
Теперь поставьте . У нас есть , поэтому мы можем заменить на , и мы получим:
Путем полиномиального интегрирования получаем:
Подключаем обратно, получаем:
.

 В статье представлена информация о функции, включая ее домен, диапазон и ключевые данные, относящиеся к построению графиков, дифференцированию и интегрированию.
В статье представлена информация о функции, включая ее домен, диапазон и ключевые данные, относящиеся к построению графиков, дифференцированию и интегрированию.