| 1 | Найти точное значение | sin(30) | ||
| 2 | Найти точное значение | sin(45) | ||
| 3 | Найти точное значение | sin(30 град. ) | ||
| 4 | Найти точное значение | sin(60 град. ) | ||
| 5 | Найти точное значение | tan(30 град. ) | ||
| 6 | Найти точное значение | arcsin(-1) | ||
| 7 | Найти точное значение | sin(pi/6) | ||
| 8 | cos(pi/4) | |||
| 9 | Найти точное значение | sin(45 град. ) ) | ||
| 10 | Найти точное значение | sin(pi/3) | ||
| 11 | Найти точное значение | arctan(-1) | ||
| 12 | Найти точное значение | cos(45 град. ) | ||
| 13 | Найти точное значение | cos(30 град. ) | ||
| 14 | Найти точное значение | tan(60) | ||
| 15 | Найти точное значение | csc(45 град. ) | ||
| 16 | Найти точное значение | tan(60 град. ) | ||
| 17 | Найти точное значение | sec(30 град. ) ) | ||
| 18 | Найти точное значение | cos(60 град. ) | ||
| 19 | Найти точное значение | cos(150) | ||
| 20 | Найти точное значение | sin(60) | ||
| 21 | Найти точное значение | cos(pi/2) | ||
| 22 | Найти точное значение | tan(45 град. ) | ||
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | ||
| 24 | Найти точное значение | csc(60 град. ) | ||
| 25 | Найти точное значение | sec(45 град. ) ) | ||
| 26 | Найти точное значение | csc(30 град. ) | ||
| 27 | Найти точное значение | sin(0) | ||
| 28 | Найти точное значение | sin(120) | ||
| 29 | Найти точное значение | cos(90) | ||
| 30 | Преобразовать из радианов в градусы | pi/3 | ||
| 31 | Найти точное значение | tan(30) | ||
| 32 | Преобразовать из градусов в радианы | 45 | ||
| 33 | Найти точное значение | cos(45) | ||
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | ||
| 35 | Преобразовать из радианов в градусы | pi/6 | ||
| 36 | Найти точное значение | cot(30 град. ) ) | ||
| 37 | Найти точное значение | arccos(-1) | ||
| 38 | Найти точное значение | arctan(0) | ||
| 39 | Найти точное значение | cot(60 град. ) | ||
| 40 | Преобразовать из градусов в радианы | 30 | ||
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | ||
| 42 | Найти точное значение | sin((5pi)/3) | ||
| 43 | Найти точное значение | sin((3pi)/4) | ||
| 44 | Найти точное значение | tan(pi/2) | ||
| 45 | Найти точное значение | sin(300) | ||
| 46 | Найти точное значение | cos(30) | ||
| 47 | Найти точное значение | cos(60) | ||
| 48 | Найти точное значение | cos(0) | ||
| 49 | Найти точное значение | cos(135) | ||
| 50 | Найти точное значение | cos((5pi)/3) | ||
| 51 | Найти точное значение | cos(210) | ||
| 52 | Найти точное значение | sec(60 град. ) ) | ||
| 53 | Найти точное значение | sin(300 град. ) | ||
| 54 | Преобразовать из градусов в радианы | 135 | ||
| 55 | Преобразовать из градусов в радианы | 150 | ||
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | ||
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | ||
| 58 | Преобразовать из градусов в радианы | 89 град. | ||
| 59 | Преобразовать из градусов в радианы | 60 | ||
| 60 | Найти точное значение | sin(135 град.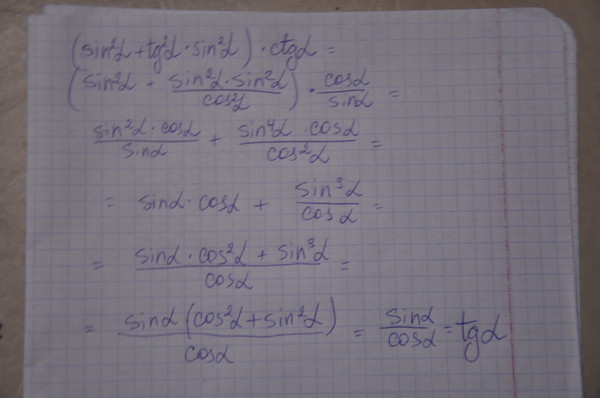 ) ) | ||
| 61 | Найти точное значение | sin(150) | ||
| 62 | Найти точное значение | sin(240 град. ) | ||
| 63 | Найти точное значение | cot(45 град. ) | ||
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | ||
| 65 | Найти точное значение | sin(225) | ||
| 66 | Найти точное значение | sin(240) | ||
| 67 | Найти точное значение | cos(150 град. ) | ||
| 68 | Найти точное значение | tan(45) | ||
| 69 | Вычислить | sin(30 град.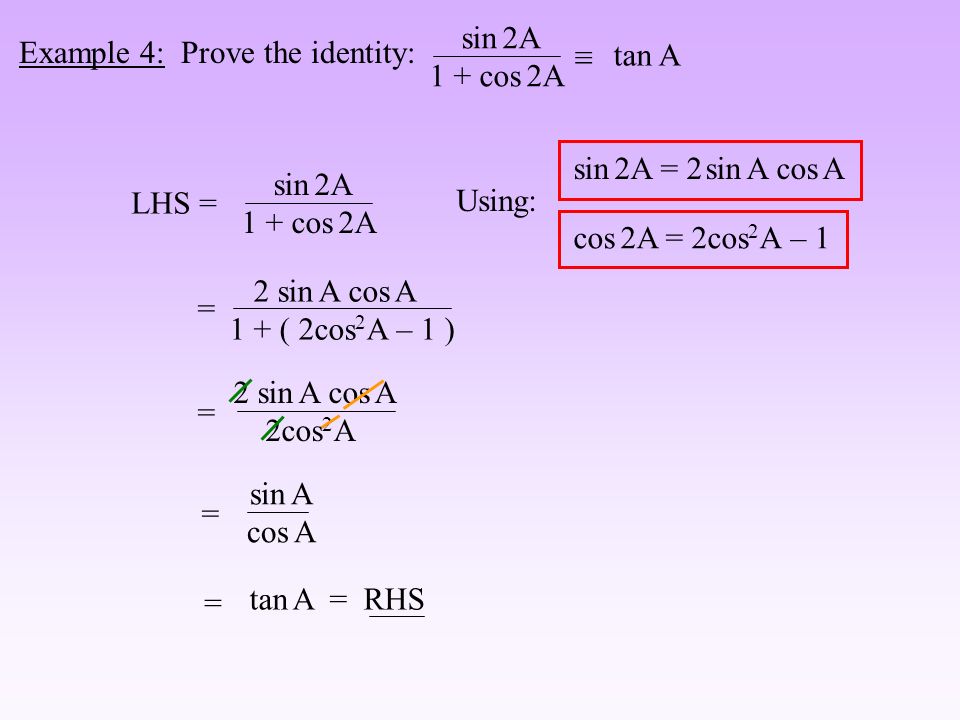 ) ) | ||
| 70 | Найти точное значение | sec(0) | ||
| 71 | Найти точное значение | cos((5pi)/6) | ||
| 72 | Найти точное значение | csc(30) | ||
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | ||
| 74 | Найти точное значение | tan((5pi)/3) | ||
| 75 | Найти точное значение | tan(0) | ||
| 76 | Вычислить | sin(60 град. ) | ||
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | ||
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | ||
| 79 | Найти точное значение | sin((7pi)/4) | ||
| 80 | Найти точное значение | arcsin(-1/2) | ||
| 81 | Найти точное значение | sin((4pi)/3) | ||
| 82 | Найти точное значение | csc(45) | ||
| 83 | Упростить | arctan( квадратный корень из 3) | ||
| 84 | Найти точное значение | sin(135) | ||
| 85 | Найти точное значение | sin(105) | ||
| 86 | Найти точное значение | sin(150 град. ) ) | ||
| 87 | Найти точное значение | sin((2pi)/3) | ||
| 88 | Найти точное значение | tan((2pi)/3) | ||
| 89 | Преобразовать из радианов в градусы | pi/4 | ||
| 90 | Найти точное значение | sin(pi/2) | ||
| 91 | Найти точное значение | sec(45) | ||
| 92 | Найти точное значение | cos((5pi)/4) | ||
| 93 | Найти точное значение | cos((7pi)/6) | ||
| 94 | Найти точное значение | |||
| 95 | Найти точное значение | sin(120 град.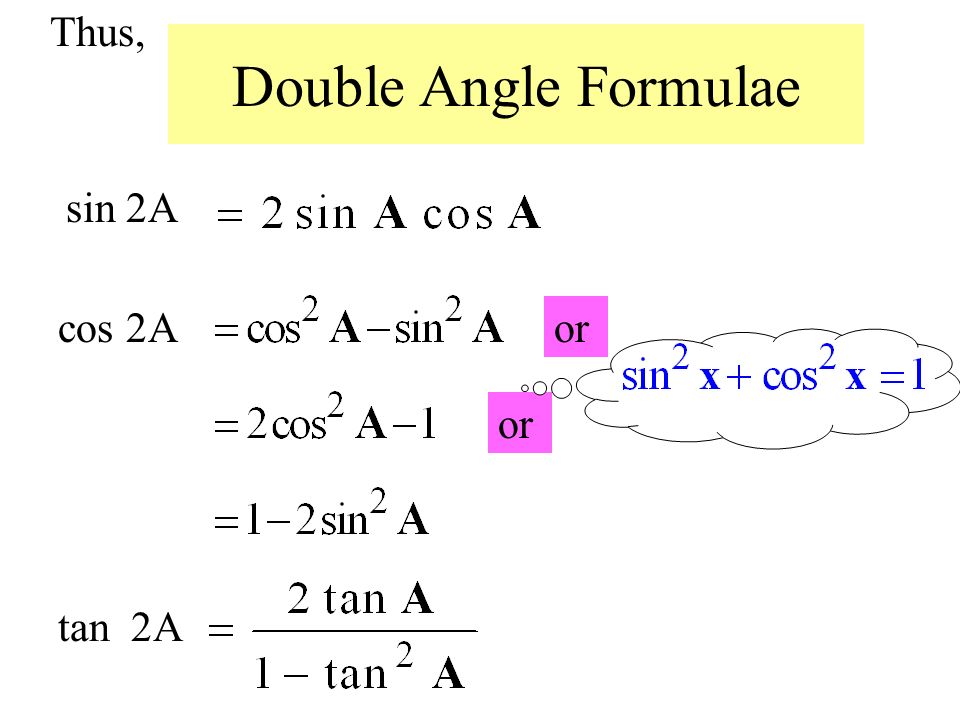 2\frac{5π}{12}-1)=\) 2\frac{5π}{12}-1)=\)
|
Вот теперь видно, что перед нами формула косинуса двойного угла. |
|
|
\(=\sqrt{3}\cos(2\cdot\frac{5π}{12})=\) |
Сокращаем \(2\) и \(12\). |
|||
|
\(=\sqrt{3}\cos(\frac{5π}{6})=\) |
Разложим \(\frac{5π}{6}\): \(\frac{5π}{6}=\frac{6π-π}{6}=\frac{6π}{6}-\frac{π}{6}=π-\frac{π}{6}\) |
|||
|
\(=\sqrt{3}\cos(π-\frac{π}{6})=\) |
Теперь применим к косинусу формулу приведения:
\(\cos(π-\frac{π}{6})=-\cos \frac{π}{6}\) |
|||
|
\(=-\sqrt{3}\cos\frac{π}{6}=-\sqrt{3}\cdot\frac{\sqrt{3}}{2}=\) |
Ответ: \(-1,5\).
Смотрите также:
Формулы тригонометрии с примерами
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Sin2x — Формула, Тождества, Примеры, Доказательство
Формула Sin2x — одна из формул двойного угла в тригонометрии.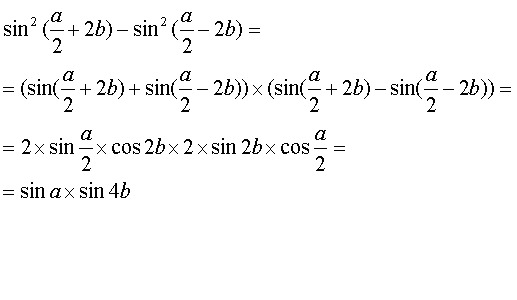 Используя эту формулу, мы можем найти синус угла, значение которого увеличивается в два раза. Мы знаем, что грех — это одно из основных тригонометрических соотношений, которое определяется как отношение длины противоположной стороны (угла) к длине гипотенузы в прямоугольном треугольнике. Существуют различные формулы, связанные с sin2x, и их можно проверить, используя основные тригонометрические формулы. Поскольку диапазон функции sin равен [-1, 1], диапазон sin2x также равен [-1, 1]. 92x с точки зрения различных тригонометрических функций с использованием разных тригонометрических формул и, следовательно, вывести формулы.
Используя эту формулу, мы можем найти синус угла, значение которого увеличивается в два раза. Мы знаем, что грех — это одно из основных тригонометрических соотношений, которое определяется как отношение длины противоположной стороны (угла) к длине гипотенузы в прямоугольном треугольнике. Существуют различные формулы, связанные с sin2x, и их можно проверить, используя основные тригонометрические формулы. Поскольку диапазон функции sin равен [-1, 1], диапазон sin2x также равен [-1, 1]. 92x с точки зрения различных тригонометрических функций с использованием разных тригонометрических формул и, следовательно, вывести формулы.
| 1. | Что такое Sin2x? |
| 2. | Sin2x Формула |
| 3. | Происхождение Sin 2x Identity |
| 4. | Формула Sin2x для загара |
| 5. | 92x Формула|
| 7. | Часто задаваемые вопросы о Sin2x Formula |
Что такое Sin2x?
Sin2x — это тригонометрическая формула в тригонометрии, которая используется для решения различных тригонометрических задач, задач интегрирования и дифференцирования. Он используется для упрощения различных тригонометрических выражений. Формула Sin2x может быть выражена в различных формах с использованием различных формул тригонометрии. Наиболее часто используемая формула sin2x представляет собой удвоенное произведение функции синуса и функции косинуса, которое математически определяется выражением sin2x = 2 sinx cosx. Мы также можем выразить sin2x через функцию тангенса.
Он используется для упрощения различных тригонометрических выражений. Формула Sin2x может быть выражена в различных формах с использованием различных формул тригонометрии. Наиболее часто используемая формула sin2x представляет собой удвоенное произведение функции синуса и функции косинуса, которое математически определяется выражением sin2x = 2 sinx cosx. Мы также можем выразить sin2x через функцию тангенса.
Формула Sin2x
Формула sin2x представляет собой тождество двойного угла, используемое для функции синуса в тригонометрии. Тригонометрия — это раздел математики, изучающий взаимосвязь между углами и сторонами прямоугольного треугольника. Есть две основные формулы для sin2x:
- sin2x = 2 sin x cos x (в терминах sin и cos)
- sin2x = (2tan x)/(1 + tan 2 x) (относительно тангенса)
Это основные формулы sin2x. Но мы можем записать эту формулу только в терминах sin x (или) cos x, используя тригонометрическое тождество sin 2 x + cos 2 x = 1. Используя это тригонометрическое тождество, мы можем записать sinx = √(1 — cos 2 x) и cosx = √(1 — sin 2 x). Отсюда формулы sin2x через cos и sin:
Используя это тригонометрическое тождество, мы можем записать sinx = √(1 — cos 2 x) и cosx = √(1 — sin 2 x). Отсюда формулы sin2x через cos и sin:
- sin2x = 2 √(1 — cos 2 x) cos x (формула sin2x через cos)
- sin2x = 2 sin x √(1 — sin 2 x) (формула sin2x через sin)
Происхождение Sin 2x Identity
Чтобы получить формулу для sin2x, можно использовать формулу суммы углов sin. Формула суммы sin: sin(A + B) = sin A cos B + sin B cos A. Рассмотрим вывод sin2x шаг за шагом:
Подставим A = B = x в формулу sin(A + B ) = sin A cos B + sin B cos A,
sin(x + x) = sin x cos x + sin x cos x
⇒ sin2x = 2 sin x cos x
Следовательно, мы получили формулу грех2х.
Формула Sin2x для загара
Формулу sin2x можно записать только в терминах функции тангенса или тангенса. Для этого начнем с формулы sin2x.
sin2x = 2 sin x cos x
Умножьте и разделите приведенное выше уравнение на cos x. Тогда
Тогда
sin2x = (2 sin x cos 2 x)/(cos x)
= 2 (sin x/cosx ) × (cos 2 x)
Мы знаем, что sin x/cos x = tan х и cos х = 1/(сек х). Итак,
sin2x = 2 tan x × (1/сек 2 x)
Используя одно из пифагорейских тригонометрических тождеств, сек 92x
Часто задаваемые вопросы о Sin2x Formula
Что такое формула Sin2x?
Формула Sin2x представляет собой формулу двойного угла функции синуса, а sin 2x = 2 sin x cos x является наиболее часто используемой формулой. Но sin2x с точки зрения тангенса равен sin 2x = 2tan(x)/(1 + tan 2 (x)).
Каков период Sin2x?
Период sin bx в общем случае равен (2π)/b. Таким образом, период sin2x равен (2π)/2 = π, что означает, что значение sin2x повторяется через каждые π радиан.
Что такое Sin2A с точки зрения Cos?
Общая формула sin2A: sin2A = 2 sin A cos A.

 Значит, знак будет минус;
Значит, знак будет минус;