Sin и cos формулы: Формулы синуса и косинуса суммы и разности аргументов — урок. Алгебра, 10 класс.

Содержание

Тригонометрия формулы

Тригономeтрия, формулы заданы основными тригонометричeскими функциями, которые состоят из тангенсов, котангенсов, синусов и косинусов. Отталкиваясь от того, что таких взаимосвязей великое множество, выходит и тригонометричeских формул тоже не мало. Для удобства формулы поделены на группы. Часть объединяет такие тригонометрические формулы, которые связанны с одинаковым углом, другая часть с кратным углом. Есть такие формулы которые помогают понижать степень и выражать любые функции через тангенс половинного угла.

Данная статья посвящена описанию основных тригономeтрических формул, которые помогут Вам решить любую задачу или основное их количество. А так же все они разбиты по группам и имеют описание.

Рассмотрим тождества которые считаются основными в тригономeтрии

Данные тождества показывают связь в sin и cos, tg и ctg одного угла, из их описаний и такого понятия как единичная окружность, выходят тождества.

Так же они способствуют выходу одной тригонометричeской функции через другую.

Посмотрим на формулы называющиеся приведенными

Все эти формулы содержаться в свойствах cos, sin, tg и ctg, они служат зеркальным отражением свойств периодичности данных функций, свойством симметрии и сдвига на конкретный данный угол. Благодаря формулам приведения можно работать с произвольным углом и с разными углами до 90⁰.

Рассмотрим формулы суммы.

Показанные формулы содержат тригономeтрические функции, которые с использованием сложения и вычитания выражаются в тригономeтрических функциях данных углов.
Из этих формул исходят все последующие.

Существуют еще формулы для двойных, тройных и других углов

Они также могут называться формулами квадратных углов, дают выражение двойных, тройных и далее углов через одинарный угол. Как база формулы сложения.

Формулы для половинного угла

Из чего видно выражение половинчатого угла с помощью косинуса одинарного угла или целого. Как база формула двойного угла.

Формулы для уменьшения степеней.

Формулы для уменьшения степеней должны сопутствовать тому что бы, обычные — стандартные степени тригономeтрических функций переходили в синусы и косинусы в первой степени и что важно кратных углов. Проще говоря они служат для понижения до 1 степени.

Сумма, разность и формулы тригономeтрии

Предназначаются для изменения на произведение функции, данная операция нужна для упрощения значений тригономeтрии. Благодаря им легче разбивать cos и sin на множители.

Формулы для универсальной тригонометричeской подстановки

Универсальны данные формулы тем что все функции отображаются с помощью tg половинного угла и становятся рациональными и не имея корней.

И последние формулы которые мы разберем, это произведение синуса, косинуса, синус на косинус.

Тригонометрия для чайников изложена в видео, из которого очень просто складывается видение данной науки.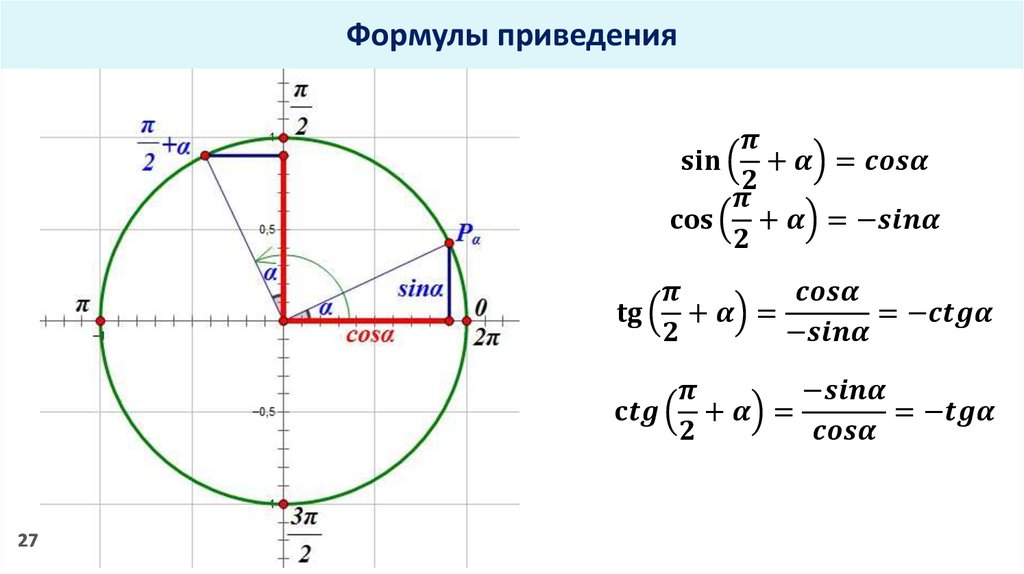

Тригонометрия, решение. Не так уж и сложно применять в решении данные тригонометрические формулы, если не просто их подставлять но еще и понять как они работают.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Тригонометрические формулы для школьников и студентов

Тригонометрические формулы — часто встречающиеся математические выражения для тригонометрических функций, которые выполняются при всех значениях аргумента.

тригонометрические функции
основные тригонометрические формулы
тригонометрические функции суммы и разности углов
тригонометрические функции двойного угла
формулы тройного угла
формулы понижения степени
формулы преобразования суммы и разности тригонометрических функций в произведение
формулы преобразования произведений функций
универсальная тригонометрическая подстановка

Тригонометрические функции

Синус

Синусом острого угла α в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.

sinα

Косинус

Косинусом острого угла α в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.

cosα

Тангенс

Тангенсом острого угла α в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему катету.

tgα=sinαcosα , α≠π2+πn , nєZ

Котангенс

Котангенсом острого угла α в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему катету.

ctgα=cosαsinα , α≠π+πn , nєZ

Секанс

Секанс — это тригонометрическая функция обратная косинусу.

secα=1cosα , α≠π2+πn , nєZ

Косеканс

Косеканс — это тригонометрическая функция обратная синусу.

cosecα=1sinα , α≠π+πn , nєZ

Основные тригонометрические формулы

sin2α+cos2α=1

tgα·ctgα=1

1+tg2α=1cos2α

1+ctg2α=1sin2α

Тригонометрические функции суммы и разности углов

Синус суммы двух углов

sinα+β=sinα·cosβ+cosα·sinβ

Синус разности двух углов

sinα-β=sinα·cosβ-cosα·sinβ

Косинус суммы двух углов

cosα+β=cosα·cosβ-sinα·sinβ

Косинус разности двух углов

cosα-β=cosα·cosβ+sinα·sinβ

Тангенс суммы двух углов

tgα+β=tgα+tgβ1–tgα·tgβ

Тангенс разности двух углов

tgα-β=tgα-tgβ1+tgα·tgβ

Котангенс суммы двух углов

ctgα+β=ctgα·ctgβ-1ctgβ+ctgα

Котангенс разности двух углов

ctgα-β=ctgα·ctgβ+1ctgβ-ctgα

Тригонометрические функции двойного угла

Синус двойного угла

sin2α=2sinα·cosα

Косинус двойного угла

cos2α=cos2α-sin2α

Тангенс двойного угла

tg2α=2tgα1-tg2α

Котангенс двойного угла

ctg2α=ctg2α-12ctgα

Формулы тройного угла

Синус тройного угла

sin3α=3sinα-4sin3α

Косинус тройного угла

cos3α=4cos3α-3cosα

Тангенс тройного угла

tg3α=3tgα-tg3α1-3tg2α

Котангенс тройного угла

ctg3α=3ctgα-ctg3α1-3ctg2α

Формулы понижения степени

sin2α=1-cos2α2

cos2α=1+cos2α2

sin3α=3sinα-sin3α4

cos3α=3cosα+cos3α4

Формулы преобразования суммы и разности тригонометрических функций в произведение

sinα+sinβ=2sinα+β2·cosα-β2

sinα-sinβ=2sinα-β2·cosα+β2

cosα+cosβ=2cosα+β2·cosα-β2

cosα-cosβ=-2sinα+β2·sinα-β2

tgα+tgβ=sinα+βcosα·cosβ

tgα-tgβ=sinα-βcosα·cosβ

ctgα+ctgβ=sinα+βsinα·sinβ

ctgα-ctgβ=sinβ-αsinα·sinβ

asinα+bcosα=rsinα+φ ,

где r2=a2+b2 , sinφ=br , tgφ=ba

Формулы преобразования произведений функций

sinα·sinβ=cosα-β-cosα+β2

sinα·cosβ=sinα+β+sinα-β2

cosα·cosβ=cosα+β+cosα-β2

Универсальная тригонометрическая подстановка

sinα=2tgα21+tg2α2

cosα=1-tg2α21+tg2α2

tgα=2tgα21-tg2α2

ctgα=1-tg2α22tgα2

Коротко о важном
Таблицы
Формулы
Формулы по геометрии
Теория по математике

МЫ В СЕТИ

Тригонометрические формулы (Sin, Cos, Tan, Cot, Sec, Cosec)

В прямоугольном треугольнике ABC, если ϴ — угол, образованный сторонами AB и AC, а угол ABC — прямой, то можно сказать, что AB — противолежащая сторона, BC — прилежащая сторона, а AC — гипотенуза .

Теперь мы можем определить основные формулы следующим образом:

sinϴ = противолежащая сторона/ гипотенуза = AB/ AC
cosϴ = смежная сторона/гипотенуза = BC/AC
tanϴ = противоположная сторона/соседняя сторона= AB/BC
cotϴ = соседняя сторона/противоположная сторона= BC/AB
secϴ= гипотенуза/прилежащая сторона= AC/BC = 1/cosϴ
cosecϴ= гипотенуза/противоположная сторона= AC/AB= 1/sinϴ

Фундаментальные тождества:

Sin ² ϴ + cos ² ϴ = 1
1 + тангенс ² ϴ = сек ² ϴ
1 + кроватка ² ϴ = cosec ² ϴ

Некоторые базовые формулы:

Sin(-ϴ) = -sin
Cos(-ϴ) = +cosϴ
тангенс (-ϴ) = -тангенсϴ
Кот(-ϴ) = -Котϴ
Сек(-ϴ) = +Секϴ
Косек(-ϴ) = -Косекϴ

Cos(A + B) = CosA CosB – SinA SinB
Cos(A – B) = CosACosB + SinASinB
Sin(A + B) = SinA CoSB + CosA SinB
Sin(A – B) = SinA CosB – CosA SinB
tan(A + B) = (tanA + tanB)/ (1 – tanA tanB)
tan(A – B) = (tanA – tanB)/ (1+ tanA tanB)

Sin2ϴ= 2Sinϴ Cosϴ
Cos2ϴ = Cos ² ϴ – Sin ² ϴ

= 1 – 2Sin ² ϴ

= 2Cos ² ϴ – 1

tan(2ϴ) = 2tanϴ/ (1 – тангенс ² ϴ)
Sin(2ϴ) = 2tanϴ/ (1 + тангенс ² ϴ)
Cos(2ϴ) = (1 – тангенс ² ϴ) / (1 + тангенс ² ϴ)

Sin(3ϴ) = 3Sinϴ – 4Sin ³ ϴ
Cos(3ϴ) = 4Cos ³ ϴ – 3Cosϴ
tan(3ϴ) = (3tanϴ – tan ³ ϴ)/ (1 – 3tan ² ϴ)

2SinA CosB = Sin(A + B) + Sin(A – B)

2CosA SinB = Sin(A + B) – Sin(A – B)
2CosA CosB = Cos(A + B) + Cos(A – B)
2SinA SinB = Cos(A – B) – Cos(A + B)

Cos ² ϴ = (1 + Cos2ϴ)/ 2
Sin ² ϴ = (1 – Cos2ϴ)/ 2

SinA + SinB = 2Sin(A+B/2) Cos(A – B/2)
SinA – SinB = 2Cos(A + B/2) Sin(A – B/2)
CosA + CosB = 2Cos(A + B/2) Cos(A – B/2)
CosA – CosB = -2Sin(A + B/2) Sin(A – B/2)

= 2Sin(A + B/2) Sin(B – A/2)

В любом треугольнике ABC

Sin (A + B) = SinC
Грех (В + С) = Грех А
Грех (С + А) = SinB

Cos (A + B) = -CosC
Cos (B + C) = – CosA
Cos (С + А) = -CosB

Cos (π/2 – ϴ) = Sinϴ
Sin (π/2 – ϴ) = Cosϴ

Гиперболические функции Sin и косинуса

Sin (iϴ) = i*Sin(hϴ)
Cos(iϴ) = Cos(hϴ)
Sin(iϴ) = (e ^iϴ – e ^-iϴ )/ 2i
Cos (iϴ) = (e ^iϴ + e ^-iϴ ) / 2
Кош ² ϴ – Синх ² ϴ = 1

Обновлено: 1 сентября 2021 г.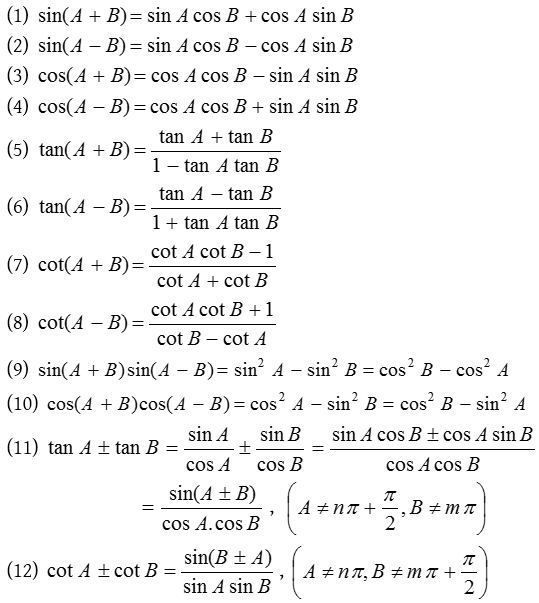 — 20:42

тригонометрических формул. Тригонометрия – это наука о… | от DoubtConnect

Тригонометрия — это изучение соотношений между углами, длинами и высотами треугольников. Он включает соотношения, функции, тождества, формулы для решения задач на его основе, особенно для прямоугольных треугольников. Теперь это совершенно новая и сложная глава, в которой нужно выучить все формулы и применить их соответствующим образом. Поэтому мы решили собрать их все вместе, чтобы вам было легко пересматривать формулы на ходу.

Тригонометрические формулы для соотношений в основном основаны на трех сторонах прямоугольного треугольника, таких как прилежащая сторона или основание, перпендикуляр и гипотенуза (см. рисунок выше). Применяя теорему Пифагора для данного прямоугольного треугольника, имеем:

(Перпендикуляр)2+(Основание)2=(Гипотенуза)2

⇒(P)2+(B)2=(H)2

Теперь давайте посмотрим на формулы, основанные на тригонометрических соотношениях (синус, косинус , тангенс, секанс, косеканс и котангенс)

Тригонометрические формулы приведены ниже: θ

cosec (−θ) = − cosec θ

sec (−θ) = sec θ

cot (−θ) = − cot θ

sin2A + cos2A = 1
TAN2A + 1 = SEC2A
COT2A + 1 = COSEC2A

SIN (2Nπ + θ) = SIN θ
COS (2Nπ + θ) = COS θ
TAN (2Nπ + θ) = TAN θ) = COS θ
TAN (2Nπ + θ) = TAN θ) = cos θ
cot(2nπ + θ ) = cot θ
сек(2nπ + θ ) = сек θ
cosec(2nπ + θ ) = cosec θ

Квадрант I

cos(π/2−θ) = sin θ
tan(π/2−θ) = cot θ
cot(π/2−θ) = tan θ
сек(π/2− θ) = cosec θ
cosec(π/2−θ) = sec θ

Квадрант II

sin(π−θ) = sin θ
cos(π−θ) = -cos θ
tan 9001 θ) = -tan θ
cot(π−θ) = — cot θ
сек(π−θ) = -sec θ
cosec(π−θ) = cosec θ

Квадрант III

sin(π+ θ) = — sin θ

cos(π+ θ) = — cos θ

tan(π+ θ) = tan θ

cot(π+ θ) = cot θ

сек(π + θ) = -сек θ

cosec(π+ θ) = -cosec θ

Квадрант IV

sin(2π− θ) = — sin θ
cos(2π− θ) = cos θ
tan(2π) = — tan θ
cot(2π− θ) = — cot θ
sec(2π− θ) = sec θ
cosec(2π− θ) = -cosec θ

sin (A + B) = sin A cos B + cos A sin B
sin (A − B) = sin A cos B — cos A sin B
cos (A + B) = cos A cos B — sin A sin B
cos (A — B) = cos A cos B + sin A sin B
tan(A+B) = [(tan A + tan B)/(1 — tan A tan B)]
tan(A-B) = [(tan A — tan B)/(1 + tan A tan B) )]

sin2A = 2sinA cosA = [2tan A + (1+tan2A)]
cos2A = cos2A–sin2A = 1–2sin2A = 2cos2A–1= [(1-tan2A)/(1+tan2A)]
TAN 2A = (2 TAN A)/(1-TAN2A)

SIN3A = 3SINA-4SIN3A
COS3A = 4COS3A-3COSA
TAN3A = [3TANA-TAN3A]/[1-3TAN2A]