Если диагонали параллелограмма равны то этот параллелограмм ромб: 1) Если в па­рал­ле­ло­грам­ме диа­го­на­ли равны, то этот па­рал­ле­ло­грамм — пря­мо­уголь­ник. 2) Если диа­го­на­ли па­рал­ле­ло­грам­ма…

Параллелограммы: ромб, прямоугольник, квадрат — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Параллелограммы

Параллелограмм
Ромб
Прямоугольник
Квадрат
Презентацию подготовила ученица 8А
класса Ольшанская Анастасия

2. Параллелограмм— это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных

Параллелограмм— это четырёхугольник, у
которого противоположные стороны попарно
параллельны, то есть лежат на параллельных
прямых.

3. Противоположные стороны параллелограмма равны. Противоположные углы параллелограмма равны. Диагонали параллелограмма

Свойства параллелограмма
Противоположные стороны параллелограмма равны.
Противоположные углы параллелограмма равны.
Диагонали параллелограмма пересекаются и точкой пересечения
делятся пополам..
Сумма углов, прилежащих к одной стороне, равна 180°.
Точка пересечения диагоналей является центром симметрии
параллелограмма.
Биссектриса отсекает от параллелограмма равнобедренный
треугольник.
Сумма всех углов равна 360°.
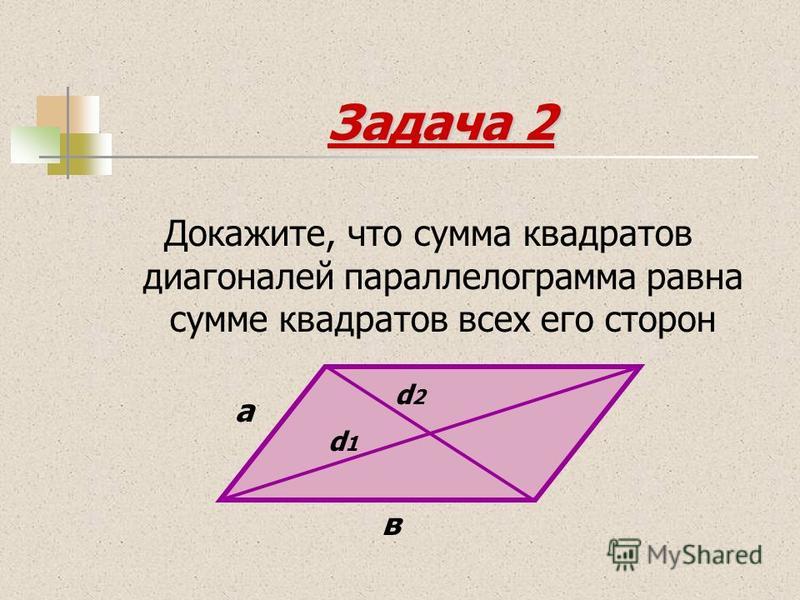
Сумма квадратов диагоналей параллелограмма равна удвоенной
сумме квадратов его двух смежных сторон.

4. Противоположные стороны попарно равны. Противоположные углы попарно равны. Диагонали делятся в точке их пересечения пополам.

Признаки параллелограмма
Противоположные стороны попарно равны.
Противоположные углы попарно равны.
Диагонали делятся в точке их пересечения
пополам.
Сумма соседних углов равна 180 градусов.
Противоположные стороны равны и
параллельны.
Сумма расстояний между серединами
противоположных сторон выпуклого
четырехугольника равна его полупериметру.
Сумма квадратов диагоналей равна сумме
квадратов сторон параллелограмма.

5. Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам). Примечание. В евклидовой геометрии для того,

Прямоугольник — параллелограмм, у которого
все углы прямые (равны 90 градусам).
Примечание. В евклидовой геометрии для того,
чтобы четырёхугольник был прямоугольником,
достаточно, чтобы хотя бы три его угла были
прямые. Четвёртый угол (в силу теоремы о сумме
углов многоугольника) также будет равен 90°.
В неевклидовой геометрии, где сумма углов
четырёхугольника не равна 360° —
прямоугольников не существует.

6. Прямоугольник является параллелограммом — его противоположные стороны попарно параллельны. Стороны прямоугольника являются его

Свойства прямоугольника
Прямоугольник является параллелограммом —
его противоположные стороны попарно
параллельны.
Стороны прямоугольника являются его высотами.
Квадрат диагонали прямоугольника равен сумме
квадратов двух его смежных сторон (по теореме
Пифагора).
Около любого прямоугольника можно описать
окружность, причем диагональ прямоугольника
равна диаметру описанной окружности (радиус
равен полудиагонали).

7. Параллелограмм является прямоугольником, если выполняется любое из условий: Если диагонали параллелограмма равны. Если квадрат

Признаки
Параллелограмм является прямоугольником, если выполняется
любое из условий:
Если диагонали параллелограмма равны.
Если квадрат диагонали параллелограмма равен сумме квадратов
смежных сторон.
Если углы параллелограмма равны.

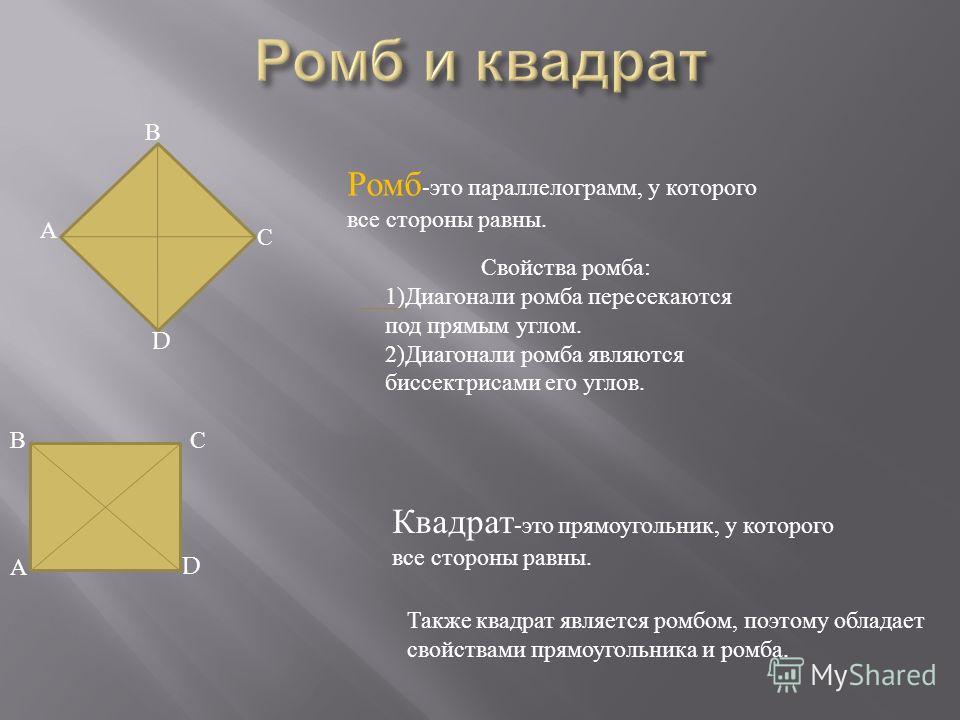
8. Ромб — это параллелограмм, у которого все стороны равны. Ромб с прямыми углами называется квадратом.

Ромб — это параллелограмм, у которого все стороны
равны. Ромб с прямыми углами называется квадратом.

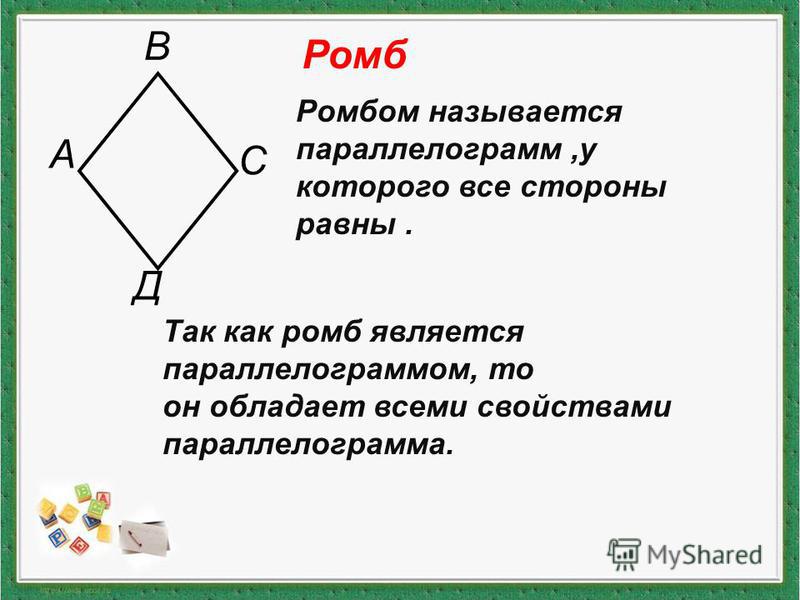
9. Ромб является параллелограммом. Его противолежащие стороны равны и попарно параллельны.

Диагонали ромба пересекаются под прямымСвойства ромба
Ромб является параллелограммом. Его противолежащие стороны
равны и попарно параллельны.
Диагонали ромба пересекаются под прямым углом и в точке
пересечения делятся пополам.
Диагонали ромба являются биссектрисами его углов .
Сумма квадратов диагоналей равна квадрату стороны, умноженному
на 4.

10. Параллелограмм  является ромбом, если выполняется одно из следующих условий: Все его стороны равны. Его диагонали пересекаются

Признаки
Параллелограмм является ромбом, если выполняется одно из
следующих условий:
Все его стороны равны.
Его диагонали пересекаются под прямым углом .
Его диагональ делит его угол пополам.

11. Квадрат — правильный четырёхугольник, у которого все углы и стороны равны.

Квадрат — правильный четырёхугольник, у которого все углы и
стороны равны.
Свойства квадрата
Равенство длин сторон.
Равенство углов( по 90 градусов).
Все углы квадрата прямые.
Диагонали квадрата равны.

English     Русский Правила

Ромб

Содержание

1. Определение ромба
2. Свойства ромба
3. Признаки ромба

Определение ромба

Определение 1. Ромб − это параллелограмм, у которого все стороны равны.

На рисунке 1 изображен ромб ABCD.

Определение 2. Ромб − это четырехугольник, у которого все стороны равны.

Ромб разделяет плоскость на две части, одна из которых называется внутренней областью ромба, а другая внешней областью ромба.

Объединение ромба и ограниченной им части плоскости также называют ромбом.

Свойства ромба

Поскольку ромб является параллелограммом, то имеет следующие свойства:

• 1. У ромба противолежащие углы равны (\( \small \angle A = \angle C, \; \angle B = \angle D. \) )
• 2. У ромба противолежащие стороны равны (\( \small AB = DC, \; BC=AD.\) )
• 3. У ромба противолежащие стороны параллельны \( \small( AB \ || \ DC, \; BC \ || \ AD).\)
• 4. У ромба соседние углы дополняют друг друга до 180° \( \small ( \angle A +\angle B=180°, \) \( \small \angle C + \angle D=180°).\)
• 5. Диагонали ромба точкой пересечения делятся пополам \( \small ( AO = OC, \) \( \small BO=OD).\)

Ромб имеет также и следующие свойства:

• 6. Диагонали ромба пересекаются под прямым углом (\( \small AC \perp BD.\) )
• 7. Диагонали ромба являются биссектрисами его углов (\( \small \angle ABD = \angle CBD, \) \( \small \angle ADB = \angle CDB, \) \( \small \angle DAC = \angle BAC, \) \( \small \angle BCA = \angle DCA. \))
• 8. В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей. 2). \)

Докажем свойства 6 и 7, сформулировав следующую теорему:

Теорема 1. Диагонали ромба перпендикулярны и являются биссектрисами его углов.

Доказательство. По определению 1, \( \small AD = DC \) (Рис.2). Следовательно треугольник \( \small DAC \) равнобедренный. Тогда \( \small \angle DCO = \angle DAO. \) Учитывая, что \( \small AO = OC \) (свойство 5 ромба), получим, что треугольники \( \small DOA \) и \( \small DOC \) равны по двум сторонам и углу между ними (см. статью Треугольники. Признаки равенства треугольников). Тогда равны углы

DOC и DOA. Но эти углы смежные и их сумма равна 180°. Следовательно \( \small \angle DOC= \angle DOA=90°. \) То есть диагонали AC и BD перпендикулярны.

Из равенства треугольников \( \small DOA \) и \( \small DOC \) также следует, что \( \small \angle CDO= \angle ADO,\) следовательно BD является биссектрисой угла ADС, то есть BD является биссектрисой ромба ABCD.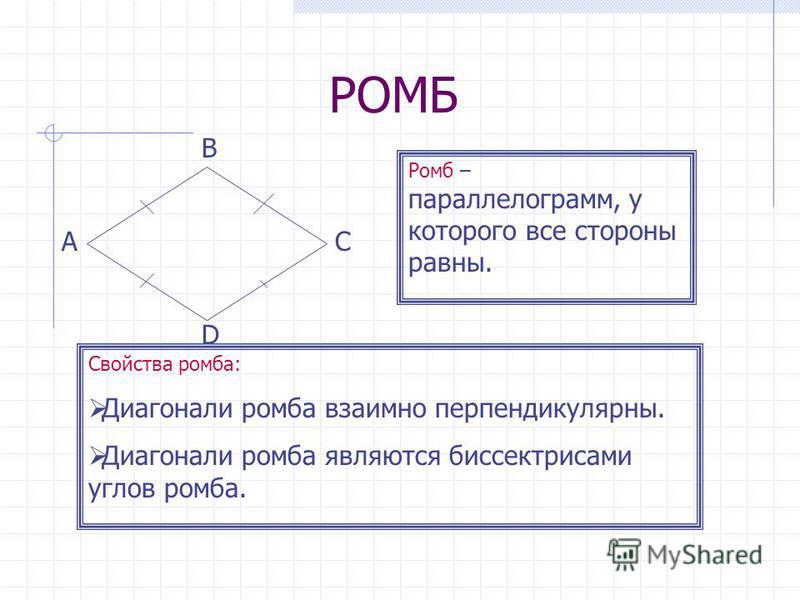

Признаки ромба

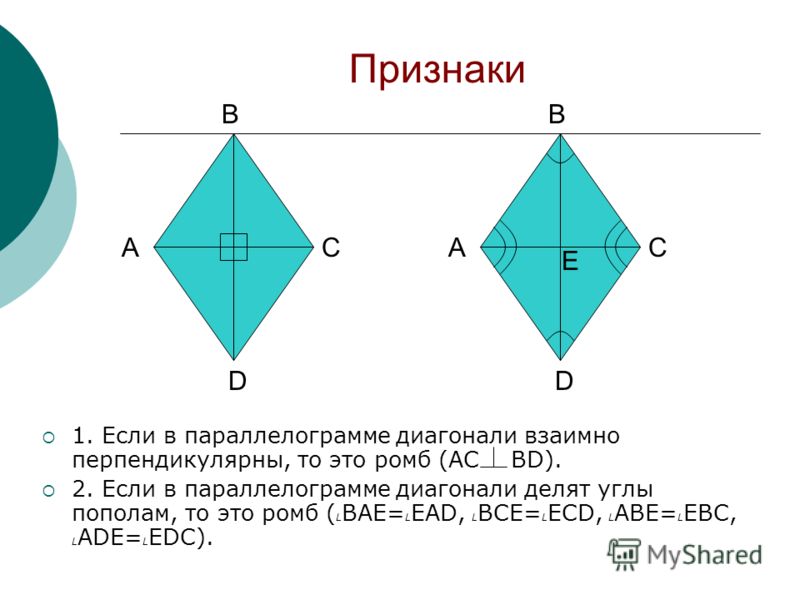
Признак 1. Если смежные стороны параллелограмма равны, то этот параллелограмм − ромб.

Доказательство. Пусть смежные стороны параллелограмма ABCD равны. То есть имеем: AB=BC (Рис.3). У параллелограмма противоположные стороны равны (Свойство 1 статьи Параллелограмм). Тогда DC=AB=BC=AD. То есть все стороны параллелограмма равны и по определению 1, этот параллелограмм является ромбом.

Признак 2. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм − ромб.

Доказательство. Пусть диагонали параллелограмма ABCD перпендикулярны (Рис.3). Рассмотрим прямоугольные треугольники AOB и COB. Так как у параллелограмма диагонали точкой пересечения разделяются пополам (Свойство 2 статьи Параллелограмм), то AO=OC. Тогда прямоугольные треугольники AOB и COB равны по двум катетам (AO=OC, BO общий катет (см. статью Прямоугольный треугольник. Свойства, признаки равенства)).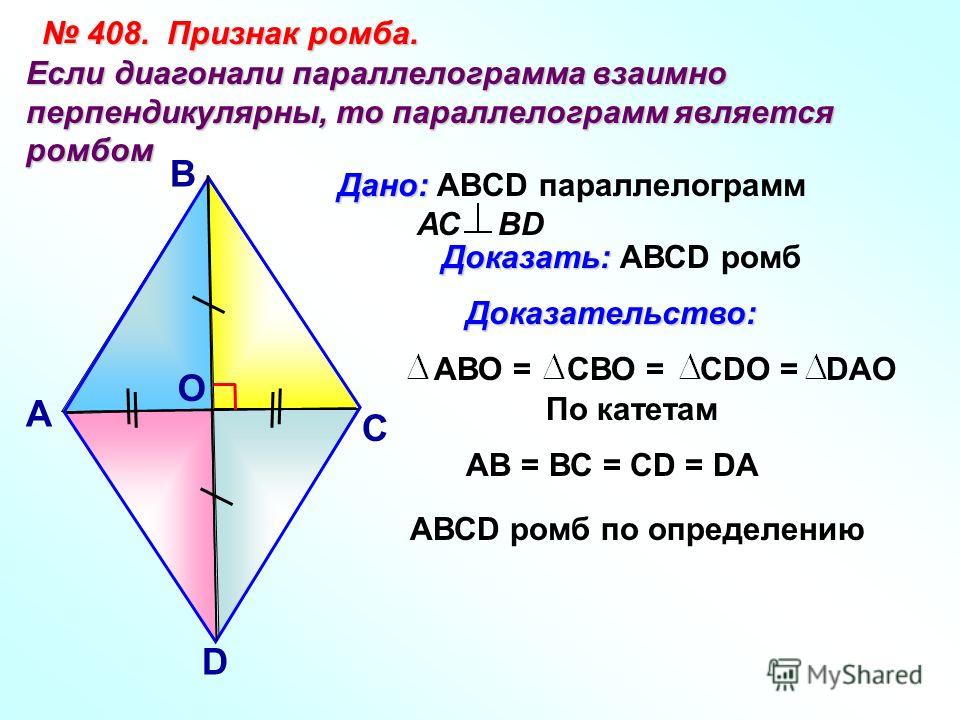 Следовательно AB=BC. Тогда по признаку 1 этот параллелограмм является ромбом.

Признак 3. Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм − ромб.

Доказательство. Пусть диагональ AC параллелограмма ABCD является биссектрисой угла BAD (Рис.4). Тогда \( \small \angle 1= \angle 2 .\) У параллелограмма ABCD \( \small AB \ || \ DC .\) Тогда для параллельных прямых AB и DC и секущей AC справедливо равенство \( \small \angle 1= \angle 4 .\) (см теорему 1 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Аналогично, для параллельных прямых BC и AD и секущей AC справедливо равенство \( \small \angle 2= \angle 3 .\) Так как \( \small \angle 1= \angle 2 ,\) то \( \small \angle 1= \angle 2=\angle 3= \angle 4 .\) Из \( \small \angle 1= \angle 3\) следует, что треугольник ABC равнобедренный (Признак 2 статьи Равнобедренный треугольник). Тогда AB=BC. У параллелограмма противоположные стороны равны (Свойство 1 статьи Параллелограмм). Тогда AB=BC=CD=DA. То есть все стороны параллелограмма равны и по определению 1, этот параллелограмм является ромбом.

Признак 4. Если стороны четырехугольника равны, то этот четырехугольник − ромб.

Доказательство. Пусть у четырехугольника все стороны равны. Тогда этот четырехугольник является параллелограммом (признак 2 статьи Параллелограмм). А по определению 1, этот параллелограмм является ромбом.

Извините! — Страница не найдена

Извините! — Страница не найдена

Пока разбираемся, возможно, поможет одна из ссылок ниже.

ДомНазад

• Класс
• Онлайн-тесты
• Ускоренный онлайн-курс JEE
• Двухлетний курс ЕГЭ 2021

• Класс
• Онлайн-курс NEET
• Серия онлайн-тестов

• Фонд CA
• CA Промежуточный
• Финал CA
• Программа CS

• Класс
• Серия испытаний
• Книги и материалы
• Тестовый зал
• Умный взломщик BBA

• Обучение в классе
• Онлайн-коучинг
• Серия испытаний
• Интеллектуальный взломщик IPM
• Книги и материалы
• ГД-ПИ

• CBSE класс 8
• CBSE класс 9
• CBSE Класс 10
• CBSE Класс 11
• CBSE Класс 12

• Обучение в классе
• Онлайн-классы CAT
• Серия тестов CAT
• МВА Жилой
• Умный взломщик CAT
• Книги и материалы
• Онлайн-классы без CAT
• Серия испытаний без CAT
• Испытательный зал
• ГД-ПИ

• Обучение в классе
• Серия испытаний
• Гражданские интервью

• Класс
• Онлайн-классы
• Серия испытаний SSC
• Корреспонденция
• Практические тесты
• Электронные книги SSC
• Пакет исследований SSC JE

• Класс
• RBI класс B
• Серия тестов банка
• Корреспонденция
• Банковские электронные книги
• Банк ПДП

• Онлайн-коучинг
• Коучинг в классе
• Серия испытаний
• Книги и материалы

• Класс
• Программа моста GRE

• Онлайн-коучинг GMAT
• Консультации по приему
• Коучинг GMAT в классе

• Стажировка
• Корпоративные программы
• Студенты колледжа
• Работающие специалисты
• Колледжи
• Школы

Что такое ромб? (Определение, форма, свойства)

Написано

Малкольм МакКинси

16 января 2023

Проверка по факту

Пол Маззал

Рамб.

стороны длины и противоположные стороны параллельны друг другу. Все ромбы — параллелограммы, но не все параллелограммы — ромбы. Противоположные внутренние углы ромба равны, а диагонали ромба всегда делят друг друга пополам под прямым углом.

Форма ромба

Каждый ромб это:

• Плоская фигура (имеет два измерения)

• Замкнутая форма (имеет внутреннюю и внешнюю)

• Четырехсторонняя фигура с прямыми сторонами)

Репетиторы

Как выглядит ромб?

В большинстве случаев ромб, который вы видите, будет нарисован так, что у него есть основание — две противоположные стороны будут горизонтальными, а нижняя сторона служит основанием фигуры.

Что такое ромб

Будьте осторожны, потому что ромб может появиться в любой ориентации. Когда он «встает», то есть внешне симметричен (его диагонали горизонтальны и вертикальны), его обычно называют ромбом.

Если вы изо всех сил пытаетесь вспомнить его название, подумайте о квадрате, в который въехал автобус, поэтому он перевернулся ( врезался  в него автобус  … ромб).

Является ли квадрат ромбом?

Все квадраты — ромбы, но не все ромбы — квадраты. Если у вас есть ромб с четырьмя равными внутренними углами, у вас есть квадрат .

Квадрат является частным случаем ромба, потому что он имеет четыре стороны одинаковой длины, а также четыре прямых угла.

Всегда ли ромб параллелограмм?

Ромб является частным случаем параллелограмма, потому что он удовлетворяет требованиям параллелограмма: четырехугольник с двумя парами параллельных сторон. Это выходит за рамки этого, чтобы также иметь четыре стороны одинаковой длины, но это все еще тип параллелограмма.

Каждый ромб, который вы видите, также будет параллелограммом, но не каждый встреченный вами параллелограмм будет ромбом.

Виды ромбов

Являются ли ромбы четырехугольниками?

Если у вас есть четырехугольник только с одной парой параллельных сторон, у вас определенно нет ромба (поскольку две его стороны не могут быть одинаковой длины). У вас есть трапеция .

Если у вас есть четырехугольник с двумя парами параллельных сторон, это не обязательно ромб; у вас может быть параллелограмм или ромб, если все четыре стороны имеют одинаковую длину.

Свойства ромба

Одной из двух характеристик, делающих ромб уникальным, является то, что его четыре стороны равны по длине или конгруэнтны. Другое идентифицирующее свойство состоит в том, что противоположные стороны параллельны.

Свойства ромба

Углы ромба

В дополнение к этим четырем сторонам ромб имеет четыре внутренних угла. Также можно построить две диагонали внутри ромба, соединив противоположные вершины (углы).

Углы ромба свойства 360 градусов

Как бы вы ни расположили эти четыре линейных объекта на своей плоской поверхности, у вас всегда будут две пары равных противоположных углов.

Начните заново с двумя вашими объектами и на этот раз сконцентрируйтесь на том, чтобы сделать из них острый угол (менее 90° ). Используйте два других объекта, чтобы соединить исходные два вверх и вправо, чтобы получилась ваша четырехсторонняя (четырехсторонняя) плоская фигура — ромб.

Посмотрите на нижний левый угол и верхний правый угол; они одинаковые. Они конгруэнтны. Посмотрите на нижний правый угол и верхний левый угол: они конгруэнтны. Противолежащие внутренние углы ромба равны.

Четыре внутренних угла ромба всегда составляют в сумме 360°.

Диагонали ромба

Замечательное и редкое свойство ромба состоит в том, что его диагонали всегда перпендикулярны друг другу. Независимо от того, какие углы вы имеете для четырех вершин ромба, диагонали ромба всегда находятся под прямым углом друг к другу.

Свойства ромба

Эти диагонали также пересекают друг друга ровно пополам. Геометры говорят, что они делят пополам друг друга. Это означает, что две диагонали делят ромб на четыре прямоугольных треугольника.

Различные названия для Rombus

Rombus может иметь три дополнительных названия:

1. Rhomb

2. Lozenge

3. Diamond

.