Конспект урока по математике на тему «Сложение и вычитание трёхзначных чисел»
Урок по математике во 2 классе
Тема: «Сложение и вычитание трёхзначных чисел»
Составитель: Ваничева А.С.,
учитель начальных классов
2013 г.
Тип урока: ОНЗ.
Образовательная цель: Узнать правило (алгоритм) сложения и вычитания трёхзначных чисел без перехода через разряд столбиком.
Деятельностная
цель: Составить алгоритм и научить им
пользоваться.
Основные структурные элементы урока:
1. Новое знание: Правила сложения и вычитания трёхзначных чисел без перехода через разряд столбиком.
2. Пробное действие: Записать пример и попробовать его решить: 353 +132 =
3. Фиксация затруднения: Я не смог решить этот пример. Я решил, но не могу доказать, что решил верно.
4. Фиксация причины затруднения: Я не знаю алгоритм ,по которому могу правильно решить эти примеры.
5. Цель деятельности учащихся: Узнать алгоритм сложения и вычитания трёхзначных чисел.
6. Фиксация нового знания:
1. ПИШУ:…………..
2. СКЛАДЫВАЮ (ВЫЧИТАЮ) ЕДИНИЦЫ.
Результат пишу под единицами.
3. СКЛАДЫВАЮ (ВЫЧИТАЮ) ДЕСЯТКИ.
Результат пишу под десятками.
4. СКЛАДЫВАЮ (ВЫЧИТАЮ) СОТНИ.
Результат пишу под сотнями.
5. ОТВЕТ:…………..
ИЛИ:
С. Д, Ед.
±
± о
о
о
Ход урока:
1. Мотивация к учебной деятельности.
Мотивация к учебной деятельности.
Учитель: — Начинается урок,
Он пойти вам должен впрок.
Постарайтесь всё понять,
Учитесь тайны открывать,
Ответы полные давайте
И на уроке не зевайте.
Учитель: — Ребята, как вы понимаете фразу: «Пойти впрок?» Как её можно соотнести с вашей учебной деятельностью? Что значит, урок должен пойти впрок?
— Какие тайны работы с трёхзначными числами вы уже открыли?
Учащиеся: — Читать, записывать, выкладывать с помощью графических моделей, представлять их в виде суммы разрядных слагаемых, сравнивать.
Учитель: — Можете ли вы сказать, что вы все тайны о трёхзначных числах открыли?
Учащиеся: — Нет
Учитель: Сегодня мы откроем ещё одну тайну при работе с трёхзначными числами.
2. Актуализация знаний и фиксация индивидуального затруднения в пробном действии.
Учитель:- Но прежде чем узнать что-то новое,
необходимо повторить кое-что из пройденного.
1).Сосчитайте в прямом порядке от 345 до 402, в обратном порядке от 605 до 597.
4). Сколько единиц каждого разряда в числе 345 (3 единицы в разряде сотен, 4 единицы в разряде десятков, 5 единиц в разряде единиц). Запишите на планшете это число. 5). Запишите на планшете число, состоящее из 3 сотен,2 десятков и 4 единицах.(324).
Учитель:- Расскажите всё ,что вы знаете о числе 324.
Учащиеся: — Оно трёхзначное; натуральное; содержит 3 сотни, 2 десятка, 4 единицы; предыдущее число 323, последующее 325; сумма цифр этого числа – 9.
:Учитель: — Найдите модель числа 425, докажите свой выбор. (В числе 425 4 сотни – они изображены большими треугольниками, 2 десятка – 2 маленьких треугольника, 5 единиц – 5 точек).
Учитель: — Выложите графическую модель числа 324.
: — Выразите это число в различных единицах счёта.
Учащиеся: — 324= 3с. 2 дес. 4ед.
324=3с. 24ед.
324=32дес. 4 ед.
-Вспомните, как записывают числа в столбик при сложении двузначных чисел? (Единицы записывают под единицами , десятки под десятками).
Учитель: — Расскажите алгоритм (эталон) сложения (вычитания) двузначных чисел в столбик. Затем вешает на доску:
1. ПИШУ:…………..
2. СКЛАДЫВАЮ (ВЫЧИТАЮ) ЕДИНИЦЫ.
Результат пишу под единицами.
3. СКЛАДЫВАЮ (ВЫЧИТАЮ) ДЕСЯТКИ.
Результат пишу под десятками.
4. ОТВЕТ:…………..
-это модель десятка, о – это модель единицы ).
Учитель вешает эталон сложения (вычитания) двузначных чисел столбиком на доску.
± о
о
о
Запишите примеры(столбиком) на планшете и решите их: 15 + 30 =
89 – 21 =
Учитель раздаёт каждому ученику листок с выражениями: Запишите выражения столбиком и решите их:
353 + 132 =
Во время выполнения задания дети
фиксируют затруднение.
Поднимите руку те, у кого нет результата. В чём ваше затруднение?
— Поднимите руку те, у кого результат неверный. В чём ваше затруднение?
— Поднимите руку те, у кого есть результат, но не может доказать, что сделал правильно. В чём ваше затруднение?
3. Выявление места и причины затруднения
Учитель: — Итак, какое задание мы выполняли?
Учащиеся — Мы попытались сложить трёхзначные числа столбиком.
Учитель: – У вас получилось? Нет. Почему? Я не знаю правила сложения трёхзначных чисел.
4. Построение проекта выхода из затруднения.
Учитель: — Какова же цель нашего урока?
Учащиеся: Узнать правило сложения трёхзначных чисел, записывая их столбиком.
Учитель: — Какая тема урока? (Сложение и вычитание трёхзначных чисел).
Учитель: — Сегодня мы с вами будем складывать и вычитать трёхзначные числа.
Чтобы правильно сложить,
Надо правильно дружить.
Если ссора иль сраженье,
Не получится сложенье.
Вычитанье, вычитанье!
Вычитанье как понять?
Это значит что-то надо
У чего-нибудь отнять.
Важные трёхзначные числа
Встали в ряд.
И такие числа
Мы будем складывать и вычитать.
А что нам понадобится для работы? (Составить план работы, вывести алгоритм сложения трёхзначных чисел ,пользуясь алгоритмом сложения двузначных чисел.)
Составляем план. Шаги плана перепутаны. Восстановите шаги плана.
1. Записать числа в столбик.
2.Сложить или вычесть.
3. Вычислить.
4. Дополнить уже известный алгоритм.
5. Реализация построения проекта.
Дети работают в группах.
Учитель: — Попробуйте
усовершенствовать известный вам эталон. Затем посмотрим , что у вас получилось
и обсудим.(Затем представитель от группы защищает свой проект).
После согласования групп эталон приобретает такой вид:
С. Д. ЕД
± ± о
ИЛИ: о
о
Учитель: — Какое дополнение вы внесли в известный эталон? (Добавили сложение единиц разряда сотен.)
— Какой шаг нужно добавить к алгоритму сложения и вычитания двузначных чисел? (СКЛАДЫВАЮ СОТНИ.
Результат пишу под сотнями.)
— Давайте проверим наш эталон на вычитании трёхзначных чисел :
564 – 153 =
Учитель открывает алгоритм:
1ПИШУ:…………..
2СКЛАДЫВАЮ (ВЫЧИТАЮ) ЕДИНИЦЫ.
Результат пишу под единицами.
3СКЛАДЫВАЮ (ВЫЧИТАЮ) ДЕСЯТКИ.
Результат пишу под десятками.
4СКЛАДЫВАЮ
(ВЫЧИТАЮ) СОТНИ.
Результат пишу под сотнями.
5ОТВЕТ:…………..
6. Первичное закрепление во внешней речи.
Учитель: — Правило вы открыли. Молодцы! Сейчас мы с ним поработаем. На планшетках записать примеры и решить их
353 + 132 =
564 – 153 =
Работа в парах по вариантам (один говорит, другой слушает):
749 — 403 =
612 + 136 =
7. Самостоятельная работа с самопроверкой
Учитель: — Мы достаточно потренировались. Что дальше? (нам надо поработать самостоятельно, чтобы проверить насколько хорошо мы поняли правило сложения и вычитания трёхзначных чисел.)
Учитель: — Выполните № 3 (1и 4 примеры) на стр. 50. Прочитайте задание. Какой вид записи выберите? ( В столбик).Дети работают в тетрадях. Затем проверяют по эталону.
Учитель: — Какие трудности возникли при решении примеров?(могут быть вычислительные ошибки при сложении и вычитании в пределах 10).
Учитель:
– Кто справился с заданием без ошибок? Поставьте себе « +».
8.Включение в систему знаний.
Учитель: — Как вы думаете, где вам пригодится знание способа сложения и вычитания трёхзначных чисел? (При решении задач, уравнений,…)
— Выполним № 4 (1 и 2 уравнения ) на стр. 51.Один ученик объясняет ход решения , остальные в тетрадях. Второе уравнение решают самостоятельно.
9. Рефлексия деятельности на уроке
Учитель: — Какие знания мы сегодня открыли на уроке?
— Как складывают и вычитают трёхзначные числа?
— Что помогло вам так легко построить новый эталон и понять его? (мы опирались на известный эталон сложения и вычитания двузначных чисел).
Учитель раздаёт каждому учащемуся листок, на котором изображено 2 лица.
Кому было всё понятно на уроке и может рассказать другим, тот дорисует нос в форме !
У кого остались затруднения, вопросы, тот дорисует нос в форме ?
Кому урок
понравился и было интересно на нём ,тот дорисует рот в форме УЛЫБКИ.
Кому урок не понравился, на нём было скучно ,тот дорисует рот в форме ПЕРЕВЁРНУТОЙ УЛЫБКИ.
Учитель: — Можете ли вы назвать себя знатоками трёхзначных чисел?
— Хорошо, я думаю, что мы это выясним на следующих уроках математики. Что нам осталось ещё запланировать? (Отработать новый способ дома, повторив алгоритм).Учитель задаёт домашнее задание, комментируя его.
Урок окончен! Всем спасибо!
Сложение и вычитание на основе разрядного состава трёхзначных чисел
Урок 41. Математика 3 класс ФГОС
Для того чтобы наглядно показать, как складывать и вычитать трёхзначные числа на основе их разрядного состава, Матюша вновь использует счётные палочки. Затем он предлагает решить несколько примеров и проверить полученные результаты.
Конспект урока «Сложение и вычитание на основе разрядного состава трёхзначных чисел»
Здравствуйте, мальчики и девочки!
Сегодня я хочу вам рассказать, как выполнять
сложение и вычитание с трёхзначными числами на основе их разрядного состава.
Но сначала давайте повторим всё то, что вы знаете о трёхзначных числах. Трёхзначные числа записываются тремя цифрами, в которых крайняя справа показывает, сколько в числе единиц. Цифра, стоящая слева, от неё показывает, сколько в числе десятков, а крайняя слева – сколько в числе сотен.
Давайте сейчас я впишу в таблицу несколько трёхзначных чисел и покажу их состав при помощи счётных палочек.
Число триста сорок пять. В нём три сотни, четыре десятка и пять единиц.
Число двести семьдесят. В нём две сотни, семь десятков и нуль единиц. То есть, единиц в этом числе нет.
Число пятьсот восемь. В нём пять сотен, нуль десятков и восемь единиц.
А теперь давайте подумаем, какие числа можно было бы сложить, чтобы получить каждое из наших чисел. Возьмём первое число, триста сорок пять.
Его можно получить из трёх сотен, то есть числа
триста, и к нему прибавить четыре десятка с пятью единицами, то есть число
сорок пять. А можно было взять сотни с десятками, число триста сорок, и к нему
прибавить пять.
А можно было взять сотни с десятками, число триста сорок, и к нему
прибавить пять.
Конечно, возможно и так: три сотни с пятью единицами – триста пять, плюс четыре десятка – сорок.
Ну, и последний вариант – сумма разрядных слагаемых – триста, плюс сорок, плюс пять.
Число двести семьдесят можно получить, сложив числа двести и семьдесят.
А число пятьсот восемь, сложив пятьсот и восемь.
Не забывайте! Для каждого разряда в трёхзначном числе есть своё место. Единицы стоят крайними справа, слева от них – десятки, а крайние слева – сотни.
А теперь я предлагаю вам найти значение вот такого выражения: сумма чисел двести шестьдесят и семь. Давайте опять посмотрим, как это происходит, в таблице.
В числе двести шестьдесят две сотни и шесть десятков. К ним надо прибавить семь единиц. Их добавляем в разряд единиц. Читаем ответ: двести шестьдесят семь.
А если к трёмстам девяти прибавить десять? Триста
девять – это три сотни и девять единиц. Прибавляем один десяток. Конечно, для
десятков есть своё собственное место. Они стоят вторыми справа. Ответ – триста
девятнадцать.
Прибавляем один десяток. Конечно, для
десятков есть своё собственное место. Они стоят вторыми справа. Ответ – триста
девятнадцать.
Запомните, ребята, когда какое-либо число прибавляют к трёхзначному числу, единицы складывают с единицами, десятки – с десятками, а сотни – с сотнями.
Ну а сейчас давайте из этих примеров составим обратные, на вычитание. Была сумма чисел: двести шестьдесят плюс семь равно двести шестьдесят семь. А теперь из двухсот шестидесяти семи вычтем семь, получится двести шестьдесят. И из двухсот шестидесяти семи вычтем двести шестьдесят, получится семь.
Следующий пример на сложение: сумма чисел триста девять и десять равна трёмстам девятнадцати. Составляем обратные примеры на вычитание. Триста девятнадцать минус десять равно триста девять. Триста девятнадцать минус триста девять равно десять.
Вы обратили внимание на то, что и при
вычитании единицы вычитаются из единиц, десятки из десятков, а сотни –
из сотен. Этим правилам надо следовать неукоснительно!
Этим правилам надо следовать неукоснительно!
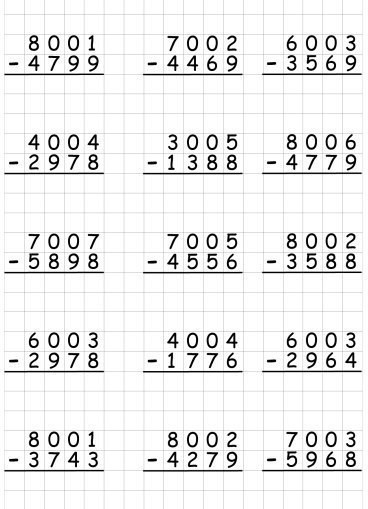
Ну а теперь я предлагаю вам самим поработать. Решите вот такие примеры:
Только не забывайте про правила:
Ну а теперь давайте проверим то, что у вас получилось.
Если вы были внимательны, то, конечно, все решили верно. Ну а если где-то ошиблись – не беда. На ошибках учатся.
Ну что, будем прощаться. Успехов вам, ребята!
Предыдущий урок 40 Сравнение трёхзначных чисел
Следующий урок 42 Определение общего количества единиц каждого разряда в числе
Получите полный комплект видеоуроков, тестов и презентаций Математика 3 класс ФГОС
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Сложение и вычитание 3-значного числа — Изучайте и решайте вопросы
Что вы понимаете под термином «сложение вещей»? Термин «сложение вещей» используется для сложения. Удаление вещей из группы, состоящей из нескольких вещей, эквивалентно вычитанию. В этой статье мы узнаем о сложении и вычитании трехзначных чисел, используя несколько творческих изображений для Лучшее понимание темы. Некоторые трехзначные рабочие листы для сложения вместе с практическими задачами на сложение предназначены для овладения понятиями. Давайте теперь начнем с обучения.
Удаление вещей из группы, состоящей из нескольких вещей, эквивалентно вычитанию. В этой статье мы узнаем о сложении и вычитании трехзначных чисел, используя несколько творческих изображений для Лучшее понимание темы. Некоторые трехзначные рабочие листы для сложения вместе с практическими задачами на сложение предназначены для овладения понятиями. Давайте теперь начнем с обучения.
Сложение и вычитание трехзначных чисел
При выполнении сложения или вычитания трехзначных чисел необходимо поместить заданные числа в столбцы в соответствии с их порядковыми значениями, такими как единицы, десятки, сотни, тысячи и т. д.
При сложении следует помнить, что складываемые числа называются слагаемыми, а результат их сложения — суммой.
При выполнении вычитания следует помнить, что вычитаемые числа называются вычитаемыми, число, из которого вычитается вычитаемое, называется уменьшаемым, а результат их вычитания называется разностью.
Действия по сложению трехзначных чисел
Если требуется сложить трехзначные числа, то сложение всегда добавляет цифры в соответствии со значением разряда. Приведены некоторые шаги для выполнения операции:
Расположите указанные числа в столбцах в зависимости от их разрядности
Начиная с разряда единиц и заканчивая разрядом десятков и сотен
Если задача связана с перегруппировкой, то есть сумма больше 9, затем поместите цифру десятков суммы на следующую цифру
Теперь добавьте цифры, на которые ставится перенос, и, наконец, добавьте перенос также, чтобы получить требуемую сумму в этом месте значение
Повторить тот же процесс до тех пор, пока сложение всех цифр не произойдет.

Например: Если мы хотим сложить 526 и 214. Мы начинаем это сложение, помещая числа в столбец в зависимости от их разрядности. Затем сложите 6 и 4, чтобы получить 10, что больше 9., поэтому воспользуемся перегруппировкой. Он добавит 1 к сумме десятков разрядов, то есть 2+1+1, что даст результат 4. Теперь возьмем сумму 5 и 2, что даст 7. Таким образом, сложение 526 и 214 равно 740.
Сложение трехзначных чисел
Этапы решения задачи вычитания трехзначных чисел
Ниже приведены шаги решения задачи вычитания трехзначных чисел:
Начиная с разряда единиц, затем переходя к разряду десятков и сотен
Если проблема связана с заимствованием, т. е. единица уменьшаемого разряда меньше единицы вычитаемого, тогда заимствуйте перенос из следующей цифры, которая после предоставления заимствования уменьшается на 1
Повторите тот же процесс, пока не произойдет полное вычитание цифр.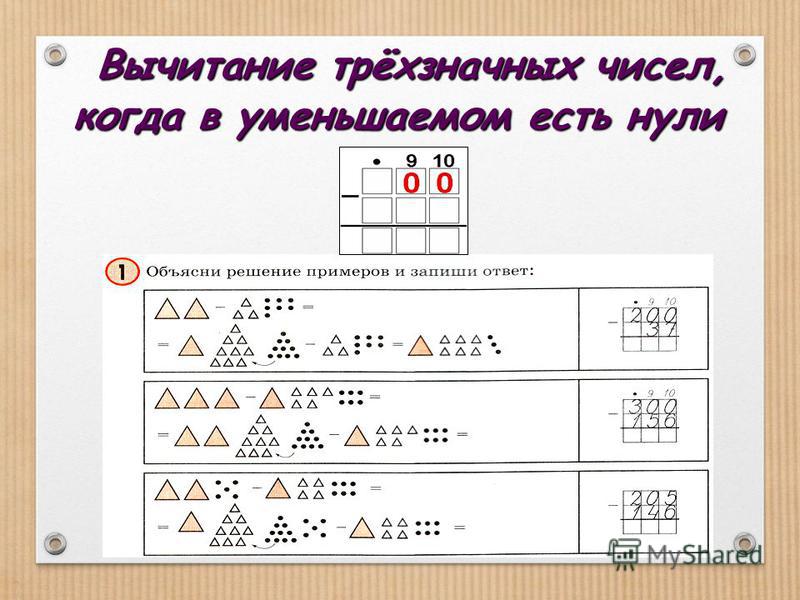
Например: Если мы хотим вычесть 203 и 110. Мы начнем вычитание справа, расставив числа в соответствии с их разрядностью, т.е. 3-0, чтобы получить 3. Так как 0 меньше 1 , мы возьмем перенос 1 из 2, а затем вычтем 1 из 10, чтобы получить 9. Теперь на месте 2 остается 1, и разница с 1 получается в 0. Таким образом, разница между 203 и 110 равна 93.
Решенные примеры
Q 1. Складываем 436 + 486.
Ответ: Некоторые шаги для выполнения сложения даны:
Расположите данные числа в столбцы в зависимости от их разрядности
Начните сложение с единиц, т.е. 6 и 6
сумма 6 и 6 равна 12, что больше 9, таким образом, поместите цифру десятков суммы, т.е. 1, на следующую цифру десятков
Теперь добавьте цифры десятков, т.
 е. 3 и 8, а также добавьте один перенос, чтобы получить сумму
е. 3 и 8, а также добавьте один перенос, чтобы получить суммуПоместите перенос разряда десятков, т. е. 1, на разряд сотен и повторите процесс сложения, т. е. 4 и 4 с одним переносом.
Таким образом, результат сложения трехзначной задачи равен 922.
Сложение трехзначных чисел
Вопросы 2. Вычтите 326 и 103.
Ответ: Дано несколько шагов для выполнения операции:
Расположите заданные числа в столбцах в зависимости от их разрядности
Начиная вычитание с единицы, т.е. 6 и 3
Asзадача не требует никаких заимствований, поэтому переходя к разряду десятков и продолжая вычислять разницу между 2 и 0, которая равна 2
Затем переходя к разряду сотен и вычитая 3 и 1, мы получаем 2
Таким образом, результат задачи на вычитание из трех цифр равен 223.
Практические задачи на вычитание и сложение
Q 1. Используя сложение с перегруппировкой, сложите 182 + 50.
Ответ: 232
92002 Q .Добавить 600 + 450.Ответ: 1050
В 3. Вычесть 512 — 100.
Ответ: 412
В 4. Укажите истинное или ложное: 650 + 420 = 1090. 3 00023 0 Истина -Рабочие листы сложения цифр
Дается трехзначное сложение с переносным рабочим листом, который должен быть решен учащимися самостоятельно, без посторонней помощи.
Рабочий лист
Резюме
Чтобы завершить тему сложения и вычитания трехзначных чисел. Математика имеет дело с группировкой чисел в соответствии с их разрядностью для выполнения определенной арифметической операции. В этой статье подробно рассмотрены шаги, выполняемые для сложения и вычитания трехзначного числа. Некоторые 3-значные дополнения с перенесенными рабочими листами также назначаются студентам для практики и овладения концепциями. Надеюсь, вам будет полезно прочитать статью. Не стесняйтесь высказывать свои сомнения в комментариях.
Надеюсь, вам будет полезно прочитать статью. Не стесняйтесь высказывать свои сомнения в комментариях.
Математические центры по вычитанию трехзначных чисел
Эти Математические центры по вычитанию трехзначных чисел помогают учащимся практиковать различные стратегии вычитания для решения трехзначных математических задач. Они идеально подходят для второклассников, которые только знакомятся с вычитанием трехзначных чисел, или для старших школьников, которым нужна дополнительная практика в использовании разрядных значений и стратегий с основанием 10.
Математические центры доступны на четырех разных уровнях и практикуют пять различных моделей и стратегий вычитания, чтобы обеспечить основу и дифференциацию для всех типов учащихся. Вычитание трехзначного числа может быть затруднено для учащихся, у которых плохое чувство числа. Этот ресурс также основан на практике числового восприятия.
Эти математические центры по вычитанию соответствуют таблицам по математике с трехзначным вычитанием.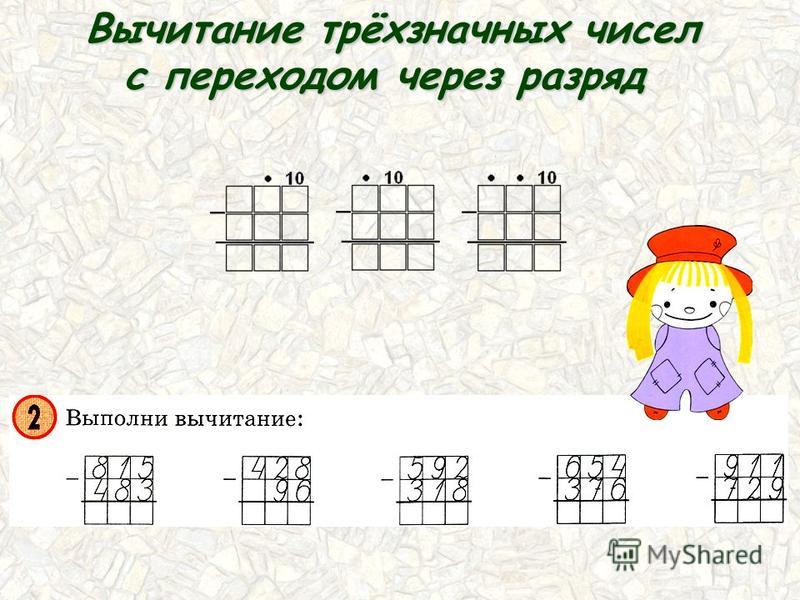 Оба ресурса используют одни и те же стратегии и модели и проходят одни и те же уровни сложности.
Оба ресурса используют одни и те же стратегии и модели и проходят одни и те же уровни сложности.
Задачи в математических центрах на вычитание переходят от простого к сложному. Они начинают с вычитания сотен и переходят к перегруппировке по всем разрядным значениям, практикуя следующие основные стратегии вычитания: использование числовой строки, использование блоков с основанием 10, разделение (также называемое разгруппированием, поэтапное сложение, добавление по разрядному значению), вычитание с помощью Vs. и Вертикальное вычитание.
Все стратегии вычитания ориентированы на разрядное значение и стратегии с основанием 10 и соответствуют общему базовому стандарту второго класса для трехзначного вычитания:
CCSS.MATH.CONTENT.2.NBT.B.7
Сложение и вычитание в пределах 1000 с использованием конкретных моделей или рисунков и стратегий, основанных на позиционном значении, свойствах операций и/или отношениях между сложением и вычитанием; связать стратегию с письменным методом.Поймите, что при сложении или вычитании трехзначных чисел добавляются или вычитаются сотни и сотни, десятки и десятки, единицы и единицы; а иногда надо составить или разложить десятки или сотни.
Четыре уровня задач на вычитание трехзначных чисел
Существуют четыре уровня задач на вычитание, помогающие учащимся перейти от вычитания двузначных чисел к вычитанию трехзначных чисел.
Четыре уровня включают в себя:
- Вычтите сотни (500 — 300)
- Вычтите сотни и десятки, без перегруппирования (740 — 320)
- no uprouping (872 — 351)
- 40172 A. uprouping 10112. Argrouping 10112. Argrouping 10112. Argrouping 10112. Argrouping 10112. A. Argrouping 1. Argrouping 10122 A. Argrouping 1. Argrouping 1011 B. Перегруппировка только десяток
C.Перегруппировка 10 ИЛИ 1(Этот уровень есть в рабочих листах, но не в математических центрах.)
D. Перегруппировка ВСЕХ разрядов, кроме 100
Каждый уровень может использоваться отдельно или, поскольку это математические центры, не рабочие листы, карточки с заданиями можно легко смешать, чтобы создать дополнительный математический центр с большим набором задач.
Этот ресурс посвящен пяти различным разрядным значениям и стратегиям с основанием 10 с некоторыми вариациями по мере усложнения задач.
Ниже приведены примеры каждой стратегии вычитания, используемой в математических центрах трехзначного вычитания.
Использование числовой строки для вычитания трехзначных чисел
Когда учащиеся используют числовую строку при вычитании, они могут считать вверх, вниз или использовать понятное число. В числовых рядах указаны указания о том, как делать прыжки для всех стратегий. Учащиеся следуют этим указаниям, а затем сопоставляют карточки с выражениями и ответами.
Есть три набора направлений. Все направления разбивают меньшее число на развернутую форму и используют стратегии позиционного значения.
Count Up
В этом наборе учащиеся начинают с меньшего числа. Учащиеся делают прыжки на 100, 10 и 1 на числовой прямой, пока не достигнут большего числа. Студент подсчитывает количество прыжков для каждого места и находит значение общего количества прыжков.
Например, 978 – 435 будут такими направлениями:
- Начните с 435.
- Сделайте прыжки на 100. Остановитесь на 935.
Сделайте прыжки на 10. Остановитесь на 975.
Сделайте прыжки на 1. Остановитесь на 978 - Сколько прыжков на 100, 10 и 1 вы сделали? Какова ценность этого числа?
Ученикам предоставляется открытая числовая строка, и они следуют указаниям, чтобы совершать прыжки.
Подсчет с использованием понятных чисел
Как только учащиеся начнут решать задачи на перегруппировку, мы добавляем стратегию использовать понятные числа .
В этой стратегии учащимся предлагается подсчитать и найти дружественные числа.
Например, направления для 536 – 354:
- Начать с 354.
- Перейти к 360. Перейти к 400.
Перейти к 500. Перейти к 530. Перейти к 536. - Найдите значение каждого прыжка и общую стоимость всех прыжков.
Обратный отсчет
Еще один набор указаний предназначен для некоторой дифференциации. В этих указаниях учащимся предлагается делать большие прыжки по разрядности.
В этих указаниях учащимся предлагается делать большие прыжки по разрядности.
Например, направления для номеров с 939 по 427:
- Начните с 939 справа от числовой строки.
- Прыжок назад четыре прыжка по 100, два прыжка по 10 и семь прыжков по 1.
- До какого числа вы прыгнули?
Для всех стратегий предусмотрены пробелы, чтобы учащиеся могли создавать свои собственные числовые ряды и заполнять пробелы своими собственными направлениями.
В качестве задания заполните нижнюю половину карточки с заданиями пустыми местами и попросите учащихся составить собственные указания. Они могут обменяться карточкой с числовой линией с кем-то еще и решить проблему, используя эти указания.
Использование блоков с основанием 10
Эта стратегия предлагает учащимся вычитать блоки с основанием 10 для сложения трехзначных чисел. Это довольно очевидно.
Разбить или разгруппировать числа
В этом разделе учащиеся расширяют каждое число до сотен, десятков и единиц.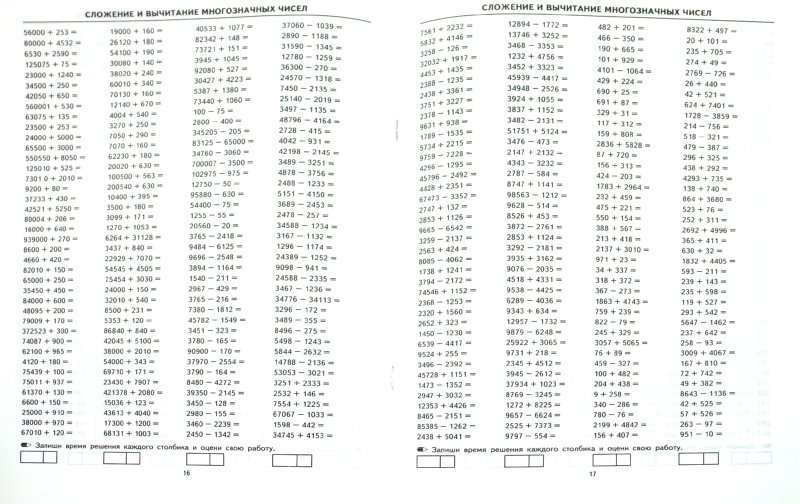 После расширения учащиеся вычитают сотни из сотен, десятки из десятков и единицы из единиц, а затем снова группируют сотни, десятки и единицы в итоговую разницу. Учащиеся перегруппировываются по значениям мест по мере необходимости.
После расширения учащиеся вычитают сотни из сотен, десятки из десятков и единицы из единиц, а затем снова группируют сотни, десятки и единицы в итоговую разницу. Учащиеся перегруппировываются по значениям мест по мере необходимости.
Вычитание с помощью Vs
Вычитание с помощью Vs — еще одна стратегия разряда, при которой учащиеся вычитают сотни из сотен, десятки из десятков и единицы из единиц. Студенты могут использовать числа или даже рисовать блоки с основанием 10.
Эти карты бывают двух форматов. Второй формат, который вы видите ниже, предлагает учащимся выбрать, добавляют ли они или вычитают десятки или единицы из предыдущего числа. Это позволяет учащимся иметь больше гибкости и использовать стратегии ментальной математики.
Вычитание по вертикали
Вычитание по вертикали — это еще один способ использования позиционного значения для вычитания, аналогичный вычитанию с помощью Vs, но по вертикали. На этих карточках с математическими задачами учащиеся вычитают сотни из сотен и пишут разницу рядом со словом сотни.

 е. 3 и 8, а также добавьте один перенос, чтобы получить сумму
е. 3 и 8, а также добавьте один перенос, чтобы получить сумму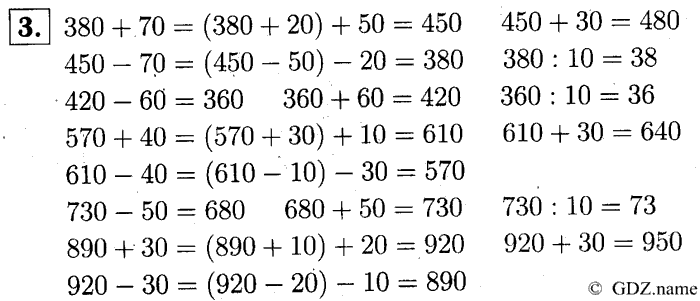 Поймите, что при сложении или вычитании трехзначных чисел добавляются или вычитаются сотни и сотни, десятки и десятки, единицы и единицы; а иногда надо составить или разложить десятки или сотни.
Поймите, что при сложении или вычитании трехзначных чисел добавляются или вычитаются сотни и сотни, десятки и десятки, единицы и единицы; а иногда надо составить или разложить десятки или сотни.