Sin квадрат x 2 sin x: Mathway | Популярные задачи

Mathway | Популярные задачи

1	Найти точное значение	sin(30)
2	Найти точное значение	sin(45)
3	Найти точное значение	sin(30 град. )
4	Найти точное значение	sin(60 град. )
5	Найти точное значение	tan(30 град. )
6	Найти точное значение	arcsin(-1)
7	Найти точное значение	sin(pi/6)
8	Найти точное значение	cos(pi/4)
9	Найти точное значение	sin(45 град. )
10	Найти точное значение	sin(pi/3)
11	Найти точное значение	arctan(-1)
12	Найти точное значение	cos(45 град. )
13	Найти точное значение	cos(30 град. )
14	Найти точное значение	tan(60)
15	Найти точное значение	csc(45 град. )
16	Найти точное значение	tan(60 град. )
17	Найти точное значение	sec(30 град. )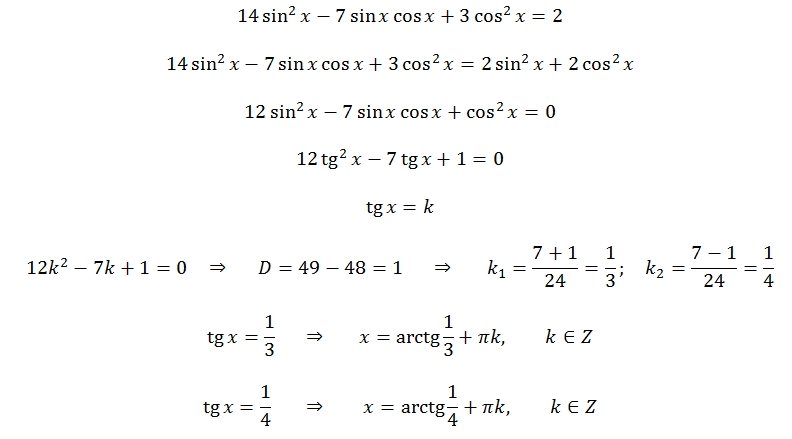
18	Найти точное значение	cos(60 град. )
19	Найти точное значение	cos(150)
20	Найти точное значение	sin(60)
21	Найти точное значение	cos(pi/2)
22	Найти точное значение	tan(45 град. )
23	Найти точное значение	arctan(- квадратный корень из 3)
24	Найти точное значение	csc(60 град. )
25	Найти точное значение	sec(45 град. )
26	Найти точное значение	csc(30 град. )
27	Найти точное значение	sin(0)
28	Найти точное значение	sin(120)
29	Найти точное значение	cos(90)
30	Преобразовать из радианов в градусы	pi/3
31	Найти точное значение	tan(30)
32	Преобразовать из градусов в радианы	45
33	Найти точное значение	cos(45)
34	Упростить	sin(theta)^2+cos(theta)^2
35	Преобразовать из радианов в градусы	pi/6
36	Найти точное значение	cot(30 град. )
37	Найти точное значение	arccos(-1)
38	Найти точное значение	arctan(0)
39	Найти точное значение	cot(60 град. )
40	Преобразовать из градусов в радианы	30
41	Преобразовать из радианов в градусы	(2pi)/3
42	Найти точное значение	sin((5pi)/3)
43	Найти точное значение	sin((3pi)/4)
44	Найти точное значение	tan(pi/2)
45	Найти точное значение	sin(300)
46	Найти точное значение	cos(30)
47	Найти точное значение	cos(60)
48	Найти точное значение	cos(0)
49	Найти точное значение	cos(135)
50	Найти точное значение	cos((5pi)/3)
51	Найти точное значение	cos(210)
52	Найти точное значение	sec(60 град. )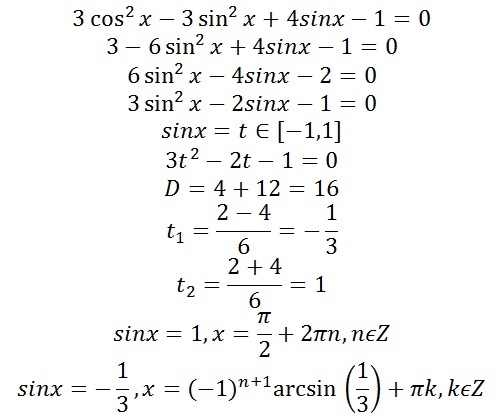
53	Найти точное значение	sin(300 град. )
54	Преобразовать из градусов в радианы	135
55	Преобразовать из градусов в радианы	150
56	Преобразовать из радианов в градусы	(5pi)/6
57	Преобразовать из радианов в градусы	(5pi)/3
58	Преобразовать из градусов в радианы	89 град.
59	Преобразовать из градусов в радианы	60
60	Найти точное значение	sin(135 град. )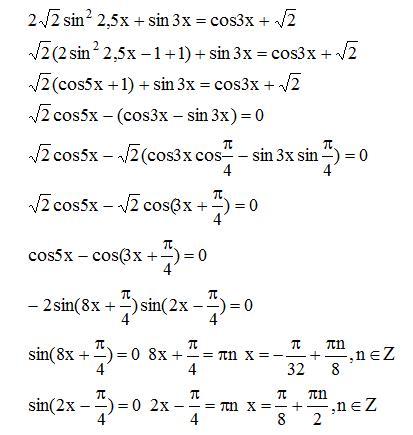
61	Найти точное значение	sin(150)
62	Найти точное значение	sin(240 град. )
63	Найти точное значение	cot(45 град. )
64	Преобразовать из радианов в градусы	(5pi)/4
65	Найти точное значение	sin(225)
66	Найти точное значение	sin(240)
67	Найти точное значение	cos(150 град. )
68	Найти точное значение	tan(45)
69	Вычислить	sin(30 град. )
70	Найти точное значение	sec(0)
71	Найти точное значение	cos((5pi)/6)
72	Найти точное значение	csc(30)
73	Найти точное значение	arcsin(( квадратный корень из 2)/2)
74	Найти точное значение	tan((5pi)/3)
75	Найти точное значение	tan(0)
76	Вычислить	sin(60 град. )
77	Найти точное значение	arctan(-( квадратный корень из 3)/3)
78	Преобразовать из радианов в градусы	(3pi)/4
79	Найти точное значение	sin((7pi)/4)
80	Найти точное значение	arcsin(-1/2)
81	Найти точное значение	sin((4pi)/3)
82	Найти точное значение	csc(45)
83	Упростить	arctan( квадратный корень из 3)
84	Найти точное значение	sin(135)
85	Найти точное значение	sin(105)
86	Найти точное значение	sin(150 град. )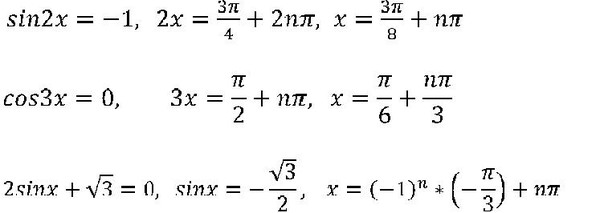
87	Найти точное значение	sin((2pi)/3)
88	Найти точное значение	tan((2pi)/3)
89	Преобразовать из радианов в градусы	pi/4
90	Найти точное значение	sin(pi/2)
91	Найти точное значение	sec(45)
92	Найти точное значение	cos((5pi)/4)
93	Найти точное значение	cos((7pi)/6)
94	Найти точное значение	arcsin(0)
95	Найти точное значение	sin(120 град. )
96	Найти точное значение	tan((7pi)/6)
97	Найти точное значение	cos(270)
98	Найти точное значение	sin((7pi)/6)
99	Найти точное значение	arcsin(-( квадратный корень из 2)/2)
100	Преобразовать из градусов в радианы	88 град.

решить уравнение sin 7x/2 sin x/2 + cos 7x/2 cos x/2 = cos23x

Пример 1.

а) Решить уравнение cos4x+cos2x=0.

б) Найдите все корни этого уравнения, принадлежащие отрезку [-π; π/3].

Решение.

а) Решаем уравнение cos4x+cos2x=0.

Применим формулу               

Tогда данное уравнение примет вид: 2cos3x⋅cosx=0. Отсюда следует, что либо cos3x=0 либо cosx=0.

• Если cos3x=0, то 3х=π/2+πn, отсюда х=π/6+πn/3, где nϵZ.
• Если cosx=0, то х=π/2+πn, где nϵZ.

Заметим, что решения уравнения cosx=0 входят в решения уравнения cos3x=0, поэтому общим решением данного уравнения будут числа x=π/6+πn/3, где nϵZ.

б) Найдём все корни этого уравнения, принадлежащие отрезку [-π; π/3].

Рассмотрим общее решение x=π/6+πn/3, где nϵZ на единичной окружности. Здесь значение πn/3 означает, что нужно брать n раз угол π/3. Отмечаем угол π/6, а затем углы, полученные поворотом угла π/6 на π/3, полученный таким образом угол π/2 опять повернём на π/3, получится угол 5π/6, затем угол 5π/6+ π/3=7π/6, следующий угол

7π/6+ π/3=9π/6=3π/2, и, наконец, 3π/2+ π/3=11π/6. Смотрите рисунок 1.

         

Все отмеченные углы рассмотрим на отрезке [-π; π/3]. Смотрим рисунок 2. Получились числа -5π/6; -π/2; -π/6; π/6.

Ответ: а) π/6+πn/3, где nϵZ; б) -5π/6; -π/2; -π/6; π/6.

Пример 2.

а) Решить уравнение cos4x-sin2x=0.

б) Найдите все корни этого уравнения, принадлежащие отрезку [0; π].

Решение.

а) Применим формулу 1-cos2α=2sin²α; тогда данное уравнение примет вид:

1-2sin²2x-sin2x=0; 2sin²2x+sin2x-1=0. Сделаем замену: sin2x=t.

Получаем равенство: 2t²+t-1=0.

У нас a-b+c=0, поэтому по методу коэффициентов t₁=-1, t₂=1/2.

• При sin2x=-1 получаем 2х=-π/2+2πn, отсюда х=-π/4+πn, где nϵZ.
• При sin2x=1/2 получаем 2х=π/6+2πn и 2х=5π/6+2πn, где nϵZ.

Тогда х=π/12+πn и х=5π/12+πn, где nϵZ.

Рассмотрим решения 2х=-π/2+2πn, 2х=π/6+2πn и 2х=5π/6+2πn на единичной окружности. Возьмём значения 2х при n=0. Углы -π/2, π/6 и 5π/6 отличаются друг от друга на значение 2π/3. Тогда общим решением будут являться числа

2х=π/6+(2π/3)n, отсюда общим решением данного уравнения будут

значения  х=π/12+(π/3)n, где nϵZ.

б) Найдём все корни этого уравнения, принадлежащие отрезку [0; π]. Для этого в общее решение х=π/12+(π/3)n, где nϵZ будем подставлять такие целые значения nϵZ,

чтобы хϵ[0; π].

Возьмём n=0, тогда х=π/12 ϵ[0; π].

При n=1 получим х= π/12+π/3= π/12+4π/12=5π/12 ϵ[0; π].

При n=2 получим х= π/12+2π/3= π/12+8π/12=9π/12=3π/4 ϵ[0; π].

При n=3 получим х= π/12+π, и это значение не входит в заданный отрезок [0; π].

Ответ: а) π/12+(π/3)n, где nϵZ; б) π/12, 5π/12, 3π/4.

Пример 3.

а) Решить уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку [π; 3π/2].

Решение.

а) Применим формулу cos(α-β)=cosα∙cosβ+sinα∙sinβ; тогда данное уравнение примет вид:

cos3x=cos²3x; cos²3x-cos3x=0;  cos3x(cos3x-1)=0;

cos3x=0 или cos3x-1=0.

• Если cos3x=0, то 3х=π/2+πn, тогда х= π/6+(π/3)n, где nϵZ.
• Если cos3x-1=0, то cos3x=1, тогда 3х=2πm, тогда х=(2π/3)m, где mϵZ.

Общие решения данного уравнения: х=π/6+(π/3)n, где nϵZ и х=(2π/3)m, где mϵZ.

б) Найдём все корни этого уравнения, принадлежащие отрезку [π; 3π/2].

Мы получили значения 3х=π/2+πn и 3х=2πm. Отметим их на единичной окружности, сделав замену 3х=t. Смотрите рисунок 3.

     

Необходимо выполнение условие хϵ[π; 3π/2]. Отсюда следует, что 3хϵ[3π; 9π/2].

Все отмеченные углы рассмотрим на отрезке [3π; 9π/2]. Смотрим рисунок 4. Получились числа 7π/2; 4π; 9π/2. Так как это значения 3х, то делим каждое из них на 3. Получим: 7π/6; 4π/3; 3π/2.

Ответ: а) π/6+(π/3)n, где nϵZ; (2π/3)m, где mϵZ.

б) 7π/6; 4π/3; 3π/2.

2 (х)=2sinx

Выберите область веб-сайта для поиска

MathAllУчебные пособияПомощь по домашним заданиямПланы уроков

Искать на этом сайте

Цитата страницы Начать эссе значок-вопрос Задайте вопрос

Начать бесплатную пробную версию

Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой Делиться 92(x)= (1-cos(2x))/2` .

Надеюсь, это поможет.

` `

См. eNotes без рекламы

Начните 48-часовую бесплатную пробную версию , чтобы получить доступ к более чем 30 000 дополнительных руководств и более чем 350 000 вопросов помощи при выполнении домашних заданий, на которые наши эксперты ответили.

Получите 48 часов бесплатного доступа

Уже зарегистрированы? Войдите здесь.

Утверждено редакцией eNotes

Задайте вопрос

Похожие вопросы

Просмотреть все

Математика

Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.

Что означают буквы R, Q, N и Z в математике?

14 Ответы воспитателя

Математика

Последний ответ опубликован 07 октября 2013 г. в 20:13:27.

Как определить, является ли это уравнение линейной или нелинейной функцией?

84 Ответы воспитателя

Математика

Последний ответ опубликован 25 февраля 2016 г. в 18:48:45.

Сколько времени (в часах) займет ваше путешествие, если вы проедете 350 км со средней скоростью 80 км/ч? Какова формула с данными: время, расстояние, скорость или скорость?

1 Ответ воспитателя

Математика

Последний ответ опубликован 09 октября 2017 г. в 00:54:39

Добавьте 1 плюс 2 плюс 3 плюс 4. . . вплоть до 100.

3 Ответа воспитателя

Математика

Последний ответ опубликован 02 сентября 2012 г. в 3:00:53.

Как ограничения (пределы исчисления) используются или применяются в повседневной жизни? Или применительно к проблемам реального мира? Мне нужно пару примеров! Спасибо! 93 6 Решить для ? cos(x)=1/2 7 Найдите x sin(x)=-1/2 8 Преобразование градусов в радианы 225 9 Решить для ? cos(x)=(квадратный корень из 2)/2 10 Найдите x cos(x)=(квадратный корень из 3)/2 11 Найдите x sin(x)=(квадратный корень из 3)/2 92=9 14 Преобразование градусов в радианы 120 градусов 15 Преобразование градусов в радианы 180 16 Найти точное значение желтовато-коричневый(195) 92-4 38 Найти точное значение грех(255) 39 Оценить основание бревна 27 из 36 40 Преобразовать из радианов в градусы 2 шт.