Sin pi t 2: Mathway | Популярные задачи

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значение sin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )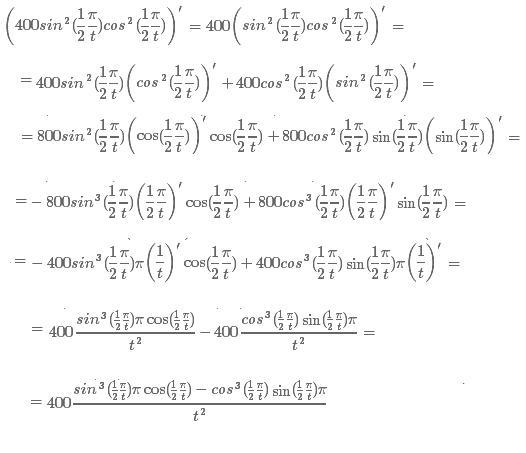
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значение arcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100
Преобразовать из градусов в радианы		88 град.

y=3sinπ(t2−x4) представляет уравнение прогрессивной волны, где t в секундах, а x в метрах. Расстояние, пройденное волной за 5 секунд, равно

Вопрос

Обновлено: 26. 04.2023

KCET ДОКУМЕНТЫ ПРЕДЫДУЩЕГО ГОДА-KARNATAKA CET 2009-PHYSICS

20 видео

РЕКЛАМА

90 002 Текст Решение

Ответ

правильный ответ B

Решение

Данное уравнение бегущей волны имеет вид y=3sinπ(t2−x4)=3sin2π(t4−x8)…………I
Стандартное уравнение прогрессивной волны:
y=y0sin2π(tT−xλ) …………………. Ii
, сравнивая I и ii, получаем
T=4s,λ=8m
Скорость волны v=λT=84=2ms−1
Расстояние, пройденное волной за время t, равно
S=vt
или S=2×5= 10 м (при t=5 с (дано))

Ответ

Пошаговое решение от экспертов, которое поможет вам в решении сомнений и получении отличных оценок на экзаменах.

Ab Padhai каро бина объявления ке

Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!

Похожие видео

Волна представлена ​​уравнением
y=y0sin[10πx−15πt+(π/3)]
, где x в метрах, а t в секундах. Уравнение представляет собой бегущую волну:

11447126

Волна распространяется в среде согласно уравнению смещения, заданному формулой y(x, t)=0,03 sin pi (2 t-0,01 x), где y и x выражены в метрах. и t в секундах. Длина волны равна

16002273

Волна представлена ​​уравнением y=7sin{π(2t−2x)}, где x в метрах, а t в секундах. Скорость волны

16002313

Уравнение прогрессивной волны: y =4 sin (4 pi t-0,04 x+pi/3), где x в метрах, а t в секундах. Скорость волны равна

112984778

Волна представлена ​​уравнением y=0.1sin(60t+2x), где x и y в метрах, а t в секундах. Это представляет собой волну

127328681

Поперечная волна, распространяющаяся вдоль оси x, представлена ​​как: y(x,t)=8,0sin(0,5πx−4πt−π4), где x в метрах, а t в секундах. Скорость волны:

350235008

Уравнение бегущей волны в среде: y=asin(100πt+π10x), где x в метрах, t в секундах. Скорость волны в среде равна

376767944

Волна представлена ​​уравнением
y = 7 sin (7πt−0,04πx+π3)
, где x в метрах, а t в секундах. Скорость волны:

415584716

Волна, описываемая уравнением y = 0,25 sin (10 pi x — 2 pi t ), где x и y в метрах, а t в секундах, представляет собой волну, бегущую вдоль :

415584874

Смещение y волны, бегущей в направлении x, определяется выражением y=(2×10−3)sin(300t−2x+π4), где x и y измеряются в метрах, а t в секундах. Скорость волны

427221760

Поперечная волна, распространяющаяся вдоль оси x, представлена ​​как
y(x,t) =80..Sin(0,5πx−4πt−π4). Где x в метрах, а t в секундах. Скорость волны:

427222250

Волна распространяется в среде в соответствии с уравнением смещения, заданным формулой y (x, t) = 0,03 sin {π(2t−0,01x)}, где y и x равны метров и t в секундах. Длина волны ………. .

427222719

Смещение y волны, бегущей в направлении x, определяется выражением y=(2×10−3)sin(300t−2x+π4), где x и y измеряются в метрах, а t в секундах. Скорость волны

427223251

Волна представлена ​​уравнением :y=Asin(10πx+15πt+π/3), где x в метрах, а t в секундах. Выражение представляет.

576405945

Текст Решение

Уравнение волны, бегущей по струне, имеет вид y=8 sin (5 x-4t), где x в метрах, а t в секундах. Затем

644162665

Текстовое решение

Калькулятор — sin(pi) — Solumaths

Грех, онлайн-исчисление

Резюме:

Тригонометрическая функция sin для вычисления синуса угла в радианах, градусов или градианов.

sin online

Описание:

Калькулятор позволяет использовать большинство из тригонометрических функций , есть возможность вычислить синус , косинус и касательная угла через одноименные функции.

Тригонометрическая функция синус отметил синус , позволяет вычислить синус угла онлайн , можно использовать разные угловые единицы: градус, градус и радианы, которые по умолчанию являются угловыми единицами.

  1. Расчет синуса

    2. Вычисление синуса угла в радианах

    Калькулятор синуса позволяет через функцию sin вычислить онлайн синус синус угла в радианах, сначала нужно выберите нужную единицу, нажав на кнопку параметров расчетного модуля. После этого можно приступать к расчетам.

    Чтобы вычислить синус онлайн от `pi/6`, введите sin(`pi/6`), после вычисления результат `1/2` возвращается.

    Обратите внимание, что функция синуса способна распознавать некоторые специальные углы и делать расчеты со специальными связанными значениями в точной форме.

    Вычислить синус угла в градусах

    Чтобы вычислить синус угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.

    Для вычисления синуса 90, введите sin(90), после вычисления результат 1 возвращается.

    Вычислить синус угла в градусах

    Чтобы вычислить синус угла в градианах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.

    Чтобы вычислить синус 50, введите sin(50), после вычисления, возвращается результат `sqrt(2)/2`.

    Обратите внимание, что функция синуса способна распознавать некоторые специальные углы и выполнять исчисление со специальными ассоциированными точными значениями.

  2. Таблица специальных синусоидальных значений

    3. Синус допускает некоторые специальные значения, которые калькулятор может определить в точных формах. Вот таблица общих синусоидальных значений :

    9018 8
    sin(`2*pi`) `0`
    sin(`pi`) `0`
    sin(`pi/2`) `1`
    sin(`pi/4`) `sqrt(2)/2` 901 85
    грех( `pi/3`) `sqrt(3)/2`
    sin(`pi/6`) `1/2`
    sin(`2*pi/3`) `SQRT (3)/2`
    SIN (` 3*PI/4`) `SQRT (2)/2`
    SIN (` 5*PI/6`)
    SIN (`5*PI/6`)
    SIN (` 5*PI/6`)
    SIN (`5*PI/6`)
    1/2`
    sin(`0`) `0`
    sin(`-2*pi`) `0`
    sin(`-pi`) `0`
    sin(` пи/2`)`- 1`
    sin(`-pi/4`) `-sqrt(2)/2`
    sin(`-pi/3`) `-sqrt(3)/2`
    sin(`-pi/6`) `-1/2`
    sin(`-2*pi/3`) `-sqrt(3)/2`
    sin(`-3*pi/4`) `-sqrt(2)/2`
    sin(`-5*pi/6`) `-1/2`

  3. Основные свойства

    4. `AA x в RR, k в ZZ`,

  • `sin(-x)= -sin(x)`
  • `sin(x+2*k*pi)=sin(x)`
  • `sin(pi-x)=sin(x) `
  • `sin(pi+x)=-sin(x)`
  • `sin(pi/2-x)=cos(x)`
  • `sin(pi/2+x)=cos(x) `

  • Производная синуса

    • Производная синуса равна cos(x).

  • Первообразная синуса

    • Первообразная синуса равна -cos(x).

  • Свойства функции синуса

    • Функция sine является нечетной функцией, для каждого действительного x `sin(-x)=-sin(x)`. Следствием для кривой, представляющей синусоидальную функцию, является то, что она допускает начало отсчета как точку симметрии.

  • Уравнение с синусом

    • Калькулятор имеет решатель, который позволяет решать уравнение с синусом формы cos(x)=a . Расчеты для получения результата детализированы, поэтому можно будет решать уравнения типа `sin(x)=1/2` или `2*sin(x)=sqrt(2)` с этапами расчета.

    Синтаксис:

    sin(x), где x — мера угла в градусах, радианах или градах.

    Примеры:

    sin(`0`), возвращает 0

    Производная синус :

    Чтобы дифференцировать функцию синуса онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции синуса

    производная sin(x) is производная(`sin(x)`)=`cos(x)`

    Первообразная синуса :

    Калькулятор первообразной позволяет вычислить первообразную функции синуса.

    Первопроизводная sin(x) есть первопроизводная(`sin(x)`)=`-cos(x)`

    Предел синуса :

    Калькулятор предела позволяет вычислить пределы функции синуса.

    Предел sin(x) равен limit(`sin(x)`)

    Обратная функция синуса :

    обратная функция синуса представляет собой функцию арксинуса, отмеченную арксинусом.

    График синуса :

    Графический калькулятор может отображать синусоидальную функцию в заданном интервале.

    Свойство функции синуса:

    Функция синуса является нечетной функцией.

    Расчет онлайн с sin (sine)

    См. также

    Список связанных калькуляторов:

    • Арккосинус : arccos. Функция arccos позволяет вычислять арккосинус числа. Функция arccos является обратной функцией функции косинуса.
    • Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
    • Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
    • Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
    • Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
    • Косеканс: косеканс Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
    • Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
    • Тригонометрическое расширение: expand_trigo.

      No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *