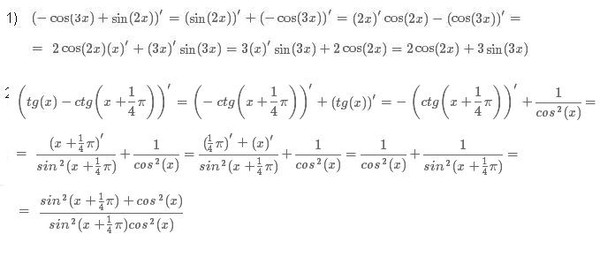Sin4X производная: Mathway | Популярные задачи

Содержание

6. Логарифмическая производная. Найти производную функции

Пример 6.1. Найти производную функции

►. Предлагаемая функция не относится к классу Тем не менее прием логарифмической производной позволяет более оптимально получить результат.

lny = 1/2(lnx + ln|x – 1 – ln|x – 2|) 

(lny)` = y`/y = 1/2(1/x + 1/(x – 1) – 1/(x–2)).

Пользуясь тем, что (lny)` = y`/y получаем

y` = (lny)`y = .◄

Пример 6.2. Найти производную степенно-показательной функции

y = .

► Логарифмируя, получим (так как 1 + 1/x > 0)

lny = xln(1 + 1/x)

Отсюда находим производные левой и правой частей

(lny)` = y`/y = ln(1 + 1/x) – 1/(1 + x).

Следовательно,

y` = (lny)`y = .

◄

1) ((sin(2x))^11x) 2) ((cos(3x))log₃^(2x))

3) ((sin(7x))^ctg(23x)) 4) ((arctg(8x))^x(45x))

5) ((arcsin(9x))^(5x)) 6) ((arccos(7x))^ln(56x))

7) ((log₃₇(3x))^arccos(55x)) 8) ((log₅₅(5x))^arcsin(56x))

9) ((sin(2x))^arccos(59x)) 10) ((cos(8x))^arcctg(803x))

11) ((tg(12x))^arctg(172x)) 12) ((log₃₃(22x))^tg(11x))

13) ((log₈(23x))^cosec(9x)) 14) ((log₅(16x))^sec(8x))

15) ((log₃(51x))^sin(4x)) 16) (log₃₄x³ln31x)

17) (85ln(x²+2x+17)) 18) (89log₃₇(ax+b))

19) (62ln(e^x+x⁴)) 20) (92log(arccos

2x))

21) (77e3^12x) 22) (11x^sinx)

23) (999(arcsinx)^5x) 24) (logx)^logx

25) (17sinx)^arcsinx 26) (65cos51x)^arcctgx

27) ((9tgx)^2sinx) 28) ((91thx)^shx)

29) (7earccosx²lnx) 30) (log³⁴x)^lnx

7.

Неявные функции

Пример 7.1. Уравнение x²+ y²= 1 неявно определяет на интервале (-1,1) две функции:

y₁(x) = ,

y₂(x) = .

Найти их производные, не используя явных выражений.

►Пусть y(x) — любая из этих функций. Тогда, дифференцируя по x тождество

x²+ y²(x) = 1,

получим

2x + 2y(x)y`(x) = 0.

Отсюда

y`(x) = –x/y(x),

т. е.

y`1(x) = –x/y1(x) = – , y`2(x) = – .◄

Пример 7.2. Уравнение arctg(y/x) = ln задаёт неявную функцию. Найти ее производную.

► Продифференцировав равенство arctg(y/x) = ln получим

откуда

y` = (xy). ◄

Найти производную неяной функции y = f(x), определяемой уравнением

1) sin(xy) + 2x = 3^xy2) cos(xy)+2^x = 5^xy

3) tg(xy) + 5^x = 8^xy4) arccos(x²y) + log₂x = 11^xy

5) cos(xy⁴) + arcsin(23x³) = 22^xy6) sin(xy) + 2x = 3^xy

7) x

3 + y⁴= xy 8) 5x⁷+ y⁸= x⁸y8

9) 5x⁶+ y⁹= xy9 10) 8x⁹+ y⁷= x⁷y²

11) 4x⁶+ y³= x⁵y²12) log₅(xy³) + arcsin(9x⁵) = 19^xy

13) log₈(xy⁸) + arcsin(4x⁷) = 18^xy14) log₉(xy⁹) + arcsin(2x⁹) = 1995^xy

15) log₂(xy⁴) + arcsin(3x³) = 19^xy 16)
x²^{+
2xy – y}²^=
2x

^17)
y²^{=
2px 18)} = 1

19) 20)

21) arctg = ln 22) x³– 2x²y²+ 5x + y – 5 = 0

23) e^xy+ xy = e 24) 2ylny = x

25) e^xsiny – e^ycosx = 0 26) sin(xy) + cos(xy) = 0

27) 2^x+2^y= 2^x+y 28) x – y = arcsinx – arcsiny

29) x^y= y^x 30)

8.

Найти производную функции заданной параметрически

Пример 8.1. Найти y`_x если, x = cos²t, y = sint, t(0,/2).

► Воспользовавшись формулой : (y`_x= y`_t/x`_t) получим

x`_t= –2costsint, y`_t= cost, y`_x= – 1/2sint◄

Пример 8.2. Найти y`_x если, x = acos³t, y = bsin³t, t(0,/2)

► Функции x(t) и y(t) дифференцируемы при всех t, и x`_t= –3acos²t·sint  0 на интервале (0,/2). Действуя по аналогии с предыдущим примером находим

y`_x= y`_t/x`_t= , t(0,/2) ◄

1) 2) 3) 4)

5) 6) 7) 8)

9) 10) 11) 12)

13) 14) 15) 16)

17) 18) 19) 20)

21) 22) 23) 24)

25) 26) 27) 28)

29) 30)

Мэтуэй | Популярные задачи

92) 9(3x) по отношению к x

92+1

1	Найти производную — d/dx	бревно натуральное х
2	Оценить интеграл	интеграл натурального логарифма x относительно x
3	Найти производную — d/dx
21	Оценить интеграл	интеграл от 0 до 1 кубического корня из 1+7x относительно x
22	Найти производную — d/dx	грех(2x)
23	Найти производную — d/dx
41	Оценить интеграл	интеграл от cos(2x) относительно x
42	Найти производную — d/dx	1/(корень квадратный из х)
43	Оценка интеграла 9бесконечность
45	Найти производную — d/dx	х/2
46	Найти производную — d/dx	-cos(x)
47	Найти производную — d/dx	грех(3x)
68	Оценить интеграл	интеграл от sin(x) по x
69	Найти производную — d/dx	угловой синус(х)
70	Оценить предел	ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х
85	Найти производную — d/dx	лог х
86	Найти производную — d/dx	арктан(х)
87	Найти производную — d/dx	бревно натуральное 5х92

Найдите из первого принципа производные следующих функций

Класс 9

Класс 8

Класс 7

Класс 6

IIT JEE

Exam
- JEE MAINS
- JEE ADVANCED
- X BOARDS 909 12
- XII ПЛАТЫ
- NEET
  - Новый Предыдущий год (по годам)
  - Физика Предыдущий год
  - Химия Предыдущий год
  - Биология Предыдущий год
  - Новый Все образцы работ
  - Образцы работ Биология 9 0912
  - Образцы статей по физике
  - Образцы работ по химии

Скачать PDF-файлы 12
Класс 7
Класс 6

Экзаменационный уголок

Онлайн-класс

Викторина

909 06

Ask Doubt в WhatsApp

Поиск Doubtnut

Английский словарь

Toppers Talk

Блог

Скачать

Получить приложение

Вопрос

Обновлено: 26.

04.2023

CHHAYA PUBLICATION-DIFFERENTIATION-Short AnswerType Questions

20 видео

লিখিত জবাব

Ответ

Правильный ответ: 4cos4x

1027

Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке!

সংশ্লিষ্ট

प्रथम सिद्धान्त स े sinx का अवकलज ज्ञात कीजिए

226122442

01:56

Найдите производную следующих функций из первых принципов :
sin(x+1)

441775410

03:12

प्रथम सिध्दान्त से फलन का अवकलज ज् ञात कीजिए |
−x

456495936

01:48

का अवकलज ज्ञात कीजिए |
sin(x+1)

456495942

Текстовое решение

Найдите производную следующих функций из первого принципа:
sin(x+1)

515787752

03:1 0

Найдите производную следующего функции из первого принципа:
sin(x+1)

516948825