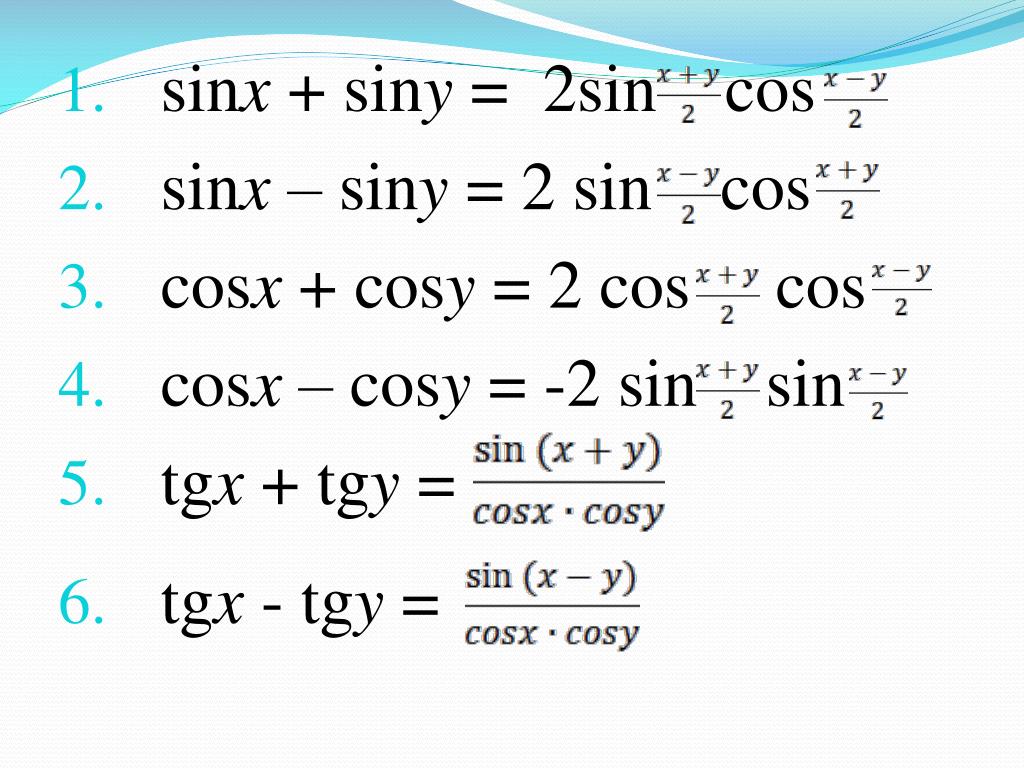Sin5X как разложить: Mathway | Популярные задачи

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )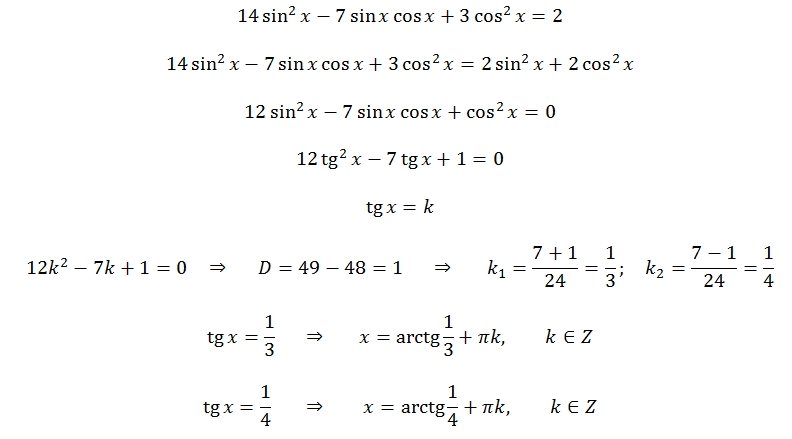
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значение
cos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значение
sin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Пример разложения функции в ряд Фурье

Примеры разложения функции в ряд Фурье

Пример 1

Спектр сигнала, показанного ниже в виде периодической смены знака перед единицей (+/- 1)

Пример постепенного приближения исходной функции суммой гармонических членов разложения

Пример 2

Вид графика функции У(Х)

Разложение на гармонические составляющие имеет вид:

У(Х) = 4/π [sinx — 1/9 sin(3x) + 1/25 sin(5x) – 1/49 sin(7x) + …]

Спектральное представление примера 2. Из графика спектра и формулы видно, что более высокочастотные составляющие стали меньше по амплитуде по сравнению с примером 1.

Пример 3.

Это не синусоида, это функция вида

У(Х) = Х(π – Х) на отрезке 0≤ Х ≤ π

График внешне очень близок к синусоиде, но некоторые отличия ведут к появлению в спектральном разложении дополнительных составляющих.

У(Х) = 8/π [sinx + 1/27 sin(3x) + 1/125 sin(5x) + 1/343 sin(7x) + …]

Амплитуда дополнительных составляющих стала еще меньше по сравнению с примерами 1 и 2, поэтому в спектральном разложении заметно выделяется первая гармоника

Спектральное представление примера 3

Вывод: из примеров 1-3 видно, что чем больше исходный сигнал похож на синусоиду, тем меньше влияние гармоник более высоких частот.

Пример 4 Спектр модулированного сигнала (эта ситуация наиболее часто встречается при диагностике состояния роторных механизмов)

На графике показана синусоида с частотой ɷ, модулированная другой синусоидой с частотой Ω. При этом ɷ>> Ω.

В аналитическом виде сигнал имеет вид:

S(t) = A(1 – R sin Ωt) sinɷt =

= A sin ɷt + AR/2 cos(ɷ — Ω)t – AR/2 cos(ɷ +Ω)t

Спектр такого разложения кроме основной гармоники на частоте ɷ будет иметь две боковые составляющие на частотах (ɷ — Ω) и (ɷ + Ω)

Спектральное представление примера 4

Замечание: Если модулирующая функция будет не в виде гармонического сигнала, а в виде более сложной зависимости, в спектральном разложении появятся дополнительные боковые составляющие на частотах (ɷ — кΩ) и (ɷ + кΩ), где к=1, 2, … n. В практике эксплуатации механизмов установлено, что по мере износа и деградации механизмов количество боковых составляющих растет

как решить уравнение sinx-sin5x=0?

Выберите область веб-сайта для поиска

MathAllУчебные пособияПомощь по домашним заданиямПланы уроков

Искать на этом сайте

Цитата страницы Начать эссе значок-вопрос Задайте вопрос

Начать бесплатную пробную версию

Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой Делиться

Ссылайтесь на эту страницу следующим образом:

«как решить уравнение sinx-sin5x=0?» eNotes Editorial , 9 июня 2010 г., https://www.enotes.com/homework-help/how-solve-equation-sinx-sin5x-0-177081. По состоянию на 28 апреля 2023 г.

Ответы экспертов

sinx-sin5x=0

Мы знаем, что sinx-siny= 2cos(x+y)/2 * sin(x-y)/2

==> sinx-sin5x= 0

==> 2cos (3x) sin(-2x)=0

==> -2cos3x * sin2x =0

==> sin2x=0 или cos3x=0

когда sin2x=0 ==> 2x= 2npi n=0,1,2 …

==> x= npi

когда cos3x= 0 ==> 3x= (2n+1)pi n=0 ,1,2,…

==> x= [(2n+1)/3]pi

Тогда x= {npi, (2n+1)pi}  n=0,1,2…

См. eNotes без рекламы

Начните с 48-часовой бесплатной пробной версией , чтобы получить доступ к более чем 30 000 дополнительных руководств и более чем 350 000 вопросов помощи при выполнении домашних заданий, на которые ответили наши эксперты.

Получите 48 часов бесплатного доступа

Уже зарегистрированы? Войдите здесь.

Утверждено редакцией eNotes

Задайте вопрос

Похожие вопросы

Просмотреть все

Математика

Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.

Что означают буквы R, Q, N и Z в математике?

14 Ответы педагога

Математика

Последний ответ опубликован 25 февраля 2016 г. в 18:48:45.

Сколько времени (в часах) займет ваше путешествие, если вы проедете 350 км со средней скоростью 80 км/ч? Какова формула с данными: время, расстояние, скорость или скорость?

1 Ответ учителя

Математика

Последний ответ опубликован 09 октября 2017 г. в 00:54:39

Добавьте 1 плюс 2 плюс 3 плюс 4. . . вплоть до 100.

3 Ответа воспитателя

Математика

Последний ответ опубликован 02 сентября 2012 г. в 3:00:53.

Как ограничения (пределы исчисления) используются или применяются в повседневной жизни? Или применительно к проблемам реального мира? Мне нужно пару примеров! Спасибо!

1 Ответ учителя

Математика

Последний ответ опубликован 23 мая 2012 г. в 2:05:32. 9Икс».

1 Ответ воспитателя

интегрирование — Интеграл от $\int \frac{\sin(3x)}{\sin(5x)} \, dx$

спросил

Изменено 10 месяцев назад

Просмотрено 918 раз

$\begingroup$

Как найти интеграл от

$$\int \frac{\sin(3x)}{\sin(5x)}dx$$

Я написал $\sin(3x)=\sin(8x-5x)$, но получилось $\frac{\sin(8x) \cos(5x)}{\sin(5x)}$.

Что мне делать?

  • интегрирование
  • неопределенные интегралы
  • тригонометрические интегралы

$\endgroup$

10

$\begingroup$

Используйте $\;\sin3x=\sin(5x-2x)=\sin5x\cos2x-\sin2x\cos5x$ :

$$\frac{\sin3x}{\sin5x}=\cos 2x-\sin2x\frac{\cos5x}{\sin5x}$$

Теперь обратите внимание, что

$$\int\frac{\cos kx}{\sin kx}dx=\frac1k\,\log|\sin kx|+C$$

и теперь возможно интегрирование по частям поможет.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *