Как сделать из косинуса синус: Как из косинуса сделать синус. Примеры с решениями задач на использование тригонометрических тождеств

Содержание

Теорема косинусов и синусов треугольника. Формулы и примеры

Поможем понять и полюбить математику

Начать учиться

240.8K

9 класс — насыщенное новыми знаниями время. Чтобы не запутаться в теории по геометрии, рекомендуем сделать карточки с информацией по каждой теме. В этой статье вы найдете самое важное про теорему косинусов.

Формулировка и доказательство теоремы косинусов

Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Формула Теоремы Пифагора:

a²> + b²> = c²>, где a, b — катеты, с — гипотенуза.

Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Формула теоремы косинусов:

a² = b² + c² — 2bc cos α

В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:

BC² = (x₂ — x₁)² + (y₂ — y₁)²

В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).

cos²α + sin²α = 1 — основное тригонометрическое тождество.

BC² = a² = (b cos α — c)² + b²sin²α = b²cos²α + b²sin²α — 2bc cos α + c² = b²(cos²α + sin²α) — 2bc cos α + c²

Что и требовалось доказать.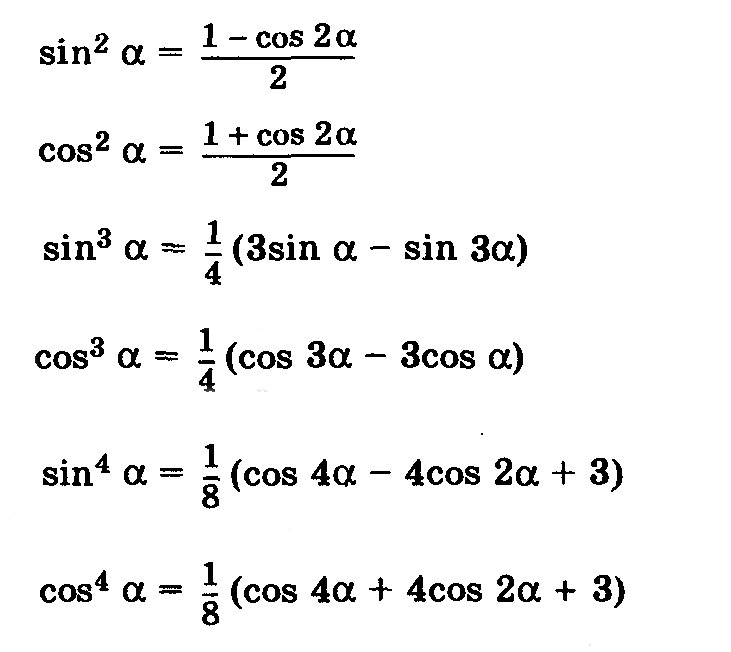

Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.

С помощью теоремы косинусов можно найти косинус угла треугольника:

Когда b² + c² — a² > 0, угол α будет острым.
Когда b² + c² — a² = 0, угол α будет прямым.
Когда b² + c² — a² < 0, угол α будет тупым.

Запоминаем

Когда угол α прямой, то теорема косинусов превращаеся в теорему Пифагора.

Сформулируем еще одно доказательство теоремы косинусов.

Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:

AD = b × cos α,
DB = c – b × cos α.

Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:

h² = b² — (b × cos α)²
h² = a² — (c – b × cos α)²

Приравниваем правые части уравнений:

b² — (b × cos α)² = a² — (c — b × cos α)²

либо

a² = b² + c² — 2bc × cos α

Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.

Определим стороны b и c:

b² = a² + c² — 2ac × cos β;
c² = a² + b² — 2ab × cos γ.

Узнай, какие профессии будущего тебе подойдут

Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Формулировка теоремы для каждой из сторон треугольника

Теорема косинусов справедлива для всех сторон треугольника, то есть:

a² = b² + c² — 2bc cos α

b² = c² + a² — 2ca cos β

c² = a² + b² — 2ab cos γ

Теорема косинусов может быть использована для любого вида треугольника.

Косинусы углов треугольника

Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:

Аналогично:

Определение угла с помощью косинуса

А теперь обратим внимание на углы.

Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).

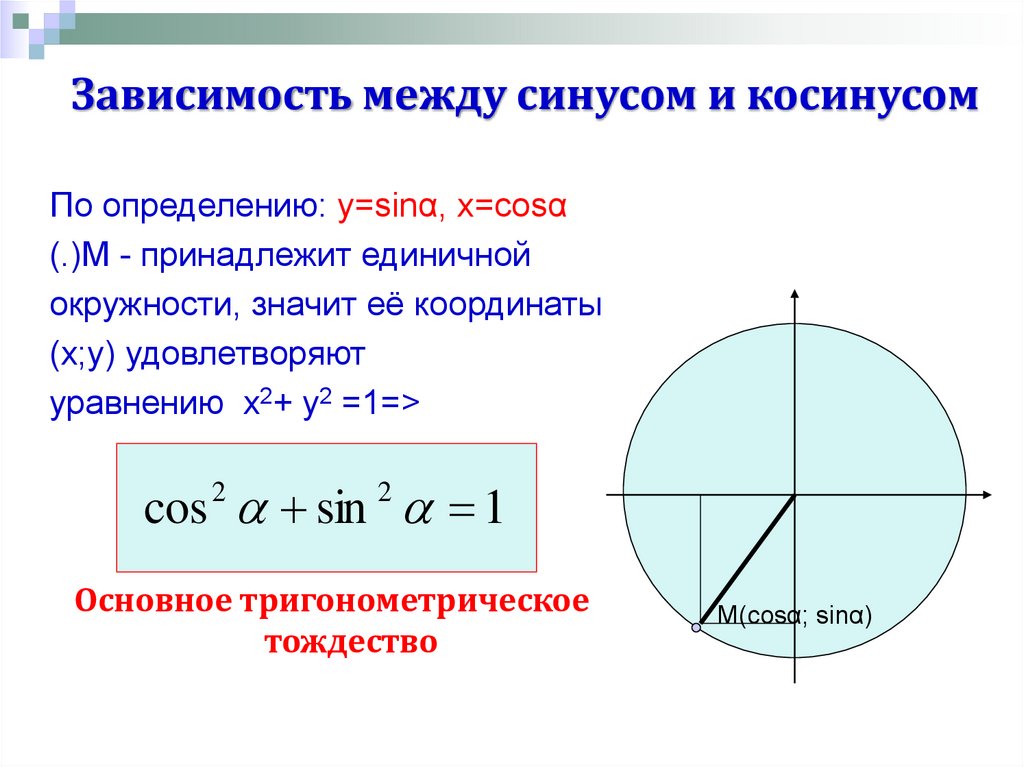
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.

Рассмотрение пределов изменения cos α и sin α

Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.

Предел изменения косинуса:

-1 < cos α < 1.

Предел изменения синуса: 0 < sin α ≤ 1.

Если cos α > 0, то α ∈ (0°;90°)
Если cos α < 0, то α ∈ (90°;180°)
Если cos α = 0, то α = 90°

Примеры решения задач

При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.

Пример 1. Дан треугольник АВС. Найти длину СМ.

∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.

Как решаем:

Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B:

Из треугольника СМВ по теореме косинусов найдём СМ:

Ответ: СМ = .

Пример 2. Дан треугольник АВС, в котором a2 + b2 < c2. Доказать, что ∠C — тупой угол.

Как доказываем:

Для доказательства нужно вспомнить теорему косинусов для угла ∠C:

Так как a² + b² < c², то cos C < 0, следовательно, ∠C — тупой.

Что и требовалось доказать.

Эта задача нам показала, что с помощью теоремы косинусов можно определить тупой угол или острый.

Если c² = a² + b², то ∠C = 90°.

Если c² < a² + b², то ∠C — острый.

Больше объяснений по этой и другим темам вы найдете в справочнике по математике — с формулами, чертежами и примерами решения задач.

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

Теоремы, которые точно пригодятся на ЕГЭ

К следующей статье

156.8K

Векторное произведение векторов

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс

Приближение синуса и косинуса полиномом 2 степени / Habr

На сайте habr.com/ru уже были похожие публикации осенью 2021 года:

Как посчитать синус быстрее всех

Как посчитать синус быстро

Не на Habr Как сделать быструю функцию для вычисления синуса? топик начат в 2003 году последний отклик в 2020 году. 5 … ) , а обычной параболой поведенной через точки 1,2,3 как на рисунке.

Точки 1 и 2 базовые, размещаются с определенным задаваемым шагом. В скрипте Scilab это переменная step. Координаты точки 3 будем вычислять таким образом, чтобы в ней было максимальное отклонение синуса ( или косинуса ) от отрезка 1-2.

Ниже приведены скрипты на Scilab для расчета коэффициентов полинома второй степени на интервале [ 0 … pi /2] и графики отклонений для от функций синуса и косинуса .

Расчет коэффициентов для синуса на Scilab

/// синус
function [a,b,c]=  koef_parabola(x1,y1,x2,y2,x3,y3)
   /// расчет коэффициентов параболы по 3 точкам 
    a1= y3 -  ( x3*(y2-y1)+ x2*y1 -x1*y2 )/( x2-x1)
    a2=   x3*( x3-x1-x2 ) + x1*x2  
    a= a1 /a2
    b =( y2-y1)/( x2-x1) - a*( x1+x2)
    c=( x2*y1 - x1*y2) / (x2-x1)   + a * x1*x2
endfunction
kol_int =12   /// количество интервалов на отрезке 0 ... %pi/ 2
kol_funct =kol_int+1
step =%pi/ ( 2*kol_int)  /// шаг
point0_x =0:step:%pi/ 2
point0_sin = cos(point0_x)
aa_sin =1:1:(kol_int)
bb_sin =1:1:(kol_int)
cc_sin =1:1:(kol_int)
    xx1=0
    yy1=1
for ii=1:1:kol_int
    xx2=xx1+step
    yy2=cos(xx2)
    wsp1 =(yy2-yy1)/(xx2-xx1)  /// наклон
    xx3=asin(-wsp1)   /// координаты центральной точки
    yy3= sqrt( 1- wsp1^2)  ///  cos(xx3)
     [aa,bb,cc]=koef_parabola( xx1,yy1,xx2,yy2,xx3,yy3)
     aa_sin(ii)=aa
     bb_sin(ii)=bb
     cc_sin(ii)=cc         
     xx1=xx2
     yy1=yy2
end
 ///вывод шага и коэффициентов
 disp( step,aa_sin,bb_sin,cc_sin) 
    xx1=0
   xx2=step 
for ii=1:1:kol_int
int01=[xx1:0. 2 -b1*int01-c1 ) )
   xx1=xx1+step
   xx2=xx2+step 
end

Пример отклонений для синуса

график отклонений полинома второй степени от синуса на интервале 0 … Пи/ 2 при разбиении на 8 интервалов ( размер интервала =Пи/ 16 примерно = 0.196 )

Расчет коэффициентов для косинуса на Scilab

function [a, b, c]=koef_parabola(x1, y1, x2, y2, x3, y3)
   /// расчет коэффициентов параболы по 3 точкам 
    a1= y3 -  ( x3*(y2-y1)+ x2*y1 -x1*y2 )/( x2-x1)
    a2=   x3*( x3-x1-x2 ) + x1*x2  
    a= a1 /a2
    b =( y2-y1)/( x2-x1) - a*( x1+x2)
    c=( x2*y1 - x1*y2) / (x2-x1)   + a * x1*x2
endfunction
kol_int =12   /// количество интервалов на отрезке 0 ... %pi/ 2
kol_funct =kol_int+1
step =%pi/ ( 2kol_int)  /// шаг
point0_x =0:step:%pi/ 2
point0_sin = cos(point0_x)
aa_sin =1:1:(kol_int)
bb_sin =1:1:(kol_int)
cc_sin =1:1:(kol_int)
xx1=0
yy1=1
for ii=1:1:kol_int
xx2=xx1+step
yy2=cos(xx2)
wsp1 =(yy2-yy1)/(xx2-xx1)  /// наклон
xx3=asin(-wsp1)   /// координаты центральной точки
yy3= sqrt( 1- wsp1^2)  ///  cos(xx3)
[aa,bb,cc]=koef_parabola( xx1,yy1,xx2,yy2,xx3,yy3)
aa_sin(ii)=aa
bb_sin(ii)=bb
cc_sin(ii)=cc
xx1=xx2
yy1=yy2
end
///вывод шага и коэффициентов
disp( step,aa_sin,bb_sin,cc_sin)
xx1=0
xx2=step
for ii=1:1:kol_int
int01=[xx1:0. 2 -b1*int01-c1 ) )
xx1=xx1+step
xx2=xx2+step
end

Пример отклонений для косинуса

график отклонений полинома второй степени от синуса на интервале 0 … Пи/ 2 при разбиении на 12 интервалов

Синус таблица коэффициентов полинома степени 2 для 8 интервалов

( шаг Пи / 16 )

Я не привожу кода на каком либо языке или псевдокода, дабы не засорять публикацию, каждый желающий может подобрать себе коэффициенты полинома степени 2 для аппроксимации и написать свою функцию. По значению аргумента x вычисляем номер интервала, запоминаем коэффициенты и подставляем из в формулу полинома

тригонометрия — Преобразование комбинации функций синуса и косинуса в функцию синуса или косинуса

Предположим, что $y=a\sin\theta \pm b\cos\theta$

комбинацию функций синуса и косинуса трудно анализировать. Итак, мы пытаемся преобразовать все выражение в выражение, состоящее только из одной тригонометрической функции, то есть либо функции синуса, либо функции косинуса.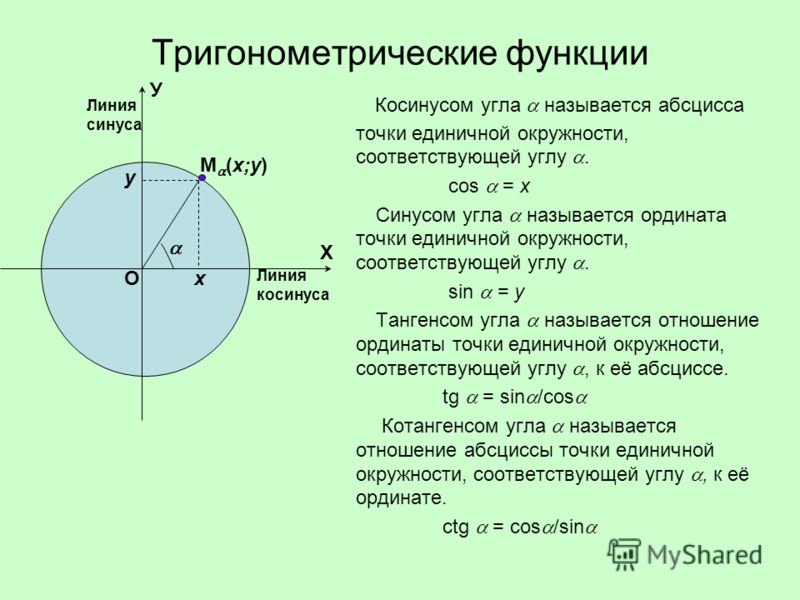 2\theta$, что равно единице. 92}\sin(\theta \pm \alpha)$

Единица измерения Окружность: функции синуса и косинуса

Результаты обучения

Найдите значения функции для синуса и косинуса специальных углов.
Определение области определения и диапазона функций синуса и косинуса.
Используйте опорные углы для оценки тригонометрических функций.
Вычислите значения синуса и косинуса с помощью калькулятора.

Чтобы определить наши тригонометрические функции, мы начнем с рисования единичной окружности с центром в начале координат и радиусом 1, как показано на рисунке 2. Угол (в радианах), который пересекает [латекс]t[/латекс], образует дуга длиной [латекс]s[/латекс]. Используя формулу [latex]s=rt[/latex] и зная, что [latex]r=1[/latex], мы видим, что для единичный круг , [латекс]s=t[/латекс].

Напомним, что оси x- и y- делят координатную плоскость на четыре четверти, называемые квадрантами. Мы помечаем эти квадранты, чтобы имитировать направление положительного угла. Четыре квадранта обозначены I, II, III и IV.

Для любого угла [латекс]t[/латекс] мы можем пометить пересечение конечной стороны и единичного круга его координатами [латекс]\влево(х,у\вправо)[/латекс]. Координаты [латекс]х[/латекс] и [латекс]у[/латекс] будут выходами тригонометрических функций [латекс]f\left(t\right)=\cos t[/латекс] и [латекс] f\left(t\right)=\sin t[/latex] соответственно. Это означает [латекс]x=\cos t[/латекс] и [латекс]у=\sin t[/латекс].

Рисунок 2. Единичная окружность, центральный угол которой равен [латекс]t[/латекс] радианам

A Общее примечание: Единичная окружность

0\right)[/latex] и радиус [latex]1[/latex] . В единичном круге длина пересекаемой дуги равна радианной мере центрального угла [латекс]1[/латекс].

Пусть [латекс]\влево(х,у\вправо)[/латекс] будет концом единичной окружности дуги с длиной дуги [латекс]s[/латекс]. Координаты [латекс]\влево(х,у\вправо)[/латекс] этой точки можно описать как функции угла.

Определение функций синуса и косинуса

Теперь, когда мы пометили нашу единичную окружность, мы можем узнать, как координаты [латекс]\влево(х,у\вправо)[/латекс] относятся к длине дуги и углу . Функция синуса связывает действительное число [latex]t[/latex] с y -координатой точки, где соответствующий угол пересекает единичную окружность. Точнее, синус угла [latex]t[/latex] равен y -значению конечной точки на единичной окружности дуги длины [latex]t[/latex]. На рисунке 2 синус равен [latex]y[/latex]. Как и все функции, синусоидальная функция имеет вход и выход. Его вход является мерой угла; его выход y -координата соответствующей точки на единичной окружности.

Функция косинуса угла [latex]t[/latex] равна x -значению конечной точки на единичной окружности дуги длины [latex]t[/latex]. На рисунке 3 косинус равен [latex]x[/latex].

. {2} [ /латекс]. Имейте в виду, что многие калькуляторы и компьютеры не распознают стенографию. Если вы сомневаетесь, используйте дополнительные скобки при вводе вычислений в калькулятор или компьютер.

Общее примечание: функции синуса и косинуса

Если [latex]t[/latex] является действительным числом и точка [latex]\left(x,y\right)[/latex] на единичной окружности соответствует угол [латекс]t[/латекс], затем

[латекс]\cos t=x[/латекс]

[латекс]\sin t=y[/латекс]

Как: Дана точка

P [латекс]\влево(х,у\вправо)[/латекс] на единичной окружности, соответствующей углу [латекс]t[/латекс], найдите синус и косинус.
Синус [latex]t[/latex] равен y -координата точки [latex]P:\sin t=y[/latex].
Косинус [latex]t[/latex] равен x -координате точки [latex]P: \text{cos}t=x[/latex].
Пример 1. Нахождение значений функции для синуса и косинуса
Точка [latex]P[/latex] — это точка на единичной окружности, соответствующая углу [latex]t[/latex], как показано на рисунке 4. Найдите [латекс]\cos\left(t\right)[/latex] и [латекс]\text{sin}\left(t\right)[/latex].
Рисунок 4
Показать решение
Попробуйте
Некоторый угол [latex]t[/latex] соответствует точке на единичной окружности в точке [latex]\left(-\frac{\sqrt{2}}{2},\frac{\ sqrt{2}}{2}\right)[/latex], как показано на рисунке 5. Найдите [latex]\cos t[/latex] и [latex]\sin t[/latex].
Рисунок 5
Показать решение
Нахождение синусов и косинусов углов на оси
Для четырехугольных углов соответствующая точка на единичной окружности приходится на 9{2}t=1[/latex], известный как Пифагорейская идентичность .
Мы можем использовать тождество Пифагора, чтобы найти косинус угла, если мы знаем синус, или наоборот. Однако, поскольку уравнение дает два решения, нам нужно дополнительное знание угла, чтобы выбрать решение с правильным знаком. Если мы знаем квадрант, в котором находится угол, мы можем легко выбрать правильное решение.
Общее примечание: Пифагорейская идентичность
Пифагорейская идентичность 9{2}t=1[/latex]
Как сделать: Зная синус некоторого угла [latex]t[/latex] и его положение в квадранте, найдите косинус [latex]t[/latex].
Подставить известное значение [латекс]\sin\left(t\right)[/латекс] в тождество Пифагора.
Найдите [латекс]\cos\left(t\right)[/латекс].
Выберите решение с соответствующим знаком для значений x в квадранте, где находится [латекс]t[/латекс].
Пример 3. Нахождение косинуса по синусу или синуса по косинусу
Если [латекс]\sin \left(t\right)=\frac{3}{7}[/latex] и [latex]t[/latex] находится во втором квадранте, найти [latex]\cos \ влево(т\вправо)[/латекс].
Показать раствор
Попробуйте
Если [латекс]\cos \left(t\right)=\frac{24}{25}[/latex] и [латекс]t[/латекс] находится в четвертом квадранте, найдите [латекс ]\sin\left(t\right)[/латекс].
Показать решение
Попробуйте
Нахождение синусов и косинусов специальных углов
Мы уже изучили некоторые свойства специальных углов, например преобразование радианов в градусы. Мы также можем вычислить синусы и косинусы специальных углов, используя 9\circ [/latex] треугольник является равнобедренным треугольником, поэтому координаты x и y соответствующей точки на окружности совпадают. Поскольку значения x- и y одинаковы, значения синуса и косинуса также будут равны. Рис. 9 Это означает, что радиус лежит вдоль линии [латекс]у=х[/латекс]. Радиус единичной окружности равен 1. Итак, прямоугольный треугольник, образованный под линией [latex]y=x[/latex], имеет стороны [latex]x[/latex] и [latex]y\text{ }\left (y=x\right)[/latex], а радиус = 1,9{2}=\frac{1}{2}\\ x=\pm \frac{1}{\sqrt{2}}\end{gathered}[/latex]
В квадранте I [latex]x= \frac{1}{\sqrt{2}}[/latex].
В [латекс]t=\frac{\pi }{4}[/латекс] или 45 градусов, x\right)=\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right) \\ x=\frac{1}{\sqrt{2 }},y=\frac{1}{\sqrt{2}}\\ \cos t=\frac{1}{\sqrt{2}},\sin t=\frac{1}{\sqrt{2 }} \end{gathered}[/latex]
Если мы затем рационализируем знаменатели, то получим
9\circ [/latex], как показано на рисунке 12.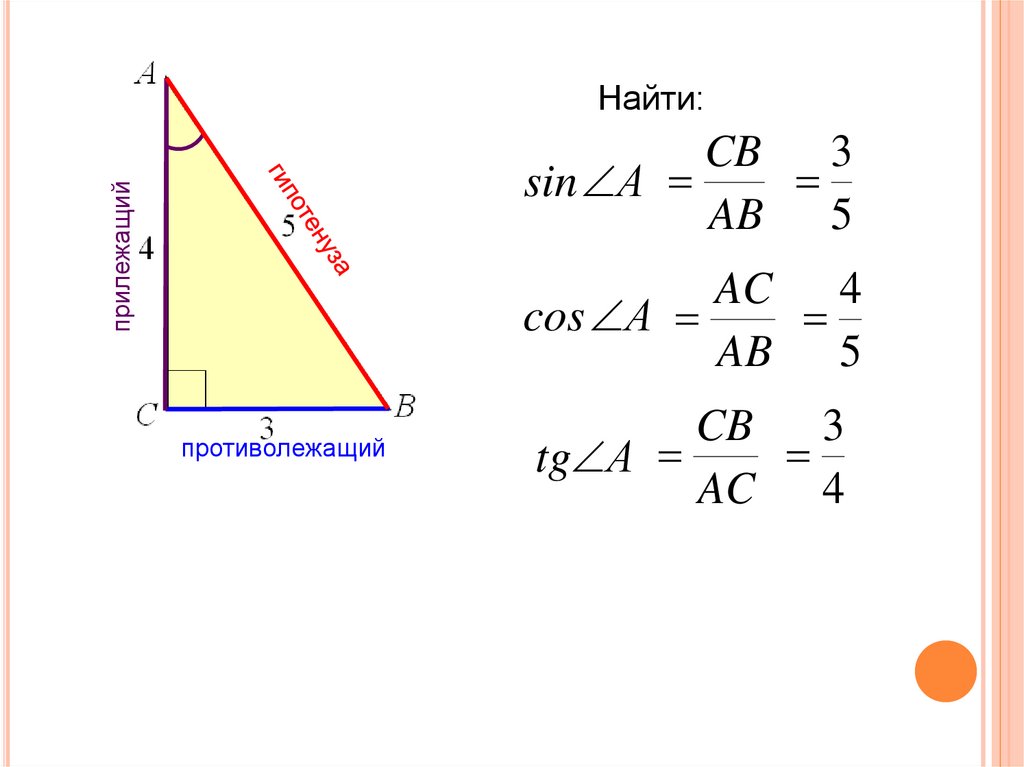
Рисунок 11

Рисунок 12
Поскольку все углы равны, стороны также равны. Вертикальная линия имеет длину [latex]2y[/latex], и поскольку все стороны равны, мы также можем заключить, что [latex]r=2y[/latex] или [latex]y=\frac{1}{2 }р[/латекс]. Поскольку [латекс]\sin t=y[/латекс] ,
[латекс]\sin \left(\frac{\pi }{6}\right)=\frac{1}{2}r[/latex]
А так как [latex]r=1[/latex] в нашем 9\circ [/латекс]. Теперь у нас есть равносторонний треугольник. Поскольку каждая сторона равностороннего треугольника [латекс]ABC[/латекс] имеет одинаковую длину, и мы знаем, что одна сторона является радиусом единичной окружности, длина всех сторон должна быть равна 1.
Рисунок 13
Угол [латекс]ABD[/латекс] равен 30°. Итак, если число двойное, угол [латекс]АВС[/латекс] равен 60°. [latex]BD[/latex] является серединным перпендикуляром к [latex]AC[/latex], поэтому он делит [latex]AC[/latex] пополам. Это означает, что [latex]AD[/latex] — это [latex]\frac{1}{2}[/latex] радиус, или [latex]\frac{1}{2}[/latex]. Обратите внимание, что [latex]AD[/latex] — это 9\circ [/latex] равны [латекс]\left(\frac{1}{2},\frac{\sqrt{3}}{2}\right)\[/latex], поэтому мы можем найти синус и косинус.
[латекс] \ begin {собраны} \ влево (x, y \ вправо) = \ влево (\ frac {1} {2}, \ frac {\ sqrt {3}} {2} \ right) \\ x =\ frac {1} {2}, y = \ frac {\ sqrt {3}} {2} \\ \ cos t = \ frac {1} {2}, \ sin t = \ frac {\ sqrt {3 }}{2} \end{gathered}[/latex]
Теперь мы нашли значения косинуса и синуса для всех наиболее часто встречающихся углов в первом квадранте единичной окружности. В таблице ниже приведены эти значения.
Угол 0 [латекс]\frac{\pi }{6}[/латекс], или 30° [латекс]\frac{\pi }{4}[/латекс], или 45° [латекс]\frac{\pi }{3}[/латекс], или 60° [латекс]\frac{\pi }{2}[/латекс], или 90°
Косинус 1 [латекс]\frac{\sqrt{3}}{2}[/латекс] [латекс]\frac{\sqrt{2}}{2}[/латекс] [латекс]\фракция{1}{2}[/латекс] 0
Синус 0 [латекс]\фракция{1}{2}[/латекс] [латекс]\frac{\sqrt{2}}{2}[/латекс] [латекс]\frac{\sqrt{3}}{2}[/латекс] 1
На рисунке 14 показаны общие углы в первом квадранте единичной окружности.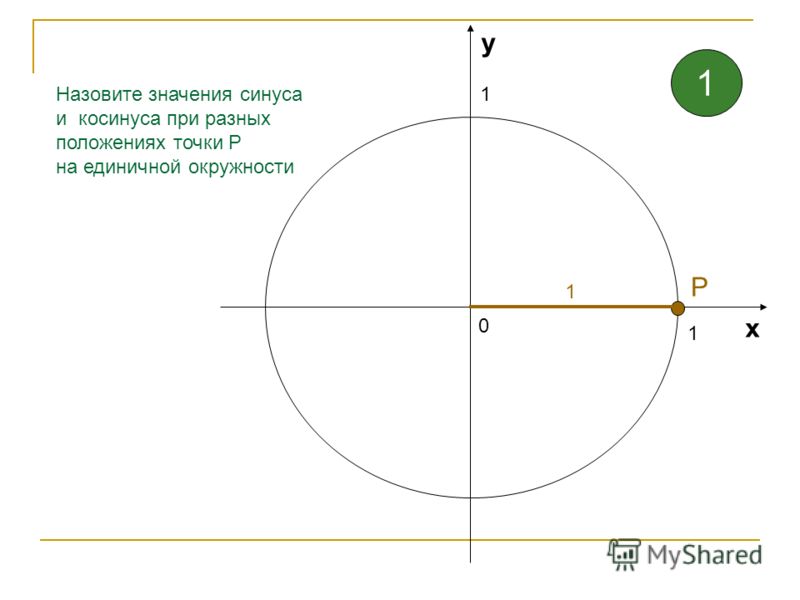 Рис. 140066 специальные углы , обращаемся к компьютеру или калькулятору. Имейте в виду : Большинство калькуляторов можно установить в режим «градусы» или «радианы», которые сообщают калькулятору единицы измерения для входного значения. Когда мы оцениваем [латекс]\cos \left(30\right)[/латекс] на нашем калькуляторе, он будет оценивать его как косинус 30 градусов, если калькулятор находится в режиме градусов, или как косинус 30 радиан, если калькулятор находится в радианном режиме.
Как: Зная угол в радианах, используйте графический калькулятор, чтобы найти косинус.

Если в калькуляторе есть режимы в градусах и в радианах, установите его в режим в радианах.
Нажмите клавишу COS.
Введите значение угла в радианах и нажмите клавишу закрытия скобок «)».
Нажмите ВВОД.
Пример 4. Использование графического калькулятора для нахождения синуса и косинуса
Вычислите значение [latex]\cos \left(\frac{5\pi }{3}\right)[/latex] с помощью графического калькулятора или компьютера.

Показать решение
Попробуй
Вычислить [латекс]\sin\left(\frac{\pi }{3}\right)[/latex].
Показать решение

Определение области определения и диапазона функций синуса и косинуса
Теперь, когда мы можем найти синус и косинус угла, нам нужно обсудить их области определения и диапазоны. Каковы области определения функций синуса и косинуса? То есть, каковы наименьшее и наибольшее числа, которые могут быть входными данными функций? Поскольку углы меньше 0 и углы больше [латекс]2\пи [/латекс] все еще могут быть изображены на единичном круге и имеют реальные значения [латекс]x,y[/латекс] и [латекс]r[/ латекс], нет нижнего или верхнего предела углов, которые могут быть входными данными для функций синуса и косинуса.
Входными данными для функций синуса и косинуса является вращение от положительной x -ось, и это может быть любое действительное число.
Каковы диапазоны функций синуса и косинуса? Каковы наименьшее и максимальное возможные значения их выхода? Мы можем увидеть ответы, исследуя единичный круг , как показано на рисунке 15. Границы координаты x равны [латекс]\лево[-1,1\право][/латекс]. Границы координаты y также равны [латекс]\влево[-1,1\вправо][/латекс]. Таким образом, диапазон функций синуса и косинуса составляет [латекс]\влево[-1,1\вправо][/латекс].
Рисунок 15
Мы обсудили нахождение синуса и косинуса для углов в первом квадранте, но что, если наш угол находится в другом квадранте? Для любого заданного угла в первом квадранте существует угол во втором квадранте с таким же значением синуса. Поскольку значением синуса является координата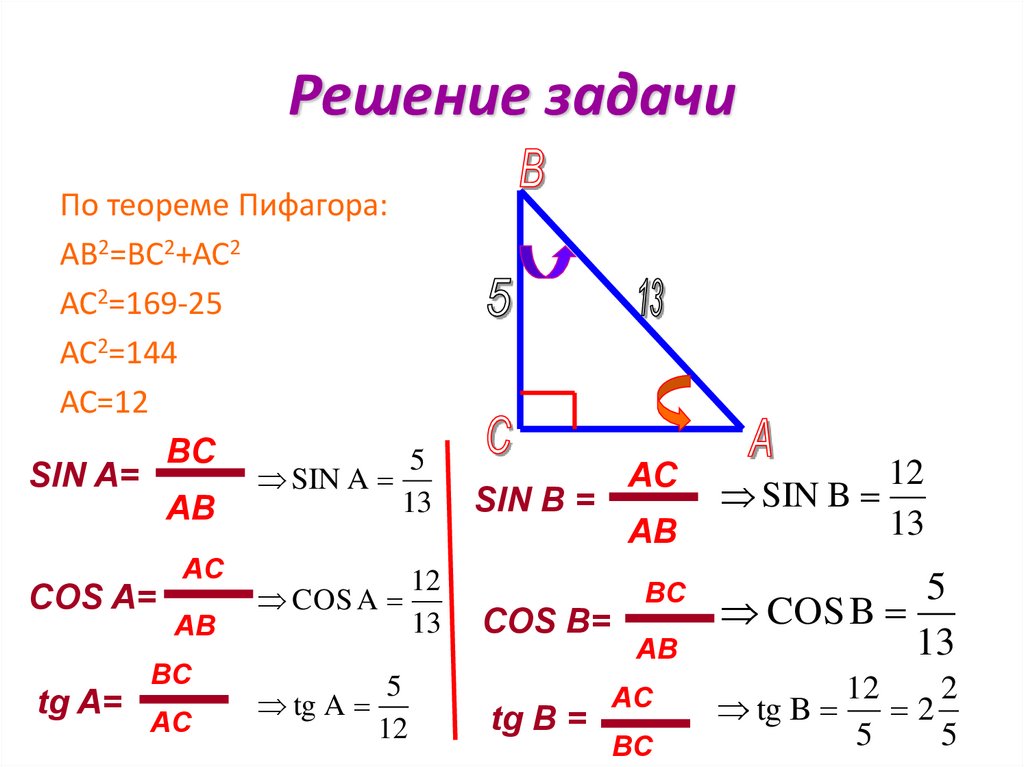
y на единичной окружности, другой угол с таким же синусом будет иметь такое же значение y , но противоположное значение x . Следовательно, его значение косинуса будет противоположно значению косинуса первого угла.
Аналогично, в четвертом квадранте будет угол с тем же косинусом, что и исходный угол. Угол с тем же косинусом будет иметь такое же значение x , но будет иметь противоположное значение y . Следовательно, его значение синуса будет противоположно значению синуса исходного угла.
Как показано на рисунке 16, угол [латекс]\альфа [/латекс] имеет то же значение синуса, что и угол [латекс]t[/латекс]; значения косинуса противоположны. Угол [латекс]\бета [/латекс] имеет то же значение косинуса, что и угол [латекс]t[/латекс]; значения синуса противоположны.
[латекс]\begin{array}{ccc}\sin \left(t\right)=\sin \left(\alpha \right)\hfill & \text{and}\hfill & \cos \left(t \right)=-\cos \left(\alpha \right)\hfill \\ \sin \left(t\right)=-\sin \left(\beta \right)\hfill & \text{and}\hfill & \cos \left(t\right)=\cos \left(\beta \right)\hfill \end{array}[/latex]
Рисунок 16
острый угол, [латекс]t[/латекс], образованный конечной стороной угла [латекс]t[/латекс] и горизонтальной осью.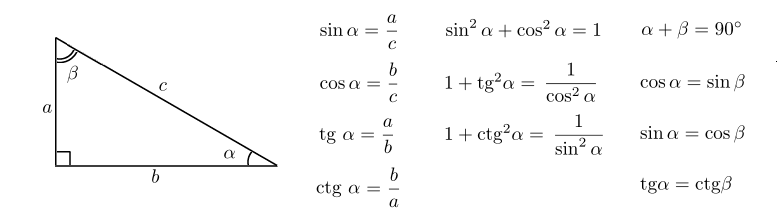 \circ \mathrm{-t}|[/латекс]. 9\circ [/latex], как показано на рисунке 18.
Рисунок 18
Показать решение
Попробуйте
Найдите исходный угол [латекс]\фракция{5\пи }{3}[/латекс].
Показать решение
Использование опорных углов
Теперь давайте еще раз рассмотрим колесо обозрения, представленное в начале этого раздела. Предположим, всадник делает снимок, остановившись в двадцати футах над уровнем земли. Затем всадник вращается на три четверти круга. Какова новая высота всадника? Чтобы ответить на такие вопросы, как этот, нам нужно оценить функции синуса или косинуса при углах, превышающих 90 градусов или под отрицательным углом . Опорные углы позволяют вычислять тригонометрические функции для углов вне первого квадранта. Их также можно использовать для нахождения [латексных]\левых(х,у\правых)[/латексных] координат для этих углов. Мы будем использовать опорный угол угла поворота в сочетании с квадрантом, в котором лежит конечная сторона угла.
Использование опорных углов для вычисления тригонометрических функций
Мы можем найти косинус и синус любого угла в любом квадранте, если знаем косинус или синус его опорного угла. Абсолютные значения косинуса и синуса угла такие же, как у опорного угла. Знак зависит от квадранта исходного угла. Косинус будет положительным или отрицательным в зависимости от знака числа 9.0070 x — значения в этом квадранте. Синус будет положительным или отрицательным в зависимости от знака значений и в этом квадранте.
Общее примечание: использование опорных углов для нахождения косинуса и синуса
Углы имеют косинусы и синусы с тем же абсолютным значением, что и их опорные углы. Знак (положительный или отрицательный) можно определить по квадранту угла.
Как сделать: по заданному углу в стандартном положении найдите опорный угол, а также косинус и синус исходного угла.

Измерьте угол между конечной стороной заданного угла и горизонтальной осью. Это опорный угол.
Определите значения косинуса и синуса опорного угла.
Присвойте косинусу тот же знак, что и значениям x в квадранте исходного угла.
Присвойте синусу тот же знак, что и y -значения в квадранте исходного угла.
Пример 6. Использование опорных углов для нахождения синуса и косинуса 9\circ \right)[/латекс].
б. Используйте опорный угол [латекс]-\frac{\pi }{6}[/латекс], чтобы найти [латекс]\cos\left(-\frac{\pi }{6}\right)[/латекс] и [латекс]\sin\left(-\frac{\pi}{6}\right)[/латекс].
Показать решение
Попробуйте
Использование опорных углов для нахождения координат
Теперь, когда мы научились находить значения косинуса и синуса для специальных углов в первом квадранте, мы можем использовать симметрию и опорные углы для заполнения значений косинуса и синуса для остальные специальные углы на единичной окружности. Они показаны на рисунке 19. . Потратьте время, чтобы узнать [латексные]\левые(х,у\правые)[/латексные] координаты всех главных углов в первом квадранте.
Помимо изучения значений специальных углов, мы можем использовать эталонные углы для нахождения [латексных]\левых(х,у\правых)[/латексных] координат любой точки на единичной окружности, используя то, что мы знаем об эталонных углы вместе с тождествами
[латекс]\begin{gathered}x=\cos t \\ y=\sin t \end{gathered}[/latex]
Сначала находим опорный угол, соответствующий заданному угол. Затем мы берем значения синуса и косинуса опорный угол , и присвойте им знаки, соответствующие y – и x -значениям квадранта.
Как сделать: Зная угол точки на окружности и радиус окружности, найдите [латекс]\влево(х,у\вправо)[/латекс] координаты точки.
Найдите опорный угол, измерив наименьший угол относительно оси x .
Найдите косинус и синус опорного угла.
Определите соответствующие знаки для [latex]x[/latex] и [latex]y[/latex]
в данном квадранте.
Пример 7. Использование единичного круга для поиска координат
Найдите координаты точки на единичном круге под углом [латекс]\фрак{7\пи }{6}[/латекс].
Показать решение
Попробуйте
Найдите координаты точки на единичной окружности под углом [latex]\frac{5\pi }{3}[/latex].
Показать решение
Ключевые уравнения
Косинус [латекс]\cos t=x[/латекс] 9{2}t=1[/латекс]
Ключевые понятия
Нахождение значений функции для синуса и косинуса начинается с рисования единичной окружности с центром в начале координат и радиусом в 1 единицу.
Используя единичную окружность, синус угла [latex]t[/latex] равен y -значению конечной точки единичной окружности дуги длины [latex]t[/latex], тогда как косинус угла угол [latex]t[/latex] равен x -значению конечной точки.
Значения синуса и косинуса наиболее непосредственно определяются, когда соответствующая точка на единичной окружности попадает на ось.
Когда синус или косинус известны, мы можем использовать тождество Пифагора, чтобы найти другое. Тождество Пифагора также полезно для определения синусов и косинусов специальных углов.
Калькуляторы и программы для построения графиков полезны для нахождения синусов и косинусов, если известна правильная процедура ввода информации.
Областью определения функций синуса и косинуса являются все действительные числа.
Диапазон функций синуса и косинуса: [латекс]\влево[-1,1\вправо][/латекс].
Синус и косинус угла имеют то же абсолютное значение, что и синус и косинус исходного угла.
Знаки синуса и косинуса определяются из значений x – и y в квадранте исходного угла.
Опорный угол угла — это размерный угол, [latex]t[/latex],
образованный конечной стороной угла [latex]t[/latex] и горизонтальной осью.
No related posts.