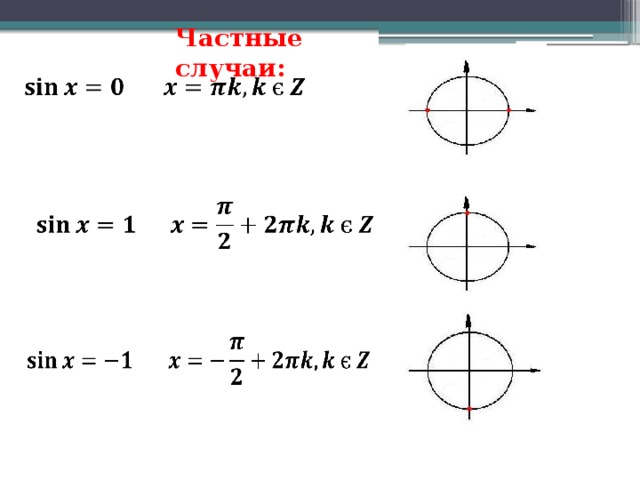
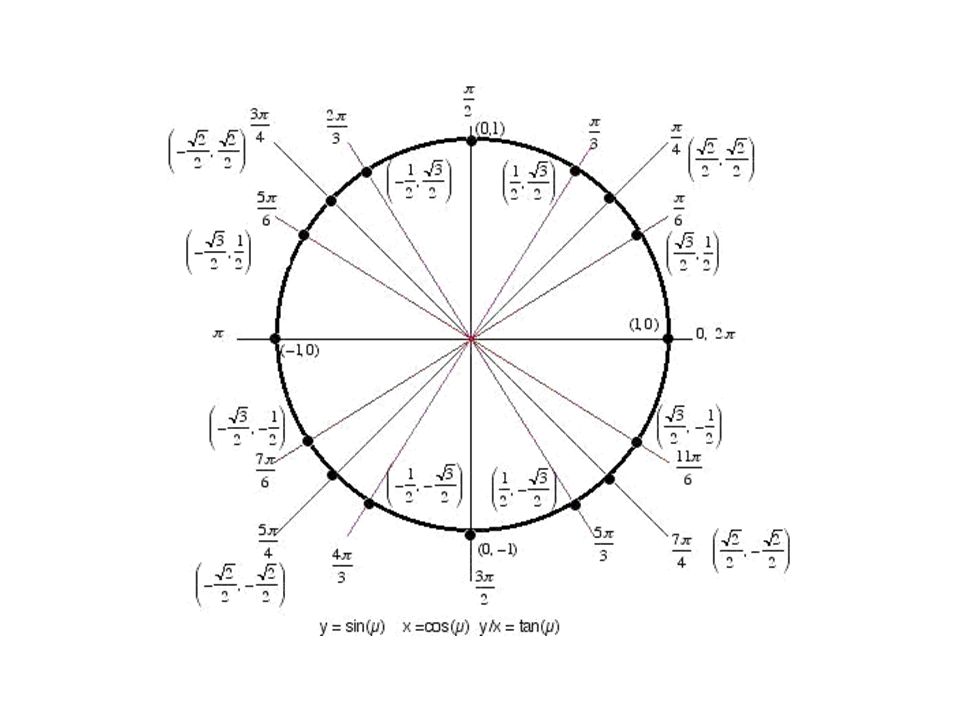
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град.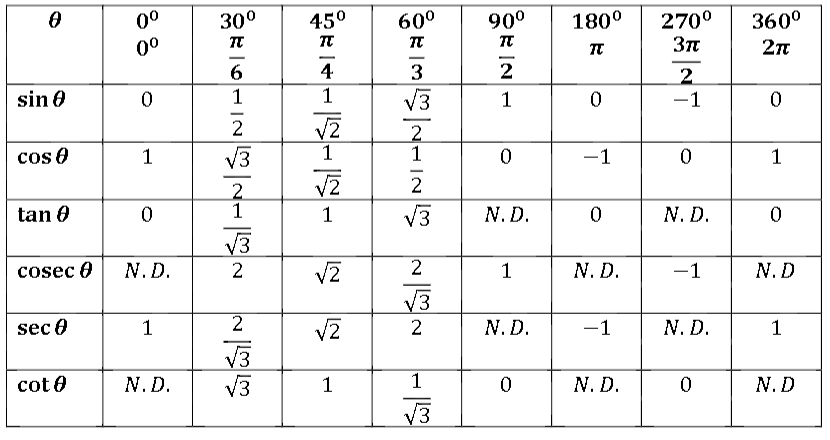 ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град.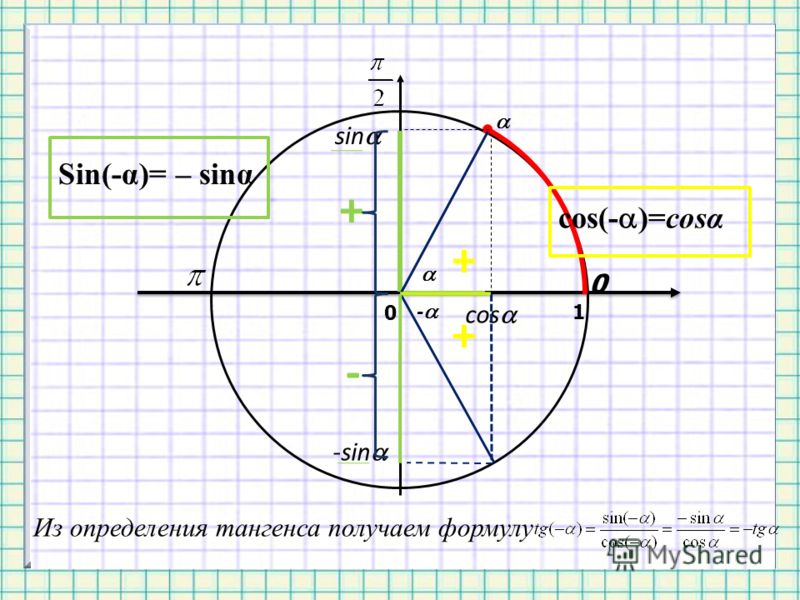 ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | sin(120 град. ) ) | ||
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Таблица синусов.
Таблица синусов Таблица косинусов Таблица тангенсов Таблица котангенсов Таблица Брадиса: синусы, косинусы, тангенсы и котангенсыСкачать таблицу синусов
Таблица синусов — это записанные в таблицу посчитанные значения синусов углов от 0° до 360°. Используя таблицу синусов вы сможете провести расчеты даже если под руками не окажется инженерного калькулятора. Чтобы узнать значение синуса от нужного Вам угла достаточно найти его в таблице.
Используя таблицу синусов вы сможете провести расчеты даже если под руками не окажется инженерного калькулятора. Чтобы узнать значение синуса от нужного Вам угла достаточно найти его в таблице.
Калькулятор — синус угла
sin(°) = 0
Калькулятор — арксинус угла
arcsin() = 90°
Таблица синусов в радианах
| α | 0 | π6 | π4 | π3 | π2 | π | 3π2 | 2π |
| sin α | 0 | 12 | √32 | 1 | 0 | -1 | 0 |
Таблица синусов углов от 0° до 180°
| sin(0°) = 0 sin(1°) = 0.017452 sin(2°) = 0.034899 sin(3°) = 0.052336 sin(4°) = 0.069756 sin(5°) = 0.087156 sin(6°) = 0.104528 sin(7°) = 0. 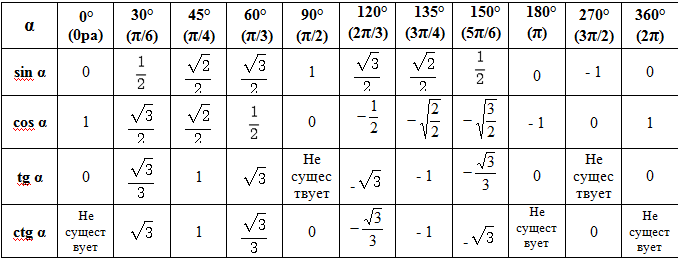 121869 121869sin(8°) = 0.139173 sin(9°) = 0.156434 sin(10°) = 0.173648 sin(11°) = 0.190809 sin(12°) = 0.207912 sin(13°) = 0.224951 sin(14°) = 0.241922 sin(15°) = 0.258819 sin(16°) = 0.275637 sin(17°) = 0.292372 sin(18°) = 0.309017 sin(19°) = 0.325568 sin(20°) = 0.34202 sin(21°) = 0.358368 sin(22°) = 0.374607 sin(23°) = 0.390731 sin(24°) = 0.406737 sin(25°) = 0.422618 sin(26°) = 0.438371 sin(27°) = 0.45399 sin(28°) = 0.469472 sin(29°) = 0.48481 sin(30°) = 0.5 sin(31°) = 0.515038 sin(32°) = 0.529919 sin(33°) = 0.544639 sin(34°) = 0.559193 sin(35°) = 0.573576 sin(36°) = 0.587785 sin(37°) = 0.601815 sin(38°) = 0.615661 sin(39°) = 0.62932 sin(40°) = 0.642788 sin(41°) = 0.656059 sin(42°) = 0.669131 sin(43°) = 0.681998 sin(44°) = 0.694658 sin(45°) = 0.707107 | sin(46°) = 0.71934 sin(47°) = 0.731354 sin(48°) = 0.743145 sin(49°) = 0. 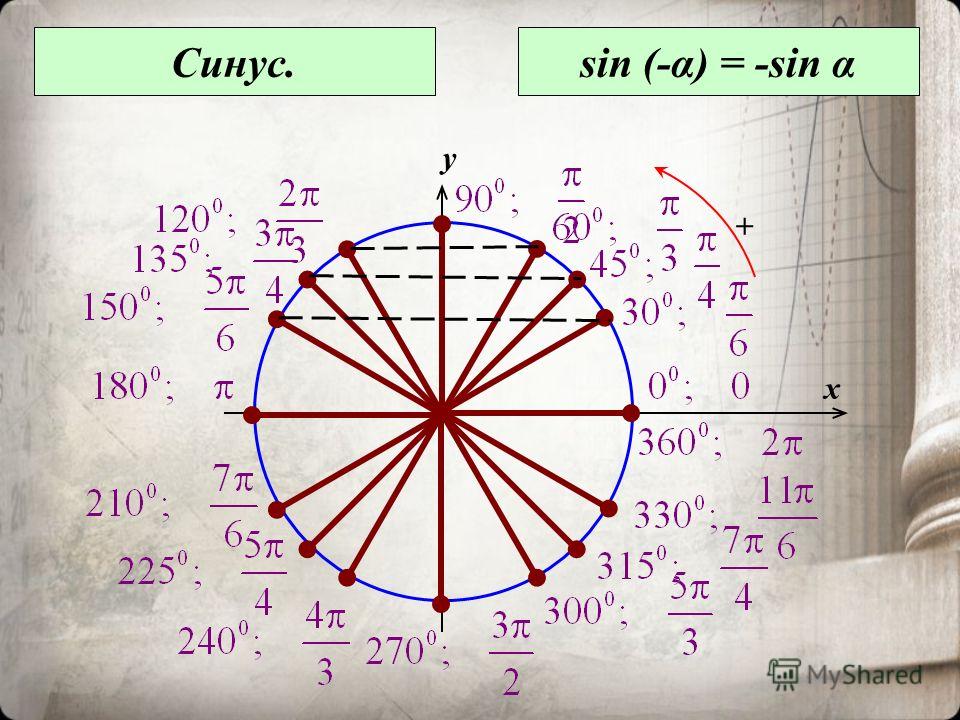 75471 75471sin(50°) = 0.766044 sin(51°) = 0.777146 sin(52°) = 0.788011 sin(53°) = 0.798636 sin(54°) = 0.809017 sin(55°) = 0.819152 sin(56°) = 0.829038 sin(57°) = 0.838671 sin(58°) = 0.848048 sin(59°) = 0.857167 sin(60°) = 0.866025 sin(61°) = 0.87462 sin(62°) = 0.882948 sin(63°) = 0.891007 sin(64°) = 0.898794 sin(65°) = 0.906308 sin(66°) = 0.913545 sin(67°) = 0.920505 sin(68°) = 0.927184 sin(69°) = 0.93358 sin(70°) = 0.939693 sin(71°) = 0.945519 sin(72°) = 0.951057 sin(73°) = 0.956305 sin(74°) = 0.961262 sin(75°) = 0.965926 sin(76°) = 0.970296 sin(77°) = 0.97437 sin(78°) = 0.978148 sin(79°) = 0.981627 sin(80°) = 0.984808 sin(81°) = 0.987688 sin(82°) = 0.990268 sin(83°) = 0.992546 sin(84°) = 0.994522 sin(85°) = 0.996195 sin(86°) = 0.997564 sin(87°) = 0.99863 sin(88°) = 0.999391 sin(89°) = 0.999848 sin(90°) = 1 | sin(91°) = 0.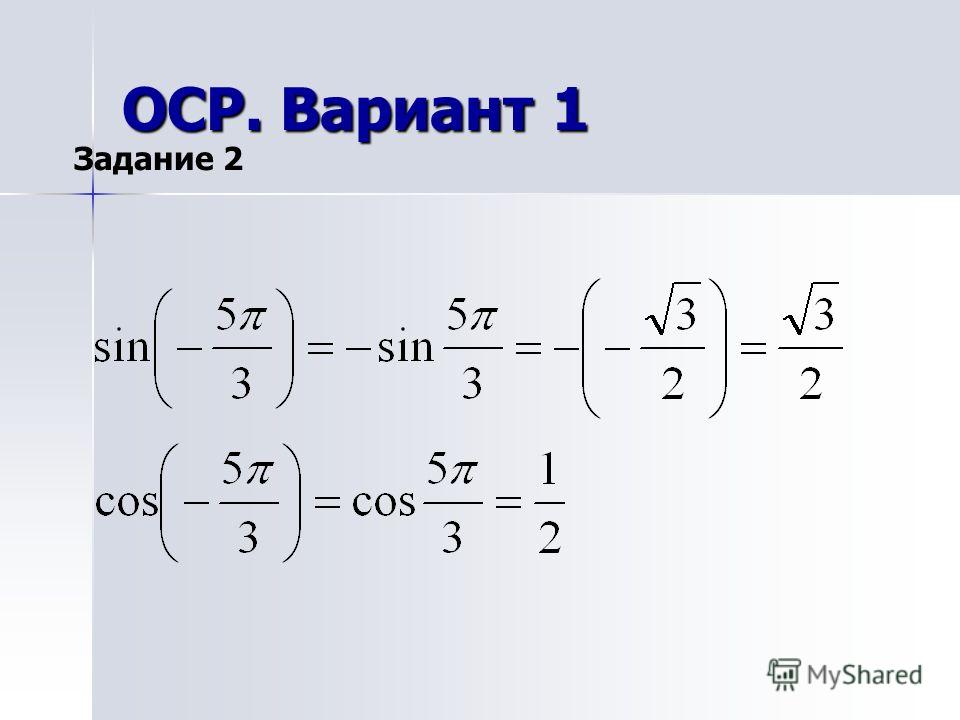 999848 999848sin(92°) = 0.999391 sin(93°) = 0.99863 sin(94°) = 0.997564 sin(95°) = 0.996195 sin(96°) = 0.994522 sin(97°) = 0.992546 sin(98°) = 0.990268 sin(99°) = 0.987688 sin(100°) = 0.984808 sin(101°) = 0.981627 sin(102°) = 0.978148 sin(103°) = 0.97437 sin(104°) = 0.970296 sin(105°) = 0.965926 sin(106°) = 0.961262 sin(107°) = 0.956305 sin(108°) = 0.951057 sin(109°) = 0.945519 sin(110°) = 0.939693 sin(111°) = 0.93358 sin(112°) = 0.927184 sin(113°) = 0.920505 sin(114°) = 0.913545 sin(115°) = 0.906308 sin(116°) = 0.898794 sin(117°) = 0.891007 sin(118°) = 0.882948 sin(119°) = 0.87462 sin(120°) = 0.866025 sin(121°) = 0.857167 sin(122°) = 0.848048 sin(123°) = 0.838671 sin(124°) = 0.829038 sin(125°) = 0.819152 sin(126°) = 0.809017 sin(127°) = 0.798636 sin(128°) = 0.788011 sin(129°) = 0.777146 sin(130°) = 0.766044 sin(131°) = 0.75471 sin(132°) = 0.  743145 743145sin(133°) = 0.731354 sin(134°) = 0.71934 sin(135°) = 0.707107 | sin(136°) = 0.694658 sin(137°) = 0.681998 sin(138°) = 0.669131 sin(139°) = 0.656059 sin(140°) = 0.642788 sin(141°) = 0.62932 sin(142°) = 0.615661 sin(143°) = 0.601815 sin(144°) = 0.587785 sin(145°) = 0.573576 sin(146°) = 0.559193 sin(147°) = 0.544639 sin(148°) = 0.529919 sin(149°) = 0.515038 sin(150°) = 0.5 sin(151°) = 0.48481 sin(152°) = 0.469472 sin(153°) = 0.45399 sin(154°) = 0.438371 sin(155°) = 0.422618 sin(156°) = 0.406737 sin(157°) = 0.390731 sin(158°) = 0.374607 sin(159°) = 0.358368 sin(160°) = 0.34202 sin(161°) = 0.325568 sin(162°) = 0.309017 sin(163°) = 0.292372 sin(164°) = 0.275637 sin(165°) = 0.258819 sin(166°) = 0.241922 sin(167°) = 0.224951 sin(168°) = 0.207912 sin(169°) = 0.190809 sin(170°) = 0.173648 sin(171°) = 0.156434 sin(172°) = 0.139173 sin(173°) = 0.  121869 121869sin(174°) = 0.104528 sin(175°) = 0.087156 sin(176°) = 0.069756 sin(177°) = 0.052336 sin(178°) = 0.034899 sin(179°) = 0.017452 sin(180°) = 0 |
Таблица синусов углов от 181° до 360°
| sin(181°) = -0.017452 sin(182°) = -0.034899 sin(183°) = -0.052336 sin(184°) = -0.069756 sin(185°) = -0.087156 sin(186°) = -0.104528 sin(187°) = -0.121869 sin(188°) = -0.139173 sin(189°) = -0.156434 sin(190°) = -0.173648 sin(191°) = -0.190809 sin(192°) = -0.207912 sin(193°) = -0.224951 sin(194°) = -0.241922 sin(195°) = -0.258819 sin(196°) = -0.275637 sin(197°) = -0.292372 sin(198°) = -0.309017 sin(199°) = -0.325568 sin(200°) = -0.34202 sin(201°) = -0.358368 sin(202°) = -0.374607 sin(203°) = -0.390731 sin(204°) = -0.406737 sin(205°) = -0.422618 sin(206°) = -0.438371 sin(207°) = -0.45399 sin(208°) = -0.  469472 469472sin(209°) = -0.48481 sin(210°) = -0.5 sin(211°) = -0.515038 sin(212°) = -0.529919 sin(213°) = -0.544639 sin(214°) = -0.559193 sin(215°) = -0.573576 sin(216°) = -0.587785 sin(217°) = -0.601815 sin(218°) = -0.615661 sin(219°) = -0.62932 sin(220°) = -0.642788 sin(221°) = -0.656059 sin(222°) = -0.669131 sin(223°) = -0.681998 sin(224°) = -0.694658 sin(225°) = -0.707107 | sin(226°) = -0.71934 sin(227°) = -0.731354 sin(228°) = -0.743145 sin(229°) = -0.75471 sin(230°) = -0.766044 sin(231°) = -0.777146 sin(232°) = -0.788011 sin(233°) = -0.798636 sin(234°) = -0.809017 sin(235°) = -0.819152 sin(236°) = -0.829038 sin(237°) = -0.838671 sin(238°) = -0.848048 sin(239°) = -0.857167 sin(240°) = -0.866025 sin(241°) = -0.87462 sin(242°) = -0.882948 sin(243°) = -0.891007 sin(244°) = -0.898794 sin(245°) = -0.906308 sin(246°) = -0.913545 sin(247°) = -0.  920505 920505sin(248°) = -0.927184 sin(249°) = -0.93358 sin(250°) = -0.939693 sin(251°) = -0.945519 sin(252°) = -0.951057 sin(253°) = -0.956305 sin(254°) = -0.961262 sin(255°) = -0.965926 sin(256°) = -0.970296 sin(257°) = -0.97437 sin(258°) = -0.978148 sin(259°) = -0.981627 sin(260°) = -0.984808 sin(261°) = -0.987688 sin(262°) = -0.990268 sin(263°) = -0.992546 sin(264°) = -0.994522 sin(265°) = -0.996195 sin(266°) = -0.997564 sin(267°) = -0.99863 sin(268°) = -0.999391 sin(269°) = -0.999848 sin(270°) = -1 | sin(271°) = -0.999848 sin(272°) = -0.999391 sin(273°) = -0.99863 sin(274°) = -0.997564 sin(275°) = -0.996195 sin(276°) = -0.994522 sin(277°) = -0.992546 sin(278°) = -0.990268 sin(279°) = -0.987688 sin(280°) = -0.984808 sin(281°) = -0.981627 sin(282°) = -0.978148 sin(283°) = -0.97437 sin(284°) = -0.970296 sin(285°) = -0.965926 sin(286°) = -0.  961262 961262sin(287°) = -0.956305 sin(288°) = -0.951057 sin(289°) = -0.945519 sin(290°) = -0.939693 sin(291°) = -0.93358 sin(292°) = -0.927184 sin(293°) = -0.920505 sin(294°) = -0.913545 sin(295°) = -0.906308 sin(296°) = -0.898794 sin(297°) = -0.891007 sin(298°) = -0.882948 sin(299°) = -0.87462 sin(300°) = -0.866025 sin(301°) = -0.857167 sin(302°) = -0.848048 sin(303°) = -0.838671 sin(304°) = -0.829038 sin(305°) = -0.819152 sin(306°) = -0.809017 sin(307°) = -0.798636 sin(308°) = -0.788011 sin(309°) = -0.777146 sin(310°) = -0.766044 sin(311°) = -0.75471 sin(312°) = -0.743145 sin(313°) = -0.731354 sin(314°) = -0.71934 sin(315°) = -0.707107 | sin(316°) = -0.694658 sin(317°) = -0.681998 sin(318°) = -0.669131 sin(319°) = -0.656059 sin(320°) = -0.642788 sin(321°) = -0.62932 sin(322°) = -0.615661 sin(323°) = -0.601815 sin(324°) = -0.587785 sin(325°) = -0.  573576 573576sin(326°) = -0.559193 sin(327°) = -0.544639 sin(328°) = -0.529919 sin(329°) = -0.515038 sin(330°) = -0.5 sin(331°) = -0.48481 sin(332°) = -0.469472 sin(333°) = -0.45399 sin(334°) = -0.438371 sin(335°) = -0.422618 sin(336°) = -0.406737 sin(337°) = -0.390731 sin(338°) = -0.374607 sin(339°) = -0.358368 sin(340°) = -0.34202 sin(341°) = -0.325568 sin(342°) = -0.309017 sin(343°) = -0.292372 sin(344°) = -0.275637 sin(345°) = -0.258819 sin(346°) = -0.241922 sin(347°) = -0.224951 sin(348°) = -0.207912 sin(349°) = -0.190809 sin(350°) = -0.173648 sin(351°) = -0.156434 sin(352°) = -0.139173 sin(353°) = -0.121869 sin(354°) = -0.104528 sin(355°) = -0.087156 sin(356°) = -0.069756 sin(357°) = -0.052336 sin(358°) = -0.034899 sin(359°) = -0.017452 sin(360°) = 0 |
Таблицы значений тригонометрических функций Таблица Брадиса: синусы, косинусы, тангенсы и котангенсы Таблица синусов Таблица косинусов Таблица тангенсов Таблица котангенсов Сводная таблица тригонометрических функций
Тригонометрические формулы
Все таблицы и формулы
Таблица синусов для школьников и студентов
Таблица синусов необходима для вычислений, связанных со значениями тригонометрических функций.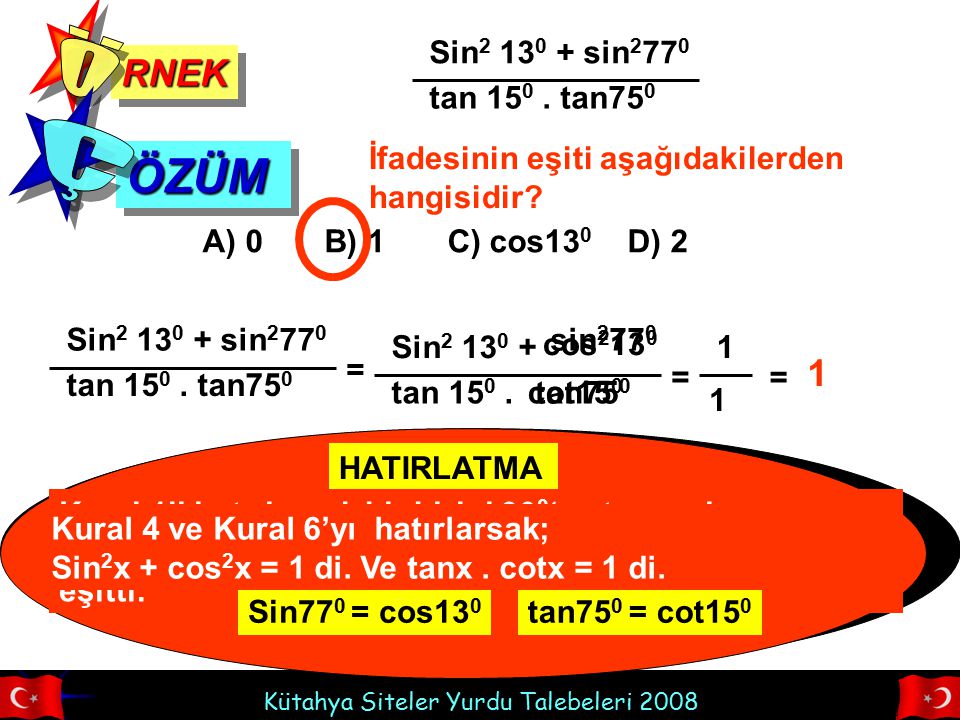
Обратите внимание на то, что значения синусов углов находятся в пределах от -1 до 1.
Также легко запомнить, что значения sin 0° = sin 360° = 0.
sin 1° — sin 90°
sin 1° = 0.01745
sin 2° = 0.03490
sin 3° = 0.05234
sin 4° = 0.06976
sin 5° = 0.08716
sin 6° = 0.10453
sin 7° = 0.12187
sin 8° = 0.13917
sin 9° = 0.15643
sin 10° = 0.17365
sin 11° = 0.19081
sin 12° = 0.20791
sin 13° = 0.22495
sin 14° = 0.24192
sin 15° = 0.25882
sin 16° = 0.27564
sin 17° = 0.29237
sin 18° = 0.30902
sin 19° = 0.32557
sin 20° = 0.34202
sin 21° = 0.35837
sin 22° = 0.37461
sin 23° = 0.39073
sin 24° = 0.40674
sin 25° = 0.42262
sin 26° = 0.43837
sin 27° = 0.45399
sin 28° = 0.46947
sin 29° = 0.48481
sin 30° = 0.50000
sin 31° = 0.51504
sin 32° = 0.52992
sin 33° = 0.54464
sin 34° = 0.55919
sin 35° = 0.57358
sin 36° = 0.58779
sin 37° = 0. 60182
60182
sin 38° = 0.61566
sin 39° = 0.62932
sin 40° = 0.64279
sin 41° = 0.65606
sin 42° = 0.66913
sin 43° = 0.68200
sin 44° = 0.69466
sin 45° = 0.70711
sin 46° = 0.71934
sin 47° = 0.73135
sin 48° = 0.74314
sin 49° = 0.75471
sin 50° = 0.76604
sin 51° = 0.77715
sin 52° = 0.78801
sin 53° = 0.79864
sin 54° = 0.80902
sin 55° = 0.81915
sin 56° = 0.82904
sin 57° = 0.83867
sin 58° = 0.84805
sin 59° = 0.85717
sin 60° = 0.86603
sin 61° = 0.87462
sin 62° = 0.88295
sin 63° = 0.89101
sin 64° = 0.89879
sin 65° = 0.90631
sin 66° = 0.91355
sin 67° = 0.92050
sin 68° = 0.92718
sin 69° = 0.93358
sin 70° = 0.93969
sin 71° = 0.94552
sin 72° = 0.95106
sin 73° = 0.95630
sin 74° = 0.96126
sin 75° = 0.96593
sin 76° = 0.97030
sin 77° = 0.97437
sin 78° = 0.97815
sin 79° = 0.98163
sin 80° = 0.98481
sin 81° = 0.98769
sin 82° = 0.99027
sin 83° = 0. 99255
99255
sin 84° = 0.99452
sin 85° = 0.99619
sin 86° = 0.99756
sin 87° = 0.99863
sin 88° = 0.99939
sin 89° = 0.99985
sin 90° = 1.00000
sin 91° — sin 180°
sin 91° = 0.99985
sin 92° = 0.99939
sin 93° = 0.99863
sin 94° = 0.99756
sin 95° = 0.99619
sin 96° = 0.99452
sin 97° = 0.99255
sin 98° = 0.99027
sin 99° = 0.98769
sin 100° = 0.98481
sin 101° = 0.98163
sin 102° = 0.97815
sin 103° = 0.97437
sin 104° = 0.97030
sin 105° = 0.96593
sin 106° = 0.96126
sin 107° = 0.95630
sin 108° = 0.95106
sin 109° = 0.94552
sin 110° = 0.93969
sin 111° = 0.93358
sin 112° = 0.92718
sin 113° = 0.92050
sin 114° = 0.91355
sin 115° = 0.90631
sin 116° = 0.89879
sin 117° = 0.89101
sin 118° = 0.88295
sin 119° = 0.87462
sin 120° = 0.86603
sin 121° = 0.85717
sin 122° = 0.84805
sin 123° = 0.83867
sin 124° = 0.82904
sin 125° = 0. 81915
81915
sin 126° = 0.80902
sin 127° = 0.79864
sin 128° = 0.78801
sin 129° = 0.77715
sin 130° = 0.76604
sin 131° = 0.75471
sin 132° = 0.74314
sin 133° = 0.73135
sin 134° = 0.71934
sin 135° = 0.70711
sin 136° = 0.69466
sin 137° = 0.68200
sin 138° = 0.66913
sin 139° = 0.65606
sin 140° = 0.64279
sin 141° = 0.62932
sin 142° = 0.61566
sin 143° = 0.60182
sin 144° = 0.58779
sin 145° = 0.57358
sin 146° = 0.55919
sin 147° = 0.54464
sin 148° = 0.52992
sin 149° = 0.51504
sin 150° = 0.50000
sin 151° = 0.48481
sin 152° = 0.46947
sin 153° = 0.45399
sin 154° = 0.43837
sin 155° = 0.42262
sin 156° = 0.40674
sin 157° = 0.39073
sin 158° = 0.37461
sin 159° = 0.35837
sin 160° = 0.34202
sin 161° = 0.32557
sin 162° = 0.30902
sin 163° = 0.29237
sin 164° = 0.27564
sin 165° = 0.25882
sin 166° = 0.24192
sin 167° = 0.22495
sin 168° = 0.20791
sin 169° = 0. 19081
19081
sin 170° = 0.17365
sin 171° = 0.15643
sin 172° = 0.13917
sin 173° = 0.12187
sin 174° = 0.10453
sin 175° = 0.08716
sin 176° = 0.06976
sin 177° = 0.05234
sin 178° = 0.03490
sin 179° = 0.01745
sin 180° = 0.00000
sin 181° — sin 270°
sin 181° = -0.01745
sin 182° = -0.03490
sin 183° = -0.05234
sin 184° = -0.06976
sin 185° = -0.08716
sin 186° = -0.10453
sin 187° = -0.12187
sin 188° = -0.13917
sin 189° = -0.15643
sin 190° = -0.17365
sin 191° = -0.19081
sin 192° = -0.20791
sin 193° = -0.22495
sin 194° = -0.24192
sin 195° = -0.25882
sin 196° = -0.27564
sin 197° = -0.29237
sin 198° = -0.30902
sin 199° = -0.32557
sin 200° = -0.34202
sin 201° = -0.35837
sin 202° = -0.37461
sin 203° = -0.39073
sin 204° = -0.40674
sin 205° = -0.42262
sin 206° = -0.43837
sin 207° = -0.45399
sin 208° = -0.46947
sin 209° = -0. 48481
48481
sin 210° = -0.50000
sin 211° = -0.51504
sin 212° = -0.52992
sin 213° = -0.54464
sin 214° = -0.55919
sin 215° = -0.57358
sin 216° = -0.58779
sin 217° = -0.60182
sin 218° = -0.61566
sin 219° = -0.62932
sin 220° = -0.64279
sin 221° = -0.65606
sin 222° = -0.66913
sin 223° = -0.68200
sin 224° = -0.69466
sin 225° = -0.70711
sin 226° = -0.71934
sin 227° = -0.73135
sin 228° = -0.74314
sin 229° = -0.75471
sin 230° = -0.76604
sin 231° = -0.77715
sin 232° = -0.78801
sin 233° = -0.79864
sin 234° = -0.80902
sin 235° = -0.81915
sin 236° = -0.82904
sin 237° = -0.83867
sin 238° = -0.84805
sin 239° = -0.85717
sin 240° = -0.86603
sin 241° = -0.87462
sin 242° = -0.88295
sin 243° = -0.89101
sin 244° = -0.89879
sin 245° = -0.90631
sin 246° = -0.91355
sin 247° = -0.92050
sin 248° = -0.92718
sin 249° = -0.93358
sin 250° = -0.93969
sin 251° = -0. 94552
94552
sin 252° = -0.95106
sin 253° = -0.95630
sin 254° = -0.96126
sin 255° = -0.96593
sin 256° = -0.97030
sin 257° = -0.97437
sin 258° = -0.97815
sin 259° = -0.98163
sin 260° = -0.98481
sin 261° = -0.98769
sin 262° = -0.99027
sin 263° = -0.99255
sin 264° = -0.99452
sin 265° = -0.99619
sin 266° = -0.99756
sin 267° = -0.99863
sin 268° = -0.99939
sin 269° = -0.99985
sin 270° = -1.00000
sin 271° — sin 360°
sin 271° = -0.99985
sin 272° = -0.99939
sin 273° = -0.99863
sin 274° = -0.99756
sin 275° = -0.99619
sin 276° = -0.99452
sin 277° = -0.99255
sin 278° = -0.99027
sin 279° = -0.98769
sin 280° = -0.98481
sin 281° = -0.98163
sin 282° = -0.97815
sin 283° = -0.97437
sin 284° = -0.97030
sin 285° = -0.96593
sin 286° = -0.96126
sin 287° = -0.95630
sin 288° = -0.95106
sin 289° = -0.94552
sin 290° = -0. 93969
93969
sin 291° = -0.93358
sin 292° = -0.92718
sin 293° = -0.92050
sin 294° = -0.91355
sin 295° = -0.90631
sin 296° = -0.89879
sin 297° = -0.89101
sin 298° = -0.88295
sin 299° = -0.87462
sin 300° = -0.86603
sin 301° = -0.85717
sin 302° = -0.84805
sin 303° = -0.83867
sin 304° = -0.82904
sin 305° = -0.81915
sin 306° = -0.80902
sin 307° = -0.79864
sin 308° = -0.78801
sin 309° = -0.77715
sin 310° = -0.76604
sin 311° = -0.75471
sin 312° = -0.74314
sin 313° = -0.73135
sin 314° = -0.71934
sin 315° = -0.70711
sin 316° = -0.69466
sin 317° = -0.68200
sin 318° = -0.66913
sin 319° = -0.65606
sin 320° = -0.64279
sin 321° = -0.62932
sin 322° = -0.61566
sin 323° = -0.60182
sin 324° = -0.58779
sin 325° = -0.57358
sin 326° = -0.55919
sin 327° = -0.54464
sin 328° = -0.52992
sin 329° = -0.51504
sin 330° = -0.50000
sin 331° = -0.48481
sin 332° = -0. 46947
46947
sin 333° = -0.45399
sin 334° = -0.43837
sin 335° = -0.42262
sin 336° = -0.40674
sin 337° = -0.39073
sin 338° = -0.37461
sin 339° = -0.35837
sin 340° = -0.34202
sin 341° = -0.32557
sin 342° = -0.30902
sin 343° = -0.29237
sin 344° = -0.27564
sin 345° = -0.25882
sin 346° = -0.24192
sin 347° = -0.22495
sin 348° = -0.20791
sin 349° = -0.19081
sin 350° = -0.17365
sin 351° = -0.15643
sin 352° = -0.13917
sin 353° = -0.12187
sin 354° = -0.10453
sin 355° = -0.08716
sin 356° = -0.06976
sin 357° = -0.05234
sin 358° = -0.03490
sin 359° = -0.01745
sin 360° = 0.00000
- Коротко о важном
- Таблицы
- Формулы
- Формулы по геометрии
- Теория по математике
от 0 до 360 градусов
Таблица синусов – это рассчитанные значения синусов от 0 до 360 градусов.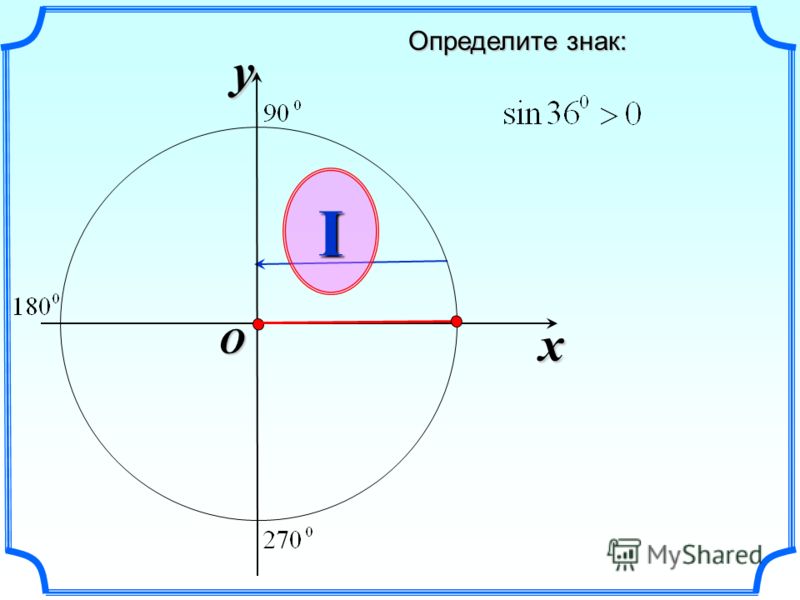 Она выручит, если вдруг потребуется выполнить расчеты, в которых фигурирует синус угла, а под рукой не будет калькулятора.
Она выручит, если вдруг потребуется выполнить расчеты, в которых фигурирует синус угла, а под рукой не будет калькулятора.
Пользоваться таблицей очень просто – находим нужный нам градус и в колонке справа от него этой же строке будет указано посчитанное значение синуса. Для удобства информация разделена на две части.
- Таблица синусов от 0° до 180°
- Таблица синусов от 181° до 360°
Таблица синусов от 0° до 180°
| sin (0°) | 0 | ||||
| sin (1°) | 0,017452 | sin (61°) | 0,87462 | sin (121°) | 0,857167 |
| sin (2°) | 0,034899 | sin (62°) | 0,882948 | sin (122°) | 0,848048 |
| sin (3°) | 0,052336 | sin (63°) | 0,891007 | sin (123°) | 0,838671 |
| sin (4°) | 0,069756 | sin (64°) | 0,898794 | sin (124°) | 0,829038 |
| sin (5°) | 0,087156 | sin (65°) | 0,906308 | sin (125°) | 0,819152 |
| sin (6°) | 0,104528 | sin (66°) | 0,913545 | sin (126°) | 0,809017 |
| sin (7°) | 0,121869 | sin (67°) | 0,920505 | sin (127°) | 0,798636 |
| sin (8°) | 0,139173 | sin (68°) | 0,927184 | sin (128°) | 0,788011 |
| sin (9°) | 0,156434 | sin (69°) | 0,93358 | sin (129°) | 0,777146 |
| sin (10°) | 0,173648 | sin (70°) | 0,939693 | sin (130°) | 0,766044 |
| sin (11°) | 0,190809 | sin (71°) | 0,945519 | sin (131°) | 0,75471 |
| sin (12°) | 0,207912 | sin (72°) | 0,951057 | sin (132°) | 0,743145 |
| sin (13°) | 0,224951 | sin (73°) | 0,956305 | sin (133°) | 0,731354 |
| sin (14°) | 0,241922 | sin (74°) | 0,961262 | sin (134°) | 0,71934 |
| sin (15°) | 0,258819 | sin (75°) | 0,965926 | sin (135°) | 0,707107 |
| sin (16°) | 0,275637 | sin (76°) | 0,970296 | sin (136°) | 0,694658 |
| sin (17°) | 0,292372 | sin (77°) | 0,97437 | sin (137°) | 0,681998 |
| sin (18°) | 0,309017 | sin (78°) | 0,978148 | sin (138°) | 0,669131 |
| sin (19°) | 0,325568 | sin (79°) | 0,981627 | sin (139°) | 0,656059 |
| sin (20°) | 0,34202 | sin (80°) | 0,984808 | sin (140°) | 0,642788 |
| sin (21°) | 0,358368 | sin (81°) | 0,987688 | sin (141°) | 0,62932 |
| sin (22°) | 0,374607 | sin (82°) | 0,990268 | sin (142°) | 0,615661 |
| sin (23°) | 0,390731 | sin (83°) | 0,992546 | sin (143°) | 0,601815 |
| sin (24°) | 0,406737 | sin (84°) | 0,994522 | sin (144°) | 0,587785 |
| sin (25°) | 0,422618 | sin (85°) | 0,996195 | sin (145°) | 0,573576 |
| sin (26°) | 0,438371 | sin (86°) | 0,997564 | sin (146°) | 0,559193 |
| sin (27°) | 0,45399 | sin (87°) | 0,99863 | sin (147°) | 0,544639 |
| sin (28°) | 0,469472 | sin (88°) | 0,999391 | sin (148°) | 0,529919 |
| sin (29°) | 0,48481 | sin (89°) | 0,999848 | sin (149°) | 0,515038 |
| sin (30°) | 0,5 | sin (90°) | 1 | sin (150°) | 0,5 |
| sin (31°) | 0,515038 | sin (91°) | 0,999848 | sin (151°) | 0,48481 |
| sin (32°) | 0,529919 | sin (92°) | 0,999391 | sin (152°) | 0,469472 |
| sin (33°) | 0,544639 | sin (93°) | 0,99863 | sin (153°) | 0,45399 |
| sin (34°) | 0,559193 | sin (94°) | 0,997564 | sin (154°) | 0,438371 |
| sin (35°) | 0,573576 | sin (95°) | 0,996195 | sin (155°) | 0,422618 |
| sin (36°) | 0,587785 | sin (96°) | 0,994522 | sin (156°) | 0,406737 |
| sin (37°) | 0,601815 | sin (97°) | 0,992546 | sin (157°) | 0,390731 |
| sin (38°) | 0,615661 | sin (98°) | 0,990268 | sin (158°) | 0,374607 |
| sin (39°) | 0,62932 | sin (99°) | 0,987688 | sin (159°) | 0,358368 |
| sin (40°) | 0,642788 | sin (100°) | 0,984808 | sin (160°) | 0,34202 |
| sin (41°) | 0,656059 | sin (101°) | 0,981627 | sin (161°) | 0,325568 |
| sin (42°) | 0,669131 | sin (102°) | 0,978148 | sin (162°) | 0,309017 |
| sin (43°) | 0,681998 | sin (103°) | 0,97437 | sin (163°) | 0,292372 |
| sin (44°) | 0,694658 | sin (104°) | 0,970296 | sin (164°) | 0,275637 |
| sin (45°) | 0,707107 | sin (105°) | 0,965926 | sin (165°) | 0,258819 |
| sin (46°) | 0,71934 | sin (106°) | 0,961262 | sin (166°) | 0,241922 |
| sin (47°) | 0,731354 | sin (107°) | 0,956305 | sin (167°) | 0,224951 |
| sin (48°) | 0,743145 | sin (108°) | 0,951057 | sin (168°) | 0,207912 |
| sin (49°) | 0,75471 | sin (109°) | 0,945519 | sin (169°) | 0,190809 |
| sin (50°) | 0,766044 | sin (110°) | 0,939693 | sin (170°) | 0,173648 |
| sin (51°) | 0,777146 | sin (111°) | 0,93358 | sin (171°) | 0,156434 |
| sin (52°) | 0,788011 | sin (112°) | 0,927184 | sin (172°) | 0,139173 |
| sin (53°) | 0,798636 | sin (113°) | 0,920505 | sin (173°) | 0,121869 |
| sin (54°) | 0,809017 | sin (114°) | 0,913545 | sin (174°) | 0,104528 |
| sin (55°) | 0,819152 | sin (115°) | 0,906308 | sin (175°) | 0,087156 |
| sin (56°) | 0,829038 | sin (116°) | 0,898794 | sin (176°) | 0,069756 |
| sin (57°) | 0,838671 | sin (117°) | 0,891007 | sin (177°) | 0,052336 |
| sin (58°) | 0,848048 | sin (118°) | 0,882948 | sin (178°) | 0,034899 |
| sin (59°) | 0,857167 | sin (119°) | 0,87462 | sin (179°) | 0,017452 |
| sin (60°) | 0,866025 | sin (120°) | 0,866025 | sin (180°) | 0 |
Таблица синусов от 181° до 360°
Sin 130 градусов — Найдите значение Sin 130 градусов
LearnPracticeDownload
Значение sin 130 градусов равно 0,7660444. . . . Sin 130 градусов в радианах записывается как sin (130° × π/180°), то есть sin (13π/18) или sin (2,268928…). В этой статье мы обсудим способы нахождения значения sin 130 градусов на примерах.
. . . Sin 130 градусов в радианах записывается как sin (130° × π/180°), то есть sin (13π/18) или sin (2,268928…). В этой статье мы обсудим способы нахождения значения sin 130 градусов на примерах.
- Sin 130°: 0,7660444. . .
- Sin (-130 градусов): -0,7660444. . .
- Sin 130° в радианах: sin (13π/18) или sin (2,2689280 . . .)
Сколько стоит грех 130 градусов?
Значение sin 130 градусов в десятичной системе равно 0,766044443. . .. Sin 130 градусов также можно выразить с помощью эквивалента заданного угла (130 градусов) в радианах (2,26892 . . .).
Используя преобразование градусов в радианы, мы знаем, что θ в радианах = θ в градусах × (pi/180°)
⇒ 130 градусов = 130° × (π/180°) рад = 13π/18 или 2,2689. . .
∴ sin 130° = sin(2,2689) = 0,7660444. . .
Объяснение:
Для sin 130 градусов угол 130° лежит между 90° и 180° (второй квадрант). Поскольку функция синуса положительна во втором квадранте, значение sin 130° = 0,7660444. . .
Поскольку функция синуса положительна во втором квадранте, значение sin 130° = 0,7660444. . .
Поскольку функция синуса является периодической функцией, мы можем представить sin 130° как sin 130 градусов = sin(130° + n × 360°), n ∈ Z.
⇒ sin 130° = sin 490° = sin 850° и так далее.
Примечание: Поскольку синус является нечетной функцией, значение sin(-130°) = -sin(130°).
Методы нахождения значения Sin 130 градусов
Функция синуса положительна во 2-м квадранте. Значение sin 130° равно 0,76604. . .. Мы можем найти значение sin 130 градусов по:
- Используя Unit Circle
- Использование тригонометрических функций
Sin 130 градусов с помощью единичной окружности
Чтобы найти значение sin 130 градусов с помощью единичной окружности:
- Поверните ‘r’ против часовой стрелки, чтобы образовать угол 130° с положительной осью x.
- Грех в 130 градусов равен координате y (0,766) точки пересечения (-0,6428, 0,766) единичной окружности и r.

Следовательно, значение sin 130° = y = 0,766 (приблизительно)
Sin 130° в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить sin 130 градусов как:
- ± √(1-cos² (130°))
- ± тангенс 130°/√(1 + тангенс²(130°))
- ± 1/√(1 + раскладушка²(130°))
- ± √(сек²(130°) — 1)/сек 130°
- 1/косек 130°
Примечание. Поскольку 130° лежит во 2-м квадранте, конечное значение sin 130° будет положительным.
Мы можем использовать тригонометрические тождества для представления sin 130° как
- sin(180° — 130°) = sin 50°
- -sin(180° + 130°) = -sin 310°
- cos(90° — 130°) = cos(-40°)
- -cos(90° + 130°) = -cos 220°
☛ Также проверьте:
- грех 18 градусов
- грех 60 градусов
- грех 90 градусов
- грех 230 градусов
- грех 12 градусов
- грех 83 градуса
Примеры использования Sin 130 градусов
Пример 1: Используя значение sin 130°, решите: (1-cos²(130°)).

Решение:
Мы знаем, (1-cos²(130°)) = (sin²(130°)) = 0,5868
⇒ (1-cos²(130°)) = 0,5868Пример 2: Упростить: 2 (sin 130°/sin 490°)
Решение:
Мы знаем sin 130° = sin 490°
⇒ 2 sin 130°/sin 490° = 2(sin 130°/sin 130°)
= 2(1) = 2Пример 3: Найдите значение sin 130°, если cosec 130° равно 1,3054.
Решение:
Поскольку sin 130° = 1/csc 130°
⇒ sin 130° = 1/1,3054 = 0,766
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы о Sin 130 Degrees
Что такое Sin 130 Degrees?
Sin 130 градусов — значение тригонометрической функции синуса для угла, равного 130 градусам. Значение sin 130° равно 0,766 (приблизительно).
Значение sin 130° равно 0,766 (приблизительно).
Каково значение Sin 130° в пересчете на Cosec 130°?
Поскольку функция косеканса является обратной величиной функции синуса, мы можем записать sin 130° как 1/cosec(130°). Значение cosec 130° равно 1,30540.
Каково значение Sin 130 градусов в пересчете на Tan 130°?
Мы знаем, что, используя тригонометрические тождества, мы можем записать sin 130° как -tan 130°/√(1 + tan²(130°)). Здесь значение тангенса 130° равно -1,19.1753.
Как найти Sin 130° в терминах других тригонометрических функций?
Используя формулу тригонометрии, значение sin 130° может быть выражено через другие тригонометрические функции следующим образом:
- ± √(1-cos²(130°))
- ± тангенс 130°/√(1 + тангенс²(130°))
- ± 1/√(1 + раскладушка²(130°))
- ± √(сек²(130°) — 1)/сек 130°
- 1/косек 130°
☛ Также проверьте: таблицу тригонометрии
Как найти значение Sin 130 градусов?
Значение sin 130 градусов можно рассчитать, построив угол 130° с осью x и затем найдя координаты соответствующей точки (-0,6428, 0,766) на единичной окружности. Значение sin 130° равно координате y (0,766). ∴ sin 130° = 0,766.
Значение sin 130° равно координате y (0,766). ∴ sin 130° = 0,766.
Скачать БЕСПЛАТНО учебные материалы
Тригонометрия
Рабочие листы по математике и
визуальные учебные программы
| 1 | Найдите точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктический(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | соз(150) | |
| 20 | Найдите точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | Преобразование градусов в радианы | 45 | 92|
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктический(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | желтовато-коричневый (пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найдите точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найдите точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желто-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | желтовато-коричневый ((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-(квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 шт.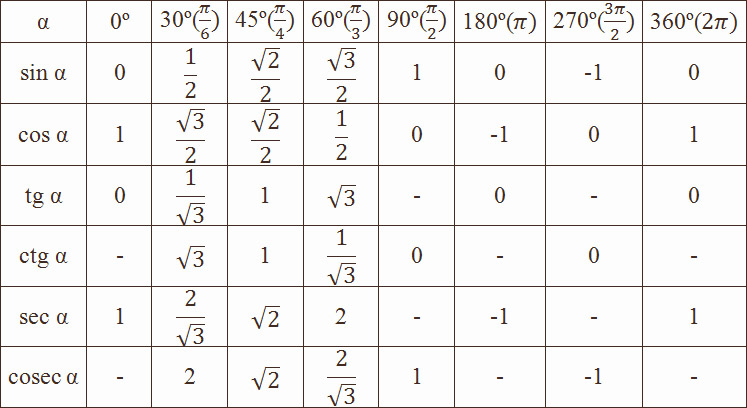 )/4 )/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан( квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | грех((2pi)/3) | |
| 88 | Найти точное значение | желтовато-коричневый ((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
130 Сравнение гармонической фазовой визуализации с локальным моделированием синусоидальной волны для оценки циркулярной деформации миокарда с использованием помеченных сердечно-сосудистых магнитно-резонансных изображений
Текст статьи
Меню статьи
- Статья
Текст - Артикул
информация - Цитата
Инструменты - Поделиться
- Быстрое реагирование
- Артикул
Метрика - Оповещения
BCS Abstracts 2011
130 Сравнение гармонической фазовой визуализации с локальным моделированием синусоидальной волны для оценки окружной деформации миокарда с использованием помеченных сердечно-сосудистых магнитно-резонансных изображений
- A N BORG1,
- C A Miller1,
- C D Steadman2,
- G P McCann2,
- M Schmitt1
- 1
- УНИВЕРСИТЕЛЬНА1177
- 2 NIHR Лестерское отделение биомедицинских исследований сердечно-сосудистых заболеваний, Лестер, Великобритания
Резюме
Введение Оценка деформации миокарда обещает стать важным количественным инструментом в ранней диагностике и лечении кардиологических заболеваний.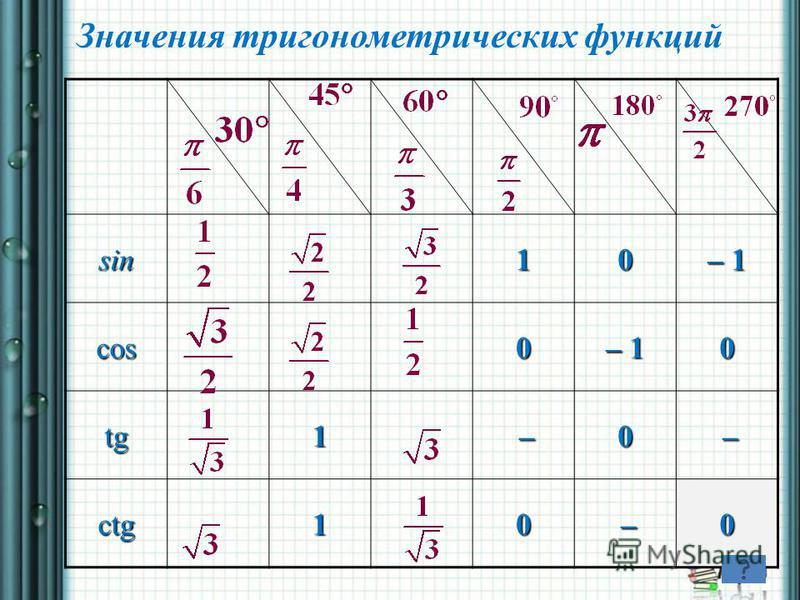 Достижения в программном обеспечении для обработки изображений облегчили быстрый и клинически осуществимый анализ деформации по маркированным изображениям сердечного магнитного резонанса (CMR). Гармонический фазовый анализ (HARP) или моделирование локальной синусоиды (SinMod) можно использовать для автоматического определения деформации. Мы получили помеченные изображения CMR для сравнения измерений окружной деформации левого желудочка (LV), полученных с использованием HARP с методом SinMod.
Достижения в программном обеспечении для обработки изображений облегчили быстрый и клинически осуществимый анализ деформации по маркированным изображениям сердечного магнитного резонанса (CMR). Гармонический фазовый анализ (HARP) или моделирование локальной синусоиды (SinMod) можно использовать для автоматического определения деформации. Мы получили помеченные изображения CMR для сравнения измерений окружной деформации левого желудочка (LV), полученных с использованием HARP с методом SinMod.
Методы Были включены 10 нормальных контролей, 10 пациентов с гипертрофической и 10 дилатационной кардиомиопатией (средний возраст 46,6 ± 14,8 лет). Пространственная модуляция намагниченности с использованием короткоосевых срезов ЛЖ на уровне середины желудочка с временным разрешением 30–50 мс была получена с использованием сканера 1,5 Тесла (Siemens Avanto) с 32-канальной катушкой. Глобальные и сегментарные трансмуральные пиковые периферические деформации (ε см3 ) измеряли с использованием HARP (Diagnosoft, США, версия 2.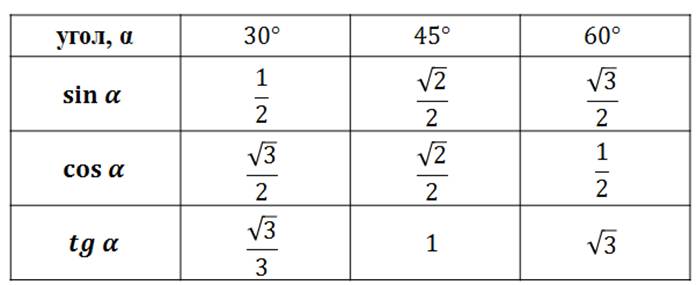 7) и SinMod (InTag, Лионский университет, Франция, версия 3.6.1). Перед запуском алгоритма оба метода включают ручное отслеживание границ эндокарда и эпикарда и локализацию точек прикрепления правого желудочка к перегородке в одном кадре. Согласованность между HARP и SinMod оценивали с помощью коэффициента корреляции Спирмена R и методов Бленда-Альтмана. Повторные измерения проводились на 10 случайно выбранных сканах для оценки воспроизводимости.
7) и SinMod (InTag, Лионский университет, Франция, версия 3.6.1). Перед запуском алгоритма оба метода включают ручное отслеживание границ эндокарда и эпикарда и локализацию точек прикрепления правого желудочка к перегородке в одном кадре. Согласованность между HARP и SinMod оценивали с помощью коэффициента корреляции Спирмена R и методов Бленда-Альтмана. Повторные измерения проводились на 10 случайно выбранных сканах для оценки воспроизводимости.
Результаты Был достигнут высокий уровень согласия между HARP и SinMod для глобального ε куб.см (HARP — разность средних значений SinMod: −0,12%, 95% пределы согласия: от −5,69% до 5,45%, R=0,83, p<0,001) (Аннотация 130 рис. 1). Согласие было намного ниже для сегментарного ε cc , варьируя от очень плохого в латеральных сегментах до скромного в нижне-септальных сегментах (Таблица 1 резюме 130). Время анализа с использованием SinMod было значительно меньше, чем для HARP (84 ± 42 против 201 ± 120 с, p = 0,02). Воспроизводимость между и внутри наблюдателя была чрезвычайно высокой для SinMod измерений глобального ε куб.см (между наблюдателем R=0,99, коэффициент повторяемости (RC) 2,14; внутри наблюдателя R=0,99, RC 1,49). Воспроизводимость глобальных измерений ε см3 с помощью HARP была несколько ниже, но все же высокой (между наблюдателями R=0,89, RC 4,80; внутри наблюдателя R=0,98, RC 2,73). В сегментарных измерениях ε см3 с использованием обоих методов, особенно с HARP, наблюдалась гораздо большая вариабельность (резюме 130, рис. 2).
Воспроизводимость между и внутри наблюдателя была чрезвычайно высокой для SinMod измерений глобального ε куб.см (между наблюдателем R=0,99, коэффициент повторяемости (RC) 2,14; внутри наблюдателя R=0,99, RC 1,49). Воспроизводимость глобальных измерений ε см3 с помощью HARP была несколько ниже, но все же высокой (между наблюдателями R=0,89, RC 4,80; внутри наблюдателя R=0,98, RC 2,73). В сегментарных измерениях ε см3 с использованием обоих методов, особенно с HARP, наблюдалась гораздо большая вариабельность (резюме 130, рис. 2).
Аннотация 130 Рисунок 1
Аннотация 130 Таблица 1
Abstract 130 Рисунок 2
Изменчивость между наблюдателями и внутри них для моделирования локальной синусоидальной волны HARP: коэффициенты повторяемости.
Выводы Методы HARP и SinMod демонстрируют высокий уровень согласованности для оценки глобальной трансмуральной окружной деформации среднего желудочка с хорошей воспроизводимостью для обоих методов.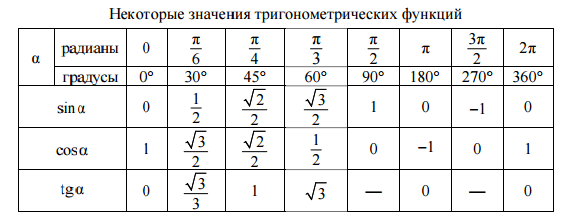 Согласие намного ниже для сегментных измерений; плохая воспроизводимость сегментарных измерений с использованием обоих методов, вероятно, отражает вариативность пользователей в идентификации точек прикрепления к перегородке правого желудочка и отслеживании контуров.
Согласие намного ниже для сегментных измерений; плохая воспроизводимость сегментарных измерений с использованием обоих методов, вероятно, отражает вариативность пользователей в идентификации точек прикрепления к перегородке правого желудочка и отслеживании контуров.
- Strain
- myocardial tagging
- left ventricular function
http://dx.doi.org/10.1136/heartjnl-2011-300198.130
Statistics from Altmetric.com
Request Permissions
If you wish to повторное использование любой части этой статьи или всей этой статьи. Воспользуйтесь приведенной ниже ссылкой, которая приведет вас к службе RightsLink Центра проверки авторских прав. Вы сможете получить быструю цену и мгновенное разрешение на повторное использование контента различными способами.
- штамм
- Myocardial Tagging
- Функция левого желудочка
Прочтите полный текст или загрузите PDF:
Подписаться
Войдите в систему с использованием вашего Username and Password
для личных Accounds Or Accounms ascounts accounts 9000.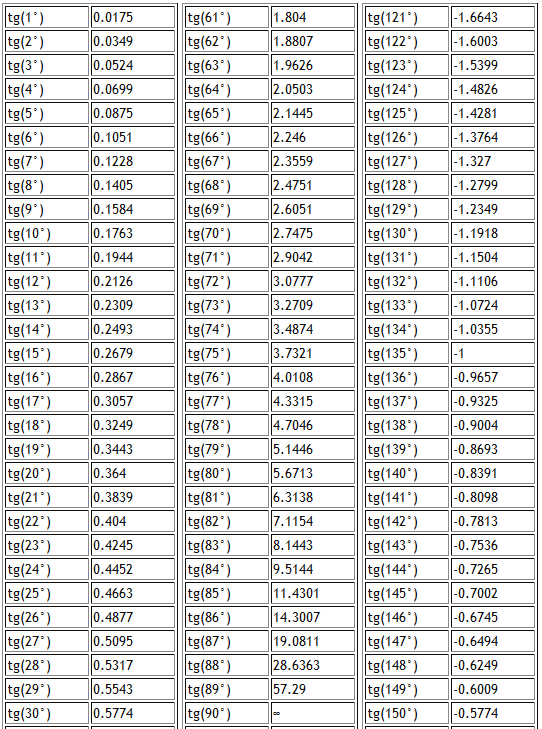 *
*
Пароль *
Забыли данные для входа? Зарегистрировать новую учетную запись?
Забыли имя пользователя или пароль?
Многоцентровое сравнение укороченных двухфазных разрядов и стандартных монофазных разрядов с затухающей синусоидой для трансторакальной желудочковой дефибрилляции. Трансторакальные исследователи
Клинические испытания
. 1996 15 ноября; 94 (10): 2507-14.
doi: 10.1161/01.cir.94.10.2507.
Г Х Барди 1 , Ф.Э. Марчлински, А.Д. Шарма, С.Дж. Уорли, Р.М. Лучери, Р.Йи, Б.Д. Гальперин, С.Л. Феллоуз, Т.С. Ахерн, Д.А.
принадлежность
- 1 Медицинский факультет Вашингтонского университета (Сиэтл), США. [email protected]
- PMID: 8921795
- DOI:
10.
 1161/01.cir.94.10.2507
1161/01.cir.94.10.2507
Клинические испытания
GH Bardy et al. Тираж. .
. 1996 15 ноября; 94 (10): 2507-14.
doi: 10.1161/01.cir.94.10.2507.
Авторы
Г Х Барди 1 , Ф.Э. Марчлински, А.Д. Шарма, С.Дж. Уорли, Р.М. Лучери, Р.Йи, Б.Д. Гальперин, С.Л. Феллоуз, Т.С. Ахерн, Д.А. Чилсон, Д.Л. Пакер, Д.Дж. Уилбер, Т.А. Маттиони, Р. Редди, Р.А. принадлежность
- 1 Медицинский факультет Вашингтонского университета (Сиэтл), США. [email protected]
- PMID: 8921795
- DOI:
10.
 1161/01.cir.94.10.2507
1161/01.cir.94.10.2507
Абстрактный
Фон: Наиболее важным фактором для улучшения внебольничной выживаемости пациентов с фибрилляцией желудочков является ранняя дефибрилляция. Этого можно достичь, если широко распространить небольшие, легкие и недорогие автоматические наружные дефибрилляторы. Поскольку размер и стоимость автоматического наружного дефибриллятора напрямую зависят от формы волны дефибрилляции, а также из-за положительного опыта использования усеченных двухфазных волн в имплантируемых кардиовертерах-дефибрилляторах, мы сравнили эффективность усеченной двухфазной волны с эффективностью стандартной затухающей синусоидальной монофазной волны для трансторакальной дефибрилляции. дефибрилляция.
Методы и результаты: Основная цель этого многоцентрового, проспективного, рандомизированного, слепого исследования состояла в том, чтобы сравнить эффективность первого разряда трансторакальной дефибрилляции укороченной двухфазной волны 130 Дж с эффективностью стандартной монофазной затухающей синусоидальной волны 200 Дж с использованием передних торакальных подушечек в грудной клетке.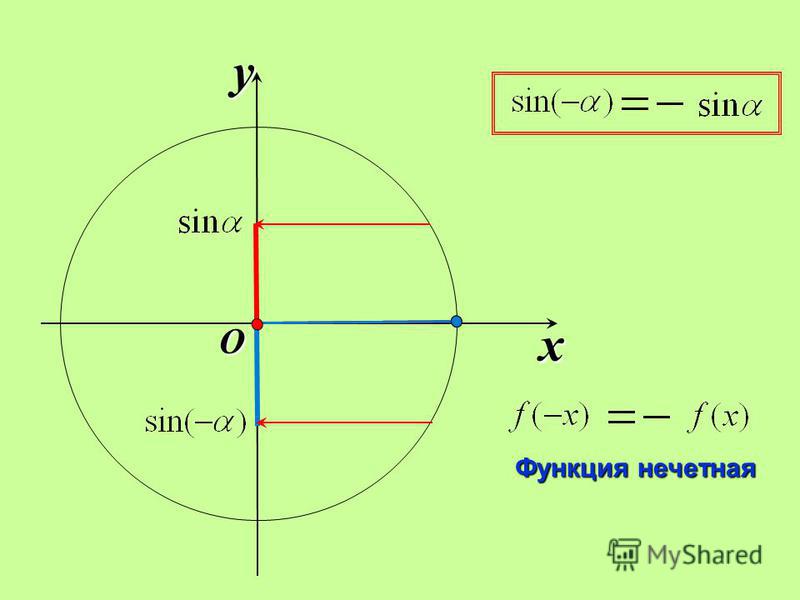 курс тестирования имплантируемого кардиовертера-дефибриллятора. После трансторакальной дефибрилляции также исследовали ЭКГ с подушками. После исключения данных о 24 пациентах, которые не соответствовали всем критериям протокола, результаты 29Было проанализировано 4 пациента. Укороченный двухфазный импульс 130 Дж и монофазный импульс с затухающей синусоидой 200 Дж привели к эффективности первого разряда 86% и 86% соответственно (P = 0,97). Уровни сегмента ST, измеренные через 10 секунд после разряда у 151 пациента с синусовым ритмом, составили -0,26 ± 1,58 и -1,86 ± 1,93 мм для разрядов силой 130 и 200 Дж соответственно (P < 0,0001).
курс тестирования имплантируемого кардиовертера-дефибриллятора. После трансторакальной дефибрилляции также исследовали ЭКГ с подушками. После исключения данных о 24 пациентах, которые не соответствовали всем критериям протокола, результаты 29Было проанализировано 4 пациента. Укороченный двухфазный импульс 130 Дж и монофазный импульс с затухающей синусоидой 200 Дж привели к эффективности первого разряда 86% и 86% соответственно (P = 0,97). Уровни сегмента ST, измеренные через 10 секунд после разряда у 151 пациента с синусовым ритмом, составили -0,26 ± 1,58 и -1,86 ± 1,93 мм для разрядов силой 130 и 200 Дж соответственно (P < 0,0001).
Выводы: Мы обнаружили, что двухфазные укороченные трансторакальные разряды мощностью 130 Дж вызывают дефибрилляцию так же, как монофазные разряды с затухающими синусоидальными волнами мощностью 200 Дж, которые традиционно используются в стандартных трансторакальных дефибрилляторах, и приводят к меньшему количеству аномалий ЭКГ после разряда.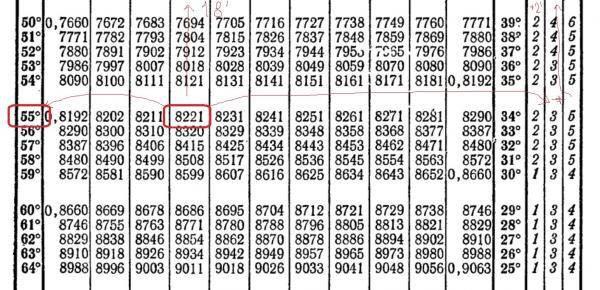
Похожие статьи
Двухфазные и монофазные волны для трансторакальной дефибрилляции при внебольничной остановке сердца.
Faddy SC, Jennings PA. Фэдди С.К. и др. Cochrane Database Syst Rev. 2016 Feb 10;2(2):CD006762. doi: 10.1002/14651858.CD006762.pub2. Кокрановская система базы данных, ред. 2016 г. PMID: 260 Бесплатная статья ЧВК. Обзор.
Укороченные двухфазные импульсы для трансторакальной дефибрилляции.
Барди Г.Х., Глинер Б.Е., Куденчук П.Дж., Пул Дж.Е., Долак Г.Л., Джонс Г.К., Андерсон Дж., Траутман С., Джонсон Г. Барди Г.Х. и соавт. Тираж. 1995 15 марта; 91 (6): 1768-74. doi: 10.1161/01.cir.91.6.1768. Тираж. 1995. PMID: 7882486 Клиническое испытание.
Двухфазная трансторакальная дефибрилляция вызывает меньше изменений сегмента ST на ЭКГ после разряда.

Редди Р.К., Глева М.Дж., Глинер Б.Е., Долак Г.Л., Куденчук П.Дж., Пул Дж.Е., Барди Г.Х. Редди Р.К. и др. Энн Эмерг Мед. 1997 авг; 30 (2): 127-34. doi: 10.1016/s0196-0644(97)70130-6. Энн Эмерг Мед. 1997. PMID: 9250633 Клиническое испытание.
Сравнение нового прямолинейного двухфазного сигнала с затухающим синусоидальным монофазным сигналом для трансторакальной желудочковой дефибрилляции. Исследователи ZOLL.
Миттал С., Аяти С., Штейн К.М., Найт Б.П., Моради Ф., Шварцман Д., Кавлович Д., Платиа Э.В., Калкинс Х., Чоу П.Дж., Миллер Дж.М., Уортон Дж.М., Сун Р.Дж., Слотвинер Д.Дж., Марковиц С.М., Лерман Б.Б. Миттал С. и др. J Am Coll Кардиол. 1999 1 ноября; 34 (5): 1595-601. doi: 10.1016/s0735-1097(99)00363-0. J Am Coll Кардиол. 1999. PMID: 10551711 Клиническое испытание.
Монофазный и двухфазный шок для трансторакальной конверсии мерцательной аритмии: систематический обзор и сетевой метаанализ.

Инасиу Дж.Ф., да Роса Мдос С., Шах Дж., Росарио Дж., Виссоци Дж.Р., Маника А.Л., Родригес К.Г. Инасио Дж. Ф. и соавт. Реанимация. 2016 март; 100:66-75. doi: 10.1016/j.resuscitation.2015.12.009. Epub 2016 8 января. Реанимация. 2016. PMID: 26777209 Обзор.
Посмотреть все похожие статьи
Цитируется
Использование наносекундных разрядов для дефибрилляции сердца.
Нойбер Ю.Ю., Варгезе Ф., Пахомов А.Г., Землян К.В. Neuber JU и соавт. Биоэлектричество. 2019 1 декабря; 1 (4): 240-246. doi: 10.1089/bioe.2019.0030. Epub 2019 12 декабря. Биоэлектричество. 2019. PMID: 32685917 Бесплатная статья ЧВК. Обзор.
Возбуждение и повреждение взрослых желудочковых кардиомиоцитов электрическим током от нано до миллисекунд.

Семенов И., Григорьев С., Нойбер Ю.Ю., Землян С.В., Пахомова О.Н., Кашиола М., Пахомов А.Г. Семенов И. и др. Научный представитель 2018 г. 29 мая;8(1):8233. doi: 10.1038/s41598-018-26521-2. Научный представитель 2018. PMID: 29844431 Бесплатная статья ЧВК.
Роль пикового тока в конверсии у пациентов с фибрилляцией желудочков.
Анантараман В., Ван П.В., Тай С.Ю., Мэннинг П.Г., Лим С.Х., Чуа С.Дж., Мохан Т., Рабинд А.С., Видья С., Хао Ю. Анантараман В. и др. Singapore Med J. 2017 Jul; 58 (7): 432-437. doi: 10.11622/smedj.2017070. Сингапур Med J. 2017. PMID: 28741007 Бесплатная статья ЧВК. Клиническое испытание.
Двухфазные и монофазные волны для трансторакальной дефибрилляции при внебольничной остановке сердца.

Faddy SC, Jennings PA. Фэдди С.К. и др. Cochrane Database Syst Rev. 2016 Feb 10;2(2):CD006762. doi: 10.1002/14651858.CD006762.pub2. Кокрановская система базы данных, ред. 2016 г. PMID: 260 Бесплатная статья ЧВК. Обзор.
Сравнение монофазной и двухфазной дефибрилляции у детей с внебольничной остановкой сердца: общенациональное популяционное исследование в Японии.
Танабэ С., Ясунага Х., Койке С., Акахане М., Огава Т., Хоригучи Х., Хатанака Т., Йокота Х., Имамура Т. Танабе С. и др. Критический уход. 2012 13 ноября; 16 (6): R219. дои: 10.1186/cc11864. Критический уход. 2012. PMID: 23148767 Бесплатная статья ЧВК.
Просмотреть все статьи «Цитируется по»
Типы публикаций
термины MeSH
NCCI Jobs — Сотрудник по питанию (ME/NIN/SIN/130/052022)
Информация о работе Офицер ПИТАНИЯ (ME/NIN/SIN/130/052022) — повторная реклама Информация об НПО
Название НПО Миссия Восток
Веб-сайт
http://www. missioneast.org/
missioneast.org/
Контактное лицо HR
Контактный адрес электронной почты
Информация о работе
Срок действия контракта 6 месяцев
мухафаза Ниневия
Смена работы 9до 17:00
Национальность Национальный
Рабочее время Полный рабочий день
Опубликовано 20.06.2022
Требования
Минимальное образование Степень бакалавра
Название степени
Минимальный опыт 2 Год
Требуется Поездка 50%
Рабочий статус
Количество рабочих мест 1
Дата публикации
20. 06.2022
06.2022
Крайний срок Дата 2022-07-04
Расположение
[Синджар, Ирак]
Описание
Справочная информация:
Mission East, основанная в Дании в 1991 году, является международной гуманитарной организацией и организацией по развитию, осуществляющей программы помощи при стихийных бедствиях и развития на Ближнем Востоке, в Восточной Европе и Азии.
В Ираке Миссия Восток оказывает помощь как в удовлетворении неотложных основных потребностей лиц, перемещенных в результате насилия, так и в долгосрочной поддержке репатриантов и ВПЛ в условиях длительного перемещения. Наша текущая программа включает непродовольственные товары и приют, денежные переводы, помощь WASH, поддержку средств к существованию, защиту и психосоциальную поддержку, осуществляемую через многоцелевые общественные центры.
Дополнительную информацию о Mission East можно найти по адресу: https://missioneast.org
Должность:
Сотрудник по мониторингу, оценке, подотчетности и обучению (MEAL) — это должность в подразделении MEAL Миссия Восток — Ирак в офисном поле Мосула. Под руководством координатора MEAL сотрудник MEAL будет планировать, разрабатывать, организовывать и координировать сбор, компиляцию, консолидацию и анализ данных для мониторинга хода выполнения проекта, результатов и воздействия. Сотрудник по MEAL также предоставит обратную связь для процессов планирования и обеспечения лучшей системы управления данными. Сотрудник MEAL будет поддерживать настройку системы MEAL и будет нести ответственность за разработку и обслуживание баз данных и укрепление системы, а также за наращивание потенциала персонала Восточной миссии. Это включает в себя сбор, компиляцию и анализ соответствующих данных, конкретно основанных на индикаторах процесса проекта, результатов, результатов и воздействия.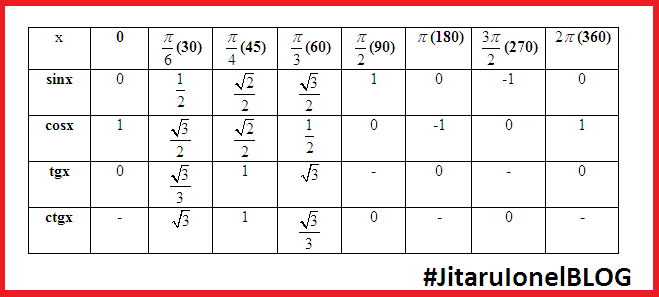 Действующий сотрудник также будет способствовать документированию извлеченных уроков по мере развития проектов.
Действующий сотрудник также будет способствовать документированию извлеченных уроков по мере развития проектов.
Основные обязанности и ответственность:
Должностные обязанности:
- Поддержка в создании систем ПИТАНИЯ, включая принципы и рекомендации.
- Помощь в обучении, мониторинге и оценке, сборе данных, интервью, опросах и т. д.
- Поддерживать отчетность по проектам, инструменты MEAL, формы отслеживания и отчетности, отчеты о мониторинге, предложения, отчеты для доноров, оценки и другую информацию о проекте.
- Разработка форм XLS и помощь в анализе и компиляции данных для измерения прогресса.
- Координация и работа с членами программных и проектных групп для обеспечения соблюдения стандартов качества (обучение, поставки и т. д.)
- Планирование и разработка процессов сбора качественных и количественных данных (с разбивкой по полу), реализация плана мониторинга, операционные системы баз данных.

- Поддержка в создании системы ПИТАНИЯ, включающей стандарты и рекомендации ПИТАНИЯ, включая Принципы ME.
- Помощь в обучении, мониторинге и оценке, сборе данных, интервью, опросах и т. д.
- Поддерживать отчетность по проектам, инструменты MEAL, формы отслеживания и отчетности, отчеты о мониторинге, предложения, отчеты для доноров, оценки и другую информацию о проекте.
- Разработка форм XLS и помощь в анализе и компиляции данных для измерения прогресса.
- Координация и работа с членами программных и проектных групп для обеспечения соблюдения стандартов качества (обучение, поставки и т. д.)
- Планирование и разработка процессов сбора качественных и количественных данных (с разбивкой по полу), реализация плана мониторинга, операционные системы баз данных.
Квалификация и предпочтительные навыки
Требуемая квалификация:
Требуется: степень бакалавра в области социальных наук, исследований в области развития, статистики или в других смежных областях.
Необходимые компетенции: —
Технические навыки.
Требуется:
- Опыт работы не менее 2 лет.
- Высокая организованность, внимание к деталям и сильные количественные и качественные аналитические навыки; Проектирование базы данных и управление ею.
- Владение компьютером, особенно Microsoft Word, Excel, Power Point; СПСС, КОБО.
- Хорошие устные и письменные навыки общения и межличностного общения.
- Твердая вера в качество, честность, командную работу, гендерное равенство, коллективный подход и устойчивость.
Прочие требования:
Миссия Восток поддерживает высокие стандарты во всех аспектах охраны и осуждает все формы жестокого обращения и эксплуатации, придерживается подхода абсолютной нетерпимости ко всем жестокому обращению и эксплуатации в отношении детей или уязвимых лиц и стремится гарантировать, что никакие — человек подвергается риску жестокого обращения со стороны его представителей. В соответствии с организационной политикой:
В соответствии с организационной политикой:
- Ввиду характера этой роли, потенциально требующей взаимодействия с уязвимыми лицами (включая ситуации, когда существует потенциальный дисбаланс власти), вам необходимо будет предоставить как самооценку, так и официальное свидетельство о предыдущем хорошем поведении.
- Профессиональные рекомендации будут запрошены и приняты для успешного кандидата.
- Все сотрудники Mission East обязаны подписать наш Кодекс поведения и Обязательства по защите детей.
Mission East придерживается высоких стандартов в области борьбы с терроризмом (COTER) и соблюдения правил санкций. Mission East проведет тщательную проверку биографических данных успешных кандидатов перед приемом на работу, включая проверку санкционных списков SDN.
Как применить
Квалифицированные кандидаты должны отправить свое резюме на английском языке по адресу iraqvacancy@missioneast.



 1161/01.cir.94.10.2507
1161/01.cir.94.10.2507 1161/01.cir.94.10.2507
1161/01.cir.94.10.2507