| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.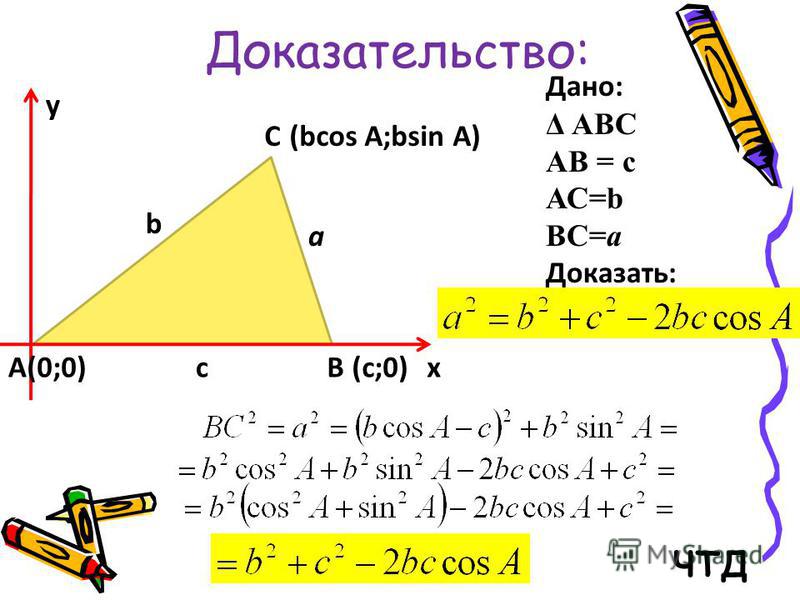 ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | arcsin(-1/2) | ||
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.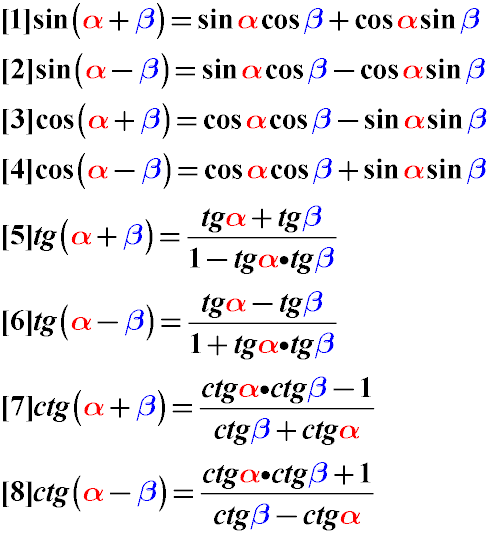 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град.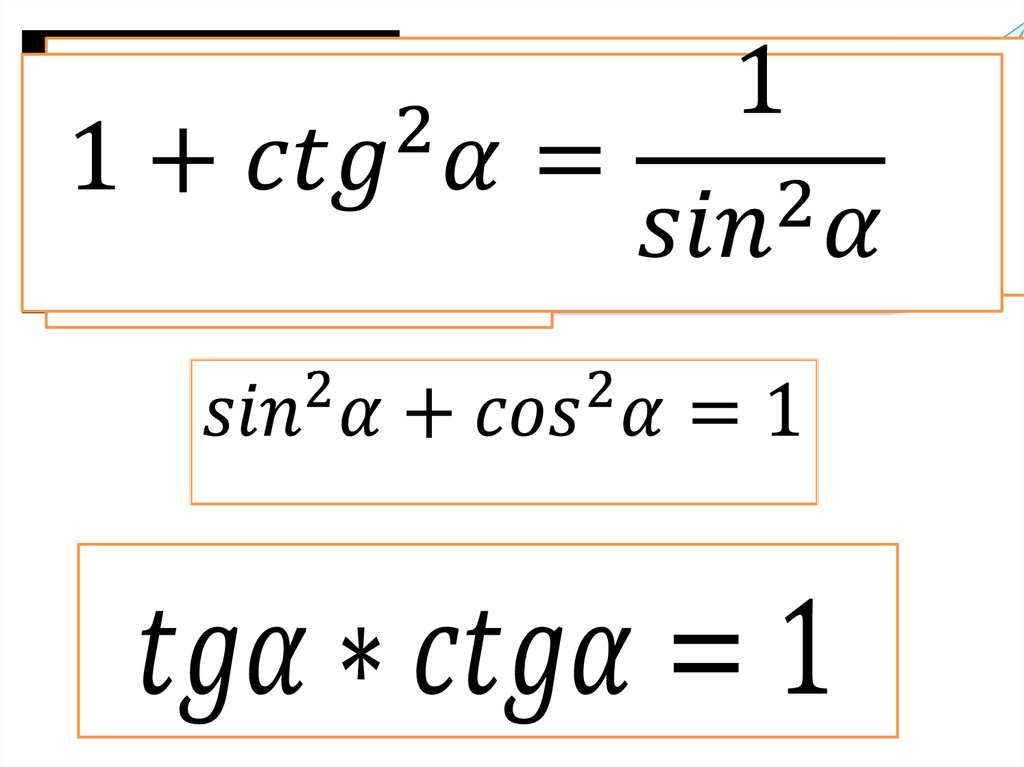 ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
100 формул тригонометрия. Основные тригонометрические формулы и тождества sin, cos, tg, ctg. Основные тригонометрические формулы
Вы можете заказать подробное решение вашей задачи !!!
Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше. n arcsin a + \pi n, n \in Z`
n arcsin a + \pi n, n \in Z`
2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| \leq 1` имеет бесконечное множество решений.
Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`
Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + \pi n, n \in Z`
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + \pi n, n \in Z`
Формулы корней тригонометрических уравнений в таблице
Для синуса:
Для косинуса:
Для тангенса и котангенса:
Формулы решения уравнений, содержащих обратные тригонометрические функции:
Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Основные формулы тригонометрии — это формулы, устанавливающие связи между основными тригонометрическими функциями. Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений.
 Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных формул можно решить практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь сами формулы, а не их вывод, которому будут посвящены отдельные статьи.
Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных формул можно решить практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь сами формулы, а не их вывод, которому будут посвящены отдельные статьи.Yandex.RTB R-A-339285-1
Основные тождества тригонометрии
Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.
Тригонометрические тождества
sin 2 a + cos 2 a = 1 t g α = sin α cos α , c t g α = cos α sin α t g α · c t g α = 1 t g 2 α + 1 = 1 cos 2 α , c t g 2 α + 1 = 1 sin 2 α
Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).
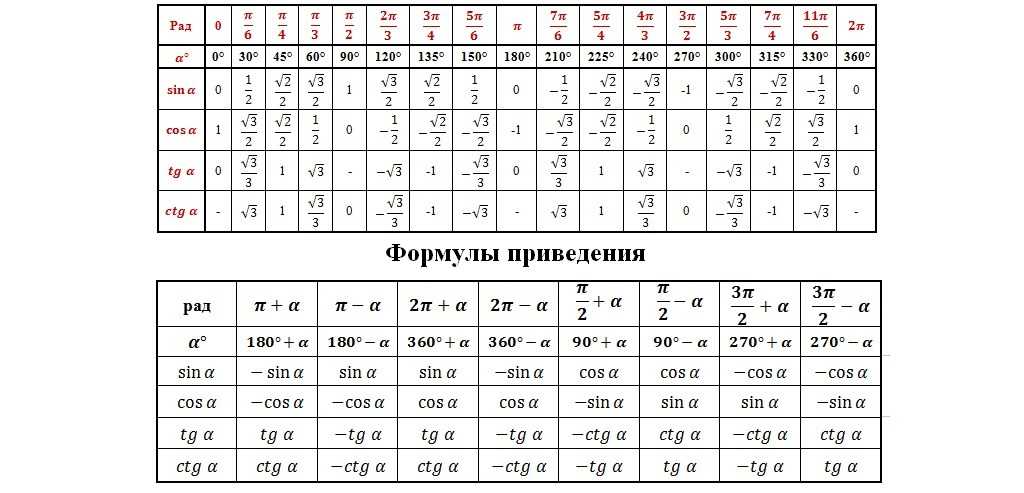
Формулы приведения
Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.

Формулы приведения
sin α + 2 π z = sin α , cos α + 2 π z = cos α t g α + 2 π z = t g α , c t g α + 2 π z = c t g α sin — α + 2 π z = — sin α , cos — α + 2 π z = cos α t g — α + 2 π z = — t g α , c t g — α + 2 π z = — c t g α sin π 2 + α + 2 π z = cos α , cos π 2 + α + 2 π z = — sin α t g π 2 + α + 2 π z = — c t g α , c t g π 2 + α + 2 π z = — t g α sin π 2 — α + 2 π z = cos α , cos π 2 — α + 2 π z = sin α t g π 2 — α + 2 π z = c t g α , c t g π 2 — α + 2 π z = t g α sin π + α + 2 π z = — sin α , cos π + α + 2 π z = — cos α t g π + α + 2 π z = t g α , c t g π + α + 2 π z = c t g α sin π — α + 2 π z = sin α , cos π — α + 2 π z = — cos α t g π — α + 2 π z = — t g α , c t g π — α + 2 π z = — c t g α sin 3 π 2 + α + 2 π z = — cos α , cos 3 π 2 + α + 2 π z = sin α t g 3 π 2 + α + 2 π z = — c t g α , c t g 3 π 2 + α + 2 π z = — t g α sin 3 π 2 — α + 2 π z = — cos α , cos 3 π 2 — α + 2 π z = — sin α t g 3 π 2 — α + 2 π z = c t g α , c t g 3 π 2 — α + 2 π z = t g α
Формулы приведения являются следствием периодичности тригонометрических функций.

Тригонометрические формулы сложения
Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.
Тригонометрические формулы сложения
sin α ± β = sin α · cos β ± cos α · sin β cos α + β = cos α · cos β — sin α · sin β cos α — β = cos α · cos β + sin α · sin β t g α ± β = t g α ± t g β 1 ± t g α · t g β c t g α ± β = — 1 ± c t g α · c t g β c t g α ± c t g β
На основе формул сложения выводятся тригонометрические формулы кратного угла.
Формулы кратного угла: двойного, тройного и т.д.
Формулы двойного и тройного угла
sin 2 α = 2 · sin α · cos α cos 2 α = cos 2 α — sin 2 α , cos 2 α = 1 — 2 sin 2 α , cos 2 α = 2 cos 2 α — 1 t g 2 α = 2 · t g α 1 — t g 2 α с t g 2 α = с t g 2 α — 1 2 · с t g α sin 3 α = 3 sin α · cos 2 α — sin 3 α , sin 3 α = 3 sin α — 4 sin 3 α cos 3 α = cos 3 α — 3 sin 2 α · cos α , cos 3 α = — 3 cos α + 4 cos 3 α t g 3 α = 3 t g α — t g 3 α 1 — 3 t g 2 α c t g 3 α = c t g 3 α — 3 c t g α 3 c t g 2 α — 1
Формулы половинного угла
Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.

Формулы половинного угла
sin 2 α 2 = 1 — cos α 2 cos 2 α 2 = 1 + cos α 2 t g 2 α 2 = 1 — cos α 1 + cos α c t g 2 α 2 = 1 + cos α 1 — cos α
Формулы понижения степени
Формулы понижения степени
sin 2 α = 1 — cos 2 α 2 cos 2 α = 1 + cos 2 α 2 sin 3 α = 3 sin α — sin 3 α 4 cos 3 α = 3 cos α + cos 3 α 4 sin 4 α = 3 — 4 cos 2 α + cos 4 α 8 cos 4 α = 3 + 4 cos 2 α + cos 4 α 8
Часто при расчетах действовать с громоздктми степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:
Общий вид формул понижения степени
для четных n
sin n α = C n 2 n 2 n + 1 2 n — 1 ∑ k = 0 n 2 — 1 (- 1) n 2 — k · C k n · cos ((n — 2 k) α) cos n α = C n 2 n 2 n + 1 2 n — 1 ∑ k = 0 n 2 — 1 C k n · cos ((n — 2 k) α)
для нечетных n
sin n α = 1 2 n — 1 ∑ k = 0 n — 1 2 (- 1) n — 1 2 — k · C k n · sin ((n — 2 k) α) cos n α = 1 2 n — 1 ∑ k = 0 n — 1 2 C k n · cos ((n — 2 k) α)
Сумма и разность тригонометрических функций
Разность и сумму тригонометрических функций можно представить в виде произведения.
 Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.
Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.Сумма и разность тригонометрических функций
sin α + sin β = 2 sin α + β 2 · cos α — β 2 sin α — sin β = 2 sin α — β 2 · cos α + β 2 cos α + cos β = 2 cos α + β 2 · cos α — β 2 cos α — cos β = — 2 sin α + β 2 · sin α — β 2 , cos α — cos β = 2 sin α + β 2 · sin β — α 2
Произведение тригонометрических функций
Если формулы суммы и разности функций позволяют перейти к их произведению, то формулы произведения тригонометрических функций осуществляют обратный переход — от произведения к сумме. Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.
Формулы произведения тригонометрических функций
sin α · sin β = 1 2 · (cos (α — β) — cos (α + β)) cos α · cos β = 1 2 · (cos (α — β) + cos (α + β)) sin α · cos β = 1 2 · (sin (α — β) + sin (α + β))
Универсальная тригонометрическая подстановка
Все основные тригонометрические функции — синус, косинус, тангенс и котангенс, — могут быть выражены через тангенс половинного угла.

Универсальная тригонометрическая подстановка
sin α = 2 t g α 2 1 + t g 2 α 2 cos α = 1 — t g 2 α 2 1 + t g 2 α 2 t g α = 2 t g α 2 1 — t g 2 α 2 c t g α = 1 — t g 2 α 2 2 t g α 2
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом и котангенсом — задаются тригонометрическими формулами . А так как связей между тригонометрическими функциями достаточно много, то этим объясняется и обилие тригонометрических формул. Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.
В этой статье мы по порядку перечислим все основные тригонометрические формулы, которых достаточно для решения подавляющего большинства задач тригонометрии. Для удобства запоминания и использования будем группировать их по назначению, и заносить в таблицы.

Навигация по странице.
Основные тригонометрические тождества
Основные тригонометрические тождества задают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Они вытекают из определения синуса, косинуса, тангенса и котангенса, а также понятия единичной окружности . Они позволяют выразить одну тригонометрическую функцию через любую другую.
Подробное описание этих формул тригонометрии, их вывод и примеры применения смотрите в статье .
Формулы приведения
Формулы приведения следуют из свойств синуса, косинуса, тангенса и котангенса , то есть, они отражают свойство периодичности тригонометрических функций, свойство симметричности, а также свойство сдвига на данный угол. Эти тригонометрические формулы позволяют от работы с произвольными углами переходить к работе с углами в пределах от нуля до 90 градусов.
Обоснование этих формул, мнемоническое правило для их запоминания и примеры их применения можно изучить в статье .

Формулы сложения
Тригонометрические формулы сложения показывают, как тригонометрические функции суммы или разности двух углов выражаются через тригонометрические функции этих углов. Эти формулы служат базой для вывода следующих ниже тригонометрических формул.
Формулы двойного, тройного и т.д. угла
Формулы двойного, тройного и т.д. угла (их еще называют формулами кратного угла) показывают, как тригонометрические функции двойных, тройных и т.д. углов () выражаются через тригонометрические функции одинарного угла . Их вывод базируется на формулах сложения.
Более детальная информация собрана в статье формулы двойного, тройного и т.д. угла .
Формулы половинного угла
Формулы половинного угла показывают, как тригонометрические функции половинного угла выражаются через косинус целого угла . Эти тригонометрические формулы следуют из формул двойного угла.
Их вывод и примеры применения можно посмотреть в статье .

Формулы понижения степени
Тригонометрические формулы понижения степени призваны содействовать переходу от натуральных степеней тригонометрических функций к синусам и косинусам в первой степени, но кратных углов. Иными словами, они позволяют понижать степени тригонометрических функций до первой.
Формулы суммы и разности тригонометрических функций
Основное предназначение формул суммы и разности тригонометрических функций заключается в переходе к произведению функций, что очень полезно при упрощении тригонометрических выражений. Указанные формулы также широко используются при решении тригонометрических уравнений, так как позволяют раскладывать на множители сумму и разность синусов и косинусов.
Формулы произведения синусов, косинусов и синуса на косинус
Переход от произведения тригонометрических функций к сумме или разности осуществляется посредством формул произведения синусов, косинусов и синуса на косинус .

Универсальная тригонометрическая подстановка
Обзор основных формул тригонометрии завершаем формулами, выражающими тригонометрические функции через тангенс половинного угла. Такая замена получила название универсальной тригонометрической подстановки . Ее удобство заключается в том, что все тригонометрические функции выражаются через тангенс половинного угла рационально без корней.
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.
 — 384 с.: ил.- ISBN 5-09-013651-3.
— 384 с.: ил.- ISBN 5-09-013651-3. - Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
Copyright by cleverstudents
Все права защищены.
Охраняется законом об авторском праве. Ни одну часть сайта , включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.Для решения некоторых задач будет полезной таблица тригонометрических тождеств, которая позволит гораздо проще совершать преобразования функций:
Простейшие тригонометрические тождества
Частное от деления синуса угла альфа на косинус того же угла равно тангенсу этого угла (Формула 1). См. также доказательство правильности преобразования простейших тригонометрических тождеств .
Частное от деления косинуса угла альфа на синус того же угла равно котангенсу этого же угла (Формула 2)
Секанс угла равен единице, деленной на косинус этого же самого угла (Формула 3)
Сумма квадратов синуса и косинуса одного и того же угла равна единице (Формула 4). см. также доказательство суммы квадратов косинуса и синуса .
см. также доказательство суммы квадратов косинуса и синуса .
Сумма единицы и тангенса угла равна отношению единицы к квадрату косинуса этого угла (Формула 5)
Единица плюс котангенс угла равна частному от деления единицы на синус квадрат этого угла (Формула 6)
Произведение тангенса на котангенс одного и того же угла равно единице (Формула 7).Преобразование отрицательных углов тригонометрических функций (четность и нечетность)
Для того, чтобы избавиться от отрицательного значения градусной меры угла при вычислении синуса, косинуса или тангенса, можно воспользоваться следующими тригонометрическими преобразованиями (тождествами), основанными на принципах четности или нечетности тригонометрических функций.
Как видно, косинус и секанс является четной функцией , синус, тангенс и котангенс — нечетные функции .
Синус отрицательного угла равен отрицательному значению синуса этого же самого положительного угла (минус синус альфа).

Косинус «минус альфа» даст тоже самое значение, что и косинус угла альфа.
Тангенс минус альфа равен минус тангенс альфа.Формулы приведения двойного угла (синус, косинус, тангенс и котангенс двойного угла)
Если необходимо разделить угол пополам, или наоборот, перейти от двойного угла к одинарному, можно воспользоваться следующими тригонометрическими тождествами:
Преобразование двойного угла (синуса двойного угла, косинуса двойного угла и тангенса двойного угла ) в одинарный происходит по следующим правилам:
Синус двойного угла равен удвоенному произведению синуса на косинус одинарного угла
Косинус двойного угла равен разности квадрата косинуса одинарного угла и квадрата синуса этого угла
Косинус двойного угла равен удвоенному квадрату косинуса одинарного угла минус единица
Косинус двойного угла равен единице минус двойной синус квадрат одинарного угла
Тангенс двойного угла равен дроби, числитель которой — удвоенный тангенс одинарного угла, а знаменатель равен единице минус тангенс квадрат одинарного угла.

Котангенс двойного угла равен дроби, числитель которой — квадрат котангенса одинарного угла минус единица, а знаменатель равен удвоенному котангенсу одинарного угла
Формулы универсальной тригонометрической подстановки
Указанные ниже формулы преобразования могут пригодиться, когда нужно аргумент тригонометрической функции (sin α, cos α, tg α) разделить на два и привести выражение к значению половины угла. Из значения α получаем α/2 .
Данные формулы называются формулами универсальной тригонометрической подстановки . Их ценность заключается в том, что тригонометрическое выражение с их помощью сводится к выражению тангенса половины угла, вне зависимости от того, какие тригонометрические функции (sin cos tg ctg) были в выражении изначально. После этого уравнение с тангенсом половины угла решить гораздо проще.
Тригонометрические тождества преобразования половины угла
Указанные ниже формулы тригонометрического преобразования половинной величины угла к его целому значению.

Значение аргумента тригонометрической функции α/2 приводится к значению аргумента тригонометрической функции α.Тригонометрические формулы сложения углов
cos (α — β) = cos α · cos β + sin α · sin β
sin (α + β) = sin α · cos β + sin β · cos α
sin (α — β) = sin α · cos β — sin β · cos α
cos (α + β) = cos α · cos β — sin α · sin βТангенс и котангенс суммы углов альфа и бета могут быть преобразованы по следующим правилам преобразования тригонометрических функций:
Тангенс суммы углов равен дроби, числитель которой — сумма тангенса первого и тангенса второго угла, а знаменатель — единица минус произведение тангенса первого угла на тангенс второго угла.
Тангенс разности углов равен дроби, числитель которой равен разности тангенса уменьшаемого угла и тангенса вычитаемого угла, а знаменатель — единице плюс произведение тангенсов этих углов.
Котангенс суммы углов равен дроби, числитель которой равен произведению котангенсов этих углов плюс единица, а знаменатель равен разности котангенса второго угла и котангенса первого угла.

Котангенс разности углов равен дроби, числитель которой — произведение котангенсов этих углов минус единица, а знаменатель равен сумме котангенсов этих углов.
Данные тригонометрические тождества удобно применять, когда нужно вычислить, например, тангенс 105 градусов (tg 105). Если его представить как tg (45 + 60), то можно воспользоваться приведенными тождественными преобразованиями тангенса суммы углов, после чего просто подставить табличные значения тангенса 45 и тангенса 60 градусов.
Формулы преобразования суммы или разности тригонометрических функций
Выражения, представляющие собой сумму вида sin α + sin β можно преобразовать с помощью следующих формул:
Формулы тройного угла — преобразование sin3α cos3α tg3α в sinα cosα tgα
Иногда необходимо преобразовать тройную величину угла так, чтобы аргументом тригонометрической функции вместо 3α стал угол α.
В этом случае можно воспользоваться формулами (тождествами) преобразования тройного угла:Формулы преобразования произведения тригонометрических функций
Если возникает необходимость преобразовать произведение синусов разных углов косинусов разных углов или даже произведения синуса на косинус, то можно воспользоваться следующими тригонометрическими тождествами:
В этом случае произведение функций синуса, косинуса или тангенса разных углов будет преобразовано в сумму или разность.
Формулы приведения тригонометрических функций
Пользоваться таблицей приведения нужно следующим образом. В строке выбираем функцию, которая нас интересует. В столбце — угол. Например, синус угла (α+90) на пересечении первой строки и первого столбца выясняем, что sin (α+90) = cos α .
2 альфа=1Тригонометрия
Ифеома Р.
спросил 26.11.21Подписаться І 1
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Осман А. ответил 26.11.21
Репетитор
5 (34)
Профессор инженерной математики – тригонометрия и геометрия
Смотрите таких репетиторов
Смотрите таких репетиторов
Докажите, что: COS 2 ∝ + SIN 2 ∝ = 1
.
 0034 с углом ∝ по оси x. Thus, base = x, height = y, hypotenuses = r
0034 с углом ∝ по оси x. Thus, base = x, height = y, hypotenuses = r Given/Known: sin ∝ = y/r cos ∝ = x/r x 2 + y 2 = R 2
Доказательство: COS 2 ∝ + SIN 2 33333343334333433. 10033 333333333333333333333333 гг. в Правая сторона = 1)
COS 2 ∝ + SIN 2 ∝ = 1
(COSE ∝) 88 88 88 88 88 88 88 888 88 888 888 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 88 888 88 88 88 888 88 88 88 88 8.
 = 1
= 1( X / R ) 2 + ( Y / R ) 2 = 1
(x 2 / R 2 ) + (Y 2 / R 2) + (Y 2 / R 2 2) + (Y 2 / R ) = 1
( x 2 + у 2 ) / (r 2 ) = 1
( R 2 ) / (R 2 ) = 1
1 = 1 <= Заключитель
Голосовать за 0 голос против
Подробнее
Отчет
Сидни П. ответил 26.11.21
Репетитор
4.9(1532)
Репетитор по астрономии, физике, химии и математике
Смотрите таких репетиторов
Смотрите таких репетиторов
Постройте прямоугольный треугольник (первый квадрант проще всего) с гипотенузой = 1, смежной стороной x и противоположной стороной y.
 Итак, cos α = x/1, sin α = y/1. По теореме Пифагора и подстановке x 2 + y 2 = 1 2 = 1 = cos 2 α + sin 2 α.
Итак, cos α = x/1, sin α = y/1. По теореме Пифагора и подстановке x 2 + y 2 = 1 2 = 1 = cos 2 α + sin 2 α.Голосовать за 0 голос против
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.

Формулы двойного и половинного угла
Формулы двойного и половинного углаВ этом разделе мы поговорим о формулах двойного и половинного углов, а также о некоторых дополнительных тригонометрических тождествах.
Формулы двойного угла
Формулы двойного угла записываются в виде sin(2*угол), cos(2*угол) и tan(2*угол). Их можно использовать для упрощения уравнений или применять непосредственно к некоторым классам задач. Мы получим формулу для греха (2 * угол). Для cos(2*угол) и tan(2*угол) мы просто приведем результаты. На рисунке справа показаны два прямоугольных треугольника, которые являются отражением друг друга. Оба имеют гипотенузу длины 1. Горизонтальный катет обоих треугольников равен cos(theta). Это происходит от cos(theta) = смежная сторона/гипотенуза. Решая для соседней стороны, мы получаем гипотенузу * cos (тета), но гипотенуза равна 1, поэтому окончательный ответ — просто cos (тета). Угол между горизонтальной осью и гипотенузой равен тета для обоих треугольников, поэтому общий угол внутри треугольника равен тета + тета или 2 * тета.
 Теперь, используя закон синусов, мы можем написать:
Теперь, используя закон синусов, мы можем написать:- sin(2*тета)/2*sin(тета) = sin(альфа)/1
- sin(alpha) также можно записать как cos(theta)/1 (противоположная сторона гипотенузы)
- подставив это в наше первое выражение, получим sin(2*theat)/2*sin(theta) = cos(theta)
- нахождение sin(2*theta) дает sin(2*theta) = 2*sin(theta)*cos(theta)
Теперь у нас есть формула, которая гласит: sin(2*theta) = 2*sin(theta)*cos(theta). Важно отметить, что sin(2*theta) НЕ РАВНО 2*sin(theta). Чтобы взять пример, мы будем использовать формулу для вычисления греха дважды 30 или . На основе нашей формулы это будет записано так:
- sin(2*30 o ) = 2*sin(30 o )*cos(30 o )
- = 2*(0,5)*(0,866) = 0,8660
В тексте приведены формулы двойного угла для синуса, косинуса и тангенса. Формулы следующие:
- sin(2*тета) = 2*sin(тета)*cos(тета)
- cos(2*theta) = cos 2 (theta) — sin 2 (theta)
- Альтернативная форма: cos(2*theta) = 1 — 2*sin 2 (тета)
- Альтернативная форма: cos(2*тета) = 2*cos 2 (тета) — 1
- тангенс(2*тета) = [2*тангенс(тета)]/[1 — тангенс 2 (тета)]
Формулы половинного угла
Точно так же, как формулы двойного угла имеют дело с проблемой нахождения тригонометрической функции удвоенного угла (2*тета), формулы половинного угла решают проблему нахождения тригонометрической функции половины угла (тета/2).
 Формулы половинного угла, которые мы будем использовать, показаны справа. Обратите внимание, что перед формулами синуса и косинуса и одной из версий формулы тангента стоит знак + или -. Это означает, что вы сначала определите, будет ли результат положительным или отрицательным. Как вы будете определять это?
Формулы половинного угла, которые мы будем использовать, показаны справа. Обратите внимание, что перед формулами синуса и косинуса и одной из версий формулы тангента стоит знак + или -. Это означает, что вы сначала определите, будет ли результат положительным или отрицательным. Как вы будете определять это?Возьмите исходную задачу и определите заданные пределы угла. Например, если вам говорят, что угол находится в квадранте II, вы знаете, что угол должен быть между 90 o и 180 o . Разделив на 2, мы знаем, что половинный угол (тета/2) должен быть между 45 o и 90 o . Это делает его углом первого квадранта и соответствующим знаком является +. Давайте выполним несколько примеров задач, чтобы освоить это определение:
- Бета — угол третьего квадранта
- Beta находится между 180 o и 270 o
- Разделив на 2, мы знаем, что Beta/2 должен быть между 90 o и 135 o (второй квадрант)
- Если нам нужен косинус бета/2, мы используем знак -.


 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных формул можно решить практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь сами формулы, а не их вывод, которому будут посвящены отдельные статьи.
Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных формул можно решить практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь сами формулы, а не их вывод, которому будут посвящены отдельные статьи.


 Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.
Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.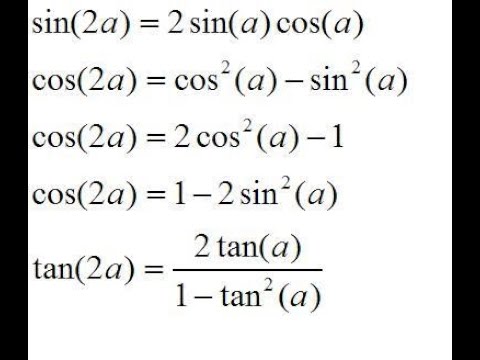



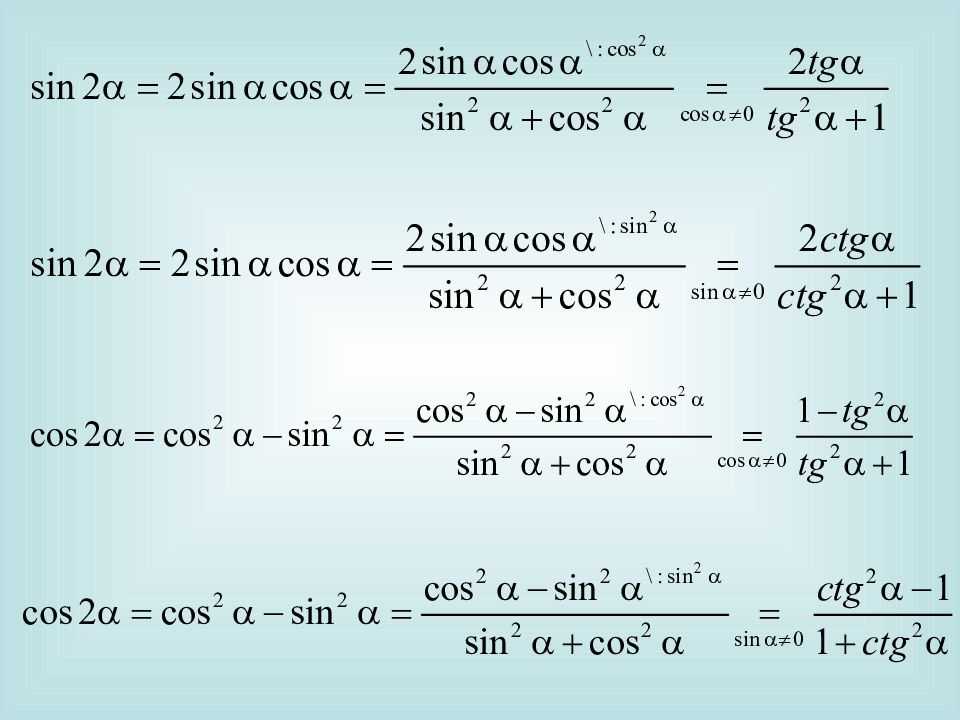 — 384 с.: ил.- ISBN 5-09-013651-3.
— 384 с.: ил.- ISBN 5-09-013651-3. см. также доказательство суммы квадратов косинуса и синуса .
см. также доказательство суммы квадратов косинуса и синуса .

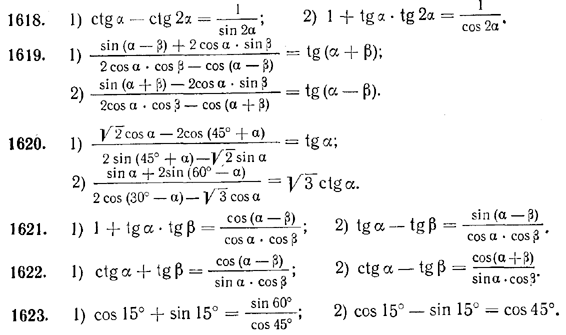

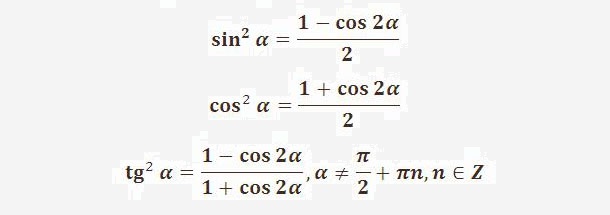
 0034 с углом ∝ по оси x. Thus, base = x, height = y, hypotenuses = r
0034 с углом ∝ по оси x. Thus, base = x, height = y, hypotenuses = r  = 1
= 1 Итак, cos α = x/1, sin α = y/1. По теореме Пифагора и подстановке x 2 + y 2 = 1 2 = 1 = cos 2 α + sin 2 α.
Итак, cos α = x/1, sin α = y/1. По теореме Пифагора и подстановке x 2 + y 2 = 1 2 = 1 = cos 2 α + sin 2 α.
 Теперь, используя закон синусов, мы можем написать:
Теперь, используя закон синусов, мы можем написать: Формулы половинного угла, которые мы будем использовать, показаны справа. Обратите внимание, что перед формулами синуса и косинуса и одной из версий формулы тангента стоит знак + или -. Это означает, что вы сначала определите, будет ли результат положительным или отрицательным. Как вы будете определять это?
Формулы половинного угла, которые мы будем использовать, показаны справа. Обратите внимание, что перед формулами синуса и косинуса и одной из версий формулы тангента стоит знак + или -. Это означает, что вы сначала определите, будет ли результат положительным или отрицательным. Как вы будете определять это?