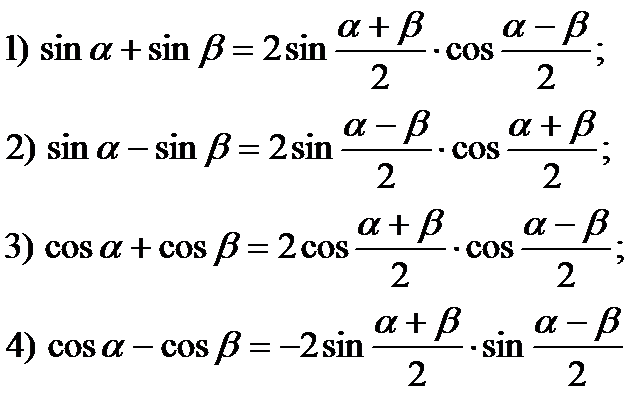Тригонометрические тождества и преобразования. Все формулы по тригонометрии Формулы приведения тригонометрических функций
В тригонометрии многие формулы легче вывести, чем вызубрить. Косинус двойного угла — замечательная формула! Она позволяет получить формулы понижения степени и формулы половинного угла.
Итак, нам нужны косинус двойного угла и тригонометрическая единица:
Они даже похожи: в формуле косинуса двойного угла — разность квадратов косинуса и синуса, а в тригонометрической единице — их сумма. Если из тригонометрической единицы выразить косинус:
и подставить его в косинус двойного угла, то получим:
Это — еще одна формула косинуса двойного угла:
Эта формула — ключ к получению формулы понижения степени:
Итак, формула понижения степени синуса:
Если в ней угол альфа заменить на половинный угол альфа пополам, а двойной угол два альфа — на угол альфа, то получим формулу половинного угла для синуса:
Теперь из тригонометрической единицы выразим синус:
Подставим это выражение в формулу косинуса двойного угла:
Получили еще одну формулу косинуса двойного угла:
Эта формула — ключ к нахождению формулы понижения степени косинуса и половинного угла для косинуса.
Таким образом, формула понижения степени косинуса:
Если в ней заменить α на α/2, а 2α — на α, то получим формулу половинного аргумента для косинуса:
Так как тангенс — отношение синуса к косинусу то формула для тангенса:
Котангенс — отношение косинуса к синусу. Поэтому формула для котангенса:
Конечно, в процессе упрощения тригонометрических выражений формулы половинного угла или понижения степени нет смысла каждый раз выводить. Гораздо проще перед собой положить листик с формулами. И упрощение продвинется быстрее, и зрительная память включится на запоминание.
Но несколько раз вывести эти формулы все же стоит. Тогда вы будете абсолютно уверены в том, что на экзамене, когда нет возможности воспользоваться шпаргалкой, вы без труда их получите, если возникнет необходимость.
На этой странице вы найдете все основные тригонометрические формулы, которые помогут вам решать многие упражнения, значительно упростив само выражение.
Тригонометрические формулы — математические равенства для тригонометрических функций, которые выполняются при всех допустимых значениях аргумента.
Формулами задаются соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом, котангенсом.
Синус угла – это координата y точки (ордината) на единичной окружности. Косинус угла – это координата x точки (абсцисса).
Тангенс и котангенс – это, соответственно, соотношения синуса к косинусу и наоборот.
`sin \ \alpha, \ cos \ \alpha`
`tg \ \alpha=\frac{sin\ \alpha}{cos \ \alpha},` ` \alpha\ne\frac\pi2+\pi n, \ n \in Z`
`ctg \ \alpha=\frac{cos\ \alpha}{sin\ \alpha},` ` \alpha\ne\pi+\pi n, \ n \in Z`
И две, которые используются реже – секанс, косеканс. Они обозначают соотношения 1 к косинусу и синусу.
`sec \ \alpha=\frac{1}{cos\ \alpha},` ` \alpha\ne\frac\pi2+\pi n,\ n \in Z`
`cosec \ \alpha=\frac{1}{sin \ \alpha},` ` \alpha\ne\pi+\pi n,\ n \in Z`
Из определений тригонометрических функций видно, какие знаки они имеют в каждой четверти.
2 \alpha,` ` \alpha\ne\pi n, \ n \in Z`
Формулы суммы и разности углов тригонометрических функций
Формулы сложения и вычитания аргументов выражают тригонометрические функции суммы или разности двух углов через тригонометрические функции этих углов.
`sin(\alpha+\beta)=` `sin \ \alpha\ cos \ \beta+cos \ \alpha\ sin \ \beta`
`sin(\alpha-\beta)=` `sin \ \alpha\ cos \ \beta-cos \ \alpha\ sin \ \beta`
`cos(\alpha-\beta)=` `cos \ \alpha\ cos \ \beta+sin \ \alpha\ sin \ \beta`
`tg(\alpha+\beta)=\frac{tg \ \alpha+tg \ \beta}{1-tg \ \alpha\ tg \ \beta}`
`tg(\alpha-\beta)=\frac{tg \ \alpha-tg \ \beta}{1+tg \ \alpha \ tg \ \beta}`
`ctg(\alpha+\beta)=\frac{ctg \ \alpha \ ctg \ \beta-1}{ctg \ \beta+ctg \ \alpha}`
`ctg(\alpha-\beta)=\frac{ctg \ \alpha\ ctg \ \beta+1}{ctg \ \beta-ctg \ \alpha}`
Формулы двойного угла
`sin \ 2\alpha=2 \ sin \ \alpha \ cos \ \alpha=` `\frac {2 \ tg \ \alpha}{1+tg^2 \alpha}=\frac {2 \ ctg \ \alpha}{1+ctg^2 \alpha}=` `\frac 2{tg \ \alpha+ctg \ \alpha}`
`cos \ 2\alpha=cos^2 \alpha-sin^2 \alpha=` `1-2 \ sin^2 \alpha=2 \ cos^2 \alpha-1=` `\frac{1-tg^2\alpha}{1+tg^2\alpha}=\frac{ctg^2\alpha-1}{ctg^2\alpha+1}=` `\frac{ctg \ \alpha-tg \ \alpha}{ctg \ \alpha+tg \ \alpha}`
`tg \ 2\alpha=\frac{2 \ tg \ \alpha}{1-tg^2 \alpha}=` `\frac{2 \ ctg \ \alpha}{ctg^2 \alpha-1}=` `\frac 2{ \ ctg \ \alpha-tg \ \alpha}`
`ctg \ 2\alpha=\frac{ctg^2 \alpha-1}{2 \ ctg \ \alpha}=` `\frac { \ ctg \ \alpha-tg \ \alpha}2`
Формулы тройного угла
`sin \ 3\alpha=3 \ sin \ \alpha-4sin^3 \alpha`
`cos \ 3\alpha=4cos^3 \alpha-3 \ cos \ \alpha`
`tg \ 3\alpha=\frac{3 \ tg \ \alpha-tg^3 \alpha}{1-3 \ tg^2 \alpha}`
`ctg \ 3\alpha=\frac{ctg^3 \alpha-3 \ ctg \ \alpha}{3 \ ctg^2 \alpha-1}`
Формулы половинного угла
`sin \ \frac \alpha 2=\pm \sqrt{\frac {1-cos \ \alpha}2}`
`cos \ \frac \alpha 2=\pm \sqrt{\frac {1+cos \ \alpha}2}`
`tg \ \frac \alpha 2=\pm \sqrt{\frac {1-cos \ \alpha}{1+cos \ \alpha}}=` `\frac {sin \ \alpha}{1+cos \ \alpha}=\frac {1-cos \ \alpha}{sin \ \alpha}`
`ctg \ \frac \alpha 2=\pm \sqrt{\frac {1+cos \ \alpha}{1-cos \ \alpha}}=` `\frac {sin \ \alpha}{1-cos \ \alpha}=\frac {1+cos \ \alpha}{sin \ \alpha}`
Формулы половинных, двойных и тройных аргументов выражают функции `sin, \ cos, \ tg, \ ctg` этих аргументов (`\frac{\alpha}2, \ 2\alpha, \ 3\alpha,… `) через эти ж функции аргумента `\alpha`.
4 \alpha=\frac{3+4cos \ 2\alpha+cos \ 4\alpha}8`
Формулы суммы и разности тригонометрических функций
Формулы являют собой преобразования суммы и разности тригонометрических функций разных аргументов в произведение.
`sin \ \alpha+sin \ \beta=` `2 \ sin \frac{\alpha+\beta}2 \ cos \frac{\alpha-\beta}2`
`sin \ \alpha-sin \ \beta=` `2 \ cos \frac{\alpha+\beta}2 \ sin \frac{\alpha-\beta}2`
`cos \ \alpha+cos \ \beta=` `2 \ cos \frac{\alpha+\beta}2 \ cos \frac{\alpha-\beta}2`
`cos \ \alpha-cos \ \beta=` `-2 \ sin \frac{\alpha+\beta}2 \ sin \frac{\alpha-\beta}2=` `2 \ sin \frac{\alpha+\beta}2 \ sin \frac{\beta-\alpha}2`
`tg \ \alpha \pm tg \ \beta=\frac{sin(\alpha \pm \beta)}{cos \ \alpha \ cos \ \beta}`
`ctg \ \alpha \pm ctg \ \beta=\frac{sin(\beta \pm \alpha)}{sin \ \alpha \ sin \ \beta}`
`tg \ \alpha \pm ctg \ \beta=` `\pm \frac{cos(\alpha \mp \beta)}{cos \ \alpha \ sin \ \beta}`
Здесь происходит преобразование сложения и вычитаний функций одного аргумента в произведение.
2 (\frac {\pi} 4-\frac{\alpha}2)`
`1 \pm tg \ \alpha=\frac{sin(\frac{\pi}4 \pm \alpha)}{cos \frac{\pi}4 \ cos \ \alpha}=` `\frac{\sqrt{2} sin(\frac{\pi}4 \pm \alpha)}{cos \ \alpha}`
`1 \pm tg \ \alpha \ tg \ \beta=\frac{cos(\alpha \mp \beta)}{cos \ \alpha \ cos \ \beta};` ` \ ctg \ \alpha \ ctg \ \beta \pm 1=\frac{cos(\alpha \mp \beta)}{sin \ \alpha \ sin \ \beta}`
Формулы преобразования произведений функций
Формулы преобразования произведения тригонометрических функций с аргументами `\alpha` и `\beta` в сумму (разность) этих аргументов.
`sin \ \alpha \ sin \ \beta =` `\frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{2}`
`sin\alpha \ cos\beta =` `\frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{2}`
`cos \ \alpha \ cos \ \beta =` `\frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{2}`
`tg \ \alpha \ tg \ \beta =` `\frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{cos(\alpha — \beta)+cos(\alpha + \beta)} =` `\frac{tg \ \alpha + tg \ \beta}{ctg \ \alpha + ctg \ \beta}`
`ctg \ \alpha \ ctg \ \beta =` `\frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{cos(\alpha — \beta)-cos(\alpha + \beta)} =` `\frac{ctg \ \alpha + ctg \ \beta}{tg \ \alpha + tg \ \beta}`
`tg \ \alpha \ ctg \ \beta =` `\frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{sin(\alpha + \beta)-sin(\alpha — \beta)}`
Универсальная тригонометрическая подстановка
Эти формулы выражают тригонометрические функции через тангенс половинного угла.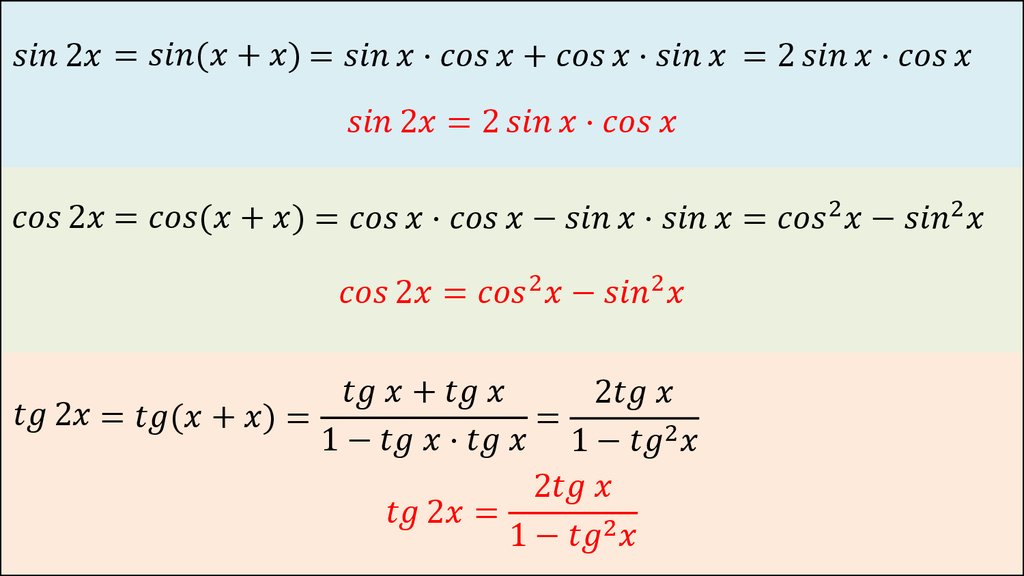
2 \alpha}}=\frac 1{tg \ \alpha}`
Тригонометрия в буквальном смысле переводится, как «измерение треугольников». Она начинает изучаться еще в школе, и продолжается более детально в ВУЗах. Поэтому основные формулы по тригонометрии нужны, начиная еще с 10 класса, а также для сдачи ЕГЭ. Они обозначают связи между функциями, а поскольку этих связей много, то и самых формул есть немало. Запомнить их все нелегко, да и не надо – при необходимости их все можно вывести.
Тригонометрические формулы применяются в интегральном исчислении, а также при тригонометрических упрощениях, вычислениях, преобразованиях.
Для решения некоторых задач будет полезной таблица тригонометрических тождеств, которая позволит гораздо проще совершать преобразования функций:
Простейшие тригонометрические тождества
Частное от деления синуса угла альфа на косинус того же угла равно тангенсу этого угла (Формула 1). См. также доказательство правильности преобразования простейших тригонометрических тождеств .
Частное от деления косинуса угла альфа на синус того же угла равно котангенсу этого же угла (Формула 2)
Секанс угла равен единице, деленной на косинус этого же самого угла (Формула 3)
Сумма квадратов синуса и косинуса одного и того же угла равна единице (Формула 4). см. также доказательство суммы квадратов косинуса и синуса .
Сумма единицы и тангенса угла равна отношению единицы к квадрату косинуса этого угла (Формула 5)
Единица плюс котангенс угла равна частному от деления единицы на синус квадрат этого угла (Формула 6)
Произведение тангенса на котангенс одного и того же угла равно единице (Формула 7).
Преобразование отрицательных углов тригонометрических функций (четность и нечетность)
Для того, чтобы избавиться от отрицательного значения градусной меры угла при вычислении синуса, косинуса или тангенса, можно воспользоваться следующими тригонометрическими преобразованиями (тождествами), основанными на принципах четности или нечетности тригонометрических функций.
Как видно, косинус и секанс является четной функцией , синус, тангенс и котангенс — нечетные функции .
Синус отрицательного угла равен отрицательному значению синуса этого же самого положительного угла (минус синус альфа).
Тангенс минус альфа равен минус тангенс альфа.
Формулы приведения двойного угла (синус, косинус, тангенс и котангенс двойного угла)
Если необходимо разделить угол пополам, или наоборот, перейти от двойного угла к одинарному, можно воспользоваться следующими тригонометрическими тождествами:
Преобразование двойного угла (синуса двойного угла, косинуса двойного угла и тангенса двойного угла ) в одинарный происходит по следующим правилам:
Синус двойного угла равен удвоенному произведению синуса на косинус одинарного угла
Косинус двойного угла равен разности квадрата косинуса одинарного угла и квадрата синуса этого угла
Косинус двойного угла равен удвоенному квадрату косинуса одинарного угла минус единица
Косинус двойного угла равен единице минус двойной синус квадрат одинарного угла
Тангенс двойного угла равен дроби, числитель которой — удвоенный тангенс одинарного угла, а знаменатель равен единице минус тангенс квадрат одинарного угла.
Котангенс двойного угла равен дроби, числитель которой — квадрат котангенса одинарного угла минус единица, а знаменатель равен удвоенному котангенсу одинарного угла
Формулы универсальной тригонометрической подстановки
Указанные ниже формулы преобразования могут пригодиться, когда нужно аргумент тригонометрической функции (sin α, cos α, tg α) разделить на два и привести выражение к значению половины угла. Из значения α получаем α/2 .
Данные формулы называются формулами универсальной тригонометрической подстановки . Их ценность заключается в том, что тригонометрическое выражение с их помощью сводится к выражению тангенса половины угла, вне зависимости от того, какие тригонометрические функции (sin cos tg ctg) были в выражении изначально. После этого уравнение с тангенсом половины угла решить гораздо проще.
Тригонометрические тождества преобразования половины угла
Указанные ниже формулы тригонометрического преобразования половинной величины угла к его целому значению.
Значение аргумента тригонометрической функции α/2 приводится к значению аргумента тригонометрической функции α.
Тригонометрические формулы сложения углов
cos (α — β) = cos α · cos β + sin α · sin β
sin (α + β) = sin α · cos β + sin β · cos α
sin (α — β) = sin α · cos β — sin β · cos α
cos (α + β) = cos α · cos β — sin α · sin β
Тангенс и котангенс суммы углов альфа и бета могут быть преобразованы по следующим правилам преобразования тригонометрических функций:
Тангенс суммы углов равен дроби, числитель которой — сумма тангенса первого и тангенса второго угла, а знаменатель — единица минус произведение тангенса первого угла на тангенс второго угла.
Тангенс разности углов равен дроби, числитель которой равен разности тангенса уменьшаемого угла и тангенса вычитаемого угла, а знаменатель — единице плюс произведение тангенсов этих углов.
Котангенс суммы углов равен дроби, числитель которой равен произведению котангенсов этих углов плюс единица, а знаменатель равен разности котангенса второго угла и котангенса первого угла.
Котангенс разности углов равен дроби, числитель которой — произведение котангенсов этих углов минус единица, а знаменатель равен сумме котангенсов этих углов.
Данные тригонометрические тождества удобно применять, когда нужно вычислить, например, тангенс 105 градусов (tg 105). Если его представить как tg (45 + 60), то можно воспользоваться приведенными тождественными преобразованиями тангенса суммы углов, после чего просто подставить табличные значения тангенса 45 и тангенса 60 градусов.
Формулы преобразования суммы или разности тригонометрических функций
Выражения, представляющие собой сумму вида sin α + sin β можно преобразовать с помощью следующих формул:
Формулы тройного угла — преобразование sin3α cos3α tg3α в sinα cosα tgα
Иногда необходимо преобразовать тройную величину угла так, чтобы аргументом тригонометрической функции вместо 3α стал угол α.
В этом случае можно воспользоваться формулами (тождествами) преобразования тройного угла:
Формулы преобразования произведения тригонометрических функций
Если возникает необходимость преобразовать произведение синусов разных углов косинусов разных углов или даже произведения синуса на косинус, то можно воспользоваться следующими тригонометрическими тождествами:
В этом случае произведение функций синуса, косинуса или тангенса разных углов будет преобразовано в сумму или разность.
Формулы приведения тригонометрических функций
Пользоваться таблицей приведения нужно следующим образом. В строке выбираем функцию, которая нас интересует. В столбце — угол. Например, синус угла (α+90) на пересечении первой строки и первого столбца выясняем, что sin (α+90) = cos α .
Тригонометрические формулы, которые нужны в высшей математике
Следующие несколько фактов и формул нужно просто запомнить наизусть!
Без них ваша учёба может закончиться самым скверным образом.
Во-первых, на практике очень часто используют нечётность синуса и чётность косинуса, а именно, выносят «минус» из-под синуса: , например, , и уничтожают минус под косинусом: , например, . Минус, кстати, выносится и у тангенса с котангенсом.
Осуществимы и обратные действия – «минус» можно «затолкать» под синус:
или поставить его под косинусом: .
Особо подчёркиваю, что здесь мы не получаем каких-то новых функций! Эти преобразования равносильны или, как говорят математики,
тождественны.
В частности, и – это две совершенно одинаковые функции, просто запись разная. Одна
запись удобна в одних задачах, другая – в других.
Ещё одна ходовая вещь, которую нужно запомнить «намертво» – это основное тригонометрическое тождество:
Аргумент может быть любым: и т.д. И обратно, единицу можно превратить в нужную сумму, например:
Чуть позже мы выведем из этого тождества ещё несколько полезных формул.
Внимательные читатели ещё в прошлой главе подметили, что тангенс и котангенс – это два взаимно
обратных отношения: (для допустимых углов)
и, наоборот: . По правилу
пропорции обе функции можно расположить на одном этаже, и тогда мы получаем формулу .
Тангенс можно выразить через синус и косинус: , и,
соответственно, котангенс равен обратному отношению: .
Теперь немного расслабьтесь, поскольку критически важные формулы позади, и вы спасены 🙂 Вся прелесть математики состоит в том, что знать нужно
немного, и из этого немного можно вывести очень много! Иногда даже маленькую Вселенную. Получим несколько полезных формул из основного
тригонометрического тождества. Прежде всего, здесь напрашивается выразить синус через косинус и наоборот:
Когда ставить «плюс», а когда «минус» мы узнаем под занавес курса, в ходе изучения тригонометрических
неравенств.
Если тождество разделить почленно на или , то получим ещё две полезные формулы, которые
используются в некоторых задачах высшей математики:
Думал не говорить, но всё-таки скажу: не путайте записи и . В первом случае в квадрате находится синус: , а во втором – его аргумент: и, конечно, это не одно и то же: .
И ещё раз заостряю внимание, что параметр «альфа» может быть не только буковкой «икс», но и сложной функцией! Все формулы
работают:
и так далее.
Следующая группа – это формулы двойного угла:
и более редкий тангенс: .
Примеры использования:
Мегапопулярные формулы понижения степени:
Запоминать их не нужно, сами запомнятся :). Натыкаться будете на каждом шагу.
Примеры:
Разумеется, все рассматриваемые формулы работают и в обратном направлении, так, степень иногда требуется и повысить:
Ну и еще куча похожих друг на друга формул. Сразу скажу, что них есть одно замечательное свойство – упорно не запоминаться. Я сотни раз искал их в справочнике, так и не запомнилась ни одна. Итак, для произвольных углов «альфа» и «бета» справедливо следующее.
Раз:
Два:
Три:
Есть еще аналогичные формулы для тангенсов и котангенсов, но о них не будем, в 99,9% случаях – не встретите.
Да и перечисленные формулы
встречаются довольно редко. Но встречаются. Поэтому примеры употребления (1-я формула из каждой группы):
5.6. Обратные тригонометрические функции
5.4. Периодичность и взаимосвязь функций. Формулы приведения
| Оглавление |
\circ \), происходит от тот факт, что GeoGebra может показывать только эти углы.Используя тождества \(\sin(-\beta)=-\sin(\beta)\) и \(\cos(-\beta)=\cos(\beta)\) получаем:
\[\sin(\alpha-\beta)=\sin(\alpha + (-\beta))=\sin \alpha \cos (-\beta) + \cos \alpha \sin (-\beta)= \sin\alpha\cos\beta — \cos\alpha\sin\beta\]
Формула сложения для косинуса
Загрузить рабочий лист GeoGebra
Измените углы, чтобы увидеть наблюдения во всех четырех квадрантах. 9\цирк\).\[-\cos(\alpha ‘ +\beta )=-\cos \alpha ‘ \cos \beta +\sin \alpha ‘ \sin\beta = \sin\alpha\cos\beta+\sin\beta\cos \альфа\]
Аналогичным образом можно доказать, что все формулы сложения верны для всех углов.