Синус числа: Как найти синус и косинус без тригонометрической таблицы?

alexxlab / / Разное

1.2.3 Синус, косинус, тангенс и котангенс числа

Итак, напоминаем, что при рассмотрении тригонометрических функций мы рассматриваем окружность, которая имеет единичный радиус. Данное упрощение используется для удобства. Все отношения справедливы для произвольных окружностей, с произвольным радиусом.

Пример. Давайте построим точки на единичной окружности, которые будут соответствовать повороту радиус-вектора на угол  

Решение. За начало отсчета принимаем точку Р0. Угол, равный нулю радиан совпадает с данной точкой.

Мы знаем, что граничными считаются углы 0, π/2, π, 3π/2, 2π. Если использовать угол π/2 и разделить первую четверть на 3 равных части, то первое от начала отсчета разделение будет соответствовать углу π/6. На графике данная точка имеет место Рπ/6.

Чтобы получить угол π/4, необходимо прямой угол разделить на две части. Если необходимо отметить угол с отрицательным аргументом, необходимо пойти по часовой стрелке от начальной точки. Например, точка — π/4 будет находиться симметрично относительно оси ОХ в 4 четверти.

Давайте теперь вспомним, каким образом исчисляются углы, выраженные в радианной мере. Чему, например, соответствует в радианах π/4? Чтобы это узнать, следует числовое значение числа π разделить на 4.

3,14 : 4 = 0,78, если углу π/2 соответствует 3,14 : 2 = 1,57. Следовательно, на окружности угол, равный единице будет лежать выше π/4, но ниже π/2. Отрицательное значение угла симметрично положительному относительно оси ОХ.

Таким же образом следует найти и местонахождение угла, равного 2. Так как граничному прямому углу соответствует значение 1,57, то угол, равный двум, будет находиться во второй четверти.

Можно убедиться, что каждому числу соответствует своя ордината и абсцисса на плоскости.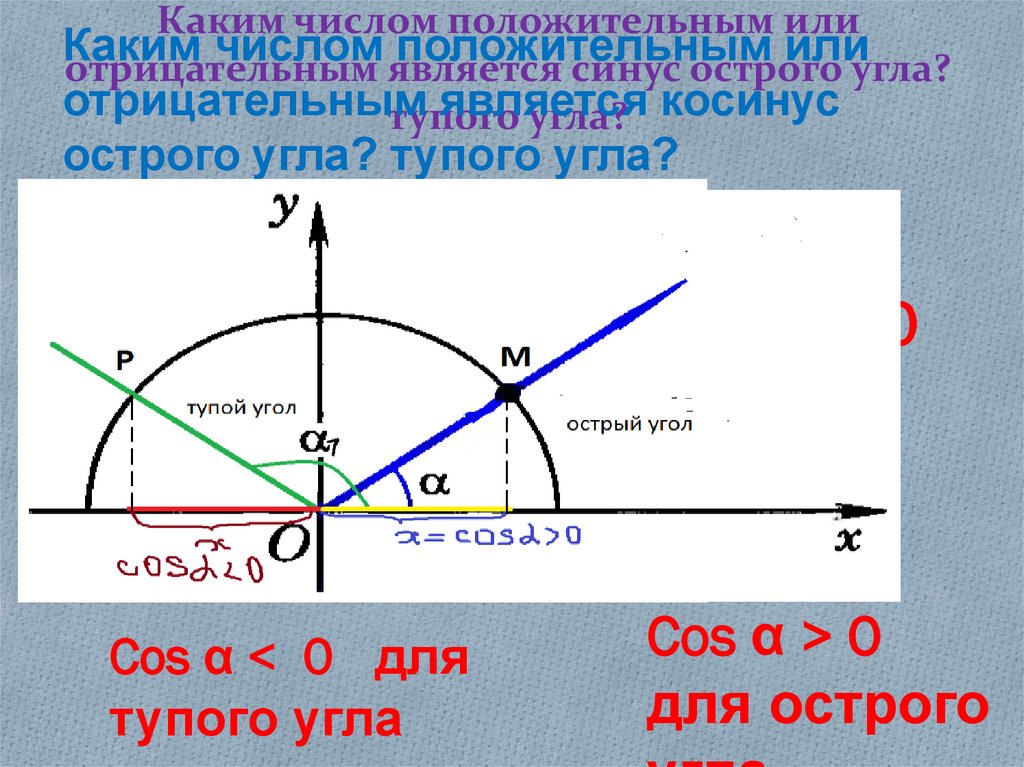

Отсюда можно сделать вывод, что: 

Синус некоторого числа — это значение ординаты на плоскости, которая соответствует точке этого числа на единичной окружности.

Косинус некоторого числа — это значение абсциссы на плоскости, которая соответствует точке этого числа на единичной окружности.

Тангенс некоторого числа — это значение, полученное в результате отношения синуса к косинусу, иначе говоря, отношение ординаты к абсциссе.

Котангенс некоторого числа — это значение, полученное в результате отношения косинуса к синусу, иначе говоря, отношение абсциссы к ординате.

Синус и косинус имеют период, равный 6,28. Тангенс и котангенс имеет период, равный 3,14.



  • 3.4 Характерные химические свойства углеводородов: алканов, циклоалканов, алкенов, диенов, алкинов, ароматических углеводородов
  • 2.3 Характерные химические свойства простых веществ неметаллов: водорода, галогенов, кислорода, серы, азота, фосфора, углерода, кремния
  • 2. 2 Характерные химические свойства и получение простых веществ — металлов: щелочных, щелочноземельных, алюминия; переходных элементов (меди, цинка, хрома, железа)
  • 1.2.4 Общая характеристика неметаллов IVA – VIIA групп в связи с их положением в Периодической системе химических элементов Д.И.Менделеева и особенностями строения их атомов
  • 1.2.1 Синус, косинус, тангенс, котангенс произвольного угла
    • Вконтакте
    • Сайт

    Mathway | Популярные задачи

    1Найти точное значениеsin(30)
    2Найти точное значениеsin(45)
    3Найти точное значениеsin(30 град. )
    4Найти точное значениеsin(60 град. )
    5Найти точное значениеtan(30 град. )
    6Найти точное значение
    arcsin(-1)
    7Найти точное значениеsin(pi/6)
    8Найти точное значениеcos(pi/4)
    9Найти точное значениеsin(45 град. )
    10Найти точное значениеsin(pi/3)
    11Найти точное значениеarctan(-1)
    12Найти точное значениеcos(45 град. )
    13Найти точное значениеcos(30 град. )
    14Найти точное значениеtan(60)
    15Найти точное значениеcsc(45 град. )
    16Найти точное значениеtan(60 град. )
    17Найти точное значениеsec(30 град. )
    18Найти точное значениеcos(60 град. )
    19Найти точное значениеcos(150)
    20Найти точное значениеsin(60)
    21Найти точное значениеcos(pi/2)
    22Найти точное значениеtan(45 град. )
    23Найти точное значениеarctan(- квадратный корень из 3)
    24Найти точное значениеcsc(60 град. )
    25Найти точное значениеsec(45 град. )
    26
    Найти точное значение    		csc(30 град. )
    27Найти точное значениеsin(0)
    28Найти точное значениеsin(120)
    29Найти точное значениеcos(90)
    30Преобразовать из радианов в градусыpi/3
    31Найти точное значениеtan(30)
    32Преобразовать из градусов в радианы45
    33Найти точное значениеcos(45)
    34Упроститьsin(theta)^2+cos(theta)^2
    35Преобразовать из радианов в градусыpi/6
    36Найти точное значениеcot(30 град. )
    37Найти точное значениеarccos(-1)
    38Найти точное значениеarctan(0)
    39Найти точное значениеcot(60 град. )
    40Преобразовать из градусов в радианы30
    41Преобразовать из радианов в градусы(2pi)/3
    42Найти точное значениеsin((5pi)/3)
    43Найти точное значениеsin((3pi)/4)
    44Найти точное значениеtan(pi/2)
    45Найти точное значениеsin(300)
    46Найти точное значениеcos(30)
    47Найти точное значениеcos(60)
    48Найти точное значениеcos(0)
    49Найти точное значениеcos(135)
    50Найти точное значениеcos((5pi)/3)
    51Найти точное значениеcos(210)
    52Найти точное значениеsec(60 град. )
    53Найти точное значениеsin(300 град. )
    54Преобразовать из градусов в радианы135
    55Преобразовать из градусов в радианы150
    56Преобразовать из радианов в градусы(5pi)/6
    57Преобразовать из радианов в градусы(5pi)/3
    58Преобразовать из градусов в радианы89 град.
    59Преобразовать из градусов в радианы60
    60Найти точное значениеsin(135 град. )
    61Найти точное значениеsin(150)
    62Найти точное значениеsin(240 град. )
    63Найти точное значениеcot(45 град. )
    64Преобразовать из радианов в градусы(5pi)/4
    65Найти точное значениеsin(225)
    66Найти точное значениеsin(240)
    67Найти точное значениеcos(150 град. )
    68Найти точное значениеtan(45)
    69Вычислитьsin(30 град. )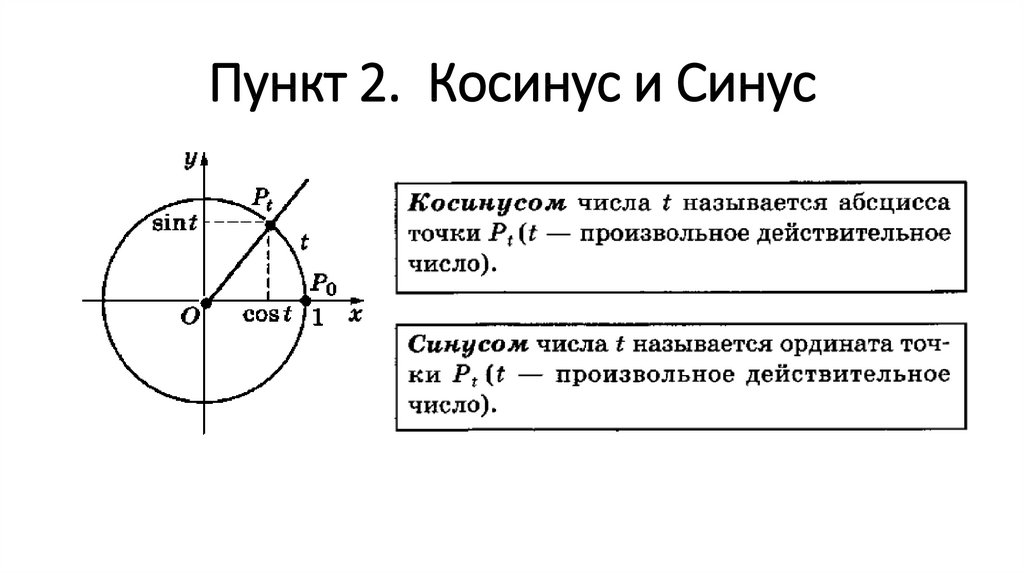
    70Найти точное значениеsec(0)
    71Найти точное значениеcos((5pi)/6)
    72Найти точное значениеcsc(30)
    73Найти точное значениеarcsin(( квадратный корень из 2)/2)
    74Найти точное значениеtan((5pi)/3)
    75Найти точное значениеtan(0)
    76Вычислитьsin(60 град. )
    77Найти точное значениеarctan(-( квадратный корень из 3)/3)
    78Преобразовать из радианов в градусы(3pi)/4
    79Найти точное значениеsin((7pi)/4)
    80Найти точное значениеarcsin(-1/2)
    81Найти точное значениеsin((4pi)/3)
    82Найти точное значениеcsc(45)
    83Упроститьarctan( квадратный корень из 3)
    84Найти точное значениеsin(135)
    85Найти точное значениеsin(105)
    86Найти точное значениеsin(150 град. )
    87Найти точное значениеsin((2pi)/3)
    88Найти точное значениеtan((2pi)/3)
    89Преобразовать из радианов в градусыpi/4
    90Найти точное значениеsin(pi/2)
    91Найти точное значениеsec(45)
    92Найти точное значениеcos((5pi)/4)
    93Найти точное значениеcos((7pi)/6)
    94Найти точное значениеarcsin(0)
    95Найти точное значениеsin(120 град. )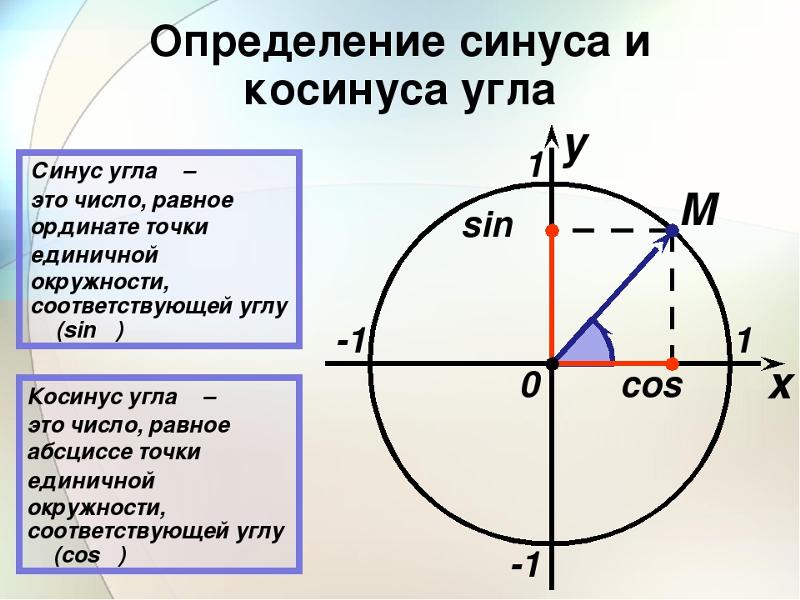
    96Найти точное значениеtan((7pi)/6)
    97Найти точное значениеcos(270)
    98Найти точное значениеsin((7pi)/6)
    99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
    100Преобразовать из градусов в радианы88 град.
    Исчисление

    — что такое синус вещественного числа

    Попробуйте ответить на этот вопрос, сначала просто взглянув на изображения (щелкните средней кнопкой мыши, чтобы увеличить их в новой вкладке).
    Если этого недостаточно, попробуйте прочитать описание.

    Где ввод в радианах:

    Представьте себе круг, как черный ниже: Для удобства назовем направление вверх на этой диаграмме «север».
    Представьте, что вы сидите на круге у красной точки в машине с очень точным счетчиком пробега.
    Вы можете представить, что транспортное средство — это вагон поезда, а черный кружок — это путь, если это поможет.
    Теперь представьте, что вы путешествуете по кругу и очерчиваете оранжевую дугу.
    Предположим, вы остановились в какой-то момент. Показания одометра х .
    (Вы можете представить себе, что это мили, километры, мегаметры или другие общие единицы измерения, которые кто-то решил назвать «радианами».) чтобы достичь исходной широты.
    Другими словами, «синус» x  – это то, как далеко вы находитесь на север от горизонтальной синей линии.

    Если вы прошли более половины круга и находитесь в «южной» половине, это расстояние будет отрицательным числом.
    Если вы прошли ровно половину круга или весь круг, это будет 0.


    Если вы прошли одну четверть пути, это будет 1.
    Если вы прошли три четверти пути, это будет -1.

    Радиус круга — это расстояние между центром и любой точкой на его краю. (Тот факт, что это постоянное значение, делает его кругом.)
    Центр этого круга находится в месте пересечения синих линий, а расстояние от этого центра до красной точки (точки на внешнем краю круга) равно 1.
    Это означает, что радиус этой окружности равен 1.
    (Любая окружность с радиусом 1 получает специальное название «единичная окружность», но на самом деле вам не нужно знать это, чтобы понять это объяснение.)

    9 окружности0003 диаметр (расстояние поперек круга через середину) всегда в два раза больше радиуса.
    Следовательно, диаметр этого круга равен 2.

    $\pi$ определяется как отношение диаметра круга к его длине окружности (расстоянию вокруг внешнего края круга). Так как $\pi$ = окружности / диаметр , окружности = диаметра * $\pi$, а длина окружности этого круга равна 2$\pi$.

    Как только одометр покажет 2$\pi$, вы вернетесь туда, откуда начали. Если вы продолжите движение, вы будете отслеживать тот же путь, и для каждого показания одометра расстояние, которое вам придется пройти на юг, чтобы достичь той же широты, с которой вы начали, точно такое же, как когда ваш одометр показывал 2 $\pi$ меньше, чем сейчас. Другими словами, значение синуса будет точно таким же, как и в прошлый раз, когда вы были там.
    Вот почему функция синуса периодична (то есть повторяется).
    $sin(x) = sin(x-2\pi) = sin(x+2\pi)$.

    Где ввод в градусах:

    Представьте себе круг, как черный ниже:
    Для удобства назовем направление вверх на этой диаграмме севером.
    Представьте, что в точке пересечения синих линий стоит обелиск, который виден отовсюду на круге.
    Представьте, что вы сидите на круге у красной точки, в одной единице к востоку от обелиска.
    Представьте, что линия между этим обелиском и вашей отправной точкой постоянно отмечена тем, что я назову «положительной горизонтальной осью».
    Теперь представьте, что вы путешествуете по кругу и очерчиваете оранжевую дугу.
    Предположим, вы остановились в какой-то точке и провели фиолетовую линию между тем, где вы находитесь, и обелиском. Назовем угол, который проходит от положительной горизонтальной оси к этой линии, $\theta$.

    «Синус» $\theta$ — это расстояние, которое вам придется пройти на юг, чтобы достичь исходной широты.
    Другими словами, «синус» $\theta$  – это то, как далеко вы находитесь на север от горизонтальной синей линии.

    Если вы прошли более половины круга и находитесь в «южной» половине, это расстояние будет отрицательным числом.
    Если вы прошли ровно половину круга или весь круг, это будет 0.
    Если вы прошли одну четверть пути, это будет 1.
    Если вы прошли три четверти пути, это будет -1.

    Как только вы вернетесь к тому, с чего начали, $\theta$ будет равно 360 градусам, потому что в круге 360 градусов (по определению).
    Если вы продолжите движение, вы будете отслеживать тот же путь, и для точки, которую вы достигнете снова, значение синуса будет точно таким же, как и в прошлый раз, когда вы были там.
    Вот почему функция синуса является периодической (что означает, что она повторяется).
    $sin(\theta) = sin(\theta-360°) = sin(\theta+360°)$.

    Дополнительное пояснение: косинус

    В обоих примерах косинус от x, или $\theta$, — это расстояние, которое вам придется пройти « на запад », чтобы достичь вертикальной синей линии.
    Другими словами, это то, как далеко вы находитесь «на восток» от вертикальной синей линии.
    Если вы нарисовали горизонтальную линию между концом дуги и вертикальной синей линией, это будет длина этой линии.
    Это длина синей стороны треугольника на второй диаграмме выше (где длина дуги по-прежнему равна x ).
    В начальной точке это 1.
    В «западной» половине круга это отрицательное число.
    Если вы прошли ровно половину пути, будет -1.
    Если вы прошли четверть круга или три четверти круга, это будет 0,9.0004 Косинус периодичен так же, как и синус; вы могли бы последовательно написать «cos» вместо «sin» в приведенных выше строках формулы (которые имеют два знака =), и каждый из них все равно будет правильным.

    Математики называют местонахождение обелиска «происхождением», но я решил не использовать этот термин здесь, чтобы избежать путаницы с более распространенным определением «происхождения», а именно «где вы начали», потому что это относится к другое место в повествовании, лежащем в основе этого ответа. Я также сделал альтернативную версию второй диаграммы, в которой вместо этого используется «происхождение».

    В этом сообщении также используется слово «линия» в нескольких местах, где «отрезок линии» был бы более правильным; Я думаю, что смысл понятен в контексте, и используемый здесь язык лучше облегчает понимание.

    тригонометрия — Какой самый эффективный способ вычисления синуса рационального числа?

    Точные ответы могут не иметь замкнутой формы для достаточно малых углов, но общий метод таков:

    Допустим, мы знаем точный ответ на $\sin(u)$ и теперь хотим вычислить $\sin(\frac{u} {к})$ 92}$$

    Чтобы получить выражение вида

    $$\sin(k \theta) = НЕКОТОРЫЕ \ ВОЛОСАТЫЕ \ АЛГЕБРАИЧЕСКИЕ \ БЕСПОРЯДОК \ ДЛЯ \ ДОСТАТОЧНО \ БОЛЬШИЕ \ K$$

    Тем не менее теперь мы можем «решить » наше уравнение выше для $\sin(\theta)$, которое позволяет нам выразить

    $$\sin(\theta) = F(\sin(k\theta))$$

    Где F — это, как правило, более сложное, обратное алгебраическому выражению ранее.

    No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *