Определение тригонометрических функций
Справочник по математике для школьников и абитуриентов / Элементарная математика
Рассмотрим вначале тригонометрические функции острого угла, которые можно ввести с помощью прямоугольного треугольника (рис. 1).
Пусть в прямоугольном треугольнике
:
(отношение противолежащего катета к гипотенузе).
Рис.1
(отношение прилежащего катета к гипотенузе).
(отношение противолежащего катета к прилежащему).
(отношение прилежащего катета к противолежащему).
Из последних двух равенств следует, что .
Рассмотрим тригонометрические функции произвольных значений аргумента.
Имеем прямоугольную систему координат хОу на плоскости и круг единичного радиуса, имеющий центр в начале координат (рис. 2). Такой круг называется единичным кругом или тригонометрическим кругом.
Рис.2
Отметим на оси Ох справа от начала координат точку
, лежащую на тригонометрическом круге: . Радиус называется начальным радиусом. При повороте начального радиуса около центра O на угол точка переходит в некоторую точку .
Синусом угла называется отношение ординаты точки к радиусу.
Косинусом угла называется отношение абсциссы точки к радиусу.
Таким образом, . Поскольку R=l, то . x и y можно рассматривать как проекции на оси координат единичного вектора . Таким образом, можно утверждать, что синус угла а равен ординате, а косинус — абсциссе вектора единичной длины, исходящего из начала координат и образующего с положительным направлением оси Ох угол . Так как координаты любой точки единичной окружности удовлетворяют уравнению , то . Соотношение называется основным тригонометрическим тождеством.
Тангенсом угла называется отношение ординаты точки к ее абсциссе:
.
Котангенсом угла называется отношение абсциссы точки к ее ординате:
.
Прямая (рис. 3) называется осью тангенсов.
Рис.3
Каждому углу
можно поставить в соответствие точку Т на оси тангенсов, являющуюся точкой пересечения конечной стороны угла (или ее продолжения) с осью тангенсов (рис. 4).
Рис.4
Тангенс угла
равен ординате соответствующей точки Т на оси тангенсов.
Прямая (рис. 5) называется осью котангенсов.
Рис.5
Каждому углу
можно поставить в соответствие точку на оси котангенсов, являющуюся точкой пересечения конечной стороны угла (или ее продолжения) с осью котангенсов (рис. 6).
Рис.6
Котангенс угла
равен абсциссе соответствующей точки на оси котангенсов.
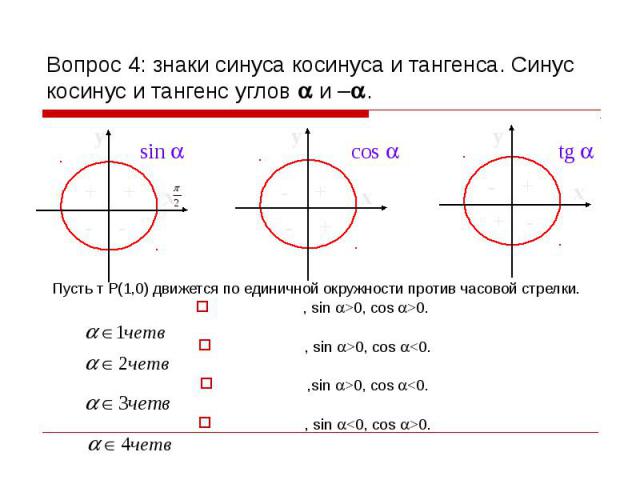
Знаки тригонометрических функций
в различных четвертях (квадрантах) даны на рис.
7.
Рис.7
Приведем таблицу значений тригонометрических функций некоторых углов, которые наиболее часто используются на практике (табл. 1).
Таблица 1
Символ
(бесконечность) означает, что или при соответствующих значениях аргумента не определены и принимают сколь угодно большие значения по модулю.
Секансом угла (обозначение ) называется величина, обратная , т. е. .
Косекансом угла (обозначение ) называется величина, обратная , т.е. .
Математика по полочкам: 5. Модуль. Тригонометрия
МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯМодуль числа Модулем действительного числа а называют само это число, если а больше или равно нуля, и противоположное число, если а меньше нуля.
|a|=a, если a≥0;
|a|= -a, если a<0.
Геометрически |a| означает расстояние на координатной прямой от точки, изображающей число а, до начала отсчета.
Свойства модуля
1. |a|≥0
2. |a|=|-a|
3. |a*b|=|a|*|b|
4. |a:b|=|a|:|b|
5. |a+b|≤|a|+|b|
6. |a-b|≥|a|-|b|
За единицу измерения углов и дуг принимают соответственно угол в 1 градус и дугу в 1 градус.
Еще одна единица измерения величины угла — 1 радиан.
Углом в один радиан называется центральный угол, которому соответствует длина дуги, равная длине радиуса окружности.
Примеры:
1. Вычислить градусную меру угла 5 рад.
2. Вычислить радианную меру угла в 50°.
Таблица значений тригонометрических функций углов
Значения sin и cos углов 0°, 30°, 45°, 60°, 90° можно узнать, пользуясь ладонью левой руки.
Введем нумерацию пальцев:
мизинец — 0,
безымянный — 1,
средний — 2,
указательный — 3,
Пример:
Найдем sin 60°:
На ладони угол 60° соответствует указательному пальцу, т.е. n=3. Подставим n в формулу, получим:
Пример:
Найдем cos 60°:
На ладони угол 60° соответствует безымянному пальцу, т.е. n=1. Подставим n в формулу, получим:
Формулы
sin2α + cos2α=1;
УПРАЖНЕНИЯ
1.
Выпишите верные равенства:
Решение:
2. Выпишите числовые выражения, которые имеют смысл:
Решение:
3. Запишите в порядке возрастания числа:
Решение:
4. Найдите значение выражения:
а) 3∙cos 30° + 3∙sin 30°; б) 5∙sin 60°+5∙cos 60°.
Решение:
5. Вычислите:
Решение:
6.
Запишите в радианах углы:
а) 15°; 128°; 60°; б) 57°; 340°; 45°.
Решение:
7. Запишите в градусах углы:
Решение:
8. Найдите значение выражения:
Решение:
9. Вычислите (№ 1.4.42 [7]):
Решение:
10. Вычислите:
а)((sin 60°-cos60°)(cos60°+sin60°)cos30°)2;
б) ((sin 30°-cos30°)(cos30°+sin30°)sin45°)-2
Решение:
11.
Докажите, что значение суммы является целым числом:
Решение:
8 — целое число, что и требовалось доказать.
12. Вычислите:
Решение:
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Вычислите: sin220°+cos220°; tg17°×ctg17°
2. Выпишите верные равенства:
3. Найдите значение выражения:
4. Выясните, верно ли неравенство:
5. Найдите радианную меру угла: 65°; 16°.
6. Найдите градусную меру угла:.
7. Вычислите:
tg245°+ cos30°-sin230° + 0,75 :
tg260°; 5tg30° + 2sin245°
+ ctg30°- tg45°.
8. Найдите значение выражения:
9. Найдите значение разности:
10. Докажите неравенство:
ПРОВЕРЬТЕ СЕБЯ
Use Coordinates of Points to Find Values of Trigonometry Functions
By: Mary Jane Sterling and
Updated: 07-12-2021
From The Book: Trigonometry For Dummies
Trigonometry For Dummies
Explore Book Buy On Amazon
Один из способов найти значения триггерных функций для углов — использовать координаты точек на окружности, центр которой находится в начале координат. Впуская позитив x -ось будет начальной стороной угла, вы можете использовать координаты точки пересечения конечной стороны с окружностью для определения триггерных функций.
На рисунке показана окружность радиусом r с углом, проведенным в стандартном положении.
Уравнение окружности: x 2 + y 2 = r 2 . На основании этого уравнения и координат точки ( x , y ), где крайняя сторона угла пересекает окружность, шесть триггерных функций для тета угла определяются следующим образом: точку ( x,y ) на ось x-. На следующем рисунке показан такой прямоугольный треугольник.
Помните, что значение x- находится справа (или слева) от начала координат, а значение y- выше (или ниже) x- оси — и используйте эти значения как длины сторон треугольника. Следовательно, сторона, противоположная углу тета, равна y , значению координаты y-. Смежная сторона x , значение координаты x-.
Обратите внимание, что, например, для углов во втором квадранте значения x- отрицательны, а значения y- положительны.
Однако радиус всегда является положительным числом. С x-значения отрицательные, а значения y- положительные, вы видите, что синус и косеканс положительны, но все остальные функции отрицательны, потому что все они имеют x в своих отношениях.
Эта статья из книги:
- Тригонометрия для чайников,
Об авторе книги:
Мэри Джейн Стерлинг — автор Алгебра I для чайников и многие другие названия для чайников . Она преподает математику в Университете Брэдли в Пеории, штат Иллинойс, уже более 30 лет, и ей нравилось работать с будущими руководителями предприятий, физиотерапевтами, учителями и многими другими.
Эту статью можно найти в категории:
- Тригонометрия,
10.
1 Полярные координатыПодобно тому, как мы описываем кривые на плоскости, используя уравнения, содержащие $x$ и $y$, поэтому мы можем описать кривые, используя уравнения, содержащие $r$ и $\тета$. Наиболее распространены уравнения вида $r=f(\theta)$.
Пример 10.1.1. Нарисуйте кривую, заданную $r=2$. Все точки с $r=2$ находятся в расстояние 2 от начала координат, поэтому $r=2$ описывает окружность радиуса 2 с центром в начале координат. $\квадрат$
Пример 10.1.2. Нарисуйте кривую, заданную $r=1+\cos\theta$. Мы сначала рассмотрим
$y=1+\cos x$, как на рисунке 10.1.2. Как $\theta$ идет
через значения в $[0,2\pi]$, значение $r$ отслеживает значение
$y$, образуя «кардиоидную»
форма рисунка 10.1.2.
Например, когда $\theta=\pi/2$, $r=1+\cos(\pi/2)=1$, мы наносим на график
точка на расстоянии 1 от начала координат по положительной оси $y$, которая
находится под углом $\pi/2$ к положительной оси $x$. Когда
$\theta=7\pi/4$, $\ds r=1+\cos(7\pi/4)=1+\sqrt2/2\приблизительно 1,71$, а
соответствующая точка появляется в четвертом квадранте.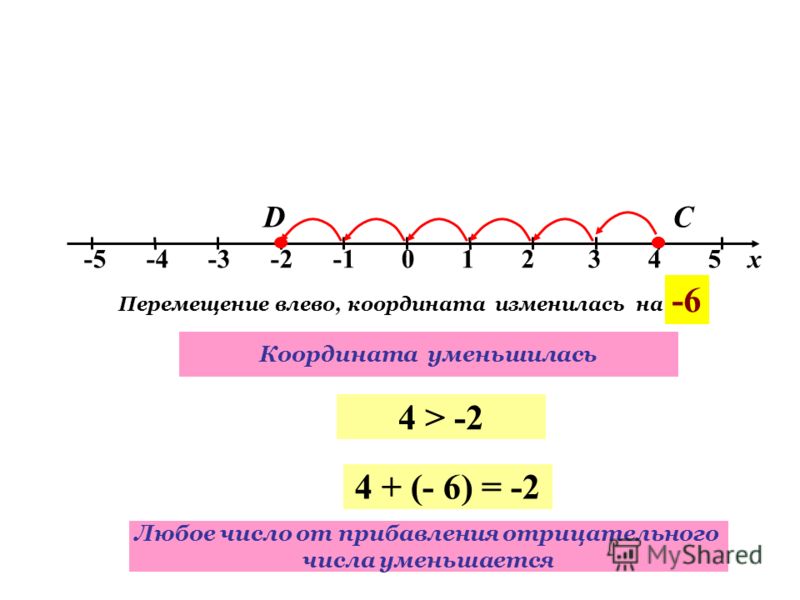
Рисунок 10.1.2. Кардиоида: $y=1+\cos x$ слева, $r=1+\cos\theta$ справа Правильно. Вы можете перетащить красную точку на графике слева и последует соответствующая точка справа.
Каждой точке на плоскости соответствует ровно одна пара чисел в прямоугольной системе координат; каждая точка связана с бесконечное число пар в полярных координатах. В кардиоидной Например, мы рассмотрели только диапазон $0\le \theta\le2\pi$, а уже был дубликат: $(2,0)$ и $(2,2\pi)$ одинаковы точка. Действительно, каждое значение $\theta$ вне интервала $[0,2\pi)$ дублирует точку на кривой $r=1+\cos\theta$, когда $0\le\theta10.1.3. Как обычно, отрицательный угол $\theta$ означает угол отсчитывается по часовой стрелке от положительной оси $x$. Дело в на рисунке 10.1.3 также есть координаты $(2,5\pi/4)$ и $(2,-3\pi/4)$.
Рисунок 10.
1.3. Точка $(-2,\pi/4)=(2,5\pi/4)=(2,-3\pi/4)$ в полярных координатах.
Отношение между прямоугольными и полярными координатами довольно легко понять. Точка с полярными координатами $(r,\theta)$ имеет прямоугольные координаты $x=r\cos\theta$ и $y=r\sin\theta$; это сразу следует из определения синуса и косинуса функции. Используя рисунок 10.1.3 в качестве например, показанная точка имеет прямоугольные координаты $\ds x=(-2)\cos(\pi/4)=-\sqrt2\приблизительно 1,4142$ и $\ds y=(-2)\sin(\pi/4)=-\sqrt2$. Это позволяет очень легко преобразовать уравнения от прямоугольных к полярным координатам. 92\тета=1/4$. Немного алгебры превращает это в $r=\cos(t)$. Вы должны попытаться построить несколько значений $(r,\theta)$ для убедите себя, что это имеет смысл. $\квадрат$
Пример 10.1.5. Нарисуйте график полярного уравнения $r=\theta$. Здесь расстояние от
начало координат точно совпадает с углом, так что немного подумав,
ясно, что при $\theta\ge0$ мы получаем спираль
Архимед в
рисунок 10.