Свойства сочетаний.
1) 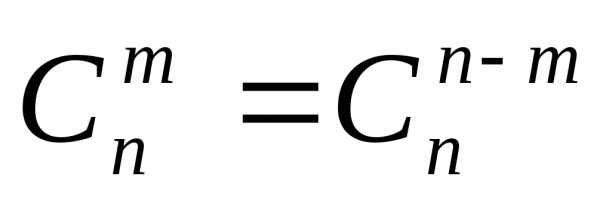 (1.8)
(1.8)
Действительно,
2) (1.9)
Покажем, что правая часть (1.9) равна левой части (1.9)
3) (1.10)
В соответствии с формулой бинома Ньютона
Пример 1. 10.
Сколькими способами можно составить дозор из трех солдат, если на заставе 20 солдат.
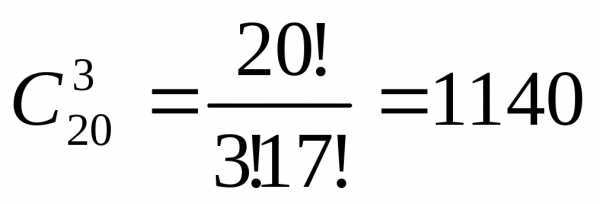
Пример 1.11.
В полуфинале первенства страны по шахматам участвуют 20 чел. В финал выходят трое. Найти число различных исходов полуфинала шахматного первенства.
Здесь нас не интересует порядок, в котором располагается первая тройка. Поэтому число исходов

Пример 1.12.
В турнире участвуют 8 игроков. Из трех человек, занявших первые места, формируется команда для поездки на соревнование. Каким количеством способов может быть сформирована команда?
Вопрос сводится к следующему: каким количеством способов можно выбрать трех человек из восьми? (порядок выбора роли не играет) По определению – это число сочетаний из восьми по три:
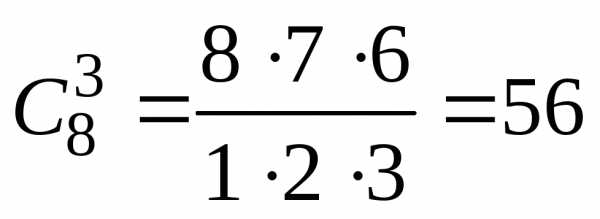 .
.
Пример 1.13.
В магазине 12 сортов пирожных. Покупатель хочет купить шесть разных пирожных. Сколько вариантов выбора у него есть?
Решение
Количество способов выбора здесь
.
В последнем примере было поставлено ограничение – разные пирожные. Если же ограничение снять, то количество вариантов выбора возрастет. Для того чтобы подсчитать количество способов выбора шести любых пирожных из 12 сортов (количество пирожных каждого сорта полагается неограниченным), нужно ввести еще одно определение – сочетание с повторениями.
Рассмотрим
неограниченное количество предметов 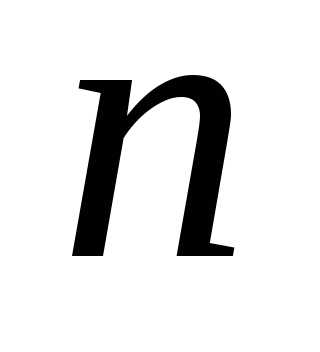 различных сортов. Пусть предметы одного
сорта не различаются.
различных сортов. Пусть предметы одного
сорта не различаются.
Сочетания с повторениями
Сочетанием
с повторениями из 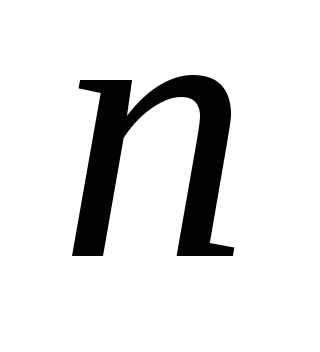 элементов по
элементов по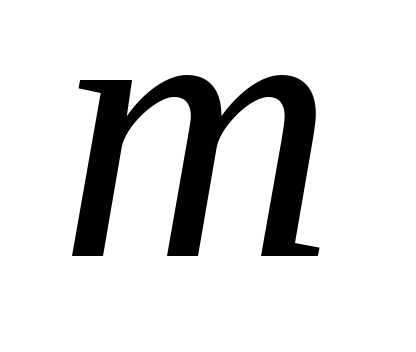 называется
выборка
называется
выборка 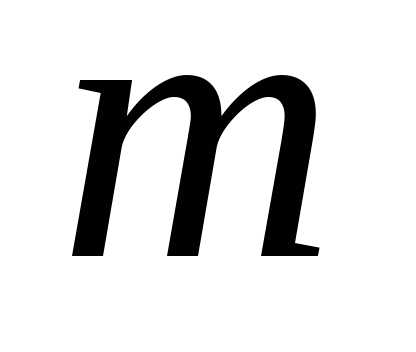 предметов из неограниченного количества
предметов
предметов из неограниченного количества
предметов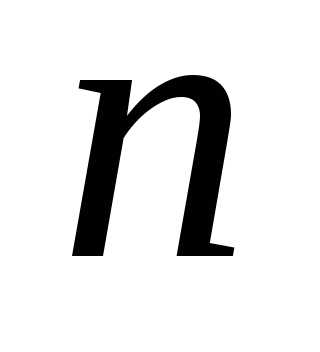
Число
вариантов выбора или количество таких
сочетаний обычно обозначается  и вычисляется по формуле
и вычисляется по формуле
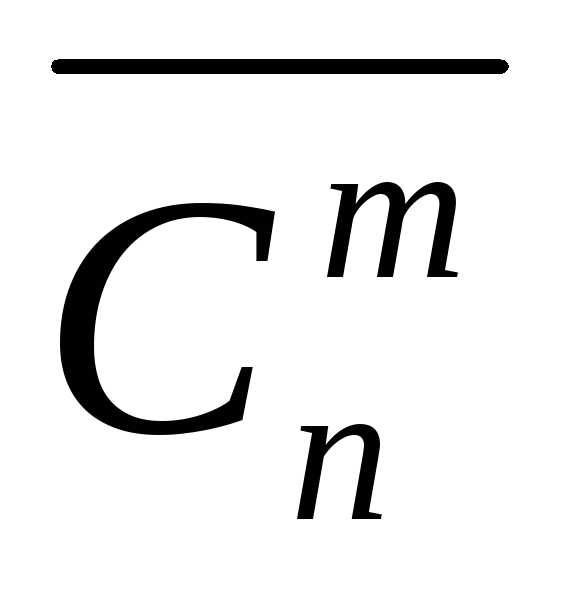 .
(1.11)
.
(1.11)
Каждое
сочетание полностью определяется , если
указать, сколько элементов каждого из 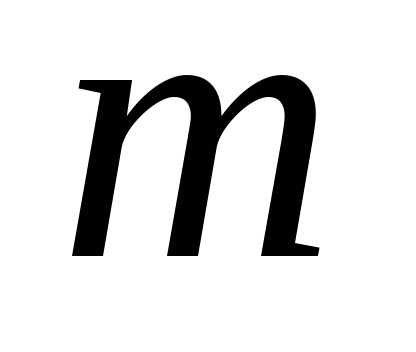 типов в него входит. Назовем кратностью
элемента число повторений данного
элемента в сочетании с повторениями.
Например, в сочетанииэлемент
типов в него входит. Назовем кратностью
элемента число повторений данного
элемента в сочетании с повторениями.
Например, в сочетанииэлемент имеет кратность
имеет кратность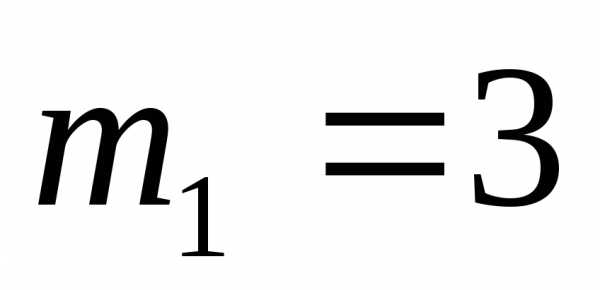 ,
элемент
,
элемент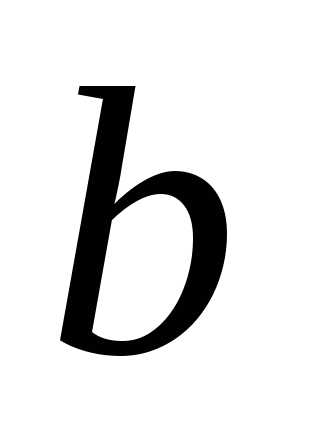
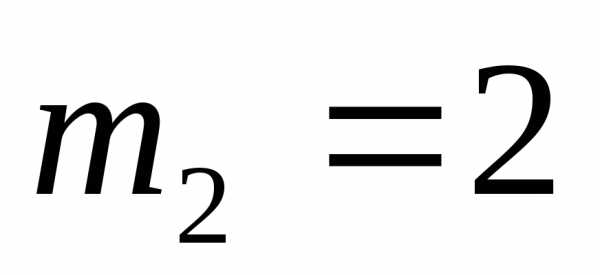 ,
элемент
,
элемент имеет кратность
имеет кратность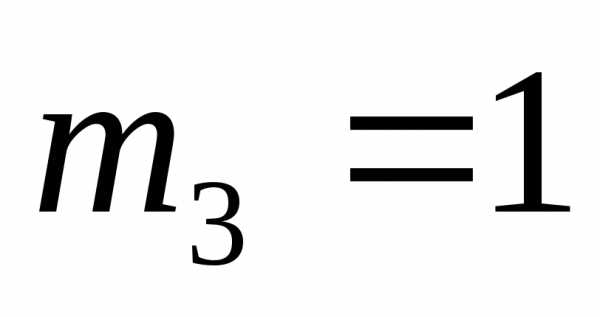 ,
элемент
,
элемент имеет кратность
имеет кратность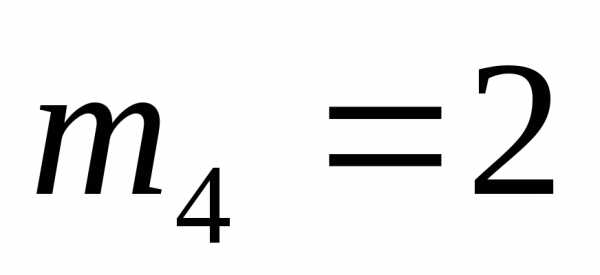 .
Сумма всех кратностей равна порядку
сочетания,
т.е..
Поставим каждому сочетанию в соответствие
последовательность из нулей и единиц,
составленную по такому правилу: напишем
подряд столько единиц, сколько элементов
первого типа в него входит, затем нуль,
затем напишем столько единиц, сколько
элементов второго типа в него входит,
затем нуль и т.д. Например, сочетанию с
повторениями
.
Сумма всех кратностей равна порядку
сочетания,
т.е..
Поставим каждому сочетанию в соответствие
последовательность из нулей и единиц,
составленную по такому правилу: напишем
подряд столько единиц, сколько элементов
первого типа в него входит, затем нуль,
затем напишем столько единиц, сколько
элементов второго типа в него входит,
затем нуль и т.д. Например, сочетанию с
повторениями соответствует последовательность
11101101011. Если некоторый элемент не
содержится в данном сочетании с
повторениями, т.е. его кратность равна
нулю, то тогда группа единиц не пишется
и в последовательности появится 0 по
меньшей мере два раза. В элементах
последовательности из нулей и единиц,
соответствующих сочетаниям с повторениями
из
соответствует последовательность
11101101011. Если некоторый элемент не
содержится в данном сочетании с
повторениями, т.е. его кратность равна
нулю, то тогда группа единиц не пишется
и в последовательности появится 0 по
меньшей мере два раза. В элементах
последовательности из нулей и единиц,
соответствующих сочетаниям с повторениями
из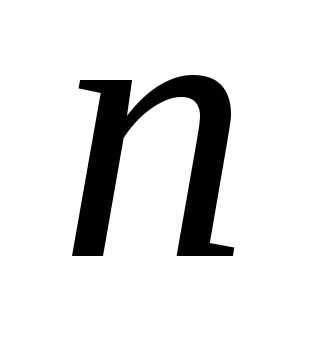
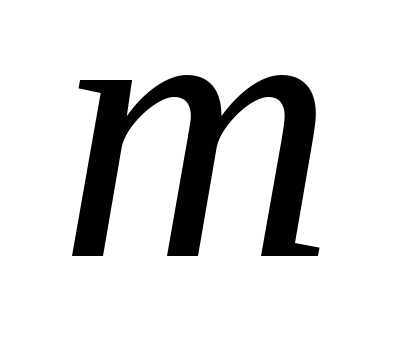 цифра 1 встречается
цифра 1 встречается раз, а цифра 0 встречается
раз, а цифра 0 встречается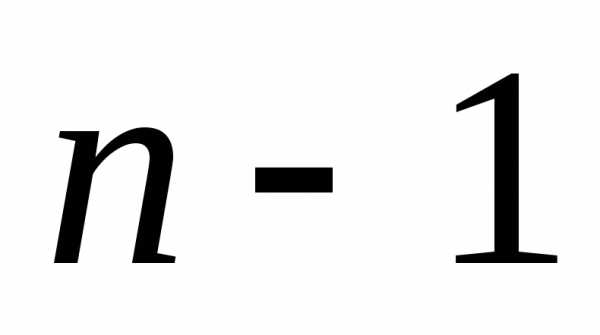 раз. Для сочетания
раз. Для сочетания соответственно 8 и 3. Всевозможные
сочетания с повторениями получатся,
если подвергнуть перестановке нули и
единицы в соответствующей последовательности.
соответственно 8 и 3. Всевозможные
сочетания с повторениями получатся,
если подвергнуть перестановке нули и
единицы в соответствующей последовательности. Каждому
сочетанию с повторениями из 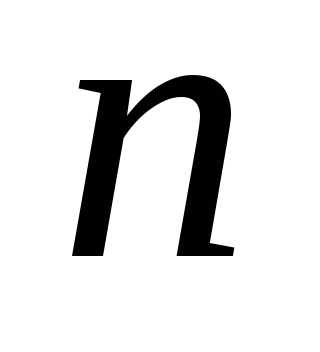 элементов по
элементов по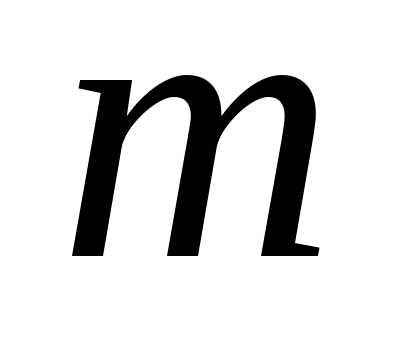 соответствует последовательность из
соответствует последовательность из единиц и
единиц и
 элементов по
элементов по равно числу последовательностей из
равно числу последовательностей из единиц и
единиц и нулей. Это число определяется числом
перестановок с повторениями
нулей. Это число определяется числом
перестановок с повторениями, т.е. .
Например,
сочетания из 4-х элементов 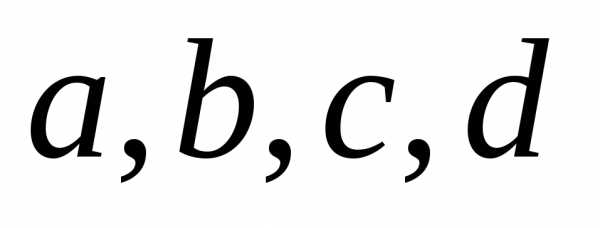 по 2 с повторениями будут.
Им соответствуют следующие последовательности
из нулей и единиц
по 2 с повторениями будут.
Им соответствуют следующие последовательности
из нулей и единиц
Пример 1.14.
В магазине 12 сортов пирожных. Покупатель хочет купить шесть пирожных, не обязательно разных. Сколько вариантов выбора у него есть?
Здесь производится выбор шести предметов из неограниченного количества предметов 12-ти различных сортов.
,
то есть шесть пирожных, не обязательно разных, можно выбрать 12376 способами.
studfiles.net
Сочетания кириллических шрифтов: Таблица, советы, примеры
В мире есть много красивых шрифтов, но не все из них идеально подойдут для вашего проекта. Комбинирование шрифтов может быть очень важным и увлекательным процессом во время создания дизайна. Идеальное сочетание начертаний может сделать ваш проект действительно потрясающим и при этом читабельным.
В этом материале я собрал особенности сочетания шрифтов, примеры использования Безопасных шрифтов и шрифтов из Google fonts, а так же разместил таблицу сочетаемости кириллических шрифтов.
Таблица сочетания шрифтов
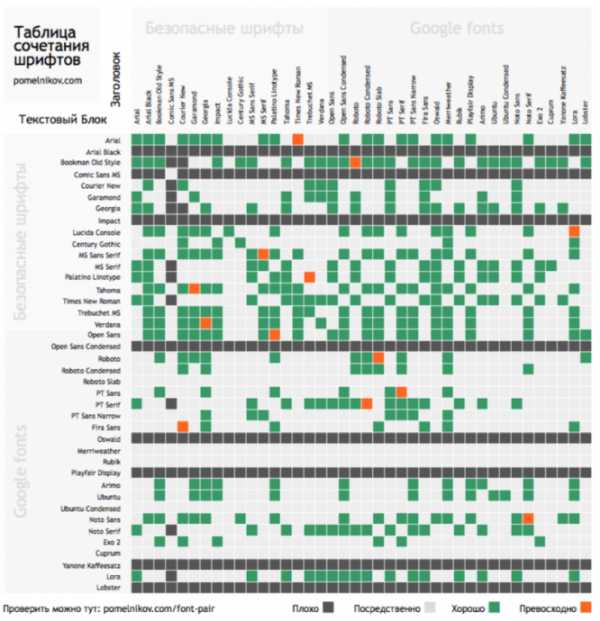 Скачать таблицу в .pdf
Скачать таблицу в .pdf
Проверить сочетания в интерактивной таблице
Мы живём среди текстов. Мы разговариваем с окружающими нас людьми, читаем книги, газеты, журналы, замечаем таблички и вывески, биллборды и надписи на заборах. Каждый день, читая тексты и воспринимая их на слух, мы получаем огромное количество информации.
Обычно грамотному человеку-носителю языка не приходит в голову вслушиваться в красоту звуков речи или всматриваться в форму букв и их расположение. Однако мы можем рассуждать, нравится нам или нет звучание незнакомых слов на чужом языке, или находить в буквах непривычной письменности загадочные узоры. Грамотный человек читает текст и получает из него информацию. Тем не менее, воспринимать текст (на знакомом языке) можно очень по-разному, в зависимости от его предназначения.
В процессе чтения глаза привыкают к основному шрифту и они утомляются, если заголовки, оглавление и второстепенный текст набраны шрифтами разной гарнитуры, не гармонирующими с основным шрифтом. Поэтому, при подборе шрифтов достаточно остановиться на одном–двух шрифтах, а акценты расставлять за счет размера, цвета и начертания.
Важно учитывать характер и объем материала, с которым вы работаете. Это почти полностью сплошной текстовый массив? Много ли там заголовков и подзаголовков? Работая с целой группой шрифтов, используйте их строго по назначению, не путайте “роли”; если подзаголовок уже набран вами одним шрифтом, то и для остальных подзаголовков применяйте этот же шрифт. Пусть будет видно, для чего предназначен каждый из них.
Основные составляющие шрифтов
Каркас

Базовая форма по которой построен шрифт. Каркас определяет общие пропорции элементов буквы, ширину букв, высоту строчных букв (x-height) и высоту заглавных (cap-height), форму скруглений и скосов, основные принципы построения.
Насыщенность
 Отношение толщины основных штрихов к высоте прямого знака, основная толщина (жирность) шрифта. Изменения этого отношения образуют сверхсветлое (Ultra Light, Extra Light, Thin), Светлое (Light), нормальное (Book, Regular, Roman), Полужирное (Medium, Demi Bold, Semibold), Жирное (Bold, Heavy), сверхжирное (Extra Bold, Black, Ultra Bold) начертания.
Отношение толщины основных штрихов к высоте прямого знака, основная толщина (жирность) шрифта. Изменения этого отношения образуют сверхсветлое (Ultra Light, Extra Light, Thin), Светлое (Light), нормальное (Book, Regular, Roman), Полужирное (Medium, Demi Bold, Semibold), Жирное (Bold, Heavy), сверхжирное (Extra Bold, Black, Ultra Bold) начертания.
Базовая форма по которой построен шрифт. Каркас определяет общие пропорции элементов буквы, ширину букв, высоту строчных букв (x-height) и высоту заглавных (cap-height), форму скруглений и скосов, основные принципы построения.
Аксессуары
 Элементы дополняющие шрифт, придающие ему стиль и особенности. К аксессуарам относят засечки, декор, фактуры, росчерки, скругления, узоры, особые элементы и эффекты.
Элементы дополняющие шрифт, придающие ему стиль и особенности. К аксессуарам относят засечки, декор, фактуры, росчерки, скругления, узоры, особые элементы и эффекты.
Семейство, гарнитура, шрифт, начертание
«Семейство» — это набор связанных гарнитур объединенный общим стилем (serif, sans-serif, mono, condensed и др.), например Pt Sans, Pt Serif и Pt Mono входят в семейство Public type (Pt), a Roboto, Roboto Slab и Roboto Сondensed входят в семейство Roboto.
«Гарнитура» — это набор шрифтов, часть шрифтового семейства, объединенная общим дизайн-решением содержащая различные начертания и насыщенность. Гарнитура обычно содержит алфавитно-цифровые, пунктуационные знаки и специальные символы. Roboto или Pt Serif, например, — это гарнитуры.
«Шрифт» — это графический рисунок начертаний букв и знаков, составляющих единую стилистическую и композиционную систему, набор символов определенного размера и рисунка, в конкретной насыщенности и стиле. Roboto Bold или Roboto Italic, например — это шрифт, файл, который вы используете в своей системе.
«Начертание» — это графическая разновидность шрифта в пределах одной гарнитуры. Характеризуются едиными стилевыми особенностями рисунка, определенными пропорциями (узкое, нормальное, широкое и др.), насыщенностью (светлое, полужирное, жирное и др.), постановкой очка, или наклоном знаков (прямое, курсивное или наклонное), декоративной обработкой контура знаков (контурное, оконтуренное, оттененное и др.).
Гарнитура «Exo 2» имеет 18 начертаний с насыщенностью и наклоном знаков
Гарнитура «Zamenhof» имеет 4 начертания c декоративной обработкой контура знаков
Анатомия шрифтов
 Жмя на картинку для хорошего качества
Жмя на картинку для хорошего качества
Правила сочетания шрифтов
Удачные парные комбинации образуются по принципу гармонии или контраста, но не путём несовместимого противопоставления. То есть, выбранные вами шрифты могут вместе составить удачное сочетание, если у них есть некие общие черты, либо наоборот, если они совершенно разные. Однако, признаков несовместимости у различных пар шрифтов довольно много, слишком большое сходство — один из них.
Гармоничные сочетания
Гармоничное сочетание строиться на шрифтах со схожим каркасом и должно иметь наименьшее количество контрастов 1-4. Приемлем контраст в размере, насыщенности, начертании и аксессуарах.
Контраст размера
Наиболее часто используемый прием, особое внимание уделяется подбору одной «богатой» гарнитуры. К контрасту размера также относят набор в верхнем регистре (прописными знаками). Иногда разработчики шрифтов создают дополнительный (Акцидентный) шрифт для популярной гарнитуры.
Использование одной гарнитуры
Использование одной гарнитуры самый простой способ гармонизации шрифтов. Для подбора хорошей гарнитуры, обращайте внимание на наличие в ней нейтрального (малоконтрастного) шрифта для текстовых блоков, наличие насыщенного (жирного) шрифта, наличие курсива, минускульные цифры* (некоторые шрифты имеют оба комплекта цифр, другие только один). Также обращайте внимание на различия между знаками Il1. В некоторых гарнитурах они плохо различаются, что усложняет читаемость.
Контраст размера и насыщенности
Второй часто используемый прием для выделения текста. Насыщенность добавляет тон шрифту, хорошо привлекает внимание. Насыщенный акцидентный шрифт в этом варианте контраста может быть из другого семейства. Например насыщенная брусковая антиква (slab-serif) хорошо сочетается с антиквой переходного стиля (transitional).
Насыщенность добавляет контраст тона
Комбинации шрифтов должны иметь четкие различия для того, чтобы документ было легко читать. Если не хватает контраста, визуальная иерархия нарушается и роли, которые вы назначили различным шрифтам не будут ясны. Жирный текст всегда выглядит темнее из-за увеличенной толщины штрихов и уменьшенного внутрибуквенного просвета.
Контраст размера и начертания
Третий часто используемый прием. Начертания специально создают для выделения элементов текста. Некоторые гарнитуры имеют стандартные начертания (жирность и курсив), другие имеют уникальные отличия, часто связанные с деталями шрифта.
Курсив – от лат. cursivus – бегущий
Курсивы — это отличный вариант для подачи второстепенной информации или расстановки акцентов. Курсив становится курсивом благодаря структуре, напоминающей скорее рукописный шрифт, чем печатный. Насыщенность курсива часто соответствует насыщенности прямого шрифта, что обеспечивает приятное восприятие комбинации этих шрифтов. Вместо курсива можно подобрать декоративный шрифт (script).
Контраст размера, насыщенности и начертания
Этот способ сочетания используется реже, чем первые три, но при этом, так же хорошо создает гармоничное сочетание. Мы сначала читаем заголовки, если нас заинтересовала информация, начинаем читать текст. Поэтому каждый смысловой блок должен иметь заголовок. Заголовки должны быть контрастными и легко читаться.
Настоящий курсив всегда лучше наклона
Некоторые шрифты, например, Arial имеют курсивное начертание, другие, например, Verdana вместо курсива используют просто наклон шрифта. Курсив является более сильным средством выделения, чем наклонный шрифт, поскольку он имеет больший контраст. Вместо курсивов можно применять рукописный (декоративный) шрифт, построенный на похожем каркасе, у него должны совпадать пропорции знаков.
Контраст аксессуаров и размера
Самым распространенным аксессуаром шрифта являются засечки. Шрифты с засечками образуют самую большую и разнообразную категорию – Антиква. Антиква гармонично сочетается с Гротеском (шрифт без засечек), если их каркас и пропорции одинаковы или максимально похожи.
Использование одного семейства
Семейства строят на общем каркасе и создают вариации Антиквы (serif) и Гротеска (sans serif). Большое семейство всегда располагает массой толщин и начертаний на выбор. У некоторых гарнитур есть несколько вариаций ширины (Narrow, Condensed, Regular, Extended, etc. — узкий, уплотненный, обычный, расширенный и т.д.). Использование двух гарнитур одного семейства даст от 4 до 36 шрифтов для работы.
Контраст аксессуаров, размера и насыщенности
Насыщенность и аксессуары создают хорошую пару контрастов, совместно с размером получаем универсальный прием, в котором можем сочетать различные шрифтовые семейства.
Сочетание разных семейств
Если подобрать гарнитуры из разных семейств с одинаковым каркасом и пропорциями знаков, то это также составит гармоничное сочетание, при этом должен быть контраст аксессуаров. Например, Georgia/Verdana, это сочетание считается классическим в любых комбинациях. Чем больше семейств вы сочетаете, тем сложнее объединить их друг с другом. Оптимальным является сочетание двух семейств.
Контраст аксессуаров, размера и начертания
Курсив используют для выделения, поэтому он не подходит для больших текстовых блоков. Курсив более пластичный, соединение знаков плавное, но при сочетании нескольких семейств нужно проверять как сочетаются их курсивные начертания.
Сочетание курсивов
Нужно проверять, как смотрится курсивное начертание каждой гарнитуры. Вы можете получить хорошую комбинацию, а затем обнаружить, что курсивы не сочетаются. Овалы и внутрибуквенный просвет отличные меры измерения, в них хорошо прослеживается ось наклона. В гармоничном сочетании ось наклона курсивов должна быть одинаковой. Круглые и овальные буквы «О» не любят друг друга, поэтому их лучше не сочетать.
Контраст аксессуаров, размера, насыщенности и начертания
Каждый дополнительный вид контраста усиливает отличия шрифтов, поэтому нужно аккуратно подбирать варианты. Если количество контрастов превысит четыре, то такое сочетания уже не является гармоничным. Самый простой способ добиться гармонии в таком сочетании, сочетать гарнитуры одного семейства. Второй способ, тщательно сравнивать шрифты, выявляя их отличия.
Использование разных шрифтов
Для каждого начертания можно подобрать отдельный шрифт, не связанный семьей или гарнитурой. В таком случае необходимо подобрать шрифты с похожим каркасом и пропорциями литер, насыщенность должна совпадать для курсивного начертания и различаться для жирного. Чтобы упростить задачу напишите слово, содержащее наибольшее количество разнородных знаков, например, Нобельфайк или Handgloves, и наложите один шрифт на другой, чем меньше отличий, тем гармоничней будет ваше сочетание. Эта задача очень непростая, помочь может сервис сравнения знаков шрифта.
* «Минускульные цифры» — это старостильные цифры обладающие верхними и нижними выносными элементами. Предназначены для использования вместе со строчными буквами в тексте для сплошного чтения. Минускульные цифры часто отсутствуют в стандартном комплекте шрифтов, включаются в расширенный комплект знаков (экспертный комплект шрифта).
Контрастные сочетания
Строятся на шрифтах с максимальным количеством контраста и минимальным количеством сходства 0-3. Объединяются по общему настроению, аксессуарам, художественному стилю. Контрастные сочетания самые сложные, но и самые эффектные.
Нет сходства
Если использовать шрифты по их назначению, малоконтрастный для текстовых блоков, курсивный (рукописный) для акцентов, жирный (акцидентный) для заголовков, то можно создать контрастное сочетании вообще без сходств. Нейтральный (малоконтрастный) шрифт всегда можно сочетать с Акцидентным (высококонтрастным) или рукописным. При сочетании трех и более шрифтов допускается только одно контрастное сочетание. Такой шрифт будет акцентом внимания.
Сочетания без сходства
Одно и то же слово, набранное разными шрифтами, будет совершенно по-разному восприниматься, это свойство называют настроением шрифта. Настроение это условный признак, не имеющий классификации, шрифты которые не вызывают настроение называют нейтральными. Комбинируя шрифты, используйте настроение шрифта, чтобы создать правильную атмосферу. Лучшим решением будет использовать один шрифт с ярко выраженным настроением. Большое количество настроенческих шрифтов может смотреться перегружено и плохо сказаться на читабельности.
Сходство аксессуаров
Яркие узнаваемые детали шрифта могут стать основой для хорошего, контрастного сочетания. Например, особые засечки, оформление контуров, пластика шрифтов, заполнение знаков, декоративные элементы, толщина штрихов, соотношения между основным и соединительным штрихом.
Сходство художественного стиля
Это наиболее распространённое из контрастных сочетаний. Некоторые стили имеют свои характерные шрифты и шрифтовые сочетания. Художественные стили тесно связаны с историческими периодами, а форма шрифтов с инструментами и материалами, при помощи которых они были созданы.




Плохие сочетания
Образуются из слишком разного противопоставления шрифтов, необоснованного использования (смешивание семейств), смешения слишком разных стилей.
Плохая читаемость
Основная задача текста – передавать информацию, если шрифт плохо читается, он будет создавать напряжение у человека, который будет его читать. Нельзя жертвовать простотой и четкостью текста ради каких-то абстрактных красивостей.
Текст для сплошного чтения должен быть как можно более незаметным. Такое его качество складывается из ритмичной структуры набора, максимально привычной формы знаков и промежутков между ними, когда мозг улавливает смысл сочетания букв и заставляет глаз двигаться вперёд раньше, чем считает их формы в отдельности.
По этой же причине читатель обычно не замечает опечаток в тексте. Общая форма слова сохраняется и человек, поняв его смысл, движется дальше, так можно перепутать слова, разные по смыслу и похожие по форме. Читатель увидит скорее то слово, которое он ожидает в контексте.
Слишком похожие шрифты
Два похожих шрифта одного начертания будут постоянно путать зрителя и вносить дисгармонию. Это создает неудобство визуального восприятия, т.к. на подсознательном уровне мы чувствуем, что шрифты разные, но все равно задаемся вопросом: одинаковые это шрифты или нет? Этот диссонанс отвлекает нас от самого процесса чтения.
Шрифты моветон
Некоторые шрифты признаны дизайнерами как не красивые их использование считается плохим вкусом к ним относят: Comic sans, lobster, Curlz, Papyrus, список постоянно дополняется. Сюда так же относят шрифты плохого качества, которые имеют дефекты контура, недоработанный кернинг, разный масштаб знаков, плохое выравнивание и прочие недоработки.
Примеры сочетания шрифтов (ресурсы)
http://fontpair.co
http://typespiration.com
http://femmebot.github.io
http://100daysoffonts.com
https://www.canva.com
https://www.typotheque.com
https://fontsinuse.com
https://www.typewolf.com
https://typeconnection.com
https://justmytype.co/
https://www.typetester.org/
В комментариях можете размещать свои лучшие примеры сочетаний шрифтов, не указанные в данном материале, как в виде ссылки на комбинатор, так и в виде своих «шрифтовых» работ.
Источник: pomelnikov.com
infogra.ru
4.2. Сочетания и их свойства
Рассмотрим ситуацию, в которой из множества требуется выбрать группы, содержащиеэлементов из данных,, отличающиеся друг от друга хотя бы одним элементом. Причем порядок расположения элементов не имеет значения. Очевидно, что количество таких групп будет меньше, чем число размещений изпово столько раз, сколько существует перестановок изэлементов, а именно.
Определение 1. Подмножества, состоящие из элементов, выбранных из данных, отличающиеся друг от друга по крайней мере одним элементом (без учета порядка расположения элементов), называются сочетаниями из элементов по .
Число сочетаний обозначается символом , где– первая буква от английского словаcombination – сочетания.
Пример 1. Для участия в научной конференции требуется направить четверых сотрудников из 32 сотрудников отдела. Сколько существует вариантов выбора представителей?
Решение
Поскольку для выбора представителей важен только состав участников, но не важно, в каком порядке происходило их выдвижение, то количество всевозможных вариантов равно числу сочетаний из 32 по 4:
.
Пример 2. Решить неравенство .
Решение
В силу определения сочетаний значениями переменной могут быть только целые числа от 1 до 10. Используя формулу сочетаний, запишем неравенство в виде.
Разделим обе части неравенства на и получим. Откуда, или. Учитывая ограничения на, получаем множество решений данного неравенства.
Число обладает рядом свойств. Укажем без доказательства некоторые из них:
, в частности ;
;
.
Доказательства перечисленных свойств можно получить непосредственно из определения сочетаний.
4.3. Выборки с повторением
Перестановки, размещения и сочетания представляют собой примеры бесповторных выборок, поскольку каждый элемент множества может быть взят только один раз. Теперь рассмотрим ситуацию, при которой выбранный элемент возвращается в первоначальное множество, и его вновь можно выбирать.
Пусть дано множество, состоящее из различных элементов. Зафиксируем некоторое натуральное число и вычислим, сколько существует способов составить группы, содержащиеэлементов из данных, причем каждый изэлементов может быть выбран более одного раза. Первымэлементом может быть любой из элементов множества, т. е. для выбора первого элемента существуетспособов. Поскольку каждый элемент можно выбирать неоднократно, то второй элемент можно выбрать такжеспособами. Рассуждая подобным образом, получим, что каждый изэлементов можно выбратьспособами. Согласно комбинаторному принципу умножения получим, что общее число выборок поэлементов из данных равно . Указанная выборка называется повторной. Заметим, что ограничение, справедливое для бесповторных выборок, , не работает в случае повторяющихся элементов. Для повторных выборок числоможет быть как больше, так и меньше либо равным.
На рис. 40 представлена схема определения выборок, которой можно руководствоваться при решении задачи.
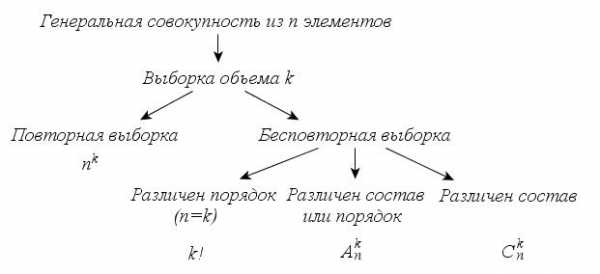
Рис. 40
Пример 1. Сколько различных пятизначных чисел можно составить из цифр 1, 2, 5, 8 при условии, что цифры в числе могут повторяться?
Решение
Из множества, содержащего различных элементов, нужно составить выборки, содержащиеэлементов. Поскольку цифры в числе могут повторяться, то общее число всевозможных выборок.
Вопросы и задачи для самостоятельного решения
Сколькими способами из группы, содержащей 15 человек, можно выбрать четверых для участия в профсоюзном собрании?
Сколько четных чисел можно составить из цифр 1, 2, 5, 4, 0?
Сколько существует вариантов ответа на тест из 10 вопросов, если на каждый вопрос требуется ответить «да» или «нет»?
Сколько различных автомобильных номеров можно составить из двух букв и идущих за ними трех цифр, если используются все буквы русского алфавита?
Сколько существует различных шестизначных телефонных номеров, которые не начинаются с цифр 0, 1, 9, 8?
Вычислите:
а) ; б); в); г).
Вычислите:
а) ; б); в); г).
Вычислите:
а) ; б); в); г).
Вычислите:
а) ; б); в); г).
Проверьте равенства:
а) ; б).
Решите уравнения:
а) ; в);
б) ; г).
studfiles.net
| 1. |
Значение выражения, содержащего формулу числа сочетаний
Сложность: лёгкое |
2 |
| 2. |
Число сочетаний
Сложность: среднее |
3 |
| 3. |
Выбор трёх элементов из группы
Сложность: среднее |
3 |
| 4. |
Число треугольников с вершинами в данных точках, расположенных на данной окружности
Сложность: среднее |
4 |
| 5. |
Выбор нескольких элементов из группы
Сложность: среднее |
3 |
| 6. |
Число сочетаний из двух групп, закон умножения
Сложность: среднее |
4 |
| 7. |
Количество хорд, проведённых через данное число точек окружности
Сложность: среднее |
3 |
| 8. |
Количество участников турнира, дано число проведённых игр
Сложность: среднее |
4 |
| 9. |
Варианты выбора цветов для букета
Сложность: среднее |
4 |
| 10. |
Выбор нескольких элементов из нескольких групп
Сложность: среднее |
4 |
| 11. |
Варианты выбора нескольких элементов из двух групп
Сложность: среднее |
3 |
| 12. |
Способы формирования группы людей
Сложность: среднее |
3 |
| 13. |
Число сочетаний из двух групп
Сложность: среднее |
4 |
| 14. |
Способы раздачи карт игрокам
Сложность: среднее |
3 |
| 15. |
Варианты состава группы людей, законы сложения и умножения
Сложность: сложное |
5 |
| 16. |
Сочетания и законы сложения, умножения
Сложность: сложное |
5 |
| 17. |
Расположение шариков в ряд и круг
Сложность: сложное |
5 |
www.yaklass.ru
сочетания с повторениями — 3 Августа 2015 — Примеры решений задач
Пусть имеется три элемента (n = 3): a, b и c. Тогда из этих трёх элементов можно составить шесть сочетаний с повторениями по два элемента (k = 2): ab, ac, bc, aa, bb, cc (порядок неважен!)
Общее число сочетаний с повторениями определяется по формуле
Пример 1. В почтовом отделении продаются открытки 10 сортов. Сколькими способами можно купить в нем 12 открыток? 8 открыток? Сколькими способами можно купить 8 различных открыток?
Решение. Данная задача на отыскание числа сочетаний с повторениями из n = 10 элементов по k = 12 (k =8). Следовательно,
.
В случае, когда требуется купить 8 различных открыток, получим сочетания без повторений:
.
Задачи.
1. Сколькими способами можно распределить 5 одинаковых предметов между тремя лицами?
2. В студенческой столовой продают сосиски в тесте, ватрушки и пончики. Сколькими способами можно приобрести пять пирожков?
Пример 3. В кондитерской имеется 3 вида пирожных. Сколькими способами можно купить 9 пирожных?
Решение. В задаче требуется найти число всевозможных групп по 9 элементов, которые можно составить из данных трех различных элементов, причем указанные элементы в каждой группе могут повторяться, а сами группы отличаются друг от друга хотя бы одним элементом. Это задача на отыскание числа сочетаний с повторениями из трех элементов по девять. Следовательно,
Пример 4. В почтовом отделении продаются открытки 10 сортов. Сколькими способами можно купить в нем 12 открыток? 8 открыток? Сколькими способами можно купить 8 различных открыток?
Решение. Данная задача на отыскание числа сочетаний с повторениями из 10 элементов по 10. Следовательно,
, .
В случае, когда требуется купить 8 различных открыток, получим сочетания без повторений:
.
Пример 5. Сколько всего чисел (не больше 100000) можно составить из цифр 1, 2, 3, 4 и 5 в каждом из которых цифры расположены в неубывающем порядке?
Решение. Это задача о числе сочетаний из пяти цифр по одному, по два, по три, по четыре и по пяти с повторениями в каждом случае. Поскольку , , , , , то существует чисел, удовлетворяющих условию задачи.
Упражнения
1. Сколькими способами Буратино, кот Базилио и лиса Алиса могут поделить между собой 5 одинаковых золотых монет?
Ответ: .
2. В кондитерской имеется пять разных сортов пирожных. Сколькими способами можно выбрать набор из четырёх пирожных?
Ответ: .
3. Сколько существует треугольников, длины сторон которых принимают одно из значений 4, 5, 6, 7?
Ответ: .
4. Сколько можно построить различных прямоугольных параллелепипедов, длина каждого ребра которых является целым числом от 1 до 10?
Ответ: .
www.reshim.su
Kibbe Dramatic. Примеры сочетаний. — Красота, вдохновленная природой
Я решила, что небесполезно будет посмотреть на примеры комбинаций предметов гардероба, составленных в разных цветовых схемах, для разных целей, но все с учетом рекомендаций Kibbe Dramatic.









Как я уже упоминала, производители начинают продажу вещей в стиле 40-х гг. Осенне-зимняя коллекция ZARA
color-harmony.livejournal.com
Сочетания
Вот в этих комбинациях порядок не важен. Сочетания трех букв (А, В, С), взятых 2 по 2, следующие: АВ, АС и ВС. Разницы между парами АВ и ВА мы не видим. Легко заметить, что для одинакового количества элементов чисел при сочетании всегда меньше, чем при размещении: $V_{3,2}=6, C_{3,2}=3$.
Это самый простой пример сочетаний, при дальнейшем разборе темы примеры будут посложнее. Если же этот материал кажется очень сложным, и вам тяжело разобраться где сочетание, а где перестановка, и что такое размещение — помочь здесь сможет онлайн репетитор по математике.
Построить таблицу с сочетаниями гораздо легче и быстрее, чем таблицу с размещениями. Однако численный расчет, наоборот, получается сложнее. Количество комбинаций с элементами m взятыми из n по n, вычисляется следующим образом:
$C_{m,n}=\frac {m!}{n! \times (m-n)!}$
Таким образом, количество сочетаний, которое мы можем получить с 6 элементами, взятыми из 3 по 3, будет: $C_{6,3}= \frac {6!}{3! \times (6-3)!}=\frac {6 \times 5\times 4\times 3\times 2\times 1}{3\times 2\times 1 \times (3\times 2\times 1 )}=20$.
В математике это выражение $ \frac {m!}{n! \times (m-n)!}$ обычно представляется в таком виде $\left( \begin{array} {c} m \\ n \end{array} \right)$ и называется биноминальный коэффициент.
Биноминальные коэффициенты часто появляются в алгебре, и иногда их вычисление может быть несколько затруднительным. Существует треугольный способ расположения биноминальных коэффициентов, облегчающий расчеты. Он известен как треугольник Паскаля и строится следующим образом:
Каждое число является суммой двух расположенных над ним чисел. Эти числа полностью соответствуют следующему расположению биноминальных коэффициентов: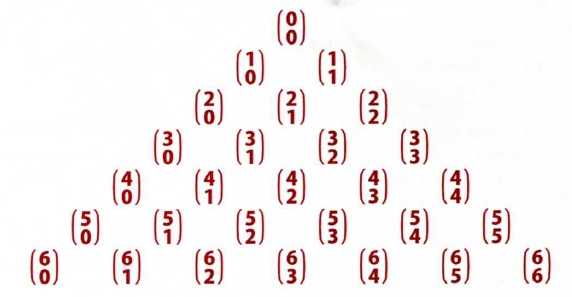
Чтобы узнать биноминальный коэффициент, нужно лишь найти его эквивалент в первой таблице.
Например, $\left( \begin{array} {c} 5 \\ 2 \end{array} \right)$ находится на третьем месте в предпоследнем ряду, и в первой таблице ему соответствует число 10. Треугольник Паскаля можно сделать любого размера и использовать его как шпаргалку. Имея перед глазами обе таблицы, можно быстро решать подобные задачи: мы имеем урну с пронумерованными от 1 до 6 шарами. Выбираем наугад 4 из них. Вопрос: сколько возможно различных сочетаний?
$\left( \begin{array} {c} 6 \\ 4 \end{array} \right)=15$
Возьмем в качестве примера испанскую лотерею «Да Примитива». В ней необходимо отгадать 6 номеров из 49. Итак, встает вопрос: сколько групп из 6 разных чисел мы можем создать, имея 49 номеров? Тут не важен порядок, так как билет с номерами (2, 16, 21, 32, 47, 49) такой же выигрышный, как и с номерами (2, 47, 21, 32, 16, 49). Разговор идет о сочетаниях. А именно, о количестве комбинаций из 49 чисел, взятых из 6 по 6. Нам необходимо рассчитать значение биноминального коэффициента $С_{49,6}$. Мы можем попробовать нарисовать треугольник Паскаля в 49 рядов, но, в любом случае, этот расчет не сложен, так как его можно сильно облегчить: $\left( \begin{array} {c} 49 \\ 6 \end{array} \right)=\frac {49!}{6! \times (49-6)!}= \frac {49!}{6! \times 43!}=\frac {49 \times 48 \times 47 \times 46 \times 45 \times 44}{6 \times 5 \times 4 \times 3 \times 2 \times 1}=13983816$
Итак, чтобы точно выиграть в лотерее «Ла Примитива», стоимость билета которой не превышает одного евро, нужно вложить в билеты около 14 млн. Конечно, это абсолютно невыгодно, но ведь сам выигрыш приносит огромное удовлетворение.
Материалы по теме:
Поделиться с друзьями:
Загрузка…matemonline.com
