Тема Градусная и радианная меры угла и дуги. Синус, косинус, тангенс и котангенс произвольного угла. Значения синуса, косинуса, тангенса и котангенса углов. Тригонометрические функции и их свойства
Тема Градусная и радианная меры угла и дуги. Синус, косинус, тангенс и котангенс произвольного угла. Значения синуса, косинуса, тангенса и котангенса углов. Тригонометрические функции и их свойства СОР 9-3А (2)
1 2 Байланысты:
1 2 ©melimde.com 2023 | Басты бет жиынтық бағалау Сабақ тақырыбы бағдарламасына сәйкес Сабақтың мақсаты тоқсан бойынша сәйкес оқыту ғылым министрлігі бағалауға арналған Реферат тақырыбы Сабақ жоспары оқыту мақсаттары жиынтық бағалауға арналған тапсырмалар білім беретін бағалау тапсырмалары Қазақстан тарихы Қазақстан республикасы мерзімді жоспар жиынтық бағалаудың тоқсанға арналған жалпы білім нтізбелік тақырыптық республикасы білім бекіту туралы Зертханалық жұмыс Жалпы ережелер арналған жиынтық болып табылады Қазақстан республикасының арналған әдістемелік Мектепке дейінгі Қысқа мерзімді оқыту әдістемесі Қазақ әдебиеті рсетілетін қызмет Инклюзивті білім білім берудің тақырыптық жоспар бағалаудың тапсырмалары атындағы жалпы пайда болуы пәнінен тоқсанға туралы жалпы әдістемелік ұсыныстар коммуналдық мемлекеттік қарым қатынас мемлекеттік мекемесі Жұмыс бағдарламасы | ||||||||||||||||||||||||||
Анимированные синус и косинус
Анимированные синус и косинусАнимированные синус и косинус
Элементарные определения: синус, cosine
Таблица запуска: синус и косинус
Подробная информация о: синус, косинус
Unit Circle: вводная страница
- Синус и косинус
Эта страница содержит более подробное описание поведение синуса (вертикальная составляющая угла или отношение противоположного катета к гипотенузе) и косинус (горизонтальная составляющая угла или отношение прилежащего катета к гипотенузе).
 Для более широкого обзора триггерных функций см. страницу Unit Circle.
Для более широкого обзора триггерных функций см. страницу Unit Circle.- При нуле градусов, ноль радианов
Как только вы избавитесь от того факта, что вы работать с треугольником, имеющим угол 0° и длину стороны 0, легко.
Вертикальный катет равен 0, поэтому синус равен 0.
Горизонтальный катет равен радиусу, который равен 1. Следовательно, косинус равен 1.
Далее рассмотрим другой способ сказать то же самое, но описав сам угол и единичный круг, а не только треугольник. Вертикальная составляющая угла отсутствует: Вертикальная составляющая угла равна 0, поэтому синус 0° равен 0.
Горизонтальная составляющая угла настолько велика, насколько это возможно. Радиус равен 1, поэтому горизонтальная составляющая равна 1: косинус 0° равен 1.
- В первом квадранте
При увеличении угла от 0° до 90° синус увеличивается от 0 до 1.

При увеличении угла от 0° до 90°, косинус уменьшается от 1 до 0.
- На 90 градусов, /2 радиана
Опять у вас есть угол 0° и сторона длиной 0.
На этот раз вертикальный катет равен 1, как и радиус, поэтому синус равен 1.
Горизонтальный катет равен 0, так как горизонтальной составляющей треугольника нет, поэтому косинус равен 0,
Рассмотрим сам угол и единичную окружность. отсутствует горизонтальная составляющая угол: горизонтальная составляющая угла равна 0, поэтому косинус 90° равен 0.
Вертикальная составляющая угла настолько велика, насколько это возможно. Радиус равен 1, поэтому вертикальная составляющая равна 1: синус 90° равен 1.
- Во втором квадранте
По мере увеличения угла от 90° до 180° синус уменьшается от его максимальное значение от 1 до значения 0.

По мере увеличения угла от 90° до 180° косинус увеличивается по величине, но теперь отрицательное значение. Косинус идет от 0 до -1.
- На 180 градусов, Радиан
Опять угол 0° и сторона с длиной 0. Значения указаны выше.
Снова рассмотрим сам центральный угол и единичную окружность. нет вертикальной составляющей угла: вертикальная составляющая угла равна 0, поэтому синус 180 ° равен 0.
Горизонтальная составляющая угла настолько велика, насколько это возможно, но она также отрицательна. Горизонтальная составляющая равна -1: косинус 180° равен -1.
- В третьем квадранте
Координаты x и y в третьем квадранте отрицательны.
Поскольку гипотенуза равна +1, и синус, и косинус должны быть отрицательными.

При увеличении угла от 180° до 270° синус увеличивается в величина, но теперь отрицательная, поэтому синус уменьшается от 0 до -1.
При увеличении угла от 180° до 270° косинус уменьшается в величина, но теперь отрицательная, поэтому косинус увеличивается с минимума -1 до значения 0,
- На 270 градусов, 3/2 радиана
Опять у вас есть угол 0° и сторона с длиной 0. Значения указаны выше.
Рассмотрим сам центральный угол и единичную окружность. Горизонтальная составляющая отсутствует. угла: горизонтальная составляющая угла равна 0, поэтому косинус 270° равен 0.
Вертикальная составляющая угла равна радиусу, но также имеет отрицательное значение. Вертикальная составляющая равна -1: синус 270° равен -1.
- В четвертом квадранте
При увеличении угла с 270° до 360° синус увеличивается с -1 до 0.

При увеличении угла с 270° до 360° косинус увеличивается с от 0 до +1.
© 2006, Agnes Azzolino www.mathnstuff.com/math/spoken/here/2class/330/unitsin.htm |
Angle and Trigonometry Functions
| template | |
| genType | acos (genType const &x) |
| template | |
| genType | acosh (genType const &x) |
| template | |
| genType | asin (genType const &x) |
| template | |
| genType | asinh (genType const &x) |
| template | |
| genType | atan (genType const &y, genType const &x) |
| template | |
| genType | atan (genType const &y_over_x) |
| template | |
| genType | atanh (genType const &x) |
| template | |
| genType | cos (genType const &angle) |
| template | |
| genType | cosh (genType const &angle) |
| template | |
| genType | градусов (genType const &radians) |
| template | |
| genType | radians (genType const °rees) |
| template | |
| genType | sin (genType const &angle) |
| template | |
| genType | sinh (genType const &angle) |
| template | |
| genType | tan (genType const &angle) |
| template | |
| genType | tanh (genType const &angle) |
Function parameters specified в качестве угла предполагается, что они выражены в радианах.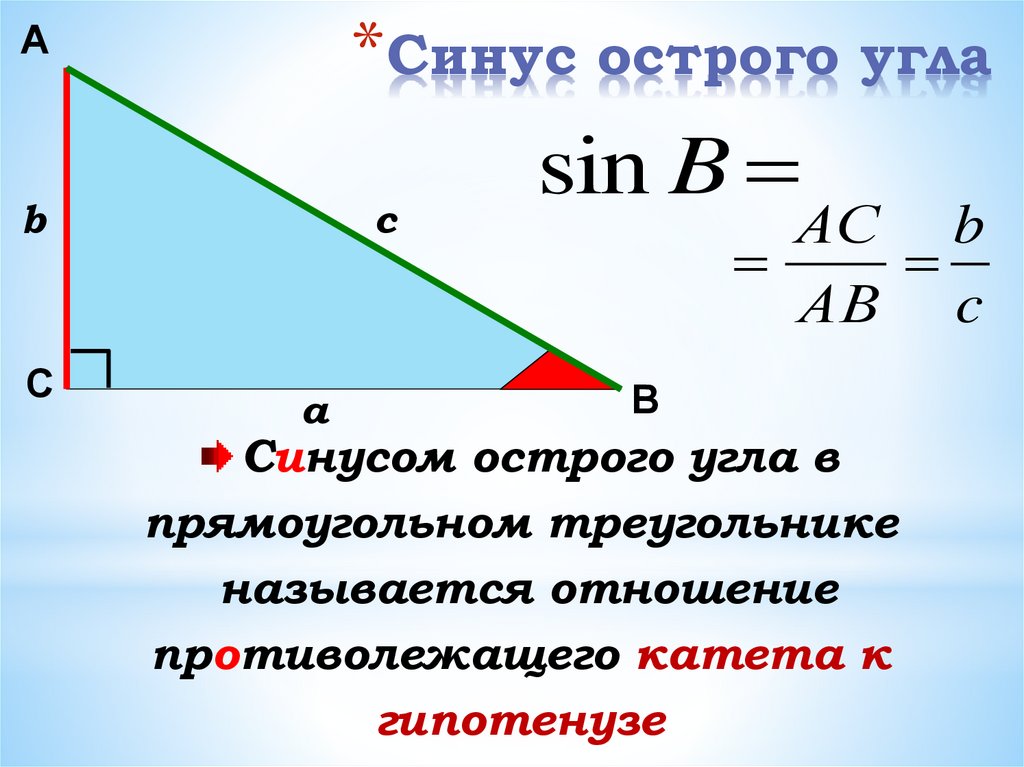
Ни в коем случае ни одна из этих функций не приведет к ошибке деления на ноль. Если делитель отношения равен 0, то результаты будут неопределенными.
Все они работают покомпонентно. Описание для каждого компонента.
| genType glm::acos | ( | genType константа и | х | ) |
Арккосинус.
Возвращает угол, синус которого равен x. Диапазон значений, возвращаемых этой функцией, равен [0, PI]. Результаты не определены, если |x| > 1.
- Параметры шаблона
genType Скалярные или векторные типы с плавающей запятой.
- См. также
- Страница руководства GLSL acos
- Спецификация GLSL 4.20.8, раздел 8.1 Функции угла и тригонометрии
| genType glm::acosh | ( | genType константа и | х | ) |
Арктический гиперболический косинус; возвращает неотрицательное обратное значение cosh.
Результаты не определены, если x < 1.
- Параметры шаблона
genType Скалярные или векторные типы с плавающей запятой.
- См. также
- Страница руководства GLSL acosh
- Спецификация GLSL 4.20.8, раздел 8.1 Функции углов и тригонометрии
| genType glm::asin | ( | genType константа и | х | ) |
Арксинус.
Возвращает угол, синус которого равен x. Диапазон значений, возвращаемых этой функцией, составляет [-PI/2, PI/2]. Результаты не определены, если |x| > 1.
- Параметры шаблона
genType Скалярные или векторные типы с плавающей запятой.
- См. также
- GLSL справочная страница
- Спецификация GLSL 4.
 20.8, раздел 8.1 Функции углов и тригонометрии
20.8, раздел 8.1 Функции углов и тригонометрии
| genType glm::asinh | ( | genType константа и | х | ) |
Дуговой гиперболический синус; возвращает обратное значение sinh.
- Параметры шаблона
genType Скалярные или векторные типы с плавающей запятой.
- См. также
- GLSL asinh справочная страница
- Спецификация GLSL 4.20.8, раздел 8.1 Угловые и тригонометрические функции
| genType glm::atan | ( | genType константа и | у , |
| genType константа и | x | ||
| ) |
Арктангенс.
Возвращает угол, тангенс которого равен y/x. Знаки x и y используются для определения того, в каком квадранте находится угол. Диапазон значений, возвращаемых этой функцией, равен [-PI, PI]. Результаты не определены, если x и y равны 0.
- Параметры шаблона
genType Скалярные или векторные типы с плавающей запятой.
- См. также
- справочная страница GLSL atan
- Спецификация GLSL 4.20.8, раздел 8.1 Функции угла и тригонометрии
На это ссылается glm::atan2().
| genType glm::atan | ( | genType константа и | y_over_x | ) |
Арктангенс.
Возвращает угол, тангенс которого равен y_over_x. Диапазон значений, возвращаемых этой функцией, составляет [-PI/2, PI/2].
- Параметры шаблона
genType Скалярные или векторные типы с плавающей запятой. 
- См. также
- справочная страница GLSL atan
- Спецификация GLSL 4.20.8, раздел 8.1 Угловые и тригонометрические функции
| genType glm::atanh | ( | genType константа и | х | ) |
Арктический гиперболический тангенс; возвращает обратное значение tanh.
Результаты не определены, если abs(x) >= 1.
- Параметры шаблона
genType Скалярные или векторные типы с плавающей запятой.
- См. также
- справочная страница GLSL atanh
- Спецификация GLSL 4.20.8, раздел 8.1 Функции угла и тригонометрии
| genType glm::cos | ( | genType константа и | уголок | ) |
Стандартная тригонометрическая функция косинуса.
Значения, возвращаемые этой функцией, будут находиться в диапазоне [-1, 1].
- Параметры шаблона
genType Скалярные или векторные типы с плавающей запятой.
- См. также
- справочная страница GLSL cos
- Спецификация GLSL 4.20.8, раздел 8.1 Функции угла и тригонометрии
| genType glm::cosh | ( | genType константа и | уголок | ) |
Возвращает функцию гиперболического косинуса, (exp(x) + exp(-x)) / 2.
- Параметры шаблона
genType Скалярные или векторные типы с плавающей запятой.
- См. также
- справочная страница GLSL cosh
- Спецификация GLSL 4.20.8, раздел 8.1 Функции угла и тригонометрии
| genType glm::degrees | ( | genType константа и | радиан | ) |
Преобразует радианы в градусы и возвращает результат.
- Параметры шаблона
genType Скалярные или векторные типы с плавающей запятой.
- См. также
- Справочная страница градусов GLSL
- Спецификация GLSL 4.20.8, раздел 8.1 Угловые и тригонометрические функции
| genType glm::radians | ( | genType константа и | градусов | ) |
Преобразует градусы в радианы и возвращает результат.
- Параметры шаблона
genType Скалярные или векторные типы с плавающей запятой.
- См. также
- Страница руководства GLSL в радианах
- Спецификация GLSL 4.20.8, раздел 8.1 Функции угла и тригонометрии
| genType glm::sin | ( | genType константа и | уголок | ) |
Стандартная тригонометрическая функция синуса.
Значения, возвращаемые этой функцией, будут находиться в диапазоне [-1, 1].
- Параметры шаблона
genType Скалярные или векторные типы с плавающей запятой.
- См. также
- Страница руководства sin GLSL
- Спецификация GLSL 4.20.8, раздел 8.1 Угловые и тригонометрические функции
| genType glm::sinh | ( | genType константа и | уголок | ) |
Возвращает функцию гиперболического синуса, (exp(x) — exp(-x)) / 2.
- Параметры шаблона
genType Скалярные или векторные типы с плавающей запятой.
- См. также
- Страница руководства GLSL
- Спецификация GLSL 4.20.8, раздел 8.1 Функции угла и тригонометрии
| genType glm::tan | ( | genType константа и | уголок | ) |
Стандартная функция тригонометрического тангенса.

 3А «Тригонометрия» Алгебра 9 класс
3А «Тригонометрия» Алгебра 9 класс
 Для более широкого обзора триггерных функций см. страницу Unit Circle.
Для более широкого обзора триггерных функций см. страницу Unit Circle.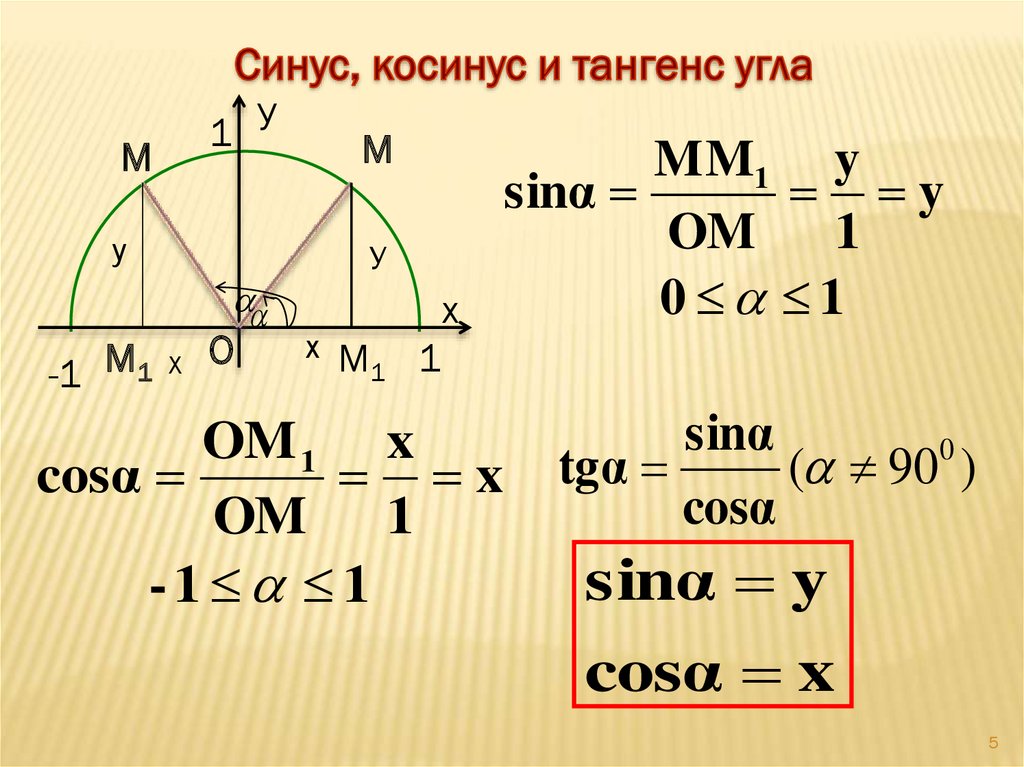


 20.8, раздел 8.1 Функции углов и тригонометрии
20.8, раздел 8.1 Функции углов и тригонометрии