Конспект занятия «Тангенс и котангенс произвольного угла»
Тема: Тангенс и котангенс произвольного угла
Цель занятия: сформировать понятия тангенса и котангенса произвольного угла и умение находить значение тангенса на единичной окружности (предполагается, что по окончании урока учащиеся будут знать понятия «тангенса» и «котангенса», отличать их, смогут находить значения данных выражений на единичной окружности).
Задачи занятия:
Обучающие: закрепить определение синуса, косинуса, тангенса и котангенса; закрепить навык нахождения значений синуса, косинуса, тангенса с помощью единичной окружности; закрепить навык применения основного тригонометрического тождества
Развивающие: развивать мыслительные операции, логическое мышление.
Воспитательные: способствовать развитию умения делать выводы и обобщения, воспитывать самостоятельность.
Тип занятия: комбинированный
Материалы и оборудование: мел, доска, карточки с заданиями для диагностики домашнего задания, карточки для самостоятельной работы.
Технологическая карта занятия:
Этап занятия | Деятельность преподавателя | Деятельность учащихся | Формы организации |
Организационный момент | Проверка наличия учащихся на занятии. Объявление темы занятия | Подготовка к работе | Фронтальная |
Проверка домашнего задания | Задание высокого уровня сложности записывается на доске, комментируется учеником с высоким уровнем подготовки. Задание среднего уровня сложности проверяется путем комментирования с места. | Проверяют точность и корректируют ход решения домашнего задания в тетради | Фронтальная, индивидуальная |
Актуализация знаний | Раздает карточки с заданиями для закрепления определения и свойств синуса и косинуса произвольного угла; закрепление, уточнение и систематизация знаний учащихся (Приложение 1) | Заполнение карточек. Взаимопроверка (меняются с соседом по парте карточками для проверки точности ответа). | Индивидуальная парная |
Изучение нового материала | Изложение нового материала. Фронтальная беседа с учащимися. Постановка проблемных вопросов. (Приложение 2) | Слушают преподавателя. Запись материала в тетрадь. Ответы на вопросы преподавателя. Участвуют в беседе. | Фронтальная |
Формирование новых умений и способов деятельности | Пошаговое выполнение заданий по новой теме у доски. (Приложение 3) | Несколько учащихся с помощью преподавателя решают задачи у доски. Остальные самостоятельно решают и сверяют решение | Индивидуальна, коллективная |
Закрепление знаний и способов деятельности | Консультирует, оказывает помощь в решении предложенных задач, корректирует знания. № 2.86, 2.89 (нечет)– В ходе решения закрепляется навыки определения знака выражения. № 2.91(нечет) –В ходе решения закрепляется умение нахождения значения выражения. № 2. 96(нечет) – задание применение свойств тангенса, котангенса, синуса и косинуса. | Решают задачи из учебного пособия. Защита задачи: демонстрация решения у доски с частичным пояснением. | Индивидуальнаяколлективная |
Контроль знаний и способов деятельности | Инструктаж по выполнению самостоятельной работы. (Приложение 4) | Выполняют самостоятельную работу. | Индивидуальная |
Домашнее задание | Инструктирует учащихся по выполнению домашней работы. Составить опорную схему про тангенс и котангенс произвольного угла (аналогичную той, которую заполняли про синус и косинус на уроке) | Записывают задания. Задают интересующие вопросы | Индивидуальная |
Итоги занятия. | Организует фронтальную беседу, подведение итогов занятия | Высказывание собственного мнения, обобщение изученного | Коллективная, индивидуальная |
Приложение 1
Карточка №1 «Определение и свойства синуса и косинуса»
cos 𝛼 sin 𝛼
Свойства: 1. Множества значений 2. Наименьшее и наибольшее значение
3. Нули 4. Промежутки знакопостоянства |
Приложение 2
Теоретические сведения «Тангенс и котангенс произвольного угла»
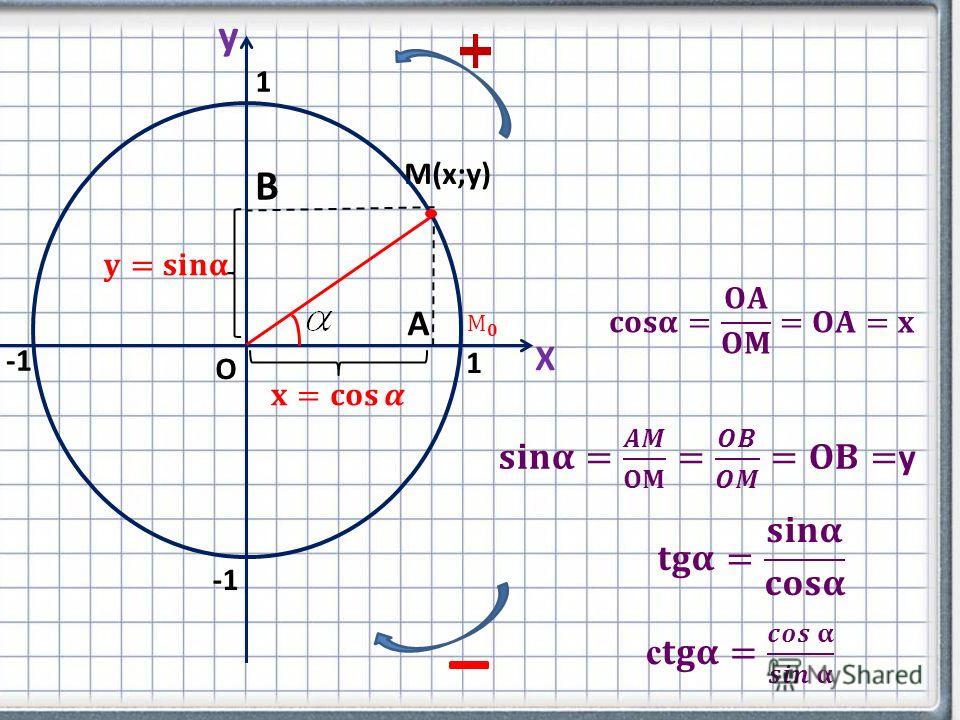
Рассмотрим числовую окружность в координатной плоскости. Дано произвольное число Ему соответствует единственная точка на окружности. У точки есть две координаты (рис. 1).
Координату назвали косинусом числа координату синусом числа
Тангенсом числа называется отношение синуса к косинусу Котангенсом называется отношение косинуса к синусу .
Определим связь между тангенсом и котангенсом.
Проведем через точку A0 (1; 0) прямую t перпендикулярную оси Ох. Она будет касательной к единичной окружности. Эта прямая t называется линией тангенсов. Если то прямая ОA пересекает линию тангенсов t в точке Т. Ордината точки Т равна .
(На партах будут присутствовать шаблоны с единичной окружностью, учащимся нужно будет только дописывать недостающие обозначения )
Построим теперь линию котангенсов. Через (0; 1) прямую с перпендикулярную оси Оу. Она будет касательной к единичной окружности. Эта прямая с называется линией котангенсов. Если то прямая ОA пересекает линию котангенсов с в точке С. Абсцисса точки С равна .
(На партах будут присутствовать шаблоны с единичной окружностью )
Рассмотрим теперь свойства тангенса и котангенса.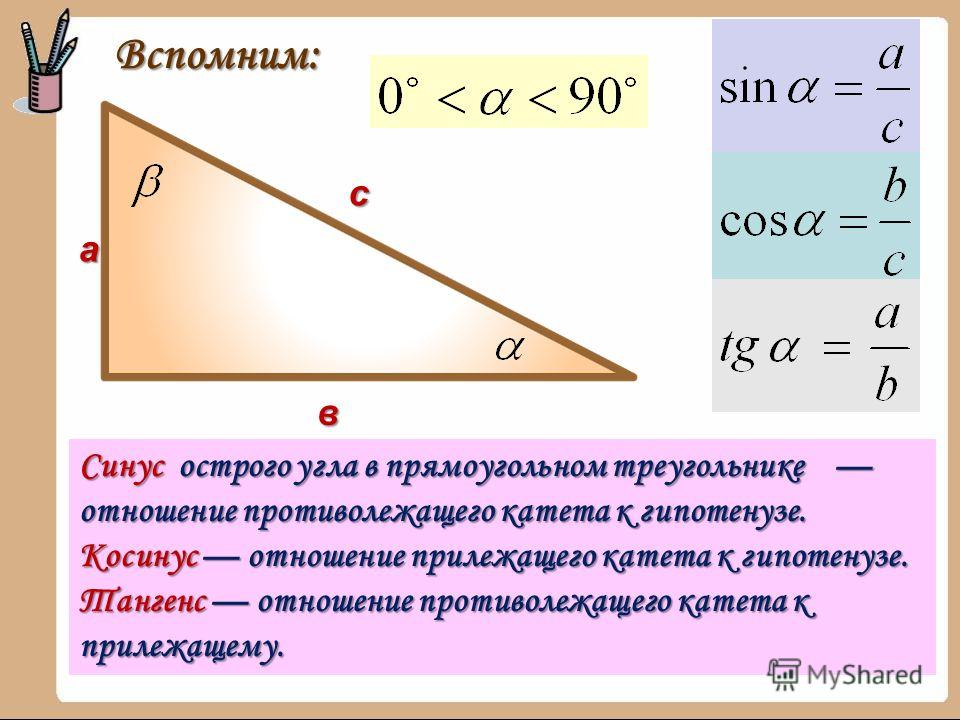
1. Множество значений.
Чему равен тангенс угла на рисунке?
О: Тангенс угла на рисунке равен ординате точки Т
У: Если угол 𝛼 будет равен 80О, то где будет значение этого угла на рисунке?
О: Проведем луч до пересечения с осью тангенсов. Получим точку. Ордината этой точи и будет равняться тангенсу 80О.
У: Если угол 𝛼 будет равен -60О? 140?
О: Аналогично.
У: Какой вывод мы можем сделать про множество значений тангенса?
О: Множеством значения выражения tg𝛼 является множество всех действительных чисел.
У: А для котангенса что будет являться множеством значений? Ответ обоснуйте.
О: Множеством значения выражения сtg𝛼 является множество всех действительных чисел. Рассуждения аналогичны как и для tg𝛼.
2. Нули.
Нули.
У: Пользуясь рисунком, скажите, где тангенс равен нулю?
О: Тангенс равен нулю в точке A0 (1; 0) и симметричной ей относительно начала координат.
У: Какой угол поворота соответствует этим точкам?
О:
У: Назовите нули котангенса.
О:
3. Промежутки знакопостоянства.
У: Знак значений выражения тангенса также можно установить с помощью единичной окружности и оси тангенсов.
Т. К. тангенс равен ординате точки, то тангенс будет положителен только в первой и третьей четверти.
Пользуясь рисунком, укажите промежутки знакопостоянства котангенса.
О: Котангенс будет положителен в первой и третьей четверти.
Вычислим тангенсы и котангенсы основных углов.
Для любого допустимого:
Приложение 3
Пример 1.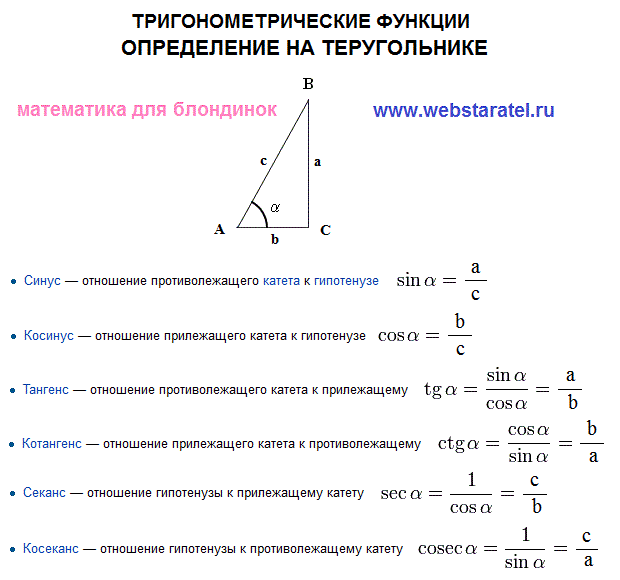 Найти
Найти
Решение:
Пример 2. Решить уравнение
Решение:
Найдем на линии тангенсов точку проведём прямую через эту точку и начало координат и получим две точки пересечения с окружностью – .
Ответ:
Пример 3. Решить уравнение
Решение :
Ответ:
Пример 4: Найти
Пример 5: Найдите: , , .
Решение.
Так угол лежит в 3 четверти, то
Ответ: 0,6 ;; .
Приложение 4
Самостоятельная работа по теме «Синус, косинус, тангенс произвольного угла»
Вариант 1 | Вариант 2 |
Задание № 1 Найдите значение выражения: Задание 2. Задание 3. Найдите знак произведения, используя правило знаков по четвертям: . Задание 4. Сравните с нулем выражение: Задание 5. Решить уравнение | Задание № 1 Найдите значение выражения: Задание 2. В какой четверти оканчивается угол α, если tg α0 и sin α 0? Задание 3. Найдите знак произведения, используя правило знаков по четвертям: . Задание 4. Сравните с нулем выражение: Задание 5. Решить уравнение |
Вариант 3 | Вариант 4 |
Задание № 1 Найдите значение выражения: Задание 2. В какой четверти оканчивается угол α, если tg α 0 и cos α Задание 3. Найдите знак произведения, используя правило знаков по четвертям: . Задание 4. Сравните с нулем выражение: Задание 5. Решить уравнение | Задание № 1 Найдите значение выражения: Задание 2. В какой четверти оканчивается угол α, если tg α0 и sin α Задание 3. Найдите знак произведения, используя правило знаков по четвертям: . Задание 4. Сравните с нулем выражение: Задание 5. Решить уравнение |
Дистанционный репетитор — онлайн-репетиторы России и зарубежья
КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?
Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!
КАК ВЫБРАТЬ репетитора
Выбрать репетитора самостоятельно
ИЛИ
Позвонить и Вам поможет специалист
8 (800) 333 58 91
* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК
ПОДАТЬ ЗАЯВКУ
Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41
Выбранные репетиторы
Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.
Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных
Вы также можете воспользоваться
расширенной формой подачи заявки
Как оплачивать и СКОЛЬКО ЭТО СТОИТ
от
800 до 5000 ₽
за 60 мин.
и зависит
ОТ ОПЫТА и
квалификации
репетитора
ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)
ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)
Оплата непосредственно репетитору, удобным для Вас способом
Почему я выбираю DisTTutor
БЫСТРЫЙ ПОДБОР
РЕПЕТИТОРА И
ИНДИВИДУАЛЬНЫЙ ПОДХОД
ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА
ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ
НАДЕЖНОСТЬ И ОПЫТ.
DisTTutor на рынке с 2008 года.
ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА
ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО
376114 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
уже сделали свой выбор
И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах
Владимир Александрович Кузьмин
«
Тренинг у Кузьмина В. А. проходил в экстремальных условиях. Мой модем совершенно не держал соединение. За время часового тренинга связь прерывалась практически постоянно. Ясно, что в таких условиях чрезвычайно непросто чему-то учить.
Однако Владимир Александрович проявил удивительную выдержку и терпение. Неоднократно он перезванивал мне на сотовый телефон, чтобы дать пояснения или комментарии.
Ценой больших усилий нам удалось рассмотреть три программы: ConceptDraw MINDMAP Professional Ru, GeoGebra и Ultra Flash Video FLV Converter. Владимир Александрович открыл мне курс на платформе dist-tutor.info и научил подключать и настраивать Виртуальный кабинет, порекомендовав изучать возможности этого ресурса, чтобы постепенно уходить от использования Skype.
«
Вячеслав Юрьевич Матыкин
Чулпан Равилевна Насырова
«
Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!
«
Алина Крякина
Надежда Васильевна Токарева
«
Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания. Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
«
Эльмира Есеноманова
Ольга Александровна Мухаметзянова
«
Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.
«
Оксана Александровна
Клиентам
- Репетиторы по математике
- Репетиторы по русскому языку
- Репетиторы по химии
- Репетиторы по биологии
- Репетиторы английского языка
- Репетиторы немецкого языка
Репетиторам
- Регистрация
- Публичная оферта
- Библиотека
- Бан-лист репетиторов
Партнеры
- ChemSchool
-
PREPY.
 RU
RU
- Class
Тригонометрические функции общего угла
До сих пор мы имели дело с прямоугольными треугольниками и рассматривали тригонометрические функции острого угла. В этом разделе мы распространяем определение тригонометрических функций на любые углы.
Единица окружности и углов
Для нахождения триггерных функций произвольного угла удобно использовать единичную окружность. Единичная окружность — это окружность радиусом, равным единице, с центром в начале декартовой плоскости. 9\circ — \alpha.\)
Единица окружности Определения синуса и косинуса
Пусть \(\alpha\) — любой угол в стандартном положении на единичной окружности. Предположим, что крайняя сторона угла пересекает окружность в точке \(M\left( {x,y} \right).\)
Синус угла \(\alpha\) определяется как
\[\sin\alpha = \frac{y}{r}\]
Аналогично функция косинуса определяется на координатной плоскости по формуле
\[\cos\alpha = \frac{x}{r}\]
Эти выражения соответствуют определению синуса и косинуса в прямоугольном треугольнике.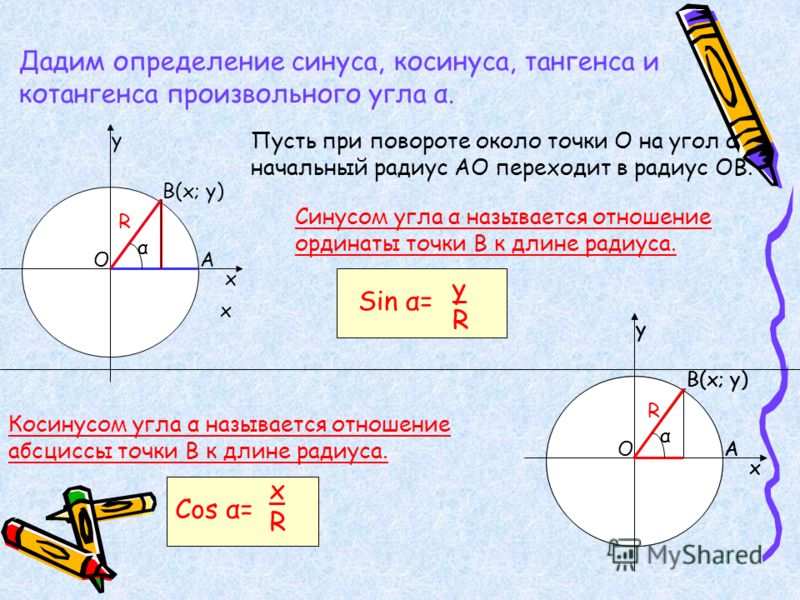 Действительно, треугольник \(ОАМ\) на рисунке \(1\) прямоугольный. В этом треугольнике радиус \(r = OM\) является гипотенузой, а координаты \(y-\) и \(x-\) образуют соответственно противолежащий и прилежащий катеты.
Действительно, треугольник \(ОАМ\) на рисунке \(1\) прямоугольный. В этом треугольнике радиус \(r = OM\) является гипотенузой, а координаты \(y-\) и \(x-\) образуют соответственно противолежащий и прилежащий катеты.
Поскольку мы рассматриваем единичную окружность, расстояние \(r\) равно \(1\) для любой точки \(\left( {x,y} \right)\) окружности:
92}} = 1.\]Таким образом, синус и косинус угла \(\alpha\) можно просто определить как координаты \(y\) и \(x\) точки \(M\left( {x,y} \right )\) определяется углом \(\alpha:\)
\[\sin \alpha = y ,\;\;\cos \alpha = x.\]
Когда угол \(\alpha\) измеряется в радианах, мы можем рассматривать любые действительные значения \(\alpha.\) Таким образом, определение синуса и косинуса единичной окружности является более общим, чем в прямоугольном треугольнике.
Определения единичной окружности касательной и котангенса
Снова рассмотрим единичную окружность и угол \(\alpha\) в стандартном положении.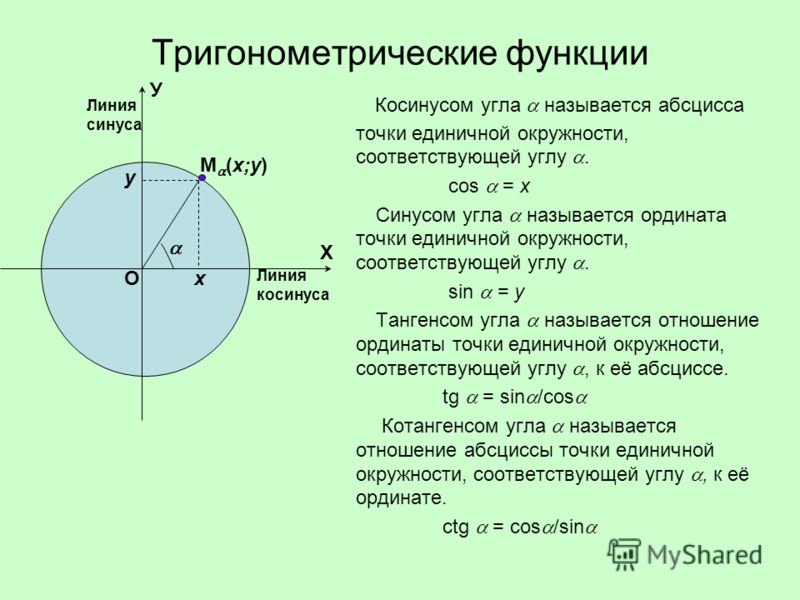 Угол \(\alpha\) определяет положение точки \(M\left( {x,y} \right)\) на окружности.
Угол \(\alpha\) определяет положение точки \(M\left( {x,y} \right)\) на окружности.
Тангенс \(\alpha\) на координатной плоскости определяется как
\[\tan\alpha = \frac{y}{x}\]
Функция тангенса выражается через синус и косинус в форме
\[\ tan \ alpha = \ frac {y} {x} = \ frac {{\ frac {y} {r}}} {{\ frac {x} {r}}} = \ frac {{\ sin \альфа}}{{\cos \альфа}}.\]
Как видите, функция касательной определена в точках, где \(\cos \alpha = x = 0.\)
На единичной окружности на рисунке \(3,\) значение функции тангенса отображается вертикальной отрезком \(BK\), проходящим через точку \(B\left( {1,0} \right). \) Действительно, треугольники \(ОАМ\) и \(ОВК\) подобны. Следовательно,
\[\frac{{AM}}{{OA}} = \frac{{BK}}{{OB}}.\]
Здесь \(AM= OS = y = \sin \alpha,\) \(OA = x = \cos \alpha,\) \(OB = 1.\) Следовательно,
\[BK = \frac{{AM}}{{OA}} \times OB = \frac{{\sin \alpha}}{{\cos \alpha}} \times 1 = \tan \alpha .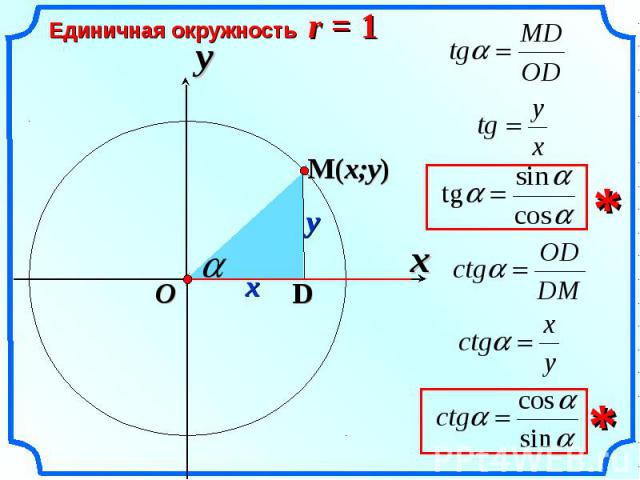 \]
\]
Котангенс угла \(\alpha\) равен
\[\cot\alpha = \frac{x}{y}\]
Мы также можем выразить функцию котангенса как отношение косинуса к синусу:
\[\ cot \ alpha = \ frac {x} {y} = \ frac {{\ frac {x} {r}}} {{\ frac {y} {r}}} = \ frac {{\ cos \альфа}}{{\sin\альфа}}.\]
Функция котангенса не определена в точках, где \(\sin \alpha = y = 0.\)
На рисунке \(3\) выше котангенс \(\alpha\) численно равен длине горизонтального сегмента \(PL.\) Поскольку треугольники \(OSM\) и \(OPL\) похожи, у нас
\[\frac{{SM}}{{OS}} = \frac{{PL}}{{OP}}.\]
Затем
\[PL = \frac{{SM}}{{OS}} \times OP = \frac{{\cos \alpha}}{{\sin \alpha}} \times 1 = \cot \alpha .\]
Определения единичной окружности секанса и косеканса
Секанс является обратной величиной косинуса. Поэтому он определяется по формуле
\[\sec\alpha = \frac{1}{\cos\alpha} = \frac{r}{x}\]
В единичной окружности внизу секущая функция \(\альфа\) представлена отрезком \(ОК.


 Концентрация внимания на наиболее эффективных приёмах.
Концентрация внимания на наиболее эффективных приёмах. Оказание индивидуальной помощи и корректировки.
Оказание индивидуальной помощи и корректировки.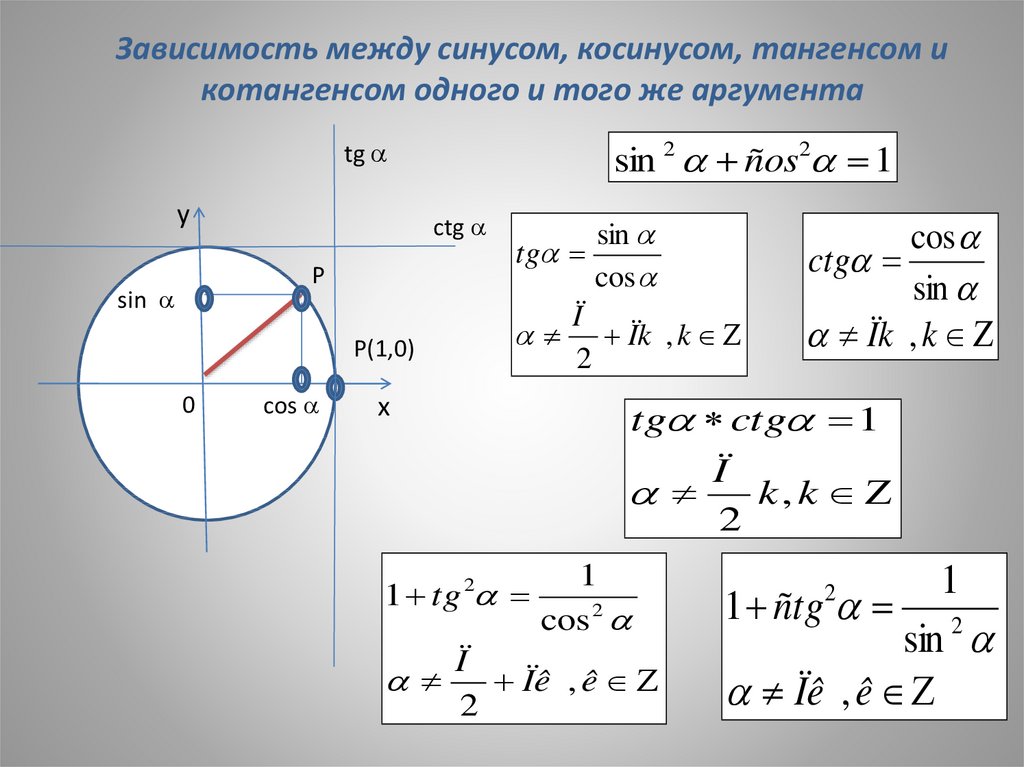 е.
е.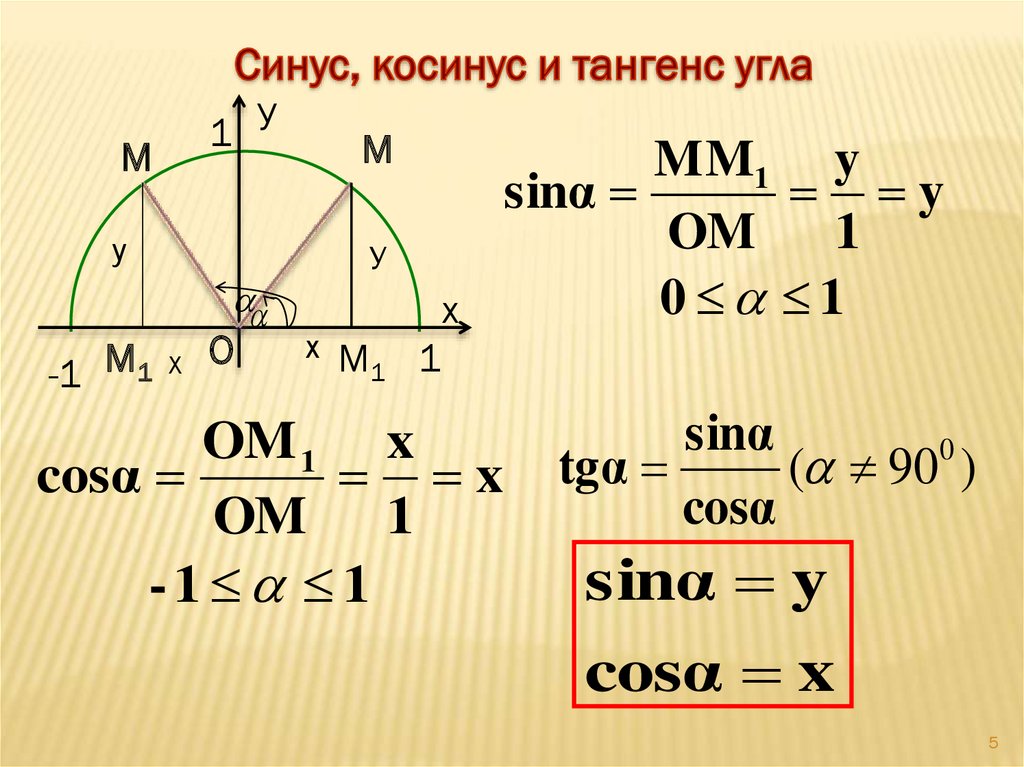 В какой четверти оканчивается угол α, если tg α cos α
В какой четверти оканчивается угол α, если tg α cos α
 RU
RU