Видеоурок по алгебре 10 класс тема Синус, косинус, тангенс на числовой окружности
Тригонометрические формулы
Решение тригонометрических уравнений и неравенств
Предел последовательности. Предел функции
Производная
Применение непрерывности и производной
Применение производной к использованию функций
Показать все темы
7 8 9 10 11
Поделиться
0
0
07:27
Если точка M числовой окружности соответствует числу t, то абсциссу точки M называют косинусом числа t и обозначают cost, а ординату точки M называют синусом числа t и обозначают sint.
Видео-урок: вычисление тригонометрических отношений по значению другого отношения
Стенограмма видео
На этом уроке мы научимся находить значение тригонометрической функции по заданному значению другой тригонометрической функции.
Прежде чем мы начнем, давайте подумаем о некоторой информации, которую мы уже должны знать. Тригонометрические функции могут быть определены через определенные отношения сторон прямоугольных треугольников. Рассмотрим угол при вершине 𝐴. У нас есть три основных отношения sin, cos и tan этого угла. Синусоидальная зависимость — это длина противоположной стороны относительно гипотенузы. Отношение косинуса — это длина соседней стороны относительно гипотенузы. А касательное отношение — это длина противоположной стороны относительно длины соседней стороны.
В треугольнике, который мы нарисовали, если мы используем угол 𝜃 при вершине 𝐴, длина противоположной стороны будет строчной 𝑎. А гипотенуза — это всегда длина стороны, противоположной прямому углу.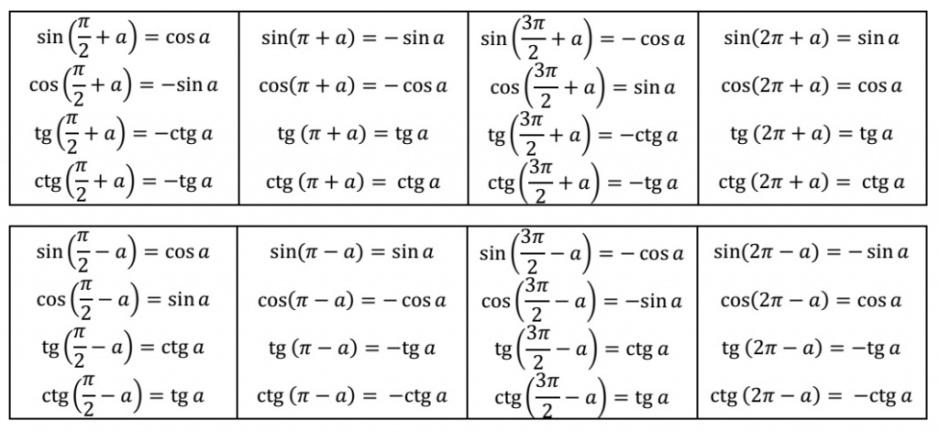
В нашем случае это будет строчная 𝑐. Чтобы найти отношение косинуса этого треугольника, длина соседней стороны обозначается строчной буквой 𝑏, а гипотенуза по-прежнему равна 𝑐, что делает касательную связь 𝑎 над 𝑏.
В дополнение к этим трем основным триггерным функциям у нас есть арккосеканс, секанс и котангенс. Косеканс является обратным к синусу, а гипотенуза — к противоположному синусу. Здесь у нас было бы 𝑐 над 𝑎. Секанс обратен косинусу, гипотенузе относительно прилежащего. В этом случае у нас было бы 𝑐 над 𝑏. Отношение котангенса является обратным отношению тангенса. Это длина смежной стороны относительно длины противоположной стороны. В данном случае 𝑏 больше 𝑎.
Многие люди помнят синус, косинус и тангенс во фразе SOH CAH TOA. Синус противоположен гипотенузе. Косинус — это прилежащий к гипотенузе. А тангенс противоположен соседнему.
Когда мы имеем дело с тригонометрией прямоугольного треугольника, все углы меньше 90 градусов. А когда все углы меньше 90 градусов, все шесть этих отношений положительны.
Но иногда мы имеем дело с углами больше 90 градусов. И когда это происходит, некоторые из этих отношений становятся негативными. Давайте вспомним, что происходит с этими большими углами.
Мы можем думать об этом с точки зрения координатной сетки. Иногда с этими углами мы используем градусы, а иногда — радианы. И когда мы измеряем такой угол, мы начинаем с правой стороны оси 𝑥 и измеряем, пока не дойдем до интересующей нас линии. Угол, который я нарисовал здесь, будет находиться где-то между 90 и 180 градусами. . Если бы мы знали, что этот угол равен 135 градусам, мы могли бы использовать калькулятор, чтобы найти sin, cos и тангенс этого угла. Наш калькулятор даст нам положительное значение 0,07 для sin, отрицательное 0,707 для cos и отрицательное значение для tan.
Этот шаблон — положительное значение синуса, отрицательное значение косинуса и отрицательное значение тангенса — будет верным для всех углов, находящихся в диапазоне от 90 до 180 градусов. Если бы мы нарисовали здесь прямоугольный треугольник, длина гипотенузы была бы равна единице, а каждая из сторон была бы равна квадратному корню из двух из двух.
Мы знаем это, потому что этот угол должен быть 45 градусов.
Это показывает, что мы все еще можем использовать тригонометрию прямоугольного треугольника. Мы по-прежнему можем использовать длины сторон для формирования соотношений для вычисления углов, превышающих 9.0. Для этого запоминаем положительные и отрицательные триггерные отношения на координатной сетке. И для этого мы используем диаграмму CAST, которая выглядит так.
Если мы начнем с первого квадранта с буквы А, это говорит нам о том, что все отношения положительны, что мы уже обсуждали. Отношения синуса, косинуса и тангенса от нуля до 90 градусов положительны. Переходя ко второму квадранту, S говорит нам, что только синус положительный. Любые углы, лежащие между 90 и 180 градусов будут иметь положительное отношение синуса и отрицательное отношение косинуса и тангенса.
В третьем квадранте буква Т говорит нам о положительном отношении касательной. Это означает, что в третьем квадранте отношения синуса и косинуса будут отрицательными.
И, наконец, в четвертом квадранте буква С говорит нам, что отношение косинуса положительное. Соотношение косинуса положительное, а отношения синуса и тангенса любого угла в четвертом квадранте будут отрицательными.
Знание шести триггерных функций и диаграммы CAST — основные инструменты, которые мы будем использовать при решении примеров задач. Давайте посмотрим на один сейчас.
Найдите csc числа 𝜃, учитывая, что тангенс числа 𝜃 равен 24 больше семи и что cos числа 𝜃 меньше нуля.
Нам дан тангенс угла 24 на семь. И нам нужно найти csc этого же угла при условии, что cos 𝜃 меньше нуля. Это означает, что наш cos отрицательный, а загар положительный. Это действительно важная информация. Прежде чем мы двинемся дальше, напомним себе об отношениях синуса, косинуса и тангенса и их обратных косекансе, секансе и котангенсе. В дополнение к этому мы можем набросать диаграмму CAST, которая поможет нам определить, в какой квадрант попадает интересующий нас угол.
Поскольку мы знаем, что тангенс положителен, мы можем сказать, что он попадет либо в первый, либо в третий квадрант.
Однако, поскольку косинус отрицательный, этот угол не может попасть в первый квадрант. В первом квадранте у нас есть 𝐴, потому что все три отношения положительны. В третьем квадранте только тангенс положителен, а синус и косинус отрицательны. И поэтому мы можем сказать, что наш угол будет лежать в третьем квадранте и набросать что-то вроде этого. Для нашего угла 𝜃, поскольку мы знаем, что тангенс равен 24 на семь, а тангенс противоположен длинам соседних сторон, мы знаем две из трех сторон.
Нам нужно нарисовать прямоугольный треугольник в третьем квадранте. Пусть это будет наш ракурс 𝜃. И тогда мы можем обозначить длину противоположной стороны как 24, а длину смежной стороны — как семь. Очевидно, мы не нарисовали это полностью в масштабе. Чтобы найти csc 𝜃, нам нужна гипотенуза напротив. И на данный момент у нас должно быть достаточно информации, чтобы распознать, что нам нужно решить теорему Пифагора.
Если мы допустим, что гипотенуза равна 𝑐, мы знаем, что 𝑎 в квадрате плюс 𝑏 в квадрате равно 𝑐 в квадрате, что даст нам 49плюс 576.
𝑐 в квадрате равно 625. Извлекая квадратный корень из обеих сторон, мы находим, что 𝑐 равно 25. Теперь, когда мы знаем гипотенузу, мы можем написать 25 вместо противоположного, 24. Но это не окончательный ответ. Нам нужно тщательно подумать о том, является ли это положительным или отрицательным решением.
Поскольку он попадает в третий квадрант, значения синуса и косинуса будут отрицательными. А поскольку значение косеканса является обратным значением синуса, оно будет иметь тот же знак, что и функция синуса. csc этого угла должен быть отрицательным. В этих условиях csc 𝜃 равно отрицательному значению 25 на 24.
Давайте посмотрим на другой пример.
Учитывая, что csc числа 𝜃 меньше семи на шесть, а тангенс числа 𝜃 больше нуля, найдите cos числа 𝜃.
Давайте подумаем об информации, которую нам дали. Мы знаем, что csc этого угла меньше семи на шесть, и мы знаем, что тангенс положителен. Мы хотим запомнить шесть триггерных функций. Поскольку нам дали csc 𝜃, нам дали гипотенузу напротив.
И так как мы ищем cos этого угла, мы ищем длину смежного катета над гипотенузой. Но есть еще одна информация, которую нам нужно учитывать. И это положение этого угла на координатной сетке.
Мы знаем, что тангенс положителен. Тангенс угла положителен только в первом и третьем квадрантах. Но мы также знаем, что косеканс отрицательный. А если косеканс отрицательный, то и синус будет отрицательным. В первом квадранте все три отношения положительны. В третьем квадранте тангенс положителен, но отношения синуса и косинуса отрицательны. А это значит, что мы знаем, что наше отношение, наше косинусное отношение, должно быть отрицательным.
Итак, мы знаем, что гипотенуза равна семи, а длина противоположной стороны равна шести. Чтобы решить нашу задачу, нам нужно знать длину смежной стороны. Если мы подумаем об этом с точки зрения прямоугольного треугольника, меры длин сторон должны быть положительными, потому что расстояние всегда измеряется положительными значениями. А это значит, что нам нужно использовать абсолютное значение гипотенузы.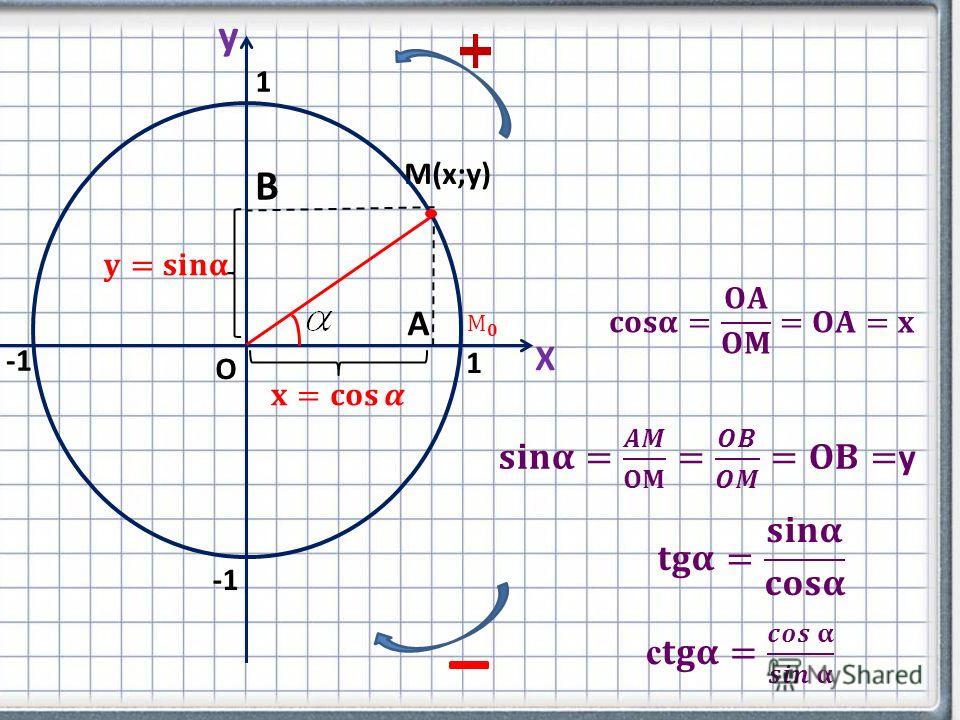
Вместо отрицательной семерки будет положительная семерка. А длина противоположной стороны будет равна шести.
Мы знаем, что можем использовать теорему Пифагора, чтобы найти эту третью недостающую длину стороны, длину соседней стороны. Поэтому мы говорим, что шесть в квадрате плюс 𝑏 в квадрате равняется семи в квадрате. 36 плюс 𝑏 в квадрате равно 49. Вычитая 36 с каждой стороны, мы получаем 𝑏 в квадрате равно 13. Отсюда мы берем квадратный корень из обеих сторон, чтобы найти недостающую длину стороны, которая равна квадратному корню из 13. Наше соотношение косинусов равно длина смежной стороны, квадратный корень из 13, по гипотенузе, которая, как мы уже знаем, равна семи. И поскольку это попадает в третий квадрант, это отношение косинуса должно быть отрицательным. И это делает наш окончательный ответ отрицательным квадратным корнем из 13 больше семи.
В этом примере нам дан диапазон измерения угла в радианах, который мы используем.
Учитывая, что кроватка 𝜃 равна отрицательным трем половинкам, где 𝜋 больше двух меньше, чем 𝜃, что меньше 𝜋, оцените сек в квадрате 𝜃 без использования калькулятора.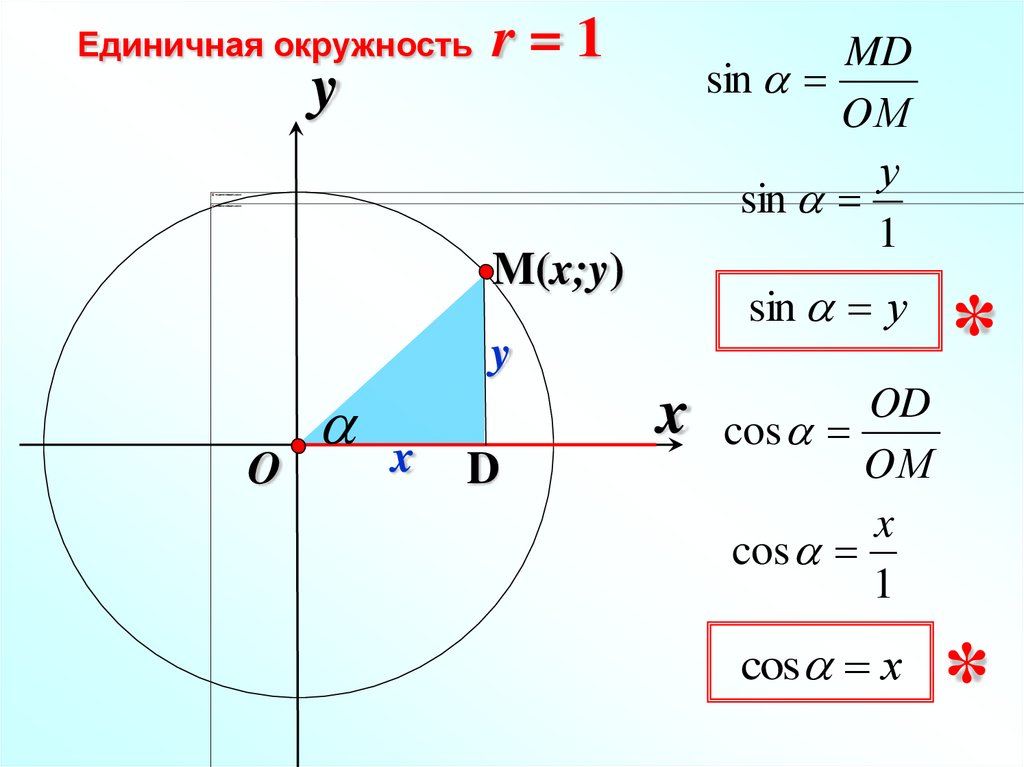
Прежде чем делать что-либо еще, будет полезно определить место, куда должна упасть эта 𝜃. Он падает между 𝜋 больше двух и 𝜋. Итак, мы рисуем координатную сетку и обозначаем ее мерами в радианах. Если 𝜃 попадает между 𝜋 больше двух и 𝜋, то 𝜃 попадет где-то во второй квадрант. Если мы нарисуем линию и наш угол 𝜃, мы сможем сделать набросок прямоугольного треугольника.
После этого нам нужно вспомнить наши триггерные связи. Поскольку мы знаем, что cot нашего угла меньше, чем три на два, мы знаем, что три представляют собой длину смежной стороны, а два представляют длину противоположной стороны. Мы можем использовать эту информацию, чтобы пометить этот эскиз. Наша цель — найти сек в квадрате 𝜃. Для этого умножим сек 𝜃 на сек 𝜃.
Эта секущая представляет собой гипотенузу длины смежной стороны. Но чтобы решить эту задачу, нам нужно выяснить, что такое гипотенуза. Для этого мы можем использовать теорему Пифагора. Два в квадрате плюс три в квадрате равно квадрату гипотенузы.
Это будет четыре плюс девять, 13 равно квадрату гипотенузы, что означает, что гипотенуза равна квадратному корню из 13.
Но здесь нужно быть очень осторожным. Мы должны рассмотреть, поскольку наш угол попадает в этот второй квадрант, будет ли секущая положительной или отрицательной. Для этого мы можем использовать диаграмму CAST. Мы уже знаем, что нас интересует второй квадрант. И поскольку здесь есть буква S, это говорит нам о том, что отношение синуса положительное, а отношения косинуса и тангенса будут отрицательными.
секанс обратен косинусу. И это означает, что если значение косинуса отрицательно, значение секанса будет отрицательным. Поскольку секанс — это гипотенуза по длине соседней стороны, у нас есть квадратный корень из 13 из трех, но мы знаем, что это значение должно быть отрицательным. И это делает сек из 𝜃 отрицательным квадратным корнем из 13 больше трех. сек в квадрате будет отрицательным квадратным корнем из 13 более трех, умноженным на отрицательный квадратный корень из 13 более трех.
Два минуса становятся плюсами. Квадратный корень из 13, умноженный на квадратный корень из 13, равен 13. А трижды три — девять. В этих условиях сек в квадрате 𝜃 составляет 13 больше девяти.
В нашем последнем примере нам снова дан диапазон значений, которым может быть наш 𝜃. Кроме того, у нас есть значение синуса, и нам нужно найти значение csc, в два раза превышающее значение 𝜃.
Учитывая, что грех 𝜃 равен отрицательной одной трети, где 𝜃 находится между 𝜋 и тремя 𝜋 больше двух, оцените csc двух 𝜃 без использования калькулятора. Подсказка: пусть csc двух 𝜃 будет равно единице, умноженной на два, умноженных на sin 𝜃, умноженных на cos 𝜃.
Всегда хорошо начинать с того, что есть. Грех 𝜃 составляет минус одну треть, а 𝜃 находится между 𝜋 и тремя 𝜋 больше двух. Если мы подумаем о квадрантах между 𝜋 и тремя 𝜋 над двумя, мы имеем дело с углом, который попадает в третий квадрант. Но мы не знаем, что это за угол, поэтому мы можем просто нарисовать угол 𝜃.
Но прежде чем мы двинемся дальше, было бы неплохо подумать о том, что мы пытаемся найти.
Если мы хотим найти csc двух 𝜃, нам нужны две части информации. Нам нужно знать грех 𝜃 и причину 𝜃. Но нам уже дан грех 𝜃, что составляет минус одну треть. А это значит, что единственное, что нам нужно для решения этой задачи, — это cos 𝜃.
Если нам дан грех 𝜃, как мы можем найти cos 𝜃? Ну, во-первых, мы думаем об этих отношениях. Синус равен противоположному по гипотенузе, а косинус равен прилежащему по гипотенузе. Поскольку у нас есть грех 𝜃, равный отрицательной одной трети, мы можем сказать, что длина противоположной стороны равна единице, а длина стороны гипотенузы равна трем. Мы можем нарисовать этот прямоугольный треугольник на координатной сетке, где длина противоположной стороны равна единице, а длина стороны гипотенузы равна трем.
Глядя на этот набросок, мы понимаем, что он немного неправильный. Что-то вроде этого немного больше в масштабе. Нам нужно найти эту недостающую сторону. Поэтому воспользуемся теоремой Пифагора. Когда мы это делаем, мы получаем, что 𝑏 равно квадратному корню из восьми.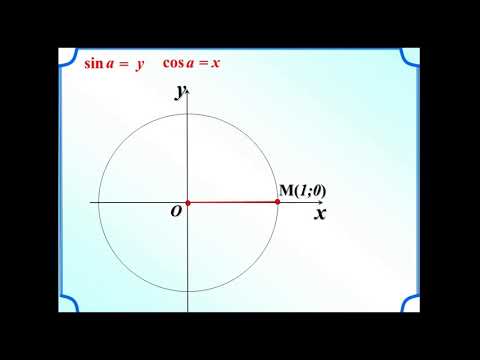
И это можно упростить до 𝑏, равного удвоенному квадратному корню из двух. Теперь, когда мы знаем, что длина смежной стороны в два раза больше квадратного корня из двух, мы можем записать косинус 𝜃 как отрицательный, умноженный на квадратный корень из двух на три.
Мы знаем, что косинус будет отрицательным, так как наш угол лежит в третьем квадранте. Диаграмма CAST говорит нам, что в третьем квадранте синус отрицательный, косинус отрицательный, а тангенс положительный. Таким образом, мы подставляем наше значение для cos 𝜃. Мы можем переписать это так: один разделить на два умножить на минус одну треть умножить на минус два умножить на квадратный корень из двух на три.
Мы хотим перемножить три числителя вместе, что даст нам четыре положительных числа, умноженных на квадратный корень из двух. А в знаменателях трижды три девять. Чтобы разделить единицу на это значение, мы умножаем на его обратную величину. И наш последний шаг — рационализировать знаменатель, который дает нам девять умноженных на квадратный корень из двух из восьми.
Ключевым моментом здесь является знание шести триггерных функций и использование диаграммы CAST для определения их положения на координатной сетке.
TRIG-RATIOS-QUIZ-ANSWERS-Google SUCHE
ALLBILDERVIDEOSNEWSMAPSSHOPPINGBücher
SUCOOPTIONEN
Коэффициент Триг. Если вам даны гипотенуза и другая сторона прямоугольного треугольника, какое тригонометрическое отношение вы, вероятно, используете? варианты ответов. Синус или тангенс.
ВИКТОРИНА по тригонометрическим отношениям | Викторина по геометрии — Викторина
quizizz.com › admin › викторина по тригонометрическим отношениям
В. Найдите ИЗМЕРЕНИЕ НЕДОПУСТИМОГО УГЛА (в правом верхнем углу) показанного прямоугольного треугольника. варианты ответов. 90∘. 50∘. 40∘. НЕ МОЖЕТ БЫТЬ ОПРЕДЕЛЕН.
Карточки для викторины по тригонометрическим отношениям — Quizlet
quizlet.com › карточки для викторины по тригонометрическим отношениям
Изучите с помощью Quizlet и запомните карточки, содержащие такие термины, как Какое из следующих соотношений используется для нахождения синуса угла в прямоугольном треугольнике?, .
..
Викторина по тригонометрическим отношениям: тест по математике! — ProProfs
www.proprofs.com › … › Математика › Тригонометрия
22.03.2022 · Попробуйте эту замечательную викторину по тригонометрическим отношениям: тест по математике! викторина, которая была предпринята 9698 раз заядлыми … Вопросы и ответы.
Тест тригонометрических отношений — BestMaths
bestmaths.net › year-levels › year-10 › year-10-topics
Каково значение синуса угла A? А. 1.25. Б. 0,8. С. 0,75. Д. 0,25. Ответ 5:.
Тригонометрические отношения MCQ [Бесплатный PDF] — Ответ на объективный вопрос …
testbook.com › Математика › Тригонометрия
Получите вопросы с несколькими вариантами ответа на тригонометрические отношения (MCQ Quiz) с ответами и подробными решениями. Загрузите эту бесплатную викторину MCQ по тригонометрическим отношениям в формате Pdf и …
[PDF] Basic Trig Quiz-Geometry
www.
wappingersschools.org › cms › lib01 › Centricity › Domain › B…
На прилагаемой диаграмме прямоугольного треугольника ABC, угол ∠B прямой, AB = 8,. ВС = 15, а СА = 17. Какое отношение равно 8,17? A. грех A. B. грех C.
Trig Ratios — Проверка на повторение 1 — Портал — Class Mathematics
classmathematics.com.au › maths-5-2 › trigonometry
Trig Ratios — Проверка на повторение 1 … Для следующей дроби напишите правильный тригонометрический отношение между углами A в данном треугольнике a b. Отвечать.
Тест и рабочий лист — Как найти тригонометрические отношения — Study.com
Study.com › академия › практика › тест-рабочий лист-ч…
Выберите ответ и нажмите «Далее». В конце вы получите свой балл и ответы. вопрос 1 из 3. Найдите значение …
Вопросы с несколькими вариантами ответа на тригонометрические отношения онлайн с. 1
mcqlearn.com › 8 класс › математика › тригонометрические отношения с несколькими вариантами ответов.