Понятие геометрического вектора.Основные определения, связанные с этим понятием (длина вект.,равенство вект.,нуль-вектор, коллиниарный и компланарный вект.,орт вектора.
Геометрический вектор-направленный отрезок, который можно перемещать параллельно ему самому. Направленный отрезок с началом в точке A и концом в точке B обозначается AB. Векторы обозначаются строчными латинскими буквами со стрелками: ↗а,↗в….
Таким образом, два направленных отрезка ∕AB и ∕CD, имеющие одинаковые длины и направления, изображают один и тот же вектор ↗а, и именно в этом случае будет равенство между векторами и направленными отрезками, например:↗а=∕АВ=∕СD
Длиной (или модулем)вектора ∕AB называется
расстояние между точками A и B.
Будем считать, что единица измерения
длин выбрана и, говоря о длинах отрезков,
не будем указывать, какой единицей они
измеряются.
Модуль вектора∕ AB обозначается
символом |∕AB|.
Вектор нулевой длины называется нулевым и
обозначается символом ↗0.
Векторы,
лежащие на параллельных или совпадающих
прямых, называются
Если угол между векторами равен π/2, то векторы называются ортогональными.
Линейные операции с геометрическими векторами. Законы, которые удовлетворяют эти операции. Разность векторов. Коллиниарные векторы.
Векторы, лежащие на параллельных или совпадающих прямых, называются коллинеарными.
Под линей.операц.над вект.понимают операции сложения,вычетания вект.и умнож.вект.на число.
1 )пусть А и В произведение вект. А
/ ОА=/а
/а /в
/а /в
О /а + /в Р
Правило треугольника: /ОВ=/а+/в Сумму
2х вект.
можно найти по правилу пар-ма.
В этом случае /а и /в откладывают от 1
(.) : /ОС=/а+/в
/а А
О С
/а+/в
/в В
2) разность /а и /в:
/с=/а-/в /в+/с=/а /в+/с=/а
А
/а
О
/в В
Заметим,что в пар-ме,построенном на /а и /в, одна диагональ сумма /а и /в, а др.разностью /а и /в.: /а-/в=/а+/в
/а
/а+/в
/в
3)произведение
/а на число λ-/λа такой, что длина |/ λ
а|=|/ λ |*|/а| и направление / λ совпадает
с направлением /а, если λ>0 и направление
/λ противополож.
/а, если λ<0.
Из определения произведения вект.на число следует св-ва этого произвед.
1)/в=/ λа, то /а||/в
2)/а=|/а|*/а◦(орта)
Каждый вектор= произвед.его модуля на орту. св-ва л.о.над вект.:
1)переместит: /а+/в=/в+/а
2)сочитательн. /а+(/в+/с)=(/а+/в)+/с
Λ1/а(λ2/а)=(λ1*λ2)/а
3)распределительн. (/а+/в)λ=λ/а+λ/в
(λ1+λ2)/а=λ1/а+λ2/а
Эти св-ва позволяют проводить преобразования в л.о. над вект.,также,как в обычной алгебре,т.е.менять местами слагаемые,вводить скобки,группировать,выносить за скобки.
ДЕЛЕНИЕ ОТРЕЗКА В ЗАДАННОМ ОТНОШЕНИИ
допустим,дано:
М(х;у)
А(х1;у1) В(х2;у2)
Будем говорить М делит АВ в отношении λ,где λ>0 |АМ|/|МВ|=λ
Заметим,что
в данном определении важен порядок в
котор.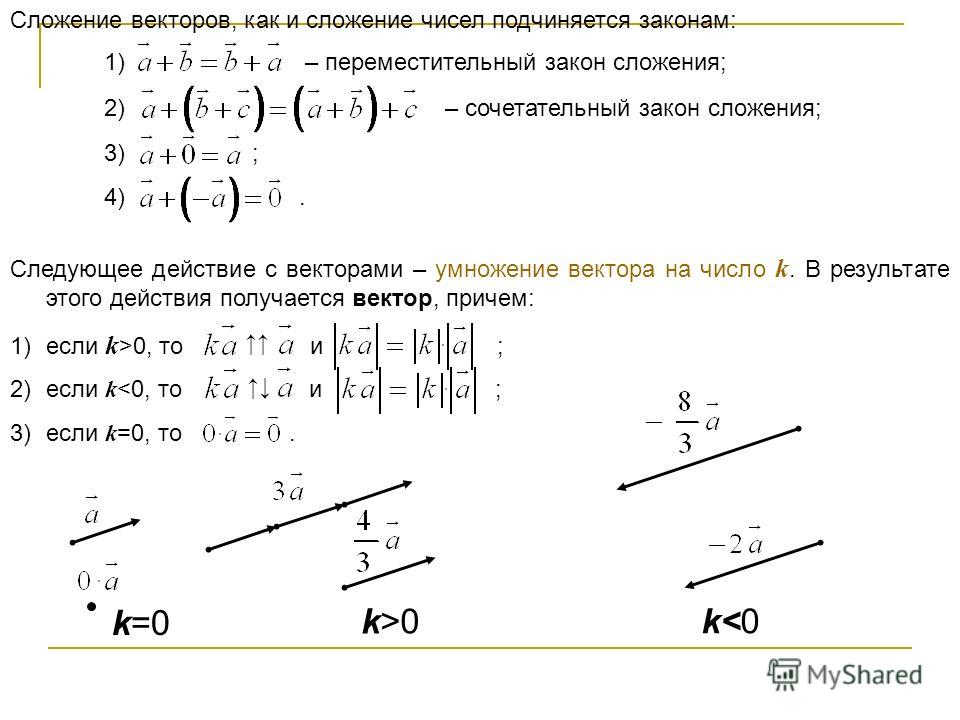
указаны концы отрезка АВ. (.)А
нач.отр.,В конец. Задача состоит в
том,чтобы определить корд.(.)М, делящая
отрезок в отнош.λ,если известны корд.(.)
А и В.
Х=(х1+λх2)/(1+λ) (плоскость,пространство)
ПОНЯТИЕ РАДИУС ВЕКТОРА.РАЗЛОЖЕНИЕ ПРОИЗВОЛЬНОГО ВЕКТОРА ПО ОРТАМ КООРДИНАТНЫХ ОСЕЙ НА ПЛ. И В ПРОСТР.
Радиус-вектор точки — это называется вектор, начало которого совпадает с началом системы координат, а конец — с данной точкой.
Рассмотрим в прост.прямоуг.СК Оxyz. Выделим на корд.осях Ох,Оу,Оz единичные векторы(орты),обозначаемые /I,/j,/k.
z M 3
ϒ
/а М
/k М2
О ᵝ у
/i ԃ /j
х М1 N Выберем
произвольный /а прост.
и совместим его
начало с нач.координат:/а=/ОМ.
Найдем проекции /а на корд.оси. проведем через конец вектора/ОМ плоскости,параллельные корд. Плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через М1,М2,М3. Получим прямоугольный параллелепипед,одной из диагоналей которого является вектор/ОМ. Тогда прХ/а=|/ОМ1|,прУ/а=|/ОМ2|,прZ/а=|/ОМ3|.по определению суммы нечкольких векторов находим /а=/ОМ1+/M1N+/NМ.а т.к./M1N=/OM2,/NM=/OM3,то /а=/ОМ1+/ОМ2+/ОМ3.но /ОЬ1=|/ОМ1|*/i, /ОМ2=|/ОМ2|*/i, /ОМ3=|/ОМ3|*/к. обозначим проекции вектора /а=/ОМ на оси Ох,Оу,Оz соответственно через ах,ау,аz,т.е. |/ОМ1|=ах, |/ОМ2|=ау,|/ОМ3|=аz. Тогда из равенства=> /а=ах*/i+ay*/j+az*/k. Эта формула явл.основ. в векторном исчислении и назыв.разложением вект.по ортам корд осей. ах,ау,аz-коорд.вект.
ОглавлениеВВЕДЕНИЕЧАСТЬ ПЕРВАЯ. ВЕКТОРНАЯ АЛГЕБРА Глава I. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ 2. Скаляры и векторы. 3. Равенство векторов. 4. Скользящие и приложенные векторные величины. 5. Модуль вектора. 6. Орт вектора. 7. Угол между двумя векторами. § 2. Сложение векторов 1. Сложение двух векторов. 2. Сложение более чем двух векторов.  3. Модуль суммы. 4. Законы сложения. § 3. Вычитание векторов § 4. Умножение и деление вектора на скаляр 2. Законы умножения вектора на скаляр. 3. Деление вектора на скаляр. 4. Выражение вектора через его модуль и орт. § 5. Линейные зависимости между векторами 2. Коллинеарные векторы. 3. Компланарные векторы. 4. Разложение вектора по трем некомпланарным векторам. 5. Метод координат. Глава II. ТЕОРИЯ ПРОЕКЦИЙ. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ § 2. Основные теоремы о скалярных проекциях § 3. Прямоугольная система координат в пространстве 1. Правая и левая прямоугольные системы координат. 2. Разложение вектора по ортам осей 3. Линейные операции над векторами в координатной форме. 4. Радиус-вектор и координаты точки. 5. Определение вектора по его началу и концу. 6. Деление отрезка в данном отношении. Глава III. ПРОИЗВЕДЕНИЯ ДВУХ ВЕКТОРОВ § 1. Скалярное произведение двух векторов 2. 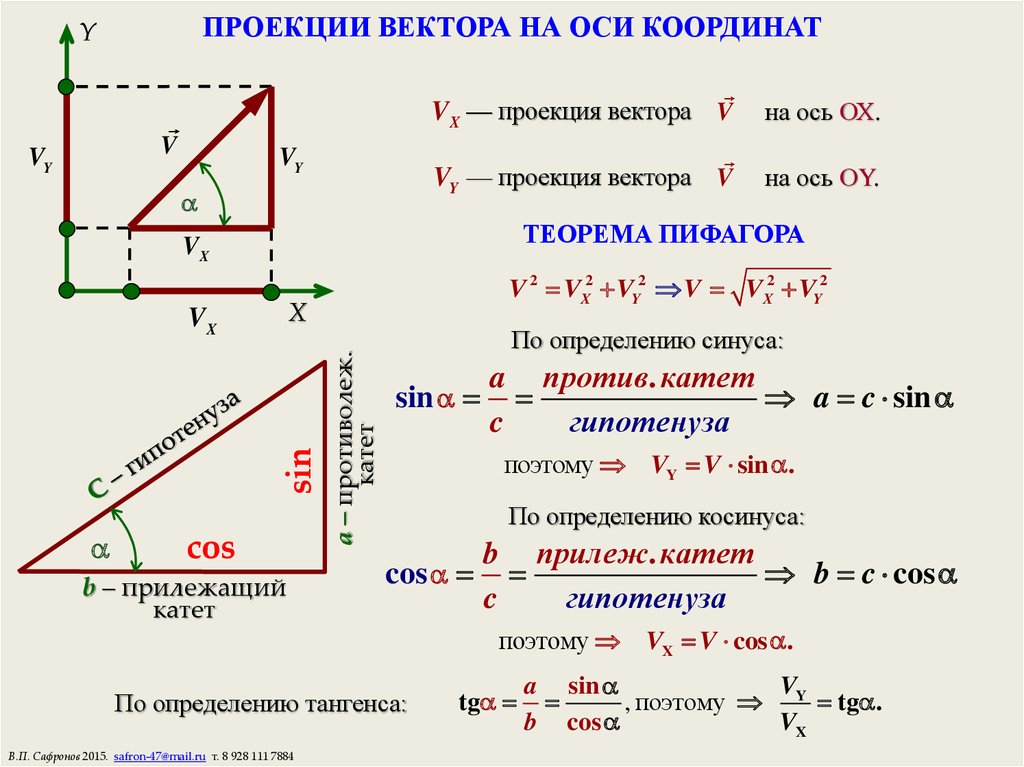 Работа силы.3. Определение. 4. Равенство скалярного произведения нулю. 5. Законы скалярного умножения. 7. Скалярные произведения координатных ортов. 8. Скалярное произведение в координатной форме. 9. Неопределенность действия, обратного скалярному умножению. § 2. Векторное произведение двух векторов 3. Условия равенства нулю векторного произведения. 4. Законы векторного умножения. 5. Векторные произведения координатных ортов. 6. Определители. 7. Векторное произведение в координатной форме. 8. Неопределенность действия, обратного векторному умножению. Глава IV. ПРОИЗВЕДЕНИЯ ТРЕХ ВЕКТОРОВ § 1. Простейшее произведение трех векторов § 2. Векторно-векторное произведение трех векторов 3. Правило разложения векторно-векторного произведения. § 3. Векторно-скалярное произведение трех векторов 2. Законы векторно-скалярного умножения 3. Обращение в нуль векторно-скалярного произведения трех векторов. 4. Векторно-скалярное произведение в координатной форме.  § 4. Выражение векторно-скалярного произведения через скалярные произведения Глава V. ФУНКЦИИ ВЕКТОРОВ § 1. Произведения четырех векторов 2. Выражение скалярного произведения двух векторных произведений (а x b), (р x q) через скалярные произведения. 4. Разложение вектора (a, b, c) по векторным произведениям b x с, c x a, а x b § 2. Произведения пяти и шести векторов 2. Разложение вектора (a, b, c) (m x n) по векторам a, b, c. 3. Выражение произведения двух смешанных произведений (a, b, c) (l, m, n) через скалярные произведения. § 3. Основные теоремы о функциях векторов 1. Рациональные функции векторов. 2. Элементарные функции векторов. 3. Произвольные скалярные функции от векторов. 4. Произвольные векторные функции векторов. Глава VI. ОСНОВНЫЕ ЗАДАЧИ § 2. Основные задачи, связанные со скалярным умножением векторов § 3. Основные задачи, связанные с векторным умножением векторов § 4.  Основные задачи, связанные с произведениями трех и более векторов§ 5. Простейшие векторные уравнения § 6. Геометрические инварианты фигур 2. Треугольник. 3. Полные системы инвариантов треугольника. 4. Тетраэдр. 5. Полные системы инвариантов тетраэдра. 6. Гексаэдр с треугольными гранями. ЧАСТЬ ВТОРАЯ. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ § 1. Векторы, зависящие от скаляра 2. Вектор-функция в координатной форме. 3. Годограф вектора. 4. Предел вектора. § 2. Дифференцирование вектора по скаляру 2. Геометрический смысл производной вектора по скаляру. 3. Механический смысл производной. 5. Дифференциал вектора. 6. Инвариантность дифференциала. 7. Связь дифференциала вектора с его приращением. § 3. Формула Тейлора Глава VIII. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ЛИНИИ В ПРОСТРАНСТВЕ § 1. Основные дифференциально-геометрические понятия, связанные с линией 2. Касательная. 3. Соприкасающаяся плоскость. 4. Главная нормаль и бинормаль.  5. Кривизна. 6. Кручение. 7. Длина дуги. § 2. Основные формулы дифференциальной геометрии линий в пространстве 1. Дуга как параметр. Дифференциал дуги. 2. Орт касательной. Первая основная формула. 3. Инвариантность геометрических понятий. 4. Главная нормаль и кривизна. Вторая основная формула. 5. Бинормаль и кручение. Третья основная формула. 6. Винтовая линия. § 3. Сопровождающий трехгранник 2. Система дифференциальных уравнений движения сопровождающего трехгранника. 3. Расположение линии относительно сопровождающего трехгранника. 4. Линии без кривизны. 5. Линии без кручения. § 4. Инвариантные формулы Глава IX. ПЛОСКИЕ ЛИНИИ § 1. Дифференциальные уравнения плоской линии § 2. Кривизна плоской линии § 3. Круг кривизны § 4. Эволюта § 5. Эвольвента Глава X. ПРИЛОЖЕНИЯ К МЕХАНИКЕ § 1. Скорость и ускорение точки § 2. Движение твердого тела вокруг неподвижной точки 2. Формула Эйлера. 3.  Угловая скорость.4. Доказательстве существования угловой скорости твердого тела. § 3. Относительная производная вектора 2. Абсолютная и относительная производные вектора. 3. Общий случай движения твердого тела. Глава XI. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ § 1. Векторные функции нескольких скалярных аргументов § 2. Параметризованная поверхность 2. Поверхность в декартовых координатах. 3. Параметрическая сеть. 4. Линия на параметризованной поверхности. § 3. Касательная плоскость и нормаль 3. Нормальный вектор. 4. Преобразование параметров. § 4. Площадь области на поверхности 2. Площадь области на поверхности. 3. Формула для вычисления площади поверхности, заданной уравнением z=z(x,y). 4. Элемент площади поверхности. 5. Векторный элемент площади поверхности. § 5. Первая квадратичная форма поверхности 2. Внутренняя геометрия поверхности. 3. Длина дуги линии на поверхности. 4. Угол между линиями на поверхности.  5. Площадь области на поверхности. § 6. Вторая квадратичная форма поверхности 2. Нормальная кривизна линии на поверхности. 3. Теорема Менье. § 7. Главные направления и главные кривизны поверхности 2. Главные направления на поверхности. 3. Перпендикулярность главных направлений. 4. Формула Эйлера. 5. Полная и средняя кривизны поверхности. ЧАСТЬ ТРЕТЬЯ. ТЕОРИЯ ПОЛЯ § 1. Функция поля. Поверхности уровня § 2. Градиент поля 2. Первая теорема о градиенте. § 3. Производная по направлению 2. Выражение производной по направлению через градиент. 3. Вторая теорема о градиенте. § 4. Направляющие косинусы нормали поверхности Глава XIII. КРИВОЛИНЕЙНЫЙ И ПОВЕРХНОСТНЫЙ ИНТЕГРАЛЫ § 1. Криволинейный интеграл как определенный интеграл от сложной функции 2. Криволинейный интеграл от линейной формы по произвольной кривой. 3. Основные свойства криволинейного интеграла. 4. Обобщенный криволинейный интеграл. 5. Примеры.  § 2. Криволинейный интеграл как предел криволипейной интегральной суммы § 3. Поверхностный интеграл как двойной интеграл от сложной функции 2. Определение простейшего поверхностного интеграла. 3. Поверхностный интеграл от билинейной формы по произвольной поверхности. § 4. Поверхностный интеграл как предел поверхностной интегральной суммы § 5. Поверхностный интеграл в параметрической форме 2. Параметрический поверхностный интеграл. 3. Поверхностный интеграл как предел суммы. § 6. Кратный интеграл как предел обобщенной интегральной суммы 2. Обобщение основной теоремы о кратном интеграле. Глава XIV. ВЕКТОРНОЕ ПОЛЕ И ЕГО ИНТЕГРАЛЬНЫЕ ИНВАРИАНТЫ § 1. Векторное поле § 2. Векторные линии § 3. Циркуляция поля вдоль линии § 4. Поток поля через поверхность Глава XV. ТЕОРЕМА ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ПОЛЯ § 1. Формула Остроградского § 2. Дивергенция поля 2. Дивергенция как предел отношения. 3. Гидромеханический смысл дивергенции.  4. Теорема Остроградского. Глава XVI. ТЕОРЕМА СТОКСА. РОТАЦИЯ ПОЛЯ § 1. Формула Стокса § 2. Ротация поля § 3. Оператор Гамильтона Глава XVII. СПЕЦИАЛЬНЫЕ ВЕКТОРНЫЕ ПОЛЯ § 1. Потенциальное поле 3. Циркуляция потенциального поля по замкнутому контуру. 4. Циркуляция потенциального поля между двумя точками. 5. Потенциал. 6. Элемент циркуляции. 7. Характеристические признаки потенциального поля. 8. Вычисление потенциала. 9. Центральное поле. 10. Вихревые шнуры. § 2. Соленоидальное поле 3. Поток соленоидального поля через замкнутую поверхность. 4. Трубчатое строение соленоидального поля. 5. Векторный потенциал. 6. Характеристические признаки соленоидального поля. 7. Источники и стоки. § 3. Потенциальное несжимаемое поле Глава XVIII. ПРОСТЕЙШИЕ ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ § 1. Электростатическое поле точечного заряда 2. Дивергенция поля точечного заряда. 3. Поток поля точечного заряда через замкнутую поверхность.  4. Ротация поля точечного заряда. 5. Потенциал поля точечного заряда. § 2. Электростатическое поле системы точечных зарядов 2. Дивергенция и ротация поля системы точечных зарядов. 3. Поток поля системы точечных зарядов через замкнутую поверхность. 4. Потенциал поля системы точечных зарядов. 5. Непрерывно распределенный заряд. § 3. Магнитное поле тока 2. Напряженность магнитного поля тока, текущего по бесконечному прямолинейному проводу. 3. Векторные линии поля H. 4. Потенциал поля Н. 5. Провод как вихревой шнур. Глава XIX. ВЕКТОРНОЕ ПОЛЕ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ § 1. Криволинейные координаты 3. Координатные поверхности и линии. 4. Линейный элемент. 5. Элемент объема. 6. Подвижной репер. 7. Векторное поле в криволиненных координатах. § 2. Дифференциальные операции в криволинейных координатах 2. Дивергенция в криволинейных координатах. 3. Ротация в криволинейных координатах. § 3. Ортогональные координаты § 4.  Цилиндрические координаты2. Линейный элемент и элемент объема в цилиндрических координатах. 3. Дифференциальные операции в цилиндрических координатах. § 5. Сферические координаты |
Ф. Элементы векторного исчисления. М., 1975 г. — 336 с.
Как найти единичный касательный вектор — Криста Кинг Математика
Формула для единичного касательного вектора
Чтобы найти единичный касательный вектор для векторной функции, мы используем формулу
???T(t)=\frac{r'(t)}{||r'(t )||}???
где???r'(t)??? является производной векторной функции ???r(t)=r(t)_1\bold i+r(t)_2\bold j+r(t)_3\bold k??? и т??? дано.
Привет! Я Криста. 92}???
Как найти единичный касательный вектор к векторной функции при определенном значении параметра
Пройти курс
Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого.
3\bold i+6t\bold j+4t\ln(t)\bold k???.Получить доступ к полному курсу Calculus 3
Начать
Изучение математикиКриста Кинг математика, изучение онлайн, онлайн-курс, онлайн-математика, исчисление iii, исчисление 3, исчисление iii, вычисление 3, векторное исчисление, векторное исчисление, единичный тангенс вектор, единичный вектор, векторная функция
0 лайковЕдиничный тангенс и единичные векторы нормали
Единичный тангенс и единичные векторы нормали
Единичный касательный вектор
Производная векторной функции дает новую векторную функцию
которая касается заданной кривой. Аналог наклона
касательная — это направление касательной. Так как вектор
содержит величину и направление, вектор скорости содержит больше
информации, чем нам нужно.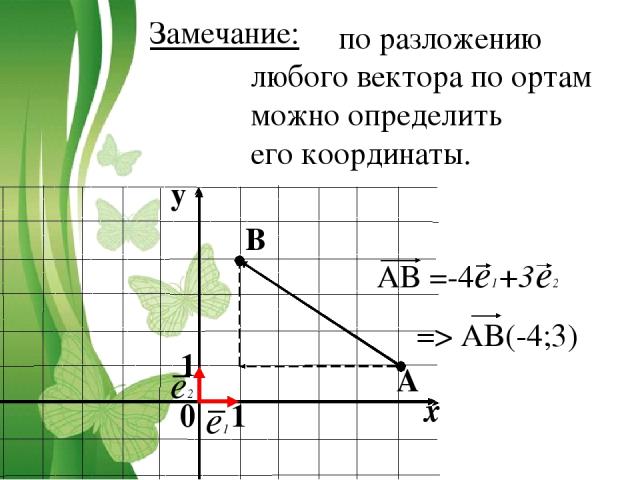
Мы можем лишить вектор его величины на
деление на его величину.
Определение единичного касательного вектора Пусть r (t) — дифференцируемый вектор со значением функция и v (t) = r ‘(t) — вектор скорости. Затем мы определяем единичный касательный вектор как как единичный вектор в направлении вектора скорости. v (т)
|
Пример
Позволять
р (т) = t i + e t j — 3t 2 k
Найти Т (т) и Т (0).
Решение
Мы есть
v (t) = r ‘(t) = i + e t j — 6 т к
и
Чтобы найти единичный касательный вектор, мы просто делим
Кому найти T(0) подставьте 0 к получить
Нормальный вектор главной единицы
Нормальный вектор — это перпендикулярный вектор.
Дан вектор v в
пространстве бесконечно много перпендикулярных векторов. Наша цель —
выберите специальный вектор, который является нормальным к единичному касательному вектору.
Геометрически для непрямой кривой этот вектор является единственным вектором, который
указать на кривую. Алгебраически мы можем вычислить вектор, используя
следующее определение.
| Определение основной единицы нормального
Вектор Пусть r (t) — дифференцируемая векторнозначная функция и пусть T (t) — единичный касательный вектор. Затем главный единичный вектор нормали N (t) определяется Т’ (т)
|
Сравнивая это с формулой для единицы
касательный вектор, если мы думаем об единичном касательном векторе как о векторе со значением
функции, то главный единичный вектор нормали является единичным касательным вектором
единичная функция касательного вектора.
Вы обнаружите, что нахождение принципала
единичный вектор нормали почти всегда громоздок. Частное правило обычно
поднимает свою уродливую голову.
Пример
Найти единичный вектор нормали для векторнозначной функции
r (t) = t i + t 2 j
и нарисуйте кривую, единичный тангенс и единичные векторы нормали, когда t = 1.
Решение
Первый находим единичный касательный вектор
Сейчас используйте правило отношения, чтобы найти Т ‘(т)
С единичный вектор в направлении данного вектора будет таким же после умножив вектор на положительную скалярную величину, мы можем упростить, умножив на фактор
первый множитель избавляется от знаменателя, а второй множитель избавляется от
дробная мощность. У нас есть
Сейчас делим на величину (после первого деления на 2) чтобы получить
Сейчас вставьте 1 для обоих векторов касательной единицы, чтобы получить
На рисунке ниже показан график и два вектора.
Тангенциальные и нормальные компоненты Ускорение
Представьте, что вы едете вниз с Эха
Поднимитесь на вершину Майерса, и у вас откажут тормоза. Когда вы едете на вас
столкнется с двумя силами (кроме силы террора), которые изменят
скорость. Под действием силы тяжести автомобиль будет увеличиваться в
скорость. Второе изменение скорости будет вызвано движением автомобиля вокруг
Кривая. Первая составляющая ускорения называется тангенциальный
компонент ускорения и второй
называется нормальной составляющей ускорения . Как вы можете догадаться, тангенциальная составляющая ускорения направлена в сторону
единичный касательный вектор и нормальная составляющая ускорения находятся в
направление главного единичного вектора нормали. Когда у нас есть T и N ,
легко найти эти два компонента. У нас есть
Тангенциальные и нормальные компоненты Ускорение Тангенциальная составляющая ускорения и нормальная составляющая ускорения и a = a N N + а Т Т |
Доказательство
Первое уведомление что
против = || против || Т и T ‘ = || Т ‘|| N
Взяв производную от обоих сторон дает
a = v ‘ = || против ||’ Т + ||v|| Т’ = || против ||’ Т + || против || || Т’ || N
Это
говорит нам, что вектор ускорения находится в плоскости, содержащей единицу
касательный вектор и единичный вектор нормали.