Формулы приведения вывод. Выражение синуса через косинус
Для использования формул приведения существует два правила.
1. Если угол можно представить в виде (π/2 ±a) или (3*π/2 ±a), то название функции меняется sin на cos, cos на sin, tg на ctg, ctg на tg. Если же угол можно представить в виде (π ±a) или (2*π ±a), то название функции остается без изменений.
Посмотрите на рисунок ниже, там схематично изображено, когда следует менять знак, а когда нет.
2. Правило «каким ты был, таким ты и остался».
Знак приведенной функции остается прежним. Если исходная функция имела знак «плюс», то и приведенная функция имеет знак «плюс». Если исходная функция имела знак «минус», то и приведенная функция имеет знак «минус».
На рисунке ниже представлены знаки основных тригонометрических функций в зависимости от четверти.
Вычислить Sin(150˚)
Воспользуемся формулами приведения:
Sin(150˚) находится во второй четверти, по рисунку видим что знак sin в этой четверти равен +.
Теперь 150˚ = 90˚ +60˚. 90˚ это π/2. То есть имеем дело со случаем π/2+60, следовательно по первому правилу меняем функцию с sin на cos. В итоге получаем Sin(150˚) = cos(60˚) = ½.
При желании все формулы приведения можно свести в одну таблицу. Но все же легче запомнить эти два правила и пользоваться ими.
Тема урока
- Изменение синуса, косинуса и тангенса при возрастании угла.
Цели урока
- Познакомиться с новыми определениями и вспомнить некоторые уже изученные.
- Познакомится с закономерностью изменений значений синуса косинуса и тангенса при возрастании угла.
- Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
- Воспитательные — посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.

Задачи урока
- Проверить знания учащихся.
План урока
- Повторение ранее изученного материала.
- Задачи на повторение.
- Изменение синуса, косинуса и тангенса при возрастании угла.
- Практическое применение.
Повторение ранее изученного материала
Начнем с самого начала и вспомним то что будет полезно освежить в памяти. Что же такое синус, косинус и тангенс и к какому разделу геометрии относятся эти понятия.
Тригонометрия — это такое сложное греческое слово: тригонон — треугольник, метро — мерять. Стало быть по-гречески это означает: мерятся треугольниками.
Предмети > Математика > Математика 8 класс
Как запомнить формулы приведения тригонометрических функций? Это легко, если использовать ассоциацию.Данная ассоциация придумана не мной. Как уже говорилось, хорошая ассоциация должна «цеплять», то есть вызывать яркие эмоции. Не могу назвать эмоции, вызываемые этой ассоциацией, позитивными.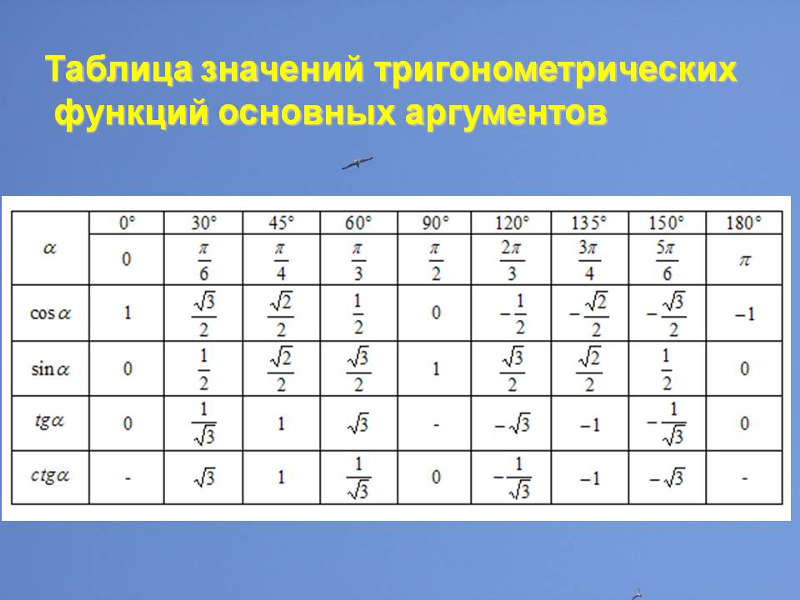
Формулы приведения имеют вид: sin(πn/2±α), cos(πn/2±α), tg(πn/2±α), ctg(πn/2±α). Запоминаем, что +α дает движение против часовой стрелки, — α — движение по часовой стрелке.
Для работы с формулами приведения нужны два пункта:
1) ставим знак, который имеет начальная функция (в учебниках пишут: приводимая. Но, чтобы не запутаться, лучше назвать ее начальной), если считать α углом I четверти, то есть маленьким.
2) Горизонтальный диаметр — π±α, 2π±α, 3π±α… — в общем, когда нет дроби — название функции не меняет. Вертикальный π/2±α, 3π/2±α, 5π/2±α…- когда дробь есть — название функции меняет: синус — на косинус, косинус — на синус, тангенс — на котангенс и котангенс — на тангенс.
Теперь, собственно, ассоциация:
вертикальный диаметр (есть дробь) —
пьяный стоит. Что с ним случится рано
или поздно? Правильно, упадет.
Название функции изменится.
Если же диаметр горизонтальный — пьяный уже лежит. Спит, наверное. С ним уже ничего не случится, он уже принял горизонтальное положение. Соответственно, название функции не меняется.
То есть sin(π/2±α), sin(3π/2±α), sin(5π/2±α) и т.д. дают ±cosα,
а sin(π±α), sin(2π±α), sin(3π±α), … — ±sinα.
Как , уже знаем.
Как это работает? Смотрим на примерах.
1) cos(π/2+α)=?
Становимся на π/2. Поскольку +α — значит, идем вперед, против часовой стрелки. Попадаем во II четверть, где косинус имеет знак «-«. Название функции меняется («пьяный стоит», значит — упадет). Итак,
cos(π/2+α)=-sin α.
Становимся на 2π. Так как -α — идем назад, то есть по часовой стрелке. Попадаем в IV четверть, где тангенс имеет знак «-«. Название функции не меняется (диаметр горизонтальный, «пьяный уже лежит»). Таким образом, tg(2π-α)=- tgα.
3) ctg²(3π/2-α)=?
Примеры, в которых функция возводится в четную степень, решаются еще проще. Четная степень «-» убирает, то есть надо только выяснить, меняется название функции или остается. Диаметр вертикальный (есть дробь, «пьяный стоит», упадет), название функции меняется. Получаем: ctg²(3π/2-α)= tg²α.
Четная степень «-» убирает, то есть надо только выяснить, меняется название функции или остается. Диаметр вертикальный (есть дробь, «пьяный стоит», упадет), название функции меняется. Получаем: ctg²(3π/2-α)= tg²α.
И еще одна задача B11 на ту же тему — из реального ЕГЭ по математике.
Задача. Найдите значение выражения:
В этом коротком видеоуроке мы узнаем, как применять формулы приведения для решения реальных задач B11 из ЕГЭ по математике. Как вы видите, перед нами — два тригонометрических выражения, каждое из которых содержит синусы и косинусы, а также довольно зверские числовые аргументы.
Прежде чем решать эти задачи, давайте вспомним, что такое формулы приведения. Итак, если у нас есть выражения вида:
То мы можем избавиться от первого слагаемого (вида k
· π/2) по специальным правилам. Начертим тригонометрическую окружность, отметим на ней основные точки: 0, π/2; π; 3π/2 и 2π. Затем смотрим на первое слагаемое под знаком тригонометрической функции.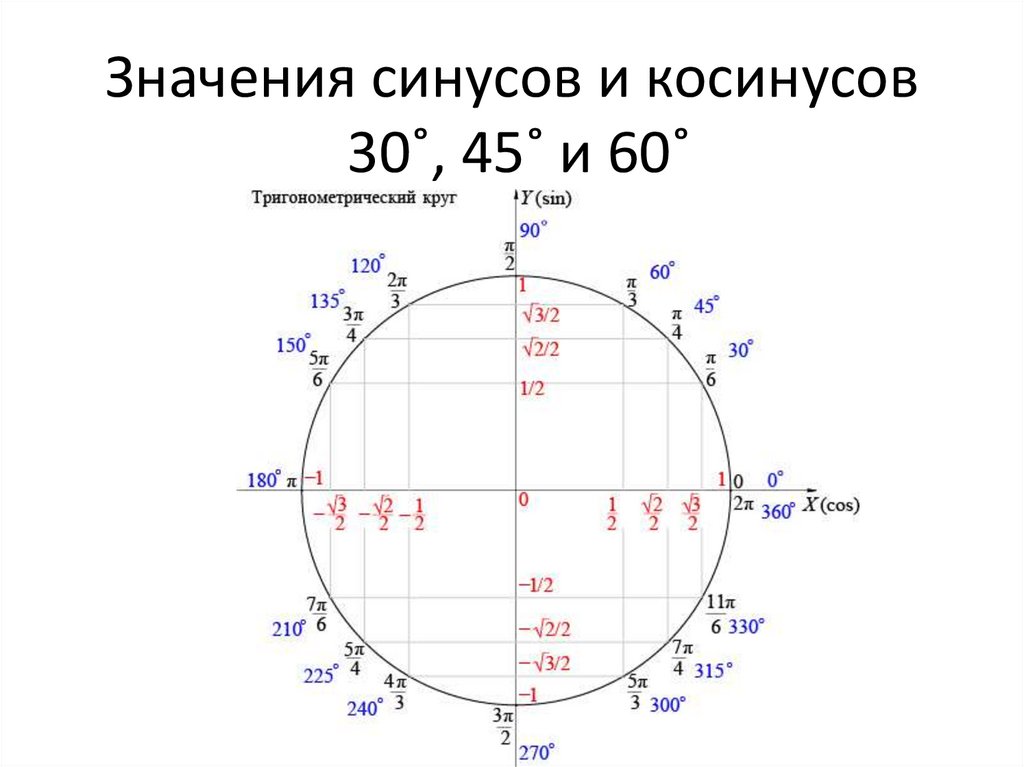 Имеем:
Имеем:
- Если интересующее нас слагаемое лежит на вертикальной оси тригонометрического круга (например: 3π/2; π/2 и т.д.), то исходная функция заменяется на ко-функцию: синус заменяется косинусом, а косинус — наоборот, синусом.
- Если же наше слагаемое лежит на горизонтальной оси, то исходная функция не меняется. Просто убираем первое слагаемое в выражении — и все.
Таким образом, мы получим тригонометрическую функцию, не содержащую слагаемых вида k · π/2. Однако на этом работа с формулами приведения не заканчивается. Дело в том, что перед нашей новой функцией, полученной после «отбрасывания» первого слагаемого, может стоять знак плюс или минус. Как определить этот знак? Вот сейчас и узнаем.
Представим, что угол α, оставшийся внутри тригонометрической функции после преобразований, имеет очень малую градусную меру. Но что значит «малая мера»? Допустим, α ∈ (0; 30°) — этого вполне достаточно. Рассмотрим для примера функцию:
Тогда, следуя нашим предположениям, что α ∈ (0; 30°), заключаем, что угол 3π/2 − α лежит в третьей координатной четверти, т. е. 3π/2 − α ∈ (π; 3π/2). Вспоминаем знак исходной функции, т.е. y
= sin x
на этом интервале. Очевидно, что синус в третьей координатной четверти отрицателен, поскольку по определению синус — это ордината конца подвижного радиуса (короче синус — это координата y
). Ну, а координата y
в нижней полуплоскости всегда принимает отрицательные значения. Значит, и в третьей четверти y
тоже отрицателен.
е. 3π/2 − α ∈ (π; 3π/2). Вспоминаем знак исходной функции, т.е. y
= sin x
на этом интервале. Очевидно, что синус в третьей координатной четверти отрицателен, поскольку по определению синус — это ордината конца подвижного радиуса (короче синус — это координата y
). Ну, а координата y
в нижней полуплоскости всегда принимает отрицательные значения. Значит, и в третьей четверти y
тоже отрицателен.
На основании этих размышлений мы можем записать окончательное выражение:
Задача B11 — 1 вариант
Вот эти же самые приемы вполне подходят для решения задачи B11 из ЕГЭ по математике. Разница лишь в том, что во многих реальных задачах B11 вместо радианной меры (т.е. чисел π, π/2, 2π и т.д.) используется градусная мера (т.е. 90°, 180°, 270° и т.д.). Давайте посмотрим на первую задачу:
Сначала разберемся с числителем. cos 41° — это нетабличное значение, поэтому мы ничего не можем сделать с ним. Пока так и оставим.
Теперь смотрим на знаменатель:
sin 131° = sin (90° + 41°) = cos 41°
Очевидно, что перед нами формула приведения, поэтому синус заменился на косинус. Кроме того, угол 41° лежит на отрезке (0°; 90°), т.е. в первой координатной четверти — именно так, как требуется для применения формул приведения. Но тогда 90° + 41° — это вторая координатная четверть. Исходная функция y
= sin x
там положительна, поэтому мы и поставили перед косинусом на последнем шаге знак «плюс» (другими словами не поставили ничего).
Кроме того, угол 41° лежит на отрезке (0°; 90°), т.е. в первой координатной четверти — именно так, как требуется для применения формул приведения. Но тогда 90° + 41° — это вторая координатная четверть. Исходная функция y
= sin x
там положительна, поэтому мы и поставили перед косинусом на последнем шаге знак «плюс» (другими словами не поставили ничего).
Осталось разобраться с последним элементом:
cos 240° = cos (180° + 60°) = −cos 60° = −0,5
Здесь мы видим, что 180° — это горизонтальная ось. Следовательно, сама функция не поменяется: был косинус — и останется тоже косинус. Но вновь возникает вопрос: плюс или минус будет стоять перед полученным выражением cos 60°? Заметим, что 180° — это третья координатная четверть. Косинус там отрицательный, следовательно, перед косинусом в итоге будет стоять знак «минус». Итого, получаем конструкцию −cos 60° = −0,5 — это табличное значение, поэтому все легко считается.
Теперь подставляем полученные числа в исходную формулу и получаем:
Как видим, число cos 41° в числителе и знаменателе дроби легко сокращается, и остается обычное выражение, которое равно −10.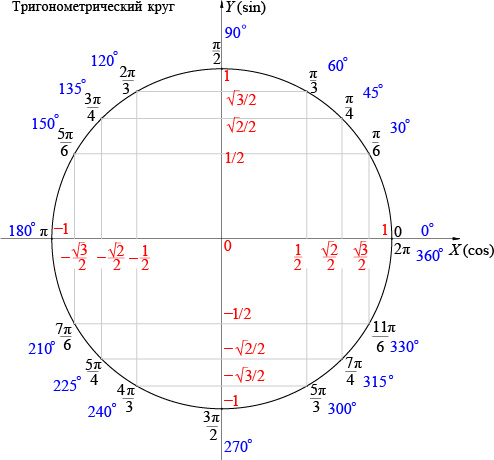 При этом минус можно либо вынести и поставить перед знаком дроби, либо «держать» рядом со вторым множителем до самого последнего шага вычислений. Ответ в любом случае получится −10. Все, задача B11 решена!
При этом минус можно либо вынести и поставить перед знаком дроби, либо «держать» рядом со вторым множителем до самого последнего шага вычислений. Ответ в любом случае получится −10. Все, задача B11 решена!
Задача B14 — 2 вариант
Переходим ко второй задаче. Перед нами снова дробь:
Ну, 27° у нас лежит в первой координатной четверти, поэтому здесь ничего менять не будем. А вот sin 117° надо расписать (пока без всякого квадрата):
sin 117° = sin (90° + 27°) = cos 27°
Очевидно, перед нами снова формула приведения
Возвращаемся к исходному выражению, которое требуется вычислить:
Как видим, в знаменателе после преобразований возникло основное тригонометрическое тождество: sin 2 27° + cos 2 27° = 1. Итого −4: 1 = −4 — вот мы и нашли ответ ко второй задаче B11.
Итого −4: 1 = −4 — вот мы и нашли ответ ко второй задаче B11.
Как видите, с помощью формул приведения такие задачи из ЕГЭ по математике решаются буквально в пару строчек. Никаких синусов суммы и косинусов разности. Все, что нам нужно помнить — это только тригонометрический круг.
Они относятся к разделу «тригонометрия» в математике. Суть их заключается в приведении тригонометрических функций углов к более «простому» виду. О важности их знания написать можно много. Этих формул аж 32 штуки!
Не пугайтесь, учить их не надо, как и многие другие формулы в курсе математики. Лишней информацией голову забивать не нужно, необходимо запоминать «ключики» или законы, и вспомнить или вывести нужную формулу проблемой не будет. Кстати, когда я пишу в статьях «… нужно выучить!!!» – это значит, что действительно, это необходимо именно выучить.
Если вы с формулами приведения не знакомы, то простота их вывода вас приятно удивит – есть «закон», при помощи которого это легко сделать. И любую из 32 формул вы напишите за 5 секунд.
И любую из 32 формул вы напишите за 5 секунд.
Перечислю лишь некоторые задачи, которые будут на ЕГЭ по математике, где без знания этих формул есть большая вероятность потерпеть фиаско в решении. Например:
– задачи на решение прямоугольного треугольника, где речь идёт о внешнем угле, да и задачах на внутренние углы некоторые из этих формул тоже необходимы.
– задачи на вычисление значений тригонометрических выражений; преобразования числовых тригонометрических выражений; преобразования буквенных тригонометрических выражений.
– задачи на касательную и геометрический смысл касательной, требуется формула приведения для тангенса, а также другие задачи.
– стереометрические задачи, по ходу решения не редко требуется определить синус или косинус угла, который лежит в пределах от 90 до 180 градусов.
И это лишь те моменты, которые касаются ЕГЭ. А в самом курсе алгебры есть множество задач, при решении которых, без знания формул приведения просто не обойтись.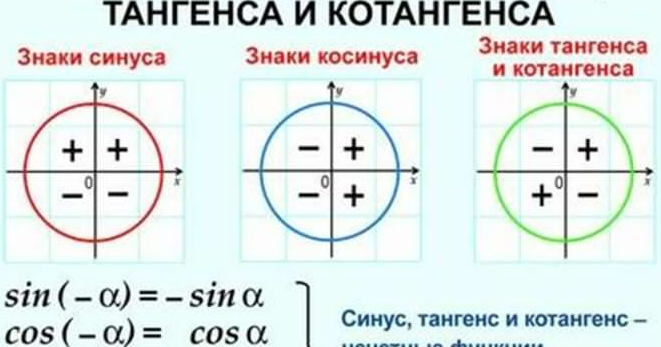
Так что же к чему приводится и как оговоренные формулы упрощают для нас решение задач?
Например, вам нужно определить синус, косинус, тангенс или котангенс любого угла от 0 до 450 градусов:
угол альфа лежит пределах от 0 до 90 градусов
* * *
Итак, необходимо уяснить «закон», который здесь работает:
1. Определите знак функции в соответствующей четверти.
Напомню их:
2. Запомните следующее:
функция изменяется на кофункцию
функция на кофункцию не изменяется
Что означает понятие — функция изменяется на кофункцию?
Ответ: синус меняется на косинус или наоборот, тангенс на котангенс или наоборот.
Вот и всё!
Теперь по представленному закону запишем несколько формул приведения самостоятельно:
Данный угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Функцию на кофункцию не меняем, так как у нас 180 градусов, значит:
Угол лежит в первой четверти, синус в первой четверти положителен. Не меняем функцию на кофункцию, так как у нас 360 градусов, значит:
Не меняем функцию на кофункцию, так как у нас 360 градусов, значит:
Вот вам ещё дополнительное подтверждение того, что синусы смежных углов равны:
Угол лежит во второй четверти, синус во второй четверти положителен. Не меняем функцию на кофункцию, так как у нас 180 градусов, значит:
Проработайте мысленно или письменно каждую формулу, и вы убедитесь, что ничего сложного нет.
***
В статье на решение был отмечен такой факт – синус одного острого угла в прямоугольном треугольнике равен косинусу другого острого угла в нём.
Формула половинного угла — Тригонометрические формулы половинного угла и примеры решения
Иногда очень важно определить значение тригонометрических функций для половинных углов. Например, используя некоторую формулу половинного угла, мы можем преобразовать выражение с показателями степени в выражение без показателей степени, и углы которого кратны исходному углу. Следует отметить, что мы получаем формулы половинного угла из формул двойного угла. И sin (2A), и cos (2A) получаются из формулы двойного угла для косинуса.
И sin (2A), и cos (2A) получаются из формулы двойного угла для косинуса.
Формула тождеств половинного угла следующая:
\[\text{Синус половинного угла} : sin(\frac{a}{2}) = \pm \sqrt{\frac{( 1 — cos a)}{2}}\]
\[\text{Косинус половины угла}: cos(\frac{a}{2}) = \pm \sqrt{\frac{(1 +cosa)}{2}}\]
\[\text{Тангенс половинного угла}: tan(\frac{a}{2}) = \frac{1 — cosa}{sina} = \ frac{sina}{1+cosa}\]
Формула половины угла
Вот математическое представление тригонометрических формул половины угла:
\[sin(\frac{\theta}{2}) = \pm \sqrt{\frac{1 — cos(\theta)}{2}}\] \[ cos(\frac{\theta}{2}) = \pm \sqrt{\frac{1 + cos(\theta)}{2}}\] \[tan(\frac{\theta}{2} ) = \frac{sin(\theta)}{1 + cos(\theta)} = \frac{1 — cos(\theta)}{sin(\theta)}\] |
Двойной угол и тождества половинного угла
Некоторые случаи формул сумм и разностей для синуса и косинуса порождают так называемые тождества двойного угла и тождества половинного угла.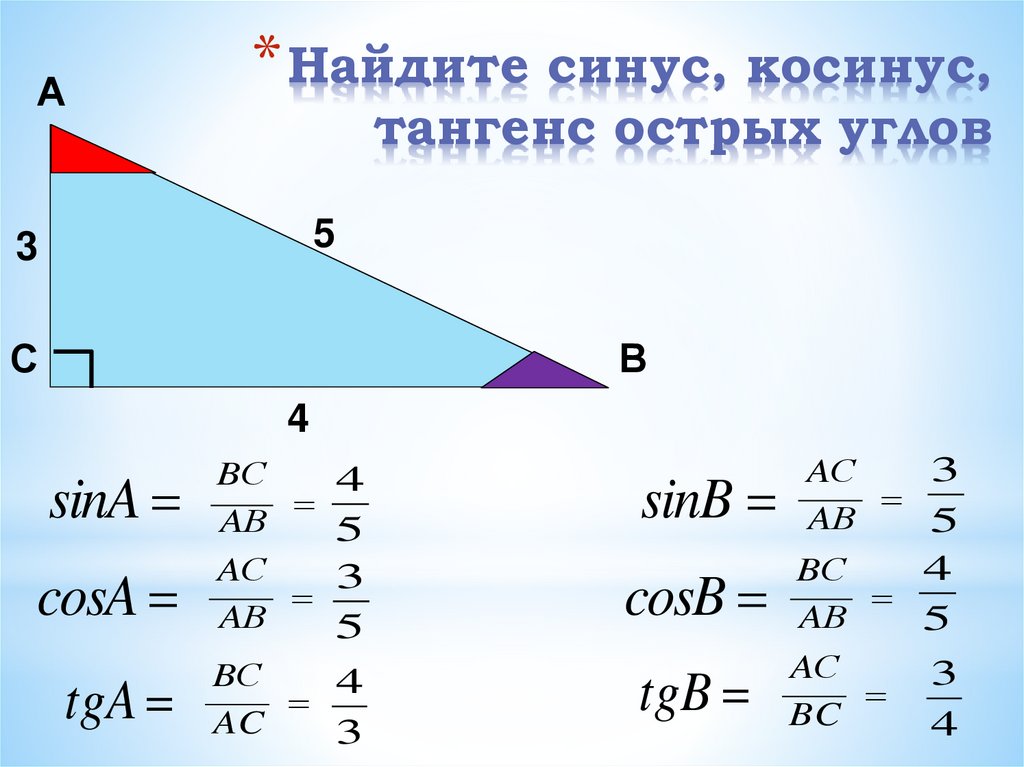 Сначала мы начнем с включения тождества суммы для синуса, как указано в справочнике, докажем, что
Сначала мы начнем с включения тождества суммы для синуса, как указано в справочнике, докажем, что
\[\begin{vmatrix} sin \alpha & sin \beta & sin \gamma \\cos \alpha & cos \beta & cos\gamma \\sin 2 \alpha & sin 2 \beta & sin 2 \gamma \ end{vmatrix}\]
Таким же образом, для косинуса cos 2 α – sin 2 α)
Применяя свойство Пифагора sin 2α + cos 2α =1, мы можем получить два дополнительных тождества косинуса, т.е.
COS 2α = COS 2 α- SIN 2 α
COS 2α = [1- SIN 2 α]- SIN 2 α
COS 2α = 1-2 SIN 2 α
COS 2α = COS 2 α — SIN 2 α
COS 2α = COS 2 α — [1 — COS 2 α]
COS 2α = 2COS 2 α — 1
the = 2COS 2 α — 1
the. тождества половинного угла для синуса и косинуса получены из двух тождеств косинуса, объясненных выше.
Cos 2α = 2cos 9{2} (A) = \ frac {\ frac {(1-cos (2A))} {2}}{\ frac {(1 + cos (2A))} {2}} = \ frac { 1-cos (2A)}{1 +cos(2A)}\]
Снова заменив A на (1/2)A, получим
\[tan = [\frac{A}{2}] = \pm \sqrt {\frac{1 — cosA}{1 + cosA}}\]
Тригонометрические углы и их обозначения
На самом деле это использование греческих букв, таких как альфа (α), бета (β), тета (θ) и гамма (γ) для обозначения углов. Он представляет знаки тригонометрических функций в каждом квадранте. Широко используются несколько различных единиц измерения угла, включая градусы, радианы и градианы (гоны): например,
1 полный круг (поворот) = 360° = 2π радиан = 400 гон.
Несмотря на то, что это специально не аннотировано (°) для градусов или (g) для градианов, предполагается, что все значения углов даны в радианах.
Графическое представление, показанное ниже, изображает некоторые распространенные углы и их значения, а также преобразование основных тригонометрических функций:
(Изображение будет загружено в ближайшее время)
Решенные примеры
Пример 1: Найдите абсолютное значение для косинуса 165°, используя полуугловые тождества. 9{\circ}}{2}}\]
9{\circ}}{2}}\]
= \[\pm \sqrt{\frac{1 — 0,866}{2}}\] …
= \[0,2588\]
Таким образом, наша ответ: sin 15° = 0,2588
Помните, здесь берется положительное значение, поскольку 15° находится в 1-м квадранте.
Ключевые факты
В задачах с формулой половинного угла для синуса и косинуса обратите внимание, что знак плюс/минус стоит перед каждым квадратным корнем (коренным).
Положительный или отрицательный ответ зависит от того, в каком квадранте находится новый полуугол.
Формула тангенса половины угла не имеет знака ± перед, поэтому вышеприведенное не относится к касательным.
Заключение
Статья очень полезна учащимся для понимания концепции формул половинного угла.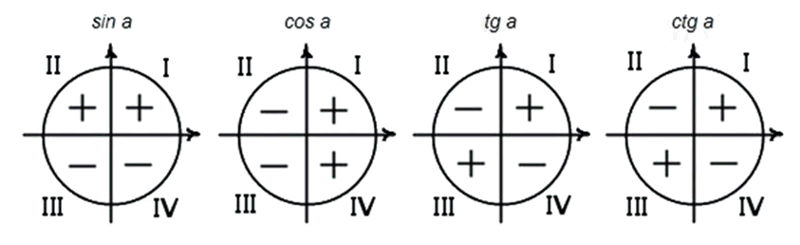 Предоставляются все важные формулы половинного угла и их преобразование. Решенные примеры помогут учащимся применять формулу половинного угла в задачах.
Предоставляются все важные формулы половинного угла и их преобразование. Решенные примеры помогут учащимся применять формулу половинного угла в задачах.
Формула касательного половинного угла Видео | Shmoop
Комарам нужен кофеин, как и всем нам. Не думал бы, что весь день суетиться и жалить людей, ваша энергия ?
имеет только деньги Триг Спрингс. В Half Angle-os все деньги конвертируются с использованием
следующей формулы: Тангенс u над 2 равен единице минус косинус
u над синусом u. Как Видо преобразует свои деньги в правильную сумму
для столь необходимого ему кофе? Прежде всего, мы видим, что тангенс числа пи
более 8 можно переписать как ? умножить на 4.
Если мы сделаем это, то сможем избавиться от знаменателя 2 в нашей формуле.
Тогда, если мы подставим тангенс числа пи на 4 in вместо u, мы получим следующее: больше 4.
Так как косинус числа пи больше 4 равен квадратному корню из 2 больше 2, а синус числа пи больше
4 равно квадратному корню из 2 из 2 É Наша формула принимает следующий вид:
1 минус квадратный корень из 2 из 2 из 2 из 90 2 из 2 из 2 из 2.
Слишком большое количество терминов только приносит проблемы… Во-первых, чтобы упростить числитель, мы можем подвести оба термина к одному общему знаменателю. Давайте сделаем это, умножив 1 на 2 на 2,
чтобы получить 2 на 2 минус корень 2 на 2. Мы вычитаем дроби, вычитая через
числитель дробей и сохраняя знаменатель одинаковым, поэтому мы получаем 2 минус
корень 2 над 2 сверху большей дроби. Мы ненавидим дроби в знаменателе, поэтому давайте
умножим числитель, 2 минус корень 2 из 2É на обратную величину знаменателя до
избавиться от него.

