Синус, косинус и тангенс острого угла прямоугольного треугольника
Синус, косинус и тангенс острого угла прямоугольного треугольника
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 🙂
Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается . Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .
Угол обозначается соответствующей греческой буквой .
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Катет , лежащий напротив угла , называется противолежащим (по отношению к углу ). Другой катет , который лежит на одной из сторон угла , называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.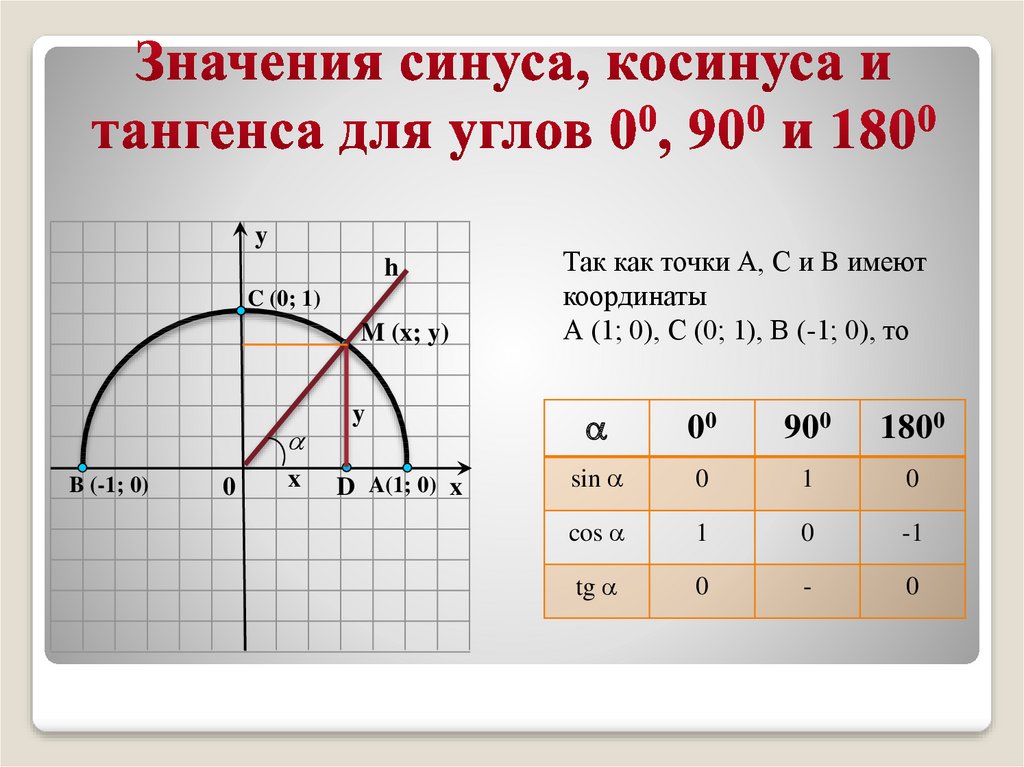
Давайте докажем некоторые из них.
- Сумма углов любого треугольника равна . Значит, сумма двух острых углов прямоугольного треугольника равнa .
- С одной стороны, как отношение противолежащего катета к гипотенузе. С другой стороны, , поскольку для угла катет а будет прилежащим.Получаем, что . Иными словами, .
- Возьмем теорему Пифагора: . Поделим обе части на : Мы получили основное тригонометрическое тождество.
- Поделив обе части основного тригонометрического тождества на , получим: Это значит, что если нам дан тангенс острого угла , то мы сразу можем найти его косинус. Аналогично,
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Мы знаем, что сумма углов любого треугольника равна .
Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до .
| 0 | |||||
| 0 | |||||
| 0 | |||||
| 0 | − | ||||
| − | 0 |
Обратите внимание на два красных прочерка в таблице.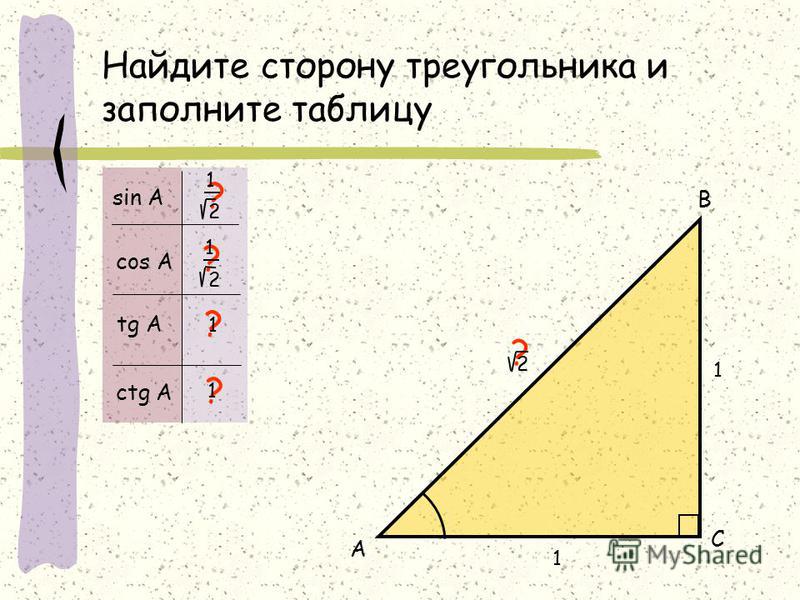 При соответствующих значениях углов тангенс и котангенс не существуют.
При соответствующих значениях углов тангенс и котангенс не существуют.
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
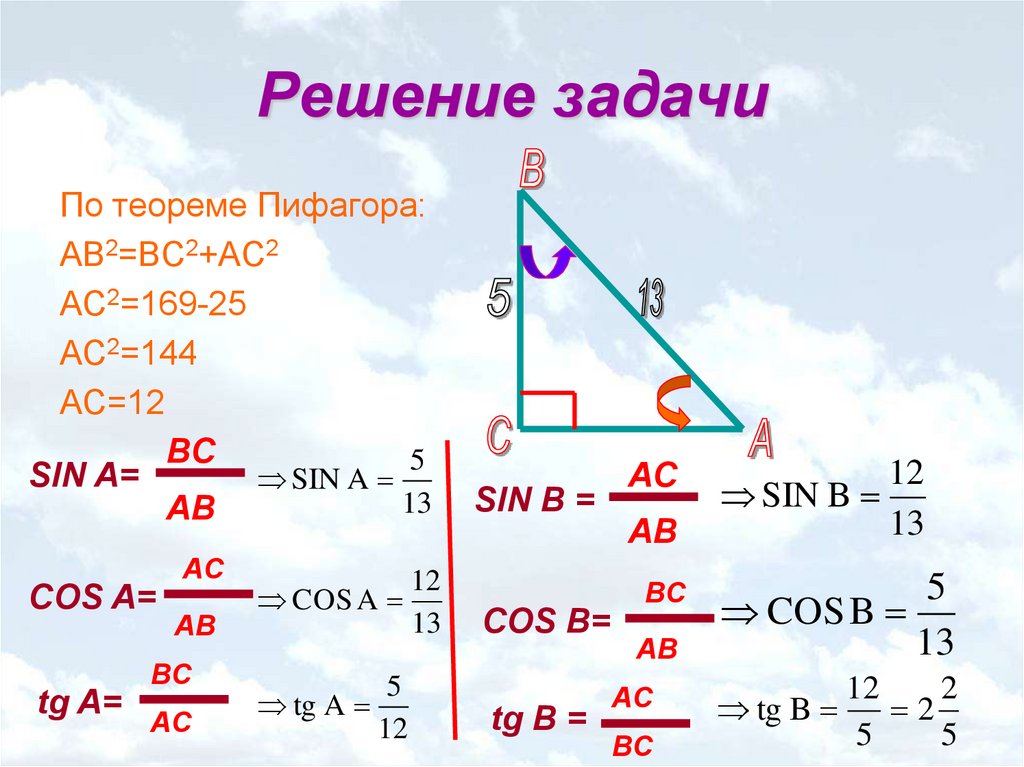
1. В треугольнике угол равен , . Найдите .
Задача решается за четыре секунды.
Поскольку , .
2. В треугольнике угол равен , , . Найдите .
Имеем:
Отсюда
Найдем по теореме Пифагора.
Задача решена.
Часто в задачах встречаются треугольники с углами и или с углами и . Основные соотношения для них запоминайте наизусть!
Для треугольника с углами и катет, лежащий напротив угла в , равен половине гипотенузы.Треугольник с углами и — равнобедренный. В нем гипотенуза в раз больше катета.
План урока»Синус,косинус,тангенс острого угла в прямоугольном треугольнике»
Урок математики в 8 классе по теме: «Синус, косинус и тангенс острого угла прямоугольного треугольника»
Учитель математики Чиндарева Наталия Николаевна
Цели урока:
Образовательные:
Закрепить понятия синуса, косинуса и тангенса
острого угла прямоугольного треугольника; формулу тангенса угла как отношения
синуса к косинусу этого угла и основное тригонометрическое тождество.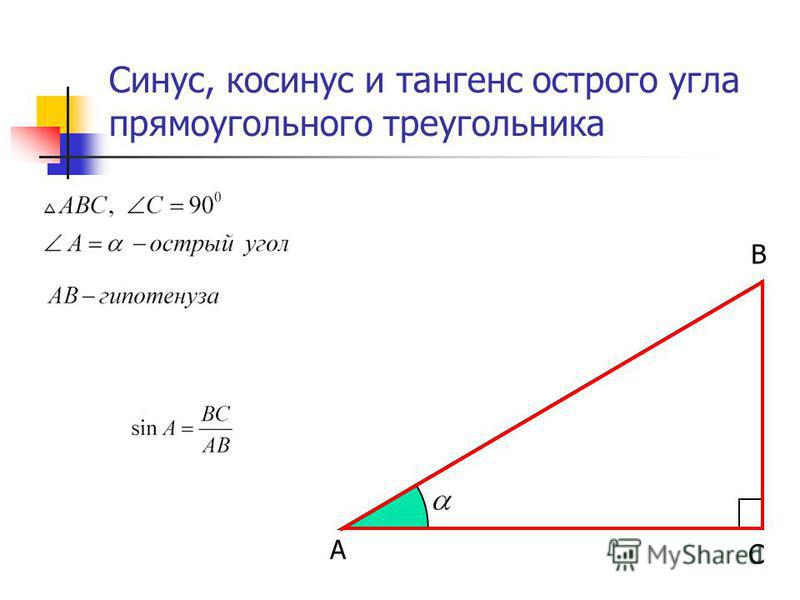
Развивающие:
развивать способности к самостоятельному планированию и организации работы; навыки коррекции собственной деятельности через применение информационных технологий; умение обобщать, абстрагировать и конкретизировать знания.
Воспитательные:
воспитывать познавательный интерес к математике, информационную культуру и культуру общения, самостоятельность, способность к коллективной работе.
Оборудование: презентация по теме (Приложение1), цветной мел, раздаточный справочный материал, лист с задачами из открытого Банка заданий ФИПИ.
Тип урока: урок обобщения и систематизации знаний
Методы: проблемно-поисковый, индуктивный, метод групповой работы, самостоятельной работы.
Ход урока:
I. Организационный момент:
Здравствуйте, ребята. Я очень рада видеть
вас, меня зовут Наталия Николаевна, сегодня я буду вести у вас урок геометрии.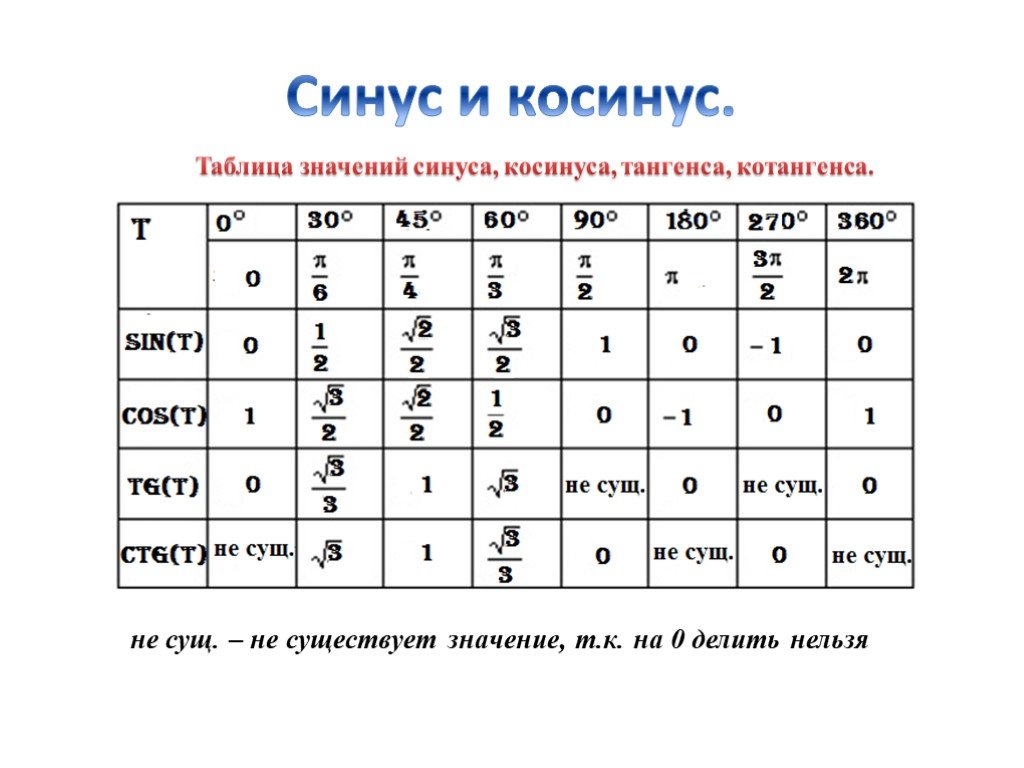 По мнению итальянского физика, механика, астронома, философа и математика
Галилео Галилея: «Геометрия является самым могущественным средством для
изощрения наших умственных способностей и дает нам возможность правильно
мыслить и рассуждать» (Слайд1)
По мнению итальянского физика, механика, астронома, философа и математика
Галилео Галилея: «Геометрия является самым могущественным средством для
изощрения наших умственных способностей и дает нам возможность правильно
мыслить и рассуждать» (Слайд1)
Один мудрец сказал: «Высшее проявление духа – разум, высшее проявление разума – геометрия. Клетка геометрии – это треугольник, он так же неисчерпаем, как и Вселенная» (Слайд2)
Сегодня мы продолжим с вами беседу о прямоугольном треугольнике.
II. Повторение ранее изученного: Для проверки основных знаний по прямоугольному треугольнику проведём математический диктант.
Математический диктант: (Слайды 3- 8)
1.Закончи предложение: «Треугольник, у которого один угол прямой
называется…»
А) остроугольный; Б) равнобедренный; В) равносторонний; Г) прямоугольный
2. Отметь прямоугольный треугольник:
А) Б) В) Г)
3. Как называются стороны в прямоугольном
треугольнике?
Как называются стороны в прямоугольном
треугольнике?
А) боковые стороны
Б) основания
В) катеты и гипотенуза
Г) параллельные стороны
4. Один из острых углов прямоугольного треугольника равен 30°, чему равен другой острый угол?
А) 90°; Б) 60°; В) 30°; С) 180° .
5. Выберите формулу площади прямоугольного треугольника:
А) S = a·b; Б) S = a·h; B) S = a·b·sin α; Г) S =√p(p-a)(p-b)(p-c)
6. Катет прямоугольного треугольника, лежащий напротив угла в 30°, равен 15см. Чему равна гипотенуза?
А) 15см; Б) 7,5см; В) 20см; Г) 30см
Ответы: (Слайд 9)
1 | 2 | 3 | 4 | 5 | 6 |
Г | Б | В | Б | А | Г |
(Слайд10)
Оценка «5» — все
верные ответы.
Оценка «4» — 5 верных ответов.
Оценка «3» — 4 верных
ответа.
«Надо ещё повторить» — менее 4 верных ответов.
III. Повторение по теме: «Синус, косинус и тангенс острого угла прямоугольного треугольника» Откройте тетради и запишите число и тему урока.
Цель нашего урока: (Слайд 11)
Наверное, многие из вас задавались вопросом: Почему в геометрии особое внимание уделяется прямоугольному треугольнику, хотя не часто встречаются предметы подобной формы? (Слайд12)
Ответ на этот вопрос
очень прост: Как в химии изучают вначале элементы, а затем – их соединения, в
биологии – одноклеточные, а потом – многоклеточные организмы, так и в геометрии
сначала изучают точки, отрезки и треугольники, из которых состоят другие
геометрические фигуры.
Повторение изученных компетенций и способов действий:
1. Понятия катетов, прилежащих и противолежащих к углу. (Слайд 13)
2. Понятия синуса, косинуса, тангенса острого угла прямоугольного треугольника, их обозначения. (Слайды 14-17)
3. Основного тригонометрического равенства
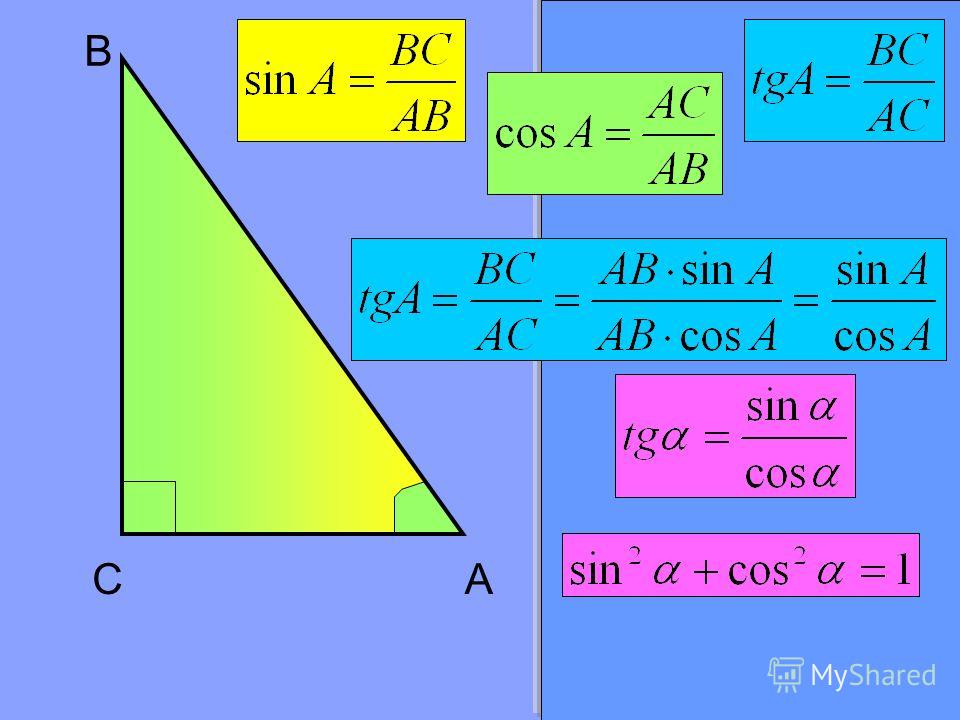
Пусть АВС – прямоугольный треугольник с прямым углом С и острым углом при вершине А, равным .
В
С А
АВ – гипотенуза
ВС — катет
АС — катет
Синусом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.
Косинусом острого угла в прямоугольном
треугольнике называется отношение прилежащего катета к гипотенузе.
Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.
Котангенсом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему.
Эти правила позволяют, зная одну из сторон прямоугольного треугольника и острый угол, находить две другие стороны; зная две стороны, находить острые углы. (Слайд 18)
a = c sin α a = b tg α
b = c cos α b = a ctg α (Слайд 19)
Основное тригонометрическое тождество. (Слайд 20)
sin2A + cos2A = 1
Используя формулы синуса и косинуса получаем
sin2A + cos2A =
по теореме Пифагора BC2 + AC2 = AB2, отсюда следует sin2A + cos2A = 1
Применяя основное тригонометрическое тождество
и формулы синуса, косинуса и тангенса можно вычислить значения синуса,
косинуса и тангенса для углов 300, 450, 600. (Слайд 21)
(Слайд 21)
На доске:
Ребята, кажется очень много формул, но этого не нужно страшиться, ведь зная определение синуса, косинуса и тангенса острого угла прямоугольного треугольника, вы всегда сможете вывести все остальные формулы.
Дело в том, что я не раз наблюдала, как учащиеся с трудом вспоминают данные определения. Они прекрасно помнят, что катет относится к гипотенузе, а вот какой из них — забывают и путают. Цена ошибки, как вы знаете на экзамене – это потерянный балл.
IV. Решение задач (устно): 1) (Слайд 25)
Дан прямоугольный треугольник с прямым углом А, найдите синусы, косинусы, тангенсы углов В и С, если известно, что его катеты равны 3 и 4.
Все ли данные у нас есть для решения задачи?
То есть неизвестна гипотенуза, как нам ее найти?
2) Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
| 4) На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный
треугольник. |
3) Найдите тангенс угла АОВ, изображённого на рисунке.
| 5) Два острых угла прямоугольного треугольника относятся как 4:5. Найдите больший острый угол. Ответ дайте в градусах. |
Таким образом, мы с вами приоткрыли дверь нового для вас раздела математики — тригонометрии — науки, изучающей связи между сторонами и углами в треугольнике. Истоки тригонометрии уходят в далекую древность, когда у людей возникла потребность следить за небесными светилами и по этим наблюдениям вести календарь, рассчитывали сроки сева, время разлива рек; ориентировались в пути по звездам.
V.Физминутка (Слайды 22-24)
VI. Решение задач:
1. В треугольнике ABC угол C равен 90°, BC=4, sinA=0,8. Найдите AB.
2. В
треугольнике ABC угол C равен 90°, BC=2, cosB=0,4.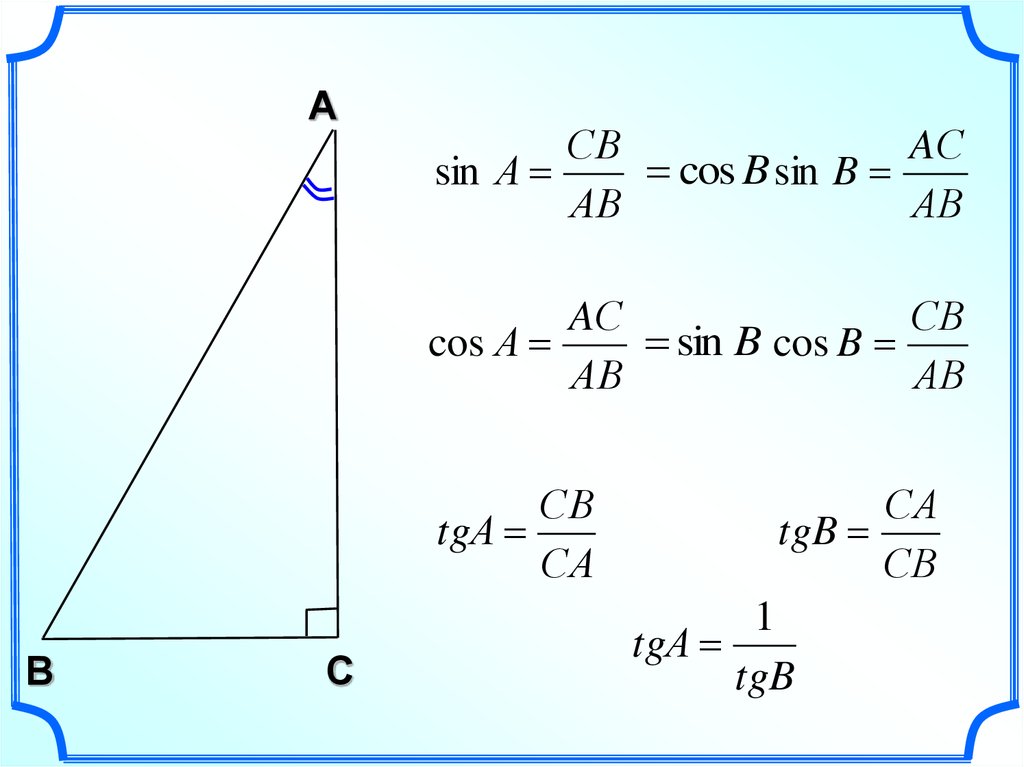 Найдите AB.
Найдите AB.
3. В треугольнике ABC угол C равен 90°, AC=8, tg A=0,75. Найдите AB.
4. В остроугольном треугольнике ABC высота AH равна 36, а сторона AB равна 45. Найдите cos B.
5. Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Разминка. Какое из следующих утверждений верно?
1) Тангенс любого острого угла меньше единицы.
2) Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
3) Сумма острых углов прямоугольного треугольника равна 90 градусам.
4) Один из углов треугольника всегда не превышает 60 градусов.
5) В прямоугольном треугольнике гипотенуза равна сумме катетов.
6) Сумма углов любого треугольника равна 180° .
Задачи повышенной трудности:
Найдите тангенс угла AOB.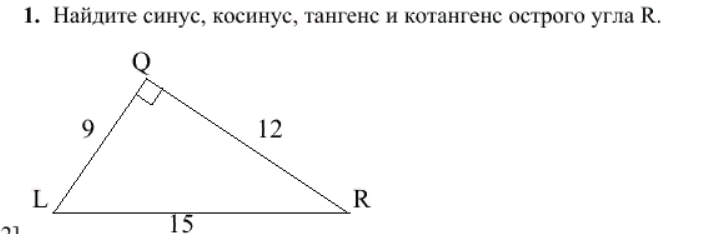
VII. Задания на дом:
1) Найдите тангенс угла AOB, изображённого на рисунке.
2) Катеты прямоугольного треугольника равны 8 и 6. Найдите синус наименьшего угла этого треугольника.
3) В треугольнике ABC угол C равен 90°, AC=10, tg A=0,1. Найдите BC.
4) В треугольнике ABC известно, что AB=BC, а высота AH делит сторону BC на отрезки BH=64 и CH=16. Найдите cos B.
5) Сторона ромба равна 30, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
6) Найдите тангенс угла AOB.
Решение прикладной задачи:
1.Найти высоту дерева, если расстояние от наблюдателя до ствола дерева равно 9 м, а угол, под которым он видит макушку дерева, равен 300. (Слайд 26)
VIII. Рефлексия: (Слайд 30)
Рефлексия: (Слайд 30)
Сегодня на уроке
Я узнал …
Я научился …
Мне понравилось …
Я затруднялся …
Моё настроение …
Информационные материалы.
- Пифагор. Занимательная математика. Халамайзер А.Я. Москва
- Живая математика. Перельман Я. И. Москва «Наука» 1978 г.
- Большая энциклопедия Кирилла и Мефодия, 8 CD-ROM, 2002 г.
- Электронные ресурсы сайта «Сеть творческих учителей»
- Электронные ресурсы сайта «Фестиваль педагогических идей «Открытый урок»
- Учебно-методическое пособие. Взаимосвязь теории с практикой в процессе изучения математики. Возняк Г.М., Маланюк М.П. Киев. «Радянська школа»
Вычисление синуса и косинуса под особыми острыми углами — Понятие
Если вы хотите невероятно облегчить свою математическую жизнь, запомните значения синуса и косинуса для пи/3, пи/4 и пи/6, а также 0, пи /2 и пи. Эти значения постоянно появляются в задачах и доказательствах по тригонометрии и до исчисления. При вычислении синуса также полезно запомнить преобразование радианов в градусы для этих значений; например, чтобы помнить, что pi/6 эквивалентно 30.
Эти значения постоянно появляются в задачах и доказательствах по тригонометрии и до исчисления. При вычислении синуса также полезно запомнить преобразование радианов в градусы для этих значений; например, чтобы помнить, что pi/6 эквивалентно 30.
синус косинус определение единичного круга синуса и косинуса углы в стандартном положении
Я хочу поговорить об очень важном определении синуса и косинуса. Теперь вы, возможно, помните из геометрии определение синуса и косинуса прямоугольного треугольника, которое начинается с прямоугольного треугольника, и мы обозначим 3 стороны x, y и z, острый угол здесь — тета, а это прямой угол. Мы определили косинус теты как сторону, примыкающую к тете, деленную на гипотенузу. И под соседним мы подразумеваем сторону, которая находится рядом с тета, это гипотенуза, длинная сторона прямоугольного треугольника, и поэтому это означает, что x больше z. Синус определяется как сторона, противоположная тете y относительно гипотенузы, поэтому y больше z.
Синус определяется как сторона, противоположная тете y относительно гипотенузы, поэтому y больше z.
Проблема с этим определением в том, что оно работает только для острых углов. Это означает, что тета должна быть между 0 и 90 градусами вправо, иначе этот треугольник не будет иметь смысла, поэтому одна из вещей, которую мы делаем в предварительном исчислении, — расширяем это определение, чтобы оно включало все углы. Хорошо, вот как выглядит угол в стандартном положении. В стандартном положении вы рисуете угол так, чтобы его вершина находилась в начале координат на плоскости координат. Это начальная сторона, это конечная сторона, и вы можете думать об угле как о вращении, как если бы конечная сторона начиналась здесь и вращалась на угол тета, заканчивающийся здесь.
Теперь прибавьте к этому углу в стандартном положении единичную окружность, окружность с радиусом 1 x в квадрате плюс у в квадрате равно 1, здесь это окружность. Теперь, чтобы сориентироваться, когда у вас есть радиус окружности 1, он пройдет через точку 1, 0 пройдет через точку 0, 1 минус 1, 0 и 0 минус 1. Тот же угол, который мы хотим отметить точка, в которой крайняя сторона пересекает единичную окружность. Эта точка будет иметь координаты x, y, мы определяем косинус как значение x и синус как значение y. Эта точка, конечно, будет уникальной, она будет однозначно зависеть от тета угла, поэтому для разных тета углов вы получите разные значения синуса и косинуса, но эта идея здесь позволит нам измерить синус и косинус для любого угла вообще. . Это сработает для острых углов, когда тета находится здесь в первом квадранте.
Тот же угол, который мы хотим отметить точка, в которой крайняя сторона пересекает единичную окружность. Эта точка будет иметь координаты x, y, мы определяем косинус как значение x и синус как значение y. Эта точка, конечно, будет уникальной, она будет однозначно зависеть от тета угла, поэтому для разных тета углов вы получите разные значения синуса и косинуса, но эта идея здесь позволит нам измерить синус и косинус для любого угла вообще. . Это сработает для острых углов, когда тета находится здесь в первом квадранте.
Это будет работать для 0 градусов, 90 градусов и любого другого угла, так что сила определений единичного круга заключается в том, что они работают для всех углов, которые мы будем использовать для остальной части курса тригонометрии.
Тригонометрические отношения – определение, формулы, примеры
Тригонометрические отношения – это отношения длин сторон треугольника. Эти соотношения в тригонометрии относятся к отношению сторон прямоугольного треугольника к соответствующему углу.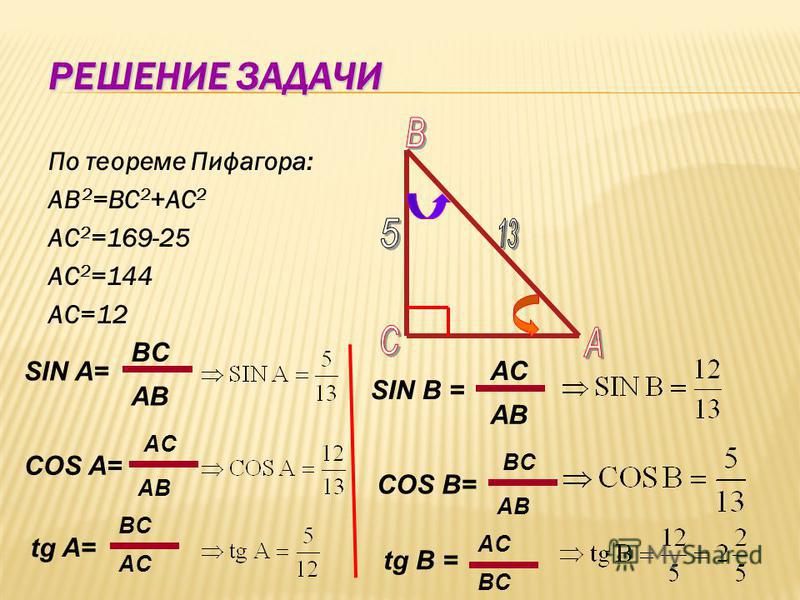 Основными тригонометрическими отношениями являются sin, cos и tan, а именно соотношения синуса, косинуса и тангенса. Другие важные триггерные отношения, cosec, sec и cot, можно получить, используя sin, cos и tan соответственно.
Основными тригонометрическими отношениями являются sin, cos и tan, а именно соотношения синуса, косинуса и тангенса. Другие важные триггерные отношения, cosec, sec и cot, можно получить, используя sin, cos и tan соответственно.
Слово «Тригонометрия» произошло от слов «Тригонон», что означает «треугольник», и «Метрон», что означает «измерять». Это раздел математики, изучающий отношения между углами и сторонами прямоугольного треугольника. На самом деле тригонометрия — один из самых древних предметов, который изучают ученые всего мира. Давайте подробно разберемся с тригонометрическими отношениями в следующих разделах.
| 1. | Что такое тригонометрические отношения? |
| 2. | Формулы тригонометрических отношений |
| 3. | Таблица тригонометрических соотношений |
| 4. | Тождества тригонометрических соотношений |
5. | Часто задаваемые вопросы о тригонометрических соотношениях |
Что такое тригонометрические отношения?
В тригонометрии существует шесть тригонометрических отношений, а именно: синус, косинус, тангенс, секанс, косеканс и котангенс. Эти соотношения записываются как sin, cos, tan, sec, cosec(или csc) и cot. Давайте посмотрим на прямоугольный треугольник, показанный ниже. Тригонометрические отношения можно использовать для определения отношений любых двух сторон из трех сторон прямоугольного треугольника с точки зрения соответствующих углов.
Значения этих тригонометрических соотношений можно рассчитать, используя меру острого угла θ в прямоугольном треугольнике, приведенную ниже. Это означает, что значение отношения любых двух сторон треугольника здесь зависит от угла C. Мы можем альтернативно найти значения этих тригонометрических отношений для угла A. Кроме того, только основание и перпендикуляр будут меняться местами для данного прямоугольного треугольника в тот случай.
Эти шесть тригонометрических соотношений можно определить как
Синус: Отношение синуса для любого заданного угла определяется как отношение перпендикуляра к гипотенузе. В данном треугольнике синус угла θ может быть задан как sin θ = AB/AC.
Косинус: Отношение косинуса для любого заданного угла определяется как отношение основания к гипотенузе. В данном треугольнике косинус угла θ может быть задан как cos θ = BC/AC.
Тангенс: Коэффициент тангенса для любого заданного угла определяется как отношение перпендикуляра к основанию. В данном треугольнике тангенс угла θ может быть задан как tan θ = AB/BC.
Косеканс: Коэффициент косеканса для любого заданного угла определяется как отношение гипотенузы к перпендикуляру. В данном треугольнике косеканс угла θ может быть задан как cosec θ = AC/AB.
Секанс: отношение секанса для любого данного угла определяется как отношение гипотенузы к основанию. В данном треугольнике секанс угла θ может быть задан как, sec θ = AC/BC.
Котангенс: Отношение котангенса для любого заданного угла определяется как отношение основания к перпендикуляру. В данном треугольнике котангенс угла θ может быть задан как ctg θ = BC/AB.
Давайте подробно разберем эти и другие формулы тригонометрических соотношений в следующем разделе.
Формулы тригонометрических отношений
Тригонометрические соотношения можно рассчитать, взяв отношение любых двух сторон прямоугольного треугольника. Мы можем вычислить третью сторону, используя теорему Пифагора, зная меру двух других сторон. Мы можем использовать сокращенную форму тригонометрических отношений, чтобы сравнить длину любых двух сторон с углом в основании. Угол θ является острым (θ < 90º) и обычно измеряется относительно положительной оси x против часовой стрелки. Формулы основных тригонометрических соотношений приведены ниже:
- sin θ = Перпендикуляр/Гипотенуза
- cos θ = основание/гипотенуза
- тангенс θ = Перпендикуляр/Основание
- с θ = гипотенуза/основание
- cosec θ = гипотенуза/перпендикуляр
- кроватка θ = основание/перпендикуляр
Теперь рассмотрим формулы обратных тригонометрических соотношений вышеупомянутых тригонометрических соотношений. Как мы наблюдаем, мы замечаем, что sin θ является обратной величиной cosec θ, cos θ является обратной величиной sec θ, tan θ является обратной величиной cot θ, и наоборот. Итак, новый набор формул для тригонометрических отношений:
Как мы наблюдаем, мы замечаем, что sin θ является обратной величиной cosec θ, cos θ является обратной величиной sec θ, tan θ является обратной величиной cot θ, и наоборот. Итак, новый набор формул для тригонометрических отношений:
- sin θ = 1/косек θ
- cos θ = 1/сек θ
- загар θ = 1/кот θ
- cosec θ = 1/sin θ
- сек θ = 1/cos θ
- раскладушка θ = 1/загар θ
Таблица тригонометрических соотношений
В таблице тригонометрических соотношений мы используем значения тригонометрических соотношений для стандартных углов 0°, 30°, 45°, 60° и 90°. Легко предсказать значения таблицы и использовать таблицу в качестве справочной информации для расчета значений тригонометрических отношений для различных других углов, используя формулы тригонометрических отношений для существующих шаблонов в пределах тригонометрических отношений и даже между углами. Теперь суммируем значения тригонометрических соотношений для конкретных углов в таблице ниже:
Тождества тригонометрических соотношений
Существует множество тождеств тригонометрических соотношений, которые мы используем, чтобы упростить наши вычисления.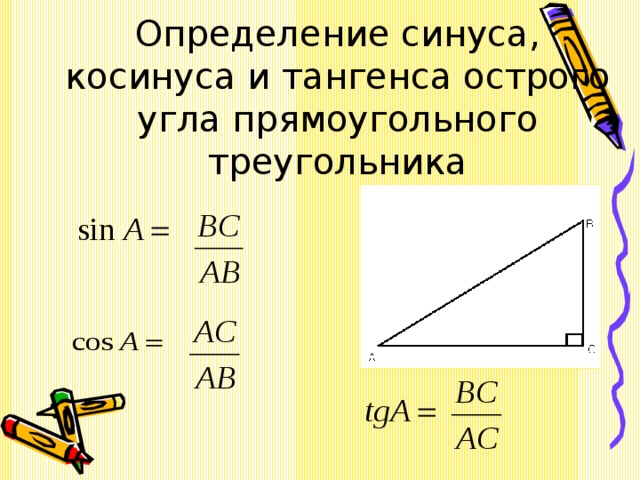 К ним относятся тождества дополнительных углов, дополнительных углов, тождества Пифагора и тождества суммы, разности, произведения.
К ним относятся тождества дополнительных углов, дополнительных углов, тождества Пифагора и тождества суммы, разности, произведения.
Тригонометрические отношения дополнительных углов Тождества
Дополнительные углы представляют собой пару двух углов, сумма которых равна 90°. Дополнение угла θ равно (90° — θ). Тригонометрические отношения дополнительных углов:
- sin (90°- θ) = cos θ
- cos (90°- θ) = sin θ
- косек (90°-θ) = сек θ
- сек (90°-θ) = cosec θ
- загар (90°- θ) = детская кроватка θ
- кроватка (90°- θ) = загар θ
Тождества пифагорейских тригонометрических отношений
Тождества пифагорейских тригонометрических отношений в тригонометрии выводятся из теоремы Пифагора. Применяя теорему Пифагора к прямоугольному треугольнику ниже, мы получаем:
Opposite 2 + Adjacent 2 = Hypotenuse 2
Dividing both sides by Hypotenuse 2
Opposite 2 /Hypotenuse 2 + Adjacent 2 /Hypotenuse 2 = Hypotenuse 2 / Гипотенуза 2
- sin 2 θ + cos 2 θ = 1
Это одно из важных пифагорейских тождеств.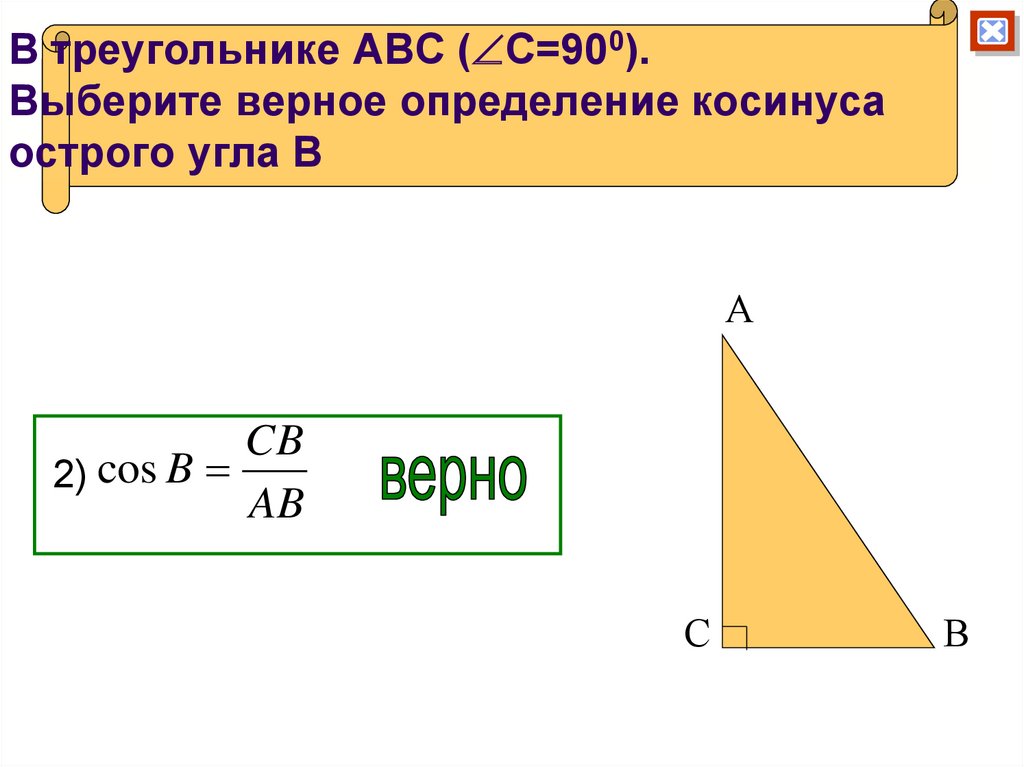 Таким же образом мы можем вывести два других тождества пифагорейских тригонометрических соотношений:
Таким же образом мы можем вывести два других тождества пифагорейских тригонометрических соотношений:
- sin 2 θ + cos 2 θ = 1
- 1 + тангенс 2 θ = сек 2 θ
- 1 + детская кроватка 2 θ = cosec 2 θ
Тождества суммы, разности, произведения тригонометрических отношений
Тождества суммы, разности и произведения тригонометрических отношений включают формулы sin(A+B), sin(A-B), cos(A+B), cos(A-B), и т. д.
- sin (A + B) = sin A cos B + cos A sin B
- sin (A — B) = sin A cos B — cos A sin B
- cos (A + B) = cos A cos B — sin A sin B
- cos (A — B) = cos A cos B + sin A sin B
- tan (A + B) = (tan A + tan B)/ (1 — tan A tan B)
- тангенс (A — B) = (тангенс A — тангенс B)/ (1 + тангенс A тангенс B)
- детская кроватка (A + B) = (детская кроватка A детская кроватка B — 1)/(детская кроватка B — детская кроватка A)
- детская кроватка (A — B) = (детская кроватка A детская кроватка B + 1)/(детская кроватка B — детская кроватка A)
- 2 sin A⋅cos B = sin(A + B) + sin(A — B)
- 2 cos A⋅cos B = cos(A + B) + cos(A — B)
- 2 sin A⋅sin B = cos(A — B) — cos(A + B)
Тригонометрические тождества половинных, двойных и тройных углов
Тождества тригонометрических отношений двойного угла
Тригонометрические тождества двойного угла можно получить, используя формулы суммы и разности.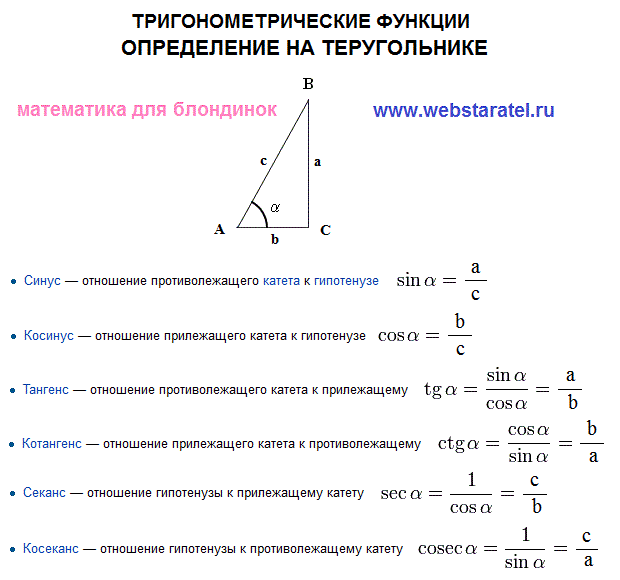
Например, из приведенной выше формулы sin (A+B) = sin A cos B + cos A sin B
Подставим здесь A = B = θ с обеих сторон, получим:
sin (θ + θ) = sinθ cosθ + cosθ sinθ
sin 2θ = 2 sinθ cosθ
Таким же образом мы можем вывести другие тождества двойного угла.
- sin 2θ = 2 sinθ cosθ
- cos 2θ = cos 2 θ — sin 2 θ
cos 2θ = 2 cos 2 θ — 1
cos 2θ = 1 — 2 sin 2 θ
cos 2θ = (1 — тангенс 2 θ)/(1 + тангенс 2 θ) - тангенс 2θ = (2 тангенс θ)/ (1 — тангенс 2 θ)
- сек 2θ = сек 2 θ/(2-сек 2 θ)
- cosec 2θ = (sec θ. cosec θ)/2
- раскладушка 2θ = (раскладушка θ — загар θ)/2
Тождества тригонометрических отношений половины угла
Используя одну из приведенных выше формул двойного угла,
cos 2θ = 1 — 2 sin 2 θ
2 sin 2 θ = 1- cos 2θ
sin 2 θ = (1 — cos 2θ)/(2)
sin θ = ±√[(1 — cos 2θ)/2]
Замена θ на θ/2 с обеих сторон,
sin (θ/2) = ±√[(1 — cos θ)/2]
Это формула полуугла синуса.
Таким же образом можно вывести и другие формулы половинного угла.
- sin (θ/2) = ±√[(1 — cos θ)/2]
- cos (θ/2) = ±√[(1 + cos θ)/2]
- тангенс (θ/2) = ±√[(1 — cos θ)(1 + cosθ)]
Тождества тригонометрических соотношений тройного угла
- sin 3θ = 3sin θ — 4sin 3 θ
- cos 3θ = 4cos 3 θ — 3cos θ
- тангенс 3θ = (3тангенс θ — тангенс 3 θ)/(1 — 3тангенс 2 θ)
Связанные темы:
- Тригонометрия
- Тригонометрические тождества
- Тригонометрическая таблица
- Тригонометрические формулы
Важные замечания по тригонометрическим отношениям:
- Значения тригонометрических отношений не меняются при изменении длин сторон треугольника, если угол остается неизменным.
- Все тригонометрические функции имеют периодический характер.

- Тригонометрические отношения используются для нахождения недостающих сторон или углов в треугольнике.
Примеры тригонометрических соотношений
Пример 1: В прямоугольном треугольнике ABC с прямым углом в точке B гипотенуза AC = 10 единиц, основание BC = 8 единиц и перпендикуляр AB = 6 единиц, и если ∠ACB = θ, то найдите тригонометрические соотношения tan θ, sin θ и cos θ.
Решение:
Мы знаем,
sin θ = перпендикуляр/гипотенузаcos θ = основание/гипотенуза
tan θ = перпендикуляр/основание
⇒ sin θ = 6/10 = 3/5
⇒ cos θ = 8/10 = 4/5
5
⇒ тангенс θ = 6/8 = 3/4
Ответ: sin θ, cos θ и тангенс θ для данного треугольника равны 3/5, 4/5 и 3/4 соответственно.
Пример 2: Здание находится на расстоянии 210 футов от точки А на земле. Найдите высоту здания, если tg θ = 4/3?
Решение: Получившийся треугольник является прямоугольным.
 Теперь примените тригонометрическое соотношение tanθ для расчета высоты здания.
Теперь примените тригонометрическое соотношение tanθ для расчета высоты здания.tan θ = Перпендикуляр/Основание
4/3 = Высота/210 футов
Высота = (4 × 210/3) = 280 футов
Ответ: Высота здания 280 футов.
Пример 3: Прямоугольный треугольник в точке C, AB = 29 единиц и AC = 20 единиц. Можете ли вы проверить идентичность тригонометрических соотношений cos 2 θ + sin 2 θ = 1 при использовании этих значений?
Решение: Мы найдем BC, используя теорему Pythagorean,
BC = √ (AB 2 — AC 2 )
= √ (29 2 — 20 2 )
69
2
69
2
6 2
6 2 2 2 2 2 — 20 2 ) 2 — 20 2 ) 2 — 20 2
) 2 — 20 2
) 2 — 20 2
) 841 2 — 400 2 )
= √441
= 21
Теперь давайте определим значения sinθ и cosθ
sinθ = ac/ab = 20/29
cosθ = bc/ab = 21 /29
Теперь проверим личность.

cos 2 θ + sin 2 θ = (21/29) 2 + (20/29) 2 = (400 + 441)/841 = 1
:900 тождество тригонометрических соотношений проверяется.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Забронируйте бесплатный пробный урок
Практические вопросы по тригонометрическим отношениям
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о тригонометрических соотношениях
Как найти тригонометрические соотношения?
Тригонометрические отношения можно рассчитать, используя заданный острый угол или определяя отношения сторон прямоугольного треугольника. Используемые формулы тригонометрических соотношений:
- sin θ = Перпендикуляр/Гипотенуза
- cos θ = основание/гипотенуза
- тангенс θ = Перпендикуляр/Основание
- с θ = гипотенуза/основание
- cosec θ = гипотенуза/перпендикуляр
- кроватка θ = основание/перпендикуляр
Что такое шесть тригонометрических соотношений?
Шесть основных тригонометрических соотношений: синус, косинус, тангенс, косеканс, секанс и котангенс.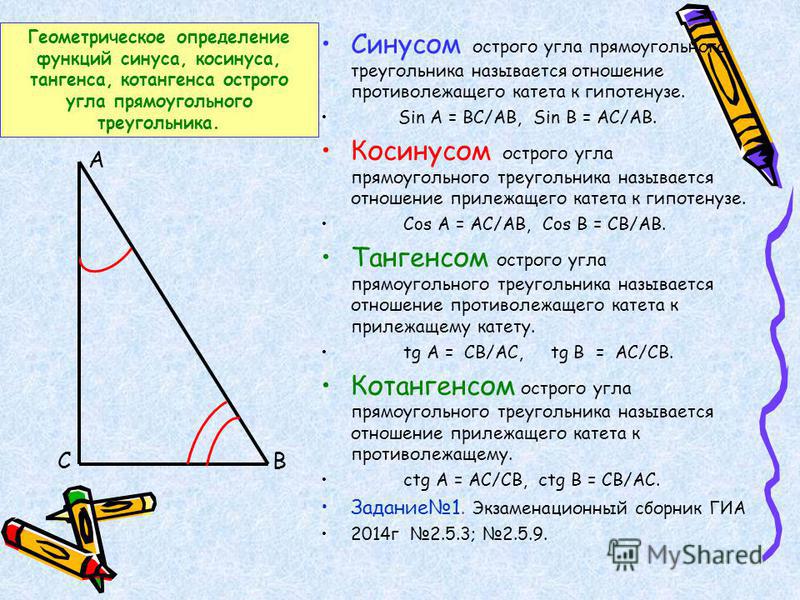

 Найдите длину его большего катета.
Найдите длину его большего катета.
 Теперь примените тригонометрическое соотношение tanθ для расчета высоты здания.
Теперь примените тригонометрическое соотношение tanθ для расчета высоты здания.