Синусы и косинусы основных углов таблица: Таблицы значений основных тригонометрических функций: синуса, косинуса, тангенса, котангенса

Содержание

Все, что вам нужно знать об углах тригонометрии

Что такое углы тригонометрии?

Угол образован соединением двух лучей, имеющих один и тот же конец. Стороны угла называются лучами, а вершина угла — общим концом. Расстояние между лучами используется для расчета угла. Мера угла определяется направлением лучей относительно друг друга.

Углы часто определяются с точки зрения поворота в тригонометрии. Рассмотрим один луч, который вращается на заданное расстояние вокруг своего конца. Угол образован лучом в его начальном положении до поворота и лучом в его конечном или конечном положении после поворота. Здесь данная вершина является точкой, вокруг которой вращается луч. Измерение угла определяется величиной вращения. Начальная сторона угла относится к лучу в его начальном положении до поворота. Терминальная сторона вышеупомянутого угла относится к лучу в его конечном положении после поворота. Если вращение было против часовой стрелки, образовавшийся угол положительный; если вращение было по часовой стрелке, угол отрицательный.

Углы, образованные отношениями тригонометрических функций, известны как тригонометрические углы. Изучение связи между углами и сторонами треугольника известно как тригонометрия. Значение угла находится в диапазоне от 0 до 360 градусов. В тригонометрии ключевые углы равны 0°, 30°, 45°, 60°, 90°, 180°, 270° и 360°. Синус, косинус, тангенс, косеканс, секанс и котангенс — это шесть важных тригонометрических соотношений или функций.

Давайте посмотрим на определение угла и связанные с ним термины, прежде чем мы перейдем к триггерным углам.

Градусы и радианы

Градусы и радианы — два наиболее часто используемых измерения углов. Градус является наиболее распространенной единицей измерения угла. Попробуйте разделить круг на 360 равных частей и найти правильный угол, используя 900. Кроме того, каждый градус делится на 60 минут, которые затем делятся на 60 секунд. °, ‘ и ” — символы градусов, минут и секунд соответственно. Угловые минуты и угловые секунды — это другие термины для обозначения минут и секунд.

Углы используются для измерения в радианах в дополнение к практической геометрии в математике. Радиус окружности с углом 1 радиан определяет длину дуги. Потому что длина окружности всего круга равна 2r.

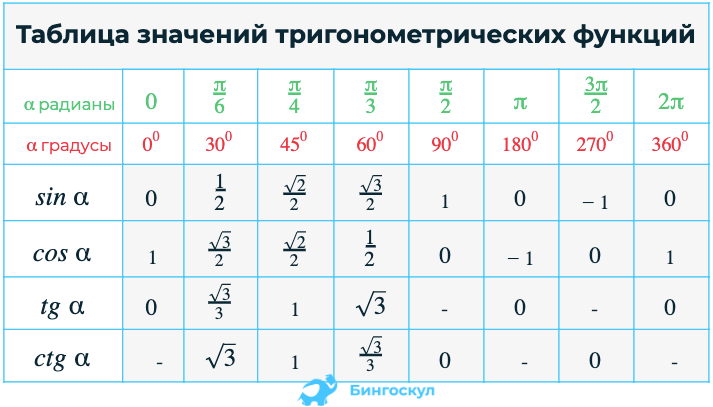
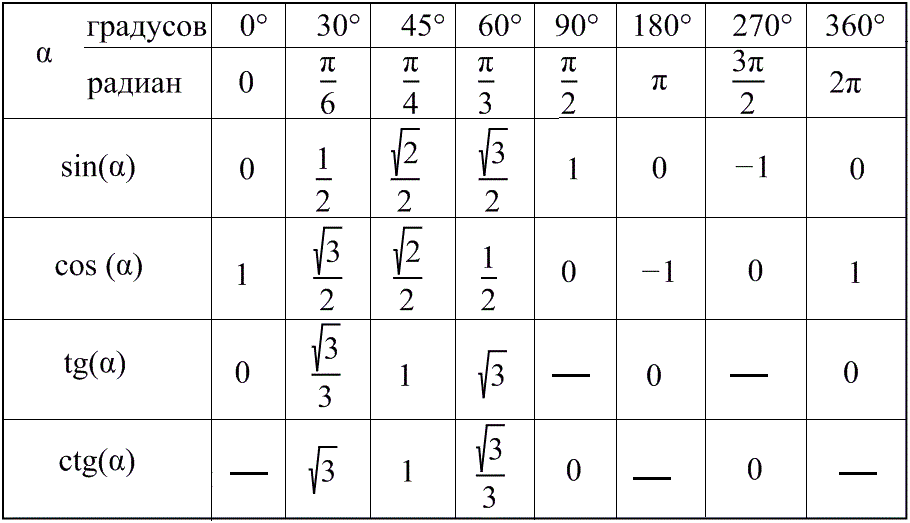
Тригонометрические таблицы всех углов

Таблица тригонометрических соотношений поможет нам в определении значений стандартных тригонометрических углов.

0°, 30°, 45°, 60° и 90° являются стандартными углами для тригонометрических соотношений.

При решении тригонометрических задач решающее значение имеют значения тригонометрических отношений стандартных углов. В результате необходимо запомнить значение тригонометрических отношений этих стандартных углов. Синус, косинус и тангенс стандартных углов перечислены в таблице ниже.

Тригонометрическая таблица настолько важна, что без нее невозможно решить многочисленные тригонометрические задачи. Значения нескольких тригонометрических функций можно найти в таблице тригонометрии.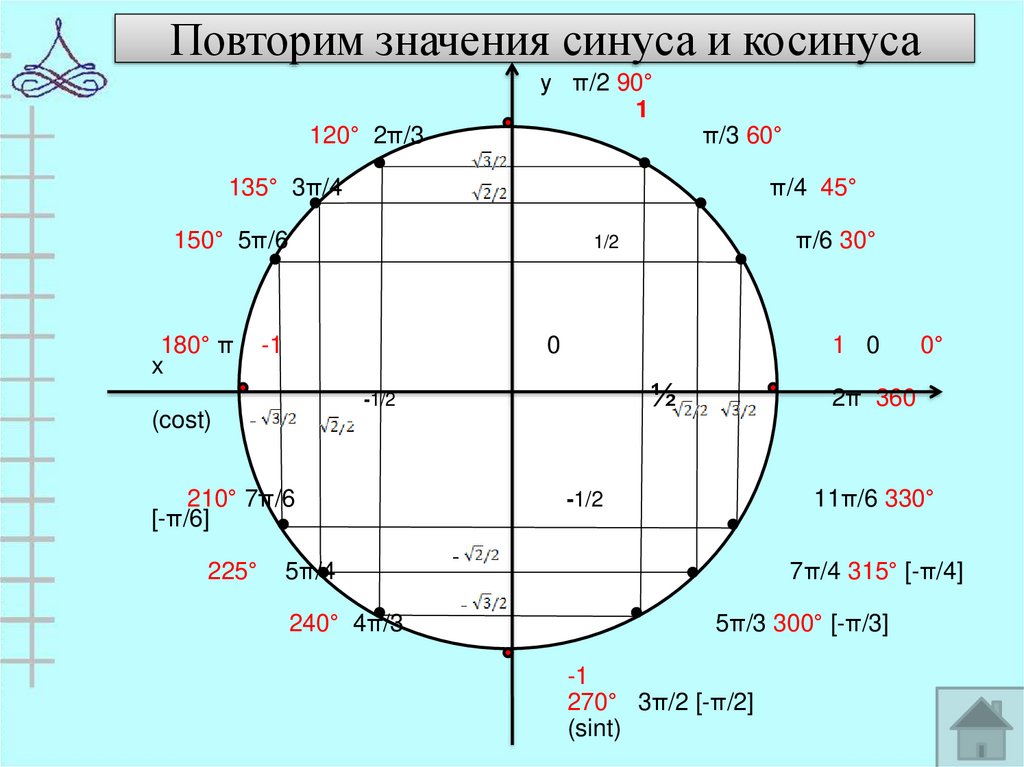 В таблице также показано, как тригонометрические функции или отношения связаны друг с другом.

Тригонометрические отношения соотносятся друг с другом в таблице тригонометрических значений с вариациями в принятии различных тригонометрических отношений сина, косинуса, секанса, косеканса, тангенса и котангенса. Калькуляторы и сложные компьютеры могут генерировать тригонометрические функции по запросу, но они должны использовать специальные библиотеки математических кодов. Эти тригонометрические таблицы значительно упростят вам работу. Вам нужно только запомнить эту таблицу, и большинство сумм будет просто ответить.

Angles	0°	30°	45°	60°	90°
SinA	0	1/2	1/√2	√3/2	1
CosA	1	√3/2	1/√2	1/2	0
tanA	0	1/√3	1	√ 3	Not defined
SecA	1	2/√3	√2	2	0
cosecA	0	2	√2	2/√3	1
cotA	Not defined	√3	1	2	0

Однако при использовании тригонометрических соотношений могут быть некоторые различия.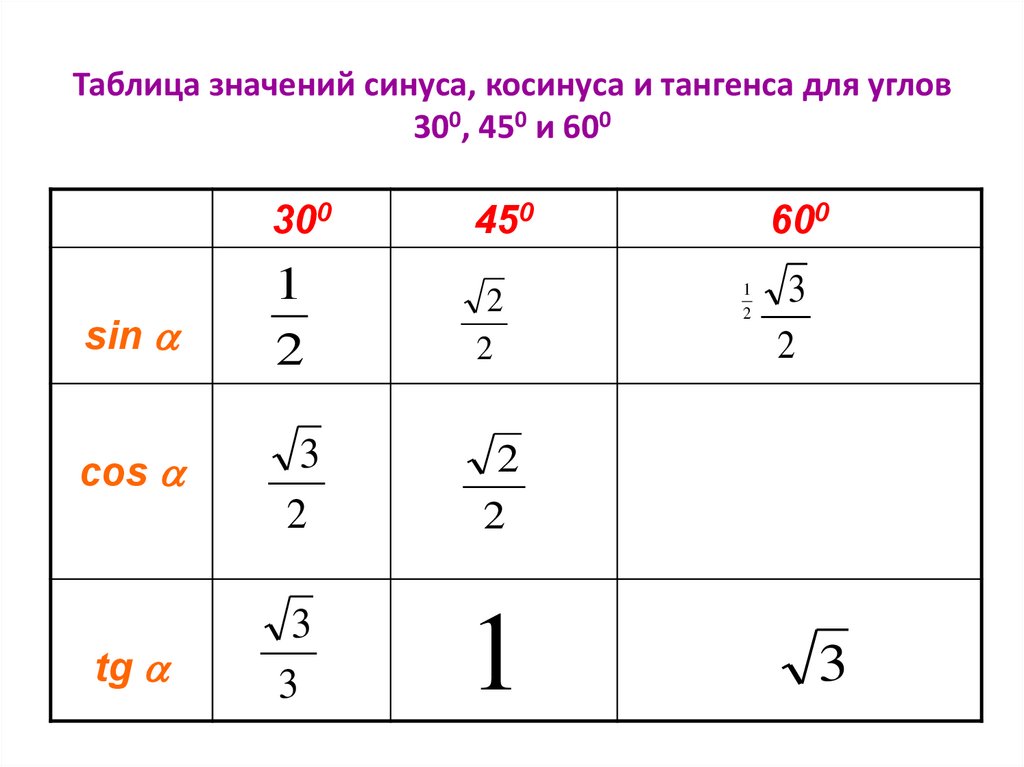 Функции тригонометрии чаще всего используются при общем измерении прямоугольного треугольника. Вы можете рассчитать общую площадь треугольника, используя подходящие формулы тригонометрии.

Однако при использовании альтернативных тригонометрических соотношений могут быть некоторые отличия в конкретном случае. Функции тригонометрии чаще всего используются при общем измерении прямоугольного треугольника. Вы можете рассчитать общую площадь треугольника, используя подходящие формулы тригонометрии.

Формулы тригонометрических углов

Дополнительные углы

Sin(π-a) = sin a

Cos(π-a)= -cos a

0 0 0 0 0 9 0 0 0 0 9 0 0 0 0 0 9 0 0 0 0 0 9 0 0 0 0 0 9 0 0 0 0 0 9 (π-a) = -cot a

Дополнительные углы

Sin(π/2-a)= cos a

Cos(π/2-a) = sin a

Tan(π/2-a) )= cot a

Тождества суммы и разности

sin(x+y)=sinxcosy+cosxsiny

cos(x+y) = cosxcosy-sinxsiny

tan(x+y)=(tanx+tany)/( 1+tanxtany)

Sin(x-y)= sinxcosy-cosxsiny

cos(x–y) = sinxsiny+cosxcosy

Tan(x-y) = ( tanx-tany)/ (1+ tanxtany)

Тождества с двумя углами

sin(2x) = 2sin(x)cos(x)
Cos(2x)= cos2x-sin2x

Тройное тождество

sin 3 A= 3 sin A – 4 sin3A

Cos3A= 4cos3A-3cosA

Tan3A=3tan1-3tan2A0007

Заключение

В этой статье мы рассмотрели всю тригонометрию и ее формулы.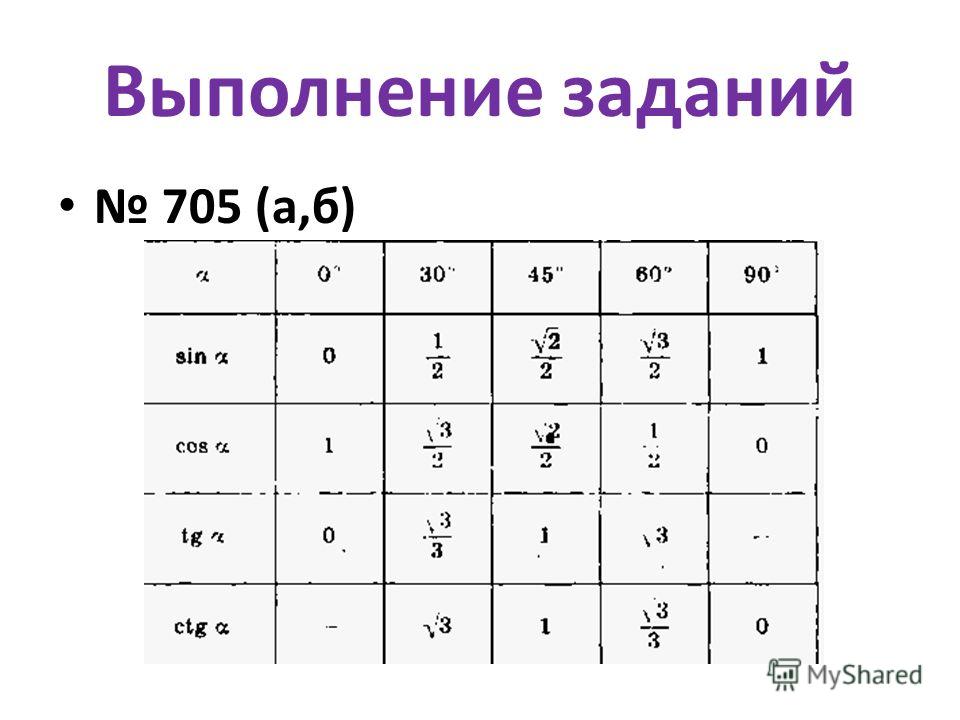 Что такое углы тригонометрии, и мы также видели различные углы с таблицей. Мы соединили все углы тригонометрии, и это родственная формула. Мы также рассмотрели все углы тригонометрии и связанные с ними формулы, которые помогут нам разобраться с различными вопросами.

Введение в тригонометрию – The Math Doctors

(Архивный вопрос недели)

Пока я показываю некоторые недавние объяснения основных методов тригонометрии, самое время взглянуть на еще более простое объяснение основ предмета для начинающих.

Тригонометрия прямоугольного треугольника

Вот вопрос от 2001 года:

 Тригонометрия в двух словах
Я учусь в 8-м классе, и на уроке математики мы занимаемся тригонометрией (синус косинус гипотенуза). Но  что такое тригонометрия?  Можешь дать мне 9?0003 хорошие простые вопросы  по тригонометрии, так что я могу попробовать его использовать? Спасибо.

Это требует непугающего введения в тему, которое покажет часть силы триггера, не показывая сложных частей.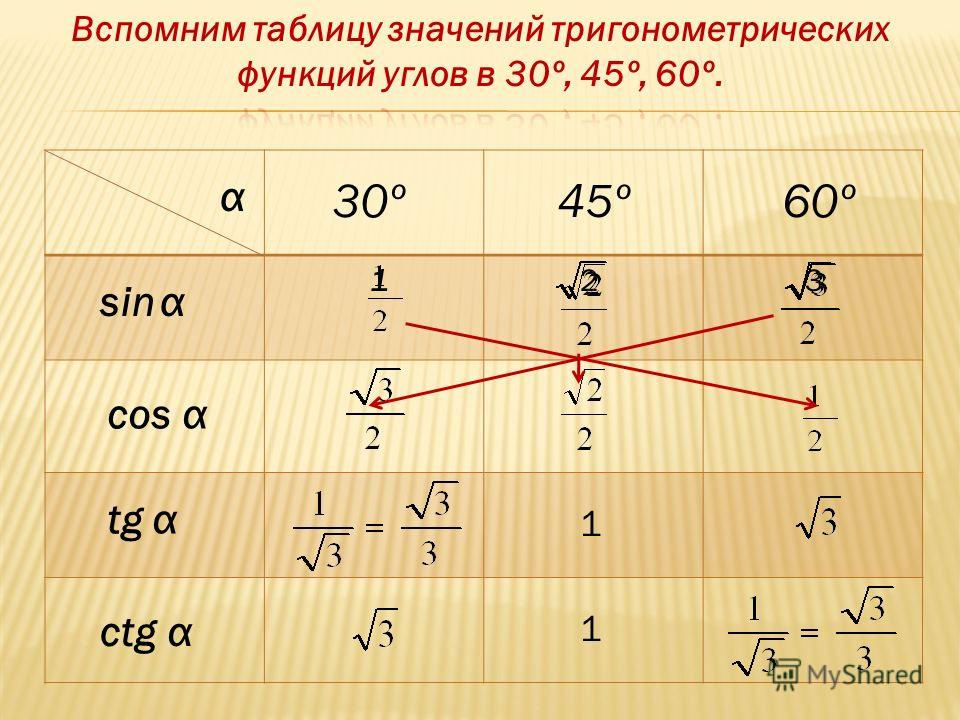 Доктор Ян принял вызов:

 Привет, Джимми!
Хотите верьте, хотите нет, но я только что провел часть прошлых выходных, объясняя тригонометрию своей матери, которая была расстроена, потому что около 50 лет назад она хотела стать радиотехником на флоте, но оказалась помощницей фармацевта, потому что не могла получить прикол тригонометрии. Итак, я собираюсь рассказать вам то, что я сказал ей.

Лучше всего сказать тому, кто только знакомится с предметом, может быть то же самое, что вы сказали бы тому, кто боролся с этим. Обзор того, что это такое, дает общую картину, не запутываясь в деталях, может помочь любому.

Тригонометрия обычно вводится с использованием прямоугольных треугольников, и именно здесь доктор Ян:

 Когда у вас есть прямоугольный треугольник,
           
          /|
         / б |
     С / |
       / | А
      / |
     /_а___|
        Б
в основном есть пять вещей, которые вы можете знать об этом: длины сторон (A, B и C) и меры острых углов (a и b).  Третий угол всегда равен 92)
И , если вы знаете угол , a или b, вы можете вычесть его из 90, чтобы получить другой:
  a + b = 90

Обратите внимание, что его запись противоположна тому, что мы обычно видим; он использует прописные буквы для длины сторон и строчные буквы для углов. Более типичная картина выглядела бы так:

Но это всего лишь общепринятое соглашение, а не математическая необходимость.

Теорема Пифагора и сумма углов позволяют найти недостающую сторону из двух заданных сторон или недостающий угол из двух заданных углов (один равен 90°). Там, где необходима собственно тригонометрия, нужно обрабатывать отношения 90 335 между 90 336 сторонами и углами, смешивая их вместе.

Тригонометрические функции (соотношения)

 Но  что если вы знаете стороны  и хотите знать углы? Или вы знаете угол  и сторону  и хотите знать другие стороны?
Итак, вот главная идея тригонометрии: если вы умножите все стороны прямоугольного треугольника на одно и то же число (k), вы получите треугольник другого размера, но с теми же углами:
                          /|
                         / б |
                        / |
        /| к*С / | к*А
       / б | / |
   С / | / | к*А А
     / | А / | --- = - и т.   д.
    / | / | к*В Б
   /_а___| /__а_____|
      Б к*Б
Почему это интересно? Ну, это означает, что если вы знаете отношение любых двух сторон, оно говорит вам, каковы углы.

То есть подобных треугольников имеют одинаковых углов и одинаковых отношений сторон ; таким образом, углы определяют , какими будут отношения, а отношения определяют, какими будут углы. Но в большинстве случаев на самом деле не сообщает , что они из себя представляют, пока вы не используете тригонометрию!

Есть специальные треугольники, для которых достаточно простой геометрии. Один из них является половиной равностороннего треугольника:

92) = квадрат (4 — 1) = квадрат (3) единицы длины. Теперь заметьте, что я не сказал, что такое «единица». Это может быть миля, или дюйм, или 13,5 см, или расстояние от большого пальца ноги до основания книжного шкафа на другом конце комнаты. Если я знаю, что угол а равен 60 градусам, то я знаю, что должно быть верно следующее: отношение A к C равно sqrt(3)/2 отношение B к C равно 1/2 отношение A к B равно sqrt(3)/1 И, что не менее важно, если я знаю, что для конкретного треугольника отношение А к В равно sqrt(3)/1, то угол а должен быть равен 60 градусам.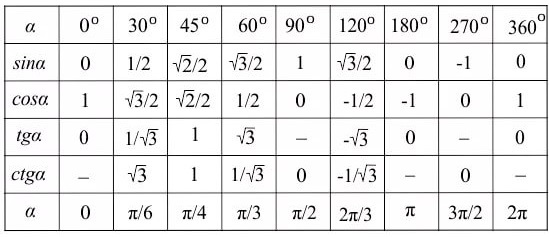

Другого угла быть не может.

Здесь показано, как угол определяет соотношение сторон, а отношение определяет угол. Сами стороны могут быть любого размера, но они должны иметь эти соотношения.

 Итак, что мы можем сделать, так это записать таблицу   , в которой мы перечислим все соотношения для всех углов интереса:
  угол отношение A/B
  ------- ---------
  0 0
  . . <= значения для других углов заполнены
  . .
  30 кв.м(3)/3
  . .
  . .
  45 1/1
  . .
  . .
  60 кв.м(3)/1
  . .
  . .
Теперь мы можем использовать эту таблицу, чтобы найти отношение A/B, если мы знаем угол a — просто найдите угол в столбце слева и прочитайте отношение из столбца справа. Или мы можем использовать ту же таблицу, чтобы найти угол a, если мы знаем отношение A/B — просто найдите отношение в столбце справа и прочитайте угол из столбца слева.

Большинство углов не имеют таких хороших соотношений; они должны быть рассчитаны как десятичные приближения (с использованием методов, которые большинству не нужно знать) и помещены в таблицы (или, в наши дни, в калькуляторы) для использования вами. Но идея та же.

А поскольку мы видим, что значение любого из этих отношений одинаково для любого треугольника с заданным углом, то каждое отношение является функцией угла .

Не хватает только имен для этих функций:

 Но вместо «отношение A/B для угла (a)» мы используем более короткое название «
  тангенс  угла a» или просто «tan(a)».
Поскольку есть три возможности, для какой пары сторон вы можете знать — A и C, B и C, A и B — у нас есть три разные функции:
  угол a => sin(a) = A/C
               потому что (а) = В / С
               загар (а) = А/В
Таким образом, мы можем составить таблицу, которая выглядит следующим образом:
  Математические страницы справочника по машинному оборудованию: таблицы триггеров
  http://www.industrialpress.com/ext/staticpages/handbook/trigpages

Образец таблицы (ссылку на которую я обновил из оригинала):

До калькуляторов (и даже сейчас, в местах, где калькуляторы обычно не доступны) нужны были гораздо более подробные таблицы.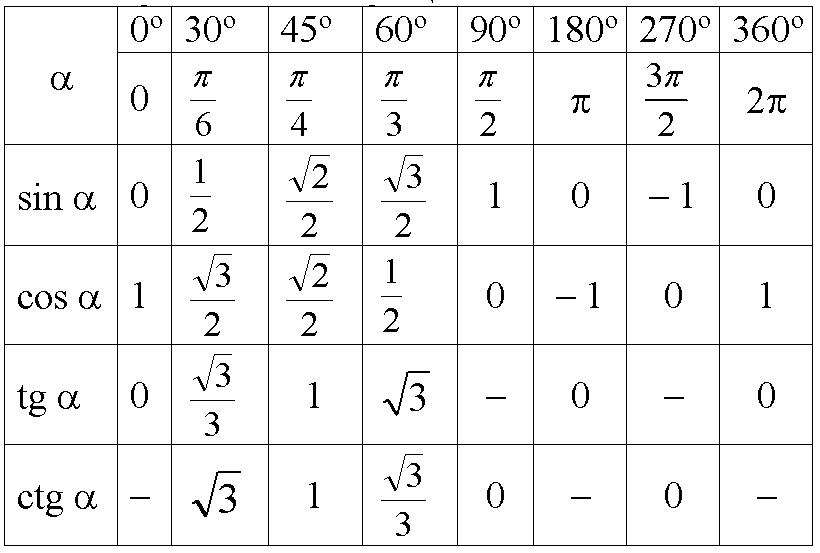

Вот пример такой таблицы для синуса.

Кстати, названия «синус», «косинус» и «тангенс», а также «секанс», «косеканс» и «котангенс» можно считать произвольными именами, которые нужно просто запомнить. Вот одна страница из Спросите доктора Математики о названиях, а другой о запоминании их значений:

 Латинское происхождение триггерных функций
Объяснение того, как работает SohCahToa

Я видел много других мнемоник для них.

 Обратите внимание, что нам не нужно включать функции sec, csc и cot, поскольку мы можем просто вычислить их из функций sin и cos:
  сек (а) = 1 / соз (а)
  csc(а) = 1/sin(а)
  cot(a) = cos(a) / sin(a)

Первые три перечисленные функции (синус, косинус и тангенс) охватывают все три пар сторон; последние три являются их обратными значениями, так что у нас есть имя для каждого возможного отношения

двух сторон (в любом порядке). Это излишне, но иногда может быть полезно, чтобы упростить формулу.
Решение прямоугольного треугольника: примеры
Теперь доктор Ян переходит к тому, как эти функции можно использовать для решения треугольника (то есть найти все недостающие части, когда вы знаете две):
Итак, сказав все это, вся суть тригонометрии такова: если у вас есть прямоугольный треугольник, в котором вы знаете одну сторону и любую другую сторону или угол, вы можете вычислить оставшиеся стороны и углы без необходимости их измерения. На самом деле, вот всех возможностей: Вы знаете, как вы находите других ---------------------------- ---------------------------------- две стороны Используйте теорему Пифагора, чтобы найти оставшуюся сторону. Используйте отношения сторон, чтобы найти углы. одну сторону и используйте функции sin, cos и tan один угол, чтобы найти остальные стороны. Другой угол равен 90 минус тот, который вы знаете.

Хорошо иметь несколько примеров, а не просто сухое общее правило:
Вот и все. Остальное — хитрости и хитрости. Например, если у вас есть треугольник типа /| / | С / | / | / | А / | /_17___| 25 это должно быть правдой, что А / 25 = тангенс (17) 25 / С = cos (17) A = 25 тангенс (17) 25 / cos (17) = C 25 * (1/cos(17)) = С 25 сек(17) = С где «sec» — это сокращение от «secant», а sec(x) — это еще один способ записи 1/cos(x). В любом случае, когда вы потратите около тысячи часов практики, вы сможете сразу же пометить треугольник: /| / | 25 сек(17) / | / | / | 25 коричневый(17) / | /_17___| 25

Используя таблицу или калькулятор, мы найдем, что вертикальная сторона равна $$25\tan(17°) \приблизительно (25)(0,3057) \приблизительно 7,64,$$, а гипотенуза равна $$\frac{25} {\cos(17°)} \приблизительно \frac{25}{0,9563} \приблизительно 26,14.$$
Обратите внимание, кстати, что на рисунке показаны только отношения, и он совсем не в масштабе; нам это не нужно. Но если бы мы нарисовали его точно, то увидели бы, что поскольку угол 17° мал, вертикальная сторона намного меньше 25, как мы и обнаружили; тогда как гипотенуза всегда длиннее любой стороны, в данном случае чуть длиннее:
Кроме того, вы сможете использовать формулы (так называемые «тождества»), например грех (х-у) = грех (х) потому что (у) - потому что (х) грех (у) делать такие трюки: грех(15) = грех(45 - 30) = грех (45) потому что (30) - потому что (45) грех (30) = (1/кв. (2))(кв.(3)/2) - (1/кв.(2))(1/2) = кв (3)/[2 кв (2)] - 1/[2 кв (2)] = [кв.(3) - 1] / кв.(2) Неясно, стоит ли способность делать эти вещи по памяти, а не по книге, тысячи часов вашей жизни. Вам придется обсудить это с законодательным собранием штата или с Департаментом образования.
Это всего лишь часть более сложных вещей, включенных в триггер. При необходимости вы можете найти такие вещи, как значения коэффициентов срабатывания, в таблице, хотя многие из них очень важны, по крайней мере, до тех пор, пока вы собираетесь активно с ними работать.
Приложения
Как насчет того, для чего можно использовать триггер? Джимми попросил несколько простых примеров задач. Многие важные приложения не могут быть поняты до более поздних курсов математики, но многие из них легко понять.
Короче говоря, это тригонометрия. Все, что вам нужно сделать, чтобы составить задачи, это нарисовать прямоугольный треугольник: /| / б | / | С / | А / | / | /_а____| Б а затем придумать к нему историю, в которой вы знаете две стороны или сторону и угол. Например, лестница прислонена к стене под углом 70 градусов к земле. Он просто касается нижней части окна в 10 футах от земли. Какой длины лестница? На каком расстоянии от стены находится нижняя часть лестницы? окно /| / | / | лестница/ | 10 футов / | / | /_70___| ?
Ответ: Тангенс угла 70° — это отношение противоположной стороны (10) к неизвестной смежной стороне, поэтому $$\frac{10}{x} = \tan(70°)$$ $$x = \ frac{10}{\tan(70°)} = \frac{10}{2,747} \приблизительно 3,64\text{ футов}$$
Чтобы превратить это в другую задачу, просто измените то, что вы знаете: окно /| / | / | 20 футов / | ? / | / | /_?____| 8 футов 9{-1}(0.4) \приблизительно 66.42°$$

Здесь мы использовали функцию арккосинуса , которая просто означает чтение таблицы в обратном направлении, чтобы найти угол, который имеет желаемый тангенс.

Или, если вам надоели лестницы и окна, придумайте другую историю, например, птица сидит на флагштоке, а солнце находится на высоте 57 градусов. Тень птицы находится в 11 футах от основания флагштока. Насколько высок флагшток? птица /| / | / | / | ? / | / | /_57___| 11 футов
Ответ: Тангенс угла 57° представляет собой отношение неизвестной противоположной стороны ( x ) к прилежащей стороне (11), поэтому $$\frac{x}{11} = \tan(57°)$$ $$x = 11\tan(57°) \приблизительно (11)(1,540) \приблизительно 16,94\текст{ футов}$$
Или один человек находится на вершине Гранд-Каньона, а другой на нижний. Они используют лазерный дальномер, чтобы определить, что они находятся на расстоянии 1200 метров друг от друга, и тому, кто внизу, приходится смотреть вверх под углом 78 градусов, чтобы увидеть того, кто выше. Насколько глубок каньон?
Ответ: синус 78° представляет собой отношение неизвестной противоположной стороны ( x ) к гипотенузе (1200), поэтому $$\frac{x}{1200} = \sin(78°)$$ $ $x = 1200\sin(78°) \приблизительно (1200)(0,9781) \приблизительно 1174\текст{ футов}$$
Некоторым людям нужна дополнительная помощь, чтобы понять, как решить, какую функцию использовать для решения треугольника; вот общее объяснение этого процесса:
Синус, косинус и тангенс: SOHCATOA
Доктор Ян заключил:
Придумывая свои собственные задачи, вы гораздо лучше поймете, почему это так полезно , и, если повезет, вы начнете понимать, почему некоторые люди вообще считают забавой . Так вот как вы придумываете проблемы. Вы решаете проблемы, придуманные другими людьми, действуя в обратном порядке. То есть вы читаете задачу и пытаетесь выяснить, что находится в вершине каждого треугольника. Затем вы пытаетесь выяснить, какие стороны и/или углы вам даны, и какой из них вы должны найти. Затем вы используете теорему Пифагора и функции sin, cos и tan, чтобы найти его.
Джимми немного преувеличил свой ответ:
Спасибо! Вы мне очень помогли и сэкономили немного денег на покупке книг по тригонометрии. Это всегда было трудным для меня на тестах, но я думаю, что смогу справиться с этим в следующий раз. Еще раз спасибо!
Нет, это не учебники! Но это делает тему более доступной.
Триггерные функции, круги и волны
Накануне другой студент задал аналогичный вопрос, который был объединен на этой странице:
Я совершенно не понимаю синуса, косинуса и тангенса. Что это такое и откуда они берутся? Все, чему меня научили, это когда их использовать и где кнопка на калькуляторе. Я пытался найти руководство или учебник для начинающих в сети, но все слишком сложно. Они даже используют синус и т. д. с кругами и волнами , тогда как я думал , что это просто сделать с треугольниками . Пожалуйста, не могли бы вы объяснить их? Я думаю, было бы очень полезно иметь пояснения на вашем сайте, так как все в моем классе могут ими пользоваться, но никто не знает, что они собой представляют на самом деле.
На этот раз Майкл знаком с тригонометрией прямоугольного треугольника, о которой говорилось выше, но интересуется более широкой картиной.
Доктор Ян ответил и на это, соединив тригонометрические функции сначала с окружностями, а затем с их графиками:
Привет Михаил! Какое отношение тригонометрия имеет к кругам? Итак, нарисуйте окружность, центр которой находится в начале координат плоскости x-y, а радиус равен 1. Теперь выберите любую точку на окружности, проведите отрезок из центра и отметьте угол a между положительной осью x и сегмент линии. 2 = 1 На самом деле, множество формул, таких как те, которые вы можете найти в FAQ Ask Dr. Math: Trigonometry Formulas, http://mathforum.org/dr.math/faq/formulas/faq.trig.html легче всего понять, если вы думаете об единичном круге, а не о треугольниках произвольного размера.
Чтобы ясно понять, почему здесь появляются синус и косинус, мы можем добавить линию, чтобы получился прямоугольный треугольник:

И какое это имеет отношение к волнам? Если вы начнете брать разные значения а и нанесете на них соответствующие значения х и у (то есть, если вы начертите х и у как функции а так, как вы обычно рисуете у как функцию х), вы получите что-то так: х х | х х х = потому что (а) | х х +------х-----------х------------ | х х | х х Икс а=0 90 180 270 360 | у | у у у = грех (а) |г у у-----------у-----------у------ | у у | у у | у а=0 90 180 270 360 Каждый график колеблется взад-вперед между 1 и -1, повторяясь каждые 360 градусов, что является другим способом сказать, что если вы двигаетесь на 360 градусов по кругу, вы в конечном итоге окажетесь там, где начали.
No related posts.