Синусы и косинусы углов все: Синус косинус и тангенс — материалы для подготовки к ЕГЭ по Математике

Тригонометрия для чайников. Урок1. Тригонометрия с нуля

Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

 

Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.

 

Синус угла – отношение противолежащего катета к гипотенузе.

sin α = Противолежащий катет гипотенуза

Косинус угла – отношение прилежащего катета к гипотенузе.

cos α = Прилежащий катет гипотенуза

Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).

tg α = Противолежащий катет Прилежащий катет

Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).

ctg α = Прилежащий катет Противолежащий катет

 

Рассмотрим прямоугольный треугольник ABC, угол C равен 90°:

sin ∠ A = C B A B

cos ∠ A = A C A B

tg ∠ A = sin ∠ A cos ∠ A = C B A C

ctg ∠ A = cos ∠ A sin ∠ A = A C C B

sin ∠ B = A C A B

cos ∠ B = B C A B

tg ∠ B = sin ∠ B cos ∠ B = A C C B

ctg ∠ B = cos ∠ B sin ∠ B = C B A C

 

Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.

Тригонометрический круг – это окружность единичного радиуса с центром в начале координат. 

Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )

На данной окружности будет три шкалы отсчета – ось x, ось y и сама окружность, на которой мы будем откладывать углы.

Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x, против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A. Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .

 

Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B) и на ось игрек (точка C).

 

Отрезок OB является проекцией отрезка OA на ось x, отрезок OC является проекцией отрезка OA на ось y.

Рассмотрим прямоугольный треугольник AOB:

cos α = O B O A = O B 1 = O B

sin α = A B O A = A B 1 = A B

Поскольку O C A B – прямоугольник, A B = C O .

Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).

 

Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :

 

Опускаем из точки A перпендикуляры к осям x и y. Точка B в этом случае будет иметь отрицательную координату по оси x. Косинус тупого угла отрицательный.

Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x.  (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y.

 

Координата по оси x – косинус угла, координата по оси y – синус угла.

Пример:

cos 150 ° = − 3 2

sin 150 ° = 1 2

 

Ещё одно замечание.

Синус тупого угла – положительная величина, а косинус – отрицательная.

Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный.

Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный.

 

sin 2 α + cos 2 α = 1

Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :

 

A B 2 + O B 2 = O A 2

sin 2 α + cos 2 α = R 2

sin 2 α + cos 2 α = 1

 

	0°	30°	45°	60°	90°
sinα	0	12	22	32	1
cosα	1	32	22	12	0
tgα	0	33	1	3	нет
ctgα	нет	3	1	33	0

 

Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!

 

Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,

можно заметить, что:

sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °

sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °

sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °

sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °

 

cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °

cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °

cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °

cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °

 

Рассмотрим тупой угол β:

 

Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:

sin ( 180 ° − α ) = sin α

cos ( 180 ° − α ) = − cos α

tg ( 180 ° − α ) = − tg α

ctg ( 180 ° − α ) = − ctg α

 

В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.

 

a sin ∠ A = b sin ∠ B = c sin ∠ C

 

Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.

 

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R

 

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

 

a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A

b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B

c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C

 

Модуль геометрия: задания, связанные с тригонометрией.

 

Скачать домашнее задание к уроку 1.

 

Тригонометрическая таблица

В статье, мы полностью разберемся, как выглядит таблица тригонометрических значений, синуса, косинуса, тангенса и котангенса . Рассмотрим основное значение тригонометрических функций, от угла в 0,30,45,60,90,…,360 градусов. И посмотрим как пользоваться данными таблицами в вычислении значения тригонометрических функций.
Первой рассмотрим таблицу косинуса, синуса, тангенса и котангенса от угла в 0, 30, 45, 60, 90,.. градусов. Определение данных величин дают определить значение функций углов в 0 и 90 градусов:

sin 0⁰=0, cos 0⁰ = 1. tg 0⁰ = 0, котангенс от 0⁰ будет неопределенным
sin 90⁰ = 1, cos 90⁰ =0, ctg90⁰ = 0,тангенс от 90⁰ будет неопределенным

Если взять прямоугольные треугольники углы которых от 30 до 90 градусов. Получим:

sin 30⁰ = 1/2, cos 30⁰ = √3/2, tg 30⁰ = √3/3, ctg 30⁰ = √3
sin 45⁰ = √2/2, cos 45⁰ = √2/2, tg 45⁰= 1, ctg 45⁰ = 1
sin 60⁰ = √3/2, cos 60⁰ = 1/2, tg 60⁰ =√3 , ctg 60⁰ = √3/3

Изобразим все полученные значения в виде тригонометрической таблицы:

Таблица синусов, косинусов, тангенсов и котангенсов!

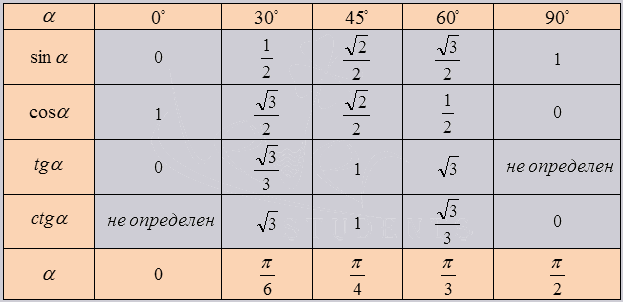
Если использовать формулу приведения, наша таблица увеличится, добавятся значения для углов до 360 градусов. Выглядеть она будет как:

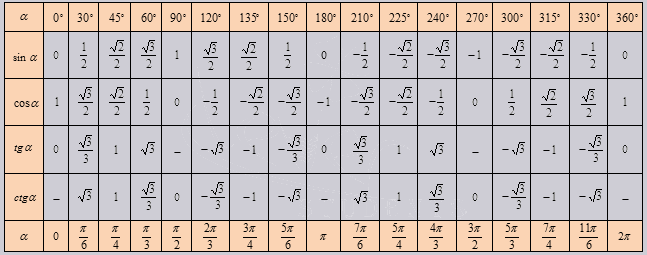
Так же исходя из свойств периодичности таблицу можно увеличить, если заменим углы на 0⁰+360⁰*z …. 330⁰+360⁰*z, в котором z является целым числом. В данной таблице возможно вычислить значение всех углов, соответствующими точками в единой окружности.

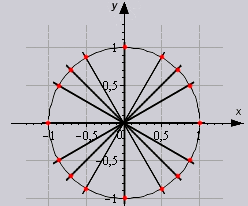
Разберем наглядно как использовать таблицу в решении.
Все очень прост. Так как нужное нам значение лежит в точке пересечения нужных нам ячеек. К примеру возьмем cos угла 60 градусов, в таблице это будет выглядеть как:

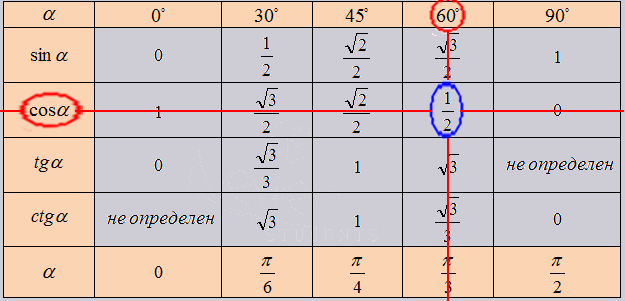
В итоговой таблице основных значений тригонометрических функций, действуем так же. Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 1020⁰ = 300⁰+360⁰*2. Найдем по таблице.

Для более поиска тригонометрических значений углов с точностью до минут используются таблицы Брадиса. Подробная инструкция как ими пользоваться на странице по ссылке.

Таблица Брадиса. Для синуса, косинуса, тангенса и котангенса.

Таблицы Брадиса поделены на несколько частей, состоят из таблиц косинуса и синуса, тангенса и котангенса — которая поделена на две части (tg угла до 90 градусов и ctg малых углов).

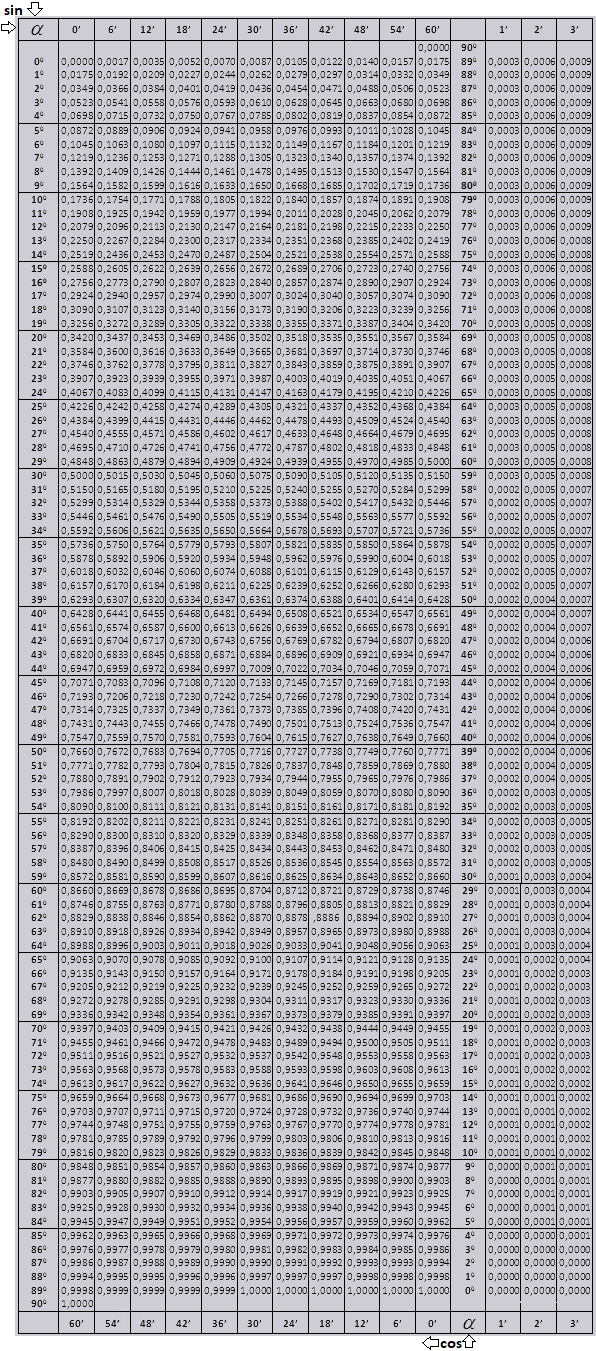
Синус и косинус

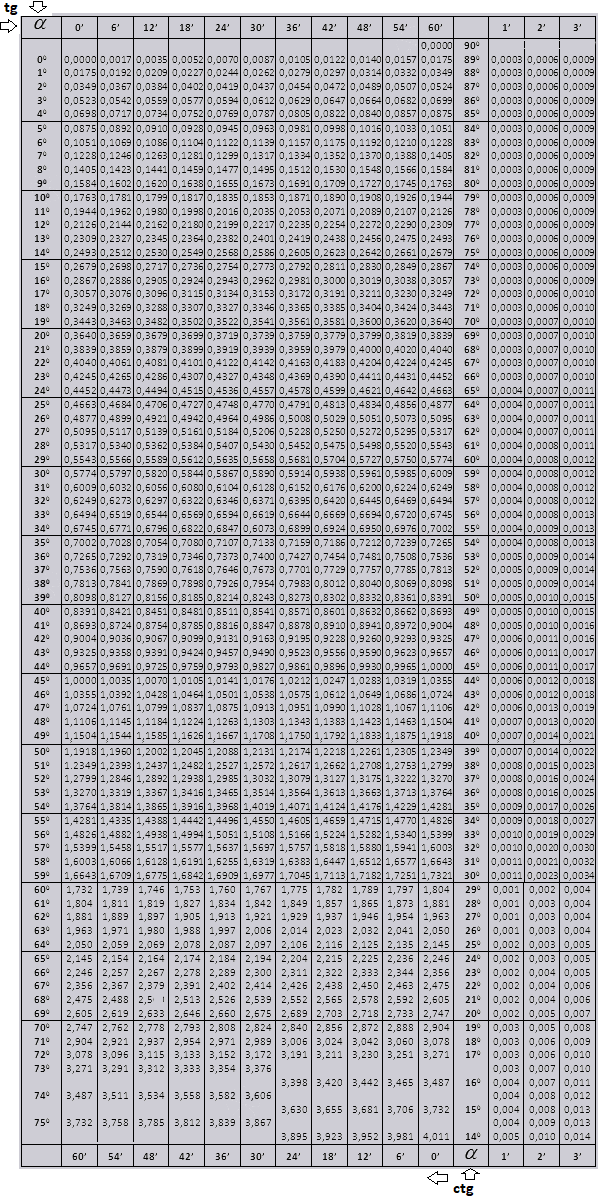
tg угла начиная с 0⁰ заканчивая 76⁰, ctg угла начиная с 14⁰ заканчивая 90⁰.

tg до 90⁰ и ctg малых углов.

Разберемся как пользоваться таблицами Брадиса в решении задач.

Найдем обозначение sin (обозначение в столбце с левого края) 42 минут (обозначение находится на верхней строчке). Путем пересечения ищем обозначение, оно = 0,3040.

Величины минут указаны с промежутком в шесть минут, как быть если нужное нам значение попадет именно в этот промежуток. Возьмем 44 минуты, а в таблице есть только 42. Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.

При sin 47 мин, берем за основу 48 мин и отнимаем от нее 1 поправку, т.е 0,3057 — 0,0003 = 0,3054

При вычислении cos работаем аналогично sin только за основу берем нижнюю строку таблицы. К примеру cos 20⁰ = 0.9397

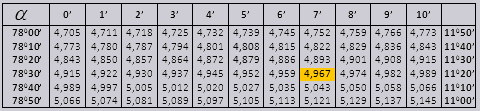
Значения tg угла до 90⁰ и cot малого угла, верны и поправок в них нет. К примеру, найти tg 78⁰ 37мин = 4,967

а ctg 20⁰ 13мин = 25,83

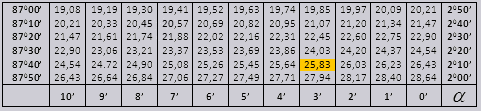
Ну вот мы и рассмотрели основные тригонометрические таблицы. Надеемся это информация была для вас крайне полезной. Свои вопросы по таблицам, если они появились, обязательно пишите в комментариях!

Заметка: Стеновые отбойники — отбойная доска для защиты стен (http://www.spi-polymer.ru/otboyniki/)

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---

Тригонометрические формулы

© Школяр. Математика (при поддержке «Ветвистого древа») 2009—2016

(1)	Основное тригонометрическое тождество	sin2(α) + cos2(α) = 1
(2)	Основное тождество через тангенс и косинус	1 + tg2(α) = 1/cos2(α)
(3)	Основное тождество через котангенс и синус	1 + ctg2(α) = 1/sin2(α)
(4)	Соотношение между тангенсом и котангенсом	tg(α)ctg(α) = 1
(5)	Синус двойного угла	sin(2α) = 2sin(α)cos(α)
(6)	Косинус двойного угла	cos(2α) = cos2(α) – sin2(α) = 2cos2(α) – 1 = 1 – 2sin2(α)
(7)	Тангенс двойного угла	tg(2α) =   2tg(α) 1 – tg2(α)
(8)	Котангенс двойного угла	ctg(2α) = ctg2(α) – 1   2ctg(α)
(9)	Синус тройного угла	sin(3α) = 3sin(α)cos2(α) – sin3(α)
(10)	Косинус тройного угла	cos(3α) = cos3(α) – 3cos(α)sin2(α)
(11)	Косинус суммы/разности	cos(α±β) = cos(α)cos(β) ∓ sin(α)sin(β)
(12)	Синус суммы/разности	sin(α±β) = sin(α)cos(β) ± cos(α)sin(β)
(13)	Тангенс суммы/разности	tg(α±β) = (tg(α) ± tg(β))/(1 ∓ tg(α)tg(β))
(14)	Котангенс суммы/разности	ctg(α±β) = (-1 ± ctg(α)ctg(β))/(ctg(&alpha) ± ctg(β))
(15)	Произведение синусов	sin(α)sin(β) = ½(cos(α–β) – cos(α+β))
(16)	Произведение косинусов	cos(α)cos(β) = ½(cos(α+β) + cos(α–β))
(17)	Произведение синуса на косинус	sin(α)cos(β) = ½(sin(α+β) + sin(α–β))
(18)	Сумма/разность синусов	sin(α) ± sin(β) = 2sin(½(α±β))cos(½(α∓β))
(19)	Сумма косинусов	cos(α) + cos(β) = 2cos(½(α+β))cos(½(α–β))
(20)	Разность косинусов	cos(α) – cos(β) = –2sin(½(α+β))sin(½(α–β))
(21)	Сумма/разность тангенсов	tg(α) ± tg(β) = sin(α±β)/cos(α)cos(β)
(22)	Формула понижения степени синуса	sin2(α) = ½(1 – cos(2α))
(23)	Формула понижения степени косинуса	cos2(α) = ½(1 + cos(2α))
(24)	Сумма/разность синуса и косинуса	sin(α) ± cos(α) = &sqrt;2sin(α±π/4)
(25)	Сумма/разность синуса и косинуса с коэффициентами	Asin(α) ± Bcos(α) = Корень(A²+B²)(sin(α ± arccos(A/Корень(A²+B²)))
(26)	Основное соотношение арксинуса и арккосинуса	arcsin(x) + arccos(x) = π/2
(27)	Основное соотношение арктангенса и арккотангенса	arctg(x) + arcctg(x) = π/2

Таблица КОСИНУСОВ для углов от 0° до 360° градусов

---

КОСИНУС (COS α) острого угла в прямоугольном треугольнике равен отношению прилежащего катета к его гипотенузе…

Малая таблица значений тригонометрических функций (в радианах и градусах)

α (радианы)	0	π/6	π/4	π/3	π/2	π	√3π/2	2π
α (градусы)	0°	30°	45°	60°	90°	180°	270°	360°
cos α (Косинус)	1	√3/2	√2/2	1/2	0	-1	0	1

…

Полная таблица косинусов для углов от 0° до  360° 

Угол в градусах	Cos (Косинус)
0°	1
1°	0.9998
2°	0.9994
3°	0.9986
4°	0.9976
5°	0.9962
6°	0.9945
7°	0.9925
8°	0.9903
9°	0.9877
10°	0.9848
11°	0.9816
12°	0.9781
13°	0.9744
14°	0.9703
15°	0.9659
16°	0.9613
17°	0.9563
18°	0.9511
19°	0.9455
20°	0.9397
21°	0.9336
22°	0.9272
23°	0.9205
24°	0.9135
25°	0.9063
26°	0.8988
27°	0.891
28°	0.8829
29°	0.8746
30°	0.866
31°	0.8572
32°	0.848
33°	0.8387
34°	0.829
35°	0.8192
36°	0.809
37°	0.7986
38°	0.788
39°	0.7771
40°	0.766
41°	0.7547
42°	0.7431
43°	0.7314
44°	0.7193
45°	0.7071
46°	0.6947
47°	0.682
48°	0.6691
49°	0.6561
50°	0.6428
51°	0.6293
52°	0.6157
53°	0.6018
54°	0.5878
55°	0.5736
56°	0.5592
57°	0.5446
58°	0.5299
59°	0.515
60°	0.5
61°	0.4848
62°	0.4695
63°	0.454
64°	0.4384
65°	0.4226
66°	0.4067
67°	0.3907
68°	0.3746
69°	0.3584
70°	0.342
71°	0.3256
72°	0.309
73°	0.2924
74°	0.2756
75°	0.2588
76°	0.2419
77°	0.225
78°	0.2079
79°	0.1908
80°	0.1736
81°	0.1564
82°	0.1392
83°	0.1219
84°	0.1045
85°	0.0872
86°	0.0698
87°	0.0523
88°	0.0349
89°	0.0175
90°	0

…

 

Таблица косинусов для углов от 91° до 180°

Угол	cos (Косинус)
91°	-0.0175
92°	-0.0349
93°	-0.0523
94°	-0.0698
95°	-0.0872
96°	-0.1045
97°	-0.1219
98°	-0.1392
99°	-0.1564
100°	-0.1736
101°	-0.1908
102°	-0.2079
103°	-0.225
104°	-0.2419
105°	-0.2588
106°	-0.2756
107°	-0.2924
108°	-0.309
109°	-0.3256
110°	-0.342
111°	-0.3584
112°	-0.3746
113°	-0.3907
114°	-0.4067
115°	-0.4226
116°	-0.4384
117°	-0.454
118°	-0.4695
119°	-0.4848
120°	-0.5
121°	-0.515
122°	-0.5299
123°	-0.5446
124°	-0.5592
125°	-0.5736
126°	-0.5878
127°	-0.6018
128°	-0.6157
129°	-0.6293
130°	-0.6428
131°	-0.6561
132°	-0.6691
133°	-0.682
134°	-0.6947
135°	-0.7071
136°	-0.7193
137°	-0.7314
138°	-0.7431
139°	-0.7547
140°	-0.766
141°	-0.7771
142°	-0.788
143°	-0.7986
144°	-0.809
145°	-0.8192
146°	-0.829
147°	-0.8387
148°	-0.848
149°	-0.8572
150°	-0.866
151°	-0.8746
152°	-0.8829
153°	-0.891
154°	-0.8988
155°	-0.9063
156°	-0.9135
157°	-0.9205
158°	-0.9272
159°	-0.9336
160°	-0.9397
161°	-0.9455
162°	-0.9511
163°	-0.9563
164°	-0.9613
165°	-0.9659
166°	-0.9703
167°	-0.9744
168°	-0.9781
169°	-0.9816
170°	-0.9848
171°	-0.9877
172°	-0.9903
173°	-0.9925
174°	-0.9945
175°	-0.9962
176°	-0.9976
177°	-0.9986
178°	-0.9994
179°	-0.9998
180°	-1

…

Таблица косинусов для углов от 180° до 270°

Угол	cos (косинус)
181°	-0.9998
182°	-0.9994
183°	-0.9986
184°	-0.9976
185°	-0.9962
186°	-0.9945
187°	-0.9925
188°	-0.9903
189°	-0.9877
190°	-0.9848
191°	-0.9816
192°	-0.9781
193°	-0.9744
194°	-0.9703
195°	-0.9659
196°	-0.9613
197°	-0.9563
198°	-0.9511
199°	-0.9455
200°	-0.9397
201°	-0.9336
202°	-0.9272
203°	-0.9205
204°	-0.9135
205°	-0.9063
206°	-0.8988
207°	-0.891
208°	-0.8829
209°	-0.8746
210°	-0.866
211°	-0.8572
212°	-0.848
213°	-0.8387
214°	-0.829
215°	-0.8192
216°	-0.809
217°	-0.7986
218°	-0.788
219°	-0.7771
220°	-0.766
221°	-0.7547
222°	-0.7431
223°	-0.7314
224°	-0.7193
225°	-0.7071
226°	-0.6947
227°	-0.682
228°	-0.6691
229°	-0.6561
230°	-0.6428
231°	-0.6293
232°	-0.6157
233°	-0.6018
234°	-0.5878
235°	-0.5736
236°	-0.5592
237°	-0.5446
238°	-0.5299
239°	-0.515
240°	-0.5
241°	-0.4848
242°	-0.4695
243°	-0.454
244°	-0.4384
245°	-0.4226
246°	-0.4067
247°	-0.3907
248°	-0.3746
249°	-0.3584
250°	-0.342
251°	-0.3256
252°	-0.309
253°	-0.2924
254°	-0.2756
255°	-0.2588
256°	-0.2419
257°	-0.225
258°	-0.2079
259°	-0.1908
260°	-0.1736
261°	-0.1564
262°	-0.1392
263°	-0.1219
264°	-0.1045
265°	-0.0872
266°	-0.0698
267°	-0.0523
268°	-0.0349
269°	-0.0175
270°	0

…

Таблица косинусов для углов от 270° до 360°

Угол	Cos (Косинус)
271°	0.0175
272°	0.0349
273°	0.0523
274°	0.0698
275°	0.0872
276°	0.1045
277°	0.1219
278°	0.1392
279°	0.1564
280°	0.1736
281°	0.1908
282°	0.2079
283°	0.225
284°	0.2419
285°	0.2588
286°	0.2756
287°	0.2924
288°	0.309
289°	0.3256
290°	0.342
291°	0.3584
292°	0.3746
293°	0.3907
294°	0.4067
295°	0.4226
296°	0.4384
297°	0.454
298°	0.4695
299°	0.4848
300°	0.5
301°	0.515
302°	0.5299
303°	0.5446
304°	0.5592
305°	0.5736
306°	0.5878
307°	0.6018
308°	0.6157
309°	0.6293
310°	0.6428
311°	0.6561
312°	0.6691
313°	0.682
314°	0.6947
315°	0.7071
316°	0.7193
317°	0.7314
318°	0.7431
319°	0.7547
320°	0.766
321°	0.7771
322°	0.788
323°	0.7986
324°	0.809
325°	0.8192
326°	0.829
327°	0.8387
328°	0.848
329°	0.8572
330°	0.866
331°	0.8746
332°	0.8829
333°	0.891
334°	0.8988
335°	0.9063
336°	0.9135
337°	0.9205
338°	0.9272
339°	0.9336
340°	0.9397
341°	0.9455
342°	0.9511
343°	0.9563
344°	0.9613
345°	0.9659
346°	0.9703
347°	0.9744
348°	0.9781
349°	0.9816
350°	0.9848
351°	0.9877
352°	0.9903
353°	0.9925
354°	0.9945
355°	0.9962
356°	0.9976
357°	0.9986
358°	0.9994
359°	0.9998
360°	1

…

Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите нужную часть таблицы, на выделенном фоне нажмите правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».

Пример

Чему равен косинус 30? …

— Ищем в таблице соответствующее значение. Правильный ответ:  0.866

---

Автор: Bill4iam

---

Техническая информация тут Перевод единиц измерения величин Таблицы числовых значений Алфавиты, номиналы, единицы Математический справочник тут Физический справочник Химический справочник Материалы Рабочие среды Оборудование Инженерное ремесло Инженерные системы Технологии и чертежи Личная жизнь инженеров Калькуляторы Поиск на сайте DPVAПоставщики оборудованияПолезные ссылкиО проектеОбратная связьОтветы на вопросы.Оглавление

Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса  / / Таблица синусов. Синусы углов от 0° — 360°. Углы с шагом в 1°. Таблица значений синусов углов. Поделиться:    Таблица синусов углов от 0° — 360°. Углы с шагом в 1°. Вариант для печати. sin(0°)=sin(360°)=0; точная, но чуть более сложная таблица ( с точностью до 1″) здесь. Углы 1° — 90° Углы 91° — 180° Углы 181° — 270° Углы 271° — 360° Угол Sin 1° sin= 0.0175 2° sin= 0.0349 3° sin= 0.0523 4° sin= 0.0698 5° sin= 0.0872 6° sin= 0.1045 7° sin= 0.1219 8° sin= 0.1392 9° sin= 0.1564 10° sin= 0.1736 11° sin= 0.1908 12° sin= 0.2079 13° sin= 0.225 14° sin= 0.2419 15° sin= 0.2588 16° sin= 0.2756 17° sin= 0.2924 18° sin= 0.309 19° sin= 0.3256 20° sin= 0.342 21° sin= 0.3584 22° sin= 0.3746 23° sin= 0.3907 24° sin= 0.4067 25° sin= 0.4226 26° sin= 0.4384 27° sin= 0.454 28° sin= 0.4695 29° sin= 0.4848 30° sin= 0.5 31° sin= 0.515 32° sin= 0.5299 33° sin= 0.5446 34° sin= 0.5592 35° sin= 0.5736 36° sin= 0.5878 37° sin= 0.6018 38° sin= 0.6157 39° sin= 0.6293 40° sin= 0.6428

90000 The Laws of Sines and Cosines 90001 90002 The 90003 Law of Sines 90004 establishes a relationship between the angles and the side lengths of ΔABC: 90005 90002 a / sin (A) = b / sin (B) = c / sin (C). 90005 90002 The relationship explains the plural «s» in 90003 Law of Sines 90004: there are 3 90003 sines 90004 after all. Another important relationship between the side lengths and the angles of a triangle is expressed by the 90003 Law of Cosines 90004. 90005 90002 c² = a² + b² — 2ab · cos (C) 90005 90002 Why do we use the plural «s» in the 90003 Law of Cosines 90004? The expression itself involves a single 90003 cosine 90004, but by rotation (or, as A.Einstein might have said, by symmetry) similar formulas are valid for other angles: 90005 90002 a² = b² + c² — 2bc · cos (A) and b² = c² + a² — 2ca · cos (B) 90005 90002 In fact, I do not know the exact sources of the existing nomenclature. But there is another plurality involved with the 90003 Law of Cosines 90004. Most of the proofs of the Law consider separately the cases of acute, right, and obtuse triangles. This is a manifestation of the fact that cosine, unlike sine, changes its sign in the range 0 ° — 180 ° of valid angles of a triangle.Sine is always positive in this range; cosine is positive up to 90 ° where it becomes 0 and is negative afterwards. 90005 90002 The essence of the 90003 Law of Cosines 90004 has been known to Euclid, who proved the obtuse case as II.12 and the acute case as II.13. Here’s how the former could be translated into plain English [Euclid, p. 403-404]: 90005 90002 90035 In obtuse-angled triangles the square on the side subtending the obtuse angle is greater than the squares on the sides containing the obtuse angle by twice the rectangle contained by one of the sides about the obtuse angle, namely that on which the perpendicular falls, and the straight line cut off outside by the perpendicular towards the obtuse angle.90036 90005 90002 With the reference to the diagram on the right, Euclid’s proof amounts to the following derivation. 90005 90002 By the Pythagorean theorem, 90005 90002 BC² = BD² + CD², 90043 AC² = AD² + CD². 90005 90002 Taking the difference we obtain, 90005 90047 90048 90049 BC² — AC² 90050 90049 = BD² — AD² 90050 90053 90048 90049 90050 90049 = (BD — AD) · (BD + AD) 90050 90053 90048 90049 90050 90049 = AB · (AB + 2AD) 90050 90053 90048 90049 90050 90049 = AB² + 2AB · AD, 90050 90053 90072 90002 which is II.12 in modern notations: BC² = AC² + AB² + 2AB · AD. (This is in fact the same proof as we used to show that the law of cosines is a direct consequence of a less general Pythagorean theorem. I am grateful to Douglas Rogers who suggested the reference to the 90003 Elements 90004. Also, the latest formula has a slightly different form discovered by Larry Hoehn that generalizes the Pythagorean theorem in a little different way.) 90005 90002 Here’s a couple of proofs from 90003 Proofs Without Words 90004 by Roger Nelsen [p.32-33]. The first one uses the power of a point with respect to a circle theorem, the other the theorem of Ptolemy. 90005 90002 90005 90002 The first proof assumes that 90084 C is acute, the second that it’s obtuse. (See if you can modify the diagrams to account for the remaining cases.) 90005 90002 In 90003 Trigonometric Delights 90004 [p. 216-217] Eli Maor employs the notion of 90003 projection 90004 to prove both Laws. 90005 90002 90005 90002 Taking projections of both AC and BC on the height h gives in all three cases 90005 90047 90048 90049 (1) 90050 90049 a · sin (B) = b · sin (A) (= h) 90050 90053 90072 90002 which proves the 90003 Law of Sines 90004 with additional identities obtained in a similar manner.(Einstein would probably rather avoid additional constructs by using a formula for the area S of a triangle: 2S = ab · sin (C) = bc · sin (A) = ca · sin (B).) If we take projections of AC and BC on AB the result will be 90005 90047 90048 90049 (2) 90050 90049 c = a · cos (B) + b · cos (A) 90050 90053 90072 90002 which is again the same in all three cases, although the sum here is 90003 algebraic 90004: one of the terms may be negative or zero. Maor remarks that it would be entirely appropriate to call the latter identity the 90003 Law of Cosines 90004 because it does contain 2 cosines with an immediate justification for the plural «s».90005 90002 The proof of the real Law now proceeds by squaring (2): 90005 90047 90048 90126 c² 90050 90128 = a² (cos B) ² + b² (cos A) ² + 2ab · cos (A) · cos (B) 90050 90053 90048 90132 90128 = a² (1 — (sin B) ²) + b² (1 — (cos A) ²) + 2ab · cos (A) · cos (B) 90050 90053 90048 90132 90128 = a² + b² — (a · sin (B)) (a · sin (B)) — (b · sin (A)) (b · sin (A)) + 2ab · cos (A) · cos (B) 90050 90053 90072 90002 Plug in equation (1): 90005 90047 90048 90126 c² 90050 90128 = a² + b² — a · sin (B) · b · sin (A) — a · sin (B) · b · sin (A) + 2ab · cos (A) · cos (B) 90050 90053 90048 90132 90128 = a² + b² + 2ab (cos (A) cos (B) — sin (A) sin (B)) 90050 90053 90048 90132 90128 = a² + b² + 2ab (cos (A + B)) 90050 90053 90048 90132 90128 = a² + b² + 2ab (cos (180 ° — C)) 90050 90053 90048 90132 90128 = a² + b² — 2ab (cos (C)) 90050 90053 90072 90002 A continuum of proofs for the 90003 Law of Cosines 90004 can be discovered by dissection [Plane & Fancy, p.38]. (However, these do not seem to work for acute angles C.) The proofs generalize that of the Pythagorean theorem by K.O. Friedrichs. The plane is now tessellated into two families of parallelograms with sides a and b and smaller angles of (C — 90 °) and squares of sides a and b. 90005 90002 90177 90178 90179 90180 This applet requires Sun’s Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun’s website at https: // www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet. 90181 90179 90005 90002 As mentioned by G. Frederickson [Plane & Fancy, p. 38-39], particular cases have been found by Rudolf Hunger (1921) and Erwin Dintzl (1931). 90005 90002 Of many other available proofs of the Law of Cosines, a proof without words is a direct generalization of Thâbit ibn Qurra’s proof of the Pythagorean proposition. There is, as well, an «unfolded variant.» Also, the Cosines Law admits a slightly different form discovered by Larry Hoehn that generalizes the Pythagorean theorem in a somewhat different way.90005 90180 References 90181 90190 90191 G. N. Frederickson, 90003 Dissections: Plane & Fancy 90004, Cambridge University Press, 1997. 90194 90191 T. L. Heath, 90003 Euclid: The Thirteen Books of the Elements 90004, v. 1, Dover, 1956 90194 90191 E. Maor, 90003 Trigonometric Delights 90004, Princeton University Press, 1998. 90194 90191 R. B. Nelsen, 90003 Proofs Without Words 90004, MAA, 1993 90194 90207 90208 90209 90208 90005 90212 | Contact | | Front page | | Contents | | Geometry | | Up | 90005 Copyright © 1996-2018 Alexander Bogomolny .90000 Sine, Cosine, Tangent 90001 90002 90003 Three Functions, but same idea. 90004 90005 90006 Right Triangle 90007 90002 Sine, Cosine and Tangent are the main functions used in Trigonometry and are based on a Right-Angled Triangle. 90005 90002 Before getting stuck into the functions, it helps to give a 90011 name 90012 to each side of a right triangle: 90013 90005 90015 90005 90017 90018 «Opposite» is opposite to the angle θ 90019 90018 «Adjacent» is adjacent (next to) to the angle θ 90019 90018 «Hypotenuse» is the long one 90019 90024 90002 90005 90002 90011 Adjacent 90012 is always next to the angle 90005 90002 And 90011 Opposite 90012 is opposite the angle 90005 90006 Sine, Cosine and Tangent 90007 90002 90011 Sine 90012, 90011 Cosine 90012 and 90011 Tangent 90012 (often shortened to 90011 sin 90012, 90011 cos 90012 and 90011 tan 90012) are each a 90011 ratio of sides 90012 of a right angled triangle: 90005 90002 90005 90002 For a given angle 90011 90003 θ 90004 90012 each ratio stays the same 90013 no matter how big or small the triangle is 90005 90002 To calculate them: 90005 90015 90011 Divide the length of one side by another side 90012 90005 90068 Example: What is the sine of 35 °? 90069 90002 90005 90002 Using this triangle (lengths are only to one decimal place): 90005 90074 90075 90076 sin (35 °) 90077 90076 = 90079 Opposite 90080 90081 Hypotenuse 90082 90077 90084 90075 90076 90077 90076 = 90079 2.8 90080 90081 4.9 90082 90077 90084 90075 90076 90077 90076 = 90011 0.57 … 90012 90077 90084 90075 90076 90077 90076 90077 90084 90075 90076 cos (35 °) 90077 90076 = 90079 Adjacent 90080 90081 Hypotenuse 90082 90077 90084 90075 90076 90077 90076 = 90079 4.0 90080 90081 4.9 90082 90077 90084 90075 90076 90077 90076 = 90011 0.82 … 90012 90077 90084 90075 90076 90077 90076 90077 90084 90075 90076 tan (35 °) 90077 90076 = 90079 Opposite 90080 90081 Adjacent 90082 90077 90084 90075 90076 90077 90076 = 90079 2.8 90080 90081 4.0 90082 90077 90084 90075 90076 90077 90076 = 90011 0.70 … 90012 90077 90084 90171 90006 Size Does Not Matter 90007 90002 The triangle can be large or small and the 90011 ratio of sides stays the same 90012.90005 90002 Only the angle changes the ratio. 90005 90002 Try dragging point «A» to change the angle and point «B» to change the size: 90005 90002 90005 90002 90005 90002 Good calculators have sin, cos and tan on them, to make it easy for you. Just put in the angle and press the button. 90005 90002 But you still need to remember 90011 what they mean 90012! 90005 90002 In picture form: 90005 90002 90005 90068 Practice Here: 90069 90006 Sohcahtoa 90007 90002 How to remember? Think 90011 «Sohcahtoa» 90012! 90005 90002 It works like this: 90005 90206 90075 90076 90002 90011 90003 Soh… 90004 90012 90005 90077 90076 90002 90011 S 90012 ine = 90011 O 90012 pposite / 90011 H 90012 ypotenuse 90005 90077 90084 90075 90076 90002 90011 90003 … cah … 90004 90012 90005 90077 90076 90002 90011 C 90012 osine = 90011 A 90012 djacent / 90011 H 90012 ypotenuse 90005 90077 90084 90075 90076 90002 90011 90003 … toa 90004 90012 90005 90077 90076 90002 90011 T 90012 angent = 90011 O 90012 pposite / 90011 A 90012 djacent 90005 90077 90084 90171 90002 You can read more about sohcahtoa… please remember it, it may help in an exam! 90005 90006 Angles From 0 ° to 360 ° 90007 90002 Move the mouse around to see how different angles (in radians or degrees) affect sine, cosine and tangent. 90005 90002 In this animation the hypotenuse is 1, making the Unit Circle. 90005 90002 Notice that the adjacent side and opposite side can be positive or negative, which makes the sine, cosine and tangent change between positive and negative values ​​also. 90005 90206 90075 90076 90003 «Why did not 90011 sin 90012 and 90013 90011 tan 90012 go to the party?» 90013 «… just 90011 cos 90012! «90004 90077 90084 90171 90002 90005 90006 Examples 90007 90068 Example: what are the sine, cosine and tangent of 30 °? 90069 90002 The classic 30 ° triangle has a hypotenuse of length 2, an opposite side of length 1 and an adjacent side of √3: 90013 90005 90015 90005 90002 Now we know the lengths, we can calculate the functions: 90013 90005 90308 90075 90076 90002 90011 Sine 90012 90005 90077 90076 90077 90076 sin (30 °) = 1/2 = 0.5 90077 90084 90075 90076 90002 90011 Cosine 90012 90005 90077 90076 90077 90076 cos (30 °) = 1.732 / 2 = 0.866 … 90077 90084 90075 90076 90002 90011 Tangent 90012 90005 90077 90076 90077 90076 tan (30 °) = 1 / 1.732 = 0.577 … 90077 90084 90171 90002 (get your calculator out and check them!) 90005 90068 Example: what are the sine, cosine and tangent of 45 °? 90069 90002 The classic 45 ° triangle has two sides of 1 and a hypotenuse of √2: 90013 90005 90015 90005 90308 90075 90076 90002 90011 Sine 90012 90005 90077 90076 90077 90076 sin (45 °) = 1/1.414 = 0.707 … 90077 90084 90075 90076 90002 90011 Cosine 90012 90005 90077 90076 90077 90076 cos (45 °) = 1 / 1.414 = 0.707 … 90077 90084 90075 90076 90002 90011 Tangent 90012 90005 90077 90076 90077 90076 tan (45 °) = 1/1 = 1 90077 90084 90171 90006 Why? 90007 90002 Why are these functions important? 90005 90017 90018 Because they let us work out angles when we know sides 90019 90018 And they let us work out sides when we know angles 90019 90024 90002 90005 90068 Example: Use the 90011 sine function 90012 to find 90011 «d» 90012 90069 90002 We know: 90005 90017 90018 The cable makes a 90011 39 ° angle 90012 with the seabed 90019 90018 The cable has a 90011 30 meter length 90012.90019 90024 90002 And we want to know «d» (the distance down). 90005 90002 Start with: sin 39 ° = opposite / hypotenuse 90005 90002 sin 39 ° = d / 30 90005 90002 Swap Sides: d / 30 = sin 39 ° 90005 90002 Use a calculator to find sin 39 °: d / 30 = 0.6293 … 90005 90002 Multiply both sides by 30: d = 0.6293 … x 30 90005 90002 d = 90011 18.88 90012 to 2 decimal places. 90005 90015 The depth «d» is 90011 18.88 m 90012 90005 90006 Exercise 90007 90002 Try this paper-based exercise where you can calculate the sine function for all angles from 0 ° to 360 °, and then graph the result.It will help you to understand these relatively simple functions. 90005 90002 You can also see Graphs of Sine, Cosine and Tangent. 90005 90002 And play with a spring that makes a sine wave. 90005 90006 Less Common Functions 90007 90002 To complete the picture, there are 3 other functions where we divide one side by another, but they are not so commonly used. 90005 90002 They are equal to 90011 1 divided by cos 90012, 90011 1 divided by sin 90012, and 90011 1 divided by tan 90012: 90005 90463 90075 90076 90002 Secant Function: 90005 90077 90076 90077 90471 90011 sec (90003 θ 90004) = 90079 Hypotenuse 90080 90081 Adjacent 90082 90012 90077 90076 90077 90076 90003 (= 1 / cos) 90004 90077 90084 90075 90076 90002 Cosecant Function: 90005 90077 90076 90077 90471 90011 csc (90003 θ 90004) = 90079 Hypotenuse 90080 90081 Opposite 90082 90012 90077 90076 90077 90076 90003 (= 1 / sin) 90004 90077 90084 90075 90076 90002 Cotangent Function: 90005 90077 90076 90077 90471 90011 cot (90003 θ 90004) = 90079 Adjacent 90080 90081 Opposite 90082 90012 90077 90076 90077 90076 90003 (= 1 / tan) 90004 90077 90084 90171 90002 90005 90002 90005 .90000 Sine Cosine Tangent Chart. Each degree with special angles 90001 90002 This table provides the decimal approximation for each angle from 0 ° through 90 °. 90003 90004 90005 90006 90007 Angle 90008 90009 90006 90007 Sine 90008 90009 90006 90007 Cosine 90008 90009 90006 90007 Tangent 90008 90009 90022 90005 90006 0 ° 90009 90006 0 90009 90006 1 90009 90006 0 90009 90022 90005 90006 1 ° 90009 90006 0.01745 90009 90006 0.99985 90009 90006 0.01746 90009 90022 90005 90006 2 ° 90009 90006 0.03490 90009 90006 0.99939 90009 90006 0.03492 90009 90022 90005 90006 3 ° 90009 90006 0.05234 90009 90006 0.99863 90009 90006 0.05241 90009 90022 90005 90006 4 ° 90009 90006 0.06976 90009 90006 0.99756 90009 90006 0.06993 90009 90022 90005 90006 5 ° 90009 90006 0.08716 90009 90006 0.99619 90009 90006 0.08749 90009 90022 90005 90006 6 ° 90009 90006 0.10453 90009 90006 0.99452 90009 90006 0.10510 90009 90022 90005 90006 7 ° 90009 90006 0.12187 90009 90006 0.99255 90009 90006 0.12278 90009 90022 90005 90006 8 ° 90009 90006 0.13917 90009 90006 0.99027 90009 90006 0.14054 90009 90022 90005 90006 9 ° 90009 90006 0.15643 90009 90006 0.98769 90009 90006 0.15838 90009 90022 90005 90006 10 ° 90009 90006 0.17365 90009 90006 0.98481 90009 90006 0.17633 90009 90022 90005 90006 11 ° 90009 90006 0.19081 90009 90006 0.98163 90009 90006 0.19438 90009 90022 90005 90006 12 ° 90009 90006 0.20791 90009 90006 0.97815 90009 90006 0.21256 90009 90022 90005 90006 13 ° 90009 90006 0.22495 90009 90006 0.97437 90009 90006 0.23087 90009 90022 90005 90006 14 ° 90009 90006 0.24192 90009 90006 0.97030 90009 90006 0.24933 90009 90022 90005 90006 15 ° 90009 90006 0.25882 90009 90006 0.96593 90009 90006 0.26795 90009 90022 90183 90004 90005 90006 90007 Angle 90008 90009 90006 90007 Sine 90008 90009 90006 90007 Cosine 90008 90009 90006 90007 Tangent 90008 90009 90022 90005 90006 31 ° 90009 90006 0.51504 90009 90006 0.85717 90009 90006 0.60086 90009 90022 90005 90006 32 ° 90009 90006 0.52992 90009 90006 0.84805 90009 90006 0.62487 90009 90022 90005 90006 33 ° 90009 90006 0.54464 90009 90006 0.83867 90009 90006 0.64941 90009 90022 90005 90006 34 ° 90009 90006 0.55919 90009 90006 0.82904 90009 90006 0.67451 90009 90022 90005 90006 35 ° 90009 90006 0.57358 90009 90006 0.81915 90009 90006 0.70021 90009 90022 90005 90006 36 ° 90009 90006 0.58779 90009 90006 0.80902 90009 90006 0.72654 90009 90022 90005 90006 37 ° 90009 90006 0.60182 90009 90006 0.79864 90009 90006 0.75355 90009 90022 90005 90006 38 ° 90009 90006 0.61566 90009 90006 0.78801 90009 90006 0.78129 90009 90022 90005 90006 39 ° 90009 90006 0.62932 90009 90006 0.77715 90009 90006 0.80978 90009 90022 90005 90006 40 ° 90009 90006 0.64279 90009 90006 0.76604 90009 90006 0.83910 90009 90022 90005 90006 41 ° 90009 90006 0.65606 90009 90006 0.75471 90009 90006 0.86929 90009 90022 90005 90006 42 ° 90009 90006 0.66913 90009 90006 0.74314 90009 90006 0.90040 90009 90022 90005 90006 43 ° 90009 90006 0.68200 90009 90006 0.73135 90009 90006 0.93252 90009 90022 90005 90006 44 ° 90009 90006 0.69466 90009 90006 0.71934 90009 90006 0.96569 90009 90022 90005 90006 45 ° 90009 90006 0.70711 or 90009 90006 0.70711 or 90009 90006 1 90009 90022 90183 90004 90005 90006 90007 Angle 90008 90009 90006 90007 Sine 90008 90009 90006 90007 Cosine 90008 90009 90006 90007 Tangent 90008 90009 90022 90005 90006 61 ° 90009 90006 0.87462 90009 90006 0.48481 90009 90006 1.80405 90009 90022 90005 90006 62 ° 90009 90006 0.88295 90009 90006 0.46947 90009 90006 1.88073 90009 90022 90005 90006 63 ° 90009 90006 0.89101 90009 90006 0.45399 90009 90006 1.96261 90009 90022 90005 90006 64 ° 90009 90006 0.89879 90009 90006 0.43837 90009 90006 2.05030 90009 90022 90005 90006 65 ° 90009 90006 0.90631 90009 90006 0.42262 90009 90006 2.14451 90009 90022 90005 90006 66 ° 90009 90006 0.91355 90009 90006 0.40674 90009 90006 2.24604 90009 90022 90005 90006 67 ° 90009 90006 0.92050 90009 90006 0.39073 90009 90006 2.35585 90009 90022 90005 90006 68 ° 90009 90006 0.92718 90009 90006 0.37461 90009 90006 2.47509 90009 90022 90005 90006 69 ° 90009 90006 0.93358 90009 90006 0.35837 90009 90006 2.60509 90009 90022 90005 90006 70 90009 90022 90183.90000 Law of Sines and Cosines — When to use each formula, video tutorial with examples and practice problems. 90001 90002 The goal of this page is to help students better understand when to use the Law of Sines and when to use the Law of Cosines 90003 90004 When to Use Law of Sines vs Cosines? 90005 90006 90002 90008 90009 90003 90004 Problem 1 90005 90002 Can you use the Law of Sines , the Law of Cosines , Or neither to solve the unknown side in triangle 1 below? 90003 Show Answer 90002 Law of Sines 90003 90002 90018 90019 Just look at it 90020.2 — 2 \ cdot 20 \ cdot 13 \ cdot cos (66) $ 90003 90004 Problem 3 90005 90002 Law of Sines 90003 90002 90018 90019 Just look at it 90020. You can always immediately look at a triangle and tell whether or not you can use the Law of Sines. 90003 90002 You need either 2 sides and the non-included angle (like this triangle) or 2 angles and the non-included side. 90003 90002 Remember, the law of sines is all about opposite pairs. 90003 90002 In this case, we have a side of length 16 opposite a known angle of $$ 115 ^ {\ circ} $$ (first opposite pair) and we want to find the angle opposite the known side of length 32 .{\ Circ})} {16} = \ frac {sin (\ red x)} {32} $ 90003 90004 Problem 4 90005 90002 Decide which formula (Law of Sines / Cosines) you would use to calculate the value of $$ \ red x $$ below? After you decide that, try to set up the equation (Do not solve — just substitute into the proper formula). 90003 Show Answer 90002 Law of Cosines 90003 90002 Since you know 3 sides, and are trying to find an angle this is Law of Cosines problem. 90003 90002 First Step $ 8 ^ 2 = 5 ^ 2 + 6 ^ 2 -2 (5) (6) \ cdot cos (\ red x) $ 90003 90004 Problem 5 90005 90002 Decide which formula (Law of Sines / Cosines) you would use to calculate the value of $$ \ red x $$ below? After you decide that, try to set up the equation (Do not solve — just substitute into the proper formula).90003 .