Персональный сайт — основные тождества, с сайта http://schoolife.ru
Вся информация с других сайтов… и не проверена…
В этой части речь идет о соотношении
Эта формула позволяет найти синус числа, если известен его косинус, и найти косинус числа, если известен его синус.
Формула выводится из известного уравнения окружности: если окружность имеет центр в начале координат, то сумма квадратов координат любой ее точки равна квадрату ее радиуса: . Так как для любого числа x на числовой окружности абсцисса равна косинусу, а ордината синусу и при этом радиус окружности равен единице, то из формулы окружности непосредственно следует:
При использовании этой формулы нужно учитывать, чему равно само число х. Если хоканчивается в первой четверти, его синус и косинус положительны, и тогда и .
Если х оканчивается во второй четверти, его синус положителен, а косинус отрицателен, и тогда и .
Если хоканчивается в третьей четверти, его синус и косинус отрицательны, и . Если же х оканчивается в четвертой четверти, его синус отрицателен, а косинус положителен, и тогда и .
Формулы для вычисления тангенса и котангенса.
Зная синус и косинус числа, мы находим его тангенс и его котангенс по определениям: , . Отсюда следует, что произведение тангенса и котангенса равно единице:
.
Поэтому, зная тангенс числа, котангенс мы находим сразу, и наоборот.
Существенно, что указанными тремя формулами можно пользоваться не всегда. Первая формула неприменима, если , вторая неприменима, если , третья неприменима во всех этих случаях, то есть при , где n — любое целое число.
Формула, связывающая косинус и тангенс.
Зная косинус, можно найти синус, а затем и тангенс. Но обратный путь — от тангенса к косинусу — более сложен. Впрочем, существует формула, которая позволяет оба эти пути проходить сразу.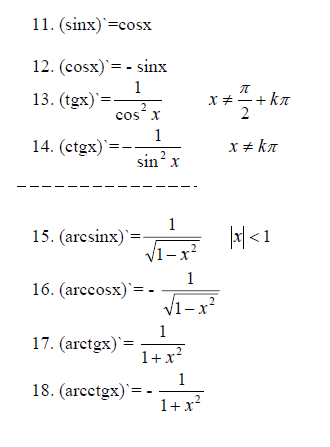
Это формула, в которой всего две функции — косинус и тангенс:.
Доказательство. , ч.т.д.
Пользоваться этой формулой можно только если .
С ее помощью можно найти тангенс числа х, если известен косинус х, и найти косинус числа х, если известен тангенс х. Однако, при этом нужно знать, в какой четверти оканчивается число х. Это скажется на операции извлечения корня. Если число х оканчивается в первой четверти, его косинус и его тангенс положительны, если во второй, — они оба отрицательны, если в третьей, то косинус отрицателен, а тангенс положителен, а если в четвертой, то косинус положителен, а тангенс отрицателен. Зная синус, можно найти косинус, а затем и котангенс. Но обратный путь — от котангенса к синусу — более сложен. Впрочем, существует формула, которая позволяет оба эти пути проходить сразу. Это формула, в которой всего две функции: синус и котангенс:
Доказательство.
2 )(два х в квадрате) — Школьные Знания.net
Все предметы
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Информатика
Українська література
Қазақ тiлi
Экономика
Музыка
Беларуская мова
Французский язык
Немецкий язык
Психология
Оʻzbek tili
Кыргыз тили
Астрономия
Физкультура и спорт
( ^-степень пример 2x^2 )(два х в квадрате)
Ответ дан
nafanya2014
1) f`(x)=(5x³-4x²)`=15x²-8x
f`(2)=15·4-8·2=44
2) f`(x)=(2sinx+cosx-ctgx)`=2(sinx)`+(cosx)`-(ctgx)`=
= 2cox-sinx+(1/sin²x)
f`(π/6)=2·cos(π/6)-sin(π/6)+(1/sin²(π/6))=(2√3/2)- (1/2)+(1/(1/4))=√3-0,5+4=3,5+√3
3) f`(x)=(3(2x-1)⁵¹)`=3·(2x-1)⁵⁰·(2x-1)`=6·(2x-1)⁵⁰
f`(2)=6·(2·2-1)⁵⁰=6·3⁵⁰
4) f«(x)=(√(2x²+1))`=(1/2√(2х²+1))·(2х²+1)`=4x/2√(2х²+1)=2х/√(2х²+1)
f`(7)=14/√99
5) f`(x)=(sinx+cosx/sinx-cosx)`=(sinx+cox)`·(sinx-cosx)-(sinx+cosx)·(sinx-cosx)`/(sinx-cosx)²=
=(cosx-sinx)(sinx-cosx)-(sinx+cosx)(cosx+sinx)/(sinx-cosx)²=
=-4(sin²x+cos²x)/(sinx-cosx)²=-4/(sinx-cosx)²
f(п/2)=-4/(1-0)²=-4
6) f`(x)=(4cos²2x)`=8cos2x·(cos2x)`=8cos2x·(-sin2x)·(2x)`=-8sin4x
f`(π/6)=-8sin(2π/3)=-8sin(π/3)=-4√3
Ejercicios con ecuaciones trigonometricas | SuperProf
Para Resolver Las Siguientes Ecuaciones Trigonométriacas es Necesario Record La Propiedad de la función inversa:
= x
1
Despejamos la, hacired aleeale areleding aellieed arielde arieldies arieldies areelieed arieldies arieldies areelieed arieldies
Localizamos en la tabla el valor para
Nos ubicamos en el del seno , es decir, el eje y , ahora localizamos el valor en el eje, por ultimo nos desplazamos a los puntos que atraviesan la circunferencia y que pasan por.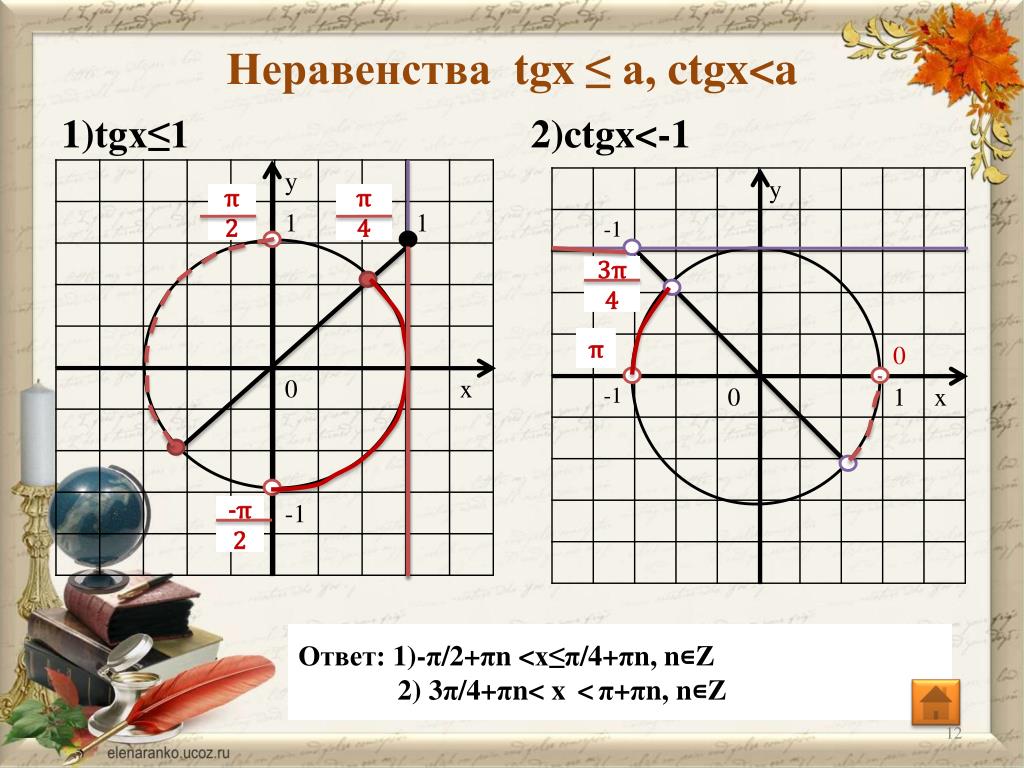
Estos valores serán el resultado de la ecuación
2
Despejamos la variable x, haciendo uso de la propiedad del inverso:
Localizamos en la tabla el valor para
Nos ubicamos en el del cos , es decir, el eje x , ahora localizamos el valor en el eje, por ultimo nos desplazamos a los puntos que atraviesan la circunferencia y que pasan por. Estos valores serán el resultado de la ecuación
3
Despejamos la variable x, haciendo uso de la propiedad del inverso:
En nuestra tabla, visualicemos una tangente de altura cero, obviamente al buscar el valor en el círculo unitario encontraremos que corresponde a cero grados, entonces:
4
Despejamos la variable x , haciendo uso de la propiedad del inverso:
Localizamos en la tabla el valor para
en el Nosubica0025 sen , es decir, el eje y , ahora localizamos el valor en el eje, por ultimo nos desplazamos a los puntos que atraviesan la circunferencia y que pasan por.
5
Despejamos la variable x, haciendo uso de la propiedad del inverso:
Localizamos en la tabla el valor пункт
Nos ubicamos en el del cos , es decir, el eje x , ahora localizamos el valor en el eje, por ultimo nos desplazamos a los puntos que atraviesan la circunferencia y que pasan por. Estos valores serán el resultado de la ecuación
6
Despejamos la variable x, haciendo uso de la propiedad del inverso:
Este ejercicio se mostró en el ejemplo a principio de la Lección donde podrás observar laпредставительствографика.
Visualizamos una recta tangente de altura , trazamos una linea desde esa altura hasta el origen y observamos el punto de intersección con la circunferencia, buscamos el valor de ese punto en nuestro círculo unitario y obtenemos el valor de la ecuación:
7
Despejamos la variable x, haciendo uso de la propiedad del inverso:
Localizamos en la el valor para
nos ubicamos en del el el valor para
nos ubicamos en del el el valor valor
nos ubic en del el el valor valor
.
es decir, el eje y , ahora localizamos el valor en el eje, por ultimo nos desplazamos a los puntos que atraviesan la circunferencia y que pasan por. Estos valores serán el resultado de la ecuación
8
Despejamos la variable x, Haciendo uso de la Propiedad del Inverso:
ubicamos en el del cos , es decir, el eje x , ahora localizamos el valor en el eje, por ultimo nos desplazamos a los puntos que atraviesan la circunferencia y que pasan por. Estos valores serán el resultado de la ecuación
Despejamos la variable x, haciendo uso de la propiedad del inverso:
ubic. , trazamos una linea desde esa altura hasta el origen y observamos el punto de intersección con la circunferencia, buscamos el valor de ese punto en nuestro círculo unitario y obtenemos el valor de la ecuación:10
Despejamos la variable x, haciendo uso de la propiedad del inverso:
localizam en la lamamos ana enamas en lamamos en lamamos en laisa enor el del sen , es decir, el eje y , ahora localizamos el valor en el eje, por ultimo nos desplazamos a los puntos que atraviesan la circunferencia y que pasan por.
Estos valores serán el resultado de la ecuación
11
Despejamos la variable x, haciendo uso de la propiedad del inverso:
9000 2 Localizam en La La La La La La La La La La La La La La La La La el del sen , es decir, el eje y , ahora localizamos el valor en el eje, por ultimo nos desplazamos a los puntos que atraviesan la circunferencia y que pasan por. Estos valores serán el resultado de la ecuación12
Despejamos la variable x, haciendo uso de la propiedad del inverso:
Localizamos en La Laba Valor Para PARA
Localizamos En La Tablor Valor Para
. cos , es decir, el eje x , ahora localizamos el valor en el eje, por ultimo nos desplazamos a los puntos que atraviesan la circunferencia y que pasan por.