1/sinx-sinx=cos(x-2π)*ctg(x-π) Доказать тождество — Учеба и наука
Лучший ответ по мнению автора | |||
| ||||||||||||||||
Другие ответы
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Боря купил 4 книги. Все книги без первой стоят 42 р., без второй — 40 р., без третьей — 38 р., без четвёртой — 36 р. Сколько стоит каждая книга?
Все книги без первой стоят 42 р., без второй — 40 р., без третьей — 38 р., без четвёртой — 36 р. Сколько стоит каждая книга?
Может ли у каждого из учащихся в классе быть ровно трое друзей в этом классе, если в классе: 1) 25 учащихся; 2) 18 учащихся ? ответ с решением
Решено
В пакете лежат несколько леденцов с разными вкусами, произведенных в разных странах. любые два леденца в пакете различаются либо вкусом, либо страной
Решено
На дне рождения у Пети нашлось трое гостей, которые вместе съели не менее 21 конфеты. Все присутствующие (гости и Петя) съели 60 конфет, причём не
Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его … 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30.
Пользуйтесь нашим приложением
Властивості sin(x), cos(x),tg(x), ctg(x)
Наведені та структуровані основні характеристики тригонометричних функцій sin(x), cos(x), tg(x), ctg(x), які є вкрай необхідними при дослідженні графіків та поведінки цих функцій, спрощенні тригонометричних виразів, обчисленні рівнянь та нерівностей.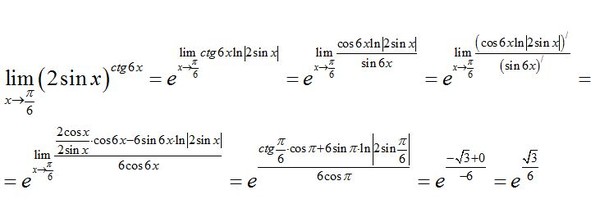
Основну частину присутніх тут формул Ви повинні вміти легко застосовувати на практичних, а для цього частину матеріалу потрібно завчити та знати.
Це не стосується всіх формул, але частину основних тригонометричних тотожностей, а також формули синуса чи косинуса подвійного кута слід запам’ятати.
Cинус y=sin(x)
Область визначення: D(y): x∈R
Область допустимих значень: E(y):y∈[-1;1], тобто -1≤sin(x)≤1.
Функція непарна: sin(-a)=sin(a).
Функція періодична з найменшим додатним періодом 2Pi: sin(a+2Pi)=sin(a).
Точки перетину з осями координат: (0,0) на осі Oy; (Pi·k;0), k∈Z на осі Ox.
Проміжки знакопостійності:
y>0, якщо x∈(2Pi·k;Pi+2Pi·k), k∈Z;
y<0, якщо x∈(Pi+2Pi·k;2Pi+2Pi·k), k∈Z.
Проміжки зростання: [-Pi/2+2Pi·k; Pi/2+2Pi·k], k∈Z, звідси ymax=1 у точках xmax=Pi/2+2Pi·k.
Проміжки спадання: [Pi/2+2Pi·k; 3Pi/2+2Pi·k], k∈Z, звідси ymin=-1 у точках xmin=-Pi/2+2Pi·k.
Косинус y=cos(x)
Область визначення: D(y): x∈R
Область значень: E(y):y∈[-1;1], тобто -1≤cos(x)≤1.
Функція парна: cos(-a)=cos(a).
Функція періодична з найменшим додатним періодом 2Pi: cos(a+2Pi)=cos(a).
Точки перетину з осями координат: (0;1) на осі Oy, (Pi/2+Pi·k;0), k∈Z на осі Ox;
Проміжки знакопостійності:
y>0, якщо x∈(-Pi/2+2Pi·k;Pi/2+2Pi·k), k∈Z;
y<0, якщо x∈(Pi/2+2Pi·k;3Pi/2+2Pi·k), k∈Z.
Проміжки зростання: [Pi+2Pi·k; 2Pi·k], k∈Z, звідси ymax=1 у точках xmax= 2Pi·k.
Проміжки спадання: [2Pi·k; Pi+2Pi·k], k∈Z, звідси ymin=-1 у точках xmin= Pi+2Pi·k.
Тангенс y=tg(x)
Область визначення: D(y):x≠Pi/2+Pi·k, k∈Z;
Область значень: E(y): y∈R, тобто -∞≤tg(x)≤+∞.
Функція непарна tg(-a)=-tg(a).
Функція періодична з найменшим додатним періодом Pi: tg(a+Pi)=tg(a).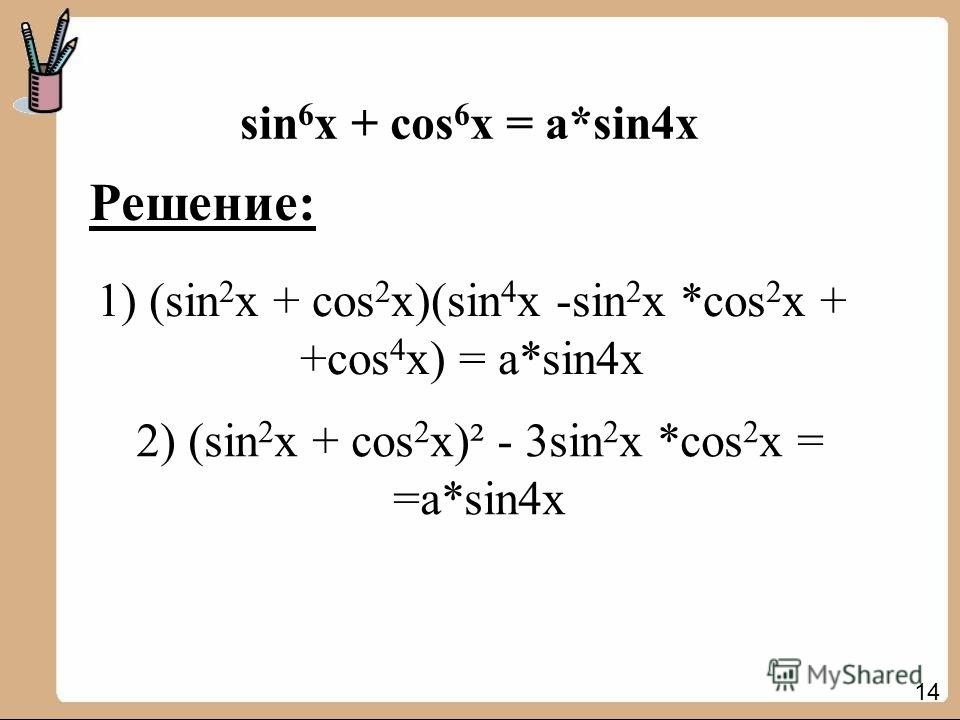
Точки перетину з осями координат: (0;0) на осі Oy; (Pi·k;0), k∈Z на осі Ox.
Проміжки знакопостійності:
y>0, якщо x∈(Pi·k;Pi/2+Pi·k), k∈Z;
y<0, якщо x∈(-Pi/2+Pi·k; Pi·k), k∈Z .
Проміжки зростання: (-Pi/2+Pi·k; Pi/2+Pi·k), k∈Z.
Найменших і найбільших значень функція не має .
Котангенс y=ctg(x)
Область визначення: D(y):x≠ Pi·k, k∈Z;
Область значень: E(y): y∈R, тобто -∞≤ctg(x)≤+∞.
Функція непарна ctg(-a)=-ctg(a).
Функція періодична з найменшим додатним періодом Pi: ctg(a+Pi)=ctg(a).
Точки перетину з осями координат:
не перетинає вісь Oy;
(Pi/2+Pi·k;0), k∈Z на осі Ox
Проміжки знакопостійності:
y>0, якщо x∈(Pi·k;Pi/2+Pi·k), k∈Z;
y<0, якщо x∈(Pi/2+Pi·k;Pi+Pi·k), k∈Z.
Проміжки спадання: (Pi·k;Pi+Pi·k), k∈Z.
Найменших і найбільших значень функція не має.
Значення тригонометричних функцій для деяких кутів:
α | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 |
sinα | 0 | 1/2 | √2/2 | √3/2 | 1 | 0 | -1 |
cosα | 1 | √3/2 | √2/2 | 1/2 | 0 | -1 | 0 |
tgα | 0 | √3/3 | 1 | √3 | — | 0 | — |
ctgα | — | √3 | 1 | √3/3 | 0 | — | 0 |
Формули зведення:
Функція | 900+α | 1800+α | 2700+α | -α | 900-α | 1800-α | 2700-α |
sinα | cosα | -sinα | -cosα | -sinα | cosα | sinα | -cosα |
cosα | -sinα | -cosα | sinα | cosα | sinα | -cosα | -sinα |
tgα | -ctgα | tgα | -ctgα | -tgα | ctgα | -tgα | ctgα |
ctgα | -tgα | ctgα | -tgα | -ctgα | tgα | -ctgα | tgα |
Знаки тригонометричних функцій:
Зв’язок між тригонометричними функціями одного аргументу:
У наведених формулах перед знаком радикала слід взяти знак «плюс» або «мінус»
залежно від того, в якій чверті лежить кут α саме так, щоб знак тригонометричної
функції, який стоїть у лівій частині збігався зі знаком величини, що стоїть у правій
частині рівності.
Основні тригонометричні тотожності
Універсальна тригонометрична підстановка
Тригонометричні функції суми і різниці аргументів
Тригонометричні функції подвійного, потрійного і половинного
аргументів
Перетворення суми тригонометричних функцій у добуток
Перетворення добутку тригонометричних функцій у суму
Далі будуть наведені відповіді до поширених на практиці прикладів з тригонометрії на знаходження значень тригонометричних виразів, розв’язування рівнянь та нерівностей на яких буде показано всю силу наведених вище формул.
Мэтуэй | Популярные задачи
92| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | |||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
тригонометрия — Если $\sin x + \cos x = \frac{\sqrt{3} + 1}{2}$, то $\tan x + \cot x=?$
спросил
Изменено 11 лет, 5 месяцев назад
Просмотрено 4к раз
$\begingroup$
Привет 🙂
Я столкнулся с проблемой.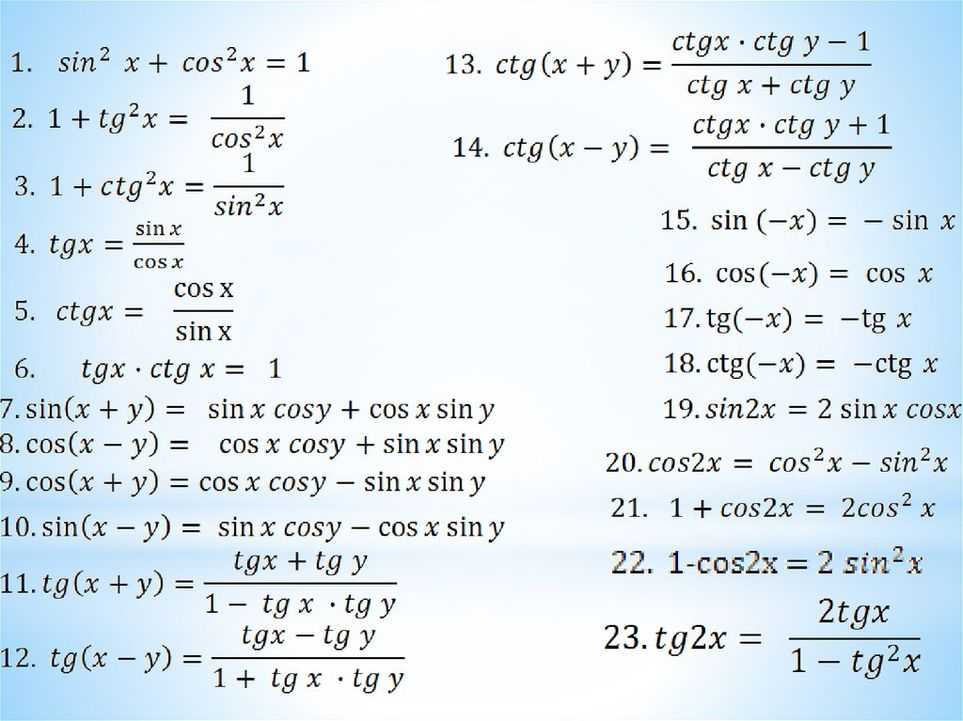 Если $\sin x + \cos x = \frac{\sqrt{3} + 1}{2}$, то сколько стоит $\tan x + \cot x$?
Если $\sin x + \cos x = \frac{\sqrt{3} + 1}{2}$, то сколько стоит $\tan x + \cot x$?
- 92 x & = \frac{4 + 2\sqrt{3}}{4}\\
1 + 2 \ sin x \ cos x &= 1 + \ frac {\ sqrt {3}} {2} \\
2 \ sin x \ cos x & = \ frac {\ sqrt {3}} {2} \\
\sin x \cos x &= \frac{\sqrt{3}}{4}\\
\tan x + \cot x = \frac{1}{\sin x\cos x} &= \frac{4\sqrt{3}}{3}.
\end{выравнивание*}
$\endgroup$
$\begingroup$
$\endgroup$
$\begingroup$
Так как $\tan x=\frac{\sin x}{\cos x}$ и $\cot x=\cdots$ (аналогично тангенсу), вы можете переписать $\tan x+\cot x$ в терминах синус и косинус. Результат можно упростить до выражения, включающего произведение синуса и косинуса. Квадрат $\sin x+\cos x$ также можно упростить до выражения, включающего произведение синуса и косинуса. Вместе это дает ответ.
Однако , в данном конкретном случае $\sin x+\cos x=\frac{\sqrt{3}+1}{2}$ настоятельно предполагает $\sin x=\frac{\sqrt{3}} {2}$ и $\cos x=\frac{1}{2}$ (или наоборот), так как это произойдет для особенно подходящего значения $x$, что усложнит вычисление $\tan x+\cot x $ просто.
$\endgroup$
$\begingroup$
Другой более общий подход заключается в решении вашего уравнения относительно $x$. Так как это линейное по $\sin x$ и $\cos x$ можно преобразовать в квадратичное уравнение в $\tan \frac{x}{2}$ (см. этот ответ): 9{2}-2y-1+\frac{1+% \sqrt{3}}{2}=0$$
и найти $y$
$$y_{1}=\frac{1}{3}\sqrt{3},y_{2}=2 -\sqrt{3}$$
Отсюда
$$x_{1}=2\arctan \frac{1}{3}\sqrt{3}=\frac{1}{3}\pi $$
или
$$x_{2}=2\arctan\left( 2-\sqrt{3}\right) =\frac{1}{6}\pi .$$
И, наконец,
$$\ tan \frac{1}{3}\pi +\cot \frac{1}{3}\pi =\frac{4}{3}\sqrt{3}$$
или
$$\tan \ frac{1}{6}\pi +\cot \frac{1}{6}\pi =\frac{4}{3}\sqrt{3}.$$
$\endgroup$
$\begingroup$
Подсказка: запишите $\tan(x) + \cot(x)$ через $\sin(x)$ и $\cos(x)$ с общим знаменателем.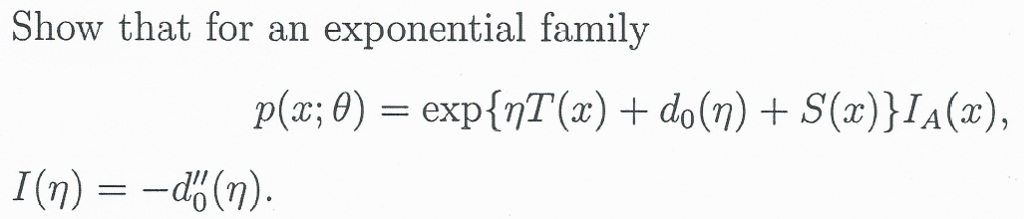

 2(x))/sin(x) = 1/sin(x) — sin(x) — что и требовалось доказать
2(x))/sin(x) = 1/sin(x) — sin(x) — что и требовалось доказать 11.16
11.16