Система линейных уравнений это: Решение систем линейных уравнений — как решать СЛАУ методами Гаусса, Крамера, подстановки и почленного сложения

Система линейных алгебраических уравнений | это… Что такое Система линейных алгебраических уравнений?

Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида

(1)

Система линейных уравнений от трёх переменных определяет набор плоскостей. Точка пересечения является решением.

Здесь  — количество уравнений, а  — количество неизвестных. x₁, x₂, …, x_n — неизвестные, которые надо определить. a₁₁, a₁₂, …, a_mn — коэффициенты системы — и b₁, b₂, … b_m — свободные члены — предполагаются известными^[1]. Индексы коэффициентов (a_ij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно

[2].

Система (1) называется однородной, если все её свободные члены равны нулю (b₁ = b₂ = … = b_m = 0), иначе — неоднородной.

Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.

Решение системы (1) — совокупность n чисел c₁, c₂, …, c_n, таких что подстановка каждого c_i вместо x_i в систему (1) обращает все её уравнения в тождества.

Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.

Совместная система вида (1) может иметь одно или более решений.

Решения c₁⁽¹⁾, c₂⁽¹⁾, …, c

_n⁽¹⁾ и c₁⁽²⁾, c₂⁽²⁾, …, c_n⁽²⁾ совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:

c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).

Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.

Содержание 1 Матричная форма 2 Эквивалентные системы линейных уравнений 3 Методы решения 3.1 Прямые методы 3.2 Итерационные методы 4 См. также 5 Примечания 6 Ссылки

Матричная форма

Система линейных уравнений может быть представлена в матричной форме как:

или:

.

Здесь  — это матрица системы,  — столбец неизвестных, а  — столбец свободных членов. Если к матрице приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.

Эквивалентные системы линейных уравнений

Системы линейных уравнений называются эквивалентными, если множество их решений совпадает, то есть любое решение одной системы одновременно является решением другой, и наоборот.

Систему, эквивалентную данной, можно получить, в частности, заменив одно из уравнений на это уравнение, умноженное на любое отличное от нуля число. Эквивалентную систему можно получить также, заменив одно из уравнений суммой этого уравнения с другим уравнением системы. В общем, замена уравнения системы на линейную комбинацию уравнений даёт систему, эквивалентную исходной.

Система линейных алгебраических уравнений

эквивалентна системе

,

где  — невырожденная матрица.

В частности, если сама матрица  — невырожденная, и для неё существует обратная матрица , то решение системы уравнений можно формально записать в виде

.

Методы решения

Прямые (или точные) методы позволяют найти решение за определённое количество шагов. Итерационные методы основаны на использовании повторяющегося процесса и позволяют получить решение в результате последовательных приближений.

Прямые методы

• Метод Гаусса
• Метод Гаусса — Жордана
• Метод Крамера
• Матричный метод
• Метод прогонки (для трёхдиагональных матриц)
• Разложение Холецкого или метод квадратных корней (для положительно-определённых симметричных и эрмитовых матриц)
• Метод вращений^[3]

Итерационные методы

Итерационные методы устанавливают процедуру уточнения определённого начального приближения к решению.

При выполнении условий сходимости они позволяют достичь любой точности просто повторением итераций. Преимущество этих методов в том, что часто они позволяют достичь решения с заранее заданной точностью быстрее, а также позволяют решать большие системы уравнений. Суть этих методов состоит в том, чтобы найти неподвижную точку матричного уравнения

,

эквивалентного начальной системе линейных алгебраических уравнений. При итерации в правой части уравнения заменяется, например, в методе Якоби (метод простой итерации) приближение, найденное на предыдущем шаге:

.

Среди итерационных методов можно отметить самые популярные:

• Метод Якоби (метод простой итерации)^{[источник не указан 277 дней]}
• Метод Гаусса — Зейделя
• Метод релаксации
• Многосеточный метод
• Метод Монтанте
• Метод Абрамова (пригоден для решения небольших СЛАУ)
• Метод обобщённых минимальных невязок (англ.)
• Метод бисопряжённых градиентов (англ. )
• Стабилизированный метод бисопряжённых градиентов (англ.)
• Квадратичный метод сопряжённых градиентов (англ.)
• Метод квази-минимальных невязок (QMR)

См. также

• Недоопределённая система
• Теорема Кронекера — Капелли
• Решение систем линейных алгебраических уравнений
• Предобуславливание

Примечания

1. ↑ В рамках данной статьи коэффициенты системы, свободные члены и неизвестные считаются действительными числами, хотя они могут быть комплексными или даже сложными математическими объектами с условием, что для них определены операции умножения и сложения.
2. ↑ Ильин В. А., Позняк Э. Г. Линейная алгебра: Учебник для вузов. — 6-е изд., стер. — М.: ФИЗМАТЛИТ, 2004. — 280 с.
3. ↑ Вержбицкий В. М. Основы численных методов. — М.: Высшая школа, 2009. — С. 80—84. — 840 с. — ISBN 9785060061239

Ссылки

• Куксенко С. П., Газизов Т. Р. Итерационные методы решения системы линейных алгебраических уравнений с плотной матрицей. — Томск: Томский государственный университет, 2007. — 208 с. ISBN 5-94621-226-5
• Решение СЛАУ онлайн
• Участник:Koctik/Решение СЛАУ на VBA

5. Системы линейных уравнений

Раздел 5. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

Системы линейных уравнений

Основные понятия

Системой линейных алгебраических уравнений,

содержащей т уравнений и п неизвестных, называется система вида

где числа а_ij, i=, j= называются коэффициентами системы, числа b_i – свободными членами. Подлежат нахождению числа х_п.

Такую систему удобно записывать в компактной матричной форме .

Здесь А – матрица коэффициентов системы, называемая основной матрицей:

,

– вектор-столбец из неизвестных х_j, – вектор-столбец из свободных членов b_i.

Расширенной матрицей системы называется матрица системы, дополненная столбцом свободных членов

.

Решением системы называется п значений неизвестных х₁=с₁, х₂=с₂, …, х_п=с_п, при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы-столбца .

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.

Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется

частным решением системы. Совокупность всех частных решений называется общим решением.

Решить систему – это значит выяснить, совместна она или не совместна. Если система совместна, то найти ее общее решение.

Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.

Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками матрицы.

Система линейных уравнений называется однородной, если все свободные члены равны нулю:

Однородная система всегда совместна, так как х₁=х₂=…=х_п=0 является решением системы.

Это решение называется нулевым или тривиальным.

Решение систем линейных уравнений

Пусть дана произвольная система т линейных уравнений с п неизвестными

Теорема 1 (Кронекера-Капелли). Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы равен рангу основной матрицы.

Теорема 2. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.

Теорема 3. Если ранг совместной системы меньше числа неизвестных, то система имеет бесконечное множество решений.

П р и м е р. Исследовать на совместность систему

Решение. , r(A)=1; , r()=2, .

Таким образом, r(A) r(), следовательно, система несовместна.

Решение невырожденных систем линейных уравнений. Формулы Крамера

Пусть дана система п линейных уравнений с п неизвестными

или в матричной форме А∙Х=В.

Основная матрица А такой системы – квадратная. Определитель этой матрицы называется определителем системы. Если определитель системы отличен от нуля, то система называется невырожденной.

Найдем решение данной системы уравнений в случае ∆0. умножив обе части уравнения А∙Х=В слева на матрицу А^1, получим А^1∙ А∙Х= А^1∙В. Поскольку А^1∙ А=Е и Е∙Х=Х, то Х= А^1∙ В. Данный способ решения системы называют матричным.

Из матричного способа вытекают формулы Крамера , где ∆ – определитель основной матрицы системы, а ∆_i – определитель, полученный из определителя ∆ путем замены i-го столбца коэффициентов столбцом из свободных членов.

П р и м е р. Решить систему

Решение. , 70, , . Значит, х₁=, х₂=.

Решение систем линейных уравнений методом Гаусса

Метод Гаусса состоит в последовательном исключении неизвестных.

Пусть дана система уравнений

Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому (в частности, треугольному) виду.

где k ≤ п, а_ii  0, i=. Коэффициенты а_ii называются главными элементами системы.

На втором этапе (обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы.

Замечания:

1. Если ступенчатая система оказывается треугольной, т. е. k=n, то исходная система имеет единственное решение. Из последнего уравнения находим х_п, из предпоследнего уравнения находим х_п1, далее поднимаясь по системе вверх, найдем все остальные неизвестные.

2. На практике удобнее работать с расширенной матрицей системы, выполняя все элементарные преобразования над ее строками. Удобно, чтобы коэффициент а₁₁ был равен 1(уравнения переставить местами, либо разделить на а₁₁1).

П р и м е р. Решить систему методом Гаусса

Решение. В результате элементарных преобразований над расширенной матрицей системы

~~~

~

исходная система свелась к ступенчатой:

Поэтому общее решение системы: x₂=5x₄ 13x₃ 3; x₁=5x₄ 8x₃ 1.

Если положить, например, х₃=х₄=0, то найдем одно из частных решений этой системы х₁=1, х₂=3, х₃=0, х₄=0.

Систем однородных линейных уравнений

Пусть дана система линейных однородных уравнений

Очевидно, что однородная система всегда совместна, она имеет нулевое (тривиальное) решение.

Теорема 4. Для того, чтобы система однородных уравнений имела ненулевое решение, необходимо и достаточно, чтобы ранг ее основной матрицы был меньше числа неизвестных, т.е. r<n.

Теорема 5. Для того, чтобы однородная система п линейных уравнений с п неизвестными имела ненулевое решение, необходимо и достаточно, чтобы определитель ее основной матрицы был равен нулю, т. е. ∆=0.

Если система имеет ненулевые решения, то ∆=0.

П р и м е р. Решить систему

Решение. , r(A)=2 , п=3. Так как r<n, то система имеет бесконечное множество решений.

, . Стало быть, х₁==2х₃, х₂==3х₃ – общее решение.

Положив х₃=0, получим одно частное решение: х₁=0, х₂=0, х₃=0. Положив х₃=1, получим второе частное решение: х₁=2, х₂=3, х₃=1 и т.д.

Вопросы для контроля

• Что такое система линейных алгебраических уравнений?

• Поясните следующие понятия: коэффициент, свободный член, основная и расширенная матрицы.

• Какими бывают системы линейных уравнений? Сформулируйте теорему Кронкера-Капелли (о совместности системы линейных уравнений).

• Перечислите и поясните методы решения систем линейных уравнений.

5

Решение систем линейных уравнений путем исключения и замены

Система линейных уравнений представляет собой набор из двух или более линейных уравнений.

Мы можем решить систему уравнений алгебраически (путем исключения или замены) или

, построив график

.

Алгебраическое решение системы уравнений похоже на решение загадки. Каждое линейное уравнение дает подсказку, необходимую для решения загадочных значений каждой переменной.

Точно так же, как ответ на загадку должен согласовываться с каждой подсказкой, значения каждой переменной в системе уравнений должны согласовываться с каждым уравнением в системе.

Это означает, что как только мы найдем значения, которые делают каждое уравнение в системе одновременно верным, мы получим наше решение.

Рассмотрим следующую систему уравнений:

x+yx+3y​=6=16​

Наша загадка: если

и

, чему равны

и

?

Мы можем решить систему уравнений методом исключения-замены:

Исключить x и найти y:

x+y=6−(x+3y=16)

---

−2y

=−10

y

=

5

Подставьте y и найдите x, используя одно из уравнений системы:

x+y=6x+5=6x=1​

Тайна раскрыта!

Обычно мы видим системы линейных уравнений с одним решением, но они также могут не иметь решений или иметь бесконечное число решений в зависимости от того, если и как пересекаются линии уравнений.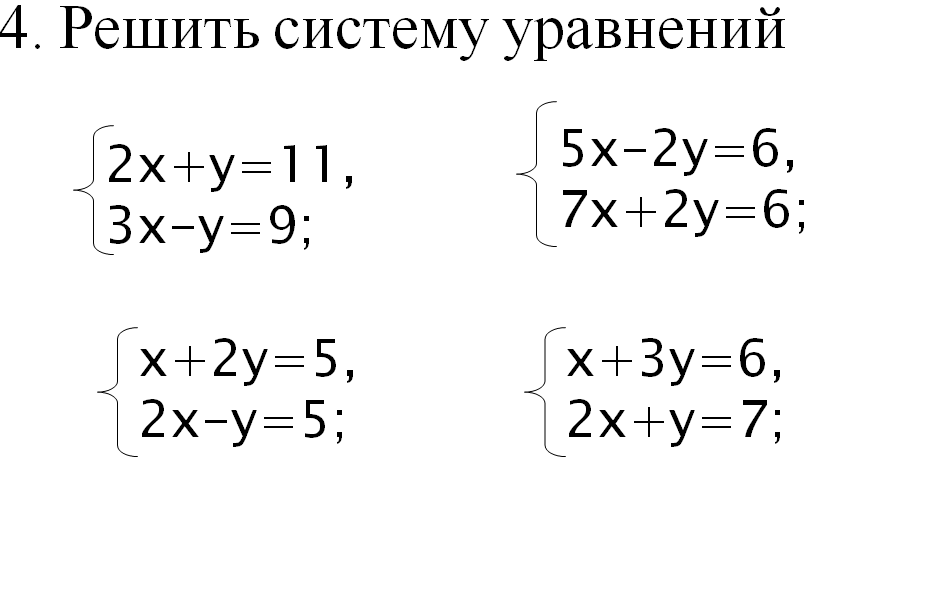

Как решить систему линейных уравнений с помощью графика?

Чтобы решить систему линейных уравнений с помощью графического метода, нам просто нужно построить график каждого уравнения в системе и найти точку пересечения всех линий.

Например, мы видим, что решение следующей системы уравнений равно (0,5):

x+yx+3y​=5=15​

Ознакомьтесь с нашим

Решением систем линейных уравнений по График

урок, чтобы узнать больше!

Ознакомьтесь с нашим калькулятором

или изучите наши уроки

и

Практикуйтесь в разделах

, чтобы больше узнать о решении систем линейных уравнений методом исключения и замены и проверить свои знания.

Вы также можете использовать меню быстрых ссылок слева, чтобы перейти к разделу по вашему выбору.

Вы также можете использовать раскрывающийся список «Быстрые ссылки» выше, чтобы перейти к разделу по вашему выбору.

Объяснение урока: Варианты решения системы линейных уравнений

В этом объяснении мы узнаем, как определить, имеет ли линейная система уравнений единственное решение, нет решения или бесконечное множество решений.

При работе с системой линейных уравнений легко предположить, что решение есть. Это решение может быть уникальным, когда все переменные имеют только одно возможное значение. В качестве альтернативы может быть бесконечно много решений, что означает, что каждая переменная может быть выражена в через некоторые независимые параметры. Хотя есть принципиальные отличия в этих двух типах решений они подобны друг другу в том смысле, что представляют системы линейных уравнений, которые действительно имеют решение. Мы широко классифицируем эти два типа решений, говоря, что они соответствуют системам линейных уравнений, которые «последовательный.» Также может случиться так, что невозможно получить решение для система линейных уравнений, и в этом случае проблема известна как «несовместимая». Например, если бы мы взяли систему линейных уравнений 𝑥+𝑦=−3,2𝑥+2𝑦=−8, тогда мы бы быстро обнаружили, что решить эту проблему невозможно. Думая в геометрическом смысле, это потому, что две линии, закодированные двумя уравнениями, параллельны, а это означает, что они никогда не пересекутся. В этом случае можно сказать, что система «непоследовательно», так как невозможно найти решение. Это можно более четко показать, переставив оба приведенных выше уравнения для 𝑦 так, чтобы они читались 𝑦=−3−𝑥,𝑦=−4−𝑥.

Теперь у нас есть 𝑦 как предмет обоих уравнений, и мы можем приравнять их, чтобы найти −3−𝑥=−4−𝑥, что сокращается, чтобы дать -3 = -4, что вопиюще абсурдно.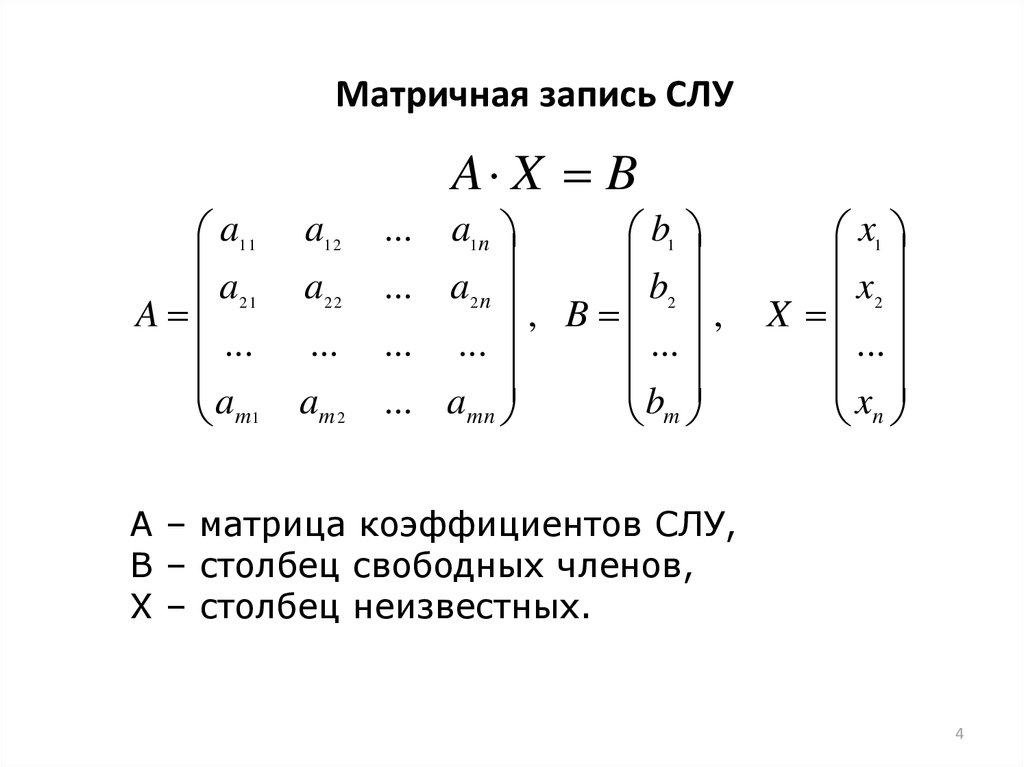 Учитывая это логическое несоответствие, мы говорим, что вся система линейных уравнений несовместна.

На основе этого предварительного примера, вероятно, стоит спросить себя, что мы могли бы ожидать увидеть, если бы мы работали с несовместной системой линейных уравнений. Возьмем, например, систему линейных уравнений 𝑥+𝑦+2𝑧=−7,2𝑥−𝑦−3𝑧=8,4𝑥−2𝑧=4.

На данном этапе не очевидно, имеет ли система линейных уравнений единственное решение, имеет ли бесконечно много решений, или вообще не имеет решений. В этом случае любой подходящий метод показал бы, что существует единственное решение со значениями 𝑥=−1,𝑦=2,𝑧=−4.

Мы отформатировали ответ очень особым образом, причины которого станут очевидны позже в объяснении. Теперь предположим, что вместо приведенной выше системы уравнений мы начали с системы линейных уравнений, которая привела нас к значениям 𝑥=−1,𝑦=2,0×𝑧=−4.

Последняя строка явно нелепа, так как предполагает, что 0=−4. В этом случае мы сказал бы, что система линейных уравнений несовместима, как это производит абсурд. Теперь мы потратим время на то, чтобы правильно определить, что это значит для системы. уравнения несовместны, перед подготовкой второго определения, которое позволит нам легче классифицировать системы уравнений как последовательное, так и непоследовательное.

Определение: Противоречащие системы линейных уравнений

Рассмотрим систему линейных уравнений от переменных 𝑥,𝑥,…,𝑥: 𝑎𝑥+𝑎𝑥 ⋯ 𝑎𝑥 = 𝑏, 𝑎𝑥+𝑎𝑥 ⋯ 𝑎𝑥 = 𝑏, ⋮⋮⋮ ⋮⋮⋮ 𝑎𝑥+𝑎𝑥 ⋯ 𝑎𝑥 = 𝑏. 

Тогда говорят, что система «непротиворечива», если существует хотя бы один набор значений для 𝑥,𝑥,…,𝑥 которые решают все уравнения. В противном случае система называется «несогласованной».

При попытке решить систему линейных уравнений наиболее распространенным методом, вероятно, является метод Гаусса-Жордана. где элементарные операции со строками используются для преобразования системы уравнений в выражение для решения, без изменения каких-либо свойств самой системы. Чаще всего это достигается тем, что сначала записывается система уравнений в удобном виде, инкапсулирующем всю информацию, которая в данном случае является соответствующим дополненным матрица коэффициентов.

Определение: расширенная матрица коэффициентов

Рассмотрим общую систему линейных уравнений с переменными 𝑥,𝑥,…,𝑥 и коэффициенты 𝑎: 𝑎𝑥+𝑎𝑥 ⋯ 𝑎𝑥 = 𝑏, 𝑎𝑥+𝑎𝑥 ⋯ 𝑎𝑥 = 𝑏, ⋮⋮⋮ ⋮⋮⋮ 𝑎𝑥+𝑎𝑥 ⋯ 𝑎𝑥 = 𝑏. 

«Расширенная матрица коэффициентов» системы ⎛⎜⎜⎜⎝𝑎𝑎 ⋯ ⋯ 𝑎𝑏 ⋮⋮ ⋱ ⋮⋮ 𝑎𝑎 ⋯ 𝑎𝑏⎞⎟⎟⎟⎠.

в переводе из систему линейных уравнений к ее расширенной матрице коэффициентов, мы по существу уже поняли одно из ключевых шагов для определения того, является ли система последовательной или противоречивой. Для пояснения этого метода возьмем дополненную матрица коэффициентов системы линейных уравнений, где есть 𝑛 уравнений с 𝑛 переменными, запись этих переменных над столбцами, которым они соответствуют:

Теперь предположим, что мы использовали элементарные операции со строками или любой другой подходящий метод для преобразования этого система в редуцированную эшелонированную форму таким образом, что каждая запись равна нулю, за исключением диагональных записей, все из которых имеют значение 1, и ̂𝑏 записи, который может принимать любые значения. Тогда запись этой матрицы коэффициентов в виде системы линейных уравнений дает 𝑥=̂𝑏,𝑥=̂𝑏,⋱⋮⋮𝑥=̂𝑏.

Это соответствует единственному решению, где 𝑥,𝑥,…,𝑥 может принимать только одно возможное значение для решения системы линейных уравнений. В этом случае система непротиворечива, так как существует хотя бы одно верное решение. Однако предположим, что у нас пришли к уменьшенной эшелонированной форме где единственная разница заключается в выделенной записи. Предположим, что ̂𝑏≠0, затем записать эту расширенную матрицу в терминах системы линейных уравнений дает 𝑥=̂𝑏,𝑥=̂𝑏,⋱⋮⋮0=̂𝑏.

Очевидно, что это не имеет никакого смысла, поскольку у нас не может быть 0≠̂𝑏, если последняя величина отлична от нуля. Таким образом, это будет представлять собой несовместимую систему. Это свойство резюмируется следующей теоремой.

Теорема: Несовместность системы линейных уравнений

Предположим, что система уравнений записана в соответствующую расширенную матрицу коэффициентов. Если эту матрицу преобразовать в эшелонированную форму и в крайнем правом столбце есть стержень, то система несовместима. Если нет опор в крайнем правом столбце, то система линейных уравнений непротиворечива.

Сводная точка — это первая ненулевая запись матрицы. Для расширенной матрицы коэффициентов, если одна из опорных точек в самой правой колонке, тогда все остальные записи в строке равны нулю. Предположим, что для переменных 𝑥,𝑥,…,𝑥 это применяется к ряду 𝑗 расширенного матрица коэффициентов после выполнения некоторого количества операций над строками. Имея первый ненулевой запись в крайнем правом столбце, это будет означать, что 0×𝑥+0×𝑥+⋯+0×𝑥=̂𝑏, где ̂𝑏≠0. Очевидно, что это невозможно, так как левая часть равна равно нулю, а правая часть — нет. Продемонстрируем один пример этого свойства на практике.

Предположим, что у нас есть система линейных уравнений 𝑥−2𝑦−𝑧=3,−3𝑥+11𝑦+5𝑧=−7,7𝑥−24𝑦−11𝑦=25.

Это может быть представлено расширенной матрицей коэффициентов ⎛⎜⎜⎝1−2−13−3115−77−24−1125⎞⎟⎟⎠.

Мы пытаемся решить эту систему, используя метод исключения Гаусса–Жордана, используя элементарные строковые операции, чтобы попытаться манипулировать матрицей в редуцированная эшелонированная форма. Сначала мы выделяем все сводные записи: ⎛⎜⎜⎝1−2−13−3115−77−24−1125⎞⎟⎟⎠.

Чтобы начать работать над формой сокращенного эшелона, мы должны удалить все ненулевые записи, которые находятся ниже оси в первом ряду. Мы используем совместные операции со строками 𝑟→𝑟+3𝑟 и 𝑟→𝑟−7𝑟 дать матрицу ⎛⎜⎜⎝1−2−1305220−10−44⎞⎟⎟⎠.

Теперь нам нужно удалить ненулевую запись, которая находится ниже опорной точки во второй строке. Это достигается с помощью операции строки 𝑟→𝑟+2𝑟, что дает матрицу ⎛⎜⎜⎝1−2−1305220008⎞⎟⎟⎠.

Эта матрица имеет эшелонированную форму, но в крайнем правом столбце есть точка опоры. Посредством теоремы выше, это означает, что система несовместна. Запись этой системы уравнений даст 𝑥−2𝑦−𝑧=3,5𝑦+2𝑧=2,0×𝑧=8.

Третье уравнение содержит ложное утверждение, подтверждающее наше утверждение о несовместимости системы.

Теперь мы приведем 3 примера, где мы должны определить, представляет ли данная расширенная матрица непротиворечивая система линейных уравнений, или непоследовательный. Если система уравнений непротиворечива, то мы также должны признать имеет ли система уравнений единственное решение или бесконечное множество решений.

Пример 1: Распознавание несовместной системы уравнений

В данной расширенной матрице ∗ обозначает произвольное число, а ■ обозначает произвольное ненулевое число. Определить, непротиворечива ли заданная расширенная матрица и, если она непротиворечива, единственно ли ее решение: ⎛⎜⎜⎜⎝■∗∗∗∗∗0■∗∗∗∗00■∗∗∗0000■∗⎞⎟⎟⎟⎠.

Ответ

Эта матрица имеет эшелонированную форму. Учитывая, что записи ■ не равны нулю, они фактически представляют собой точки поворота каждой строки. Поскольку матрица имеет ступенчатую форму и в крайнем правом столбце нет опорных точек, система уравнений непротиворечиво.

В этой системе уравнений 5 переменных, но всего уравнений всего 4. Данный что переменных больше, чем уравнений, решение не может быть единственным, поэтому решений должно быть бесконечно много.

Пример 2: Распознавание несовместимой системы уравнений

В расширенной матрице ⎛⎜⎜⎝■∗∗∗0■∗∗00■∗⎞⎟⎟⎠,∗ обозначает произвольное число и ■ обозначает ненулевое число. Определите, непротиворечива ли данная расширенная матрица. Если это непротиворечиво, решение единственно?

Ответ

Расширенная матрица имеет эшелонированную форму и в крайнем правом столбце нет сводных элементов, что означает, что соответствующая система уравнений совместна.

В этой системе 3 переменных, и если их содержат 3 уравнения, это означает, что решение должно быть единственным.

Пример 3. Распознавание несовместимой системы уравнений

В расширенной матрице ⎛⎜⎜⎜⎝■∗∗∗∗∗0■∗∗0∗0000■00000∗■■⎞⎟⎟⎟⎠,∗ обозначает произвольное число и ■ обозначает произвольное ненулевое число. Определить, непротиворечива ли данная расширенная матрица и, если она непротиворечива, то единственно ли ее решение.

Ответ

Ключ к этому вопросу находится в выделенной записи: ⎛⎜⎜⎜⎝■∗∗∗∗∗0■∗∗0∗0000■00000∗■⎞⎟⎟⎟⎠.

Если эта запись отлична от нуля, то это сводная запись. Учитывая, что расширенная матрица уже имеет эшелонированную форму, если запись * отлична от нуля, то это будет поворотным входом, и, следовательно, решение будет последовательным. Вместо того, чтобы решение было уникальным, было бы бесконечно много решений, потому что их меньше. уравнений, чем переменных в соответствующей системе.

Если запись * равна нулю, то в крайнем правом столбце будет сводная запись, что означает, что система несовместима.

Поскольку последняя запись в третьей строке равна нулю, то четвертая переменная в той же строке должна быть равна нулю. Это приводит к тому, что запись * равна нулю, тогда в крайнем правом столбце будет сводная запись, что означает, что система несовместима.

Предыдущие вопросы основывались на распознавании согласованности расширенной матрицы путем рассмотрения записи и расположение опорных точек. В двух приведенных ниже вопросах мы рассмотрим конкретные расширенные матрицы, содержащие неизвестные переменные, и мы будут использовать операции со строками, чтобы показать, как эти системы линейных уравнений можно классифицировать по этим переменным.

Пример 4. Вычисление, когда система линейных уравнений несовместима

Найдите значения ℎ, для которых расширенная матрица 2ℎ4367 согласуется.

Ответ

Мы начнем с преобразования матрицы в эшелонированную форму. Для этого сначала выделим опорные точки данной матрицы: 2ℎ4367.

Чтобы исключить ненулевую запись, расположенную ниже опорной точки в первой строке, мы используем операцию строки 𝑟→𝑟−32𝑟, что дает 2ℎ406−32ℎ1.

Эта матрица теперь имеет эшелонированную форму. Чтобы быть опорной, выделенная запись во второй строке должна быть отличной от нуля. иначе матрица приняла бы вид 2ℎ4001.

Эта матрица имеет точку опоры в крайнем правом столбце и поэтому несовместима. Чтобы избежать этого, мы должны иметь 6−32ℎ≠0, что означает, что ℎ≠4. Для любого другого значения ℎ система будет последовательный. В связи с тем, что есть одно и то же число переменных, поскольку существуют уравнения, соответствующая система будет иметь единственное решение.

Пример 5. Вычисление, когда система линейных уравнений несовместима

Найдите условия для ℎ и 𝑘, чтобы следующая расширенная матрица не имеют решения, единственное решение и бесконечно много решений: 1222ℎ𝑘.

Ответ

Выделим опорные элементы данной расширенной матрицы коэффициентов: 1222ℎ𝑘.

Чтобы преобразовать эту матрицу в эшелонированную форму, мы должны сначала исключить ненулевой элемент, который находится ниже поворот в первом ряду. Мы используем ряд операция 𝑟→𝑟−2𝑟 дать 1220ℎ−4𝑘−4.

Если ℎ−4≠0, то соответствующая система уравнений будет состоятельной. Данный что существует столько же уравнений, сколько переменных, поэтому решение должно быть единственным.

Если ℎ−4=0, то имеем матрицу 12200𝑘−4 и есть две возможности. Во-первых, 𝑘−4≠0 и в крайнем правом столбце есть точка опоры, означает, что решение несовместимо. Альтернативно, 𝑘−4=0 и нижняя строка представляет собой нулевую строку, а это означает, что существует бесконечно много решений.

В большинстве случаев невозможно сразу определить, является ли система линейных уравнений состоятельной или противоречивой. Поэтому разумнее всего предположить, что система непротиворечива, и начать поиск решения, используя нормальный метод Гаусса – Джордана устранение для достижения эшелонированной формы. При условии, что мы знаем, как распознать несогласованность системы всякий раз, когда это становится очевидным, нет ничего плохого в том, чтобы действовать так, как будто система непротиворечива. В более широком смысле линейной алгебры есть несколько способы интерпретации того, что означает, что система уравнений несовместима. Тем не менее, один общий способ попытаться понять это физически. Ранее в объяснителе у нас была система линейных уравнений 𝑥+𝑦=−3,2𝑥+2𝑦=−8, и мы переставили оба этих уравнения прямой линии, чтобы получить два уравнения 𝑦=−3−𝑥,𝑦=−4−𝑥.

Эти две прямые параллельны, а это означает, что они никогда не пересекутся. Это основа используется для понимания того, что это означает, что система линейных уравнений несовместима, но имеет больше переменных или больше уравнений. Вообще говоря, мы думаем о противоречивая система, относящаяся к прямым линиям, плоскостям, гиперплоскостям и т. д., которые не пересекаются друг друга. там явно ничего неправильно с ситуацией, когда любые два геометрических объекта не встречаются друг с другом, но необходимо чтобы иметь терминологию, чтобы различать этот случай из тех, где есть либо единственная точка встречи, либо бесконечно много точек.

Ключевые моменты

• Система уравнений является «непротиворечивой», если существует хотя бы одно решение.
• Для непротиворечивой системы может быть либо единственное решение, либо бесконечно много решений (которые выражаются через независимые параметры).
• Для противоречивой системы линейных уравнений не существует жизнеспособных решений.
• Мы распознаем непоследовательную систему, когда в крайнем правом входе любого ступенчатая матрица, соответствующая исходной расширенной матрице коэффициентов системы.

  No related posts.