Как репетитор по математике решает системы неравенств — Колпаков Александр Николаевич
Совокупность – самый распространенный тип систем неравенств в школьной программе. Знакомство с ними начинается еще в 8 классе на примере готовых к изображению линейных совокупностей. В 9 классе они трансформируются в квадратные системы, а в старших классах, когда подготовка к ЕГЭ по математике вступает в заключительную фазу, используют полный спектр изученных объектов. Ох, сколько же мучений доставляют школьнику логарифмические и иррациональные системы, модули и степени. Как же в них разобраться и сдать ЕГЭ? Многих спасает репетитор по математике, ибо только он может обеспечить точную дифференциацию заданий и объяснений под конкретные способности и знания ребенка.
Надо сказать, что школа не готовит выпускников к серьезным экзаменационным испытаниям и часто занимается обучением выполнять те или иные типовые задания при определенных ограничениях на условия. Эти ограничения создаются учебниками, стандарты заданий которых влияют на работу школьного преподавателя и тем самым создают репетитору по математике лишние проблемы при подготовке к ЕГЭ.
Школьные педагоги опираются на учебники и часто приносят на уроки далеко не лучшую технику решения систем. Рассмотрим ее подробнее.
Как репетитор по математике борется неудачной техникой решения систем?
К сожалению, многие учителя предлагают неудачную систему подхода к изображению пересечений. Рассмотрим технику, которой пользуется школьный преподаватель математики для поиска ответа в простейшем задании. Решить систему:Решается согласно учебнику. Отмечаются точки 2 и 10, и соответствующие их ответам кусочки оси заштриховываются (закрашиваются). Более толковыми преподавателями предлагается двухуровневая закраска. Для одного неравенства штриховка располагается над осью, а для другого под осью. Ответом является пересечение штриховок, то есть та часть оси, которая закрашена и сверху и снизу.
Как я устал с этим бороться… «А что здесь такого?», — спросите Вы. «Все правильно решается», — справедливо заметит любой математик. Да, вроде бы все правильно, но подумайте, во что превратится рисунок, если репетитор по математике предлагает сильному ученику систему на пересечение большого количества неравенств? Например:
Читабельность рисунка снижается даже при наличии трех штриховок.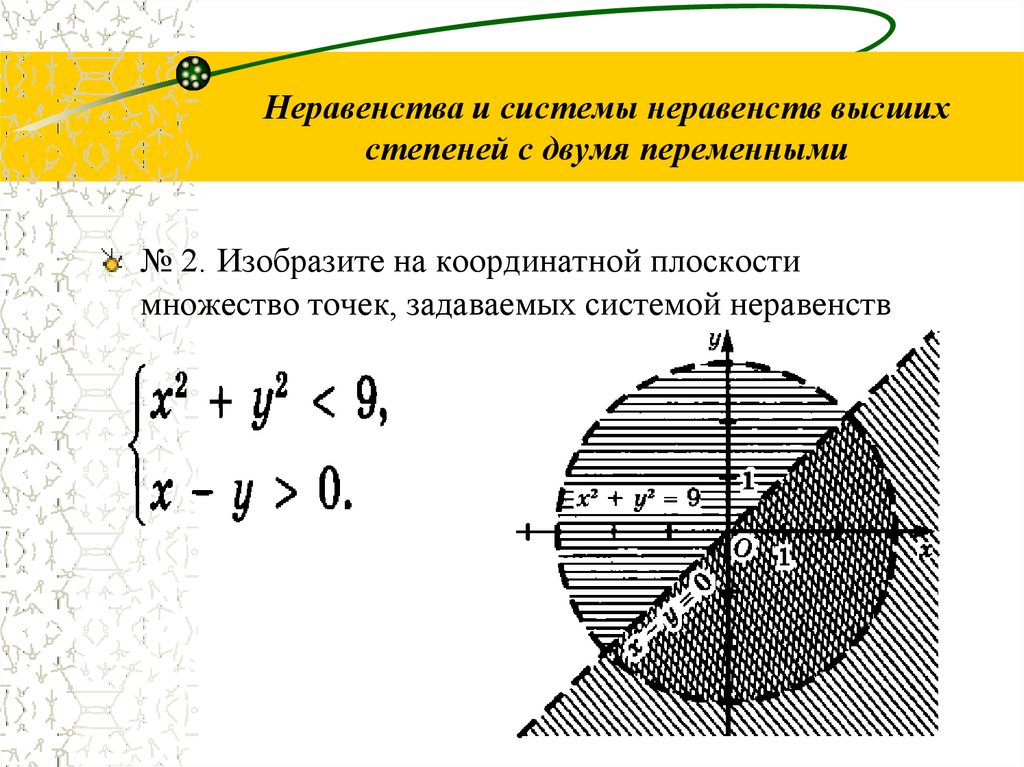
Приходится использовать многоцветную закраску или наклонять линии. А если пять неравенств, шесть, семь… ? Никакие уровни не спасут репетитора по математике от неизбежного замыливания чертежа, навала или грязи. Даже при аккуратном изображении нескольких промежутков может возникнуть ощущение, что перед нами тетрадь по математике самого неряшливого ученика на планете.
Какие правила использует репетитор по математике для поиска пересечения?
1)Ответы неравенств, находящихся внутри системы лучше всего показать на пересечении горизонтальными линиямии соответствующим образом описать их назначение. Репетитор по математике произносит: «ответ каждого неравенства мы будем показывать линией, накрывающей подходящие для него числа (точки). Если мы ищем иксы, попадающие в ответы всех неравенств, значит, нас интересуют точки, накрытые сразу всеми линиями в количестве, равном числу неравенств системы. Поэтому мы выбираем промежуток, над которым располагается столько линий, сколько имеется неравенств в системе».
2) В особых случаях репетитор по математике нумерует линии в соответствии с порядком следования неравенств в системе. Это помогает слабому ученика, которому трудно удержать в голове весь поток информации. Типичная ситуация: лучи из ответа квадратного неравенства часто принимаются как два различных ответа двух различных неравенств. При использовании номеров такая ошибка быстро даст о себе знать. Главное, чтобы ученик помнил о совпадении количеств.
3) Когда репетитор по математике заканчивает решение последнего неравенства системы, он пересекает полученные ответы. Прии этом возникает проблема их поиска. Приходится возвращаться назад и заново изучать решения. Здесь репетитору математики уместно будет использовать закраску (штриховку). Она выделяет промежуток среди довольно большого количества математических записей и других частей рисунка. Если школьник задумает перенести полученный ранее ответ на общий рисунок, он сможет быстрее его распознать. Если ответы объединяются или пересекаются между собой или с другими ответами, то лучше всего ограничиться рисунком каждого из них, а записать в виде только окончательный ответ.
Все равно в процессе пересечения используются визуальный образы множествв.
4) Даже тогда, когда репетитор занимается с сильным учеником, не стоит совмещать поиск финального ответа с каким-нибудь отдельным неравенством на одном рисунке. То есть, например, задание репетитора по математике на систему
не должно решаться одновременным изображением луча и параболы. Парабола всегда изображается отдельно.
5) В процессе переноса границ найденных промежуточных ответов на общий рисунок (или при решении одного из неравенств методом интервалов с большим количеством критических точек), репетитору по математике хорошо было бы убедить ученика использовать раздельную технику. Сначала на оси Ох равномерно расставляются отметки (черточки) для будущих точек, затем числа сравниваются и располагаются рядом с точками в порядке возрастания слева направо. В финальной части можно позаботится об их закрашивании или выкалывании. Если репетитор по математике не принимает такую системы, то ученик будет вынужден многократно переключаться от одного вида деятельнсти (пусть даже простого) к другому, тем самым снижая скорость работы и увеличивая риск ошибки.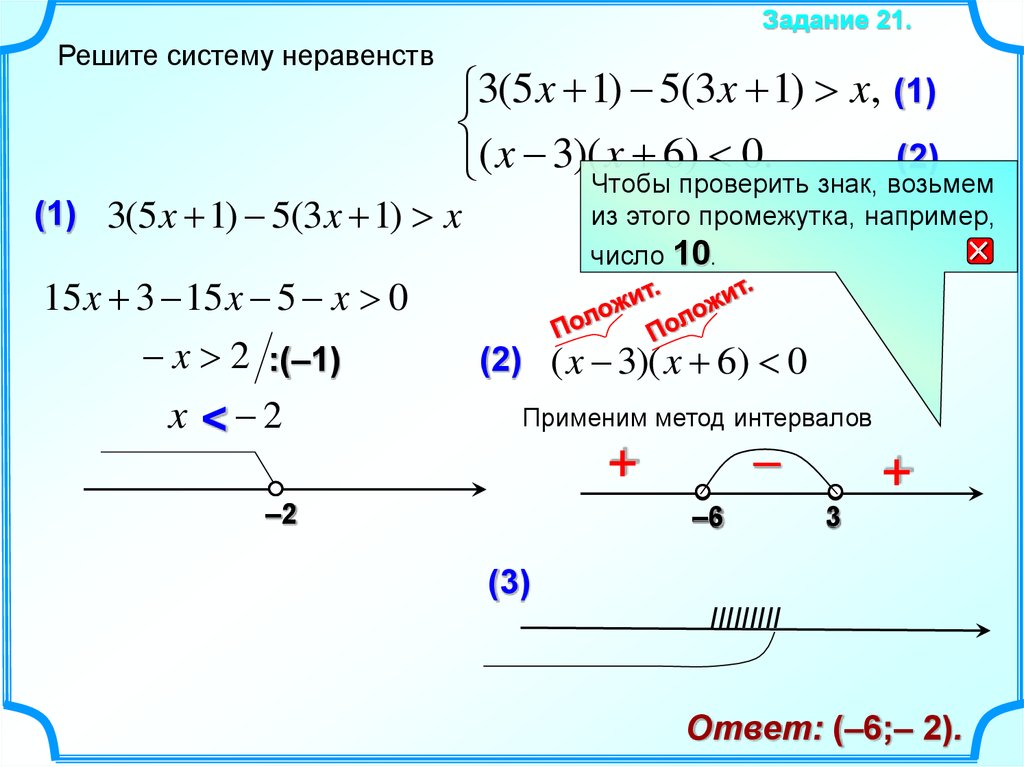
Более того, в случае возникновения трудностей в сравнении нескольких обыкновенных дробей, иррациональностей репетитор по математике может потерять равномерность распределения чисел на осик и случайно сместить их всех к правому краю. Как это происходит на практике? Например, допустим, что нам надо изобразить числа . Репетитор по математике отмечает по центру. Затем выясняет, что есть число, которое больше его и изображает правее центра. Затем оказывается, что тоже «уходит» вправо и т.д. В результате все границы промежутков скапливаются на правой половине рисунка или какие-то точки приходится вставлять между рядом расположенными. Плотное расположение точек помешает репетитору по математике расставить знаки методом интервалов на каждом них.
Заключение: Если бы не было ЕГЭ, то профильные экзамены в Вузы сохранили бы свою свободу в выборе заданий. Спектр задач вступительных экзаменов на совокупности в прошлые годы отличался завидным разнообразием их типов. Сегодня подготовка к ЕГЭ по математике — узконаправленная работа, в которой репетитору приходится разбирать системы неравенств, интегрированные в задачи, казалось бы далекие от систем.
Несмотря на заявленное ФИПИ отсутствие ограничений в задаче С3, постоянство появления логарифмов в реальных ЕГЭ вариантах и прагматизм родителей заставляют репетитора по математике действовать коньюнктурно и штамповать логарифмические задания :). Будем надеяться, что в будущем ЕГЭ станет более разноплановым и ученики начнут уделять время решению совокупностей, полученных от несложных модулей, корней и ли иных математических понятий.
Репетитор по математике, А.Н. Колпаков, Москва, Строгино.
Неравенства: типичные ошибки и проблемы их устранения
Цель исследования данной статьи — определить основные причины, вследствие которых школьники совершают ошибки при решении неравенств; разобрать способы и методы решения некоторых видов неравенств; определить пути исправления возникающих ошибок, а в лучшем случае — вообще не допустить их появления. Рассматриваемая проблема актуальна и по сей день, более того, набирает обороты.
И корни ее лежат не вовсе в специфичности конкретно неравенств или любых других видов математических задач. Значит, и пути решения проблемы также стоит искать в несколько более общих областях, о чем мы также поговорим в данной статье.
Ключевые слова: неравенства, свойства неравенств, правила неравенств.
The purpose of this article is to determine the main reasons why students make mistakes when solving inequalities; to analyze the ways and methods of solving some types of inequalities; to determine ways to correct errors that occur, and in the best case — to prevent them from appearing at all. The problem under consideration is still relevant to this day, moreover, it is gaining momentum. And its roots do not lie in the specificity of specific inequalities or any other types of mathematical problems. This means that you should also look for ways to solve the problem in a few more General areas, which we will also discuss in this article.
Keywords: inequalities, properties of inequalities, rules of inequalities.
Неравенства
Математика — наука об отношениях между объектами, о которых не известно ничего, кроме описывающих их некоторых свойств, — собственно эти свойства, качестве аксиом, положены в основание той или иной математической теории. История математики ведется издревле — от простейших операций подсчёта, измерения объектов и описания их формы. Создаются математические объекты с помощью идеализации свойств объектов реальных или других математических и записи этих свойств на формальном языке. К естественным наукам математика не относится, но широко в них используется — как для точной формулировки их содержания, так и для получения новых результатов. Математика — наука фундаментальная, поскольку она предоставляет другим наукам универсальные языковые средства; с помощью этого выявляется взаимосвязь наук, а также находятся общие законы природы.
Что же касается конкретно неравенств, то с ними начинают работать еще с детского сада. Детей учат тому, что в количественном соотношении некоторые объекты больше, а некоторые — меньше других. А есть объекты, которые равны между собой. В начальных классах продолжается изучение неравенств, там сравнивают — в какой чашке больше вишен, какое число больше, а какое меньше, далее следуют более сложные примеры, например — «4+2» больше, меньше или равно «3+3»?
Конечно, чем старше класс, тем сложнее, разнообразнее и интереснее становятся неравенства и пути нахождения их решений. Однако, стоит понимать, что сама суть неравенств и умение ее понимать находятся с человеком на протяжении всей его жизни. Да, мы об этом не задумываемся, но, тем не менее, постоянно решаем эти самые неравенства в своих бытовых делах. В этой пачке больше салфеток, но она стоит дороже, а в этой — меньше, но и стоит она дешевле. Что же выгоднее приобрести? Причем, ведь роль еще играют факторы того, сколько именно нужно сейчас салфеток и пригодятся ли потом лишние… В общем, рассуждать можно долго, этот пример приведен для того, чтобы было понятно — неравенства с нами всю жизнь и, даже если мы не используем математических формул для их решения (по крайней мере, осознанно), тема эта очень важная и актуальная.
Но прежде чем перейти к проблеме и способам ее решения, стоит немного поговорить о том, что же такое неравенство, каких видов они бывают и какие существуют пути решения.
Итак, что же такое неравенство?
Неравенство в математике — отношение, связывающее два числа или иных математических объекта с помощью одного из перечисленных ниже знаков.
Строгие неравенства
● — означает, что меньше , чем
● — означает, что больше , чем
Неравенства равносильны. Говорят, что знаки противоположны ; например, выражение «знак неравенства сменился на противоположный» означает, что заменено на или наоборот.
Нестрогие неравенства
– — означает, что меньше либо равно
– — означает, что больше либо равно
Про знаки ⩽ и ⩾ также говорят, что они противоположны .
Другие типы неравенств
– — означает, что не равно .
– — означает, что величина намного больше, чем
– — означает, что величина намного меньше, чем
Связанные определения
Неравенства с одинаковыми знаками называются одноимёнными (иногда используется термин «одного смысла» или «одинакового смысла»). Допускается двойное или даже многократное неравенство, объединяющее несколько неравенств в одно. Пример:— это краткая запись пары неравенств: и
Числовые неравенства
Числовые неравенства содержат вещественные числа (для комплексных чисел сравнение на больше-меньше не определено) и могут содержать также символы неизвестных Числовые неравенства, содержащие неизвестные величины, подразделяются (аналогично уравнениям) на алгебраические и трансцендентные.
Алгебраические неравенства, в свою очередь, подразделяются на неравенства первой степени, второй степени и так далее. Например, неравенство — алгебраическое первой степени, неравенство
— алгебраическое третьей степени, неравенство
— трансцендентное.
Существуют определенные правила решения неравенства
При решении неравенств используют следующие правила:
- Любой член неравенства можно перенести из одной части неравенства в другую с противоположным знаком, при этом знак неравенства не меняется.
- Обе части неравенства можно умножить или разделить на одно и то же положительное число, не изменив при этом знак неравенства.
- Обе части неравенства можно умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный.
Давайте рассмотрим несколько примеров.
1)
Переносим все в одну часть
Приводим к общему знаменателю
Раскрываем скобки, приводим подобные
Находим точки, в которых числитель или знаменатель равны нулю.
Отмечаем х на числовой прямой. Определяем знаки на каждом получившемся промежутке.
Записываем ответ
2)
Заменим
Раскрывая второй из модулей, запишем неравенство в виде системы
или
Ответ:
3)
Раскрываем модуль по определению
I случай
II случай
(не входит в ОДЗ)
Ответ: x=-3; x=-1.
Неравенства включены в ЕГЭ повышенной сложности. Неравенства рассматриваются в 15 пункте под C3. Эти задания рассматриваются в 2 части экзамена, задания с 13–19 с развернутым ответом (полная запись решения с обоснованием выполненных действий), проверяющих освоение математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Задания части 2 работы предназначены для проверки знаний на том уровне требований, который традиционно предъявляется ВУЗами с профильным экзаменом по математике. Поэтому для более успешной сдачи экзамена, необходимо решить вторую часть, в которую входит тема неравенства.
И вот сейчас, определив и поняв — зачем же нужно уметь решать неравенства, мы переходим к обсуждению обозначенной выше проблемы.
Ошибки, допускаемые обучающимися при решении уравнений и неравенств.
Ошибки в этой сфере встречается самые разнообразные: от неверного оформления решения до ошибок логического характера.
- Одна из самых типичных ошибок состоит в том, что учащиеся при решении уравнений и неравенств без дополнительных пояснений используют преобразования, нарушающие равносильность, что приводит к потере корней и появлению посторонних корней.
- Целая группа ошибок, а точнее будет сказать — недочетов, состоит в том, что учащиеся не уделяют должного внимания нахождению области определения уравнений, хотя именно она в ряде случаев есть ключ к решению.
- Типичной ошибкой учащихся является то, что они не владеют на нужном уровне определениями понятий, формулами, формулировками теорем, алгоритмами.
- Многие ошибки, допускаемые при решении уравнений и неравенств, являются следствием того, что учащиеся очень часто пытаются решать задачи по шаблону, привычным путем, даже не задумываясь о том, что стоит посмотреть на задачу с другой стороны.
- Ряд типичных ошибок связан с тем, что учащиеся не совсем корректно решают уравнения и неравенства на основе функционального подхода.
- При решении неравенств с помощью подстановки мы всегда сначала решаем новое неравенство относительно новой переменной, и лишь в его решении делаем переход к старой переменной. Школьники же очень часто ошибочно делают обратный переход раньше. Этого делать не следует.
- Типичная ошибка при решении уравнений, неравенств и их систем состоит в том, что неверно преобразовываются выражения.
Способы исправления и предупреждения ошибок
Как и в случае с любой проблемой, после ее обозначения и осознания, должны искаться пути решения. Иначе говорить о проблеме становится бессмысленно. Как мы видим, многие ошибки возникают у учащихся в следствие спешки или же невнимательности. А зачастую одно приводит к другому. Поэтому для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля . Эти навыки состоят из двух частей:
а) умения обнаружить ошибку;
б) умения её объяснить и исправить.
В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:
– проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;
– проверка правильности решения задач путём составления и решения задач, обратных к данной;
– оценка результата решения задачи с точки зрения здравого смысла;
– проверка аналитического решения графическим способом.
Сведению вероятности ошибок к минимуму также способствуют следующие профилактические меры:
– Тексты письменных заданий должны быть удобными для восприятия: грамотно сформулированными, хорошо читаемыми.
– Активная устная отработка основных ЗУН, регулярный разбор типичных ошибок.
– При объяснении нового материала предугадать ошибку и подобрать систему заданий на отработку правильного усвоения понятия. Акцентирование внимания на каждом элементе формулы и выполнение разнотипных заданий позволит свести ошибочность к минимуму.
– Подбирать задания, вызывающие интерес, формирующие устойчивое внимание.
– Прочному усвоению (а, значит, отсутствию ошибок) способствуют правила, удобные для запоминания, четкие алгоритмы, следуя которым заведомо придешь к намеченной цели.
Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок. В математике, как ни в какой другой науке, особенно сильна взаимосвязь материала.
Изучение и понимание последующего невозможно без знания предыдущего, отсюда возникает неизбежность повторения на каждом уроке. При объяснении нового материала следует использовать ряд определений и теорем, которые были изучены ранее. Тем самым новые знания будут основываться на уже сформировавшейся и закрепившейся базе, что приведет к лучшему усвоению материала. Поэтому так важен, особенно в математике, комплексный и систематический подход к обучению. С самых первых дней обучения важно заложить первые кирпичики той базы, на которую в дальнейшем будут надстраиваться новые знания. Несомненно, главную роль здесь играют способности самого ученика, но проявить и дать направление их развитию — тут уже как раз поле деятельности, которое зависит от таланта и способностей учителя, а также от влияния семьи и окружения. Не только в рассматриваемой сегодня теме, но и в процессе обучения в целом. Ведь, как мы видим, ошибки в решении неравенств возникают именно вследствие пробелов в образовательном процессе в целом, а не из-за специфичности конкретно данного раздела.
Так и пути решения и исправления описанных ошибок вовсе не специфичны и уникальны, они сводятся к тому, что сначала надо устранить и/или предупредить общие пробелы в знаниях, не натаскать ребенка на конкретные шаблоны, а именно научить разбираться в рассматриваемом вопросе.
Литература:
- Математика [Электронный ресурс] / Википедия — Режим доступа: https://goo-gl.ru/6qeR~s
- Неравенство [Электронный ресурс] / Википедия — Режим доступа: https://goo-gl.ru/6qeV~s
- Анализ типичных ошибок при решении неравенств [Электронный ресурс] / — Режим доступа: https://goo-gl.ru/6qeW~s
- Решение неравенств: основные ошибки и полезные лайфхаки [Электронный ресурс] / — Режим доступа: https://goo-gl.ru/6qeY~s
- Методическое пособие. Неравенства и системы неравенств [Электронный ресурс] / Инфоурок — Режим доступа: https://goo-gl.ru/6qeZ~s
- https://infourok.ru/user/ivanova-antonina-mihaylovna/blog/problemitipichnie-oshibkidopuskaemie-uchaschimisya-pri-reshenii-uravneniy-i-neravenstv-48897. html
htmlОсновные термины (генерируются автоматически): неравенство, ошибка, знак неравенства, решение неравенств, решение уравнений, путь решения, том, часть неравенства, объяснение нового материала, процесс обучения.
неравенств — Доказательство правил сложения и вычитания для систем неравенств.
Задавать вопрос
спросил
Изменено 7 лет, 3 месяца назад
Просмотрено 2к раз
$\begingroup$
Я слышал, что для системы неравенств типа:
$a
Короче говоря, мне сказали, что вы можете складывать неравенства только тогда, когда они оба имеют один и тот же знак неравенства (я полагаю, что термин «смысл»), и вы можете вычитать их только тогда, когда они не имеют.
Однако я не видел и не могу вывести доказательства того, что эти правила верны.
У кого-нибудь есть такое доказательство?
- неравенство
- арифметика
$\endgroup$
$\begingroup$
Если даны $a\lt b$ и $c\lt d$, то $a+c\lt b+c\lt b+d$
Если даны $e\gt f$ и $g\lt h$, то $ e-g\gt f-g\gt f-h$
$\endgroup$
$\begingroup$
Подсказка: $a0, \; а+х=b$. Аналогично $c
Таким же образом вы можете доказать все те утверждения, которые вы использовали.
$\endgroup$
$\begingroup$
Делайте по одной части за раз. Если a
$\endgroup$
$\begingroup$
Лучше никогда вычитать (напрямую) и никогда манипулировать неравенствами в разных смыслах. Это слишком подвержено ошибкам. Гораздо безопаснее придерживаться этих правил:
- Вы можете добавлять неравенства с тем же смыслом.
- Вы можете умножать неравенства в том же смысле, если все числа положительные.
- Если числа отрицательные, их можно умножить, но смысл неравенства должен измениться.
- Вы можете изменить знаки в неравенстве или умножить обе части на отрицательное число, но при этом изменить смысл неравенства.
$\endgroup$
Системы нелинейных уравнений и неравенств: две переменные · Precalculus
Системы нелинейных уравнений и неравенств: две переменные · Предварительное исчислениеВ этом разделе вы:
- Решите систему нелинейных уравнений с помощью подстановки.
- Решите систему нелинейных уравнений методом исключения.
- Нарисуйте график нелинейного неравенства.
- Нарисуйте график системы нелинейных неравенств.
Комета Галлея ([ссылка]) совершает оборот вокруг Солнца примерно раз в 75 лет. Его путь можно рассматривать как очень вытянутый эллипс. Другие кометы следуют аналогичным путям в космосе.
Эти орбитальные траектории можно изучать с помощью систем уравнений. Эти системы, однако, отличаются от тех, которые мы рассмотрели в предыдущем разделе, потому что уравнения не являются линейными.
В этом разделе мы рассмотрим пересечение параболы и прямой, окружности и прямой, окружности и эллипса. Методы решения систем нелинейных уравнений аналогичны методам решения линейных уравнений.
Решение системы нелинейных уравнений с помощью подстановки
Система нелинейных уравнений — это система двух или более уравнений с двумя или более переменными, содержащая хотя бы одно нелинейное уравнение. Напомним, что линейное уравнение может иметь вид Ax+By+C=0.
Любое уравнение, которое нельзя записать в этой форме в нелинейном виде. Метод подстановки, который мы использовали для линейных систем, — это тот же метод, который мы будем использовать для нелинейных систем. Мы решаем одно уравнение для одной переменной, а затем подставляем результат во второе уравнение для решения другой переменной и так далее.
Однако есть вариации возможных результатов.
Пересечение параболы и прямой
Существует три возможных типа решений системы нелинейных уравнений, включающих парабола и линия.
Возможные типы решений для точек пересечения параболы и прямой
[ссылка] иллюстрирует возможные наборы решений для системы уравнений, включающей параболу и прямую.
- Нет решения. Линия никогда не пересечет параболу.
- Одно решение. Прямая касается параболы и пересекает параболу ровно в одной точке.
- Два решения. Прямая пересекает параболу внутри и пересекает параболу в двух точках.
Дана система уравнений, содержащая прямую и параболу, найти решение.
- Решите линейное уравнение для одной из переменных.
- Подставьте выражение, полученное на первом шаге, в уравнение параболы.
- Найдите оставшуюся переменную.
- Проверьте свои решения в обоих уравнениях.
Решение системы нелинейных уравнений, представляющих параболу и прямую
Решите систему уравнений.
x−y=−1 y=x2+1
Решите первое уравнение для x
и затем подставьте полученное выражение во второе уравнение.
x−y=−1 x=y−1Найти x. y=x2+1 y=(y−1)2+1Замените x выражением.
Разверните уравнение и приравняйте его к нулю.
y=(y−1)2 =(y2−2y+1)+1 =y2−2y+20=y2−3y+2 =(y−2)(y−1)
Решение для y
дает y=2
и y=1.
Затем подставьте каждое значение для y
в первое уравнение для решения x.
Всегда подставляйте значение в линейное уравнение, чтобы проверить наличие посторонних решений.
x−y=−1x−(2)=−1 x=1x−(1)=−1 x=0
можно проверить, подставив эти (x,y)
значений в оба исходных уравнения. См. [ссылка].
**Можем ли мы заменить значения для y
во второе уравнение для решения x
в [ссылка]?**
Да, но поскольку
xвозведено в квадрат во втором уравнении, это может дать нам посторонние решения для
x.
Для y=1
y=x2+1 1=x2+1 x2=0 1=x2+1 x2=0 x=60=0
дает нам то же значение 9, что и3. решение.
Для y=2
y=x2+1 2=x2+1×2=1 x=±1=±1
*Обратите внимание, что −1
является посторонним решением.*
Решите данную систему уравнений подстановкой.
3x−y=−22×2−y=0
(−12,12)
и (2,8)
Пересечение круга и линии
Как и в случае с параболой и прямой, при решении системы уравнений, представляющей окружность и прямую, возможны три исхода.
Возможные типы решений для точек пересечения окружности и прямой
[ссылка] иллюстрирует возможные наборы решений для системы уравнений, включающей окружность и прямую.
- Нет решения. Линия не пересекает окружность.
- Одно решение. Прямая касается окружности и пересекает окружность ровно в одной точке.
- Два решения. Прямая пересекает окружность и пересекает ее в двух точках.
Дана система уравнений, содержащая прямую и окружность, найти решение.
- Решите линейное уравнение для одной из переменных.
- Подставьте выражение, полученное на первом шаге, в уравнение для окружности.
- Найдите оставшуюся переменную.
- Проверьте свои решения в обоих уравнениях.
Нахождение пересечения окружности и прямой подстановкой
Нахождение пересечения заданной окружности и заданной прямой подстановкой.
x2+y2=5 y=3x−5
Одно из уравнений уже решено для y.
Подставим y=3x−5
в уравнение окружности.
x2+(3x — 5) 2 = 5×2+9×2–30x+25 = 5 10×2–30x+20 = 0
Теперь мы учитываем и решаем для x.
10 (x2–3x+2) = 010 (x -2) (x -1) = 0 x = 2 x = 1
Замените два x -значения в исходное линейное уравнение для решения для y.
y=3(2)−5 =1y=3(1)−5 =−2
Прямая пересекает окружность в точках (2,1)
и (1,−2),
, что может быть проверяется путем подстановки этих (x,y)
значений в оба исходных уравнения. См. [ссылка].
Решите систему нелинейных уравнений.
x2+y2=10 x−3y=−10
(−1,3)
Решение системы нелинейных уравнений методом исключения
Мы видели, что подстановка часто является предпочтительным методом, когда система уравнений включает линейное уравнение и нелинейное уравнение. Однако, когда оба уравнения в системе имеют одинаковые переменные второй степени, решить их методом исключения путем сложения часто проще, чем подстановкой. Как правило, 9Исключение 0102 — гораздо более простой метод, когда система включает только два уравнения с двумя переменными (система два на два), а не система три на три, поскольку шагов меньше. В качестве примера исследуем возможные типы решений при решении системы уравнений, представляющих окружность и эллипс.
Возможные типы решений для точек пересечения окружности и эллипса
[ссылка] иллюстрирует возможные наборы решений для системы уравнений, включающей окружность и эллипс .
- Нет решения. Окружность и эллипс не пересекаются. Одна фигура находится внутри другой или круг и эллипс находятся на расстоянии друг от друга.
- Одно решение. Окружность и эллипс касаются друг друга и пересекаются ровно в одной точке.
- Два решения. Окружность и эллипс пересекаются в двух точках.
- Три решения. Окружность и эллипс пересекаются в трех точках.
- Четыре решения. Окружность и эллипс пересекаются в четырех точках.
Решение системы нелинейных уравнений, представляющих окружность и эллипс
Решение системы нелинейных уравнений.
x2+y2=26 (1)3×2+25y2=100(2)
Начнем с умножения уравнения (1) на −3,
и добавления его к уравнению (2).
(−3)(x2+y2)=(−3)(26) −3×2−3y2=−78 3×2+25y2=100 22y2=22
После того как мы решим вместе два уравнения, .
y2=1 y=±1=±1
Подставьте y=±1
в одно из уравнений и найдите x.
x2+(1) 2 = 26 x2+1 = 26 x2 = 25 x = ± 25 = ± 5×2+( — 1) 2 = 26 x2+1 = 26 x2 = 25 = ± 5
Есть четыре раствора: ( 5,1),(−5,1),(5,−1) и (−5,−1).
См. [ссылка].
Найдите набор решений для данной системы нелинейных уравнений.
4×2+y2=13 x2+y2=10
{(1,3),(1,−3),(−1,3),(−1,−3)}
График нелинейного неравенства
Все уравнения в системах, с которыми мы сталкивались до сих пор, включали равенства, но мы также можем столкнуться с системами, включающими неравенства. Мы уже научились строить графики линейных неравенств, нарисовав соответствующее уравнение, а затем заштриховав область, представленную символом неравенства . Теперь мы выполним аналогичные шаги для построения графика нелинейного неравенства, чтобы научиться решать системы нелинейных неравенств.
А нелинейное неравенство — неравенство, содержащее нелинейное выражение. График нелинейного неравенства очень похож на график линейного неравенства.
Напомним, что когда неравенство больше, y>a,
или менее, y график нарисован пунктирной линией. Когда неравенство больше или равно, y≥a, или меньше или равно, y≤a, график нарисован сплошной линией. Графики создадут области на плоскости, и мы проверим каждую область в поисках решения. Если работает одна точка региона, работает весь регион. Это область, которую мы затеняем. См. [ссылка]. Для заданного неравенства, ограниченного параболой, нарисуйте график. или ), парабола изображается сплошной линией. Построение графика неравенства для параболы Построение графика неравенства y>x2+1. Сначала начертите соответствующее уравнение y=x2+1. Так как y>x2+1 имеет символ больше, мы рисуем график пунктирной линией. Затем мы выбираем точки для проверки внутри и снаружи параболы. Проверим точки* * * (0,2) и (2,0). Одна точка явно находится внутри параболы, а другая точка явно снаружи. y>x2+12>(0)2+12>1True0>(2)2+10>5False График показан на [ссылка]. Мы видим, что множество решений состоит из всех точек внутри параболы, но не на самом графике. Теперь, когда мы научились строить графики нелинейных неравенств, мы можем научиться строить графики систем нелинейных неравенств. Система нелинейных неравенств — это система двух или более неравенств с двумя или более переменными, содержащая хотя бы одно нелинейное неравенство. Построение графика системы нелинейных неравенств аналогично построению графика системы линейных неравенств. Разница в том, что наш график может привести к большему количеству заштрихованных областей, представляющих решение, чем мы находим в системе линейных неравенств. Решением нелинейной системы неравенств является область графика, где заштрихованные области графика каждого неравенства перекрываются, или где области пересекаются, называемая возможная область . Учитывая систему нелинейных неравенств, нарисуйте график. Построение графика системы неравенств Построение графика данной системы неравенств. x2−y≤0 2×2+y≤12 Эти два уравнения явно являются параболами. Мы можем найти точки пересечения методом исключения: добавьте оба уравнения, и переменная y будет исключена. Затем мы решаем для x. x2−y=02×2+y=12\_\_\_\_\_\_\_\_\_\_\_\_ 3×2=12 x2=4 x=±2 Замените x -значения в одно из уравнений и решить для y. x2-y=0(2)2-y=04-y=0y=4(-2)2-y=04-y=0y=4 Две точки пересечения: (2,4) и (−2,4). Обратите внимание, что уравнения можно переписать следующим образом. x2 -e≤0 x2≤y y≥x22x2+y≤12 y≤ — 2×2+12 График каждого неравенства. сверху и x2−y≤0 снизу. Нарисуйте график данной системы неравенств.* * * y≥x2−1x−y≥−1 Заштрихуйте область, ограниченную двумя кривыми, над квадратичной и под прямой. Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с нелинейными уравнениями. (1) решения нет, окружность и эллипс не пересекаются; (2) одно решение, окружность и эллипс касаются друг друга; (3) два решения, окружность и эллипс пересекаются в двух точках; (4) три решения, окружность и эллипс пересекаются в трех местах; (5) четыре решения, окружность и эллипс пересекаются в четырех точках. См. [ссылка]. Объясните, может ли система двух нелинейных уравнений иметь ровно два решения. А если ровно три? Если нет, объясните почему. Нелинейная система может представлять собой две окружности, которые перекрываются и пересекаются в двух местах, следовательно, есть два решения. Нелинейная система может представлять параболу и окружность, где вершина параболы встречается с окружностью, а ветви также пересекают окружность, следовательно, три решения. При построении графика неравенства объясните, почему нам нужно проверить только одну точку, чтобы определить, является ли решением вся область? Когда вы рисуете систему неравенств, всегда ли будет допустимая область? Если да, объясните почему. Если нет, приведите пример графа неравенств, не имеющего допустимой области. Почему у него нет допустимой области? Нет. Достижимая область не требуется. Рассмотрим систему, ограниченную двумя параллельными прямыми. Одно неравенство представляет область выше верхней линии; другой представляет область ниже нижней линии. Если вы рисуете функцию доходов и затрат, объясните, как определить, в каких регионах есть прибыль. Если вы выполняете анализ безубыточности и обнаруживаете более одного решения, объясните, как бы вы определили, какое из x — значения прибыльные, а какие нет. Выберите любое число из каждого решения и подставьте в C(x) и R(x). Если C(x) , то прибыль есть. Для следующих упражнений решите систему нелинейных уравнений с помощью подстановки. х+у=4х2+у2=9 y=x−3×2+y2=9 (0,−3),(3,0) y=xx2+y2=9 y=−xx2+y2=9 (−322 322),(322,−322) x=2×2−y2=9 Для следующих упражнений решите систему нелинейных уравнений методом исключения. 4×2−9y2=364×2+9y2=36 (−3,0),(3,0) х2+у2=25х2-у2=1 2×2+4y2=42×2−4y2=25x−10 (14,−628),(14 628) у2-х2=93х2+2у2=8 x2+y2+116=2500y=2×2 (−3984,1994),(3984,1994) В следующих упражнениях используйте любой метод решения системы нелинейных уравнений. −2×2+y=−5 6x−y=9 −x2+y=2 −x+y=2 (0,2),(1,3) x2+y2=1 y=20×2−1 x2+y2=1 y=−x2 (−12(5−1),12(1−5)),(12(5−1),12(1−5)) 2×3−x2=y y=12−x 9×2+25y2=225(x−6)2+y2=1 (5,0) x4−x2=y x2+y=0 2×3−x2=y x2+y=0 (0,0) В следующих упражнениях используйте любой метод решения нелинейной системы. х2+у2=9у=3-х2 x2−y2=9 x=3 (3,0) x2−y2=9 y=3 x2−y2=9 x−y=0 Решений не существует -x2+y=2-4x+y=-1 −x2+y=2 2y=−x Решений не существует х2+у2=25х2-у2=36 x2+y2=1 y2=x2 (−22,−22),(−22,22),(22,−22),(22,22) 16×2−9y2+144=0 y2+x2=16 3×2−y2=12(x−1)2+y2=1 (2,0) 3×2−y2=12(x−1)2+y2=4 3×2−y2=12 x2+y2=16 (−7,−3),(−7,3),(7,−3),(7,3) x2−y2−6x−4y−11=0 −x2+y2=5 x2+y2−6y=7 x2+y=1 (−12(73−5),12(7−73)),(12(73−5),12(7−73)) x2+y2=6 xy=1 Для следующих упражнений постройте график неравенства. x2+y<9  х2+у2<4 Для следующих упражнений постройте график системы неравенств. Отметьте все точки пересечения. x2+y<1y>2x  x2+y<−5y>5x+10 x2+y2<253x2−y2>12  x2−y2>−4×2+y2<12 x2+3y2>163×2−y2<1  Для следующих упражнений постройте график неравенства. y≥exy≤ln(x)+5 y≤−log(x)y≤ex  Для следующих упражнений найдите решения нелинейных уравнений с двумя переменными. 4×2+1y2=245×2−2y2+4=0 6×2−1y2=81×2−6y2=18 (−270383,−23529),(−270383,23529),(270383,−23529),(270383,23529) x2-xy+y2-2=0 x+3y=4 x2-xy-2y2-6=0 x2+y2=1 Решение не существует x2+4xy−2y2−6=0 x=y+2 Для следующих упражнений решите систему неравенств. xy<1y>x x=0,y>0 and0 x2+y<3y>2x Для следующих упражнений постройте систему нелинейных уравнений, описывающую заданное поведение, а затем найдите нужные решения. Два числа в сумме дают 300. Одно число в два раза больше квадрата другого числа. Какие числа? 12, 288 Квадраты двух чисел дают в сумме 360. Второе число равно половине значения квадрата первого числа. Какие числа? Компания по производству ноутбуков определила свои функции затрат и доходов на каждый день: C(x)=3×2−10x+200 и R(x)=−2×2+100x+50. Если они хотят получать прибыль, какой диапазон ноутбуков в день они должны производить? Округлите до ближайшего числа, которое принесет прибыль. 2–20 компьютеров Компания сотовой связи имеет следующие функции затрат и доходов: C(x)=8×2−600x+21 500 и R(x)=−3×2+480x. Какой ассортимент сотовых телефонов они должны производить каждый день, чтобы была прибыль? Округлите до ближайшего числа, приносящего прибыль. Вы также можете бесплатно скачать на http://cnx.
График системы нелинейных неравенств
См. [ссылка]. Допустимая область — это область между двумя уравнениями, ограниченная 2×2+y≤12 Ключевые понятия
См. [ссылка]. Секционные упражнения
Устный
Если да, приведите пример такой системы в виде графика и объясните, почему ваш выбор дает два или три ответа.
В этом случае в обеих областях нет точек на плоскости; следовательно, нет допустимой области. Алгебраический
Графический
Расширения
Технология
Используйте калькулятор, чтобы построить график системы, чтобы подтвердить ответ. Реальные приложения
Глоссарий
Эта работа находится под лицензией Creative Commons Attribution 4.0 International License.