Скалярное произведение векторов 9 класс онлайн-подготовка на Ростелеком Лицей
Тема: Соотношения между сторонами и углами треугольника. Раздел 3. Скалярное произведение векторов
Урок: Скалярное произведение векторов
1. Тема урока, введение
Тема урока: «Скалярное произведение векторов». На этом уроке мы рассмотрим скалярное произведение векторов и решим задачи на вычисление скалярного произведения.
2. Напоминание основных сведений о векторах
Напомним кратко основные сведения, которые мы знаем о векторах.
1. Определение. Вектор – это направленный отрезок, обозначение
2. Операции с векторами.
а) Сложение векторов.
Правило параллелограмма.
Правило треугольника.
б) Умножение вектора на число.
3. Угол между векторами.
4.
Скалярное произведение векторов.
Скалярное произведение векторов – это произведение их длин на косинус угла между ними.
Заметим, что – это проекция вектора на направление вектора . Из определения следует, что скалярное произведение векторов – это число, характеризующее взаимное расположение векторов.
3. Анализ формулы скалярного произведения векторов
Рассмотрим некоторые частные случаи взаимного расположения векторов.
1. Перпендикулярные векторы.
Если , то и .
Сила в направлении не совершает никакой работы, скалярное произведение Обратно: если , то в силу равенства .
Получаем следующий важный вывод: Скалярное произведение векторов равно нулю тогда и только тогда, когда векторы перпендикулярны.
2. Коллинеарные векторы.
Рассмотрим коллинеарные векторы: они могут быть сонаправлены или противоположно направлены.
а) Сонаправленные векторы.
, поэтому Таким образом,
б) Противоположно направленные векторы.
, поэтому
Таким образом,
3. Равные векторы. Рассмотрим случай, когда
Определение: Скалярное произведение называется скалярным квадратом вектора и обозначается , . Свойство: Скалярный квадрат вектора равен квадрату его длины, .
4. Решение задач на вычисление скалярного произведения векторов
Следует научиться вычислять скалярное произведение векторов не только в частных, но и в общих случаях. Рассмотрим следующую задачу.
Задача. Вычислить скалярное произведение векторов и , если , угол между ними равен:
а)
б)
в)
а) Дано:
Найти: Решение: Ответ:
б) Дано:
Найти: Решение: или Ответ: 0.
в) Дано:
Найти:
Решение:Ответ:
5. Вычисление скалярного произведения векторов в геометрических задачах
Векторы часто присутствуют и в различных геометрических фигурах.
Рассмотрим следующую задачу.
Задача. В равностороннем треугольнике ABC со стороной a проведена высота BD. Вычислить скалярное произведение векторов:
а)
б)
в)
г)
Решение:
а) Ответ:
б) Для определения угла между векторами отложим вектор от точки
. Ответ: .
в) Ответ: 0.
г) Ответ:
6. Вычисление скалярного произведения векторов в физической задаче
Задача. К одной и той же точке приложены две силы и , действующие под углом друг к другу, причем . Найти величину равнодействующей силы .
Дано:
Найти: .
Решение:
Ответ:
7. Заключение
Итак, мы рассмотрели разные задачи на вычисление скалярного произведения векторов. На следующем уроке мы рассмотрим скалярное произведение векторов в координатах.
Список литературы
- Атанасян Л.
С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010. - Фарков А. В. Тесты по геометрии: 9 класс. К учебнику Л. С. Атанасяна и др. – М.: Экзамен, 2010.
- Погорелов А. В. Геометрия. Уч. для 7–11 кл. общеобр. учрежд. – М.: Просвещение, 1995.
С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- E-science.ru (Источник).
- Mathematics.ru (Источник).
Домашнее задание
- Атанасян Л. С. и др. Геометрия 7–9 классы. №№1041, 1042.
Свойства скалярного произведения. Скалярное произведение векторов и его свойства. Скалярный квадрат вектора.
- Альфашкола
2) \) в результате мы получаем скалярный квадрат вектора.
2 свойство. Скалярный квадрат вектора всегда больше нуля или равен нулю:
- \(\)\( \overline{a }· \overline{a }\geq0\)
3 свойство. Произведение вектора само на себя равно нулю тогда и только тогда, когда вектор является нулевым вектором:
- \( \overline{a }· \overline{a }=0\) если \( \overline{a }= \overline{0 }\)
4 свойство. Переместительное или коммутативное свойство :
- \( \overline{a }· \overline{b }= \overline{b }· \overline{a }\)
5 свойство. Распределительное или дистрибутивное свойство:
- \(( (\overline{a }+\overline{b })\overline{с }= \overline{a }· \overline{c }+\overline{b }· \overline{c })\)
6 свойство. Cочетательное или ассоциативное свойство:
- \((\lambda \overline{a })· \overline{b }= \lambda(\overline{b }· \overline{a })-\) выносим константу
7 свойство.
Если скалярное произведение двух ненулевых векторов равно нулю, то эти векторы перпендикулярны:
- \(a ≠ 0, b ≠ 0, a · b = 0 <=> a ┴ b\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Лиля Алексеевна Шевченко
Репетитор по математике
Стаж (лет)
Образование:
Армавирский государственный педагогический институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 5-9 классы.
Наталья Игоревна Шестакова
Репетитор по математике
Стаж (лет)
Образование:
Московский государственный открытый университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 1-5 классов. Я люблю математику за точность и порядок, за живость ума. Мне очень нравится работать с детьми и видеть результат работы и ними.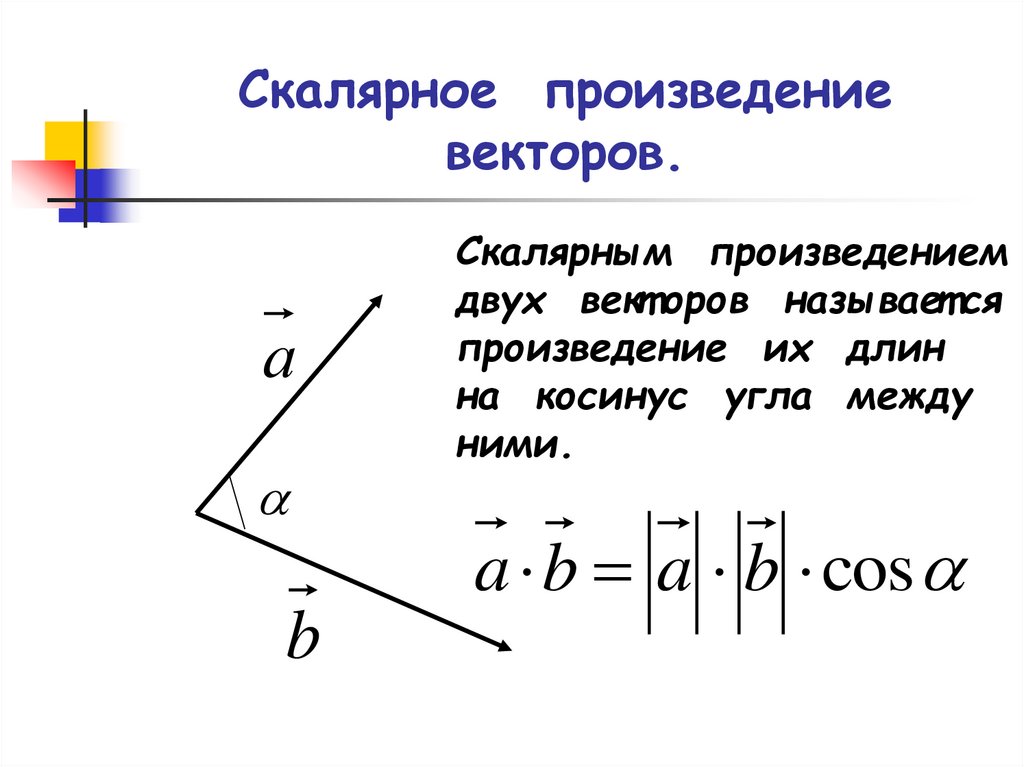
Оксана Александровна Анцыферова
Репетитор по математике
Стаж (лет)Образование:
Саратовский государственный университет им.
Н. Г. Чернышевского
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике и русскому языку 1-4 классов. Очень легко и с интересом к предметам: математика, русский язык можно относиться, если это тебе понятно! А когда педагог в доступной форме, с учетом дифференцированного подхода к каждому ребенку, может помочь освоить материал, справиться со всеми заданиями по предметам- значимый результат для современного ребенка! Подготовить ребенка к школе, помочь освоить основы грамоты, дать первоначальные математические представления — первостепенная задача для педагога, работающего профессионально и качественно!
Похожие статьи
- Основные формулы: треугольник, параллелограмм и четырехугольник
- Как быстро умножить число на 2,5
- Куб дроби
- Сколько одно число составляет в процентах от другого?
- ИВТ (Информатика и Вычислительная Техника): МФТИ
- Кринж, краш и токсик: учим подростковый сленг
- Профессиональное выгорание: как вернуть энергию?
- Как заинтересовать ребенка читать + 20 книг для школьников всех возрастов
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Формула скалярного произведения через компоненты вектора
Геометрическое определение скалярного произведения гласит, что скалярное произведение двух векторов $\vc{a}$ и $\vc{b}$ равно
$$\vc{a} \cdot \vc{b} = \|\vc{a}\| \|\vc{b}\| \cos\тета,$$
где $\theta$ — угол между векторами $\vc{a}$ и $\vc{b}$.
Хотя эта формула удобна для понимания свойств скалярного произведения,
формула скалярного произведения в терминах компонентов вектора облегчила бы вычисление скалярного произведения между двумя заданными векторами.
В качестве первого шага рассмотрим скалярное произведение между стандартными единичными векторами, т. е. векторами $\vc{i}$, $\vc{j}$ и $\vc{k}$ длины один и параллельно осям координат.
Загрузка апплета
Стандартные единичные векторы в трех измерениях. Стандартные единичные векторы в трех измерениях: $\vc{i}$ (зеленый), $\vc{j}$ (синий) и $\vc{k}$ (красный) представляют собой векторы длины один, которые указывают параллельно ось $x$, ось $y$ и ось $z$ соответственно. Перемещение их с помощью мыши не меняет вектора, поскольку они всегда указывают в положительном направлении соответствующей оси.
Дополнительная информация об апплете.
Поскольку стандартные единичные векторы ортогональны, мы немедленно заключаем, что скалярное произведение между парой различных стандартных единичных векторов равно нулю:
\начать{выравнивать*}
\vc{i} \cdot \vc{j} = \vc{i} \cdot \vc{k} = \vc{j} \cdot \vc{k}=0.
\конец{выравнивание*}
Скалярное произведение между единичным вектором и самим собой также просто вычислить.
В этом случае угол равен нулю и $\cos\theta=1$.
Учитывая, что все векторы имеют длину один, скалярные произведения равны
\начать{выравнивать*}
\vc{i} \cdot \vc{i} = \vc{j} \cdot \vc{j} = \vc{k} \cdot \vc{k}=1.
\конец{выравнивание*}
Вторым шагом является вычисление скалярного произведения двух трехмерных векторов.
\начать{выравнивать*}
\vc{a} &= (a_1,a_2,a_3) = a_1\vc{i} + a_2\vc{j}+a_3\vc{k}\\
\vc{b} &= (b_1,b_2,b_3) = b_1\vc{i} + b_2\vc{j}+b_3\vc{k}.
\конец{выравнивание*}
Для этого мы просто утверждаем, что для любых трех векторов $\vc{a}$, $\vc{b}$ и $\vc{c}$ и любого скаляра $\lambda$
\начать{выравнивать*}
(\lambda\vc{a}) \cdot \vc{b} &= \lambda(\vc{a}\cdot\vc{b}) = \vc{a} \cdot (\lambda\vc{b} )\\
(\vc{a}+\vc{b}) \cdot \vc{c} &= \vc{a} \cdot \vc{c} + \vc{b}\cdot \vc{c}.
\конец{выравнивание*}
(Эти свойства означают, что скалярное произведение является линейным.
Учитывая эти свойства и тот факт, что скалярное произведение коммутативно, мы можем разложить скалярное произведение $\vc{a} \cdot \vc{b}$ по компонентам,
\начать{выравнивать*}
\vc{a} \cdot \vc{b} &= (a_1\vc{i} + a_2\vc{j}+a_3\vc{k}) \cdot
(b_1\vc{i} + b_2\vc{j}+b_3\vc{k}) \\
&= a_1b_1 \vc{i} \cdot \vc{i} + a_2b_2\vc{j}\cdot\vc{j} + a_3b_3\vc{k}\cdot\vc{k}
\\
&\quad + (a_1b_2+a_2b_1)\vc{i}\cdot\vc{j} + (a_1b_3+a_3b_1)\vc{i}\cdot\vc{k}
\\
&\quad + (a_2b_3+a_3b_2)\vc{j}\cdot \vc{k}.
\конец{выравнивание*}
Поскольку мы знаем скалярное произведение единичных векторов, мы можем упростить формулу скалярного произведения до
\начать{собирать}
\vc{a} \cdot \vc{b} = a_1b_1+a_2b_2+a_3b_3.
\метка{dot_product_formula_3d}\тег{1}
\конец{собрать}
92$,
еще проще. Данный
\начать{выравнивать*}
\vc{a} &= (a_1,a_2) = a_1\vc{i} + a_2\vc{j}\\
\vc{b} &= (b_1,b_2) = b_1\vc{i} + b_2\vc{j},
\конец{выравнивание*}
мы можем использовать ту же формулу, но с $a_3=b_3=0$,
\начать{собирать}
\vc{a} \cdot \vc{b} = a_1b_1+a_2b_2
\label{dot_product_formula_2d}\tag{2}.
\конец{собрать}
Вооружившись уравнениями \eqref{dot_product_formula_3d} и \eqref{dot_product_formula_2d}, вы можете быстро вычислить скалярные произведения, как показано в этих примерах.
Скалярное произведение векторов
Скалярное произведение векторовСкалярное произведение и векторное произведение — это два способа умножения векторов, наиболее часто применяемые в физике и астрономии. Скалярное произведение двух векторов можно построить, взяв компонент одного вектора в направлении другого и умножив его на величину другого вектора. Это можно выразить в виде: Если векторы выражаются через единичные векторы i, j и k вдоль направлений x, y и z, скалярное произведение также может быть выражено в виде: В некоторых учебниках по математике скалярное произведение также называют «внутренним произведением» или «точечным произведением».
| Индекс Векторные понятия | ||
| Назад |
Вы можете ввести значения в любое из полей ниже. Примечание. Приведенные выше числа не будут принудительно согласованы до тех пор, пока вы не щелкнете либо по скалярному произведению, либо по углу в активной формуле выше. | Индекс Векторные понятия | ||
| Назад |
Затем щелкните символ скалярного произведения или угла. Векторы A и B не могут быть однозначно вычислены из скалярного произведения и угла. Если угол изменить, то B будет размещен вдоль оси x, а A — в плоскости xy.С геометрической точки зрения скалярное произведение полезно для нахождения направления между произвольными векторами в пространстве. Так как два выражения для произведения: включают компоненты двух векторов, и поскольку величины A и B могут быть рассчитаны из компонентов, используя: , то можно вычислить косинус угла и определить угол. Одним из важных физических применений скалярного произведения является вычисление работы: Скалярное произведение используется для выражения магнитной потенциальной энергии и потенциала электрического диполя. | Индекс Векторные понятия | ||
| Назад |
Иногда удобно представлять векторы в виде матриц-строк или столбцов, а не в виде единичных векторов, как это было сделано выше при рассмотрении скалярного произведения. Если рассматривать обычные пространственные векторы как матрицы-столбцы их компонентов x, y и z, то транспонирование этих векторов будет матрицей-строкой. Тогда мы могли бы написать для векторов A и B: Тогда матричное произведение этих двух матриц даст только одно число, являющееся суммой произведений соответствующих пространственных компонентов двух векторов. |
