Правило сложение и вычитание: Правила сложения и вычитания. — Инженерный справочник DPVA.ru / Технический справочник ДПВА / Таблицы для инженеров (ex DPVA-info)

Правила сложения и вычитания. — Инженерный справочник DPVA.ru / Технический справочник ДПВА / Таблицы для инженеров (ex DPVA-info)

		Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д.
Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница / / Техническая информация/ / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Правила сложения и вычитания. Поделиться:    Правила сложения и вычитания. 1. От перемены мест слагаемых сумма не изменится (коммутативное свойство сложения) Пример: 13+25=38, можно записать как: 25+13=38 2. Результат сложения не изменится, если соседние слагаемые заменить их суммой (ассоциативное свойство сложения). Пример: 10+13+3+5=31 можно записать как: 23+3+5=31; 26+5=31; 23+8=31 и т.д. 3. Единицы складываются с единицами, десятки с десятками и т.д. Пример: 34+11=45 (3 десяка плюс еще 1 десяток; 4 единицы плюс 1 единица). 4. Единицы вычитаются из единиц, десятки из десятков и т.д. Пример: 53-12=41 (3 единицы минус 2 единицы; 5 десятков минус 1 десяток) примечание: 10 единиц составляют один десяток. Это надо помнить при вычитании, т.к. если количество единиц у вычитаемого больше, чем у уменьшаемого, то мы можем «занять» один десяток у уменьшаемого. Пример: 41-12=29 (Для того чтобы и 1 вычесть 2, мы сначала должны «занять» единицу у десятков, получаем 11-2=9; помним, что у уменьшаемого остается на 1 десяток меньше, следовательно, остается 3 десятка и от него отнимается 1 десяток. Ответ 29). 5. Если из суммы двух слагаемых вычесть одно из них, то получится второе слагаемое. Это значит, что сложение можно проверить с помощью вычитания. Пример: 42+7=49 Для проверки из суммы вычитают одно из слагаемых: 49-7=42 или 49-42=7 Примечание: Если в результате вычитания вы не получили одно из слагаемых, значит в вашем сложении была допущена ошибка. 6. Если к разности прибавить вычитаемое, то получится уменьшаемое. Это значит, что вычитание можно проверить сложением. Пример: 69-50=19 Для проверки к разности прибавим вычитаемое: 19+50=69. Примечание: Если в результате описанной выше процедуры вы не получили уменшьшаемое, значит в вашем вычитании была допущена ошибка. Поиск в инженерном справочнике DPVA. Введите свой запрос: Дополнительная информация от Инженерного cправочника DPVA, а именно — другие подразделы данного раздела: Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая поддержка сайта: Zavarka Team	Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator

Сложение и вычитание – правила с примерами (6 класс, математика)

4.7

Средняя оценка: 4.7

Всего получено оценок: 211.

4.7

Средняя оценка: 4.7

Всего получено оценок: 211.

Сложение и вычитание – это базовые операции даже не математики, а арифметики. Но от этого они не становятся проще, хотя бы потому, что складывать и вычитать приходятся огромные числа.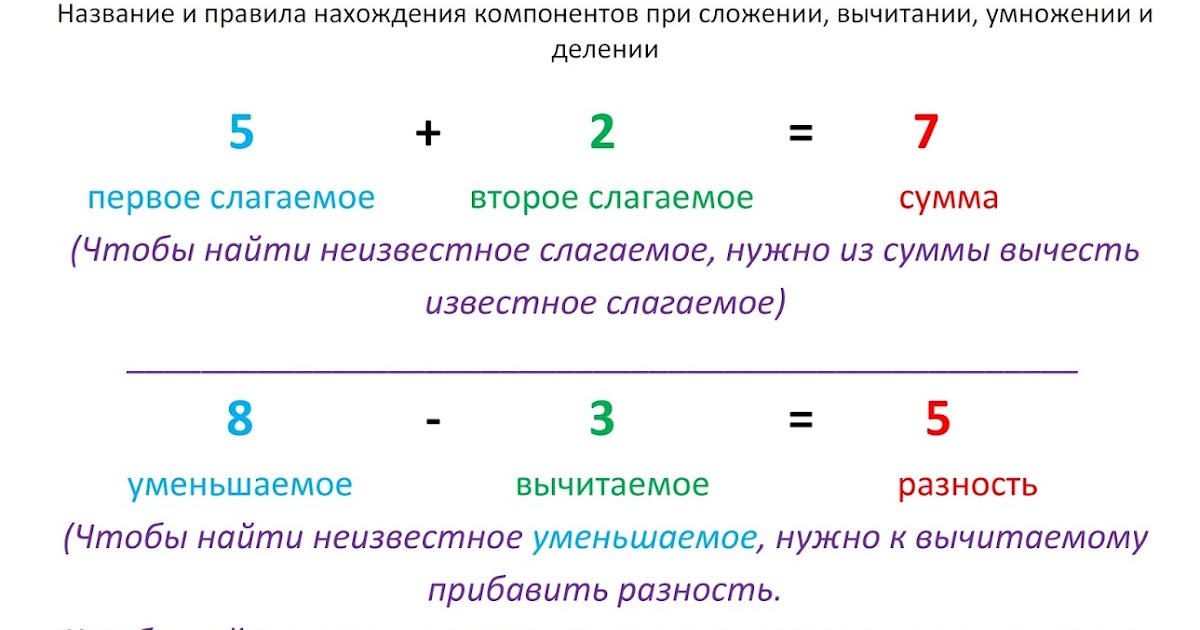 Поэтому, чтобы не допускать ошибок в курсе математики 6 класса, изучим в подробности правила сложения и вычитания.

Числовая прямая

Числовая прямая достаточно важное понятие в математике. Это прямая, которая не имеет ни начала ни конца, только отметку нуля и единичные отрезки, которые могут распространятся сколь угодно долго в обе стороны от отметки нуля.

Любое число можно отметить на числовой прямой. Вне зависимости от величины числа, его категории и знака.

При этом, вычитание и сложение – есть движение точки числа вправо или влево от нуля. При этом принято говорить, что сложение есть движение точки вправо от нуля, так как сложение подразумевает увеличение числа, а вычитание – уменьшение.

Но это скорее традиция, чем реальное правило, так как даже при сложении чисел, первое слагаемое, которое принимается за начальную точку, может уменьшиться.

Например: 18+(-5)=13 – перед нами операция сложения положительного и отрицательного числа, результатом которой стало уменьшение начального числа.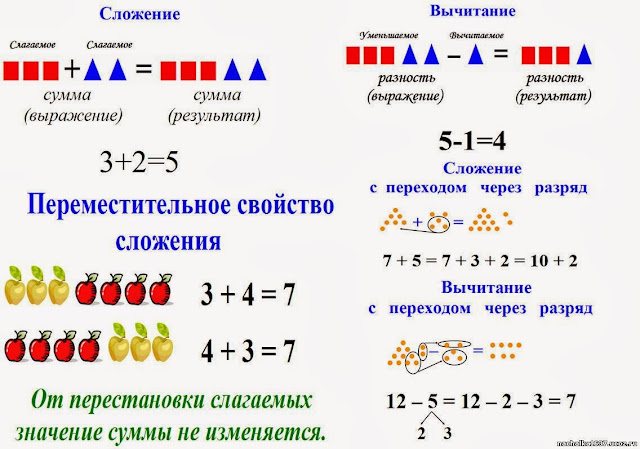 Уменьшение означает перенос влево по числовой прямой.

Рациональные и иррациональные числа

Рациональные и иррациональные числа это две разные категории сложения и вычитания. Всем привычные действия выполняют только с рациональными числами. Неважно, будут это отрицательные, положительны числа или дроби.

Иррациональными числами называют любые числа со знаком радикала, то есть корнем.

Выполнять сложение корней по тем же правилам нельзя. Поэтому используют приближенные вычисления. Конечно, результат может отличатся от реального ответа, но с этим ничего сделать не получится.

Правило знаков

Правило знаков и перенос чисел – две основы, которые позволяют не допускать ошибок при сложении и вычитании чисел. Именно правило знаков имеют в виду учителя, когда говорят «плюс на минус будет минус». На примере это правило выглядит так:

2+(-5)=2-5=-3

Оставшиеся две части гласят, что «плюс на плюс дает плюс» и «минус на минус дает минус». Запомнить эти правила легко, зато правильное их использование избавит вас от множества ошибок.

Перенос чисел

Перенос чисел более свойственен решению уравнений, но и при сложении и вычитании чисел, иногда приходится пользоваться этим свойством. Правило переноса числа из одной части выражения в другое через знак равенства гласит, что знак числа при такой операции нужно заменить на противоположный.

Свойства сложения и вычитания

Перед тем, как говорить о свойствах, нужно отметить, что в математике не разделяют понятия сложения и вычитания, называя обе операции математическим сложением. Ведь вычитание можно рассматривать как сложение положительного числа с отрицательным. Поэтому любое свойство сложения можно использовать и для вычитания.

Свойств у сложения всего два: переместительное и сочетательное. Переместительное свойство гласит: от перемены мест слагаемых, сумма не меняется. Это значит, что в больших примерах на сложение или вычитание порядок действий не имеет значения, считать можно так, как проще и удобнее ученику.

Сочетательный закон говорит о том, что если сумма чисел умножается на какое-то число, то можно каждое из слагаемых умножить на это число, а результаты сложить.

Зачастую свойства помогают сэкономить время, но куда чаще без них найти ответ просто невозможно. Поэтому стоит отработать их применение до автоматизма на различных примерах.

Что мы узнали?

Мы поговорили о сложении и вычитании. Выделили основные ошибки и разобрали наиболее сложные моменты выполнения этих операций. Поговорили о свойствах умножения и вычитания. А так же обсудили особенности числовой прямой.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Рустам Давлатов

  8/10

• Ростислав Радченко

  8/10

• Людовик Дорофеева

  5/10

Оценка статьи

4.7

Средняя оценка: 4.7

Всего получено оценок: 211.

---

А какая ваша оценка?

Правила сложения, вычитания, умножения и деления положительных и отрицательных чисел. [Решено]

Четыре основные арифметические операции, связанные с целыми числами:

• Сложение целых чисел
• Вычитание целого числа
• Умножение целых чисел
• Деление целых чисел

Ответ.

Существуют определенные правила сложения, вычитания, умножения и деления положительных и отрицательных чисел.

Прежде чем мы начнем изучать эти методы целочисленных операций, нам нужно запомнить несколько вещей. Если перед числом нет знака, значит, число положительное.

Объяснение:

В следующем содержании показаны правила сложения, вычитания, умножения и деления положительных и отрицательных чисел.

Правило сложения целых чисел:

Случай 1: знаки одинаковые

Если знаки одинаковые, добавьте и сохраните тот же знак.

• (+) + (+) = сложите числа, и ответ положительный

           Пример: 2 + 5 = 7

• (-) + (-) = сложите числа, и ответ будет отрицательным

           Пример: (-5) + (-4) = -9

Случай 2: знаки разные

Если знаки разные, вычтите числа и используйте знак большего числа.

• (+) + (-) = Вычесть числа и взять знак большего числа.

           Пример: 7 + (-3) = 4

• (-) + (+) = вычесть числа и взять знак большего числа.

          Пример: (-9) + 6 = -3

Правило вычитания целых чисел:

Чтобы вычесть число из другого числа, нужно изменить знак числа (которое нужно вычесть), а затем это число с измененным знаком прибавить к первому числу.

• (+) — (+) = изменить знак вычитаемого числа и сложить их. Результат принимает знак большего числа.

            Пример: (+6) – (+2)

                                     = (+6) + (-2) = 6 — 2 = 4

• (-) — (-) = Изменить знак вычитаемого числа и сложить их. Результат принимает знак большего числа.

           Пример: (-9) – (-6)

                         = (-9) + (+6) = -9 + 6 = -3

• (+) — (-) = Изменить знак числа для вычитания и сложения их.

           Пример: (+5) – (-3)

                         = (+5) +(+3) = 5 + 3 = 8

• (-) — (+) =  Изменить знак вычесть и сложить их. Результат всегда отрицательный

Пример: (-7) -(+2)

= (-7) + (-2) = -7 -2 = -9

Умножение и разделение целых чисел Правило:

Случай 1: Знаки одинаковы

Если знаки одинаковые, ответ всегда положительный.

• (+) × (+) = +

           Пример: 5 × 4 = 20

• (+) ÷ (+) = +

           Пример: 16 ÷ 4 = 4

• (-) × (-) = + 

           Пример: (-7) × (-9) = 63

• (-) ÷ (-) = +

            Пример: (-20) ÷ (-2) = 10

Случай 2: знаки разные

Если знаки разные, ответ всегда отрицательный.

• (+) × (-) = —

           Пример: 6 × (-10) = -60

• (+) ÷ (-) = —

           Пример: 30 ÷ (-15) = -2

• (-) × (+) = —

           Пример: -3 × 11 = 33

• (-) ÷ (+) = —

           Пример: -25 ÷ 5  = -5

Таким образом, это правила сложения, вычитания, умножения и деления положительных и отрицательных чисел.



правила сложения и вычитания целых чисел

Сложение и вычитание целых чисел немного сложнее. Сложение и вычитание — две функции, которые являются основными математическими функциями. В целых числах эта математическая функция немного сложна из-за наличие определенного знака перед числом, т.е. «-» и «+». Однако, когда вы добавляете или вычитаете два числа с одинаковым знаком, которые вы делаете, как указано, но если числа имеют разные знаки, то это другой.
Если есть вычитание между положительным и отрицательным числом, то есть сложение.

Правила сложения и вычитания целых чисел

Правила сложения и вычитания целых чисел:
1) Если два числа имеют разные знаки, такие как положительные и отрицательные, вычтите два числа и укажите знак большего числа.
2) Если два числа имеют одинаковый знак, т. е. положительные или отрицательные знаки, сложите два числа и укажите общий знак.
3) (положительный) x (положительный) = положительный знак произведения.
4) (отрицательный) x (отрицательный) = отрицательный знак произведения.
5) (положительный) x (отрицательный) = отрицательный знак произведения. Число
положительное, следовательно, знак произведения положительный
6) (отрицательный) x (положительный) = знак произведения отрицательный. Примечание: ответ сложения или вычитания между двумя числами будет иметь знак большего числа.
Решенные примеры:
1. вычесть: (-4) – (-3)
(минус) x (минус 3) = + 3
= -4 + 3
= -1.
Здесь я поставил знак большего числа, то есть (- 4).
2. Сложение: -8 + 10
= -8 + 10
= 2
3. Вычитание: -9 – (+9)
(отрицательное) x (положительное 9) = — 9
= -9 – 9
= — 18

Практика по правилам сложения и вычитания целых чисел

1. Вычесть: 6 – (-9)
2. Вычесть: 10 – (10)
3. Вычесть: 10 – (8)
4. Вычесть: 34 – (-9)
5. Вычесть: 73 – (88) )
6. Вычесть: 19 – (-29)
7. Вычесть: 15 – (23)
8. Вычесть: 54– (-34)
9. Вычесть: 0 – (38)
10. Вычесть: -34– (-18)
11. Сложить: 78+ (-12)
12. Сложить: 68 + (-56)
13. Сложение: 36 + (9)
14. Сложение: 94 + (-99)
15. Сложение: -63 + (0)
16. Сложение: 20 + (-6)
17 Сложение: -37 + (73)
18. Сложение: 48 + (-12)
19. Сложение: 78 + (-67)
20. Сложение: 5 + (23)

Правила сложения и вычитания целых чисел
Целые числа правила к 6 классу по математике
Домашняя страница

Мы в ask-math считаем, что учебные материалы должны быть бесплатными для всех. Пожалуйста, используйте содержимое этого веб-сайта для более глубокого понимания концепций. Кроме того, мы создали и разместили видеоролики на нашем YouTube.

Мы также предлагаем индивидуальные занятия / групповые занятия / помощь в выполнении домашних заданий по математике с 4 по 12 классы по алгебре, геометрии, тригонометрии, предварительному исчислению и исчислению для учащихся из США, Великобритании, Европы, Юго-Восточной Азии и ОАЭ.

No related posts.