Сколько будет если умножить х на х: сколько будет х умножить на х — Спрашивалка

Учим таблицу умножения.



Регистрация

/

ВХОД

Поиск по сайту



Поделитесь с друзьями, возможно,
им с нужна эта информация!

© Рисунок Валентины Черняевой

Ученики и ученицы!
Чтоб было проще вам считать,
Мы Пифагорову таблицу
В стихах решили написать.

По ней легко найти решенье,
Куплет достаточно прочесть,
А чтоб запомнить вычисленья,
Везде своя подсказка есть!

Ну что ж, откладывать не станем,
Тетрадь и карандаш достанем
И примемся за дело бойко.
Итак, на старт выходит ДВОЙКА!

Умножив два на единицу,
Получим ДВОЙКУ — лебедь-птицу,
Спасает каждый ученик
От этих «птичек» свой дневник.

2 х 1 = 2

Известно детям в целом мире,
Что дважды два равно ЧЕТЫРЕ.

2 х 2 = 4

Им также следует учесть,
Что дважды три получим ШЕСТЬ.

2 х 3 = 6



Два на четыре — будет ВОСЕМЬ.
И всех ребят мы очень просим
Забыть капризы, ссоры, лень
Восьмого марта — в мамин день!

2 х 4 = 8

Нам два на пять умножить нужно,
И если все возмемся дружно,
Да поднатужимся, ребятки,
То сразу попадем в ДЕСЯТКУ!

2 х 5 = 10

О том, что дважды шесть — ДВЕНАДЦАТЬ,
Вам календарь расскажет, братцы,
А в нём подсказку вам дадут
Двенадцать месяцев в году!

2 х 6 = 12

Красиво два на семь умножить
Февральский праздник нам поможет,
День всех влюбленных, помню я, —
ЧЕТЫРНАДЦАТОГО, друзья!

2 х 7 = 14

А сколько будет дважды восемь,
Десятиклассников мы спросим.
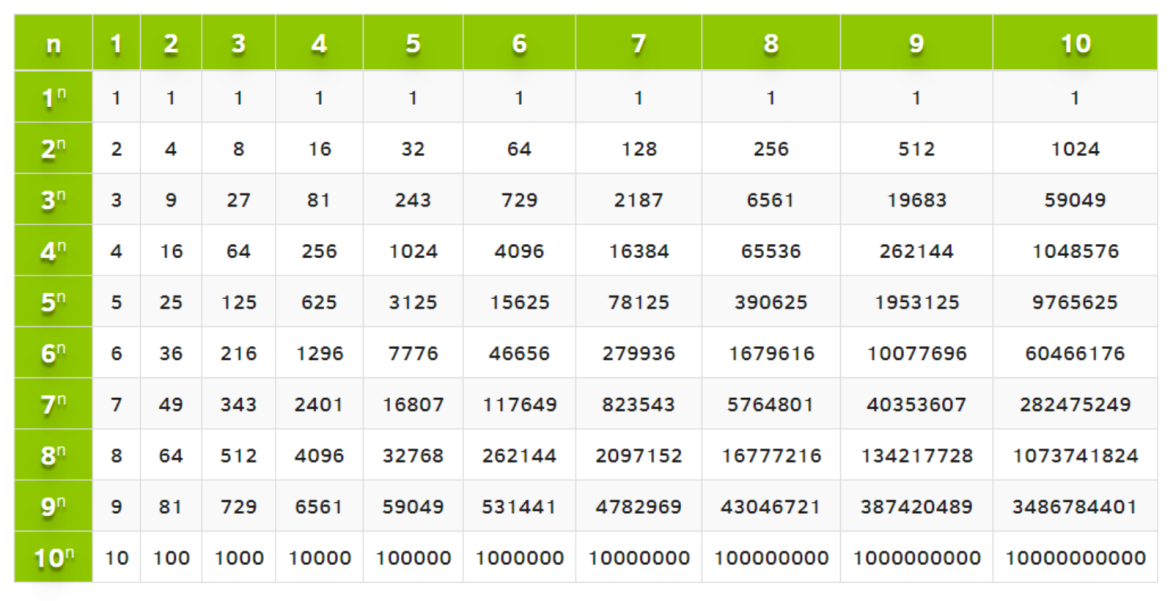
Они подскажут нам ответ,
Ведь им уже ШЕСТНАДЦАТЬ лет!

2 х 8 = 16

Запомнить надо постараться,
Что дважды девять – ВОСЕМНАДЦАТЬ.

2 х 9 = 18

И очень просто догадаться,
Что дважды десять — будет ДВАДЦАТЬ!

2 х 10 = 20

Мы хорошенько постарались
И с двойкой быстро разобрались.
Теперь, друзья, держитесь стойко,
В игру уже вступает ТРОЙКА!

ДАЛЕЕ

Автор: Марина Казарина,
специально для детского портала «Солнышко»,
опубликовано 22 марта 2004 г.

Поиск по сайту

Популярное

Снежная королева
Сказки народов мира

День рождения ребенка
Спят усталые игрушки
Развивающие компьютерные игры
Песни о маме, бабушке
Обучалки   Стихи
Шоу, спектакли, квесты, сценки
Песни: ноты, караоке

Умножение.

Как объяснить ребёнку?

• Опубликовано 17.06.2020
• by Светлана
•  в Второй класс, Для 2 класса, Для 3 класса, Математика, Первый класс

Умножение. Как объяснить ребёнку? Просто!

 

Умножение — это то же самое сложение. Только упрощённое. Не верите? Ну, как же! Смотрите сами…

 

2+2+2+2+2+2+2+2+2+2+2+2=???

 

Это же пока сосчитаешь, сколько тут двоек, да сложишь все по очереди! Тут и пенсия как раз настанет!

А умножать просто:

2 х 12 = 24 и всё!

 

И для облегчения счёта создана таблица умножения. Один раз выучил — всю жизнь пользуешься. Очень удобно!

Сначала дети учатся умножать и запоминают, как называются числа при умножении. Кажется, всё просто. Аналогично сложению. Там были слагаемые и сумма, тут множители и произведение.

Странные исправления в задачах

 

Засада начинается позже, когда начинаются задачи. Все помнят эти фотографии из родительских чатов с вопросами: За что? И почему так?

На фото было что-то типа такого:

В чём же дело?

Ведь всем же ясно, что 3х2, что 2х3 — получится одинаковое число. За что издеваются над нашими детьми?

Всё дело в логике.

 

Если пишем 3 х 2, то по условию задачи получаем: три раза мальчик нарисовал по 2 кораблика.

Если пишем 2 х 3, то получаем: по 2 кораблика мальчик нарисовал три раза.

Ну и что? Хрен редьки не слаще! Что в лоб, что по лбу! Разница-то в чём?

Тем более, что в старших классах дети всё равно будут учить переместительный закон умножения: от перемены мест множителей сумма не меняется.

Вот раньше таких проблем не было!

 

Действительно, не было!

А дело всё в том, что числа при умножении назывались иначе. Вернее, одно число называлось иначе и всё становилось на свои места!

 

И никто не путался. Сразу же ясно:

• Множимое — число, которое берут для умножения.
• Множитель — число, показывает сколько сколько раз умножили взятое число.
• Произведение — то, что получилось.

И — нет путаницы.

И задача сразу иначе звучит. Решать ее надо иначе.

Сразу следует подумать, о чём идёт речь в задаче?

О корабликах! Сколько было корабликов? Два. Два — это множимое!

Во сколько раз больше Вася нарисовал корабликов? В три! Три — это множитель!

Отсюда: верная запись: 2 х 3 = 6 (и никак иначе!)

А как же может звучать вопрос при умножении?

1. Сколько будет 2 умножить на 3?
2. Чему равно произведение чисел 2 и 3?
3. Умножь 2 на 3!
4. Перемножь числа 2 и 3!
5. Два умножили на три. Сколько стало?
6. Два увеличили в три раза. Сколько получилось?
7. Два увеличили втрое. Назови полученное число.
8. Если трижды взять два, сколько получится?
9. Трижды по два будет…
10. Первый множитель 2, второй — 3, чему равно произведение?
11. Найди произведение чисел два и три.
12. Произведение 6, первый множитель 2, чему равен второй множитель?
13. Множимое 2, множитель 3. Найди произведение.
14. Назови число, которое втрое больше, чем 2.
15. При умножении какого числа на 2 получается шесть?

А теперь давайте тренироваться!

Тест на умножение. Если Вы его не видите, значит его блокирует какая-то программа, установленная на Вашем компьютере. Обычно, блокировщик рекламы.

ТЕСТ

Тэги: математика, начальная школа, умножение

О Светлана

Копирайтер. Фрилансер. Мама ребёнка на семейном обучении.

Посмотреть все публикации созданные Светлана →

Что такое нулевое свойство умножения? Определение, примеры

Умножение любого числа на ноль, пожалуй, самая простая из всех задач! Каким бы большим ни было число, если его умножить на ноль, ответ всегда будет простым — ноль. Итак, среди всех известных вам чисел, пожалуй, проще всего выучить таблицу умножения цифры 0. 

Это связано с нулевым свойством умножения, которое гласит, что произведение любого числа на ноль всегда равно нулю. Это свойство применимо ко всем типам чисел, независимо от того, насколько они велики или малы.

Давайте узнаем об этом свойстве подробнее.

Что такое нулевое свойство умножения?

Нулевое свойство умножения определяется как «когда мы умножаем любое число на ноль, результат всегда равен нулю». Ноль не обязательно должен быть первым или вторым из чисел. Он может быть в любом месте при умножении на другое число. Это означает, что положение цифры ноль не влияет на результат умножения.

Это свойство также относится ко всем типам чисел. Это могут быть целые, десятичные или дробные числа. Итак, исход некоторых таких чисел будет следующим:

8 x 0 = 0

½ x 0 = 0

6,4 x 0 = 0

Это работает, даже если вы умножаете более двух чисел. Если вы находите произведение, скажем, трех чисел или десяти чисел, при условии, что любое из чисел в вашем выражении умножения равно нулю, конечный продукт также будет равен нулю.

0 x 1 x 2 x 3  = 0

Следует отметить, что это свойство нуля справедливо только для операции умножения. Математическая функция деления работает иначе. Это применимо даже тогда, когда деление просто обратное умножению. Итак, если бы вы разделили число на ноль, результирующий ответ не был бы равен нулю, поскольку деление на 0 не определено.

Однако свойство нуля применимо к операциям сложения и вычитания, но в этих случаях оно немного отличается. Когда вы прибавляете или вычитаете ноль из числа, в результате получается то же самое число, а не ноль.

Решенные примеры

Пример 1: Используйте нулевое свойство умножения, чтобы найти пропущенное число в данных уравнениях.

32 x 0 = __

Решение : Согласно нулевому свойству умножения,

32 x 0 = 0.

Пример 2. Используйте нулевое свойство умножения, чтобы найти ответ на пропущенное число число умножается на 0, в результате получается ноль. Следовательно, 57 x 0 = 0

Пример 3. Применяется ли свойство нуля при умножении к отрицательному числу? Если да, то каким будет результат умножения -75 на 0? Решение . Нулевое свойство умножения применимо ко всем числам, включая отрицательные числа. Таким образом, если -75 умножить на 0, в результате получится 0,9.0003

Практические задачи

1

Какое из следующих уравнений описывает нулевое свойство умножения?

50 + 0 = 50

15 x 1 = 15

75 x 0 = 0

5 + 5 = 10

Правильный ответ: 75 x 0 = 0
Нулевое свойство умножения применимо к любому числу что при умножении на 0 дает ответ 0. Из приведенных выше вариантов
только третий вариант изображает умножение числа на 0.

2

Каково произведение первых 15 целых чисел?

-5

15

5

Правильный ответ: 0
Первые 15 целых чисел равны 0, 1, 2, 3 … 14.
Согласно нулевому свойству умножения, произведение всех этих чисел будет быть 0.

3

Что из следующего является примером нулевого свойства умножения?

$\frac{2}{5} + 0 = \frac{2}{5}$

$\frac{2}{5} \times 1 = \frac{2}{5}$

$\frac{2}{5} \times 0 = 0$

$\frac{2}{5} \div1 = \frac{2}{5}$

Правильный ответ: $\frac{ 2}{5} \times 0 = 0$
Нулевое свойство умножения относится к любому числу, которое при умножении на 0 дает ответ 0. Из приведенных выше вариантов
только третий вариант изображает умножение число с 0.

Часто задаваемые вопросы

Отличается ли свойство идентичности умножения от свойства нуля умножения?

Да, согласно тождественному свойству умножения, при умножении любого числа на 1 результатом будет само число. Однако нулевое свойство умножения гласит, что при умножении любого числа на 0 в результате получается 0.

Что такое ассоциативное свойство умножения?

Согласно ассоциативному свойству умножения произведение любых трех чисел остается одним и тем же, независимо от порядка их группировки.

Является ли нулевое свойство умножения единственным свойством умножения?

Нет, нулевое свойство умножения — одно из многих свойств умножения. Некоторыми другими свойствами умножения являются коммутативность, ассоциативность и дистрибутивность.

Алгебраические выражения Обозначения переменных

• Главная /
• Алгебра /
• Алгебраические выражения /
• Темы /
• Переменные /
• Обозначения переменных

• Переменные /
• Обозначения переменных

Темы

• Введение
• Темы
• Переменные
• Переменные как неизвестные величины
• Обозначения переменных
• Константы
• Выражения и уравнения
• Объединение одинаковых терминов
• Уравнения, функции и формулы
• Приложения Toolbox
• Геометрические формулы
• Преобразование единиц измерения
• В реальном мире

  0

  0

• Примеры
• Упражнения
• Задачи Math Shack
• Условия
• Лучшее из Интернета
• викторины
• Раздаточный материал
• Содержание

•  НАЗАД
• СЛЕДУЮЩИЙ 

Помните, что математики любят сокращать вещи (сокращенно RTMLTAT). Чтобы написать «3 умножить на 4» в символах, мы могли бы написать 3 · 4, 3 × 4 или (3)(4). Чтобы записать «3 умножить на x », мы могли бы также написать 3 · x , 3 × x или (3)( x ).

Однако есть гораздо более короткий путь: напишите 3 x . При умножении числа на переменную мы можем записать число и переменную рядом. Они прекрасно ладят друг с другом, поэтому нет необходимости разделять их символом. Мы не можем сделать то же самое при умножении чисел вместе, потому что, если мы напишем 2 рядом с 4, например, мы получим 24. Если вы думаете, что 2 умножить на 4 равно 24, то, возможно, вы взяли 2 × 4 в обратном порядке. головы.

При умножении двух (или более) переменных мы также записываем переменные рядом друг с другом, чтобы показать, что они перемножаются. Например, xy означает « x умножить на y ». Это еще одна причина, по которой мы используем такие редко используемые буквы в качестве наших переменных. Если бы мы использовали a и b большую часть времени, вы могли бы увидеть ab и подумать, что мы говорим о чьей-то упаковке из шести штук.

Математическое соглашение (обычный способ ведения дел) состоит в том, чтобы писать число перед переменной при умножении чисел на переменные. Другими словами, мы пишем 3 x , а не x 3. Если вы напишите x 3 , люди, вероятно, поймут, что вы имеете в виду, но вас, вероятно, не пригласят обратно на конвенцию.

Кроме того, вы должны знать, что xy = yx , так как умножение действительных чисел коммутативно. При перемножении переменных может быть полезно записывать переменные в алфавитном порядке ( xy или xyz ), чтобы у нас был стандартный порядок их записи. Написание yx вместо xy не так плохо, как запись x 17 вместо 17 x , но в определенных кругах это все еще не одобряется. В основном кружки, посещаемые нами, математическими ботаниками. Вы насмехаетесь, но наши хмурые взгляды могут быть пугающими.

Когда мы умножаем переменную саму на себя несколько раз — почти как клонирование, но гораздо менее спорное — мы можем использовать запись степени . Например, х · х · х = х ³ . Мы можем прочитать x ³ как «три копии x », поскольку x ³ — это сокращение от трех копий x , умноженных вместе. Жаль, что нам не нужно 100 копий, потому что тогда мы получим скидку в цене.

При делении переменной на число существует несколько различных способов записи деления символами. Так как , то и оба означают « x разделить на 4″. В этом выражении x никак не может обозначать Соединенные Штаты Америки, потому что наша нация неделима. Присяга на верность, представляю.

Будьте осторожны : Безопаснее записывать деление дробью, чем через косую черту. Не то чтобы вы подверглись реальной физической опасности, если сделаете последнее, но это не рекомендуется, и вот почему.

No related posts.