График функции 1 x 3: Mathway | Популярные задачи

2

Степенная+функция — презентация онлайн

Похожие презентации:

Степенная функция

Степенная функция

Степенная функция

Степенная функция и ее график

Степенная функция. Свойства степенной функции

Степенная функция

Степенная функция и ее график

Степенная функция и её график

Свойства и график степенной функции

Степенная функция

Частные случаи степенной функции
у
2
у=х
у
=
х
у
Прямая
Парабола
х
х
у
у = х3
х
Кубическая
парабола
Гипербола
у
1
у
х
х
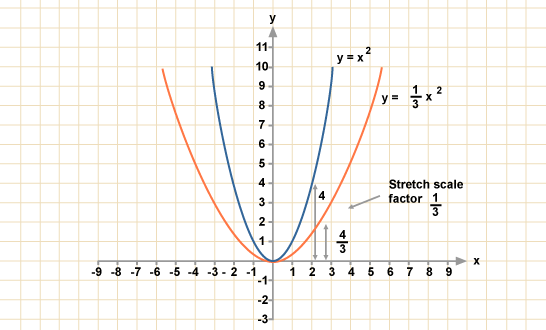
Функция вида у = хр, где р – действительное
число называется степенной функцией
Свойства и график степенной функции зависят от
свойств степени с действительным показателем, и в
частности от того, при каких значениях х и р имеет
p
смысл степень
x
Показатель р = 2n – четное натуральное число
у = х2, у = х4 , у = х6, у = х8, …

у
D( y) : x R
у = х2
Е ( y) : у 0
0
1
х
Функция у=х2n четная,
т. к. (–х)2n = х2n
Функция убывает на
промежутке
( ;0]
Функция возрастает
на промежутке [0; )
y
у = х2
у = х6
-1 0 1
x
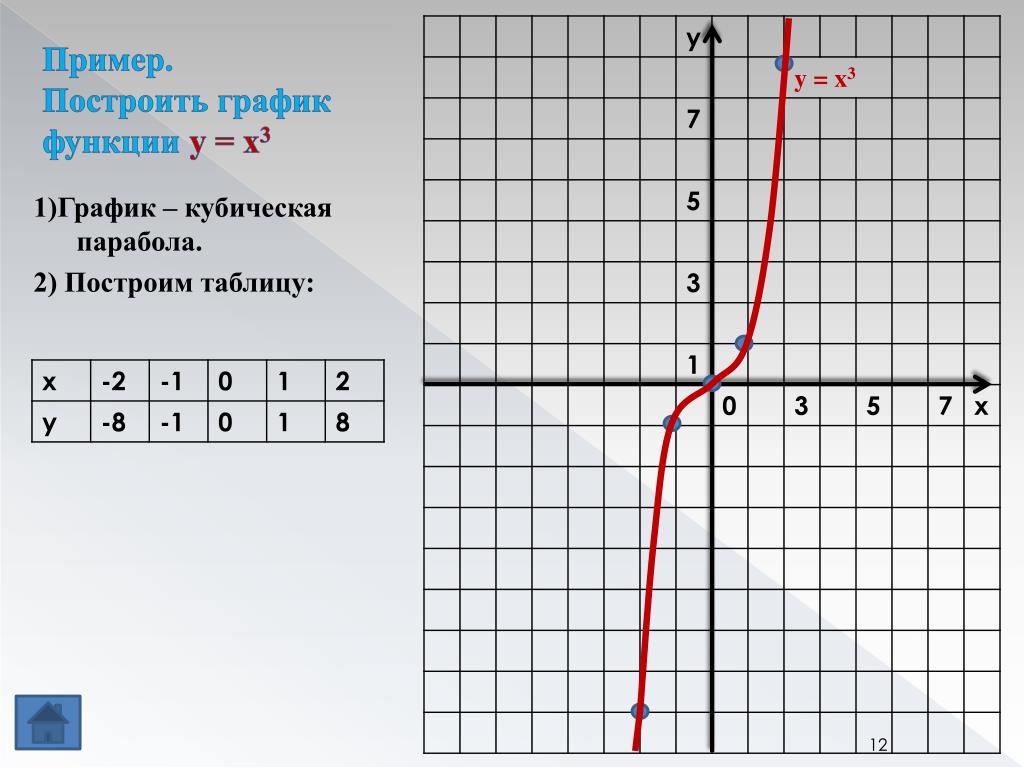
Показатель р = 2n-1 – нечетное натуральное число
у = х3, у = х5, у = х7, у = х9, …
у
D( y) : x R
Е ( y) : у R
у = х3
Функция у=х2n-1 нечетная,
т.к. (–х)2n-1 = – х2n-1
0
1
х
Функция возрастает
на промежутке ;
y
у = х3
у = х7
-1 0 1
x
Показатель р = – 2n, где n – натуральное число
у = х-2, у = х-4 , у = х-6, у = х-8, …
у
D( y) : x 0
Е ( y) : у 0
0
y х
2
1
1
y 2
х
х
Функция у=х2n четная,
т.к. (–х)-2n = х-2n
Функция возрастает на
промежутке
( ;0)
Функция убывает
на промежутке (0; )
y
у = х-2
у = х-6
-1 0 1
x
Показатель р = – (2n-1), где n – натуральное число
у = х-3, у = х-5 , у = х-7, у = х-9, …
у
D( y) : x 0
Е ( y) : у 0
0
х
1
Функция у=х-(2n-1)
нечетная,
т. к. (–х)–(2n-1) = –х–(2n-1)
Функция убывает на
y х
1
1
y
х
промежутке
( ;0)
Функция убывает
на промежутке (0; )
y
у = х-1
у = х-5
-1 0 1
x
Показатель р – положительное действительное нецелое
1
число
у = х1,3, у = х0,7, у = х2,12, у х 3 …
у
у х
у х
0
1
D( y) : x 0
4
3
1
3
Е ( y) : у 0
Функция возрастает на
х промежутке
[0; )
y
у = х0,84
у = х0,5
-1 0 1
x
y
у = х3,1
-1 0 1
у = х1,5
x
Показатель р – отрицательное действительное
1
нецелое число
3
-1,3
-0,7
-2,12
у
х
у=х , у=х , у=х
,
…
у
D( y) : x 0
Е ( y) : у 0
Функция убывает на
0
1
х промежутке
(0; )
y
у = х-3,8
у = х-0,3
-1 0 1
x
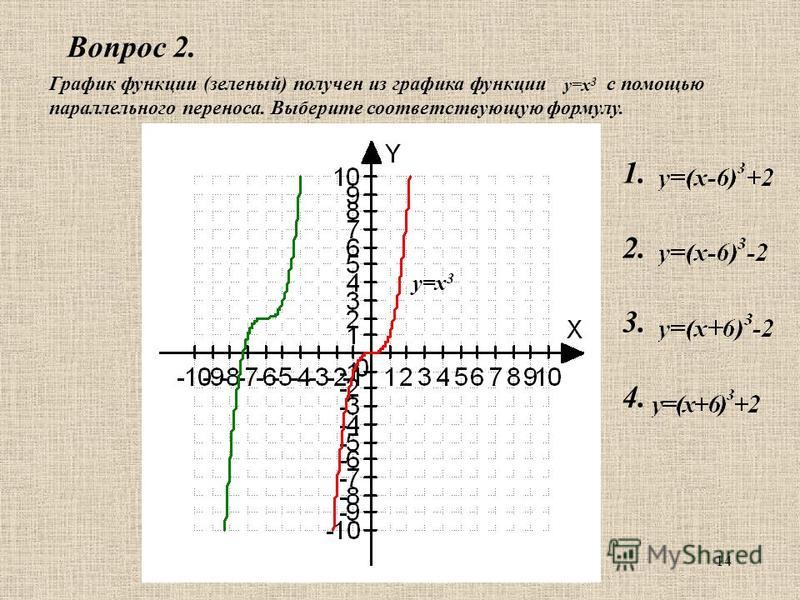
Пользуясь рисунком, найти
промежутки, на которых
e
график функции
лежит выше (ниже) графика
у
у х
функции у = х.
0
1
х
у
Пользуясь рисунком, найти
промежутки, на которых
cos 600
график функции
лежит выше (ниже) графика
у х
функции у = х.
0
1
х
Пользуясь рисунком, найти промежутки, на которых
график функции
у х
1
лежит выше (ниже) графика
функции у = х.
у
0
1
х
y
-1 0 1
у = (х + 2)-6
x
y
-1 0 1
у = х– 6 – 4
x
y
-1 0 1
у = (х+1)– 4 + 2
x
y
-1 0 1
у = (х-3)– 3+1
x
y
-1 0 1
у = (х+3)–2,5 +2
x

English     Русский Правила

Мэтуэй | Популярные задачи

92) 9(3x) по отношению к x 92+1

1	Найти производную — d/dx	бревно натуральное х
2	Оценить интеграл	интеграл натурального логарифма x относительно x
3	Найти производную — d/dx
21	Оценить интеграл	интеграл от 0 до 1 кубического корня из 1+7x относительно x
22	Найти производную — d/dx	грех(2x)
23	Найти производную — d/dx
41	Оценить интеграл	интеграл от cos(2x) относительно x
42	Найти производную — d/dx	1/(корень квадратный из х)
43	Оценка интеграла 9бесконечность
45	Найти производную — d/dx	х/2
46	Найти производную — d/dx	-cos(x)
47	Найти производную — d/dx	грех(3x)
68	Оценить интеграл	интеграл от sin(x) по x
69	Найти производную — d/dx	угловой синус(х)
70	Оценить предел	ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х
85	Найти производную — d/dx	лог х
86	Найти производную — d/dx	арктан(х)
87	Найти производную — d/dx	бревно натуральное 5х92

График функций f(x)=?x, f(x)=1/x, f(x)=x3, f(x)= 3?x, f(x)=bx, f(x) =|x| и f(x)=logb (x), где b равно 2, 10 и e, и, если применимо, анализировать ключевые атрибуты, такие как домен, диапазон, точки пересечения, симметрии, асимптотическое поведение, а также максимум и минимум заданный интервал | Стандарты Техаса | Стандарты Техасской алгебры 2 | Атрибуты функций и их обратные.

Учащийся применяет математические процессы, чтобы понять, что функции имеют определенные ключевые атрибуты, и понять взаимосвязь между функцией и ее обратной функцией.

Popular Tutorials

в График функций f(x)=?x, f(x)=1/x, f(x)=x3, f(x)= 3?x, f(x)=bx, f (x)=|x| и f(x)=logb (x), где b равно 2, 10 и e, и, если применимо, анализировать ключевые атрибуты, такие как домен, диапазон, точки пересечения, симметрии, асимптотическое поведение, и максимум и минимум с заданным интервалом

• Как построить график функции абсолютного значения?

  Построение графика уравнения абсолютного значения может быть сложным, если вы не знаете, как анализировать уравнение, чтобы найти и использовать наклон и переводы. Следуйте инструкциям, поскольку этот учебник покажет вам, как определить необходимые части уравнения и использовать их для построения графика уравнения абсолютного значения.
• Что делает константа ‘k’ в y = |x|+k?

  Когда вы изучаете перевод уравнений с абсолютными значениями, ОБЯЗАТЕЛЬНО изучите вертикальные переводы! Ознакомьтесь с этим учебным пособием и узнайте, что нужно для вертикального перевода уравнения абсолютного значения.

• Что такое функция абсолютного значения?

  Функция абсолютного значения — это просто функция, которая содержит абсолютные значения. Этот учебник дает отличное введение в эту очень полезную функцию!

• Что такое экспоненциальная функция?

  Ищете уравнение с переменной в показателе степени? У вас есть экспоненциальная функция! Узнайте об экспоненциальных функциях в этом руководстве.
• Что такое экспоненциальный рост?

  Экспоненциальные функции часто включают скорость увеличения или уменьшения чего-либо. Когда это скорость увеличения, у вас есть экспоненциальная функция роста! Проверьте эти виды экспоненциальных функций в этом уроке!

• Как построить график функции квадратного корня с помощью таблицы?

  Составление таблицы значений является полезным способом построения графика функции квадратного корня. Просто не забудьте выбрать значения x, для которых определена функция! Посмотрите обучающее видео, чтобы узнать больше.

• Как найти степень многочлена?

  Члены и многочлены не могут вызвать лихорадку, но у них есть степени! Этот учебник расскажет вам все о степени терма и многочлена и покажет, как ее найти!

• Что такое домен?

  Знаете ли вы, что отношение имеет домен? Домен отношения — это набор первых координат из упорядоченных пар. Этот учебник определяет домен отношения!

• Как перевести функцию?

  Подумайте о том, чтобы положить монетку на стол. Все, что вы делаете, это перемещаете пенни в новое место на столе. Это в основном все, что происходит, когда вы переводите функцию! Когда вы переводите функцию, вы просто перемещаете ее в новое место на координатной плоскости!

• Как преобразовать экспоненциальную форму в логарифмическую?

  Хорошо иметь задачу в экспоненциальной форме, но можно ли преобразовать ее в логарифмическую? Этот урок покажет вам этот процесс шаг за шагом!

• Как преобразовать экспоненциальную форму в натуральную логарифмическую форму?

  Преобразование экспоненциальной формы в натуральную логарифмическую проще, чем вы думаете! Следуйте этому руководству, чтобы узнать, как выполнить это преобразование.

• Как построить график экспоненциальной функции естественного основания?

  Хотите построить график экспоненциальной функции с естественным основанием? Составьте таблицу баллов! Затем нанесите точки, соедините их, и у вас есть график! Следуйте этому руководству, чтобы увидеть весь процесс шаг за шагом.

• Что такое логарифм?

  Логарифмы могут быть сложными, но они станут намного проще, если вы поймете, как они связаны с показателями степени. Следуйте вместе с учебником, чтобы узнать об этих отношениях.

• Что такое натуральный логарифм?

  Натуральный логарифм — это логарифм, имеющий особое основание. В этом уроке вы познакомитесь с натуральными логарифмами!

• Что такое экспоненциальная функция естественного основания?

  Экспоненциальная функция с естественным основанием на самом деле является функцией, которая короче своего названия! Этот учебник знакомит вас с этой специальной функцией и показывает, как она выглядит.

  No related posts.